A benchmark ab initio study of the complex potential energy surfaces of the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] reactions

Abstract

We provide the first benchmark characterization of the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] reactions utilizing the high-level explicitly-correlated CCSD(T)-F12b method with the aug-cc-pVnZ [n = 2(D), 3(T), 4(Q)] basis sets. We explore and analyze the stationary points of the elimination (E2) and substitution (S_N2) reactions, including anti-E2, syn-E2, back-side attack, front-side attack, and double inversion. In all cases, S_N2 is thermodynamically more preferred than E2. In the entrance channel of S_N2 a significant front-side complex formation is revealed, and in the product channel the global minimum of the title reactions is obtained at the hydrogen-bonded CH₃CH₂OH⋯Y⁻ complex. Similar to the OH⁻ + CH₃Y reactions, double inversion can proceed via a notably lower-energy pathway than front-side attack, moreover, for Y = I double inversion becomes barrier-less. For the transition state of the anti-E2, a prominent ZPE effect emerges, giving an opportunity for a kinetically more favored pathway than back-side attack. In addition to S_N2 and E2, other possible product channels are considered, and in most cases, the benchmark reaction enthalpies are in excellent agreement with the experimental data.

---

I. Introduction

One of the main aims in chemistry is to understand chemical reactions at an atomic level. In organic chemistry the bimolecular nucleophilic substitution (S_N2) and the base-induced bimolecular elimination (E2) are elemental reactions and the competitions of these processes have been widely studied both experimentally and theoretically over the past 40 years.^1–18 The traditional Walden-inversion and front-side attack mechanisms of S_N2 reactions were described by Ingold and co-workers in the middle of the 20th century.^19,20 In a simple S_N2 reaction, X⁻ + CH₃Y → CH₃X + Y⁻, the Walden-inversion mechanism goes through X⁻⋯CH₃Y and XCH₃⋯Y⁻ minima connected by a central [X⋯CH₃⋯Y]⁻ transition state. Concerning the front-side attack, the mechanism is defined by a high-energy [XYCH₃]⁻ transition state. In the last two decades, it has been recognized that the mechanisms of the S_N2 reactions are much more complex.^5,21–25 Among the above-described traditional double-well Walden-inversion pathway and the front-side attack retention mechanism, several direct and indirect mechanisms can be found: roundabout,²⁶ hydrogen-bond complex, front-side complex forming, double inversion,²² rebound, and stripping.²³

In 2001, Gonzales and co-workers characterized the Walden-inversion pathway of the F⁻ + CH₃Y [Y = F, Cl, OH, SH, CN, PH₂, NH₂] S_N2 reactions.²⁷ The geometries of the stationary points were optimized by CCSD(T)/TZ2P+dif, and the final single-point energies of the geometries were computed by the CCSD(T) method with the aug-cc-pVTZ basis set. Afterwards, focal-point analyses were made to obtain a more accurate description of the reaction profile.²⁸ The OH⁻ + CH₃F S_N2 reaction was investigated by Hase and co-workers,²⁹ and the dynamics simulations showed that in the exit channel the reaction occurs via the HOCH₃⋯F⁻ configuration, instead of the CH₃OH⋯F⁻ deep hydrogen-bonded minimum.³⁰ In 1987, Jorgensen et al. determined an ab initio characterization of the OH⁻ + CH₃Cl S_N2 reaction using second and third-order Møller–Plesset perturbation theory,² later direct dynamics simulations were performed by Tachikawa and co-workers.^31,32 Regarding the OH⁻ + CH₃I reaction, several theoretical and experimental studies have been carried out.^33–36 In 2012, Wester and co-workers unveiled various reaction mechanisms for OH⁻(H₂O)_n + CH₃I → CH₃OH + I⁻ + nH₂O [n = 0, 1, 2] using the crossed-beam imaging technique.³³ Recently, the novel front-side complex mechanism of these latter reactions, along with several other nucleophiles [F⁻, Cl⁻, Br⁻, I⁻], was examined.³⁷ The proton transfer and the traditional back-side attack pathways of the OH⁻ + CH₃I reaction were studied with density functional theory calculations by Xie et al.³⁵ In 2018, we reported high-level ab initio characterization of the OH⁻ + CH₃Y [Y = F, Cl, Br, I] S_N2 reactions, where the stationary points of the Walden-inversion, the front-side attack and the double-inversion pathways were computed at the CCSD(T)-F12b/aug-cc-pVQZ level of theory applying core- and post-CCSD(T) correlation corrections.³⁸ Recently, we developed full-dimensional analytical potential energy surfaces for the OH⁻ + CH₃I reaction with various ab initio methods.³⁹ It was found that at certain geometries of the potential energy surface the CCSD(T) energy breaks down resulting in an increase of the rejected unphysical trajectories in quasi-classical trajectory simulations. This problem was solved by proposing a Brueckner-type CCSD(T)-based composite method.³⁹

An evident way to extend the complexity of the X⁻ + CH₃Y reactions is to replace CH₃Y with CH₃CH₂Y. In these cases, the E2 reaction can also occur competing with the S_N2 reaction. In 1988, for F⁻ + CH₃CH₂Cl and X⁻ + CH₃CH₂X [X = F, Cl] reactions, Yamabe and co-workers determined the stationary points of the S_N2 and the E2 reactions by ab initio calculations, in order to analyze structure–reactivity variation.¹² Followed by Gronert, characterization was performed for the reactions of the F⁻ and PH₂⁻ with CH₃CH₂Cl by a higher level of calculations.¹⁴ Later, Mugnai et al. investigated the competition between S_N2 and E2 in the F⁻ + CH₃CH₂Cl reaction by molecular dynamics simulations and revealed that the initial velocity of fluoride has a different effect on the two reaction mechanisms.⁴⁰ Bento et al.³ and Zhao et al.⁴¹ defined the E2 and S_N2 pathways of the X⁻ + CH₃CH₂X [X = F, Cl] reactions, comparing the accuracy of numerous ab initio methods and density functionals. In 2009, the reactivity order of twelve nucleophiles [F⁻, Cl⁻, Br⁻, OH⁻, SH⁻, SeH⁻, NH₂⁻, PH₂⁻, AsH₂⁻, CH₃⁻, SiH₃⁻, and GeH₃⁻] toward ethyl-chloride was studied by Wu et al., and a strong correlation was found between the electronegativity of the attacking atom of the nucleophiles and the barrier heights of the S_N2 and E2 reactions.⁴² Recently, our group characterized the potential energy surface of the F⁻ + CH₃CH₂Cl reaction using a series of ab initio methods, up to the CCSD(T)-F12b method with the aug-cc-pVQZ basis set.^25,43 Comparing the benchmark results of the stationary points with lower-level methods showed that the MP2 method has an inaccuracy of 1.5–2.5 kcal mol⁻¹, in fact for some products an inaccuracy of 4.0–4.5 kcal mol⁻¹ can be recognized. In 2018, the effects of various solvents were studied for the reaction of fluoride with bromo-ethane by Satpathy et al., and the gas-phase reaction was also investigated at the CCSD(T) level.⁴⁴ Hase and co-workers examined the microsolvated F⁻(CH₃OH)_n + CH₃CH₂Br [n = 0–2] reactions and direct dynamics simulations showed that by adding methanol to the reaction, the transition states of the S_N2 reactions become more stabilized, therefore substitution dominates over elimination.⁴⁵ The F⁻ + CH₃CH₂I reaction was described by Yang et al. using several electronic structure calculations,⁴⁶ and an experimental and theoretical reaction dynamics study was performed by the collaboration of Hase and Wester groups.⁷

Following the above-mentioned studies, in this work, we provide benchmark ab initio characterization of the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] reactions. We analyze the mechanisms of the E2 and S_N2 reactions, such as anti-E2, syn-E2, back-side attack, front-side attack, and double inversion. We determine the geometries, the energies and the harmonic vibration frequencies of the stationary points using the modern explicitly-correlated CCSD(T)-F12b method with aug-cc-pVnZ [n = 2–4] basis sets. Beyond the S_N2 and the E2 reactions, we also describe several product channels on the complex potential energy surfaces.

The purpose of the present study is three-fold: (1) to the best of our knowledge, the “attitude” of the title reactions is investigated for the first time, (2) the results derived from the present work can refine our knowledge of the competition between S_N2 and E2 reactions, and (3) this benchmark characterization serves as a basis for future experimental and theoretical investigations.

II. Computational details

The geometries of the stationary points of the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] reactions are preoptimized using the second-order Møller–Plesset perturbation theory⁴⁷ (MP2) with the augmented correlation-consistent polarized-valence-double-ζ⁴⁸ (aug-cc-pVDZ) basis set. The benchmark harmonic vibrational frequencies of the stationary points are computed using the explicitly-correlated coupled-cluster singles, doubles, and perturbative triples (CCSD(T)-F12b) method⁴⁹ with the aug-cc-pVDZ basis set. To obtain the most accurate geometries for the stationary points, the CCSD(T)-F12b method is utilized with the aug-cc-pVTZ basis set.⁴⁸ The best relative energies of the stationary points are determined using the CCSD(T)-F12b method with the quadruple-ζ aug-cc-pVQZ basis set at the CCSD(T)-F12b/aug-cc-pVTZ geometries. Note that performing CCSD(T)-F12b/aug-cc-pVQZ geometry optimizations is not feasible and also unnecessary as the geometry effects on the relative energies are usually significantly less than 0.01 kcal mol⁻¹ as ref. 43 showed. For the open-shell systems [CH₃CH₂ and OHY⁻; Y = F, Cl, Br, I] restricted MP2 (RMP2) and unrestricted UCCSD(T)-F12b methods are used based on restricted open-shell Hartree–Fock (ROHF) orbitals. For Br and I, we apply small-core relativistic effective core potentials,⁵⁰ replacing the inner-core 1s²2s²2p⁶ and 1s²2s²2p⁶3s²3p⁶3d¹⁰ electrons, respectively, with the appropriate aug-cc-pVnZ-PP [n = 2–4] basis sets.

The benchmark adiabatic relative energies of the stationary points are computed as:

ΔE[CCSD(T)-F12b/aug-cc-pVQZ] + ΔZPE[CCSD(T)-F12b/aug-cc-pVDZ] (1)

where ΔE is the benchmark classical relative energy and ΔZPE is the harmonic zero-point energy correction. All the ab initio computations are performed with the MOLPRO program package.⁵¹

III. Results and discussion

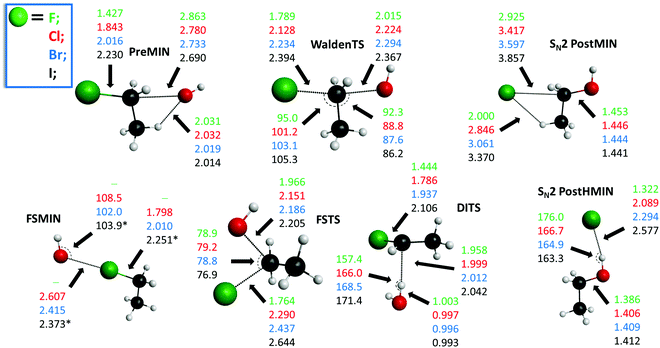
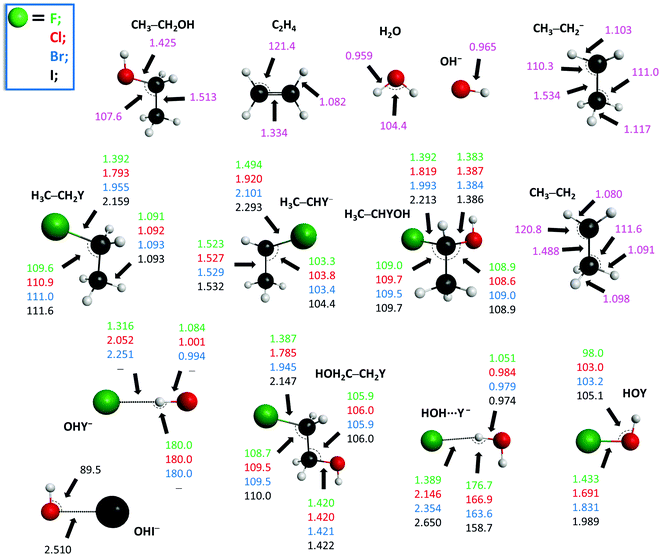
The potential energy diagrams of the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] S_N2 and E2 reactions presenting the benchmark classical and adiabatic relative energies of the stationary points are shown in Fig. 1 and 2, respectively. The geometries of the stationary points along with the most important structural parameters are given in Fig. 3 and 4. The relative energies of the minima and transition states determined at the MP2/aug-cc-pVDZ, CCSD(T)-F12b/aug-cc-pVDZ, CCSD(T)-F12b/aug-cc-pVTZ, and CCSD(T)-F12b/aug-cc-pVQZ levels of theory are presented in Table 1. Fig. 5 shows the structures of the examined product channels with the relevant bond lengths and angles. The reaction enthalpies of several product channels obtained by the above-defined levels of theory are shown in Table 2. The most accurate Cartesian coordinates of the minima, transition states, reactants, and products are given in the ESI.†

Fig. 1 Schematic potential energy surfaces of the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] S_N2 reactions showing the classical (adiabatic) CCSD(T)-F12b/aug-cc-pVQZ (+ΔZPE[CCSD(T)-F12b/aug-cc-pVDZ]) relative energies (kcal mol⁻¹) of the stationary points along the different reaction pathways, see Table 1. Results indexed by * correspond to CCSD(T)-F12b/aug-cc-pVDZ structures.

Fig. 2 Schematic potential energy surfaces of the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] E2 reactions showing the classical (adiabatic) CCSD(T)-F12b/aug-cc-pVQZ (+ΔZPE[CCSD(T)-F12b/aug-cc-pVDZ]) relative energies (kcal mol⁻¹) of the stationary points along the different reaction pathways, see Table 1.

Fig. 3 Structures of the minima and transition states corresponding to the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] S_N2 reactions showing the relevant bond lengths (Å) and angles (degree) obtained at the CCSD(T)-F12b/aug-cc-pVTZ level of theory. Results indexed by * correspond to the CCSD(T)-F12b/aug-cc-pVDZ structure.

Fig. 4 Structures of the minima and transition states corresponding to the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] E2 reactions showing the relevant bond lengths (Å) and angles (degree) obtained at the CCSD(T)-F12b/aug-cc-pVTZ level of theory.

Table 1 Benchmark classical and adiabatic energies (kcal mol⁻¹) of the stationary points relative to the reactants for the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] S_N2 and E2 reactions

OH^− + CH3CH2F	MP2	CCSD(T)-F12b			ΔZPE^e	Adiabatic^f
	DZ^a	DZ^b	TZ^c	QZ^d
a MP2/aug-cc-pVDZ. b CCSD(T)-F12b/aug-cc-pVDZ. c CCSD(T)-F12b/aug-cc-pVTZ. d CCSD(T)-F12b/aug-cc-pVQZ at CCSD(T)-F12b/aug-cc-pVTZ geometry. e ΔZPE(CCSD(T)-F12b/aug-cc-pVDZ). f QZ + ΔZPE. g CCSD(T)-F12b/aug-cc-pVTZ optimization does not converge and the CCSD(T)-F12b/aug-cc-pVQZ energy is obtained at the CCSD(T)-F12b/aug-cc-pVDZ geometry.
PreMIN	−16.63	−16.54	−16.41	−16.21	0.73	−15.48
syn-E2 PostMIN1	−40.86	−40.60	−40.40	−40.29	−0.79	−41.09
syn-E2 PostMIN2	−40.75	−40.29	−40.14	−40.08	−0.96	−41.04
SN2 PostMIN	−32.19	−31.39	−31.21	−31.09	2.24	−28.86
SN2 PostHMIN	−50.56	−50.31	−50.19	−50.02	1.34	−48.68
WaldenTS	−2.52	−0.66	−0.83	−0.59	0.64	0.05
FSTS	40.73	43.05	42.93	43.41	−0.05	43.36
DITS	24.19	21.93	22.18	22.43	−1.30	21.13

---

OH^−+ CH3CH2Cl	MP2^a	DZ^b	TZ^c	QZ^d	ΔZPE^e	Adiabatic^f
PreMIN	−18.74	−18.59	−18.54	−18.38	0.68	−17.69
anti-E2 PostMIN	−57.97	−59.16	−59.14	−59.31	0.57	−58.74
syn-E2 PostMIN1	−57.81	−59.10	−59.13	−59.32	0.14	−59.17
syn-E2 PostMIN2	−57.66	−58.79	−58.84	−59.06	0.03	−59.02
SN2 PostMIN	−60.00	−60.93	−61.01	−61.18	3.14	−58.04
SN2 PostHMIN	−68.39	−69.73	−69.94	−70.02	3.35	−66.68
FSMIN	−0.79	−2.58	−1.96	−1.79	0.56	−1.23
anti-E2 TS	−13.20	−12.58	−12.55	−12.36	−2.68	−15.04
syn-E2 TS	−3.32	−3.71	−3.45	−3.17	−3.08	−6.25
WaldenTS	−13.13	−12.84	−13.11	−12.98	0.71	−12.28
FSTS	29.17	28.64	28.61	28.87	−0.08	28.79
DITS	10.13	6.96	7.24	7.40	−0.68	6.71

---

OH^−+ CH3CH2Br	MP2^a	DZ^b	TZ^c	QZ^d	ΔZPE^e	Adiabatic^f
PreMIN	−19.29	−19.61	−19.49	−19.31	0.68	−18.64
anti-E2 PostMIN	−62.15	−65.45	−65.24	−65.50	0.88	−64.62
syn-E2 PostMIN1	−61.73	−65.10	−64.96	−65.23	0.47	−64.76
syn-E2 PostMIN2	−61.58	−64.78	−64.66	−64.95	0.19	−64.77
SN2 PostMIN	−65.51	−68.75	−68.59	−68.89	3.66	−65.22
SN2 PostHMIN	−72.61	−76.15	−76.07	−76.24	3.98	−72.27
FSMIN	−9.42	−10.47	−10.38	−10.23	0.55	−9.68
anti-E2 TS	−15.31	−15.54	−15.32	−15.14	−2.22	−17.36
syn-E2 TS	−4.75	−5.45	−5.09	−4.83	−2.90	−7.73
WaldenTS	−15.78	−16.89	−17.00	−16.86	0.80	−16.05
FSTS	24.20	22.35	22.18	22.40	0.55	22.94
DITS	7.39	4.30	4.60	4.79	−0.52	4.27

---

OH^−+ CH3CH2I	MP2^a	DZ^b	TZ^c	QZ^d	ΔZPE^e	Adiabatic^f
PreMIN	−19.93	−20.33	−20.21	−20.04	0.78	−19.26
anti-E2 PostMIN	−66.74	−70.33	−70.19	−70.65	1.10	−69.55
syn-E2 PostMIN1	−66.07	−69.79	−69.71	−70.18	0.69	−69.49
syn-E2 PostMIN2	−65.89	−69.45	−69.40	−69.88	0.45	−69.43
SN2 PostMIN	−71.58	−75.19	−75.20	−75.74	3.97	−71.77
SN2 PostHMIN	−77.35	−81.20	−81.19	−81.54	4.11	−77.43
FSMIN	−21.75	−22.99	—^g	−22.87^g	0.81	−22.06
anti-E2 TS	−17.09	−17.25	−17.01	−16.88	−1.82	−18.69
syn-E2 TS	−6.62	−7.11	−6.78	−6.57	−2.81	−9.38
WaldenTS	−18.05	−19.19	−19.21	−19.09	0.67	−18.41
FSTS	18.57	16.57	16.38	16.52	0.45	16.97
DITS	2.97	−0.54	−0.41	−0.28	−0.32	−0.60

---

Fig. 5 Structures of the reactants and various products corresponding to the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] reactions showing the relevant bond lengths (Å) and angles (degree) obtained at the CCSD(T)-F12b/aug-cc-pVTZ level of theory.

Table 2 The best available experimental and our benchmark ab initio 0 K reaction enthalpies (kcal mol⁻¹) of various product channels for the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] reactions

OH^− + CH3CH2F	MP2	CCSD(T)-F12b			ΔZPE^e	Adiabatic^f	Exp^g
	DZ^a	DZ^b	TZ^c	QZ^d
a MP2/aug-cc-pVDZ. b CCSD(T)-F12b/aug-cc-pVDZ. c CCSD(T)-F12b/aug-cc-pVTZ. d CCSD(T)-F12b/aug-cc-pVQZ at CCSD(T)-F12b/aug-cc-pVTZ geometry. e ΔZPE(CCSD(T)-F12b/aug-cc-pVDZ). f QZ + ΔZPE. g Data obtained from the latest version (1.122p) of the Active Thermochemical Tables (ATcT).^53,54 The uncertainties are derived using the Gaussian error-propagation law on the uncertainties of each 0 K enthalpy of formation provided in ATcT. h TZ + ΔZPE, because ROHF/QZ does not converge.
C2H5OH + F^−	−20.61	−19.00	−19.07	−19.22	2.19	−17.03	−17.19 ± 0.10
HOH⋯F^− + C2H4	−32.37	−31.81	−32.02	−32.20	−2.00	−34.19	—
F^− + H2O + C2H4	−5.55	−4.04	−4.29	−4.67	−2.74	−7.40	−7.81 ± 0.09
H2O + H3C–CHF^−	24.54	21.94	22.13	22.22	−2.37	19.85	—
H^− + H3C–CHFOH	27.70	20.17	21.41	21.83	−2.13	19.71	—
H^− + HOH2C–CH2F	41.64	34.24	35.53	35.93	−2.13	33.80	31.98 ± 0.25
OHF^− + CH3CH2	48.93	47.08	46.89	46.98	−4.48	42.50	—
HOF + CH3CH2^−	120.60	114.54	114.39	114.51	−3.18	111.33	111.66 ± 0.23

---

OH^− + CH3CH2Cl	MP2^a	DZ^b	TZ^c	QZ^d	ΔZPE^e	Adiabatic^f	Exp^g
C2H5OH + Cl^−	−51.88	−52.84	−53.20	−53.46	3.03	−50.43	−50.26 ± 0.08
HOH⋯Cl^− + C2H4	−51.55	−52.96	−53.47	−53.83	−0.69	−54.52	—
Cl^− + H2O + C2H4	−36.83	−37.89	−38.42	−38.91	−1.89	−40.80	−40.88 ± 0.07
H2O + H3C–CHCl^−	12.63	9.49	9.42	9.43	−1.99	7.44	—
H^− + H3C–CHClOH	32.93	26.19	27.55	28.00	−2.43	25.56	—
H^− + HOH2C–CH2Cl	40.37	33.10	34.46	34.86	−2.19	32.68	30.93 ± 0.15
OHCl^− + CH3CH2	32.00	28.58	28.13	28.07	−3.23	24.84	—
HOCl + CH3CH2^−	84.81	77.47	77.95	78.12	−2.73	75.39	75.86 ± 0.22

---

OH^− + CH3CH2Br	MP2^a	DZ^b	TZ^c	QZ^d	ΔZPE^e	Adiabatic^f	Exp^g
C2H5OH + Br^−	−58.09	−61.59	−61.57	−61.97	3.51	−58.46	−58.19 ± 0.08
HOH⋯Br^− + C2H4	−55.92	−59.67	−59.87	−60.33	−0.30	−60.63	—
Br^− + H2O + C2H4	−43.03	−46.63	−46.80	−47.42	−1.42	−48.83	−48.81 ± 0.07
H2O + H3C–CHBr^−	9.33	5.16	5.15	5.15	−1.66	3.49	—
H^− + H3C–CHBrOH	33.74	26.98	28.40	28.83	−2.41	26.42	—
H^− + HOH2C–CH2Br	40.09	32.98	34.31	34.71	−2.16	32.55	30.43 ± 0.14
OHBr^− + CH3CH2	28.11	22.38	22.24	—	−2.85	19.38^h	—
HOBr + CH3CH2^−	74.88	69.22	69.30	69.41	−2.51	66.89	67.91 ± 0.25

---

OH^− + CH3CH2I	MP2^a	DZ^b	TZ^c	QZ^d	ΔZPE^e	Adiabatic^f	Exp^g
C2H5OH + I^−	−65.06	−68.93	−69.08	−69.75	3.79	−65.96	−65.71 ± 0.13
HOH⋯I^− + C2H4	−60.87	−64.97	−65.27	−65.94	−0.13	−66.07	—
I^− + H2O + C2H4	−50.01	−53.97	−54.31	−55.20	−1.14	−56.34	−56.33 ± 0.12
H2O + H3C–CHI^−	5.14	0.64	0.51	0.42	−1.57	−1.14	—
H^− + H3C–CHIOH	35.29	28.63	30.11	30.55	−2.31	28.25	—
H^− + HOH2C–CH2I	39.62	32.55	33.91	34.32	−2.22	32.10	33.86 ± 0.61
OHI^− + CH3CH2	20.91	16.58	16.34	16.16	−2.52	13.64	—
HOI + CH3CH2^−	62.13	57.12	56.76	56.82	−2.42	54.40	55.32 ± 0.78

---

The S_N2 reactions are more exothermic than the corresponding E2 reactions, submerged by classical (adiabatic) energies of 14.6 (9.6) kcal mol⁻¹, at 0 K, in all cases, as seen in Fig. 1 and 2. The back-side attack substitution can occur via the traditional PreMIN → WaldenTS → S_N2 PostHMIN and/or S_N2 PostMIN pathway. For the S_N2 reactions, similar to OH⁻ + CH₃Y,^{21,27,29,35,38} the global minimum of the potential energy surfaces is S_N2 PostHMIN. S_N2 PostMIN is above S_N2 PostHMIN by 18.9 (19.8), 8.8 (8.6), 7.4 (7.0) and 5.8 (5.7) kcal mol⁻¹ for Y = F, Cl, Br and I, in order. Note that the S_N2 PostHMIN is the global minimum for the complex multi-channel potential energy surfaces also. In the entrance channel only one minimum is found (PreMIN), unlike the F⁻ + CH₃CH₂Cl reaction,⁴³ where a H-bonded complex was also obtained. The barrier of the Walden-inversion mechanism is significantly submerged, except for Y = F, where the classical barrier height is only −0.6 kcal mol⁻¹, and with ZPE correction it is even above the reactant asymptote by 0.1 kcal mol⁻¹. In the F⁻ + CH₃CH₂I reaction for the transition state of the back-side attack substitution, a classical energy of −16.9 kcal mol⁻¹ was revealed relative to the reactants,⁴⁶ while for the OH⁻ + CH₃CH₂I reaction, a value of −19.1 kcal mol⁻¹ is identified. The difference of these latter classical energies, 2.2 kcal mol⁻¹, is similar to the cases of the X⁻ + CH₃CH₂Cl [X = F, OH] reactions,⁴³ where a difference of 1.4 kcal mol⁻¹ is determined. As Fig. 3 shows, at WaldenTS the Y–C bond is stretched by 0.362, 0.285, 0.218 and 0.164 Å relative to the corresponding bond lengths in PreMIN for Y = F, Cl, Br and I, respectively. Considering the lengths of the H⋯Y⁻ hydrogen bond and the dissociation energy of the leaving Y⁻ at S_N2 PostHMIN, the trend is similar to the OH⁻ + CH₃Y reactions:³⁸ as the H⋯Y⁻ bond decreases the dissociation energy increases, resulting in D_e (D₀) values of 30.8 (31.6) kcal mol⁻¹ for Y = F. For Y = Cl the classical energies of PreMIN and S_N2 PostMIN are deeper by 0.3 and 16.4 kcal mol⁻¹ relative to the classical energies of the relevant stationary points for the F⁻ + CH₃CH₂Cl reaction.⁴³ Regarding the point-group symmetries of PreMIN, WaldenTS, S_N2 PostHMIN and S_N2 PostMIN, all structures have C_s symmetry.

In contrast to the above-described back-side attack mechanism, the front-side attack proceeds via high classical (adiabatic) barriers of 43.4 (43.4), 28.9 (28.8), 22.4 (22.9) and 16.5 (17.0) kcal mol⁻¹, for Y = F, Cl, Br and I, respectively, as Fig. 1 shows. In the entrance channel a front-side complex is found for Y = Cl, Br, I. In the case of F⁻ + CH₃I, an important front-side complex formation was exposed,⁵² thus, it is worth noting that in the title reaction for Y = I FSMIN is below PreMIN by 2.8 (2.8) kcal mol⁻¹. In FSMIN the arrangement of O⋯Y–C is almost collinear, and in the cases of Y = Br and I, the OH group rotates out of the C_s symmetry plane by ∼88°, leading to a C₁ symmetry structure. In all cases, FSTS has C₁ point-group symmetry. For the F⁻ + CH₃CH₂Cl reaction,⁴³ a front-side transition state with 29.6 kcal mol⁻¹ classical height was found, similar to OH⁻ + CH₃CH₂Cl, where a slightly deeper classical energy, 28.9 kcal mol⁻¹, emerges. At higher energies, besides the front-side attack, double inversion can also occur, resulting in a lower-energy retention pathway. Double inversion begins with a proton-abstraction induced inversion via DITS followed by a second inversion through WaldenTS resulting in retention of the initial configuration. Note that the trend between the barrier heights of the double inversion and the weights of the halogens is inversely proportional: 22.4 (21.1), 7.4 (6.7) and 4.8 (4.3) kcal mol⁻¹, for Y = F, Cl and Br, respectively. For Y = I, similar to OH⁻ + CH₃I,³⁸ double inversion becomes a barrierless pathway through a slightly submerged DITS with an energy of −0.3 (−0.6) kcal mol⁻¹.

Besides the S_N2 reaction, elimination can also occur by two different mechanisms: anti-E2 and syn-E2, where the simultaneously breaking C–Y and C–H bonds are in anti and syn arrangements, respectively. In the entrance channel for both E2 mechanisms the same complex (PreMIN) is found as in the back-side attack substitution, as shown in Fig. 2. All stationary points of E2 are submerged: the global minimum is anti-E2 PostMIN for anti-E2, and syn-E2 PostMIN1 for syn-E2. Anti-E2 TS is below syn-E2 TS by 9.2 (8.8), 10.3 (9.6), and 10.3 (9.3) kcal mol⁻¹ for Y = Cl, Br, and I, respectively. These latter energy differences are in agreement with the case of F⁻ + CH₃CH₂Cl, where a value of 10.6 (10.3) kcal mol⁻¹ was obtained.²⁵ For the OH⁻ + CH₃CH₂F reaction anti-E2 TS and syn-E2 TS cannot be found. Compared to the back-side attack substitution, the WaldenTS is below anti-E2 TS by 0.6 (Cl), 1.7 (Br) and 2.2 (I) kcal mol⁻¹ without taking the ZPE corrections into consideration, as seen in Fig. 2. However, the picture changes with ZPE corrections, the anti-E2 TSs get energetically more favored, thus the adiabatic barrier heights of anti-E2 TSs are below WaldenTSs by 2.8, 1.3 and 0.3 kcal mol⁻¹, for Y = Cl, Br and I respectively. This peculiarity is not unique: the same can be observed for the F⁻ + CH₃CH₂Cl reaction, indicating that the kinetic control predicts a higher reactivity for E2 reaction than for back-side attack S_N2.⁴³ Both anti-E2 TS and syn-E2 TS have C₁ symmetry; in syn-E2 TS the breaking C–H bond is lengthened by 0.122 (Cl), 0.123 (Br) and 0.109 (I) Å, however, the O–H bond of the H₂O fragment is shortened by 0.121 (Cl), 0.153 (Br) and 0.169 (I) Å relative to the corresponding bond lengths in anti-E2 TS, as shown in Fig. 4. For syn-E2, in the product channel two ion-dipole complexes are revealed (syn-E2 postMIN1 and syn-E2 postMIN2), which can lead to Y⁻⋯HOH + C₂H₄ and afterwards to the final products. It should be noted that for the Cl⁻⋯HF + C₂H₄ products of the F⁻ + CH₃CH₂Cl reaction, the D_e (D₀) dissociation energy is 23.4 (22.2) kcal mol⁻¹,^25,43 while in the case of OH⁻ + CH₃CH₂Cl D_e (D₀) values of 14.9 (13.7) kcal mol⁻¹ can be determined for Cl⁻⋯HOH, as seen in Fig. 2. Nevertheless, in the exit channel, the D_e (D₀) dissociation energy for the three-body breakup of the Cl⁻⋯C₂H₄⋯HF complex for the F⁻ + CH₃CH₂Cl reaction is around 15.4 (13.1) kcal mol⁻¹,^25,43 while in OH⁻ + CH₃CH₂Cl for anti-E2 PostMIN it is 20.4 (17.9) kcal mol⁻¹. This trend breaks for the F⁻ + CH₃CH₂I reaction: the D_e dissociation energies of I⁻⋯HF + C₂H₄ and I⁻⋯C₂H₄⋯HF are 24.7 and 16.5 kcal mol⁻¹,⁴⁶ while for the OH⁻ + CH₃CH₂I reaction the corresponding D_e values are 10.7 and 15.4 kcal mol⁻¹, in order. Concerning the structures of the stationary points: syn-E2 PostMIN2 complexes have C_s symmetry, as seen in Fig. 4, whereas for syn-E2 PostMIN1 and anti-E2 PostMIN no plane symmetry is detected.

Besides S_N2 and E2, five other product channels are investigated for the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br and I] reactions: H₂O + H₃C–CHY⁻, H⁻ + H₃C–CHYOH, H⁻ + HOH₂C–CH₂Y, OHY⁻ + CH₃CH₂, and HOY + CH₃CH₂⁻, as seen in Table 2 and Fig. 5. In all cases, the most endothermic pathway is the HOY + CH₃CH₂⁻. For Y = F, Cl, Br and I, in most cases, the H₂O + H₃C–CHY⁻, H⁻ + H₃C–CHYOH, and H⁻ + HOH₂C–CH₂Y are endothermic, and the endothermicity is increasing in the same order. All the reaction enthalpies decrease from Y = F to I, except for H⁻ + H₃C–CHYOH, where the trend is reversed. Moreover, it should also be mentioned that, except for S_N2, MP2 provides notably larger values of reaction enthalpies, than CCSD(T)-F12b. If one compares the benchmark 0 K reaction enthalpies in the present study with the available “experimental” reaction enthalpies obtained from the Active Thermochemical Tables (ATcT),^53,54 an excellent agreement can be observed, except for the H⁻ + HOH₂C–CH₂Y products, where a difference of ∼2 kcal mol⁻¹ can be eventuated. Note that the decreasing trend for the experimental reaction enthalpies of H⁻ + HOH₂C–CH₂Y breaks at Y = I, querying the accuracy of either the experimental or the benchmark ab initio energies. It should be emphasized that the sum of the post-CCSD(T) and core-correlation effects of the S_N2 channels was substantial for the OH⁻ + CH₃Y [Y = Cl, Br, I] reactions: a sum of 0.40 (Cl), 0.68 (Br) and 1.07 (I) kcal mol⁻¹ was revealed.³⁸ Therefore, to resolve this latter issue of the H⁻ + HOH₂C–CH₂Y channel, more accurate benchmark reaction enthalpies should be determined, considering post-CCSD(T) correlations, core-correlation corrections, as well as relativistic effects besides Br and I and anharmonic ZPE corrections. However, these auxiliary correction computations are out of the scope of the present work, because previous studies on S_N2 reactions showed that the chemical accuracy for most of the benchmark energies is not significantly affected by these corrections.^38,55–57

For a detailed evaluation of the accuracy of our benchmark energies, the basis-set convergence of the CCSD(T)-F12b relative energies can be analyzed. As shown in Fig. 6, the deviations of the corresponding basis sets are within ±0.65 kcal mol⁻¹ for the stationary points, excluding FSMIN in OH⁻ + CH₃CH₂Cl, where the aug-cc-pVDZ (DZ) basis set gives a 0.79 kcal mol⁻¹ deviation from aug-cc-pVQZ (QZ). Concerning the product channels, at the H⁻ + H₃C–CHYOH and H⁻ + HOH₂C–CH₂Y pathways, a large difference of almost 2 kcal mol⁻¹ can be obtained between DZ and QZ reaction enthalpies, however, due to the fast basis-set convergence of the F12 methods, aug-cc-pVTZ (TZ) provides a more reduced deviation of roughly 0.4 kcal mol⁻¹ from QZ, as seen in Fig. 7. For the reaction enthalpies of E2, the basis-set convergence is not that smooth, especially for OH⁻ + CH₃CH₂I, the difference between the TZ and QZ enthalpies is 0.89 kcal mol⁻¹. In OH⁻ + CH₃Y [Y = Cl, Br, I], a similar situation occurs, and the largest deviations in the TZ and QZ data appear for the reaction enthalpies.³⁸ For PreMIN, FSMIN, anti-E2 PostMIN, syn-E2 PostMIN1, syn-E2 PostMIN2, WaldenTS, FSTS, and DITS, in most cases, the ZPE effects are within ±1 kcal mol⁻¹, as Table 1 shows. More significant ZPE corrections can be recognized for S_N2 PostMIN and S_N2 PostHMIN, in the range of 1.3–4.2 kcal mol⁻¹. For anti-E2 TS and syn-E2 TS the ΔZPEs are between −1.8 and −3.1 kcal mol⁻¹, decreasing the barrier heights of the anti-E2 TS below WaldenTS, as discussed earlier. In respect of the product channels, as seen in Table 2, only S_N2 channels have positive ZPE corrections, from about 2.2 to 3.8 kcal mol⁻¹, all other product channels have negative and usually substantial ΔZPEs.

Fig. 6 Deviations of the CCSD(T)-F12b relative energies of the stationary points obtained by using the aug-cc-pVDZ (DZ) and aug-cc-pVTZ (TZ) basis sets with respect to the CCSD(T)-F12b/aug-cc-pVQZ (QZ) results, corresponding to the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] S_N2 and E2 reactions.

Fig. 7 Deviations of the CCSD(T)-F12b reaction enthalpies of several product channels obtained by using the aug-cc-pVDZ (DZ) and aug-cc-pVTZ (TZ) basis sets with respect to the CCSD(T)-F12b/aug-cc-pVQZ (QZ) results, corresponding to the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] reactions.

IV. Summary and conclusions

In this work, we have explored the complex potential energy surfaces of the OH⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] reactions by characterizing the stationary points of the E2 and S_N2 pathways using the explicitly-correlated CCSD(T)-F12b method. In the case of elimination, anti-E2 and syn-E2 mechanisms have been investigated, as far as for the substitution, besides the traditional back-side attack, front-side attack and double inversion have been studied. We have found that the thermodynamically most favored back-side attack substitution goes through almost the same pathway as in the F⁻ + CH₃CH₂Cl reaction.⁴³ Furthermore, in the exit channel, the dissociation energies of the leaving nucleophiles of the hydrogen-bonded CH₃CH₂OH⋯Y⁻ global minimum follow a similar trend to that for the reactions of OH⁻ with methyl-halides.³⁸ In the entrance channel, a front-side complex formation is unveiled,^23,37,52 resulting in a submerged HO⁻⋯YCH₂CH₃ minimum, especially for Y = I, where this front-side complex is below the traditional ion-dipole HO⁻⋯H₂CYCH₃ complex. The barrier heights of double inversion are reduced by 22.2 (F), 22.1 (Cl), 18.7 (Br) and 17.6 (I) kcal mol⁻¹ relative to the corresponding barriers of the front-side attack, leading to a barrierless double-inversion pathway for OH⁻ + CH₃CH₂I, similar to OH⁻ + CH₃I.³⁸ Regarding the elimination, in all cases, the pathway of the anti-E2 is lower than the syn-E2. As in F⁻ + CH₃CH₂Cl,⁴³ at the transition states of the anti-E2 notable ZPE effects occur, causing a less kinetically favorable back-side attack S_N2. It should be also highlighted that all stationary points of the E2 are submerged, as in the back-side attack substitution. Along with the S_N2 and E2, we examined several reaction enthalpies of other product channels, as well. Our benchmark reaction enthalpies are in excellent agreement with those obtained from ATcT,^53,54 except for the H⁻ + HOH₂C–CH₂Y channel, addressing, in this case, an uncertainty of either the “experimental” or the ab initio reaction enthalpies. We have also analyzed the basis-set convergence of the CCSD(T)-F12b method and the ZPE effects on the classical energies. Overall, for the first time, we have presented a high-level characterization of the title reactions, extending our knowledge on S_N2 and E2 reactions and motivating future potential energy surface developments, reaction dynamics simulations as well as experiments.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We are grateful for the financial support from the National Research, Development and Innovation Office − NKFIH (K-125317), the Ministry of Human Capacities, Hungary (20391-3/2018/FEKUSTRAT), and the Momentum (Lendület) Program of the Hungarian Academy of Sciences.

References

1. R. A. Bartsch and J. Závada, Chem. Rev., 1980, 80, 453.
2. J. D. Evanseck, J. F. Blake and W. L. Jorgensen, J. Am. Chem. Soc., 1987, 109, 2349.
3. A. P. Bento, M. Sola and F. M. Bickelhaupt, J. Chem. Theory Comput., 2008, 4, 929.
4. J. M. Garver, N. Eyet, S. M. Villano, Z. Yang and V. M. Bierbaum, Int. J. Mass Spectrom., 2011, 301, 151.
5. M. Stei, E. Carrascosa, M. A. Kainz, A. H. Kelkar, J. Meyer, I. Szabó, G. Czakó and R. Wester, Nat. Chem., 2016, 8, 151.
6. E. Carrascosa, J. Meyer and R. Wester, Chem. Soc. Rev., 2017, 46, 7498.
7. E. Carrascosa, J. Meyer, J. Zhang, M. Stei, T. Michaelsen, W. L. Hase, L. Yang and R. Wester, Nat. Commun., 2017, 8, 25.
8. E. Carrascosa, J. Meyer, T. Michaelsen, M. Stei and R. Wester, Chem. Sci., 2018, 9, 693.
9. P. Vermeeren, T. Hansen, P. Jansen, M. Swart, T. A. Hamlin and F. M. Bickelhaupt, Chem. – Eur. J., 2020, 26, 15538.
10. P. Vermeeren, T. Hansen, M. Grasser, D. R. Silva, T. A. Hamlin and F. M. Bickelhaupt, J. Org. Chem., 2020, 85, 14087.
11. L. J. de Koning and N. M. M. Nibbering, J. Am. Chem. Soc., 1987, 109, 1715.
12. T. Minato and S. Yamabe, J. Am. Chem. Soc., 1988, 110, 4586.
13. C. H. DePuy, S. Gronert, A. Mullin and V. M. Bierbaum, J. Am. Chem. Soc., 1990, 112, 8650.
14. S. Gronert, J. Am. Chem. Soc., 1991, 113, 6041.
15. F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114.
16. S. Gronert, Acc. Chem. Res., 2003, 36, 848.
17. S. Gronert, A. E. Fagin, K. Okamoto, S. Mogali and L. M. Pratt, J. Am. Chem. Soc., 2004, 126, 12977.
18. B. Ensing and M. L. Klein, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6755.
19. W. A. Cowdrey, E. D. Hughes, C. K. Ingold, S. Masterman and A. D. Scott, J. Chem. Soc., 1937, 1252.
20. C. K. Ingold, Structure and Mechanism in Organic Chemistry, Cornell Univ. Press, Ithaca, NY, 1953.
21. J. Xie, R. Otto, J. Mikosch, J. Zhang, R. Wester and W. L. Hase, Acc. Chem. Res., 2014, 47, 2960.
22. I. Szabó and G. Czakó, Nat. Commun., 2015, 6, 5972.
23. J. Xie and W. L. Hase, Science, 2016, 352, 32.
24. D. A. Tasi, Z. Fábián and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 7924.
25. G. Czakó, T. Győri, B. Olasz, D. Papp, I. Szabó, V. Tajti and D. A. Tasi, Phys. Chem. Chem. Phys., 2020, 22, 4298.
26. J. Mikosch, S. Trippel, C. Eichhorn, R. Otto, U. Lourderaj, J. X. Zhang, W. L. Hase, M. Weidemüller and R. Wester, Science, 2008, 319, 183.
27. J. M. Gonzales, R. S. Cox, S. T. Brown, W. D. Allen and H. F. Schaefer, J. Phys. Chem. A, 2001, 105, 11327.
28. J. M. Gonzales, C. Pak, R. S. Cox, W. D. Allen, H. F. Schaefer, A. G. Császár and G. Tarczay, Chem. – Eur. J., 2003, 9, 2173.
29. L. Sun, K. Song, W. L. Hase, M. Sena and J. M. Riveros, Int. J. Mass Spectrom., 2003, 227, 315.
30. L. Sun, K. Song and W. L. Hase, Science, 2002, 296, 875.
31. H. Tachikawa, M. Igarashi and T. Ishibashi, J. Phys. Chem. A, 2002, 106, 10977.
32. H. Tachikawa and M. Igarashi, Chem. Phys., 2006, 324, 639.
33. R. Otto, J. Brox, S. Trippel, M. Stei, T. Best and R. Wester, Nat. Chem., 2012, 4, 534.
34. J. Xie, R. Sun, M. R. Siebert, R. Otto, R. Wester and W. L. Hase, J. Phys. Chem. A, 2013, 117, 7162.
35. J. Xie, S. C. Kohale, W. L. Hase, S. G. Ard, J. J. Melko, N. S. Shuman and A. A. Viggiano, J. Phys. Chem. A, 2013, 117, 14019.
36. J. Xie, J. Zhang and W. L. Hase, Int. J. Mass Spectrom., 2015, 378, 14.
37. X. Ji, C. Zhao and J. Xie, Phys. Chem. Chem. Phys., 2021, 23, 6349.
38. D. A. Tasi, Z. Fábián and G. Czakó, J. Phys. Chem. A, 2018, 122, 5773.
39. D. A. Tasi, T. Győri and G. Czakó, Phys. Chem. Chem. Phys., 2020, 22, 3775.
40. M. Mugnai, G. Cardini and V. Schettino, J. Phys. Chem. A, 2003, 107, 2540.
41. Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 1104.
42. X.-P. Wu, X.-M. Sun, X.-G. Wei, Y. Ren, N.-B. Wong and W.-K. Li, J. Chem. Theory Comput., 2009, 5, 1597.
43. V. Tajti and G. Czakó, J. Phys. Chem. A, 2017, 121, 2847.
44. L. Satpathy, P. K. Sahu, P. K. Behera and B. K. Mishra, J. Phys. Chem. A, 2018, 122, 5861.
45. X. Liu, J. Zhang, L. Yang and W. L. Hase, J. Am. Chem. Soc., 2018, 140, 10995.
46. L. Yang, J. Zhang, J. Xie, X. Ma, L. Zhang, C. Zhao and W. L. Hase, J. Phys. Chem. A, 2017, 121, 1078.
47. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618.
48. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
49. T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106.
50. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113.
51. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., Molpro, version 2015.1, a package of ab initio programs, see http://www.molpro.net.
52. I. Szabó, B. Olasz and G. Czakó, J. Phys. Chem. Lett., 2017, 8, 2917.
53. D. H. Ruscic and B. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.122p of the Thermochemical Network, 2020, available at http://ATcT.anl.gov.
54. B. Ruscic, R. E. Pinzon, M. L. Morton, G. Von Laszevski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 108, 9979.
55. I. Szabó and G. Czakó, J. Phys. Chem. A, 2017, 121, 5748.
56. G. Czakó, I. Szabó and H. Telekes, J. Phys. Chem. A, 2014, 118, 646.
57. I. Szabó, H. Telekes and G. Czakó, J. Chem. Phys., 2015, 142, 244301.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates (Å) and energies (E_h) of the stationary points obtained at the CCSD(T)-F12b/aug-cc-pVTZ level of theory. See DOI: 10.1039/d1cp01303c

---