trans–cis Photoisomerization of a biomimetic cyclocurcumin analogue rationalized by molecular modelling

Abstract

Cyclocurcumin is a natural compound extracted from turmeric and showing, in addition to antiinfective, antibacterial, and intinflammatory capabilities, solvent-dependent phtoswitching ability. The solvent-dependent photochemistry of cyclocurcumin has been rationalized on the basis of a competition between π–π* and n–π* states. Recently we have reported the synthesis of a biomimetic analogue showing enhanced photochemical properties and in particular presenting photoswitching capacity in various media. In the present contribution we rely on the use of molecular modeling and simulation, incuding density functional and wavefunction based methods to explore the excited states potential energy surface landscape. We see that the addition of a carbon–carbon double bond to the core of the natural compounds favors the population of the π–π* state, whatever the choice of the solvent, and hence leads to photoisomerisation, with fluorescence reduced to only a minor channel, rationalizing the experimental observations. In addition, the two photon absorption cross section is also strongly increased compared to the parent compound, paving the way to the use in biologically oriented applications.

---

Introduction

Curcumin is a natural compound which can be isolated from turmeric rhizome¹ (Curcuma longa), and is widely used as a spice and culinary condiment.² Furthermore, while the significant pharmacological properties of curcumin^3–9 are steering high interest, more recent studies have revealed the antioxidant,¹⁰ anti-vasoconstrictive,¹¹ immune-modulating¹² and neuroprotective effects of a secondary turmeric derivative, i.e. cyclocurcumin (CC).¹³ Although, CC is extracted in small amount from turmeric, it presents interesting properties from a photochemical perspective. Indeed, CC is characterized by an α,β-unsaturated dihydropyrone core with an exocyclic double bond which can be isomerized under the proper light excitation.

CC photoswitchable properties have been scarcely exploited, or even characterized from an experimental point of view, even though they have been demonstrated and rationalized computationally, together with their dependence on the surrounding environmental factors, namely medium viscosity and polarity.^14,15 CC predominant form is constituted by the thermodynamically most stable trans-isomer. The irradiation with UVA light, λ_max = 375 nm, induces a trans to cis photoisomerization process.¹⁴ As for other well-known photoswitches, the reverse reaction can take place either thermally or photochemically after exposition to UVB light at around 300 nm. Additionally, natural CC exhibits fluorescence emission at around 500 nm, with again a noticeable dependence on the solvent.¹⁴ As a matter of fact, previous molecular modeling studies suggest that the competition between the main excited-state relaxation routes, photoisomerization and fluorescence, strongly depends on the polarity of the environment, which ultimately determines the detected outcome.¹⁵ Such competition is detrimental to the achievement of an exploitable, reproducible, and controllable function, e.g. fluorescent probe or photoswitch, especially in complex and inhomogeneous biological environments.

Although, the potential of the molecular photoswitches is still far for being fully explored, synthetic and natural photoswitches already found a wide range of applications,¹⁶ including optogenetics and imaging, biotechnology or pharmacology.¹⁷

Indeed, the main characteristics defining an ideal molecular photoswitch should comprise (i) chemical stability, (ii) low fatigue, meaning the ability of optical retuning, (iii) a large spectral difference between the two isomers allowing a selective irradiation, and (iv) a high photoisomerization quantum yield. Moreover, to be exploitable in biological applications and especially in photopharmacology a chromophore should present significant absorption in the biological optical active window, covering the 650 to 1350 nm range.¹⁸ As previously stated, the light-induced isomerization of CC is instead induced by absorption in the UVA region, therefore being inapplicable in a biological environment. Indeed, the necessity to avoid UV light for biomedical applications is due to its reduced penetration and to its potential toxicity. One way to bypass these limitations resides in exploiting non-linear absorption properties and particularly two-photon absorption (TPA). Indeed, in case of CC the simultaneous absorption of two equivalent photons with a wavelength ca. 740 nm, would be adequate to populate the isomerizing excited state.¹⁵ Additionally, TPA probability has a quadratic dependence to the light-source intensity, hence it decays more rapidly when moving away from the incident focal point, allowing for a better control of the spatial selectivity of the applied light source. Obviously, this spatial and temporal selectivity is extremely important in any potential biomedical application. Despite the fact that natural CC has a relatively high TPA cross-section compared to simple and small organic compounds, having been computationally estimated at 14 GM, its value is still too low for practical exploitation.¹⁵

With all these motivations in mind, we recently reported the design and synthesized a biomimetic analogue based on natural CC showing improved non-linear absorption properties, especially concerning significantly increased TPA cross-section, while keeping the main photoswitchable characteristics of the natural CC.¹⁹ As a matter of fact, the combination of a biomimetic strategy using synthetic and molecular design has emerged as a clearly advantageous procedure in the improvement of the photoswitching capabilities.^20,21 Indeed, we reported the first bioinspired photoswitch derived from cyclocurcumin (CC) showing that trans–cis photo-isomerization is possible and rather solvent independent. We hence propose a 2,6-γ-pyrone analogue (Fig. 1) with an additional ethylene bond compared to the 2,3-dihydro-2,6-γ-pyrone core of CC. This architecture was specifically designed to increase the planarity of the moiety and to introduce a second donor–acceptor group (aryl-ketone) conjugated within the chromophore, also increasing the global symmetry. Planar and quadrupolar structures with D–π–A–π–D systems, such as the one of pyrone, are expected to be more efficient in TPA than their dipolar analogues D–π–A, such as CC,²² as we confirmed by molecular modeling and simulations. More notably the chemical engineering provided an order of magnitude increase in the TPA cross-section.

Fig. 1 Structure of the synthetic cyclocurcumin mimetic studied, highlighting the isomerizable double bond and its dihedral angle (θ) (in green) and the structural change respect to natural cyclocurcumin (C=C_pyrone, in red).

In the present contribution we mainly focus on the study of the photoisomerization process of our biomimetic CC analogue, characterizing the nature of the involved excited states and the topology of the different potential energy surfaces (PES).

Through the use of multiconfigurational wavefunction-based techniques, and time dependent density functional theory (TD-DFT) we provide a full electronic picture of the photoisomerization process rationalizing the differences with natural CC and the role of the solvent effects in modulating the PES. A detailed knowledge of these factors is indeed crucial and instrumental to further improve the next generations of CC biomimetics yielding to more efficient photoswitches to be used in a broad spectrum of applications.

Results and discussion

As previously reported, the absorption spectrum of our prepared CC analogue was studied in different solvents and functionals. In contrast, in this work a detailed analysis of the potential energy surface is performed, focusing on the different factors ruling the isomerization process and the influence of solvent.

Firstly, natural transition orbitals (NTO) analysis^23,24 was performed to characterize the nature of the relevant excited states in terms of electronic density reorganization (see Fig. 2). Two main transitions are identified, which may play a dominant role in driving the photoswitchable behavior of the molecule. A dark state of n–π* nature is observed presenting an oscillator strength lower than 0.04 au. The brightest transition corresponds to a π–π* state centered on the isomerizable C=C π moiety. It should be noted that this transition is stabilized when computed in solution and slightly red shifting when increasing the polarity of the used solvent.¹⁹

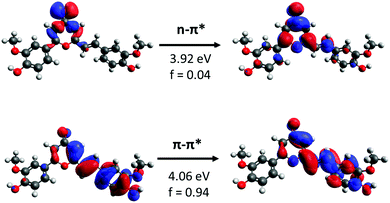Fig. 2 NTOs of the first two excited states found in a gas phase TD-DFT calculation using the CAM-B3LYP/6-31G* level.

Additionally, a third contribution of π–π* nature and involving the pyrone C=C which is coupled to the main chromophore because of the extended conjugation could also be considered. However, all the computational methodologies used agree in placing this transition at higher energies than the former along the entirety of the double-bond torsion coordinate, hence suggesting that its role on the photoisomerization is negligible.¹⁹

To validate the use of TD-DFT to include solvent effects in a more affordable manner, the energy levels of the two lowest energy states along the double-bond rotation coordinate have been benchmarked against wavefunction-based methods. This involved the use of a complete active space approach (CASSCF) and the multi state second order perturbation expansion (MS-CASPT2). In addition, to improve the representation along the conical intersection regions and the branching space the extended multi state approach (XMS-CASPT2) was used.

We observed consistently a common behavior as it was also reported in the case of the modeling of the absorption spectrum as reported in our previous contribution.¹⁹ Even though B3LYP provides an absorption spectrum whose shape is closer to the experimental results, its use to study the rotation coordinate was dismissed due to the appearance of intruder states that makes impossible the right representation of the PES along this coordinate. This is mostly due to the well-known over-stabilization of charge-transfer states, that is an issue plaguing hybrid functionals, and for that reason the long-range corrected CAM-B3LYP was chosen instead.

As reported in Table 1, the nature and order of the different excited states is consistent between the different methods used. It should be pointed that the CAM-B3LYP notably overestimates the n–π* state energy with respect to the qualitatively good description of π–π* state. The nature of the different excited states at the CAS expansion is confirmed by analysis of the molecular orbitals involved, see ESI† for further information.

Table 1 Relative energies of the relevant points along the PES at different levels of theory. The Franck–Condon energy is used as reference for the two excited state minima found

Level of theory	Electronic states	Franck–Condon	Minn–π*	Minπ–π*
a Optimized geometries at the TD-DFT level. In brackets, energy of the CASSCF optimized minimum geometries.
CASSCF	S0	0	0.84	0.87
	S1	3.64 ^1(n–π*)	2.69 ^1(n–π*)	2.98 ^1(n–π*)
	S2	5.59 ^1(π–π*)	4.22 ^1(π–π*)	4.01 ^1(π–π*)
Multistate (MS)-CASPT2	S0	0.0	1.05	1.00
	S1	3.54 ^1(n–π*)	3.31 ^1(n–π*)	3.44 ^1(n–π*)
	S2	4.82 ^1(π–π*)	4.42 ^1(π–π*)	4.00 ^1(π–π*)
Extended multistate (XMS)-CASPT2	S0	0.00	1.39	1.43
	S1	3.79 ^1(n–π*)	3.72 ^1(n–π*)	3.86 ^1(n–π*)
	S2	5.02 ^1(π–π*)	4.57 ^1(π–π*)	4.42 ^1(π–π*)
TD-DFT (CAM-B3LYP)^a	S0	0	0.33 [1.01]	0.27 [1.03]
	S1	3.92 ^1(n–π*)	3.68 [3.92] ^1(n–π*)	3.62 [4.03] ^1(π–π*)
	S2	4.06 ^1(π–π*)	4.02 [4.34] ^1(π–π*)	4.02 [4.06] ^1(n–π*)

---

Once the methodology has been evaluated, we explored the PES starting from the Franck–Condon (FC) region following the ¹(n–π*) and ¹(π–π*) states. Note that the results reported in Table 1 and in the figures detailing the isomerization pathways are obtained from CAS-SCF optimized geometries on top of which either perturbative corrections or TD-DFT calculations have been performed. In particular we may evidence two distinct minima, the lowest ¹(n–π*) and the higher ¹(π–π*), which are structurally quite close to the ground state equilibrium geometry. Note that the energy differences in the figures below is due to the use of CAS-SCF optimized geometries instead of DFT ones. In case of the ¹(π–π*) state, the corresponding minimum (Min_π–π*) is located at 4.00 eV from the Franck–Condon geometry, using the (MS)-CASPT2 approach and shows a dihedral angle of θ = 179°. This change in the dihedral angle is coupled with an elongation of the C=C bond of about 0.101 Å, which clearly shows the weakening of the double bond character and hence the feasibility of the photoisomerization. To compare the MS-CASPT2 and CAM-B3LYP level, the two previously described minima were optimized using CAM-B3LYP. The CAM-B3LYP ¹(π–π*) minimum presents a similar dihedral angle coupled with a shorter elongation of the C=C bond (0.056 Å), also being more stabilized, at 3.62 eV. Another high energy excited state minimum corresponding to the ¹(n–π*) is found displaying an almost totally planar disposition, with a dihedral angle along the isomerizable double bond of θ = −179°.

In contrast, the minimum in the ¹(n–π*) state (Min_n–π*) presents a different behavior, at CASSCF the dihedral angle remains totally planar coupled with a C=C elongation of 0.038 Å and located at 3.31 eV over FC. At CAM-B3LYP the minimum is located at 3.68 eV, higher in energy than what is observed for the ¹(π–π*) state, due to the general overestimation of its energy in CAM-B3LYP. Geometrically the ¹(n–π*) equilibrium geometry presents a fully planar conformation with a smaller elongation of only 0.006 Å. This different behavior could suggest a delayed isomerization or a non-truly isomerizable pathway following the population of this state and also points to the necessity of complementing TD-DFT methods with multireference approaches to correctly study this process, especially for the behavior of the ¹(n–π*) state. The presence of the two minima in excited state presenting similar energies is in good agreement with the Stokes-shifted fluorescent emission found experimentally.¹⁹

To begin with the exploration of the photoisomerization process, the two lower excited states were followed along the most relevant coordinate, which in a trans to cis isomerization is obviously the dihedral angle along the isomerizable bond. For that, a relaxed scan over the dihedral angle (θ), see Fig. 1, was performed in vacuo with the geometry of the two states relaxed at CAS-SCF level, and the energy corrected by single point MS-CASPT2 to include the dynamic electron correlation. This procedure is justified both by its widespread application and also by the presence of significant pathways, such as double and single bond length alternation (BLA), reminiscent to those observed in well-known photoswitches (like retinal or stilbene) as well as in natural CC that we modeled following a similar approach.¹⁵ Indeed, bond-length elongation and the change in BLA pattern represents the initial driving force which leads to the torsion of the C=C double bond and hence to photoisomerization.

As previously mentioned, both ¹(n–π* and ¹(π–π*) states can contribute to the isomerization process, for that reason we decided to compute both pathways to discriminate their role and their participation to the photoisomerization. The relaxed scans are reported in Fig. 3a for ¹(n–π*) and Fig. 3b for ¹(π–π*). From the PES depicted in Fig. 3, a deactivation pathway to the ground state can be unequivocally assumed for both states. Indeed, in either case a crossing region between S₁ and S₀ is located along the torsion coordinate, leading to a nonadiabatic crossing point funneling the population transfer between the excited and the ground state.

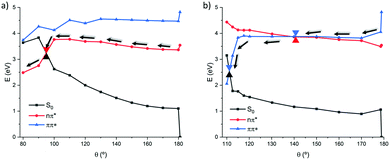Fig. 3 Relaxed scan along the torsion of the dihedral angle following the ¹(n–π*) (a) and ¹(π–π*) (b) states in the gas phase at the MS-CASPT2 level.

In more detail, the ¹(π–π*) state who is brightest and hence directly accessible upon FC excitation, yields to a local minimum in S₂ that can subsequently lead to a flat region along the torsion coordinate. All through the torsion and between dihedral values of 170 and 130 degrees, S₁ and S₂ remain almost degenerate with a maximum energy difference of only 0.1 eV. Throughout that area, a crossing point, i.e. a S₂/S₁ conical intersection (CI), can be located at ca. θ = 140°, being more delayed with respect to the natural CC which is found closer to FC. After the crossing, the S₁ PES stays almost planar until 120°, where a sudden stabilization of S₁ yields to a conical intersection with the ground state that is reached at ca. 110 degrees. The topology of the S₁/S₀ conical intersection appears quite steep and hence the completion of the isomerization in the ground state should be favorable. Representative structures on both pathways can be found in ESI,† pointing to how the isomerization undergoes.

In contrast, a steeper pathway is observed on the ¹(n–π*) PES, in which case an energy of ca. 0.4 eV needs to be overcome. While the S₁ behavior is strongly reminiscent of natural CC, the S₂ route presents significant differences. In natural CC S₂ is destabilized as a consequence of the rotation, increasing it energy to ca. 2 eV above S₁, oppositely in the biomimetic analogue a stepwise stabilization is observed that in turn can be linked to the contribution of the ¹(π–π*) state and to a delayed isomerization. This fact is also supported by the large mixing observed along these PESs, where the nature of the ground state has a great contribution of the π–π* transition. Hence, two competitive pathways can be highlighted and proposed, leading to two distinct crossing regions with the ground state. In terms of energetic considerations, the ¹(π–π*) crossing point appears favorable at lower energy, i.e. ca. 2.5 eV, as compared to the ¹(n–π*) that is found at 3.2 eV. Natural CC also presented similar profiles for the two photoisomerization pathways,¹⁵ which are characterized by barriers of 0.7 and 0.4 eV for the ¹(π–π*) and ¹(n–π*) states, respectively, that should be overcome to reach the crossing points. In case of the biomimetic analogue, the ¹(n–π*) is almost totally overlapping with the one of the natural CC, as most notably witnessed by the same energetic barrier, more significant differences can be observed for the ¹(π–π*) path. Indeed, in the biomimetic analogue the energetic barrier leading to the conical intersection is significantly lowered amounting only to less than 0.1 eV. Hence, it is evident that the ¹(π–π*) state leads to the most favorable route leading to the photoisomerization. This preference, and the smaller energetic penalty, could also yield to a more efficient photoswitching behavior, coherently with the experimental observations. Indeed, the almost barrierless pathway is in good agreement with the observed efficient isomerization process, as witnessed by the cis/trans ratio obtained after irradiation, and the very low fluorescent quantum yield found.¹⁹

The extended multi-state (X)MS-CASPT2 method (see ESI†) provides an identical picture for the ¹(n–π*) state but the ¹(π–π*) pathway yields in a crossing point at slightly lower dihedral of θ = 115° followed by sudden decay and the inversion of the state's order. Despite these differences the qualitative conclusions that can be drawn are equivalent to the ones based on (MS)-CASPT2 description.

The PES along the photoisomerization coordinate was also explored at TD-DFT level using the CAM-B3LYP functional as reported in Fig. 4, yielding a similar behavior to the one evidenced by wavefunction based methods with only minor differences. In the ¹(π–π*) path the relaxation follows a completely barrierless and flat route. However, it should be marked that the isomerization seems to be quite delayed, compared to the CAS-PT2 description, and thus an additional point was optimized as a constrained geometry at 100 degrees relaxing all the other coordinates. In contrast, the behavior of the ¹(n–π*) pathway becomes more complex compared to the simple two-states model sketched out at MS-CASPT2 level. Indeed, a stabilization of the ¹(π–π*) state is evidenced leading, at 120° to a S₂/S₁ conical intersection, after which a favorable and rather steep path to the S₁/S₀ conical intersection is opened, reaching the non-adiabatic point at around θ = 90°.

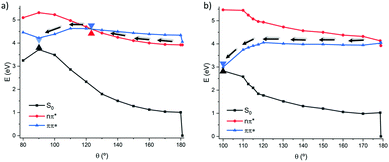Fig. 4 Relaxed scan along the torsion of the dihedral angle following the ¹(n–π*) (a) and ¹(π–π*) (b) states in the gas phase at the CAM-B3LYP level.

Note that due to the problematic description of the S₁/S₀ conical intersection at TD-DFT level, the energy degeneracy is not strictly obtained, indeed an extended branching, quasi-degeneracy region, spanning between 120 and 80° is obtained.

This fact corroborates the robustness of TD-DFT to provide at least a qualitative description of the photoisomerization process, in particular for what concerns the dominant ¹(π–π*) route.

Thus, once we have explored the photochemical features in gas phase, the solvent influence in modulating the topology of the PES is considered. Indeed, in the case of natural CC an important environmental effect, leading to the inversion of the ¹(π–π*) and ¹(n–π*) energetic order, has been observed, thus justifying the solvent-dependent isomerization quantum yields. Solvent effects are taken into account at TD-DFT level, whose accuracy has been benchmarked and through the use of implicit polarizable continuum methods (PCM). Solvent of different polarity are also considered including cyclohexane (non-polar), chloroform, dimethyl sulfoxide (polar aprotic), ethanol and water (polar protic), results are reported in Fig. 5 and ESI.† As general behavior, we found a negligible dependency on the solvent polarity compared to natural CC. Indeed, independently of the solvent used the most favorable ¹(π–π*) pathway is accessible. Similarly to what observed in vacuo, a first almost barrierless PES evolving into a down step region accessing the S₁/S₀ CI area is explored. Interestingly, polar solvents modify the relative energy differences leading to an even more stable ¹(π–π*) state and hence breaking the quasi-degeneracy between the two lowest states that is observed in gas phase or in non-polar environments.

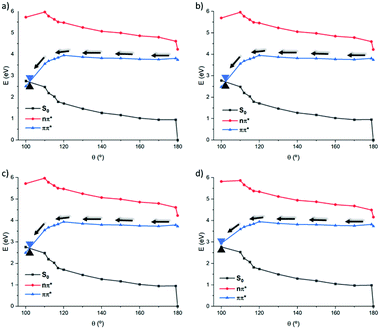Fig. 5 Most representative ¹(π–π*) pathways along the torsion (θ) in different solvents, water (a), ethanol (b), dimethyl sulfoxide (c) and chloroform (d), at the CAM-B3LYP level.

To better evaluate the influence of protic solvents, the use of explicit solvent molecules was considered in case of water. Indeed, two water molecules, interacting with the oxygen of the carbonyl, were included in the system and a relaxed scan was done along the ¹(π–π*) state at the CASSCF level (see ESI†). The optimized structures were evaluated as usual at the MS-CASPT2. This points to a clear stabilization of the ¹(π–π*) state as qualitatively observed in the previously commented TD-DFT results (Fig. 5). While a slightly delayed isomerization with a more twisted dihedral (ca. 10° lower) can be observed, the use of micro-hydration confirms the dominant role of the ¹(π–π*) in driving the isomerization process, justifying our approach based on an implicit description of the solvent.

A similar global tendency is also observed on the ¹(n–π*) pathways, see ESI,† for more details, that invariably leads to a stabilization of the ¹(π–π*) by polar solvents. As a consequence, the population of the former state is clearly favored. However, the former pathway still lays at higher energy with respect to the ¹(π–π*) channel. In contrast, in cyclohexane, i.e., a non-polar solvent, the qualitative behavior observed in vacuo is maintained.

Globally, and coherently with the experimental observations, we found a much-reduced dependence of the PES topology with the solvent polarity. Thus, isomerization appears as always possible and is favored when increasing the polarity of the solvent, minimizing the role played by radiative, fluorescence, emission. Indeed, our biomimetic CC analogue has been shown to have a very small fluorescence quantum yield. More importantly, the reduced dependence of the isomerization quantum yield on the solvent polarity is strongly beneficial to maintain the photoswitch potentiality also in inhomogeneous environments, such as interfaces and lipid bilayer, hence corroborating the possible use of our biomimetic CC analogue for biological applications. This fact is also reinforced by the fact that the TPA cross section is also strongly increased by an order of magnitude as compared with natural CC and as reported elsewhere.¹⁹

Conclusions

We report the study of the photoisomerization capabilities of biomimetic pyrone analogue of CC, recently designed and synthesized. In particular, we used molecular modeling and simulation to explore the PES topology around the crucial photoisomerization coordinate, i.e. the torsion angle around a carbon–carbon double bond. Even if this process could occur combining complex movements, the simple rotation around the isomerizable bond may be considered as the most relevant degrees of freedom as also observed for similar derivatives. Furthermore, by using relaxed scan the flexibility of the other global coordinates are, at least partially, taken implicitly into account. The absorption and later energy relaxation processes were rationalized at CASSCF//CASPT2 level to identify the critical features along the PESs, which are determining the global photochemical properties. The isomerization process was followed along the lowest and most representative ¹(n–π*) and ¹(π–π*) states, which can be easily populated by light absorption. The relaxation along the ¹(π–π*) state results in an almost barrierless deactivation pathway (barrier of ca. 0.1 eV) that leads to a crossing region with the ground state and hence to isomerization. The ¹(n–π*) state appears clearly destabilized as compared to natural CC. The latter is a most desired occurrence, since it leads to the dominant population of the ¹(π–π*) state that is characterized by a more accessible and facile isomerization. Furthermore, and in sharp contrast with natural CC, the population of the ¹(π–π*) channel is always favorable, and whatever the polarity of the medium, leading to a consistent dominance of photoisomerization over fluorescence. The almost barrierless PES should also be consistent with a rather fast process, occurring in the ps timescale. This allows the production of a more efficient photoswitch, especially functional in complex inhomogeneous biological environments, such as lipid bilayers.

Our results allow to rationalize on the one side the observed experimental evidences and on the other to clearly point to the usefulness of a rational design approach that is aimed to induce opportune chemical modification of available switches to allow tuning and controlling their photophysical and photochemical properties. This is furthermore reinforced by the increased TPA absorption that could allow overcoming the necessity of relying to UV light absorption.

In the future we plan to extend the present study, on the one side to determine by time-resolved spectroscopy the lifetime of the dominant states involved in the photoisomerization, and on the other side to model the behavior in presence of biological environments, such as lipid bilayers mimicking cellular membranes resorting to multiscale hybrid approaches.

Computational methodology

Different levels of theory have been used in, particular CASSCF//CASPT2^25,26 approaches have been considered to explore the excited states PES landscape and hence characterize the photochemistry of our compound.

As a first step the ground state geometry has been optimized at MP2 level. Subsequently, this geometry was used to compute the absorption spectrum as vertical excitations using either B3LYP²⁷ and CAM-B3LYP²⁸ functionals in the TD-DFT formalism. Note that DFT optimized Franck–Condon geometries provided less accurate excitation energies, pointing to the subtle coupling between structural and electronic effects. The nature of the excited states have also been determined using NTO formalisms.²³ On top of the MP2 optimized geometry wavefunction calculation have also been performed: MS-CASPT2//SA(4)-CASSCF^25,26 level of theory was used, firstly performing CASSCF calculation including 4 averaged states (from S₀ to S₃), followed by a multistate 2nd order perturbation theory to the CASSCF wavefunction. As can be seen in the ESI,† four different active spaces were tested, in all cases n orbital and different π and π* orbitals were included. The 10 electrons in 8 orbitals (10,8), 10 electrons in 9 orbitals (10,9), 12 electrons in 10 orbitals (12,10) and 14 electrons in 12 orbitals (14,12) were used. In all cases the π* orbital centered on the C=C_pyrone was excluded from the active space due to inconsistencies in the wavefunction and the appearance of intruder charge transfer states. This choice is also corroborated by TD-DFT calculations, since this orbital does not appear as a relevant in any of the excited state expansion. All the active spaces predicted a bright S₀ to S₂ vertical transition and a dark S₀ to S₁ state. This fact is coherent with what is found at TD-DFT level in gas phase where the ¹(n–π*) transition corresponds to S₁ and S₂ presents a ¹(π–π*) character.

Hence, as a compromise between accuracy and required computational cost, the photochemistry of cyclocurcumin was studied using the (10,9) active space. In particular, the S₁¹(n–π*) and S₂¹(π–π*) states identified at Franck–Condon were optimized at CASSCF level, reaching the respective minima whose diabatic nature was confirmed by analyzing the respective molecular orbitals. Starting from these structures, relaxed scans along the dihedral angle optimizing both S₁ and S₂ states were performed freezing the dihedral at the desired value and relaxing along all the other coordinates. In addition, the same procedure at TD-DFT level of theory using CAM-B3LYP functional was also performed. In case of explicit micro-solvent pathway, this was computed adding two water molecules and relaxing in the ¹(π–π*) state. The choice of including two water molecules was based on the analysis of a 500 ns classical molecular dynamic simulation in which our chromophore represented by generalized amber force field²⁹ was placed in a periodic water box. The analysis of the radial distribution function around the carbonyl oxygen revealed that only two solvent molecules were, in average, interacting with the chromophore.

On the optimized CASSCF structures, single point multi-state CASPT2 (MS-CASPT2) and extended multi-state CASPT2 (XMS-CASPT2)³⁰ were performed to include the necessary dynamic electron correlation. For those calculations, an imaginary shift of 0.2 a.u. without IPEA was applied to avoid the influence of intruder states.

Since TD-DFT is able to provide a qualitatively correct description of the PES landscape in vacuo when using CAM-B3LYP,²⁸ the effect of different solvents have been included at this level of theory via the PCM in state specific equilibrium conditions within the integral equation formalism variant (IEFPCM).^31,32 To this aim, the obtained CASSCF geometries were computed by single point calculations with different solvents including water, ethanol, dimethyl sulfoxide, chloroform, and cyclohexane.

In the ¹(π–π*) pathways, an extra point at 100 degrees was obtained by TD-DFT to ensure the descendent PES depicted by the CASSCF points, yielding in all cases to a quasi-degeneracy region.

For all calculations, the 6-31G* basis set was used.³³ CASSCF and CASPT2 calculations have been performed using the OpenMolcas^34,35 suite of programs while DFT and TD-DFT have been obtained employing the Gaussian16 software.³⁶

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge University of Lorraine, CNRS and the European Regional Development Funds (Programme opérationnel FEDER-FSE Lorraine et Massif des Vosges 2014-2020/“Fire Light” project: “Photo-bio-active molecules and nanoparticles”) for financial support. JP acknowledges the French Ministry of Higher Education, Research, and Innovation for his PhD grant. MS-CASPT2 and TD-DFT calculations were performed on the LPCT local computing cluster and at the computing center of the Université de Lorraine (Explor) under the project “Dancing under the light”.

References

1. M. D. Cas and R. Ghidoni, Nutrients, 2019, 11, 2147.
2. K. I. Priyadarsini, Molecules, 2014, 19, 20091–20112.
3. V. Kuptniratsaikul, P. Dajpratham, W. Taechaarpornkul, M. Buntragulpoontawee, P. Lukkanapichonchut, C. Chootip, J. Saengsuwan, K. Tantayakom and S. Laongpech, Clin. Interventions Aging, 2014, 9, 451–458.
4. R. C. Reddy, P. G. Vatsala, V. G. Keshamouni, G. Padmanaban and P. N. Rangarajan, Biochem. Biophys. Res. Commun., 2005, 326, 472–474.
5. F. Mazzolani and S. Togni, Clin. Ophthalmol., 2013, 7, 939–945.
6. L. Wright, J. Frye, B. Gorti, B. Timmermann and J. Funk, Curr. Pharm. Des., 2013, 19, 6218–6225.
7. B. B. Aggarwal and K. B. Harikumar, Int. J. Biochem. Cell Biol., 2009, 41, 40–59.
8. S. Hewlings and D. Kalman, Foods, 2017, 6, 92.
9. L. Vera-Ramirez, P. Pérez-Lopez, A. Varela-Lopez, M. Ramirez-Tortosa, M. Battino and J. L. Quiles, BioFactors, 2013, 39, 88–100.
10. Y. Li, M. Toscano, G. Mazzone and N. Russo, New J. Chem., 2018, 42, 12698–12705.
11. K. Kim, J. J. Kim, Y. Jung, J. Y. Noh, A. S. Syed, C. Y. Kim, M. Y. Lee, K. M. Lim, O. N. Bae and J. H. Chung, J. Nat. Prod., 2017, 80, 196–200.
12. M. Fu, L. Chen, L. Zhang, X. Yu and Q. Yang, Int. J. Mol. Med., 2017, 39, 1164–1172.
13. T. Ngo, K. Kim, Y. Bian, G. J. An, O. N. Bae, K. M. Lim and J. H. Chung, J. Funct. Foods, 2019, 61, 103462.
14. R. Adhikary, C. A. Barnes, R. L. Trampel, S. J. Wallace, T. W. Kee and J. W. Petrich, J. Phys. Chem. B, 2011, 115, 10707–10714.
15. M. Marazzi, A. Francés-Monerris, M. Mourer, A. Pasc and A. Monari, Phys. Chem. Chem. Phys., 2020, 22, 4749–4757.
16. C. García-Iriepa, M. Marazzi, L. M. Frutos and D. Sampedro, RSC Adv., 2013, 3, 6241–6266.
17. M. M. Lerch, M. J. Hansen, G. M. van Dam, W. Szymanski and B. L. Feringa, Angew. Chem., Int. Ed., 2016, 55, 10978–10999.
18. C. Ash, M. Dubec, K. Donne and T. Bashford, Lasers Med. Sci., 2017, 32, 1909–1918.
19. J. Pecourneau, R. Losantos, A. Monari, S. Parant, A. Pasc and M. Mourer, ChemRxiv, 2021 DOI:10.26434/chemrxiv.14236454.v1.
20. D. Sampedro, A. Migani, A. Pepi, E. Busi, R. Basosi, L. Latterini, F. Elisei, S. Fusi, F. Ponticelli, V. Zanirato and M. Olivucci, J. Am. Chem. Soc., 2004, 126, 9349–9359.
21. C. Garcia-Iriepa, M. Gueye, J. Leonard, D. Martinez-Lopez, P. J. Campos, L. M. Frutos, D. Sampedro and M. Marazzi, Phys. Chem. Chem. Phys., 2016, 18, 6742–6753.
22. M. Albota, D. Beljonne, J. L. Brédas, J. E. Ehrlich, J. Y. Fu, A. A. Heikal, S. E. Hess, T. Kogej, M. D. Levin, S. R. Marder, D. McCord-Maughon, J. W. Perry, H. Röckel, M. Rumi, G. Subramaniam, W. W. Webb, X. L. Wu and C. Xu, Science, 1998, 281, 1653–1656.
23. R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777.
24. T. Etienne, X. Assfeld and A. Monari, J. Chem. Theory Comput., 2014, 10, 3906–3914.
25. K. Andersson, P. Å. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488.
26. K. Andersson, P.-A. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218.
27. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
28. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
29. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
30. T. Shiozaki, W. Gyroffy, P. Celani and H. J. Werner, J. Chem. Phys., 2011, 135, 081106.
31. B. Mennucci, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 386–404.
32. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
33. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
34. F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541.
35. I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci and H. P. Hratchian, GAUSSIAN, Gaussian, Inc., Wallingford CT, 2016.

---

Footnote

† Electronic supplementary information (ESI) available: Benchmark of different active spaces at the CASSCF level, CASSCF orbitals in the (10,9) active space, XMS-CASPT2 energy profiles, cyclohexane ¹(π–π*) pathway and all solvent pathways at the ¹(n–π*) state. See DOI: 10.1039/d1cp01224j

---