Computational exploration of heterometal substitution into the decaniobate framework, [Nb₁₀O₂₈]⁶⁻

Abstract

The factors governing the substitution of group 4B–12B metals into the decaniobate framework are explored using density functional theory in order to ascertain whether (1) recently isolated [MNb₉O₂₈]^x− clusters are kinetic or thermodynamic products, (2) density functional theory is a sufficient level of theory to accurately predict substitution patterns in polyoxometalates where ion pairing and other effects may operate, and (3) it can be used to guide future synthetic efforts. Computations using restricted, unrestricted and open-shell density functional theory at PBE0/def2-tzvp were found to correctly predict substitution patterns in known clusters, and were subsequently used to calculate the relative energies of a large series of [MNb₉O₂₈]^x− clusters, to reveal trends and suggest potential synthetic approaches. OPBE/def2-tzvp correctly predicted favoured spin states of known substituted decametalates.

---

1 Introduction

Polyoxometalates (POMs) are generally defined as polyoxoanions of the group 5B and 6B elements V, Nb, Ta, Mo and W in their highest oxidation states.^1–4 These discrete metal oxide clusters exhibit a great structural diversity which is reflect by an equally diverse set of chemistries. However, whereas V, Mo and W POMs are relatively well-explored, until quite recently only a handful of Nb and Ta POMs were known.⁵ For example, [Nb₂₀O₅₆]⁶⁻ and [Ta₁₀O₂₈]⁶⁻ – reported in 2006⁶ and 2013,⁷ respectively-were only the third isopolyoxoniobate and second isopolyoxotantalate ever isolated.

This is likely due to practical reasons – while water-soluble monomeric oxide species of vanadium, molybdenum and tungsten are commercially available and readily speciate in response to changes in pH and concentration, this is not the case for tantalum and niobium. For these two elements syntheses have typically started by dissolution of the anhydrous oxides in molten alkali hydroxides or carbonates,^8,9 or by slow, but difficult to reproduce or scale up, hydrolysis of their penta-ethoxides.¹⁰ The discovery of hydrous niobium and tantalum oxides – niobic and tantalic acid – as being substantially more reactive starting materials than the corresponding anhydrous oxides has, together with the use of non-coordinating ammonium counterions, led to the renaissance that the field presently is undergoing,⁵ but syntheses still typically take place under hydrothermal conditions, where subtle manipulation of the reaction is challenging, although microwave methods have also been developed.¹¹ The one-pot nature of the process also requires all starting materials to be compatible, and as hydrothermal reactions are run in a autogenic pressure vessel, following the progress is difficult. Further complications stem from the difficulty in analysing the product mixture without work-up, and it appears that electrospray ionisation mass spectrometry is the method of choice for this, although the results can be ambiguous unless elements with a wide range of naturally abundant isotopes are present to aid assignment of the signals.¹²

Nonetheless, there is a rapidly growing body of work on the synthesis of novel polyoxoniobates. There are a few key structural motifs that recur among transition metal substituted polyoxoniobates. These are the Lindqvist ion ([M^z_xNb_6−xO₁₉]^(13−z)−),^13–15 the decaniobate ion ([M^z_x=1–2Nb_10−xO₂₈]^{(11−x·z)−}),^10,16–20 and the [M^xNb₁₀O³²]^(14−x)−,^20,21 and the [M₂(OH)₄Nb₁₀O₃₀]⁸⁻ ions.^20,22 In contrast, incorporation of tetrahedral p-block element centres tends to give Keggin-like ions.^16,23–25

The decaniobate [Nb₁₀O₂₈]⁶⁻ framework in particular has proven to be a useful scaffold for incorporating transition metals into a niobate cluster,^10,16–20 and is particularly interesting as, in contrast to V(V), W(VI) and Mo(VI), niobium is comparatively inert towards reduction. Redox-active, alkali-sensitive transition metals can thus be isolated in a more inert polydentate-ligand-like scaffold.

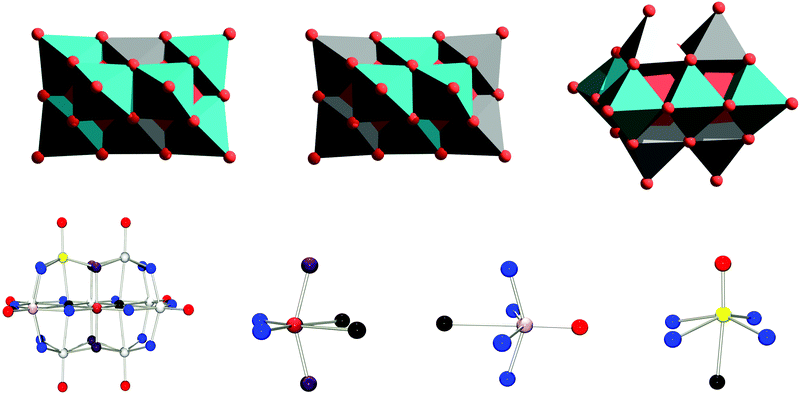
To date, Ti^IV, Cr^III, Mn^III, Fe^III, Co^II, Ni^II and Rh(III) have been inserted into the decaniobate framework to yield [M^zNb₉O₂₈]^(11−z)−.^17–20 In all cases the locus of substitution is the central position a (see Fig. 1), which lacks any terminal oxygen sites, so that only isomer A is obtained. No examples of substitution into sites b or c in niobates have been experimentally isolated. The latter type of substitution presents particular challenges in terms of identification and purification, as where there are only two equivalent a metal sites, there are four b and four c metal sites, making unambiguous characterisation via single crystal X-ray diffractometry challenging, especially for cases where the heterometal is similar to niobium in terms of electron density even where a single product can be successfully isolated and crystallised. It is also important to highlight that none of the sites have perfectly octahedral, or even tetragonal, environments, but are all distorted in different ways. The coordination numbers of in particular sites b and c are better considered as being closer to five than to six, making these sites more similar to square pyramidal sites.

Fig. 1 The distinct metal sites are highlighted in grey in the polyhedral representations. Top: from left to right, sites a, sites b and sites c. [M^zNb₉O₂₈]^(11−z)− isomers in which a single a, b or c site is occupied by a heteroatom are denoted A, B or C, respectively. Bottom: from left to right, the decaniobate ion, [Nb₁₀O₂₈]⁶⁻, drawn as ball and stick. Niobium sites a, b and c are in brown, pink and yellow, respectively. Oxygen μ₆ sites shown in black, μ₃ in violet, μ₂ in blue and terminal oxygen sites shown in red. The (from left to right) a, b and c sites in the decaniobate ion are also shown as isolated niobium atoms surrounded by oxygen atoms, to highlight their distortion from octahedral and tetragonal structures.

The use of computational methods such as density functional theory (DFT) to supplement experimental work is thus very attractive as it allows for the testing of hypotheses and selection of target molecules before engaging in time-consuming and often challenging experimental work, and there are efforts focussing on searches for doped solid state structures incorporating niobium emerging in the literature.^26,27 In the present case computation can easily be used to predict the most stable isomer, and although it won't answer whether a compound will definitely form – since other, more stable structural motifs are possible – it does offer a route to informing synthetic work as to which targets are likely to be worth focusing on. While there are examples in the literature of the use of DFT to gauge the relative energies of substitution isomers of specific polyoxometalates, this is the first systematic study.

2 Computational details

All structures were optimised at PBE0²⁸/def2-tzvp²⁹ with implicit solvation (water) using the polarizable continuum model (PCM)³⁰ in Gaussian 09D Rev. 01 (G09D) unless otherwise specified.³¹ Initial guesses for the Hartree–Fock wavefunction for spin unrestricted and restricted-open shell computations were generated using fragment guesses as implemented in G09D.

When self-consistent field (SCF) convergence was difficult to achieve, structures were first pre-optimised using looser convergence criteria; otherwise the default settings in G09D were used throughout. All structures involved in the study have the general empirical formula [M^zNb₉O₂₈]^(11−z)−.

Local structural minima were confirmed through normal mode analysis. The crystal structure of [Nb₁₀O₂₈]⁶⁻,³² was used as the starting point in the construction of isomer geometries.

3 Results and discussion

3.1 Exchange–correlation functional and basis set

Accurate density functional theory calculations rely on the judicious choice of a suitable exchange and correlation (XC) functional. The PBE0 XC functional in conjunction with the def2-tzvp basis set has previously been found to produce structures that agree well with experimentally determined solid state structures.³³ In addition, this level of theory has been used to predict ¹⁷O NMR spectra,³³ and to determine relative protonation energies³⁴ in polyoxometalates.

However, to confirm whether PBE0 is an XC suitable for computation of isomerisation energetics too, we investigated the performance of a selection of XC functionals, viz. PBE,³⁵ OPBE,^35,36 BP86,^37,38 B3LYP,^39,40 B3PW91,^39,41 PBE0,²⁸ and M06.⁴² The performances of the OPBE and PBE0 functionals were of particular interest, as the former has been suggested to be able to qualitatively accurately discriminate between different spin configurations^43,44 and the latter has been shown to yield structures that agree well with experiment.³³ However, as there are no experimental relative isomer energies that can serve as reference, we compared the XC functionals with one another for consistency for the singlet [TiNb₉O₂₈]⁷⁻ system. Single-point calculations at PW6B95-D3⁴⁵/def2-qzvp on PBE0/def2-tzvp structures were also included, as this has been demonstrated as an accurate functional for general isomerization energies.⁴⁶

It is clear from Fig. 2 that OPBE yields relative isomer energies that are consistently considerably lower than those from the other XCs investigated, which only vary between one-another in isomerisation energies by ca. one kcal mol⁻¹ or less, which is within the estimated margin of error of the method, considering that the computations do not account for specific solvation interactions and ion pairing. The fitted hybrid functional M06 is also an outlier, in that it predicts isomer B to be slightly more stable than isomer C, whereas all the other functionals predict isomer C to be more stable than B. These two functionals were therefore ruled out and not considered further. Pure DFT functionals gave somewhat lower energies than hybrid functionals, but the same trends were obtained for both types of functionals. Notably, PBE0/def-tzvp and single-point calculations using PW6B95-D3/def2-qzvp using the PBE0/def2-tzvp structure gave almost identical energies.

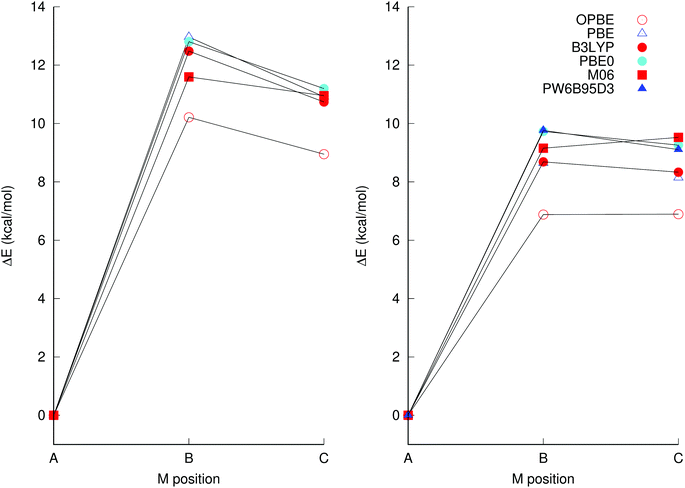Fig. 2 Energies of [TiNb₉O₂₈]⁷⁻ isomers B and C relative to A, the latter has been isolated experimentally, using the (left) def2-svp and (right) def2-tzvp basis sets in conjunction with implicit solvation through PCM. The structures were optimised using the same basis set and XC as the energies were calculated at, with the exception of the PW6B95D3/def2-qzvp calculation which used the PBE0/def2-tzvp structure. Additional XC and basis set combinations are available in Table S1 in the ESI.†

Using a specific XC, the two basis sets def2-svp and def2-tzvp give relative energies for the isomers that differ by 2 kcal mol⁻¹ or more between the basis sets, so that computation using at least def2-tzvp is required. Absolute and relative energies of [TiNb₉O₂₈]⁷⁻ at different levels of theory, including additional XC, are provided as ESI† (Table S1).

Given that PBE0 has worked well in the past,³³ and that results obtained with this functional do not differ in a meaningful way from the other functionals investigated (with the two notable exceptions above), in conjunction with the attraction of it being an “ab initio” functional,⁴⁷ the combination of PBE0 and def2-tzvp with implicit solvation through PCM was chosen for all subsequent computations.

3.2 Energetics of spin multiplicity in isomer A

The energies of different electron configurations of isomer A of a selection of [M^xNb₉O₂₈]^(11−x)− (M = Mn(III), Fe(II/III), Co(II/III), Ni(II), Ru(II/III), Rh(III), Pd(II/IV), Ir(III), Pt(IV)) species were computed using both OPBE and PBE0 in order to see whether there was any disagreement between the methods (see Table 1, and Table S5 in the ESI†). While both XC functionals found the same spin configuration to be the most stable one in a majority of cases, different spin multiplicities were predicted for Co(II), Co(III) and Ni(II). In the cases of Co(II) and Ni(II) PBE0 favoured the low-spin configurations, whereas OPBE favoured the high-spin ones. This is unexpected, as hybrid functionals such as PBE0 generally favour high-spin configurations, and pure DFT functionals like OPBE favour low-spin configurations.⁴⁸ For Co(III), however, OPBE favoured the low-spin configuration as expected whereas PBE0 favoured the high-spin one, although OPBE only predicts a difference of 0.09 kcal mol⁻¹ in favour of the low-spin state, which is well within the margin of error for the method.

Table 1 Comparison between the performance of different exchange correlation functionals in predicting the correct spin state. All computations used the def2-tzvp basis set and the PCM solvation model

Species	Experiment	PBE0	OPBE
	S calc	Predicted S^a	Predicted S
a Spin state which has lower energy for isomer A using that method.
[Fe^IIINb9O28]^8−	2.5	2.5	2.5
[Mn^IIINb9O28]^8−	2.0	2	2
[Co^IINb9O28]^9−	1.9	0.5	1.5
[Ni^IINb9O28]^9−	1.2	0	1

---

Here, however, experimental data is available for comparison. Both [Ni^IINb₉O₂₈]⁹⁻ (μ_eff = 3.2;¹⁸S_calc = 1.2) and [Co^IINb₉O₂₈]⁹⁻ (μ_eff = 4.8;¹⁹S_calc = 1.9) have been isolated, and while S_calc ignores the orbital angular momentum contribution to the total magnetic moment, the data suggest that in both cases the high-spin configurations are the more stable ones. OPBE thus predicts the correct spin state for both, whereas PBE0 – unexpectedly, given the normal bias of hybrid functionals towards high-spin states – fails.

For [Fe^IIINb₉O₂₈]⁸⁻ and [Mn^IIINb₉O₂₈]⁸⁻ both XC functionals predict that the high-spin configuration is the most stable one, in agreement with experimental data (μ_eff = 5.9; S_calc = 2.5 for Fe(III); μ_eff = 4.8; S_calc = 1.9 for Mn(III)).¹⁸

While the prediction by OPBE is qualitatively correct regarding the lower energy spin state, it isn't necessarily quantitatively reliable in terms of relative isomer energies. Conversely, while PBE0 fails to predict the lower energy spin state qualitatively, it does not necessarily imply that PBE0 does not provide correct energy differences between isomers with the same spin state, something which OPBE may not be capable of based on the significantly different relative isomer energies seen for the singlet molecule [Ti^IVNb₉O₂₈]⁷⁻. All further computations were thus done at the PBE0/def2-tzvp level in the interest of maintaining the same model chemistry as in earlier studies.^33,34

3.3 Energetics of known structures

First investigated was whether the method would predict isomer A to be the most favoured one for M = Ti^IV, Cr^III (μ_eff = 3.8; S_calc = 1.5), Mn^III (μ_eff = 4.9; S_calc = 2.0), Fe^III (μ_eff = 5.9; S_calc = 2.5), Co^II (μ_eff = 4.8; S_calc = 1.9), Ni^II (μ_eff = 3.2; S_calc = 1.2), and Rh^III as only isomer A of all these complexes have been crystallographically characterised (see Fig. 3A).^17–20 Isomer A was found to be more favoured by 9.26 (Ti(IV)), 42.39 (Cr(III), S = 3/2), 22.96 (Mn(III), S = 2), 27.94 (Fe(III), S = 5/2), 15.15 (Co(III), S = 3/2), 53.46 (Ni(III), S = 1), and 48.95 kcal mol⁻¹ (Rh(III)), respectively, relative to the second-most stable isomer. For all the isolated species the A isomer is thus shown to be the most stable one, in line with experimental observations. This suggests that isomer A is the thermodynamically favoured product in these cases, which is unsurprising given that the syntheses involve high temperatures and long reaction times.

Fig. 3 The d-block elements. A (top): [M^xNb₉O₂₈]^(11−x)− showing in green which elements for which isomer A has been isolated and characterized crystallographically. B (bottom): Predicted [M^xNb₉O₂₈]^(11−x)− isomer stabilities: where isomer A is the lowest energy isomer (green), where it is the only isomer (blue) and where it is the least stable isomer (red). The different-coloured dots in the top right corner indicate that there are oxidation states for which the behaviour is different. V(V), Co(III), Mo(VI), Ru(III) and Pd(IV) are shown – other oxidation states for these elements have different stabilities (see main text).

Having confirmed that the method predicted the correct isomer for the known compounds, next to be investigated were trends for a wider selection of d-block elements, the results of which are summarized in Fig. 3B, and Tables S2–S4 (see ESI†).

3.4 Group 4–6 complexes, and the impact of oxidation state on V, Mo and W complexes

A majority of the elements in this group are metals found together with polyoxometalates. Here, [Ti^IVNb₉O₂₈]⁷⁻ (singlet),¹⁷ and [Cr^IIINb₉O₂₈]⁸⁻ (quartet) have been isolated.¹⁹ An additional Cr(III)-functionalised niobate species is known; however, it is not isostructural with the decaniobate ion and has an empirical formula of [Cr^III₂(OH)₄Nb₁₀O₃₂]⁸⁻.²² It is important to note that both [Ti^IVNb₉O₂₈]⁷⁻ and [Cr^IIINb₉O₂₈]⁸⁻ are stable over a wider pH range than [Nb₁₀O₂₈]⁶⁻, demonstrating how heterometal substitution can be used to confer desired properties.

For M = Ti(IV), V(V), Zr(IV), Nb(V), Mo(VI), Hf(IV), Ta(V) or W(VI), isomers A, B and C were optimised using spin-restricted DFT as the corresponding species are diamagnetic (see Tables S2–S4 in the ESI†). The geometries of the titanium(IV) containing isomers are shown in Fig. 4.

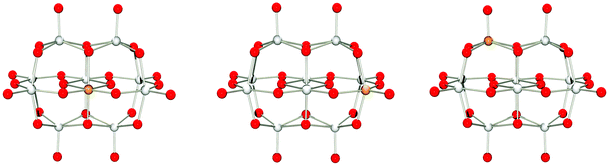Fig. 4 Isomers A, B and C (left to right) of [TiNb₉O₂₈]⁷⁻ optimized at PBE0/def2-tzvp with implicit solvation through PCM.

For the elements in group 4 – Ti(IV), Zr(IV) and Hf(IV) – isomer A is favoured, with the energy by which is it favoured increasing with the period (see Fig. S1–S4 in the ESI†). In spite of this, only the Ti(IV) complex has been isolated,¹⁷ but there is thus potential for other group IV complexes to be isolated. In the case of Ti(IV), introduction of this element increases the base tolerance of the decametalate,^49,50 and makes the charge of the cluster more negative.

In group 5, which comprises V(V), Nb(V) and Ta(V), isomer A is favoured for Ta(V) by almost 3 kcal mol⁻¹ over the second most stable isomer (B), but not for V(V), where isomer C is favoured by 7 kcal mol⁻¹, and isomer B is favoured by 4 kcal mol⁻¹ over isomer A (see Fig. 5). No examples of a Ta or V substituted decametalate structure is known, but computations here suggest that it may be possible to isolate isomer A of [Ta^VNb₉O₂₈]⁶⁻ Vanadium is known to form Kegginate and other structures with niobium, however.^24,25,51

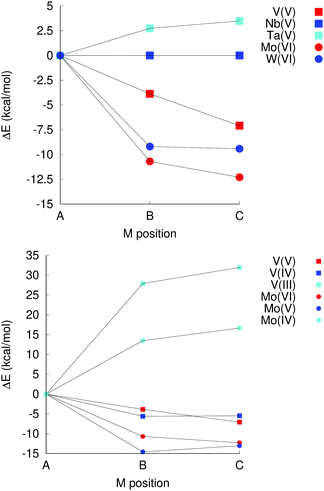Fig. 5 Left: Relative isomer energies for group 5B and 6B elements. Right: Impact of reduction on isomer energies in [M^xNb₉O²⁸]^(11−x)−; M = V or Mo.

For the elements in group 6 – Cr(III), Mo(VI) and W(VI) – the most stable isomer according to computation is A only in the case of Cr(III), with isomer C being weakly favoured over isomer B for Mo(VI) and W(VI), and significantly more stable than isomer A. [Cr^IIINb₉O₂₈]⁸⁻ is also the only one of these species that has been isolated experimentally.

The impact of oxidation states was also investigated. In [Nb^IIINb₉O₂₈]⁸⁻, there is a exceedingly weak (ca. 0.02 kcal mol⁻¹) and probably not significant bias in favour of isomers B and C, which in [Nb^IVNb₉O₂₈]⁷⁻ decreases to 5 kcal mol⁻¹ for isomer C over A, which in turn is more stable by 1 kcal mol⁻¹ than isomer B. These differences are significantly smaller than any realistic appreciation of the inherent uncertainty in the computational approach. There is thus no particular preference in terms of which site gets reduced in the decaniobate ion.

For V and Mo, however, reduction leads to a change in preferred isomer. Changing the oxidation state from V(V) to V(III) leads to a significant bias, 28 kcal mol⁻¹ in favour of isomer A instead of C as for V(V) or B as for V(IV) (Fig. 5). Similarly, while the most stable isomer of [Mo^VINb₉O₂₈]⁵⁻ is isomer C, isomer A is the most stable one for [Mo^IVNb₉O₂₈]⁷⁻. Neither species has ever been isolated; however, this observation suggests a potential synthetic approach to isomer A of [V^VNb₉O₂₈]⁶⁻ and [Mo^VINb₉O₂₈]⁵⁻ that involves introduction of V(III) or Mo(IV), followed by oxidation. Isomer A is never the preferred isomer for W(IV), W(V) or W(VI), but the difference in energy between the different isomers decreases on reduction, albeit not as dramatically as for V or Mo. This decrease in the stability of metal oxide units with terminal multiply-bonded oxygen atoms when going to lower oxidation states is consistent with the reasoning behind the oxo wall phenomenon,⁵² where additional electrons populate anti-bonding orbitals, although the coordination numbers of the metal sites are lower than six for sites b and c, even though the geometries of the sites are different from the tetragonal one (Fig. 1).

Substitution of niobium for a heterometal also distorts the [Nb₉O₂₈]¹¹⁻ framework. The energies of the [Nb₉O₂₈]¹¹⁻ scaffolds obtained by deleting on niobium atom from sites a, b or c in the decaniobate ion, [Nb₁₀O₂₈]⁶⁻ were compared with the energies of the scaffolds obtained by deleting vanadium in the V(V) and V(III) isomers (see Table S6 in the ESI†). For V(V) the energies of the scaffolds were all positive compared to the corresponding decaniobate scaffold, whereas the scaffolds from isomers A and C of the V(III)-compound were negative. That is, the niobate-frameworks with V(III) are relaxed relative to those with Nb(V), in the case of isomer A with V(III) by 104 kcal mol⁻¹. The scaffold from isomer B with V(III) was in contrast higher than the corresponding decaniobate scaffold by 590 kcal mol⁻¹. These energies bear little resemblance to the relative stabilities of the V(III) isomers, and are thus of limited qualitative use. In spite of this it is interesting to note that replacing Nb(V) with V(V) induces strain in the niobate framework, whereas replacing Nb(V) with V(III) relaxes this in isomers A and C.

3.5 Group 7–12 complexes

In this group [M^xNb₉O₂₈]^(11−x)− with M = Mn(III), Fe(III), Co(III), Ni(II) and Rh(III) have been isolated. Notably, all of these species have lower oxidation states than Nb(V), leading to an increase in the negative charge of the molecule on substitution. For all the known species, computations predict that the isolated isomer A is the most stable one, which would indicate that the isolated species are the thermodynamic products.

This is part of a broader trend, where all period four d-block elements in this group – Mn(II/III), Fe(II/III), Co(III) and Ni(II) – favour isomer A by 16 kcal mol⁻¹ or more (see Tables S2–S4 in the ESI†). No stable isomer C for [Fe^IINb₉O₂₈]⁹⁻ could be optimised, with the Fe(II) site becoming trigonal planar, with one terminal oxygen site. No isomer B or C could be optimised for Co(II), Cu(II) and Zn(II). For Co(II) and Zn(II), the heteroatom adopts a tetrahedral geometry in isomer B, with a terminal oxygen site. In the C isomer, Co(II), Cu(II) and Zn(II) all adopt a trigonal planar geometry with a terminal oxygen site. The resulting heteroniobate structures are thus no longer decametalate isomers, which is consistent with the idea of additional d-block electrons having a destabilizing influence on sites with terminal oxygen atoms. See Fig. S5–S11 in the ESI,† for these geometries.

Apart from Tc(VII), which has a much higher oxidation state than the other elements and where isomer C is favoured, all period five element in this group favour isomer A. Isomer C for Ru(II) optimises to give a trigonal planar geometry with a terminal oxygen site for the heteroatom, while Pd(II) adopts a square planar geometry with a terminal oxygen in both isomers B and C. Ag(I) takes on a linear geometry with a terminal oxygen in isomers B and C. These are thus not decametalate structures.

The behaviour in period six varies, with the higher oxidation states Re(VII) and Os(VII) favouring isomers B and C, respectively, but the lower oxidation states Ir(III) and Pt(IV) favouring isomer A. Au(III) adopts a tetrahedral geometry in isomer B and a T-shaped geometry in isomer C, while Hg(II) has a linear geometry in isomer B and a trigonal planar geometry in isomer C. In all cases do the elements occupy distorted octahedral sites in the optimised structures for isomer A.

4 Conclusions

The relative energies of isomers of [M^xNb₉O₂₈]^(11−x)− have been computed. It is interesting to note that while isomers B and C could not be optimised for some elements, isomer A could be optimised for all elements and oxidation states in the study.

There are two potential pitfalls with the computations presented above. Firstly, only the relative energies of the isomers are computed. Alternative structures, such as Kegginates, which may be lower in energy have not been considered. Thus, while the computations herein may suggest that a particular isomer is preferred, experimentally a completely different structure may be obtained due to this being thermodynamically favoured. Secondly, it is also important to note that the computations make predictions about preferred isomers, they do not guarantee that the most stable isomer is stable under conditions where particular starting materials are stable, thus further complicating the design of a synthetic strategy.

In spite of this, these computations do suggest what synthetic targets may be realisable, in addition to presenting a strategy, viz. the use of other oxidation states, to achieve targets that would not otherwise be favoured, and as such can guide synthetic efforts. The availability of a large number of computationally optimised structures can serve as a guide in resolving crystallographically obtained structures by predicting bond distances.

Finally, these computations suggest that the decaniobate derivatives that have been obtained thus far are indeed the thermodynamic products, which means that, perhaps unsurprisingly, there's an active equilibrium present under hydrothermal conditions. However, this raises the tantalising possibility of there being transient species waiting to be discovered – such as the case with [Nb₇O₂₂]^9− 53,54 – or at least captured by reaction with other species.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The author thanks the Kempe Foundation (grant JCK-2029.1) and the Swedish National Science Foundation (grant 2018-07039) for generous support. Computational resources were provided by the Swedish National Infrastructure for Computing at the National Supercomputer Centre via grant SNIC 2020/5-480.

Notes and references

1. M. T. Pope and A. Müller, Angew. Chem., Int. Ed. Engl., 1991, 30, 34–48.
2. J. M. Poblet, X. López and C. Bo, Chem. Soc. Rev., 2003, 32, 297–308.
3. Y.-F. Song and R. Tsunashima, Chem. Soc. Rev., 2012, 41, 7384–7402.
4. S.-S. Wang and G.-Y. Yang, Chem. Rev., 2015, 115, 4893–4962.
5. M. Nyman, Dalton Trans., 2011, 40, 8049–8058.
6. M. Maekawa, Y. Ozawa and A. Yagasaki, Inorg. Chem., 2006, 45, 9608–9609.
7. M. Matsumoto, Y. Ozawa, A. Yagasaki and Y. Zhe, Inorg. Chem., 2013, 52, 7825–7827.
8. W. H. Nelson and R. S. Tobias, Inorg. Chem., 1963, 2, 985–992.
9. W. H. Nelson and R. S. Tobias, Can. J. Chem., 1964, 42, 731–743.
10. E. J. Graeber and B. Morosin, Acta Crystallogr., 1977, B33, 2137–2143.
11. M. A. Rambaran, M. Pascual-Borr'as and C. A. Ohlin, Eur. J. Inorg. Chem., 2019, 3913–3918.
12. C. A. Ohlin, Chem. – Asian J., 2012, 7, 262–270.
13. I. Lindqvist, Arkiv för Kemi, 1953, 5, 247–250.
14. M. Dabbabi and M. Boyer, J. Inorg. Nucl. Chem., 1976, 38, 1011–1014.
15. J.-H. Son, J. R. Wang, F. E. Osterloh, P. Yu and W. H. Casey, Chem. Commun., 2014, 50, 836–838.
16. M. Nyman, F. Bonhomme, T. M. Alam, M. A. Rodriguez, B. R. Cherry, J. L. Krumhansl, T. M. Nenoff and A. M. Sattler, Science, 2002, 297, 996–998.
17. C. A. Ohlin, E. M. Villa, J. C. Fettinger and W. H. Casey, Dalton Trans., 2009, 2677–2678.
18. J.-H. Son, C. A. Ohlin and W. H. Casey, Dalton Trans., 2013, 42, 7529–7533.
19. J.-H. Son, J. R. Wang and W. H. Casey, Dalton Trans., 2014, 43, 17928–17933.
20. J.-H. Son and W. H. Casey, Dalton Trans., 2015, 44, 20330–20333.
21. J.-H. Son and W. H. Casey, Dalton Trans., 2013, 42, 13339–13342.
22. J.-H. Son, C. A. Ohlin and W. H. Casey, Dalton Trans., 2012, 41, 12674–12677.
23. M. Nyman, T. M. Bonhomme, F. Alam, J. B. Parise and G. M. B. Vaughan, Angew. Chem., Int. Ed., 2004, 116, 2847–2852.
24. J.-H. Son, C. A. Ohlin, E. C. Larson, P. Yu and W. H. Casey, Eur. J. Inorg. Chem., 2013, 1748–1753.
25. J.-H. Son, C. A. Ohlin, R. L. Johnson, P. Yu and W. H. Casey, Chem. – Eur. J., 2013, 19, 5191–5197.
26. X. X. Xia, A. Hermann, X. Y. Kuang, Y. Y. Jin, C. Lu and X. D. Xing, J. Phys. Chem. C, 2016, 120, 677–684.
27. M. Ren, S. Jin, D. Wei, Y. Jin, Y. Tian, C. Lu and G. L. Gutsev, Phys. Chem. Chem. Phys., 2019, 21, 21746–21752.
28. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6159.
29. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
30. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
31. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009.
32. C. A. Ohlin, E. M. Villa and W. H. Casey, Inorg. Chim. Acta, 2009, 362, 1391–1392.
33. R. Sharma, J. Zhang and C. A. Ohlin, Phys. Chem. Chem. Phys., 2016, 18, 8235–8241.
34. C. A. Ohlin and M. Pascual-Borràs, Dalton Trans., 2018, 47, 13602–13607.
35. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
36. N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403–412.
37. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
38. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
39. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
40. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
41. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
42. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
43. M. Swart, A. W. Ehlers and K. Lammertsma, Mol. Phys., 2004, 102, 2467–2474.
44. M. Swart, A. R. Groenhof, A. W. Ehlers and K. Lammertsma, J. Phys. Chem. A, 2004, 108, 5479–5483.
45. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667.
46. L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688.
47. M. G. Medvedev, I. S. Bushmarinov, J. Sun, J. P. Perdew and K. A. Lyssenko, Science, 2017, 355, 49–52.
48. S. R. Mortensen and K. P. Kepp, J. Phys. Chem. A, 2015, 119, 4041–4050.
49. E. M. Villa, C. A. Ohlin, J. R. Rustad and W. H. Casey, J. Am. Chem. Soc., 2009, 131, 16488–16492.
50. E. M. Villa, C. A. Ohlin and W. H. Casey, J. Am. Chem. Soc., 2010, 132, 5264–5272.
51. G. Guo, Y. Xu, J. Cao and C. Hu, Chem. – Eur. J., 2012, 18, 3493–3497.
52. H. B. Gray and J. R. Winkler, Acc. Chem. Res., 2018, 51, 1850–1857.
53. E. M. Villa, C. A. Ohlin, E. Balogh, T. M. Anderson, M. D. Nyman and W. H. Casey, Angew. Chem., Int. Ed., 2008, 47, 4844–4846.
54. W. G. Klemperer and K. A. Marek, Eur. J. Inorg. Chem., 2013, 1762–1771.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates and absolute and relative energies of the structures in this study. See DOI: 10.1039/d1cp01092a

---