How does the solvent composition influence the transport properties of electrolyte solutions? LiPF6 and LiFSA in EC and DMC binary solvent†
Received
4th March 2021
, Accepted 6th April 2021
First published on 8th April 2021
Abstract
In this study, we experimentally measured the viscosity, η, and ionic conductivity, σ, of the electrolyte solutions of 1 mol kg−1 of LiPF6 or LiFSA dissolved in the binary mixture solvent of EC and DMC in a temperature range of 288 ≤ T/K ≤ 328 by varying the EC content from 0 to 60 vol%, which translates into the molar fraction of EC of 0 ≤ xEC ≤ 0.7. The diffusion coefficient, D, of each species, Li+, PF6−, FSA−, EC and DMC, was determined by pulse gradient spin-echo NMR. The state of molecules around Li+ was examined using the Raman spectra of the solvents and anions; the quantitative analysis suggests that EC is about twice as much preferred as DMC in the solvation shell at low xEC, while the EC-preference decreases with an increase in xEC. The classical Stokes–Einstein relation still quantitatively holds when evaluating the hydrodynamic radius, rSt, of transporting entities from D and η, in that (i) rSt,EC and rSt,DMC without the solute do not significantly differ from those in the solution; (ii) rSt,Li roughly coincides with the size estimated from the solvation number determined by Raman spectroscopy, which implies that rSt,Li reflects the solvation shell size; and (iii) rSt,anion is close to the static size, suggesting that anions are little solvated. The increase in xEC results in a decrease in rSt for all species, among which anions are most influenced, which is consistent with the view that the highly Li+-solvating EC, with its better dielectric shielding effect than DMC, liberates the anions from Li+, whereby enhancing the anion transfer that positively contributes to the ionic conductivity until the viscosity prevails at high xEC.
1 Introduction
Lithium ion batteries (LIBs) are a daily essential for sustaining our modern civilization because of their use in mobile phones, electric vehicles, smart-grids, spacecraft, etc. Non-aqueous electrolyte solutions, an indispensable component of the LIB, provide the medium through which charge carriers transfer between electrodes. Transport phenomena in an electrolyte solution have hence been a decades-long research subject from the viewpoint of not only the fundamental aspect but also industrial interest. A binary solvent is usually used in LIBs, in which a solvent with a high dielectric constant (e.g., ethylene carbonate, EC) is mixed with another solvent with a low viscosity (e.g., dimethyl carbonate, DMC). The former is considered to play a role in dissociating the cations and anions whereas the latter in enhancing ionic movement.1 Many experimental and theoretical studies have been conducted to fully understand the role of each solvent component. As an example, the self-diffusion coefficients of the solution constituents were determined using pulse gradient spin-echo NMR to investigate the movement of ions and solvent molecules, and discuss how the solvent influences the hydrodynamic size of ions.2–4 As another example, the solvation state of Li+ in mixed solvents has been vigorously investigated using NMR,5–7 Raman/IR7–9 and electro-spray mass spectroscopy,10,11 because the solvent composition in the Li-solvation shell is considered to significantly influence the solid–electrolyte interface formation on the electrodes,11–19 as an important implication for the performance of the LIBs. While the experimental data accumulate, recent theoretical studies call for reassessing the early experimental results. For instance, Borodin et al.20,21 pointed out that different pictures can be drawn, in a somewhat paradoxical manner, about the solvation state of Li+ from the spectroscopic studies cited above, into which the theoretical insights (e.g., the sensitivity of vibrational bands) must be integrated to resolve the inconsistencies. Another issue that motivated us to take on the present study is that, although the recent progress in research has in a way helped the dichotomous controversy subside regarding whether the specific solvation exists or not, e.g., a competition between EC and DMC, in a mixed solvent, only a few experimental studies have pursued the qualitative examination of the extent to which a solvent prevails, if any, over another in solvating Li+, especially as a function of the solvent composition. In addition, we would like to relate the knowledge about the solvation state to other experimentally measurable transport properties, e.g., diffusion coefficient, whereby we can draw a comprehensive picture describing the transport phenomena in non-aqueous electrolyte solutions.
In this study, we focus on the solvent composition dependence of a variety of properties that are experimentally measurable. The systems we deal with are the 1 mol kg−1 solution of LiPF6 and LiFSA (FSA− = bis(fluorosulfonyl)amide, [N(SO2F)2]−) dissolved in the binary solvent EC/DMC while varying the EC-content from 0 to 60% by volume, where the molar ratio of the solute to the total solvent is constant. As a function of the solvent composition, the following properties were examined: the density, viscosity, ionic conductivity, solvation states around Li+ by Raman spectroscopy, as well as the self-diffusion coefficient of the solvent and ions by pulse-gradient spin-echo NMR of 1H, 7Li and 19F. Incorporating into the discussion the insight imparted in the previous experimental and theoretical studies cited above, we examine the transport properties of the electrolyte solutions in terms of the solvation state, ionic dissociation, static and hydrodynamic size of constituent species and so forth.
2 Experimental
2.1 Materials
The solvent and lithium salt (i.e., LiPF6, LiFSA, EC, DMC and GBL), lithium battery grade, were purchased from Kishida Chemical. Electrolyte solutions were prepared in an argon-filled glove box with a dew point below −70 °C to avoid water contamination. EC and DMC were mixed such that the EC content ranges between 0 and 60 vol%, which translates into the molar fraction of EC in the solvent 0 ≤ xEC ≤ 0.7 where xEC is defined later in eqn (2). The solute LiPF6 or LiFSA was dissolved in these solvents to the molality m/mol kg−1 = 1.0, in which the solvent to solute molar ratio is practically constant (cf., eqn (3)). The Raman signal from FSA− interacting with Li+ is overlaid by that from EC. We hence substituted GBL, another cyclic ester having an analogous chemical structure and high permittivity (εr = 39), for EC (εr = 90) in an experiment wherein Raman spectra from FSA− were examined on the basis of the study by Matsuda et al.10 who experimentally proved that EC and GBL have an approximately equal solvating ability, which prevails over DMC (εr = 3) in the Li+-solvation.
2.2 Density
The density, ρ, at T/K = 298 of the solvent (i.e., without a solute) and the electrolyte solution were measured using a pycnometer (nominal volume 10 cm3), the exact inner volume of which is calibrated with deionized and degassed water at the same temperature. The mean of at least two measurements was adopted.
2.3 Raman spectroscopy
A laser Raman microscope (RENISHAW, inVia Reflex, 532 nm green laser, resolution: 2 cm−1) was used for the solvent and solution at room temperature to investigate not only the solvation state of ions but also the conformer composition of DMC. The solution was filled in an air-tight quartz cell in the glove box. The exposure time was 1 s and the scattering spectrum was integrated 60 times. The wavenumber of the Raman shift was calibrated by the spectrum of a Si wafer standard. The spectra were split into each component by fitting with the pseudo-Voigt function; an example is shown in Fig. 2. When converting the peak area into a mole fraction, the activity of Raman intensity (i.e., the change in the Raman scattering factor of each vibrational mode caused by the interaction with an ion) was considered based on the quantum chemistry calculations by Borodin et al.21 The mean of two measurement runs for each sample was adopted.
2.4 Viscosity
The viscosity, η, of the electrolyte was measured using a viscosity meter (BROOK FIELD, DV-IIT) equipped with a CPA-40Z cone plate and a stainless-steel sample cup the temperature of which was controlled by flowing water from a water bath with the same specifications as that used in the conductivity measurements. The apparatus was placed in an open dry chamber with a dew point of <−50 °C to avoid water contamination. The viscosity was measured at 288 ≤ T/K ≤ 328, same as that for conductivity, after waiting for the sample temperature to sufficiently stabilize. The viscosity of the pure solvents without a solute was measured at only T/K = 298, above which it is too low and out-of-range of the apparatus. The apparatus was calibrated at each temperature using five standard oils for viscosity (NIPPON GREASE, JS2.5, JS5, JS10, JS20 and JS50). The mean of two measurements was adopted.
2.5 Ionic conductivity
The specific ionic conductivity, σ, of the electrolyte was measured in a four-electrode cell (EC frontier) in the temperature range of 288 ≤ T/K ≤ 328 by an electrochemical impedance technique using potentiogalvanostat (Ivium, CompactStat.e) equipped with a frequency response analyzer. The cell constant was determined using conductivity standard KCl aqueous solutions. The cell containing about 10 cm3 of solution was assembled and sealed in the glove box, and then, it was immersed in a water bath of which the temperature was measured by the calibrated thermocouples and controlled by a heater and coolant water within an accuracy of ±0.1 K. The cell was equilibrated at each temperature for approximately 20 min prior to the measurements. The alternative current frequency ranges from 150 to 15 kHz with a 5 mVp-0 amplitude, where the phase angle is so close to 0° that only the resistance component was observed. The impedance data were collected three times for 11 points evenly spaced with respect to the logarithm of the frequency, from which the mean of the real part was taken as the solution resistance. The conductivity was calculated from the mean of the obtained solution resistance and cell constant. Two series of measurements and calculation processes were repeated for each electrolyte, the mean of which was taken as the final result.
2.6 Pulsed gradient spin-echo (PGSE) NMR
PGSE-NMR was performed to estimate the self-diffusion coefficient, D, of the solvent molecules, lithium ion and anions using a 400 MHz spectrometer (JEOL, JMTC-400/54/JJ) with probe units adjusted to the nuclide of 1H (400 MHz), 7Li (155 MHz) and 19F (376 MHz). The stimulated echo sequence was used,22 in which a half-sine shaped gradient pulse was adopted.23,24 When the probed nuclide migrates in the duration time, Δ, according to the random walk model, the relative spin-echo intensity, M/M0, is attenuated by25| |  | (1) |
where γ is the gyromagnetic ratio that is unique for each nuclide. To determine the diffusion coefficient, D, from the slope of ln(M/M0), the pulse width of the field gradient, δ, was varied in the range of a few milliseconds while maintaining the interval of two gradient pulses, Δ, to 100 ms and the strength of the field gradient, g, to 0.9 T m−1. An example of the spin-echo intensity profile, where one can confirm good linearity, is shown in Fig. S7 (ESI†). The mean of two to four runs of measurement was adopted.
3 Results and discussion
In the present study, the solvent composition xEC is defined as the fraction of EC in the solvent (i.e., solute excluded) as| |  | (2) |
where Nα is the molar number of solvent, α = EC or DMC. The definition is analogous in Raman spectroscopy wherein EC is replaced by GBL, xGBL. Owing to the similar molecular weights of EC and DMC, the molality in the present study, m/mol kg−1 = 1.0, translates into a practically constant solvent to solute ratio as| |  | (3) |
where LiA = LiPF6 or LiFSA and the constant, f, is introduced for the discussion below. Namely, a total of 11 solvent molecules per LiA are always present either for LiPF6 or for LiFSA, which is convenient for extracting the influence of the solvent composition. Incidentally, the monotonous increase in ρ with an increase in xEC leads to a slight increase in the molarity from ca. 1.0 mol dm−3 at xEC = 0 to ca. 1.1 mol dm−3 at xEC = 0.7 for either salt system.
3.1 Molar volume—static size of the solvent and solute
Fig. 1 plots the volume per mole of solvent, Vm, for the solvent without a solute, 1 mol kg−1 of LiPF6 and 1 mol kg−1 of LiFSA solution as a function of the EC-fraction in the solvent, xEC, at T/K = 298. (N.B. Vm is defined here as the volume per mole of the solvent even for the solution, which simplifies some equations in this section.) Denoting the molar volume of each species, α, as Vm,α, one gets for the solvent (without a solute),| | | Vm = xECVm,EC + (1 − xEC)Vm,DMC | (4) |
| | | = Vm,DMC + xEC(Vm,EC − Vm,DMC), | (5) |
and for the solution of LiA salt, because Vm refers to per mole of solvent,| | 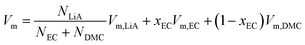 | (6) |
| | | = fVm,LiA + Vm,DMC + xEC(Vm,EC − Vm,DMC), | (7) |
where f is a constant defined in eqn (3). In general, the molar volume of each species, Vm,α, can be a function of xEC (i.e., Vm,α(xEC)). Yet parallel linearity in Fig. 1 suggests that Vm,α is almost constant and additive independent of xEC, or the excess volume is insignificant. The linear optimization of Vm(xEC) for the solvent gives the y-intercept as| | | Vm,DMC/cm3 mol−1 = 83.8 | (8) |
and the slope (Vm,EC − Vm,DMC) cm3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol−1 = −18.9, leading to
mol−1 = −18.9, leading to| | | Vm,EC/cm3 mol−1 = 64.9. | (9) |
These molar volumes of the solvent agree well with the literature.26
 |
| | Fig. 1 Volume of the system per mole of solvent, Vm, as a function of the EC-fraction, xEC, in the solvent at T/K = 298, calculated from the experimentally determined density in Table SI (ESI†). The lines are the result of the linear optimization. cf., eqn (7) and the description that follows. | |
If the excess volume is negligible also for the solution, the difference in Vm between the solvent and the solution corresponds to the molar volume of the solute, which is roughly equal to that of the anion because the static volume of Li+, 1–2 cm3 mol−1, is insignificant. The distance between parallel lines in Fig. 1 roughly yields Vm,PF6/cm3 mol−1 ∼ 50 and Vm,FSA/cm3 mol−1 ∼ 80, which, if considered spherical, translates into the static radius of
The static radius, r0, calculated here is compared with the hydrodynamic Stokes radius, rSt, determined from the transport properties in Section 3.6.
3.2 Raman spectroscopy
3.2.1 Solvent and DMC conformers.
The relevant Raman frequency from each solvent used to examine the Li+-solvation state is summarized in Table 1. We analyzed the signals from not only EC and the major cis–cis (cc) conformer of DMC, but also its minor cis–trans (ct) conformer (see for an example of peak fitting by the pseudo-Voigt function in Fig. 2(a)), which has been ignored in the previous study.8 When calculating the amount of each molecule, such as the fraction, solvation number, etc., the signal activity ratio, as/a0, calculated by Borodin et al. were taken into account.
Table 1 Raman shift (ν0: free solvent and νs: solvent solvating Li+) and signal activity ratio, as/a0
|
|
ν
0/cm−1 |
ν
s/cm−1 |
a
s/a0a |
| Obs.b |
Calc.a |
Obs.b |
Calc.a |
|
Theoretical calculation by Borodin et al. for the cluster ECnDMC4−nLi+.21
Observed in the present study.
|
| EC |
894 |
894 |
904 |
905 |
1.18 |
| DMCcc |
916 |
918 |
934 |
932 |
1.01 |
| DMCct |
860 |
860 |
873 |
875 |
1.19 |
 |
| | Fig. 2 Examples of Raman signal splitting by the pseudo-Voigt function. (a) Solvent without solute at xEC = 0.7 and (b) 1 mol kg−1 LIFSA solution at xEC = 0.7. “DMCct” and “DMCcc” stand for the cis–trans and cis–cis conformer of DMC, and “-0” and “-Li” for the free and solvating solvent, respectively. | |
As shown in Fig. S1(a) (ESI†), in the solvent without the solute, about 3.5% of DMC is in the ct conformer at xEC = 0, which monotonously increases to ca. 6% at xEC = 0.7. Assuming the thermal equilibrium between two conformers, we can calculate their energy difference, Ect − Ecc, as (cf., eqn (S1), ESI†)
| |  | (12) |
The calculated
Ect −
Ecc, also plotted in Fig. S1(a) (ESI
†), decreases from 8.5 at
xEC = 0 to 7 kJ mol
−1 at
xEC = 0.7. Katon
et al.27 experimentally determined the energy difference between these conformers to be 10.9 ± 2.1 kJ mol
−1 in pure DMC (
i.e.,
xEC = 0), which coincides with our results to within their experimental error. In the isolated gas phase,
Ect −
Ecc is theoretically calculated to be 12–13 kJ mol
−1,
7,20,28 which is higher than that in the liquid state estimated in the present study. In the condensed phase, the attraction between the higher dipoles of DMCct than that of DMCcc may stabilize the former from the isolated state. The decrease in
Ect −
Ecc with the increase in
xEC can be also caused by the further stabilization of DMCct relative to DMCcc by interacting with the still more polar EC;
cf., the dipole moment of EC, DMCcc and DMCct is respectively calculated to be 5.68 D, 0.34 D and 3.76 D by Borodin
et al.20 and 5.35 D, 0.29 D and 3.93 D by Seo
et al.7
In the solution, the Raman signals from the solvent solvating Li are clearly observed as shown in Fig. 2(b), which is an example of LiFSA dissolved in the solvent at xEC = 0.7. The addition of the solute significantly changes the fraction of DMC conformers (Fig. S1(b), ESI†). While the fraction of free DMCct remains 3–4%, another 7% of DMC turns into the ct-conformer to solvate Li+, totaling ca. 10% of DMC in the ct-conformer, which can be explained by the further stabilization of DMCct by the strong charge–dipole interaction between Li+ and DMCct. This observation agrees with the previous study by Doucey et al.29 who investigated the LiAsF6 dissolved in pure DMC using IR and Raman spectroscopy. Theoretical calculations also endorse the stabilization of the DMCct upon coordinating Li+ in isolated clusters.7,20,21 The increase in xEC, however, decreases the DMCct fraction bound to Li+ while maintaining the free DMCct fraction almost constant, and therefore, the former goes below the latter at a high xEC. This is presumably caused by two factors: (i) with the increase in xEC, as discussed below, EC expels DMC from the solvation shell into the bulk solvent, in which cc-conformer is more stable, and (ii) the increase in the EC molecules participating in the Li+ solvation renders DMCcc energetically more preferable than DMCct, because the dipoles forced to align by Li+ in the solvation shell repel each other, thereby making the less polar DMCcc favorable by staying in the shell.
3.2.2 Li+ solvation.
The fractions of each DMC conformer as well as of the EC that solvate Li+ in the solution can be converted to the average solvation number, ns, shown in Fig. 3(a). An important remark must be made here to avoid a conceptual confusion about “solvation number”. The quantity, ns, presented here is the “average” solvation number in the sense of the total number of each solvent bound to Li+ divided by the total number of Li+, a fraction of which may be paired with an anion. If we borrow the symbols used in the study by Doucey et al.,29 what is presented here corresponds to n1.
 |
| | Fig. 3 (a) Average number of solvent molecules, ns, solvating Li+ determined by Raman spectroscopy. The quantity, ns, presented here is the average number of each solvent per Li+ in the system. (b) EC to DMC ratio, ns,EC/ns,DMC, in the solvation shell and the EC-preference, PEC/DMC, defined in eqn (13). | |
In the pure DMC solvent, either for the LiPF6 or LiFSA system, about two DMCcc and 0.7 DMCct molecules solvate Li+, totalling 2.7 DMC molecules. A somewhat smaller solvation number of n1 = 2.2, yet still close to ours, is reported for 1.0–1.2 mol dm−3 LiAsF6 dissolved in pure DMC.29 When EC is added in the solvent, both DMC conformers are replaced by EC. Until xEC ≲ 0.25, the number of EC molecules that participate in the solvation exceeds that of DMC replaced by EC, and therefore, the total solvation number increases to 3.3–3.6, whereafter it saturates. For example, at xEC = 0.57, in the LiPF6 system, ns,EC = 2.3 and ns,DMC = 1.1 leading to ns = 3.4 and in the LiFSA system, ns,EC = 2.3 and ns,DMC = 1.0 leading to ns = 3.3. The free Li+ dissociated from the anion is often assumed to be solvated by four solvent molecules. The deficit of ns from four thus alludes to the ion pairing, or in other words, a certain fraction of the solvation shell around Li+ involves one anion. If we assume that exactly four solvent molecules solvate each free Li+, the number of solvent molecules, nIPs, around the ion pair [Li+·A−] can be calculated from ns in Fig. 3(a) and the degree of ionic dissociation, α, given in Fig. 8. The results are shown in Fig. S2 (ESI†), which indicates that approximately 2.5–3.0 solvent molecules are present in the solvation shell when it involves one anion. This observation is consistent with the tetra-coordinated state of Li+ as premised above; namely, the anion expels at least one of the four solvent molecules from the shell. The finding that nIPs values are smaller for LiFSA than those for LiPF6 is also consistent with the greater size of FSA− than PF6− since the former can be bidentate to Li+ with its two bulky SO2F groups on which the negative charge is mainly distributed.
The Raman study by Morita et al.8 suggests that for the 1 mol dm−3 LiPF6 solution (comparable to our case; 1 mol kg−1 = 1.15 mol dm−3) in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC = 1
DMC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume (corresponding to xEC = 0.57), ns,EC = 3.0 and ns,DMC = 1.1, which was reassessed by Borodin et al.21 by considering the Raman activity ratio, as/a0, in Table 1 to find ns,EC = 2.8 and ns,DMC = 1.2. Similarly, Borodin et al. also predicted a result close to that of ours;21 namely, they estimated ns,EC = 1.79–2.13 and ns,DMC = 1.12–1.05 (depending on the functional used in the calculation) by integrating the radial distribution function obtained by the molecular dynamics simulations for the system composed of LiPF6
1 by volume (corresponding to xEC = 0.57), ns,EC = 3.0 and ns,DMC = 1.1, which was reassessed by Borodin et al.21 by considering the Raman activity ratio, as/a0, in Table 1 to find ns,EC = 2.8 and ns,DMC = 1.2. Similarly, Borodin et al. also predicted a result close to that of ours;21 namely, they estimated ns,EC = 1.79–2.13 and ns,DMC = 1.12–1.05 (depending on the functional used in the calculation) by integrating the radial distribution function obtained by the molecular dynamics simulations for the system composed of LiPF6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC
EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC = 1
DMC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, of which the solvent composition corresponds to xEC = 0.5 and the salt concentration is close to that of ours where the solute to solvent ratio is ca. 11 as given in eqn (3). The EC-preference in solvating Li+ over DMC is also suggested in another molecular dynamics simulation of 0.1–1.0 mol dm−3 LiPF6 dissolved in EC
5, of which the solvent composition corresponds to xEC = 0.5 and the salt concentration is close to that of ours where the solute to solvent ratio is ca. 11 as given in eqn (3). The EC-preference in solvating Li+ over DMC is also suggested in another molecular dynamics simulation of 0.1–1.0 mol dm−3 LiPF6 dissolved in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC = 1
DMC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by Tenney et al.30 Bogle et al.6 also conclude, from the chemical shift of 17O NMR, the stronger interaction of EC with Li+ than DMC for the 1 mol dm−3 LiPF6 in the EC/DMC system. Matsuda et al.10 observed that the major cluster assayed by the electro-spray ionization mass spectroscopy (EIMS) from LiClO4 in EC/DMC diluted with methanol was [Li(EC)2]+ with a minor component [Li(EC)3]+, and no DMC was observed in the clusters isolated in vacuo, which testified to the EC preference in the Li+-solvation over DMC. An EIMS study by von Cresce et al.11 proved the EC dominance over DMC and EMC, another acyclic carbonate like DMC, in the clusters reached the TOF spectrometer sampled out of the 1.0–1.2 mol dm−3 solution without dispersing the solvent. This phenomenon is consistent with the quantum chemistry calculations20,21 indicating that, in the isolated state, EC binds to Li+ more strongly than DMC while its energetic advantage diminishes in the clusters surrounded by a matrix of a certain dielectric constant, thereby leaving to some extent a room for DMC to stick to Li+. As explained by Bogle et al.,6 in the EIMS measurements, the cluster loses the weakly bound DMC during traveling in the mass chamber, leaving two or three EC molecules tightly bound. From the chemical shift in NMR and the diffusion coefficient obtained by PGSE-NMR, Yang et al.5 conclude that EC is more strongly bound to Li+ than DMC and DEC in the ternary solvent system where the molar ratio is LiPF6
1 by Tenney et al.30 Bogle et al.6 also conclude, from the chemical shift of 17O NMR, the stronger interaction of EC with Li+ than DMC for the 1 mol dm−3 LiPF6 in the EC/DMC system. Matsuda et al.10 observed that the major cluster assayed by the electro-spray ionization mass spectroscopy (EIMS) from LiClO4 in EC/DMC diluted with methanol was [Li(EC)2]+ with a minor component [Li(EC)3]+, and no DMC was observed in the clusters isolated in vacuo, which testified to the EC preference in the Li+-solvation over DMC. An EIMS study by von Cresce et al.11 proved the EC dominance over DMC and EMC, another acyclic carbonate like DMC, in the clusters reached the TOF spectrometer sampled out of the 1.0–1.2 mol dm−3 solution without dispersing the solvent. This phenomenon is consistent with the quantum chemistry calculations20,21 indicating that, in the isolated state, EC binds to Li+ more strongly than DMC while its energetic advantage diminishes in the clusters surrounded by a matrix of a certain dielectric constant, thereby leaving to some extent a room for DMC to stick to Li+. As explained by Bogle et al.,6 in the EIMS measurements, the cluster loses the weakly bound DMC during traveling in the mass chamber, leaving two or three EC molecules tightly bound. From the chemical shift in NMR and the diffusion coefficient obtained by PGSE-NMR, Yang et al.5 conclude that EC is more strongly bound to Li+ than DMC and DEC in the ternary solvent system where the molar ratio is LiPF6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC
EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC
DMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC = 1
DEC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 (the solute to total solvent ratio is close to ours). The preference of PC, another cyclic carbonate as EC, over DMC is observed by 13C NMR study.31 A molecular dynamic study on the desolvation process suggests that DMC sheds first from the Li-solvation shell at the SEI in the EC/DMC solvent.19
4 (the solute to total solvent ratio is close to ours). The preference of PC, another cyclic carbonate as EC, over DMC is observed by 13C NMR study.31 A molecular dynamic study on the desolvation process suggests that DMC sheds first from the Li-solvation shell at the SEI in the EC/DMC solvent.19
While EC is confirmed to prevail in the solvation shell over DMC, the question arises as to how much? The present study enables us to quantitatively evaluate the EC-preference as a function of xEC. The EC to DMC ratio ns,EC/ns,DMC, in the solvation shell is plotted in Fig. 3(b). The theoretical prediction by Borodin et al. coincides very well with ours, namely, ns,EC/ns,DMC = 1.9 for the above mentioned system.21 If EC and DMC were equally capable of solvating Li+, this ratio should be xEC/(1 − xEC), and hence, the factor
| |  | (13) |
can be termed as the “EC-preference” that measures the EC selectivity in the solvation over DMC (
Fig. 3(b)). While at low
xEC, EC is more than twice as much preferred as DMC in the solvation shell,
PEC/DMC slightly decreases to 1.6 at
xEC = 0.7. Bogle
et al.6 also examined, as a function of the EC-content, the competitive solvation between EC and DMC for the 1 mol dm
−3 LiPF
6 in the EC/DMC system. A different picture is drawn when their results are analyzed in the same way as in the present study. Fig. S4 (ESI
†) shows the EC-preference,
PBEC/DMC, calculated from the numerical data “EC/DMC associated with Li
+” given in
Table 1 of their article. When viewed in terms of
PBEC/DMC, the EC-preference is, if any, insignificant even at low
xEC, and it becomes less than unity (
i.e., less preferred) at an EC-content greater than 30%. The discussion about this apparent inconsistency between
PEC/DMC and
PBEC/DMC is made two paragraphs later.
Another index for measuring the EC-preference over DMC in solvating Li+ can be obtained from the viewpoint of the solvation equilibrium. Instead of considering the multistep equilibrium among the solvating clusters, Lucht, Seo et al.7,32 assumed a simplified model based on the similarity in the vibrational spectra for all forms of solvating molecules. If we are to apply their model to our case, the apparent change in the free energy ΔG pertaining to the equilibrium
| | | EC·Li++ DMC ⇌ DMC·Li+ + EC | (14) |
where EC·Li
+ and DMC·Li
+ stand for EC and DMC solvating Li
+, of which the number is
Ns, and EC and DMC for the solvent molecules free from Li
+, of which the number is
Nf, is given by
| | 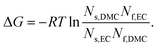 | (15) |
The result calculated from the present data is shown in Fig. S3 (ESI
†). The positive free energy, Δ
G > 0, indicates that the
reaction (14) tends to thermodynamically proceed from the right-hand side to the left-hand side, rationalizing the EC-preference over DMC. Yet the preference decreases from 3.5 to 1.5 kJ mol
−1 when
xEC increases. In the competitive solvation between PC
vs. DMC and PC
vs. DEC in the 1.2 mol dm
−3 LiPF
6 solution, Seo
et al.7 estimated Δ
G/kJ mol
−1 = 1.3 and 0.0
vs. DMC and DEC, respectively, from their IR measurements whereas the corresponding energy calculated by DFT (
ca. 8 kJ mol
−1) is, they consider, overestimated. Our result of Δ
G for EC/DMC at
xEC = 0.7 is close to their experimental one for PC/DMC, while one may consider that the value is modulated toward the calculated one at low EC-content, thereby implying the importance as well as the subtlety in taking into account the secondary (or farther) solvation environment for theoretical calculations. As in terms of
PBEC/DMC, a similar
prima facie contradiction shows up if we analyze the molar fraction of bound EC and DMC,
XECB and
XDMCB, given by Bogle
et al.6 as done in this study; namely, the free energy change is negative in most of the EC% range, the reason for which is discussed in the next paragraph.
Either in terms of PEC/DMC or ΔG, the EC-preference over DMC is evident; however, its extent diminishes when the EC-content increases in the solvent. Behind this phenomenon lies the balance between the attractive charge–dipole interaction and the repulsive interaction between multiple dipoles that are forced to align by Li+; EC is advantageous for the former effect while disadvantageous for the latter.20,21 While our observation is about the influence of EC concentration on shell composition, an analogous argument may apply in explaining the observation that the EC-dominance over DMC in the solvation diminishes when the salt concentration increases.7 The following considerations can be made about the apparent paradox in evaluating the EC-preference by PEC/DMC and PBEC/DMC, where the former is obtained from our Raman measurements and the latter from 17O NMR by Bogle et al.6 While the Raman bands used in the present study reflect the solvent molecules directly contacting Li+, the 17O NMR signals involve, as Bogle et al. state, those in the secondary solvation shell, and therefore, the total number of solvent molecules “associated with Li+” exceeds four and reaches nine. While EC is prevailing in the first solvation shell because of the strong interaction with Li+, DMC is “noncommittal but prevalent”, in the words of Bogle et al., in the greater solvation environment into which more polar EC molecules have difficulties in entering.
Based on the average nature of ns, if we assume that the number of species coordinating with Li+, including both the solvent and anion, totals four, the anion PF6− or FSA− accounts for the remaining 4 − ns,total ∼ 1.3–0.5. The neutron diffraction study of LiPF6 dissolved in pure DMC (9.6 mol%) by Kamada et al.33 concluded that one Li+ ion is surrounded by about three DMC molecules and one PF6− anion, which roughly agrees with our results at xEC = 0. The initial increase in the total number of solvent in the shell with the increase in xEC thus implies the decrease in the number of anions in the vicinity of Li+. One may interpret the deficit of the solvation number from four as an index of the fraction of ion-pairs.29 Borodin et al.21 suggests the coordination number of the P atom in PF6− around Li+ levels off at 0.5–0.6 in a system composed of EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC
DMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiPF6 = 15
LiPF6 = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (the system composition is close to ours at xEC = 0.5), which is consistent with our results (4 − ns,total ∼ 0.5).
3 (the system composition is close to ours at xEC = 0.5), which is consistent with our results (4 − ns,total ∼ 0.5).
The radius of the moving entity containing Li+, rc, which measures the average size of Li+ coordinated by the solvent and anion, is roughly estimated by
| | 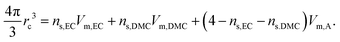 | (16) |
where the molar volumes,
Vm, are in Section 3.1. The radius,
rc, shown in Fig. S5 (ESI
†), is by and large constant at around 5 Å throughout the range of
xEC either for LiPF
6 or for LiFSA, which is comparable to the Stokes radius of Li
+ derived from the viscosity and diffusion coefficient in Section 3.6.
3.2.3 Raman signals of anions.
As indicated in Fig. 4(a), the Raman spectrum derived from the a1g mode vibration of PF6− is hardly influenced by the solvent composition. Although the signal seems to slightly red-shift (< 1 cm−1) with the increase in xEC, it is below the resolution of the spectrometer (2 cm−1). This invariance in the vibration frequency of PF6−, also observed in many other electrolyte solutions, has been occasionally considered as evidence for the high degree of dissociation of the PF6-based electrolyte. However, Han et al.34 examined the Raman signal of the solvate crystals of LiPF6 (i.e., LiPF6 co-crystallized with the solvent) and found that even in the solvate crystals, the signals derived from the contact ion pair and the solvent-shared ion pair overlap; therefore, the naive assumption of high dissociation might be problematic as it is inconsistent with the molecular dynamic simulations.35,36 In addition, in the liquid state, a strenuous rotation of PF6− is suggested even if it is in direct contact with Li+,20 which may average out the signal. Considering these previous studies, we have to conclude that the insensitive Raman frequency of PF6− cannot evidence the absence of the ion pairs in the LiPF6 system. Indeed, as discussed in Fig. 8 in Section 3.5, the degree of ionic dissociation, α, in the LiPF6 system significantly depends on xEC as in the LiFSA system.
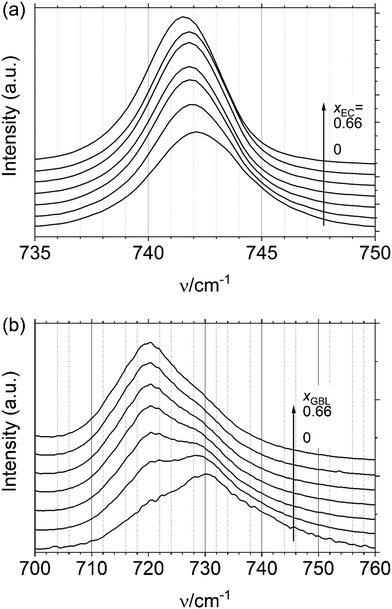 |
| | Fig. 4 Raman spectra of (a) PF6− (a1g mode) and (b) FSA−. | |
As mentioned in the Experimental section, the Raman signals from FSA− overlap with those from EC, we hence substitute GBL for EC, expecting qualitatively similar behavior. Contrary to PF6−, the Raman signal from FSA− shown in Fig. 4(b) significantly depends on xEC; the peak at νH/cm−1 = 730 gradually decreases with the increase in xGBL surpassed by the peak at νL/cm−1 = 720. Although we cannot decisively assign these peaks, if we hypothetically consider νL to be of free FSA− and νH to be of FSA− forming an ion pair with Li+ and equal activity (i.e., aionpair = afree), one can tentatively calculate the degree of dissociation, α, from the intensity ratio of these peaks; the result is shown in Fig. 8 in Section 3.5.
3.3 Viscosity
Fig. 5 shows the viscosity, η, of the solvent without the solute and the 1.0 mol kg−1 solution of LiPF6 and LiFSA at T/K = 298. Replacing DMC by more viscous fluid EC monotonously with a slight concave shape increases the solution viscosity, η, with xEC for both the solvent without the solute and the solution. Addition of the solute increases the η of the solvent 2.5–3.0 times for LiFSA and 2.5–3.5 times for LiPF6, for which the inter-ionic interaction should be responsible. While ηLiPF6 ≃ ηLiFSA at xEC = 0, the former exceeds the latter by ca. 20% at xEC > 0.4.
 |
| | Fig. 5 Solution and solvent viscosity, η, at T/K = 298. The lines are a visual guide. | |
The non-Arrhenius behavior is often observed in the temperature dependence of the viscosity and conductivity of liquids; instead, the Vogel–Tammann–Fulcher equation, for example, is utilized to analyze these properties. However, over the limited temperature range of this study (288 ≤ T/K ≤ 328), the deviation from the Arrhenius relation is not evident. The apparent activation energy associated with viscosity, Eηa, over this temperature range was thus calculated by considering fluidity, 1/η, to be a simple thermal activation process as ln(1/η) = −Eηa/RT + C, where R is the gas constant, T the absolute temperature and C a constant. As shown in Fig. S6(a) (ESI†), Eηa coincides for LiPF6 and LiFSA within the error in the linear optimization of the Arrhenius plot and similarly behaves for both salts in that Eηa drops from ca. 30 kJ mol−1 at xEC = 0 to 16–18 kJ mol−1 at xEC ∼ 0.25 and becomes constant thereafter. The reason why the less viscous solution near xEC = 0 has a higher Eηa is not clear at present. One may revisit the classical free volume model to understand the phenomenon.37 (The viscosity of the solvent without the solute at high temperature is so low and out of range of the apparatus that we could not determine its Eηa.)
3.4 Ionic conductivity
Fig. 6 plots the specific conductivity, σ, of the solution of LiPF6 and LiFSA. For either the LiPF6 or LiFSA system, the addition of EC into DMC initially increases the conductivity until it levels off at xEC ∼ 0.4, after which it decreases. Throughout the range of the measured xEC, the conductivity of the LiFSA solution is ca. 1 mS cm−1 greater than that of LiPF6 despite the greater static size of FSA− in eqn (11) than PF6− in eqn (10). When compared by their ratio, i.e., σLiFSA/σLiPF6, at xEC = 0, σLiFSA exceeds σLiPF6 by 13%. The gap shrinks to 7% at xEC ∼ 0.4 where the maximum in σ occurs, and widens again thereafter to 10% at xEC ∼ 0.7.
 |
| | Fig. 6 Specific conductivity, σ, of the 1 mol kg−1 solution of LiPF6 and LiFSA at T/K = 298. The lines are a visual guide. | |
Similar to viscosity, the non-Arrhenius behavior is not evident for conductivity over the studied temperature range. For both the LiPF6 and LiFSA systems, the apparent activation energy associated with conductivity, Eσa, over the studied temperature range (Fig. S6(b), ESI†), calculated from the Arrhenius relation, −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ = −Eσa/RT + C, monotonously increases without the extremum from ∼8 kJ mol−1 at xEC = 0 to ∼15 kJ mol−1 at xEC = 0.7. What is behind this observation that less conductive solution at low xEC has a low Eσa is inexplicable at present, to which, as in the viscosity, the free volume considerations may give a clue.38
σ = −Eσa/RT + C, monotonously increases without the extremum from ∼8 kJ mol−1 at xEC = 0 to ∼15 kJ mol−1 at xEC = 0.7. What is behind this observation that less conductive solution at low xEC has a low Eσa is inexplicable at present, to which, as in the viscosity, the free volume considerations may give a clue.38
The well-known negative correlation between η and σ—the higher the viscosity, the lower the conductivity—is quantitatively discussed when dealing with the hydrodynamic (Stokes) radius in Section 3.6.
3.5 Diffusion coefficient and degree of dissociation
Fig. 7 plots the diffusion coefficient, D, of all species in both the solvent and the solution determined by PGSE-NMR. Some of these data points were previously measured by Hayamizu et al.,2–4 with which our results agree; e.g., in pure DMC without a solute, DDMC/10−10 m2 s−1 = 26, by Hayamizu, while it was 24.8 in our study.
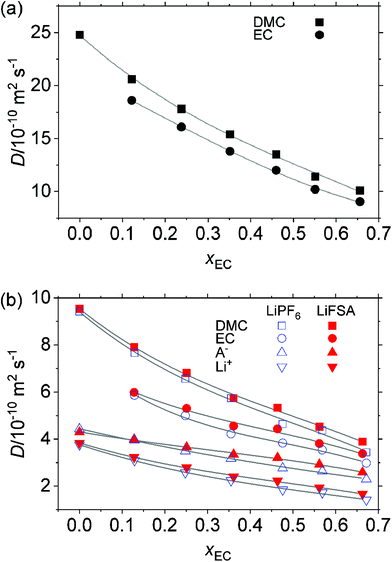 |
| | Fig. 7 Self-diffusion coefficient, D, determined by PGSE-NMR at T/K = 298. (a) Solvent without solute and (b) solution of 1 mol kg−1 LiPF6 and LiFSA. | |
Either for the solvent without solute or for the 1 mol kg−1 solution, DMC moves the fastest, followed by EC, anions and Li+ which is the slowest. As compared in Fig. 7(a and b), the addition of 1 mol kg−1 of the solute decreases the D of EC and DMC to around a third, which is a roughly opposite trend in the viscosity where η increases about three times as shown in Fig. 5. When the solute is absent (Fig. 7(a)), DDMC is close to DEC in the mixed solvent; the former is only 10–13% greater than the latter throughout the measured range of xEC. In the EC/DEC solvent system, Hayamizu et al.4 observed a similar phenomenon: while DEC and DDEC significantly differ in each pure (single component) solvent, they come close to each other when EC and DEC are mixed. In the presence of the solute (Fig. 7(b)), either for the LiPF6 or for the LiFSA system, DDMC is 33% greater than DEC at xEC = 0 and the gap gradually narrows to 15% at xEC = 0.7. This observation implies that, at low xEC, EC molecules are more hindered in their movement, concurring with the preferred solvation of EC to Li+ over DMC and its downslide with xEC as discussed in Section 3.2.2.
For all species, D decreases with an increase in xEC, which presumably stems from the increase in η. Incidentally, in the EC/DEC system, Hayamizu et al. observed that, with the increase in the EC-content, while DLi decreases, DPF6 remains almost constant.4
Not only are DLi, DEC and DDMC in the LiPF6 system close to those in the LiFSA system, but also DPF6 ≃ DFSA, despite the significant difference in the static size of the anions as in eqn (10) and (11) and significantly less than D of the solvent in the solution. As discussed below, this result is related to the pairing of anions with Li+, which drags a fraction of the anion with Li+ regardless of the anion. Although the precision of the experimental data requires certain reservation for the decisive figure, at higher xEC, D in the LiFSA system slightly exceeds that in the LiPF6 system, which, as discussed below in Section 3.6, results in the similar Stokes radius in these systems because of the cancellation between D and η.
The order of magnitude is
| | | DLi < DA < DEC < DDMC | (17) |
throughout the measured range of
xEC, which is in contrast to the order of the static size of each species discussed in Section 3.1 and reflects the hydrodynamic Stokes radius discussed below in Section 3.6. Comparing
DLi and
DA, one finds that the anions are 10–20% more mobile as a charge carrier than Li
+ at
xEC = 0, which suggest a higher transport number of the former than the latter. The gap monotonously widens to
ca. 60% at
xEC = 0.7.
The Nernst–Einstein relation relates the diffusion coefficient of charge carriers, D±, to a hypothetical molar conductivity, ΛNE, as in the present 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-salt case
1-salt case
| |  | (18) |
where
F is Faraday's constant. The molar conductivity of an electrolyte solution would hypothetically be
ΛNE if each charged particle were moving independently without correlating with others. The real molar conductivity,
Λ =
σ/
C, where
C is the molarity, is in many cases less than
ΛNE, which is usually explained by the negative contribution from the positive velocity cross-correlation between cation and anion, or in a sense viewed as an “ion pair”, and therefore, the ratio
| |  | (19) |
can be termed as the degree of dissociation of the solute in the solution.
Fig. 8 plots the
α thus calculated, in which also shown is
α estimated from the Raman intensity ratio of FSA
− in the GBL/DMC system in
Fig. 4(b) under the tentative assumption that the signal activity ratio,
as/
a0 = 1.0. Either for the LiPF
6 or LiFSA system, only 25–30% of solute dissociates in DMC, which increases to 65% at
xEC = 0.7. Our experimental results of
α roughly agree with the dynamic degree of ion dissociation,
αd, theoretically predicted by Borodin
et al.20 Analyzing the results of the molecular dynamics simulations based on topological graph theory, Tenney
et al.30 pointed out that a significant fraction of clusters has non-zero charge in pure EC and in EC
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
DMC = 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1 mixed solvent while in pure DMC neutral clusters prevail, suggesting a lower
α value in the latter. The degree of ionic dissociation,
α, estimated from the Raman signal of FSA
− is by and large in line with the one calculated from
eqn (19). If the activity ratio,
as/
a0, is accurately obtained, the coincidence can be better, thereby suggesting that for FSA
−, the vibrational spectroscopy can be applied for examining the ionic dissociation whereas for PF
6− it cannot. Insofar as the present two systems, LiPF
6 and LiFSA in EC/DMC, are concerned, the solvent composition similarly influences the ion dissociation either for PF
6− or FSA
−. Similarly in the EC/DEC solvent system,
α increases from 0.17 to 0.71 when the EC content increases from 0 to 100%.
4 This result is consistent with the notion that the high dielectric constant of EC is effective in separating the ion-pairs to increase the ionic conductivity of the electrolyte solution. The important role of dielectric shielding in determining the electrolyte conductivity has been also revealed in our recent Monte-Carlo simulations.
39,40
 |
| | Fig. 8 Degree of ionic dissociation, α, calculated from the diffusion coefficient, D, of the charge carriers and the conductivity in Section 3.4 using eqn (19) as well as α estimated from the Raman spectra of FSA− of LiFSA dissolved in GBL/DMC shown in Fig. 4(b) in Section 3.2. | |
While LiPF6 and LiFSA hardly differ in terms of α, they are distinct in terms of the transport properties; namely, the latter system has lower viscosity, η (Section 3.3), and higher ionic conductivity, σ (Section 3.4), than the former. Phenomenologically, αLiPF6 comes close to αLiFSA because both the conductivity and diffusion coefficient of ions, which are in the numerator and denominator in eqn (19), respectively, are smaller in the LiPF6 system than in the LiFSA system; the distinction between these systems hence tends to cancel out in α. The fact that the concept like the ion-pair or the degree of dissociation cannot differentiate these systems in terms of η or σ points to a limitation inherent in this concept in describing the transport phenomena, for which we make a brief remark at the end of Section 4 from the viewpoint of the two-body correlation functions.
3.6 Stokes radius
The so-called Stokes–Einstein relation surely belongs to the “classics”, for more than a century has elapsed since the Brownian motion of colloidal particles in a continuum viscous medium was theoretically examined by Einstein,41,42 whose contemporary Perrin43 experimentally determined, making use of the very Brownian motion, the Avogadro's number to secure victory of the atomism over the continuum picture of matter. Because atoms and molecules are much smaller than colloidal particles, the model is unlikely to describe their movement in a medium which itself is composed of atomistic entities. The relation has nonetheless proved suggestive in analyzing the diffusion of ions and molecules in solution.2,4,44 In the present study, we also assume that the following equation holds:| |  | (20) |
where rSt,α is the hydrodynamic (Stokes) radius of species α, k the Boltzmann constant, T the absolute temperature, c the shape factor, η the viscosity of the solution and Dα the diffusion coefficient of α. Theoretically, the factor, c, is 6 for the sphere and depends on the shape of the particle. Empirically, on the other hand, for neutral molecules whose molecular weight is close to that of EC or DMC, c roughly ranges from 3 to 4 in CCl4.44 Hayamizu et al. suggested c = 3.2 and 3.3 for GBL and PC, respectively,2 whereas Collings proposed c = 3.61 and 3.79 for benzene and carbon tetrachloride, respectively.45 To eliminate the ambiguity in c, one may take the ratio of rSt, for instance, of the ions to the solvent, as Hayamizu et al. did;3 however, in the present study, we tentatively put c = 3.5 as a mean of above mentioned empirical values to gain a rule-of-thumb size of transporting entities in the solution. (The figures of which the y-axis should be linearly re-scaled if c is modified are Fig. S7 and S9, ESI.†)
In the solvent without the solute, the Stokes radius of EC and DMC is constant independent of xEC as shown in Fig. S8 (ESI†):
| | | rSt,DMC/Å ≃ 2.5 < rSt,EC/Å ≃ 2.7. | (21) |
This suggests that the increase in
xEC decreases both the fluidity of the solvent, 1/
η, and the diffusion coefficient of its constituents to an approximately equal extent, rendering the product,
ηDα, in
eqn (20) constant. In other words, in the absence of ions, each individual EC and DMC molecule flows, as if it were, with a characteristic constant hydrodynamic radius under the friction imposed by the surrounding matrix, which is greater for EC than DMC and varies with
xEC even if the matrix itself is composed of EC and DMC. The order of
rSt is opposite to their static size in
eqn (8) and (9). We hence infer that the Stokes radius of DMC, a highly fluid liquid, can be close to its static radius whereas the viscous EC moves under a more dynamic friction than DMC to give the order
| | | r0,EC < r0,DMC ∼ rSt,DMC < rSt,EC. | (22) |
Fig. 9 shows the calculated Stokes radius, rSt, in the solutions. Disregarding the variation of rSt with xEC, which we will discuss later, one confirms in either solution the obvious trend
| | | rSt,DMC < rSt,EC < rSt,A < rSt,Li, | (23) |
where
A represents the anion (PF
6− or FSA
−). As for EC and DMC, despite the considerably higher viscosity of the solution than that of the solvent without the solute (
cf., Section 3.3), the
rSt of the solvent molecules in the presence of ions comes close to that in its absence (Fig. S8, ESI
†), although at high
xEC the radius in the solution becomes smaller than that in the solvent, which is not plausible, thereby implying the limitation of applying the Stokes–Einstein relation. While at low
xEC, the
rSt of PF
6− and FSA
− is greater than the static radius,
r0, in
eqn (10) and (11), the gap narrows at high
xEC. The lithium ion Li
+, whose static size is the smallest, has the largest Stokes radius, confirming the well-established view that Li
+ in the solution is heavily solvated by the solvent and correlated with the anions. The Stokes radius of Li
+ calculated in this section by and large agrees with
rc estimated from the solvation number determined by the Raman spectroscopy discussed in Section 3.2 (Fig. S5, ESI
†).
 |
| | Fig. 9 Stokes radius, rSt, of the ions and solvent in the solution calculated from the diffusion coefficient, D, of each component and the solution viscosity, η, based on eqn (20), where the shape factor is taken to be c = 3.5. | |
As for the variation of rSt with xEC, an obvious tendency is that it decreases for all constituents with an increase in xEC except at the highest EC-content xEC = 0.7. Let us define the rate of expansion of rSt with respect to xEC by
| |  | (24) |
and the rate of expansion of the entire system as
| |  | (25) |
where
Vm is the molar volume of the solution. If we calculate
Kα from
rSt in the range 0 ≤
xEC ≤ 0.55 and
Ksys from
Vm determined in Section 3.1, we get
| | | 0 < −Ksys ≪ −KLI ∼ −KEC ∼ −KDMC < −KA | (26) |
for either A = PF
6 or FSA. That is, the decrease in the system volume with the decrease in
xEC hardly contributes to the decrease rate of
rSt of all components, among which the anions are the most influenced by the EC-content to the extent that their Stokes radius becomes close to their static radius. This implies that the anions are liberated from the cations, not solvated by the solvent, and move under the friction from the solvent medium, which is consistent with the degree of ionic dissociation shown in
Fig. 8. The cations, on the other hand, are heavily solvated by the solvent, even if it dissociates the anions thanks to the dielectric shielding of EC, and therefore, the size of moving entity only slightly decreases or is almost invariant as shown in Fig. S5 (ESI
†). When the EC-content is too high, the high viscosity of the system is considered to prevail over the gain in separating ions by EC, thereby causing the ionic conductivity to peak out as in
Fig. 6 and the Stokes radius to bottom out as in
Fig. 9.
4 Conclusions
The present study experimentally measured a series of transport properties of the EC/DMC binary solvent with the composition 0 ≤ xEC ≤ 0.7 and its solution dissolving 1 mol kg−1 of LiPF6 and LiFSA; namely, diffusion coefficients of Li+, PF6−, FSA−, EC and DMC; the viscosity of the solvent and solution; and the ionic conductivity of the solution. Further, we employed Raman spectroscopy to quantitatively specify the species solvating Li+ in the solution and to examine the interaction between Li+ and the anions. Incorporating the experimental and theoretical results obtained in the previous studies, we can summarize the experimental insight into the transport properties of these electrolyte systems as follows.
4.1 Competitive solvation between EC and DMC
Raman spectroscopy quantified the competitive relation among EC and two conformers of DMC in the Li-solvation shell. The cis–trans conformer of DMC, which is less stable than the cis–cis conformer in vacuo, is to some extent stabilized in the solvation shell. When EC is substituted for DMC in the solvent, the former replaces the latter in the first solvation shell, and the analysis reveals that EC is about twice as preferred in the shell as DMC, although the preference somewhat decreases if xEC increases. The present result consistently appends a quantitative insight into the Li-solvation model depicted by the previous experimental and theoretical studies.
4.2 Stokes–Einstein relation
The classical Stokes–Einstein equation, which links the microscopic hydrodynamic radius and diffusion coefficient to macroscopic viscosity, still effectively holds, albeit with an ad hoc “shape factor”, when quantitatively discussing the transport phenomena. For instance, the average size of the moving entity associated with Li+ estimated from the solvation number determined by Raman spectroscopy roughly coincides with the Stokes radius of Li+ despite the independent experiments. The Stokes radius of the solvent molecules does not significantly change when the solute is added, despite the significant difference in the viscosity and diffusion coefficient between the pure solvent and the solution.
4.3 Static and hydrodynamic size of ions
The established account reconfirmed that the hydrodynamic (Stokes) radius of Li+, whose static size is the smallest among the constituents, is the greatest in the solution whereas that of the anions does not significantly differ from the static one, suggesting that Li+ is heavily solvated while the anions are not.
4.4 EC's effect in increasing conductivity
As previously considered, its high viscosity notwithstanding, EC is effective in increasing the ionic conductivity of the electrolyte solution by dissociating ion-pairs, for which the high dielectric shielding of EC is presumably responsible. The argument was substantiated in the present study by the comparison of Nernst–Einstein conductivity with real conductivity and the Raman spectra of FSA−. This effect of EC liberates the anions from Li+ as suggested in the higher extent of decrease in the Stokes radius of the anions than that of the other constituents with the increase in xEC, enhancing the contribution of the anions to the conductivity, despite the decrease in its diffusion coefficient due to the increase in the solution viscosity. On the other hand, Li+ barely receives benefits, because the EC-preference in the solvation over DMC maintains its hydrodynamic size nearly constant, or decreases it only slightly.
Based on the experimental data, the present study attempted to draw a comprehensive picture of a range of transport properties of non-aqueous electrolyte solutions. However, to reinforce the understanding obtained, not only can we extend our experiment by varying the salt concentrations or by dealing with other solute/solvent systems, but also there is room for further theoretical studies to give full play. That is, transport phenomena entail by nature the dynamic correlations among different particles, especially at a high concentration of the charge carriers, and therefore, they cannot be described in terms only of static concepts like ion-pair, solvation number, etc. Nor are they fully fathomed out by single-particle properties like Stokes radius or self-diffusion coefficient, which pertains only to auto-correlation. Recently, we demonstrated by molecular dynamics simulations46 that the reason why the real ionic conductivity of molten binary carbonates, where virtually all ions are in a sense “paired”, deviates from the Nernst–Einstein counterpart is explicable in terms of the velocity cross-correlations between cations and CO32−. As implied by Tenney et al.,30 accurately calculating the cross-correlation functions can be still computationally demanding for room-temperature electrolyte solutions containing organic molecules. Considerations analogous to molten salts would be nonetheless inevitable to fully understand the transport properties of electrolyte solutions.
Finally, from the viewpoint of battery application, the diffusion coefficient suggests that the contribution from the cation and anion to the conductivity at a given xEC is comparable in LiFSA and LiPF6 solutions; i.e., the transference number is comparable in these systems. In terms of the absolute value of the conductivity, on the other hand, LiFSA excels over LiPF6 in the EC/DMC binary solvent, which facilitates the successful operation of Li-ion batteries. However, at electrochemical potentials above 4 V vs. Li/Li+, the amide-based anions, including FSA−, corrode the Al current collector,47,48 which may limit the use of LiFSA as the main electrolyte component for high-voltage Li-ion batteries.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
A part of the present study was financially supported by JSPS KAKENHI Grant No. 19K15688. We thank Drs S. Takeda and Y. Saito of AIST for their kind assistance and advice in obtaining the PGSE-NMR measurements.
References
- K. Xu, Chem. Rev., 2004, 104, 4303–4418 CrossRef CAS PubMed.
- K. Hayamizu, Y. Aihara, S. Arai and C. Garcia-Martinez, J. Phys. Chem. B, 1999, 103, 519–524 CrossRef CAS PubMed.
- K. Hayamizu, Electrochemistry, 2003, 71, 1052–1054 CrossRef CAS.
- K. Hayamizu, J. Chem. Eng. Data, 2012, 57, 2012–2017 CrossRef CAS.
- L. Yang, A. Xiao and B. L. Lucht, J. Mol. Liq., 2010, 154, 131–133 CrossRef CAS.
- X. Bogle, R. Vazquez, S. Greenbaum, A. V. W. Cresce and K. Xu, J. Phys. Chem. Lett., 2013, 4, 1664–1668 CrossRef CAS PubMed.
- D. M. Seo, S. Reininger, M. Kutcher, K. Redmond, W. B. Euler and B. L. Lucht, J. Phys. Chem. C, 2015, 119, 14038–14046 CrossRef CAS.
- M. Morita, Y. Asai, N. Yoshimoto and M. Ishikawa, J. Chem. Soc., Faraday Trans., 1998, 94, 3451–3456 RSC.
- C. M. Burba and R. Frech, J. Phys. Chem. B, 2005, 109, 15161–15164 CrossRef CAS PubMed.
- Y. Matsuda, T. Fukushima, H. Hashimoto and R. Arakawa, J. Electrochem. Soc., 2002, 149, A1045–A1048 CrossRef CAS.
- A. von Cresce and K. Xu, Electrochem. Solid-State Lett., 2011, 14, A154–A156 CrossRef CAS.
- S. K. Jeong, M. Inaba, Y. Iriyama, T. Abe and Z. Ogumi, Electrochim. Acta, 2002, 47, 1975–1982 CrossRef CAS.
- T. Abe, H. Fukuda, Y. Iriyama and Z. Ogumi, J. Electrochem. Soc., 2004, 151, A1120–A1123 CrossRef CAS.
- K. Xu, Y. F. Lam, S. S. Zhang, T. R. Jow and T. B. Curtis, J. Phys. Chem. C, 2007, 111, 7411–7421 CrossRef CAS.
- K. Xu, J. Electrochem. Soc., 2007, 154, A162–A167 CrossRef CAS.
- Y. Yamada, Y. Iriyama, T. Abe and Z. Ogumi, Langmuir, 2009, 25, 12766–12770 CrossRef CAS PubMed.
- K. Xu, A. v. Cresce and U. Lee, Langmuir, 2010, 26, 11538–11543 CrossRef CAS PubMed.
- M. Nie, D. P. Abraham, D. M. Seo, Y. Chen, A. Bose and B. L. Lucht, J. Phys. Chem. C, 2013, 117, 25381–25389 CrossRef CAS.
- O. Borodin and D. Bedrov, J. Phys. Chem. C, 2014, 118, 18362–18371 CrossRef CAS.
- O. Borodin and G. D. Smith, J. Phys. Chem. B, 2009, 113, 1763–1776 CrossRef CAS PubMed.
- O. Borodin, M. Olguin, P. Ganesh, P. R. C. Kent, J. L. Allen and W. A. Henderson, Phys. Chem. Chem. Phys., 2016, 18, 164–175 RSC.
- H. Kataoka, Y. Saito, T. Sakai, S. Deki and T. Ikeda, J. Phys. Chem. B, 2001, 105, 2546–2550 CrossRef CAS.
- W. S. Price and P. K. Kuchel, J. Magn. Reson., 1991, 94, 133–139 Search PubMed.
- W. S. Price, K. Hayamizu, H. Ide and Y. Arata, J. Magn. Reson., 1999, 139, 205–212 CrossRef CAS PubMed.
- H. Kataoka, Y. Saito, M. Tabuchi, Y. Wada and T. Sasaki, Macromolecules, 2002, 35, 6239–6244 CrossRef CAS.
- J. Neuhaus, E. von Harbou and H. Hasse, J. Power Sources, 2018, 394, 148–159 CrossRef CAS.
- J. E. Katon and M. D. Cohen, Can. J. Chem., 1974, 52, 1994–1996 CrossRef CAS.
- Y.-X. Wang and P. B. Balbuena, Int. J. Quantum Chem., 2005, 102, 724–733 CrossRef CAS.
- L. Doucey, M. Revault, A. Lautié, A. Chaussé and R. Messina, Electrochim. Acta, 1999, 44, 2371–2377 CrossRef CAS.
- C. M. Tenney and R. T. Cygan, J. Phys. Chem. C, 2013, 117, 24673–24684 CrossRef CAS.
- V. Prakash-Reddy, M. C. Smart, K. B. Chin, B. V. Ratnakumar, S. Surampudi, J.-B. Hu, P. Yan and G. K. Surya-Prakashc, Electrochem. Solid-State Lett., 2005, 8, A294–A298 CrossRef.
- B. L. Lucht and D. B. Collum, J. Am. Chem. Soc., 1995, 117, 9863–9874 CrossRef CAS.
- Y. Kameda, S. Saito, Y. Umebayashi, K. Fujii, Y. Amo and T. Usuki, J. Mol. Liq., 2016, 217, 17–22 CrossRef CAS.
- S.-D. Han, S.-H. Yun, O. Borodin, D. M. Seo, R. D. Sommer, J. V. G. Young and W. A. Henderson, J. Phys. Chem. C, 2015, 119, 8492–8500 CrossRef CAS.
- D. M. Seo, O. Borodin, S.-D. Han, P. D. Boyle and W. A. Henderson, J. Electrochem. Soc., 2012, 159, A1489–A1500 CrossRef CAS.
- D. M. Seo, O. Borodin, D. Balogh, M. O'Connell, Q. Ly, S.-D. Han, S. Passerini and W. A. Henderson, J. Electrochem. Soc., 2013, 160, A1061–A1070 CrossRef CAS.
- P. B. Macedo and T. A. Litovitz, J. Chem. Phys., 1965, 42, 245–256 CrossRef CAS.
- T. Miyamoto and K. Shibayama, J. Appl. Phys., 1973, 44, 5372–5376 CrossRef CAS.
- H. Ozaki, K. Kuratani and T. Kiyobayashi, J. Electrochem. Soc., 2016, 163, H576–H583 CrossRef CAS.
- H. Ozaki, K. Kuratani, H. Sano and T. Kiyobayashi, J. Chem. Phys., 2017, 147, 034904 CrossRef PubMed.
- A. Einstein, Ann. Phys., 1906, 19, 289–306 CrossRef CAS.
- A. Einstein, Z. Elektrochem., 1908, 14, 235–239 CrossRef.
- J. Perrin, Ann. Chim. Phys., 1909, 18, 1–114 Search PubMed.
- J. T. Edward, J. Chem. Educ., 1970, 47, 261–270 CrossRef CAS.
- A. F. Collings and R. Mills, J. Chem. Soc., Faraday Trans., 1970, 66, 2761–2766 RSC.
- T. Kiyobayashi, T. Kojima, H. Ozaki and K. Kiyohara, J. Chem. Phys., 2019, 151, 074503 CrossRef PubMed.
- A. Abouimrane, J. Ding and I. J. Davidson, J. Power Sources, 2009, 183, 693–696 CrossRef.
- K. Park, S. Yu, C. Lee and H. Lee, J. Power Sources, 2015, 296, 197–203 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Numerical data and additional figures. See DOI: 10.1039/d1cp00967b |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article


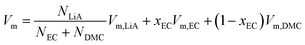
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol−1 = −18.9, leading to
mol−1 = −18.9, leading to


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC = 1
DMC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume (corresponding to xEC = 0.57), ns,EC = 3.0 and ns,DMC = 1.1, which was reassessed by Borodin et al.21 by considering the Raman activity ratio, as/a0, in Table 1 to find ns,EC = 2.8 and ns,DMC = 1.2. Similarly, Borodin et al. also predicted a result close to that of ours;21 namely, they estimated ns,EC = 1.79–2.13 and ns,DMC = 1.12–1.05 (depending on the functional used in the calculation) by integrating the radial distribution function obtained by the molecular dynamics simulations for the system composed of LiPF6
1 by volume (corresponding to xEC = 0.57), ns,EC = 3.0 and ns,DMC = 1.1, which was reassessed by Borodin et al.21 by considering the Raman activity ratio, as/a0, in Table 1 to find ns,EC = 2.8 and ns,DMC = 1.2. Similarly, Borodin et al. also predicted a result close to that of ours;21 namely, they estimated ns,EC = 1.79–2.13 and ns,DMC = 1.12–1.05 (depending on the functional used in the calculation) by integrating the radial distribution function obtained by the molecular dynamics simulations for the system composed of LiPF6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC
EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC = 1
DMC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, of which the solvent composition corresponds to xEC = 0.5 and the salt concentration is close to that of ours where the solute to solvent ratio is ca. 11 as given in eqn (3). The EC-preference in solvating Li+ over DMC is also suggested in another molecular dynamics simulation of 0.1–1.0 mol dm−3 LiPF6 dissolved in EC
5, of which the solvent composition corresponds to xEC = 0.5 and the salt concentration is close to that of ours where the solute to solvent ratio is ca. 11 as given in eqn (3). The EC-preference in solvating Li+ over DMC is also suggested in another molecular dynamics simulation of 0.1–1.0 mol dm−3 LiPF6 dissolved in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC = 1
DMC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by Tenney et al.30 Bogle et al.6 also conclude, from the chemical shift of 17O NMR, the stronger interaction of EC with Li+ than DMC for the 1 mol dm−3 LiPF6 in the EC/DMC system. Matsuda et al.10 observed that the major cluster assayed by the electro-spray ionization mass spectroscopy (EIMS) from LiClO4 in EC/DMC diluted with methanol was [Li(EC)2]+ with a minor component [Li(EC)3]+, and no DMC was observed in the clusters isolated in vacuo, which testified to the EC preference in the Li+-solvation over DMC. An EIMS study by von Cresce et al.11 proved the EC dominance over DMC and EMC, another acyclic carbonate like DMC, in the clusters reached the TOF spectrometer sampled out of the 1.0–1.2 mol dm−3 solution without dispersing the solvent. This phenomenon is consistent with the quantum chemistry calculations20,21 indicating that, in the isolated state, EC binds to Li+ more strongly than DMC while its energetic advantage diminishes in the clusters surrounded by a matrix of a certain dielectric constant, thereby leaving to some extent a room for DMC to stick to Li+. As explained by Bogle et al.,6 in the EIMS measurements, the cluster loses the weakly bound DMC during traveling in the mass chamber, leaving two or three EC molecules tightly bound. From the chemical shift in NMR and the diffusion coefficient obtained by PGSE-NMR, Yang et al.5 conclude that EC is more strongly bound to Li+ than DMC and DEC in the ternary solvent system where the molar ratio is LiPF6
1 by Tenney et al.30 Bogle et al.6 also conclude, from the chemical shift of 17O NMR, the stronger interaction of EC with Li+ than DMC for the 1 mol dm−3 LiPF6 in the EC/DMC system. Matsuda et al.10 observed that the major cluster assayed by the electro-spray ionization mass spectroscopy (EIMS) from LiClO4 in EC/DMC diluted with methanol was [Li(EC)2]+ with a minor component [Li(EC)3]+, and no DMC was observed in the clusters isolated in vacuo, which testified to the EC preference in the Li+-solvation over DMC. An EIMS study by von Cresce et al.11 proved the EC dominance over DMC and EMC, another acyclic carbonate like DMC, in the clusters reached the TOF spectrometer sampled out of the 1.0–1.2 mol dm−3 solution without dispersing the solvent. This phenomenon is consistent with the quantum chemistry calculations20,21 indicating that, in the isolated state, EC binds to Li+ more strongly than DMC while its energetic advantage diminishes in the clusters surrounded by a matrix of a certain dielectric constant, thereby leaving to some extent a room for DMC to stick to Li+. As explained by Bogle et al.,6 in the EIMS measurements, the cluster loses the weakly bound DMC during traveling in the mass chamber, leaving two or three EC molecules tightly bound. From the chemical shift in NMR and the diffusion coefficient obtained by PGSE-NMR, Yang et al.5 conclude that EC is more strongly bound to Li+ than DMC and DEC in the ternary solvent system where the molar ratio is LiPF6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC
EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC
DMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC = 1
DEC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 (the solute to total solvent ratio is close to ours). The preference of PC, another cyclic carbonate as EC, over DMC is observed by 13C NMR study.31 A molecular dynamic study on the desolvation process suggests that DMC sheds first from the Li-solvation shell at the SEI in the EC/DMC solvent.19
4 (the solute to total solvent ratio is close to ours). The preference of PC, another cyclic carbonate as EC, over DMC is observed by 13C NMR study.31 A molecular dynamic study on the desolvation process suggests that DMC sheds first from the Li-solvation shell at the SEI in the EC/DMC solvent.19
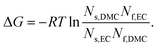
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC
DMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiPF6 = 15
LiPF6 = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (the system composition is close to ours at xEC = 0.5), which is consistent with our results (4 − ns,total ∼ 0.5).
3 (the system composition is close to ours at xEC = 0.5), which is consistent with our results (4 − ns,total ∼ 0.5).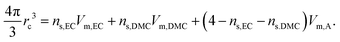

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ = −Eσa/RT + C, monotonously increases without the extremum from ∼8 kJ mol−1 at xEC = 0 to ∼15 kJ mol−1 at xEC = 0.7. What is behind this observation that less conductive solution at low xEC has a low Eσa is inexplicable at present, to which, as in the viscosity, the free volume considerations may give a clue.38
σ = −Eσa/RT + C, monotonously increases without the extremum from ∼8 kJ mol−1 at xEC = 0 to ∼15 kJ mol−1 at xEC = 0.7. What is behind this observation that less conductive solution at low xEC has a low Eσa is inexplicable at present, to which, as in the viscosity, the free volume considerations may give a clue.38
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-salt case
1-salt case

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC = 1
DMC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixed solvent while in pure DMC neutral clusters prevail, suggesting a lower α value in the latter. The degree of ionic dissociation, α, estimated from the Raman signal of FSA− is by and large in line with the one calculated from eqn (19). If the activity ratio, as/a0, is accurately obtained, the coincidence can be better, thereby suggesting that for FSA−, the vibrational spectroscopy can be applied for examining the ionic dissociation whereas for PF6− it cannot. Insofar as the present two systems, LiPF6 and LiFSA in EC/DMC, are concerned, the solvent composition similarly influences the ion dissociation either for PF6− or FSA−. Similarly in the EC/DEC solvent system, α increases from 0.17 to 0.71 when the EC content increases from 0 to 100%.4 This result is consistent with the notion that the high dielectric constant of EC is effective in separating the ion-pairs to increase the ionic conductivity of the electrolyte solution. The important role of dielectric shielding in determining the electrolyte conductivity has been also revealed in our recent Monte-Carlo simulations.39,40
1 mixed solvent while in pure DMC neutral clusters prevail, suggesting a lower α value in the latter. The degree of ionic dissociation, α, estimated from the Raman signal of FSA− is by and large in line with the one calculated from eqn (19). If the activity ratio, as/a0, is accurately obtained, the coincidence can be better, thereby suggesting that for FSA−, the vibrational spectroscopy can be applied for examining the ionic dissociation whereas for PF6− it cannot. Insofar as the present two systems, LiPF6 and LiFSA in EC/DMC, are concerned, the solvent composition similarly influences the ion dissociation either for PF6− or FSA−. Similarly in the EC/DEC solvent system, α increases from 0.17 to 0.71 when the EC content increases from 0 to 100%.4 This result is consistent with the notion that the high dielectric constant of EC is effective in separating the ion-pairs to increase the ionic conductivity of the electrolyte solution. The important role of dielectric shielding in determining the electrolyte conductivity has been also revealed in our recent Monte-Carlo simulations.39,40








