Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The effect of defect interactions on the reduction of doped ceria†
Steffen
Grieshammer
 abc
abc
aInstitute of Physical Chemistry, RWTH Aachen University, Landoltweg 2, 52056 Aachen, Germany. E-mail: grieshammer@pc.rwth-aachen.de
bHelmholtz-Institut Münster (IEK-12), Forschungszentrum Jülich GmbH, Corrensstr. 46, 48149 Münster, Germany
cJARA-HPC, Germany, Forschungszentrum Jülich & RWTH Aachen University, Germany
First published on 13th April 2021
Abstract
Doped cerium oxide is known for its reduction properties that are utilized in catalytic applications as well as in thermochemical cycling to produce solar fuels. Upon reduction of the lattice, oxygen vacancies and polarons are formed leading to a highly concentrated solution of defects in which the interactions of defects cannot be neglected anymore. In this study, the effect of defect interactions on the free energy of reduction for doped ceria with composition Ce1−x−yRExZryO2−x/2−δ was investigated by large scale Metropolis Monte Carlo multi-stage sampling simulations based on first-principles calculations. The simulations allowed the prediction of the relation between oxygen partial pressure and non-stoichiometry for the highly interacting, non-ideal system. The results show that the non-ideality observed in experiments can be traced back to the interactions of defects and allow prediction of the reduction behavior for various dopant types, dopant fractions, temperatures, and non-stoichiometries.
Introduction
Cerium oxide (ceria) is an essential material in various applications such as solid oxide fuel cells, industrial and automotive catalysis, and more recently the production of solar fuels.1–5 One of the most prominent properties of ceria is its high oxygen storage capacity (OSC) that is utilized in catalytic reactions and the two step process to produce hydrogen from water. The OSC is based on the reduction equilibrium given in eqn (1) in Kröger–Vink-notation, where the release of oxygen gas leads to the creation of oxygen vacancies and polarons, i.e. localized electrons.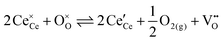 | (1) |
An even higher OSC is achieved by doping the material with rare-earth oxides (RE2O3) or zirconium oxide (ZrO2).6–10 While aliovalent rare-earth doping (eqn (2)) leads to the formation of oxygen vacancies, isovalent Zr4+ introduces no additional defects (eqn (3)) but modifies the material's properties due to the smaller size of the Zr-ions and the corresponding lattice distortions.
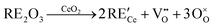 | (2) |
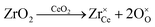 | (3) |
For an ideal, non-interacting system, the classical mass action law for eqn (1) can be expressed in terms of the molar fractions by,
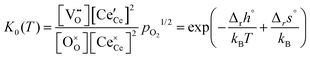 | (4) |
Therefore, the term Δrgint has to be considered, which is the contribution of defect interactions to the Gibbs energy of reduction per formula unit CeO2. Neglecting volume changes in the solid, the approximation Δrgint ≈ Δrfint is applicable. The deviation from the ideal reduction behavior can then be expressed by an excess term with the derivative of Δrfint for δ (see ESI† for details):
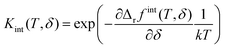 | (5) |
For the general composition Ce1−x−yRExZryO2−x/2−δ, we can write the charge and site balances as follows:
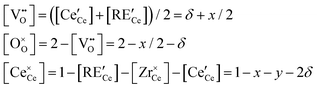 | (6) |
Inserting in eqn (4) and combining with eqn (5) results in
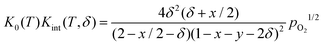 | (7) |
Rearranging yields the relationship between oxygen partial pressure pO2 and non-stoichiometry δ.
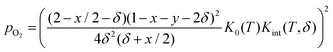 | (8) |
It is noted that K0(T) solely depends on the temperature whereas Kint(T,δ) depends on temperature and non-stoichiometry as well as dopant type and fraction.
Using the Metropolis Monte Carlo algorithm, the simulation of the defect distribution in equilibrium and the estimation of the internal energy is possible. As the direct evaluation of the free energy contribution is not possible, Valleau and Card19 suggested a multi-stage sampling approach which connects the desired distribution (T = Tmin) with the random distribution (T = ∞) by a series of consecutive distributions i with the temperature factor αi = Tmin/Ti. This approach allows the evaluation of Δrfint with respect to the ideal solution and was successfully applied in the description of the non-ideal behavior of pure and Gd-doped ceria before.17 More details are given in the ESI† and the according references.
In this paper, the effect of defect interactions on the free energy of reduction is investigated for various dopants and compositions in Ce1−x−yRExZryO2−x/2−δ using Metropolis Monte Carlo multi-stage sampling simulations based on density functional theory calculations. With the results, the deviation of the relation δ vs. pO2 from the ideal behavior is investigated.
Simulation setup
Simulations were performed with the program MOCASSIN using the built in multi-stage sampling routine as described in the ref. 2 and 21. The interactions of defects, i.e. oxygen vacancies, polarons and dopant ions, were evaluated as a sum over the number of interactions Ndij and the corresponding pair interaction energies εdij for defect pairs ij at distance d.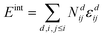 | (9) |
The relevant pair interaction energies from density functional theory (DFT) calculations were taken from ref. 16 and 18 as listed in the ESI.† These energies were obtained with the PBE functional with an on-site Coulomb interaction on cerium f-orbitals of Ueff = 5 eV. It is noted that the choice of the functional influences the values of the interactions but significant changes are not expected.24,25 Therefore, the general results of the simulations are expected to be widely independent of the applied functional.
In this study, typical rare-earth dopants for ceria were included which are distinguished by their ionic radii (Fig. 1). In addition, Zr4+ was included as a typical dopant and impurity in ceria.
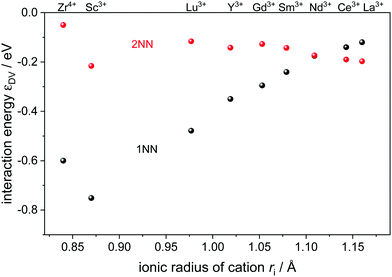 | ||
Fig. 1 Interaction energy  between an oxygen vacancy and a dopant ion or polaron in the nearest (1NN) and next nearest (2NN) neighbor position taken from ref. 16 and 18. between an oxygen vacancy and a dopant ion or polaron in the nearest (1NN) and next nearest (2NN) neighbor position taken from ref. 16 and 18. | ||
The most relevant energies are the interactions between the oxygen vacancies and the dopant ions or polarons which are represented in Fig. 1. All interactions are negative implying attraction between the cation defects and oxygen vacancies. While the interaction in next nearest neighbor (2NN) position is similar for all cations, the interaction in nearest neighbor (1NN) position depends on the ionic radius. The strength of the 1NN interaction decreases with increasing cation radius which can be explained by the tendency of smaller cations to favor a lower coordination number. This results in a strong attraction for 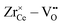 and
and 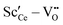 pairs that weakens for the other dopants. It is noted, that up to Sm3+ the 1NN position is energetically favorable compared to the 2NN position, whereas for Nd3+ both positions are energetically equal. For the polaron and for La3+ the 2NN position is most favorable.
pairs that weakens for the other dopants. It is noted, that up to Sm3+ the 1NN position is energetically favorable compared to the 2NN position, whereas for Nd3+ both positions are energetically equal. For the polaron and for La3+ the 2NN position is most favorable.
Simulations were conducted in 12 × 12 × 12 supercells with a total of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736 lattice positions. The dopant ions were randomly distributed and considered as immobile due to their low diffusivity.26 In contrast, polarons and oxygen vacancies are highly mobile and
736 lattice positions. The dopant ions were randomly distributed and considered as immobile due to their low diffusivity.26 In contrast, polarons and oxygen vacancies are highly mobile and 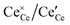 and
and 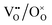 pairs were thus swapped during the simulations to obtain their equilibrium distribution. The temperature factor α was varied with a step size of 0.01 between 0 and 1 with Tmin = 773 K.
pairs were thus swapped during the simulations to obtain their equilibrium distribution. The temperature factor α was varied with a step size of 0.01 between 0 and 1 with Tmin = 773 K.
The interaction contribution Δruint to the internal energy of reduction was obtained from the simulation average of the energy states in thermodynamic equilibrium. The interaction contribution Δrfint to the free energy was obtained from the energy distributions collected in the multi-stage sampling approach (see ref. 17 or the ESI† for details). The entropy term Δrsint was calculated according to the relation S = (U − F)/T. All contributions were referenced to the stoichiometric case, thus reflecting only the contributions of defect interactions to the reduction of the lattice.
The non-stoichiometry was varied with a step size of 0.002 in the range δ ∈ [0.001…0.009] and 0.01 in the range δ ∈ [0.01…0.12]. For each simulation, 107 cycle steps were performed for equilibration of the lattice and energy states were recorded over 108 cycle steps. Twelve independent simulations with different dopant distributions were averaged for each data point. These simulation parameters are in accordance with previous simulations.17
Results and discussion
Energy contributions
The simulated interaction contributions Δruint, Δrfint, and Δrsint per formula unit CeO2 are given in Fig. 2. Internal energy Δruint and free energy Δrfint contributions are negative due to the attractive interactions between the oxygen vacancies and cation defects. The energy values become more negative with increasing non-stoichiometry as the amount of defects and thus the number of defect interactions increases. This implies that Kint > 1 according to eqn (5), thus facilitating the reduction of the lattice.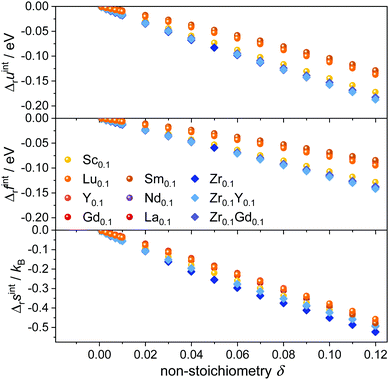 | ||
| Fig. 2 Interaction contributions per formula unit to internal energy (top), free energy (center), and entropy (bottom) at 1073 K in Ce1−x−yRExZryO2−x/2−δ for various dopants. | ||
The absolute value of the free energy is smaller than the absolute value of the internal energy, corresponding to the negative values of the entropy contribution. This is in accordance with the fact that any kind of interaction leads to an ordering of defects and thus a loss of configurational entropy compared to the ideal solution model.
Two different groups of dopants can be identified from the energies in Fig. 2 in correspondence with Fig. 1. The values are similar for the RE-dopants Lu3+, Y3+, Gd3+, Sm3+, Nd3+, and La3+ but considerably more negative for Sc3+ and Zr4+. Previous investigations revealed that the lowering of the energy during reduction is mainly due to the attractive interaction between the polarons and oxygen vacancies in 2NN position that is independent of the dopant type.16 A secondary effect is the interaction between the dopant ions and the oxygen vacancies introduced through reduction. This effect is less important for Lu3+, Y3+, Gd3+, Sm3+, Nd3+, and La3+ and consequently the results in Fig. 2 are similar. In contrast, the effect is more pronounced for Sc3+ due to a considerably stronger 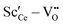 interaction. For Zr4+, this effect is even more pronounced due the fact that no oxygen vacancies are present in the stoichiometric case. This leads to the formation of favorable
interaction. For Zr4+, this effect is even more pronounced due the fact that no oxygen vacancies are present in the stoichiometric case. This leads to the formation of favorable 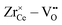 pairs during reduction and a strong decrease of the energy.18 It should be noted at this point that the composition Ce0.9Sc0.1O1.95−δ is a hypothetical case as the Sc-concentration is above the solubility limit of a few percent.23
pairs during reduction and a strong decrease of the energy.18 It should be noted at this point that the composition Ce0.9Sc0.1O1.95−δ is a hypothetical case as the Sc-concentration is above the solubility limit of a few percent.23
Dependence of non-stoichiometry on oxygen partial pressure
The relations between oxygen partial pressure and non-stoichiometry in doped ceria were obtained from eqn (8) with the respective values Kint from eqn (5) and the experimentally determined values Δrh° = 5 eV and Δrs° = 17kB for the diluted case as described in the literature.11,17 The results for the various dopants at 1073 K are presented in Fig. 3 together with the values for pure ceria and the ideal curves for pure ceria and Ce0.9RE0.1O1.95−δ according to eqn (4). Compared to the ideal behavior, all curves are shifted by 4 to 15 orders of magnitude to higher partial pressures for a given non-stoichiometry. This implies a higher reducibility due to the existence of defect interactions. As the slopes of Δrfint in Fig. 2 are negative, Kint > 1 according to eqn (5) leading to higher values of pO2 for a given value of δ according to eqn (8).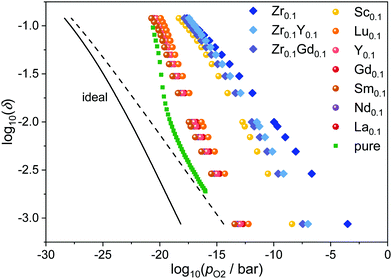 | ||
| Fig. 3 Relation between oxygen partial pressure and non-stoichiometry in Ce1−x−yRExZryO2−x/2−δ at 1073 K. The ideal behavior for CeO2−δ (dashed) and Ce0.9RE0.1O1.95−δ (solid) according to eqn (4) is indicated by the black line. Simulated values for pure ceria (squares) are taken from ref. 17. | ||
Again, the two groups of dopants can be distinguished. The RE-dopants Lu3+, Y3+, Gd3+, Sm3+, Nd3+, and La3+ with medium interactions show similar results while the Sc3+ and Zr4+ lead to reduction at considerably higher partial pressures. This reflects the finding, that doping with Sc3+ and Zr4+ leads to lower values of Δrfint.
In addition, the slopes for Sc3+ and Zr4+ are flattened compared to the other dopants, meaning that the effect of interactions is more pronounced at low non-stoichiometries while the curves approach the other RE-dopants at high non-stoichiometries. This effect is likely to originate from a saturation effect: The strong attraction between vacancies and dopants leads to an ordering of vacancies close to the dopant ions even at low non-stoichiometry. At high non-stoichiometries, these favorable positions are already occupied and additional vacancies do not increase the number of favorable interactions considerably.
Fig. 3 also shows the effect of co-doping zirconia doped ceria with a rare-earth oxide. Comparing Ce0.9Zr0.1O2−δ with Ce0.8RE0.1Zr0.1O1.95−δ, it is apparent that the co-doping with Y2O3 or Gd2O3 leads to a shift of the curves to lower partial pressures, i.e. lower reducibility. This phenomenon can be attributed to two effects, which are due to the introduction of oxygen vacancies through RE-doping in the stoichiometric case. 1. The minor effect is that the overall fraction of vacancies is increased and the fraction of oxygen ions is decreased leading to a smaller non-exponential factor in eqn (8). 2. The more important effect is that the oxygen vacancies order at the Zr-ions already in the stoichiometric, co-doped case, thus blocking these favorable positions and making the further creation of vacancies by reduction less favorable.
From the position of the curves in Fig. 3, an increase of the reducibility in the order pure ceria < RE-doped < Zr/RE-co-doped < Zr-doped can be inferred. This is well in line with experimental findings.7,27
The influence of the dopant fraction is illustrated in Fig. 4 for Ce1−xGdxO2−x/2−δ at 1073 K. In general, the curves are shifted to higher oxygen partial pressures with increasing dopant fraction as expected for an increasing amount of favorable interactions. However, above 20 at% doping, the effect seems to diminish and furthermore, the curves approach each other at high non-stoichiometries. Both observations are likely due to the saturation effect mentioned above: As the number of defects increases, the energetically favorable configurations are already occupied, leading to a diminished effect for the further reduction.
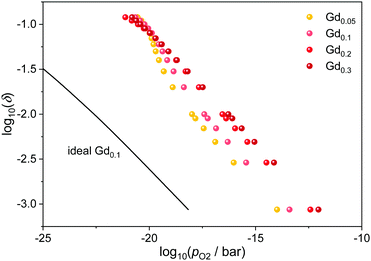 | ||
| Fig. 4 Relation between oxygen partial pressure and non-stoichiometry in Gd-doped ceria at 1073 K for different dopant fractions. The ideal behavior for Ce0.9Gd0.1O1.95−δ according to eqn (4) is indicated by the black line. | ||
The temperature influence for Ce0.9Gd0.1O1.95−δ is illustrated in Fig. 5. While all curves shift to higher partial pressures with increasing temperature, the differences between ideal and corrected curve diminish. This is due to the fact that high temperatures decrease the ordering of defects and thus the number of interacting pairs lowers. As a consequence, the impact of the defect interactions on the reduction of ceria is especially pronounced at low temperatures.
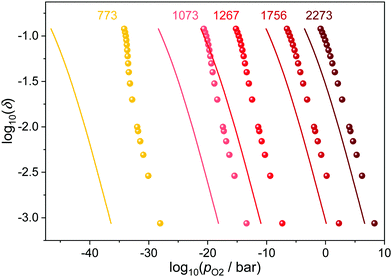 | ||
| Fig. 5 Relation between oxygen partial pressure and non-stoichiometry in Ce0.9Gd0.1O1.9−δ for different temperatures. The ideal behavior according to eqn (4) is indicated by the respective lines. | ||
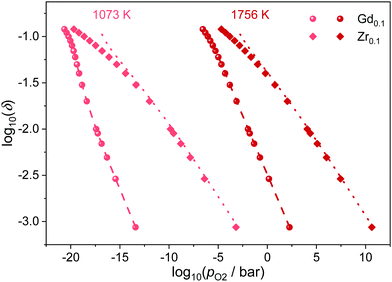
In the presented simulations, the dopant ions were distributed randomly, corresponding to the situation that can be expected for the slowly diffusing cations after quenching from high sintering temperatures. Nevertheless, long operation at elevated temperatures could lead to ordering of the dopant ions. Therefore, simulations were conducted with the dopant ions mobile, i.e. the ions are swapped during the simulations and allowed to reach their equilibrium distribution. The results are shown in Fig. 6 for Ce0.9Gd0.1O1.9−δ and Ce0.9Zr0.1O2−δ at 1073 K and 1756 K. It is apparent that the ordering has no effect on the reduction behavior of Gd-doped ceria. The same is true for Zr-doping except for a little deviation at high non-stoichiometries. Overall, the ordering of defects seems to have only little effect on the reduction, independent of temperature and dopant type.
Conclusions
The impact of defect interactions on the reduction behavior of doped ceria with the general composition Ce1−x−yRExZryO2−x/2−δ was investigated by large scale Metropolis Monte Carlo multi-stage sampling simulations based on DFT energies. The contributions of defect interactions Δrfint to the free energy of reduction were estimated and the relation between oxygen partial pressure and non-stoichiometry for the non-ideal system was predicted. The results show a clear enhancement of the reduction due to defect interactions, leading to a shift of the partial pressure to higher values by orders of magnitude. In line with experimental results, an enhancement of the non-stoichiometry in the order pure ceria < RE-doped < Zr/RE-co-doped < Zr-doped is found and the following conclusions can be drawn:• For a wide range of RE-dopants (Lu3+ to La3+) the effect on the reduction is similar as the main influence is the interaction between polaron and oxygen vacancy.
• For Sc3+ the effect is more pronounced as the strong 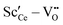 interaction plays a more important role.
interaction plays a more important role.
• The effect is even more pronounced for Zr4+ where the formation of oxygen vacancies during reduction leads to favorable 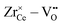 pairs.
pairs.
• The effect of interactions is especially pronounced at low temperatures, leading to stronger reduction compared to the ideal case.
• Additional co-doping of Zr-doped ceria with Gd2O3 or Y2O3 decreases the reducibility due to the vacancies introduced in the stoichiometric composition.
• Above δ > 0.1, the reduction of the lattice seems to become progressively harder irrespective of the type of dopant or the dopant fraction.
• The ordering of dopant ions seems to have only little effect on the reduction behavior.
The simulation approach allows the prediction of the deviation from the ideal reduction behavior for a broad set of dopant types, dopant fractions, temperatures, and non-stoichiometries. Although the approach, based on pair interaction energies, is relatively simple, the simulations are in good agreement with the experimentally measured trends and values.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author gratefully acknowledges the computing time granted by the JARA Vergabegremium and provided on the JARA Partition part of the supercomputer CLAIX at RWTH Aachen University.Notes and references
- H. Yao, J. Catal., 1984, 86, 254–265 CrossRef CAS.
- W. C. Chueh, C. Falter, M. Abbott, D. Scipio, P. Furler, S. M. Haile and A. Steinfeld, Science, 2010, 330, 1797–1801 CrossRef CAS PubMed.
- J. Kašpar, P. Fornasiero and M. Graziani, Catal. Today, 1999, 50, 285–298 CrossRef.
- B. C. H. Steele, Solid State Ionics, 2000, 129, 95–110 CrossRef CAS.
- R. Schmitt, A. Nenning, O. Kraynis, R. Korobko, A. I. Frenkel, I. Lubomirsky, S. M. Haile and J. L. M. Rupp, Chem. Soc. Rev., 2020, 49, 554–592 RSC.
- F. Call, M. Roeb, M. Schmücker, H. Bru, D. Curulla-Ferre, C. Sattler and R. Pitz-Paal, Am. J. Anal. Chem., 2013, 04, 37–45 CrossRef.
- F. Call, M. Roeb, M. Schmücker, C. Sattler and R. Pitz-Paal, J. Phys. Chem. C, 2015, 119, 6929–6938 CrossRef CAS.
- A. Le Gal, S. Abanades and G. Flamant, Energy Fuels, 2011, 25, 4836–4845 CrossRef CAS.
- A. Le Gal, S. Abanades, N. Bion, T. Le Mercier and V. Harlé, Energy Fuels, 2013, 27, 6068–6078 CrossRef CAS.
- Y. Hao, C.-K. Yang and S. M. Haile, Chem. Mater., 2014, 26, 6073–6082 CrossRef CAS.
- R. J. Panlener, R. N. Blumenthal and J. E. Garnier, J. Phys. Chem. Solids, 1975, 36, 1213–1222 CrossRef CAS.
- S. Wang, Solid State Ionics, 1998, 107, 73–79 CrossRef CAS.
- S. R. Bishop, K. L. Duncan and E. D. Wachsman, Electrochim. Acta, 2009, 54, 1436–1443 CrossRef CAS.
- M. Kuhn, S. R. Bishop, J. L. M. Rupp and H. L. Tuller, Acta Mater., 2013, 61, 4277–4288 CrossRef CAS.
- G. Zhou, P. R. Shah, T. Kim, P. Fornasiero and R. J. Gorte, Catal. Today, 2007, 123, 86–93 CrossRef CAS.
- S. Grieshammer, M. Nakayama and M. Martin, Phys. Chem. Chem. Phys., 2016, 18, 3804–3811 RSC.
- S. Grieshammer and M. Martin, J. Mater. Chem. A, 2017, 5, 9241–9249 RSC.
- S. Grieshammer, J. Phys. Chem. C, 2017, 121, 15078–15084 CrossRef CAS.
- J. P. Valleau, J. Chem. Phys., 1972, 57, 5457 CrossRef CAS.
- S. Eisele and S. Grieshammer, J. Comput. Chem., 2020, 41, 2663–2677 CrossRef CAS PubMed.
- S. Eisele, F. M. Draber and S. Grieshammer, Phys. Chem. Chem. Phys., 2021, 23, 4882–4891 RSC.
- S. Grieshammer, S. Eisele and J. Koettgen, J. Phys. Chem. C, 2018, 122, 18809–18817 CrossRef CAS.
- S. Grieshammer, B. O. H. Grope, J. Koettgen and M. Martin, Phys. Chem. Chem. Phys., 2014, 16, 9974 RSC.
- P. A. Zguns, A. V. Ruban and N. V. Skorodumova, Phys. Chem. Chem. Phys., 2017, 19, 26606–26620 RSC.
- S. Grieshammer, Phys. Chem. Chem. Phys., 2018, 20, 19792–19799 RSC.
- C. L. Perkins, M. A. Henderson, C. H. F. Peden and G. S. Herman, J. Vac. Sci. Technol., A, 2001, 19, 1942–1946 CrossRef CAS.
- D. Arifin, A. Ambrosini, S. A. Wilson, B. Mandal, C. L. Muhich and A. W. Weimer, Int. J. Hydrogen Energy, 2020, 45, 160–174 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00925g |
| This journal is © the Owner Societies 2021 |