Bond-forming and electron-transfer reactivity between Ar²⁺ and N₂

Abstract

Collisions between Ar²⁺ and N₂ have been studied using a coincidence technique at a centre-of-mass (CM) collision energy of 5.1 eV. Four reaction channels generating pairs of monocations are observed: Ar⁺ + N₂⁺, Ar⁺ + N⁺, ArN⁺ + N⁺ and N⁺ + N⁺. The formation of Ar⁺ + N₂⁺ is the most intense channel, displaying forward scattering but with a marked tail to higher scattering angles. This scattering, and other dynamics data, is indicative of direct electron transfer competing with a ‘sticky’ collision between the Ar²⁺ and N₂ reactants. Here Ar⁺ is generated in its ground (²P) state and N₂⁺ is primarily in the low vibrational levels of the C²Σ_u⁺ state. A minor channel involving the initial population of higher energy N₂⁺ states, lying above the dissociation asymptote to N⁺ + N, which fluoresce to stable states of N₂⁺ is also identified. The formation of Ar⁺ + N⁺ by dissociative single electron transfer again reveals the involvement of two different pathways for the initial electron transfer (direct or complexation). This reaction pathway predominantly involves excited states of Ar²⁺ (¹D and ¹S) populating N₂⁺* in its dissociative C²Σ_u⁺, 2²Π_g and D²Π_g states. Formation of ArN⁺ + N⁺ proceeds via a direct mechanism. The ArN⁺ is formed, with significant vibrational excitation, in its ground (X³Σ⁻) state. Formation of N⁺ + N⁺ is also observed as a consequence of double electron transfer forming N₂²⁺. The exoergicity of the subsequent N₂²⁺ dissociation reveals the population of the A¹Π_u and D³Π_g dication states.

---

Introduction

Doubly charged positive ions (dications) are found in a variety of energised media including the ionospheres of planets and their satelites.^1–8 As demonstrated in several studies, both atomic and molecular dications exhibit significant bimolecular reactivity following collisions with neutral species.^9–13 Indeed, the lifetimes of atomic dications in planetary ionospheres are expected to be primarily determined by such collisional processes.¹⁴ This significant dicationic reactivity suggests that dication chemistry can play a role in ionospheric processes;¹⁵ for example, dications are proposed to be involved in the chemistry of complex molecule assembly through carbon chain-growth.^14,16–19

Atomic dications have been detected in planetary ionospheres.²⁰ However, it is difficult to unambiguously detect many ionospheric molecular dications using simple mass spectrometry, the usual sampling technique. This difficulty arises because there are often monocations with the same mass to charge ratio as the target dication present in these environments.⁹ The lack of definitive detection of ionospheric molecular dications may account for the historical neglect of these species in models of ionospheric chemistry.¹⁴ In order to identify dication reactions of ionospheric interest, laboratory-based experiments to probe dicationic reactivity, along with spectroscopic identification techniques, are vital.²¹ The value of such laboratory work is shown by experiments that have identified the role molecular dications play in atmospheric erosion processes.^22–25

Following our recent study of the reactions of Ar²⁺ + O₂,²⁶ this paper presents a detailed investigation of the interactions between Ar²⁺ and N₂. This work both further elucidates the energetics, reactivity and reaction mechanisms of dications and also allows a better understanding of the relevance and influence of Ar²⁺/N₂ collisions in planetary environments.

Argon constitutes ∼1% of the Earth's atmosphere and is also found in the atmospheres of the Moon, Mercury and Mars.^27–31 In the upper reaches of these atmospheres, the formation of the Ar²⁺ dication is likely, as recognised by Thissen et al.¹⁴ The bimolecular reactivity of Ar²⁺ with a variety of rare gases and simple molecules has been studied previously.^32–38 Most of the early investigations of Ar²⁺-neutral collisions were carried out at 0.1–20 keV collision energies. At these significant collision energies only single-electron transfer (SET) and double-electron transfer (DET) channels were observed. In contrast, more recent experiments, utilising lower collision energies (<100 eV) revealed bond-forming chemistry following the interactions of Ar²⁺ with various neutral species.^26,39–44 The formation of Ar–X (X = O, N, C) bonds, detected in the above studies, confirms the bimolecular reactivity of rare gas dications as an effective route to the formation of unusual chemical species.

Nitrogen (N₂) is the dominant species in the atmospheres of the Earth and Titan, and is present in the atmospheres of other planets and satelites.^{14,15,28–31,45–47} The reactions resulting from collisions of Ar²⁺ with N₂ have been the subject of previous investigation. As noted above, at high collision energies (keV), SET and DET pathways were identified, as expected, although these studies did not probe the reactivity at an electronic state-selective level.^{32,34–36,48,49} However, in 1999, Tosi et al.³⁹ observed the formation of ArN²⁺ following the collisions of Ar²⁺ with N₂, demonstrating a more complex chemistry in this collision system than the earlier studies had indicated. Indeed, molecular ions of ArN have attracted interest due to their rare gas bond and ArN⁺ is a well-known contaminant in plasma-based mass spectrometry.^50–52 The formation of ArN⁺ has also been observed as a product of monocation-neutral^53,54 and dication-neutral reactions.⁴³ In the latter case, the production of ArN⁺ and ArNH⁺ was observed following reactions of Ar²⁺ with NH₃; the reaction proceeding via the formation of a collision complex [ArNH₃]²⁺. Computational investigations predict ArN²⁺ to be kinetically stable⁵⁵ whilst ArN⁺ is found to have the highest binding energy of the ArX⁺ (X = Li–Ne) species.⁵⁶ The stability of ArNⁿ⁺ species, and the facility of dication-neutral reactions to form new bonds, suggests that there is perhaps a richer chemistry resulting from the collisions of Ar²⁺ and N₂ than has been previously reported.

In this investigation we study collisions between Ar²⁺ and N₂, at a centre-of-mass (CM) collision energy of 5.1 eV, using position-sensitive coincidence mass spectrometry (PSCO-MS). The PSCO-MS technique involves coincident product detection via time-of-flight mass spectrometry using a position-sensitive detector. This experimental technique has been shown to provide comprehensive information on the dynamics and energetics of dicationic bimolecular reactions that generate pairs of monocationic products.^9,26,37,57 For the Ar²⁺/N₂ collision system our experiments reveal the dynamics and energetics of the SET and DET channels, including both dissociative and non-dissociative SET reactions. We see clearly that the dissociative SET reaction proceeds via two mechanisms: a long-range direct process, and a process involving the formation of a collision complex, [Ar–N₂]²⁺. We also report, for the first time, to the best of our knowledge, a bond forming channel that generates ArN⁺ + N⁺via a direct mechanism.

Experimental

Coincidence techniques involve the simultaneous detection of two or more products from a single reactive event. Bimolecular reactions of dications with neutral species often generate pairs of monocations and these pairs of ions are detected in coincidence in the PSCO-MS experiment. The PSCO-MS apparatus used in this study has been described in detail in the literature.^57–59 Briefly, a pulsed beam of dications is directed into the field-free source region of a time-of-flight mass spectrometer (TOF-MS) where the dications interact with a jet of the neutral reactant. Subsequent application of an extraction voltage to the source region allows the TOF-MS to detect the cation pairs generated from the dication-neutral interactions. The detection of these ions involves recording their arrival time, and position, at a large microchannel-plate detector. From this raw data, a list of flight times and arrival positions of the ions detected in pairs, a two-dimensional mass spectrum can be generated revealing the different reactive channels. The positional data accompanying the ionic detections shows the relative motion of the products of each reactive event, providing a detailed insight into the mechanisms of each reactive channel.⁵⁹

In this work the Ar²⁺ ions are generated, along with Ar⁺, via electron ionisation of Ar (BOC, 99.998%) by 100 eV electrons in a custom-built ion source. The positively charged argon ions are extracted from the ion source and pass through a hemispherical energy analyser to restrict the translational energy spread of the final Ar²⁺ beam to ∼0.3 eV. The continuous beam of ions exiting the hemispherical analyser is then pulsed, using a set of electrostatic deflectors, before being accelerated and focussed into a commercial velocity filter. The velocity filter is set to transmit just the ⁴⁰Ar²⁺ (m/z = 20) ions. The resulting pulsed beam of energy-constrained Ar²⁺ ions is then decelerated to less than 10 eV in the laboratory frame before entering the source region of the TOF-MS. In the source region the beam of dications is crossed with an effusive jet of N₂ (BOC, 99.998%). Single-collision conditions⁶⁰ are achieved by employing an appropriately low pressure of N₂ and, hence, most dications do not undergo a collision and only a small percentage experience one collision. Such a pressure regime ensures no secondary reactions, due to successive collisions with two N₂ molecules, influences the Ar²⁺ reactivity we observe. An electric field is applied across the TOF-MS source when the dication pulse reaches the centre of this region. This electric field accelerates positively charged species into the second electric field (acceleration region) of the TOF-MS and then on into the flight tube. At the end of the flight tube, the cations are detected by a position-sensitive detector comprising a chevron-pair of microchannel plates located in front of a dual delay-line anode.⁵⁷ The voltage pulse applied to the source region also starts the ion timing circuitry, to which the signals from the detector provide stop pulses. The experiments in this work employed both high (183 V cm⁻¹) and low (28.5 V cm⁻¹) TOF-MS source fields. As discussed in more detail below, the lower source field results in better energy resolution in the resulting PSCO-MS data. However, in these low field spectra ions with high transverse (off-axis) velocities do not reach the detector.

Signals from the detector are amplified and discriminated before being passed to a PC-based time-to-digital converter. If two ions are observed in the same TOF cycle, a coincidence event is recorded and each ion's arrival time and impact position on the detector are stored for off-line analysis. The use of single-collision conditions ensures ‘false’ coincidences are kept to a minimum. The ion pairs data can be plotted as a 2D histogram, a ‘pairs spectrum’, where the time of flights (t₁, t₂) of each ion in the pair are used as the (x, y) co-ordinates. Peaks in the pairs spectrum readily identify bimolecular reaction channels that result in a pair of positively charged product ions. Each such peak, the group of events corresponding to an individual reaction channel, can then be selected for further off-line analysis.

As shown in previous work, the positional and time of flight information for each ion of a pair can be used to generate their x, y and z velocity vectors in the laboratory frame; here the z-axis is defined by the principal axis of the TOF-MS.⁵⁷ The x and y velocity vectors of an ion are determined from the associated positional information and flight time; the z vector is determined from the deviation of the observed TOF from the expected TOF of the same ion with zero initial kinetic energy. The laboratory frame velocities are then converted into the CM frame using the initial dication velocity.⁵⁷ Often the pair of monocations resulting from the reaction between a dication and a neutral are accompanied by a neutral product: a three-body reaction. A powerful feature of the PSCO-MS experiment is that the CM velocity of such a neutral product can be determined from the CM velocities of the detected ionic products via conservation of momentum.⁵⁷

To reveal the dynamics of a given reaction channel, a CM scattering diagram (Fig. 1) can be generated from the velocities of the product ions. Such CM scattering diagrams are radial histograms that, for each event collected for a given reaction channel, plot the magnitude of the products’ CM velocity |w_i| as the radial co-ordinate and the scattering angle θ between w_i and the CM velocity of the incident dication as the angular coordinate. In the kinematics that apply in our experiment, where the dication is heavier and markedly faster than the neutral, the velocity of the incident dication is closely oriented with the velocity of the centre of mass. In our CM scattering diagrams, since 0° ≤ θ ≤ 180°, the data for one product can be shown in the upper semi-circle of the figure and the data for another product in the lower semi-circle, as the scattering of each ion is azimuthally symmetric. For three-body reactions, internal-frame scattering diagrams can be a powerful aid in interpreting the reaction dynamics. In this class of scattering diagram |w_i| is again the radial coordinate, but the angular coordinate is now the CM scattering angle with respect to CM velocity of one of the other product species.

Fig. 1 CM scattering diagram for the reaction Ar²⁺ + N₂ → Ar⁺ + N₂⁺ at a CM collision energy of 5.1 eV. The black dot indicates the position of the CM. See text for details.

From the CM velocities of the product species the total kinetic energy release (KER) T for a given reactive event can also be determined using the individual CM velocities of the products.⁵⁷ The exoergicity of the reaction ΔE can then be determined from T and the CM collision energy, E_com:

ΔE = T − E_com = −(E_products − E_reactants) (1)

where E_products and E_reactants are the relative energies of the product and reactant states respectively. If the products lie lower in energy than the reactants, the resulting exoergicity will be positive. Performing this analysis for all the events collected for a given reaction channel provides a histogram of the exoergicity of the detected reactive events. From knowledge of the available electronic states of the reactants and products the exoergicity spectrum can reveal the electronic states involved in the reaction.

Results and discussion

PSCO-MS spectra were recorded following the collisions of Ar²⁺ with N₂ at E_com = 5.1 eV. The ‘pairs’ spectrum revealed the four reaction channels shown in Table 1. The most intense channel (Rxn. I) is a non-dissociative single electron transfer process (ND-SET), producing Ar⁺ + N₂⁺. A dissociative SET (DSET) reaction, forming Ar⁺ + N⁺ + N is also observed (Rxn. II) with a slightly lower intensity than the ND-SET channel. A bond forming channel (Rxn. III) is also observed, producing ArN⁺ + N⁺. To our knowledge, the formation of ArN⁺ from the interactions of Ar²⁺ and N₂ has not been previously observed. Finally, double electron transfer (DET) is observed resulting in the formation of N⁺ + N⁺via N₂²⁺ (Rxn. IV).

Table 1 Reaction channels, following the collisions of Ar²⁺ with N₂ at a CM collision energy of 5.1 eV, with associated relative intensities (branching ratios). The modal experimental values of the total exoergicity ΔE from each reaction are reported. See text for details

Reaction	Products	Relative intensity/%	Modal experimental ΔE/eV
a The exoergicity given for Rxn. IV is the value for the N2^2+ → N^+ + N^+ dissociation.
I	Ar^+ + N2^+	43.2	5.4
II	Ar^+ + N^+ + N	41.7	6.5
III	ArN^+ + N^+	4.3	5.5
IV	Ar + N^+ + N^+	10.8	6.8^a

---

PSCO-MS experiments were also repeated at a low TOF-MS source field to yield a higher energy resolution in the exoergicity spectrum (E_com = 4.5 eV). As discussed below, these low source field experiments reveal a minor, low energy release, pathway in the ND-SET channel (Rxn. I).

Non-dissociative SET

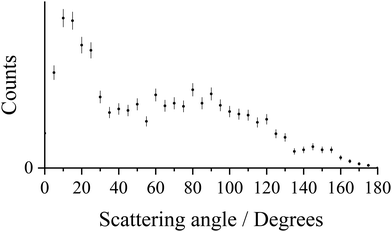
Fig. 1 shows the CM scattering diagram for the Ar⁺ + N₂⁺ product ions observed from the ND-SET reaction, Ar²⁺ + N₂ → Ar⁺ + N₂⁺. A forward scattering pattern, typical of that reported before for this class of reaction, is observed.^37,61,62 Forward scattering indicates that the velocity of the Ar⁺ product ion is predominantly oriented in the same direction as the velocity of the reactant Ar²⁺, w(Ar²⁺), while the velocity of the N₂⁺ product ion is directed anti-parallel to w(Ar²⁺). This scattering pattern is typical of a direct process, where the electron transfer occurs at a relatively large interspecies separation (3–6 Å), and is generally well represented by a Landau–Zener (LZ) formalism.^59,63–65 The scattering angles of the Ar⁺ ion (the angle between the velocity of the reactant dication w(Ar²⁺) and the velocity of the Ar⁺ product ion) are shown more clearly in Fig. 2. Fig. 2 reveals that whilst the scattering is dominated by θ < 90°, the scattering is not concentrated as intensely at lower angles as might be expected for a typical forward scattered ND-SET reaction.^37,61,62 For example, in the SET reaction between Ne²⁺ + Ar, also investigated with PSCO-MS, the Ne⁺ product was forward scattered with an angular distribution peaked at ∼15°.⁶⁵ There is also a tail in our data, to higher scattering angles, manifested in the scattering diagram (Fig. 1) by the extra ‘bumps’ involving higher velocity ions scattered between 70 < θ < 110. Both of these observations hint strongly that there is a distinct contribution to the scattering in this channel involving longer-lived association, or a ‘sticky collision’, between the reactant species, in addition to the usual direct (LZ) mechanism. As we will see below, the analysis of the N₂⁺ electronic states populated in this ND-SET channel, and the dynamics exhibited by the DSET channel, also point towards a contribution from such a non-direct reaction pathway.

Fig. 2 Histogram of the CM scattering angle θ for the product Ar⁺ ion, relative to w(Ar²⁺), for the reaction Ar²⁺ + N₂ → Ar⁺ + N₂⁺ at a CM collision energy of 5.1 eV. The error bars represent two standard deviations of the counts.

Fig. 3 shows a histogram of the exoergicities recorded in the ND-SET reaction channel, Ar²⁺ + N₂ → Ar⁺ + N₂⁺. In the exoergicity distribution, there is a maximum centred around 5.8 eV, with a full width at half maximum (FWHM) from 4.1–7.2 eV. To interpret the exoergicity spectrum for this channel, we need to consider the accessible electronic states of the reactant and product species. For these species the relevant energetic data is readily available. The Ar²⁺ beam used in this experiment has been shown to be composed of ions in the three electronic states derived from the Ar²⁺ p⁴ configuration (³P, ¹D and ¹S), with relative abundances that are approximately statistical.^26,66,67 There are two energetically accessible electronic states for the Ar⁺ product (²P and ²S).⁶⁸ The reactant N₂ molecule, admitted as an effusive beam, will be in its ground vibronic state, X¹Σ_g⁺v = 0. The ground state of N₂⁺ (X²Σ_g⁺) lies 15.58 eV above the ground state of N₂.^69,70 The lowest energy dissociation asymptote of N₂⁺ (N⁺(³P) + N(⁴S)) lies at 24.3 eV relative to N₂(X¹Σ_g⁺), which corresponds to the energy of N₂⁺(C²Σ_u⁺v = 3).^68,71 Photoionisation studies have shown that N₂⁺ states generated with a higher internal energy than 24.3 eV have dissociation lifetimes less than the timescale of our experiment and therefore will not contribute to the N₂⁺ counts observed in this channel.^71–74

Fig. 3 Experimental exoergicity spectrum for the reaction Ar²⁺ + N₂ → Ar⁺ + N₂⁺. The exoergicities for potential SET pathways (reactions (a)–(e), discussed in the text) calculated from literature values are also shown. The error bars represent two standard deviations of the associated counts.

From the above energetic considerations, we find that there are four possible ND-SET reaction pathways that match the range of exergicities^69,70 shown in Fig. 3: (a–d). Additionally, whilst pathway (e) has an exoergicty (8.9 eV) clearly outside of the observed range, if the N₂⁺(B²Σ_u⁺) product is formed with significant vibrational excitation, it could yield exoergicities in accord with our experimental observations.

Ar²⁺(³P) + N₂(X¹Σ_g⁺) → Ar⁺(²P) + N₂⁺(C²Σ_u⁺) ΔE = 4.0 eV (a)

Ar²⁺(¹D) + N₂(X¹Σ_g⁺) → Ar⁺(²P) + N₂⁺(C²Σ_u⁺) ΔE = 5.8 eV (b)

Ar²⁺(³P) + N₂(X¹Σ_g⁺) → Ar⁺(²P) + N₂⁺(D²Π_g) ΔE = 5.6 eV (c)

Ar²⁺(¹D) + N₂(X¹Σ_g⁺) → Ar⁺(²P) + N₂⁺(D²Π_g) ΔE = 7.4 eV (d)

Ar²⁺(³P) + N₂(X¹Σ_g⁺) → Ar⁺(²P) + N₂⁺(B²Σ_u⁺) ΔE = 8.9 eV (e)

The match of the calculated exoergicities of pathways (a)–(e) with the experimental spectrum is good, particularly when allowing for potential vibrational excitation of the N₂⁺ product ion. Pathways (a)–(e) are all spin-allowed and involve the formation of the Ar⁺ ion in its ground ²P state; their exoergicities are indicated in Fig. 3. Reviewing what is known of the N₂⁺ electronic states involved in these pathways is instructive. Photoelectron spectra show low intensities for the formation of N₂⁺(D²Π_g) from N₂ in this energy range due to Franck–Condon effects; in fact the D state is only stable to dissociation at significantly longer bond lengths than that of the neutral molecule. Pathway (e) involves ground state Ar²⁺(³P) and forms N₂⁺ in its B²Σ_u⁺ state. As noted above, populating the B²Σ_u⁺ state and giving an exoergicity within the observed range necessitates the state being formed with a high vibrational quantum number. The potential energy surface of the N₂⁺(B²Σ_u⁺) state has a deep well and therefore could support vibrational excitation, however, photoelectron spectra show that the first two vibrational levels, v = 0 and v = 1, are predominantly populated in a vertical transition.^69,70

In our spectra it is not possible to resolve the different N₂⁺ channels potentially involved in this ND-SET reaction. Pathways (c)–(e) involve the formation of N₂⁺(D²Π_g) or vibrationally excited levels of N₂⁺(B²Σ_u⁺). As noted above, such transitions are not favoured in a vertical transition from N₂(X¹Σ_g⁺) and previous experiments studying dicationic electron transfer have shown that the ionising transitions in the neutral are often vertical in nature.^75,76 However, ionising transitions in the neutral collison partner that produce monocations in vibrational states well outside the Franck–Condon zone have also been reported.⁷⁷ Additionally, the longer-lived association observed between the reactant species in this channel (identified above) will facilitate the formation of N₂⁺ states away from the equilibrium geometry of N₂. However, in contrast to pathways (c)–(e), pathways (a) and (b) involve the population of the lower vibrational levels of N₂⁺(C²Σ_u⁺), transitions which are favoured in the photoelectron spectrum of N₂, and are inherently more probable than transitions to the higher vibrational levels of the B²Σ_u⁺ state or D²Π_g states. Thus pathways (a) and (b), involving N₂⁺(C²Σ_u⁺), are most likely the dominant pathways in the ND-SET reaction, but a minor contribution from pathways (c)–(e) is also possible.

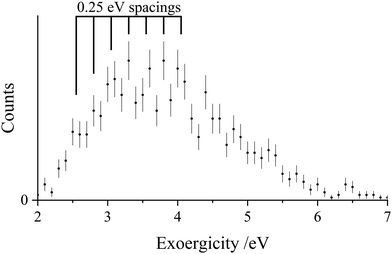
As discussed before in the literature, higher resolution energetic information is obtainable from the PSCO-MS experiment using a low TOF-MS source field.^37,57,65 In low source field experiments conducted as part of this study, the counts where the Ar⁺ ions were forward scattered relative to Ar²⁺ were masked by reactions occurring away from the source region. Thus, only events where the Ar⁺ ions were backwards scattered could be selected for analysis. Fig. 4 shows the resulting exoergicity spectrum of these back-scattered events for the ND-SET channel. As previously noted, low source field experiments do not collect product ions with high transverse velocities. Therefore, exoergicity spectra from low source field experiments discriminate in favour of events with lower exoergicities. The exoergicity of the back-scattered events in the low source field experiment (Fig. 4) ranges from ∼2.5 eV–5.5 eV. The range of exoergicities revealed in Fig. 4 are clearly present at the low energy extreme of the exoergicity distribution generated by the high source field experiment (Fig. 3). One way to account for these low exoergicities is to invoke the population of higher energy, long-lived, N₂⁺ states than those involved in pathways (a)–(e). However, given the extensive studies of N₂⁺ it is unlikely that there are previously unknown long-lived metastable states of N₂⁺ lying above the dissociation asymptote to N⁺ + N.

Fig. 4 Experimental exoergicity spectrum for the back scattered (θ(Ar⁺) > 90°) counts of the ND-SET reaction, Ar²⁺ + N₂ → Ar⁺ + N₂⁺, in the low source field experiment. A comb is shown with a line spacing of 0.25 eV. The error bars represent two standard deviations of the associated counts.

The formation of stable states of N₂⁺(X, A) in processes involving low exoergicities (2.7 eV, 1.6 eV) is possible from reactions of Ar²⁺(¹S) with N₂, if Ar⁺(²S) is generated as the atomic monocation. However, such processes cannot account for the signals around 3 eV in Fig. 4. Indeed, Ar²⁺(¹S) is a minor component of the dication beam and formation of Ar⁺(²S) from Ar²⁺(¹S) involves a two-electron transition, usually a strong indication of a disfavoured process. Thus, we do not feel such reactions can explain the form of the exoergicity spectrum (Fig. 4) at low exoergicities. A more likely explanation of these low exoergicity processes, generating long-lived N₂⁺ ions, is that the N₂⁺(C²Σ_u⁺) state is formed with an energy above the first dissociation limit, before fluorescing to a N₂⁺ bound state, most likely X²Σ_g⁺. Populating these higher vibrational levels of the C state will result in the reduced exoergicity we observe. Several of the electronic excited states of N₂⁺ higher in energy than X²Σ_g⁺, including the N₂⁺(C²Σ_u⁺) state, are known to fluoresce to lower-lying electronic states.^78–80 Since our energetic analysis above clearly shows population of bound levels of the C state, it is not unreasonable to propose higher levels of the C state are also populated, and these levels then, in competition with their dissociation, fluoresce to result in long-lived N₂⁺ ions. In Fig. 4, there is perhaps a hint of fine structure that could result from the vibrational structure of the N₂⁺ state populated in this low exoergicity region. The spacings of these features (Fig. 4) appear to be of the order of ∼0.25 eV which is the vibrational spacing of the N₂⁺(C²Σ_u⁺) state.⁶⁹ The competition between fluorescence and predissociation has been studied in depth for N₂⁺(C²Σ_u⁺).^71,81,82 Predissociation dominates over fluorescence when N₂⁺ is formed with more energy than the lowest energy dissociation asymptote (24.3 eV).^82–84 However, predissociation of the C state will not generate counts in this ND-SET channel, but instead contributes to the counts in the DSET channel, Rxn II., as discussed below. So although the yield of the C state fluorescence is low, the long-lived N₂⁺ ions resulting from this emissive process will be sensitively detected in the low-field spectrum.

To summarise, the ND-SET reaction forming Ar⁺ + N₂⁺ is the dominant channel resulting from the collisions of Ar²⁺ and N₂. A broadly forward scattering dynamic was observed, indicative of a direct, long-range electron transfer, but with a significant tail to higher scattering angles, indicative of a competitive mechanism involving a longer-lived association between the reactant species. After the electron transfer, Ar⁺ is generated in its ground (²P) state and N₂⁺ is likely predominantly generated in its C²Σ_u⁺ state, with perhaps a minor contribution from the B²Σ_u⁺ and D²Π_g states. The high dissociation threshold of N₂⁺ and the involvement of the most abundant Ar²⁺ states present in the beam explain why this ND-SET reaction is the most intense product channel in the Ar²⁺ + N₂ collision system.

Dissociative single electron transfer

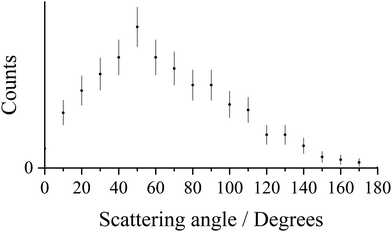
The pairs spectrum we record following collisions of Ar²⁺ with N₂ shows a clear peak corresponding to the formation of Ar⁺ + N⁺: a DSET reaction. The general mechanism for dicationic DSET reactions has been well investigated,^{37,64,85–87} and involves an initial LZ style single electron transfer, populating a product cation in a dissociative state (e.g. N₂⁺*), followed by subsequent dissociation of that ion. In the CM scattering diagram these dynamics result in strong forward scattering (Fig. 5a), with the velocity of the Ar⁺ product w(Ar⁺) strongly oriented with w(Ar²⁺). The scattering angles of the Ar⁺ ions are shown in more detail in Fig. 6 which reveals a bimodal distribution: a large peak at low scattering angles, consistent with a direct mechanism, along with an additional broad peak at higher scattering angles. This secondary peak has a broad maximum close to 90°, typical of processes involving isotropic scattering associated with a longer temporal association between the Ar²⁺ and N₂ species. That is, the involvement of a collision complex, as also suggested by the ND-SET data discussed above. Again, it seems clear that both a direct mechanism and a mechanism involving complexation are operating in this channel.

Fig. 5 Scattering diagrams for the reaction Ar²⁺ + N₂ → Ar⁺ + N⁺ + N at a CM collision energy of 5.1 eV. (a) CM scattering diagram showing the scattering of N⁺ and Ar⁺ relative to the incident dication velocity, w(Ar²⁺). (b) Internal frame scattering diagram showing the scattering of N⁺ and N relative to the velocity of the Ar⁺ product ion. In part (b) the labelled vector, (1), represents 0.30 cm μs⁻¹.

Fig. 6 Histogram for the CM scattering angles for the product Ar⁺ ion, relative to w(Ar²⁺), for the reaction Ar²⁺ + N₂ → Ar⁺ + N⁺ + N at a CM collision energy of 5.1 eV. The error bars represent two standard deviations of the counts.

Fig. 5b shows the internal frame scattering of the N⁺ and N products, relative to the velocity of the Ar⁺ product. The N⁺ and N fragments are clearly both back-scattered, away from the Ar⁺ product ion, confirming that any complex between the N₂ and Ar²⁺ initially dissociates into N₂⁺* + Ar⁺. Fig. 5b also clearly shows that the N⁺ ion flies away from the Ar⁺ ion with a greater velocity than the N product. Such a signature has been observed before in DSET reactions,^26,37 and indicates the N₂⁺* ion dissociates in the Coulomb field of the Ar⁺, and the N⁺ product is subsequently further accelerated. An estimate of the lifetime of the N₂⁺* species generated in this DSET reaction can be determined by a simple electrostatic model to reproduce the additional velocity of the N⁺ species with respect to the nitrogen atom. The difference in the velocities of the N⁺ and N fragments corresponds to dissociation of the N₂⁺* at an average distance of 11 ± 0.5 Å from the Ar⁺, equating to an N₂⁺ lifetime of approximately 100 fs. The N₂⁺* lifetime calculated here is comparable to our previous estimates of the lifetime of N₂⁺* formed from collisions of Ne²⁺ with N₂,⁸⁵ as well as that of O₂⁺* formed in the Ar²⁺ + O₂ system.²⁶

The experimentally determined total exoergicity of the DSET reaction, (see Fig. S1 in the ESI†) for forming Ar⁺ + N⁺ + N, has a peak at 6.5 eV with a FWHM from 4.4 eV–8.0 eV. The bulk of the counts in this spectrum can be accounted for by contributions from the first and second excited states of Ar²⁺ (¹D and ¹S) forming N⁺ + N at the three lowest energy dissociation limits of N₂⁺ together with Ar⁺(²P).^68,88 The three channels involving Ar²⁺(¹S) result in nominal exoergicities of 7.4 eV, 5.5 eV, and 5.0 eV, in good accord with the bulk of the exoergicity distribution. Additionally, minor structure towards lower exoergicities could point to the involvement of Ar²⁺(³P) or N⁺(¹S).

Considering the higher energy events in the exoergicity spectrum (Fig. S1, ESI†) we note that, as previously discussed, if N₂⁺ is formed with an energy of over 24.33 eV relative to the ground state of N₂ (equivalent to N₂⁺(C²Σ_u⁺v = 3)) and does not fluoresce, it will dissociate within the lifetime of our experiment and therefore can contribute the DSET channel.^71–74 The maximum energy that can be released from Ar²⁺(¹S) accepting an electron to form the ground state monocation, Ar⁺(²P), is 31.75 eV. Therefore, the maximum exoergicity in this channel is 7.42 eV if we restrict ourselves to the p⁴ states of Ar²⁺. There are a significant number of counts observed in this channel above this theoretical maximum of 7.4 eV (∼30%, see Fig. S1, ESI†). These higher energy events are too numerous and extend to too high an energy to be explained by the spread in the translation energy of the Ar²⁺ ions in the beam (FWHM = 0.3 eV). One possible source for these higher energy events is higher lying excited Ar²⁺ energy states in the beam. However, we see little evidence of such states in other channels in this collison system, or in our previous work involving Ar²⁺.^26,37,67 However, the clear observation of a significant complexation pathway in this reaction channel provides an explanation for these high energy events. Specifically, if the translational energy of the Ar²⁺ in the beam can be coupled into the reaction, a process that is not normally involved in the direct SET mechanism⁹ but is perfectly feasible when complexation is involved, exoergicities of up to ∼12.5 eV are perfectly possible. The Ar⁺ scattering angle distribution of the high exoergicity events (>7.4 eV) is dominated by the peak centered at 90°, indicating a link with the complexation pathway. Thus, it seems highly likely that the high energy tail in the exoergicity distribution is yet another signature of complexation competing with direct electron transfer in this collision system.

If we consider the DSET reaction to be predominantly stepwise, the exoergicity of the initial electron transfer step (forming Ar⁺ and N₂⁺*) can be estimated using the N₂⁺* precursor velocity. The N₂⁺* precursor velocity is determined, on an event-wise basis, via conservation of momentum from the Ar⁺ velocity. Using this method, which neglects any small contribution to the Ar⁺ velocity from interaction with the final N⁺ product, we find the exoergicity for the initial electron transfer step to have a broad peak centred at 5.0 eV and with a FWHM from 2.9 eV–6.4 eV, as shown in Fig. 7. Exoergicity distributions for such primary electron transfer reactions of dications are commonly peaked between 2 and 6 eV due to such exoergicities favouring the net curve crossing probability as predicted in the LZ model.^64,89

Fig. 7 Exoergicity spectrum for the initial electron transfer reaction in the DSET channel, Ar²⁺ + N₂ → Ar⁺ + N₂⁺*. The literature exoergicities are identified in Table 2. The error bars represent two standard deviations of the associated counts.

As discussed above, this DSET channel, producing Ar⁺ + N⁺ + N, mostly involves Ar²⁺(¹D and ¹S), and results in the formation of N₂⁺* in a dissociative state. The dissociative states of N₂⁺* that best fit the exoergicity data in Fig. 7 are: the C²Σ_u⁺ state (v > 2), the 2²Π_g state, and the continuum of the D²Π_g state (E ∼26 eV), all of which lie in the Franck–Condon region of the N₂ ground state.⁷⁰ Photoelectron spectra from Baltzer et al.⁷⁰ show that the 2²Π_g state overlaps with the C²Σ_u⁺ state around the Franck–Condon region, overlying the D continuum, and these states are therefore indistinguishable in our experiment. We detail in Table 2 the possible pathways contributing to this channel, the exoergicities of which are marked on Fig. 7. Pathways (i) and (j) match well with the peak of the observed experimental exoergicity distribution, and involve the formation of N₂⁺(C²Σ_u⁺) and N₂⁺(D²Π_g) respectively. Pathway (h) also involves the formation of D²Π_g with Ar²⁺(¹D). There are also possible smaller contributions from pathways (f) and (g), which populate the higher lying F²Σ_g⁺ and G²Π_u or H²Π_u states of N₂⁺; structures that hint at these reactions can be seen in the exoergicity spectrum (Fig. 7). Additionally, pathway (k) could contribute to this channel, involving Ar²⁺(¹S) generating N₂⁺(C²Σ_u⁺). Of course, the observed exoergicities will be broadened by the population of the N₂⁺ species in a range of vibrational states.

Table 2 Exoergicities for primary electron transfer reactions in the DSET channel, Ar²⁺ + N₂(X¹Σ_g⁺) → Ar⁺(²P) + N₂⁺*, this electron transfer populates a dissociative state of the molecular nitrogen cation

Pathway	Ar^2+ state	N2^+ state	Exoergicity/eV
(f)	^1S	G^2Πu or H^2Πu	1.8
(g)	^1S	F^2Σg^+	3.0
(h)	^1D	D^2Πg	3.4
(i)	^1D	C^2Σu^+ at predissociaton limit	5.0
(j)	^1S	D^2Πg	5.8
(k)	^1S	C^2Σu^+ at predissociaton limit	7.4

---

The exoergicity of the final N₂⁺* dissociation can also be evaluated by determining the velocities of the N⁺ and N products, on an event by event basis, in the frame of the N₂⁺* precursor velocity.²⁶ This exoergicity spectrum (Fig. 8) has a maximum at 0.9 eV with a FWHM extending from 0.1 eV–2.3 eV. To interpret this exoergicity, we must consider previous studies of N₂⁺ dissociation. As noted above, the dissociation threshold, corresponding to the lowest energy N⁺ + N asymptote, L1 (N⁺(³P) + N(⁴S⁰), Table 3), lies at ∼24.3 eV above the molecular ground state and corresponds to N₂⁺(C²Σ_u⁺v = 3).^71–73 At energies above the second dissociation limit, L2 (N⁺(¹D) + N(⁴S⁰), ∼26.2 eV, Table 3), there is competition between dissociation to L1 and L2.^88,90,91 In studies of N₂ excitation, at the energies involved in the processes we see in our experiment (24.3–32 eV), the C²Σ_u⁺ state is the dominant state populated in photoelectron spectra and dissociation to the three lowest energy dissociation asymptotes is observed, with lifetimes of the order of nanoseconds.^{69,70,74,79,92–95} The predissociation of N₂⁺(C²Σ_u⁺) is thought to occur via several mechanisms including by spin orbit coupling to the ²Σ_u⁻ state then transition to the continuum of ⁴Π_u.^{71,93,96–98}

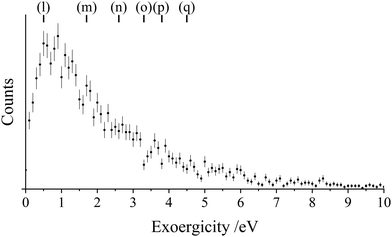Fig. 8 Experimental exoergicity spectrum for the dissociation of the N₂⁺* product to form N⁺ and N. The literature exoergicities marked at the top are shown in Table 3. The error bars represent two standard deviation of the counts. See text for details.

Table 3 Possible exoergicities calculated from literature values for the dissociation of N₂⁺*. L1, L2 and L3 are the three lowest energy dissociation asymptotes forming N⁺ + N

Pathway	N2^+ state	N^+ + N states	Exoergicity/eV
(l)	C^2Σu^+ or 2^2Πg at (E = 24.8eV)	N^+(^3P) + N(^4S^0) (L1)	0.5
(m)	D^2Πg	N^+(^3P) + N(^4S^0) (L1)	1.7
(n)	F^2Σg^+	N^+(^1D) + N(^4S^0) (L2)	2.6
(o)	G^2Πu or H^2Πu	N^+(^3P) + N(^2D^0) (L3)	3.3
(p)	G^2Πu or H^2Πu	N^+(^1D) + N(^4S^0) (L2)	3.8
(q)	F^2Σg^+	N^+(^3P) + N(^4S^0) (L1)	4.5

---

In previous experiments probing the dissociation of N₂⁺*, produced via electron impact or photoionisation, kinetic energy releases of 0.5 eV–8 eV were observed.^90,99 The maximum theoretical exoergicity for N₂⁺* dissociation in this channel, under the energy constraints of the current study, is 7.4 eV, arising when Ar²⁺(¹S) is involved and N₂⁺* dissociates to the lowest energy dissociation limit, L1. Considering the maximum theoretical exoergicity available in this system (7.4 eV), the exoergicity observed in this study matches nicely with the previous experiments characterising N₂⁺* dissociation.

The shape of the exoergicity spectrum we see for the dissociation of N₂⁺* (Fig. 8) can be associated with the pathways shown in Table 3. The main contributions are clearly from the C²Σ_u⁺/2²Π_g or the D²Π_g states dissociating to L1, in satisfying accord with the assignment made above that the initial electron transfer step populates these ionic states. Additionally there are potentially minor contributions from the involvement of some of the higher energy excited states of N₂⁺. These states were also implicated in the above anaylsis of the initial electron transfer, showing a coherent description of the electron transfer state selectivity is emerging.

To summarise, dissociative single electron transfer is the second most intense channel following the collisions of Ar²⁺ and N₂ at a collision energy of 5.1 eV. The scattering angles of the Ar⁺ product ion (Fig. 6) show that two mechanisms are involved in the initial electron transfer: a direct, Landau–Zener process where the electron transfer occurs at long range, and a process involving the formation of a complex [Ar–N₂]²⁺. In this channel, electron transfer predominantly involves N₂ and Ar²⁺ (¹D and ¹S), forming Ar⁺(²P), and N₂⁺* formed in the dissociative C²Σ_u⁺, 2²Π_g and D²Π_g states. These N₂⁺* ions then fragment, a dissociation slightly perturbed by the field of the Ar⁺ product, primarily to the lowest energy dissociation asymptote, N⁺(³P) + N(⁴S⁰). The lifetime of N₂⁺* before it dissociates was determined to be ∼100 fs, comparable to estimates for N₂⁺* generated in similar experiments.⁸⁵ There is a spread in the observed exoergicities due to minor contributions from the involvement of Ar²⁺(³P), N₂⁺(F²Σ_g⁺) and N₂⁺(G²Π_u or H²Π_u) and higher energy dissociation limits of N⁺ + N.

Chemical bond formation

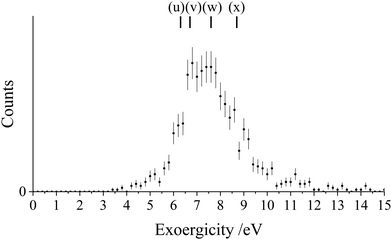
Fig. 9 shows the CM scattering of the ArN⁺ and N⁺ products observed from the previously unreported bond forming channel, Rxn. III. Fig. 9 shows that the ArN⁺ product ion is scattered with a marked bias towards lower scattering angles. This bias can be seen more clearly in the histogram of ArN⁺ scattering angles, shown in Fig. 10. This form of the scattering suggests a stripping-style mechanism where an N⁻ is transferred between the N₂ and Ar²⁺ species at a relatively large interspecies separation. This style of direct mechanism is similar to that found in our previous work with the analogous channel in the Ar²⁺ + O₂ system, forming ArO⁺.²⁶ The more usual mechanism observed for a chemical bond forming reaction between a dication and neutral species involves a ‘long-lived’ association between the reactant species with a lifetime of at least several rotations of this collision complex.^59,61 However, direct mechanisms for bond forming reactions between dications and neutral species have been previously reported.³⁷ The scattering data shown here shows little evidence for a long-lived association between the reactants. If such a complex survived for long enough to undergo several rotations, the relationship of the direction of approach of the reactant species would be scrambled and both product fragments would be scattered effectively isotropically about the CM, as has been observed before in other collision systems.^62,100 It is interesting that formation of ArN⁺ from the Ar²⁺ + N₂ system proceeds via a direct mechanism rather than complexation, particularly given the clear evidence of complexation observed in the SET channels. The formation of new chemical bonds via direct processes is well-established in dication reactions and the experimental data clearly imply that complexation does not provide a viable route to populate long-lived states of ArN⁺.

Fig. 9 CM scattering diagram for the reaction Ar²⁺ + N₂ → ArN⁺ + N⁺ at a CM collision energy of 5.1 eV. The scattering of N⁺ and ArN⁺ are shown relative to the incident dication velocity, w(Ar²⁺). See text for details.

Fig. 10 Histogram of the CM scattering angles for the product ArN⁺ ion, relative to w(Ar²⁺), for the reaction Ar²⁺ + N₂ → ArN⁺ + N⁺ at a CM collision energy of 5.1 eV. The error bars represent two standard deviations of the counts.

Fig. 11 shows the experimental exoergicity distribution observed for the bond-forming reaction (Rxn. III). The exoergicity maximum is at 5.5 eV, and the FWHM is from 3.5 eV–9.0 eV. To interpret this exoergicity we note that several states of ArN⁺ have been identified theoretically.^51,56,101 The ground state, X³Σ⁻, and first excited state, A³Π, are both lower in energy than the Ar(¹S⁰) + N⁺(³P⁰) dissociation asymptote and their formation has been reported from the reactions of N₂⁺ + Ar and Ar⁺ + N₂ respectively.⁵³ Here we will consider just the ground state, X³Σ⁻, which is well bound with a significant dissociation energy (∼2.1 eV). The minimum of the ArN⁺(A³Π) state lies just below the Ar(¹S⁰) + N⁺(³P⁰) dissociation asymptote. Thus, we would not expect to populate long-lived, and hence detectable, ArN⁺(A³Π) states with the level of vibrational excitation that we expect to result from a long-range N⁻ abstraction from N₂ by Ar²⁺.

Fig. 11 Experimental exoergicity spectrum for the reaction producing ArN⁺ and N⁺ from Ar²⁺ and N₂ at a CM collision energy of 5.1 eV. The exoergicities for potential reaction pathways calculated from literature values are shown (reactions (r)–(t), discussed in the text).^56,68 The error bars represent two standard deviations of the associated counts. See text for details.

From consideration of the calculated ArN⁺ energies and literature values for known N⁺ and Ar²⁺ states, reaction pathways (r)–(t) provide a very good match to the exoergicity distribution observed for this channel.^56,68 Pathways (s) and (t) result from the production of ArN⁺(X³Σ⁻) and N⁺ in its ground state (³P) from the two lowest energy Ar²⁺ states in our beam (³P and ¹D). Pathway (r) results in the formation of N⁺ in its first excited state, ¹D. Note that these pathways are all spin allowed. Of course, the formation of vibrationally excited ArN⁺, which we expect due to the long-range N⁻ abstraction from N₂ by Ar²⁺, will act to spread (decrease) the nominal exoergicity of the reaction, in accord with the spread in the exoergicity data in Fig. 11.

Ar²⁺(³P) + N₂(X¹Σ_g⁺) → ArN⁺(X³Σ⁻) + N⁺(¹D) ΔE = 4.7 eV (r)

Ar²⁺(³P) + N₂(X¹Σ_g⁺) → ArN⁺(X³Σ⁻) + N⁺(³P) ΔE = 6.6 eV (s)

Ar²⁺(¹D) + N₂(X¹Σ_g⁺) → ArN⁺(X³Σ⁻) + N⁺(³P) ΔE = 8.3 eV (t)

The formation of ArN⁺ from the collisions of Ar²⁺ and N₂ has not been previously reported, to the best of our knowledge. This study therefore offers another potential source for the formation of ArN⁺ species detected in Ar/N₂ plasmas.^50,51 The scattering shows that, unusually, this reaction proceeds via a direct mechanism. The relative intensity for this channel is high (4.3%) compared with typical bond forming dication-neutral reactions, showing an affinity to form the Ar–N bond.^{41–43,102–107}

Dissociative double electron transfer

Rxn. IV from the Ar²⁺/N₂ collison system results in the formation of N⁺ + N⁺ and has relative intensity of 10.8%. From the dynamics it is clear that this channel originates from double electron transfer (DET), via the formation of N₂²⁺, as the N⁺ + N⁺ ions are effectively isotropically scattered about the velocity of the N₂ reactant. Such DET reactions are commonly observed in dicationic collision systems,^37,108,109 where two electrons transfer from N₂ to the Ar²⁺ ion and the nascent N₂²⁺ ion then dissociates. As discussed in more detail in our previous work,^26,37 dicationic DET usually favours a concerted mechanism in which the product and reactant asymptotes lie close in energy (<1 eV).³⁷ The Ar²⁺ ground state (³P) and first two excited states (¹D and ¹S) have energies of 43.4 eV, 45.1 eV and 47.5 eV above the ground state of Ar respectively.⁶⁸ There are several dissociative states of N₂²⁺ that lie at a comparable energy to these Ar²⁺ states relative to the ground state of N₂.^69,110,111 Therefore, concerted DET would be expected to occur in the Ar²⁺ + N₂ system. The dissociation of N₂²⁺ into N⁺ + N⁺ has been well studied. In 1996, Lundqvist et al.¹¹⁰ reported the kinetic energies of N₂²⁺ dissociation revealing energy releases of 6.7–7 eV corresponding to the v = 7–10 levels of the A¹Π_u state dissociating to the lowest energy N⁺ + N⁺ asymptote, D1(N⁺(³P) + N⁺(³P)). Lundqvist et al. also observed peaks at 7.6 and 7.7 eV, corresponding to the N₂²⁺(D³Π_g) v = 0 and v = 1 levels dissociating to D1. In Lundqvist's study of the dissociation of N₂²⁺ the dominant contribution is from the lowest energy N⁺ + N⁺ dissociation asymptote.

From analysis of the N⁺ ion velocities, we see the exoergicity for the dissociation of N₂²⁺ in the DET channel has a maximum centred at 7.2 eV with a FWHM from 6.2–8.6 eV, shown in Fig. 12. The experimental exoergicity distribution is a good match with the observations of Lundqvist et al.¹¹⁰ (see Fig. 12) and also agrees well with energy releases reported in other studies of N₂²⁺ dissociation.^112–116 Therefore, it seems clear that the nascent N₂²⁺ is generated in the A¹Π_u and D³Π_g states which predominantly dissociate to form pairs of N⁺(³P) ions.

Fig. 12 Experimental exoergicity spectrum for the dissociation of N₂²⁺, formed in an initial DET reaction between Ar²⁺ and N₂, to form N⁺ and N⁺. The exoergicities for potential N₂²⁺ dissociation pathways calculated from literature values are also shown: (u) N₂²⁺(E = Ar²⁺(¹D)) → N⁺(³P) + N⁺(³P), (v) N₂²⁺(A¹Π_u, v = 7) → N⁺(³P) + N⁺(³P), (w) N₂²⁺(D³Π_g, v = 0) → N⁺(³P) + N⁺(³P) and (x) N₂²⁺(E = Ar²⁺(¹S)) → N⁺(³P) + N⁺(³P). The error bars represent two standard deviations of the associated counts. See text for details.

Conclusions

Collisions between Ar²⁺ and N₂ have been studied using a coincidence technique at a CM collision energy of 5.1 eV. Four reaction channels generating pairs of monocations are observed, producing: Ar⁺ + N₂⁺, Ar⁺ + N⁺, ArN⁺ + N⁺ and N⁺ + N⁺. The formation of Ar⁺ + N₂⁺ is the most intense channel, displaying forward scattering but with a marked tail to higher scattering angles. This scattering is indicative of direct electron transfer competing with a ‘sticky’ collision between the Ar²⁺ and N₂ reactants. After the electron transfer, Ar⁺ is generated in its ground (²P) state and N₂⁺ is primarily in the low vibrational levels of the C²Σ_u⁺ state, with contributions from the B²Σ_u⁺ state and D²Π_g states. The exoergicity distribution in this channel also indicates a minor contribution to the formation of N₂⁺via the initial population of higher energy N₂⁺ states, lying above the dissociation asymptote to N⁺ + N, which fluoresce to stable states of N₂⁺.

The formation of Ar⁺ + N⁺ results from dissociative single electron transfer. The scattering in this channel again reveals the involvement of two different pathways for the initial electron transfer: a long-range direct process, and a process involving the formation of a complex, [ArN₂]²⁺. Satisfyingly, the operation of these same pathways was extracted from the data for the non-dissociative channel. Despite the differing dynamics, the electronic states involved in this dissociative electron transfer reaction appear the same for both routes. That is, the excited states of Ar²⁺ (¹D and ¹S) are involved in the initial electron transfer, populating N₂⁺* in its dissociative C²Σ_u⁺, 2²Π_g and D²Π_g states. The nascent N₂⁺* then quickly dissociates, primarily to the lowest energy dissociation asymptote, N⁺(³P) + N(⁴S).

We also observe the formation of ArN⁺ + N⁺ which has not been previously reported. The scattering shows that this bond-forming reaction proceeds via a direct mechanism. The molecular ion ArN⁺ is formed, with significant vibrational excitation, in its X³Σ⁻ state. Finally, the formation of N⁺ + N⁺ is observed, resulting from double electron transfer that initially generates N₂²⁺ which subsequently dissociates. The exoergicity of the N₂²⁺ dissociation is in good agreement with previous studies of the dissociation of the isolated dication, formed in a vertical transition from the neutral molecule, which involve the dissociation of the A¹Π_u and D³Π_g dication states.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the financial support of the EPSRC (EP/J010839/1), the Leverhulme Trust (RPG-2017-309) and UCL.

References

1. C. Simon, J. Lilensten, O. Dutuit, R. Thissen, O. Witasse, C. Alcaraz and H. Soldi-Lose, Ann. Geophys., 2005, 23, 781–797.
2. H. S. Bridge, J. W. Belcher, A. J. Lazarus, J. D. Sullivan, R. L. McNutt, F. Bagenal, J. D. Scudder, E. C. Sittler, G. L. Siscoe, V. M. Vasyliunas, C. K. Goertz and C. M. Yeates, Science, 1979, 204, 987–991.
3. S. Ghosh, K. K. Mahajan, J. M. Grebowsky and N. Nath, J. Geophys. Res., 1995, 100, 23983–23991.
4. J. H. Hoffman, C. Y. Johnson, J. C. Holmes and J. M. Young, J. Geophys. Res., 1969, 74, 6281–6290.
5. E. Dubinin, R. Modolo, M. Fraenz, J. Woch, G. Chanteur, F. Duru, F. Akalin, D. Gurnett, R. Lundin, S. Barabash, J. D. Winningham, R. Frahm, J. J. Plaut and G. Picardi, J. Geophys. Res.: Space Phys., 2008, 113, A10217.
6. J. Lilensten, O. Witasse, C. Simon, H. Soldi-Lose, O. Dutuit, R. Thissen and C. Alcaraz, Geophys. Res. Lett., 2005, 32, L03203.
7. J. Lilensten, C. Simon, O. Witasse, O. Dutuit, R. Thissen and C. Alcaraz, Icarus, 2005, 174, 285–288.
8. O. Witasse, O. Dutuit, J. Lilensten, R. Thissen, J. Zabka, C. Alcaraz, P.-L. Blelly, S. W. Bougher, S. Engel, L. H. Andersen and K. Seiersen, Geophys. Res. Lett., 2002, 29, 104.
9. S. D. Price, J. D. Fletcher, F. E. Gossan and M. A. Parkes, Int. Rev. Phys. Chem., 2017, 36, 145–183.
10. D. Ascenzi, J. Aysina, E. L. Zins, D. Schröder, J. Žabka, C. Alcaraz, S. D. Price and J. Roithová, Phys. Chem. Chem. Phys., 2011, 13, 18330–18338.
11. J. Roithová, H. Schwarz and D. Schröder, Chem. – Eur. J., 2009, 15, 9995–9999.
12. W. Wolff, H. Luna, R. Schuch, N. D. Cariatore, S. Otranto, F. Turco, D. Fregenal, G. Bernardi and S. Suárez, Phys. Rev. A, 2016, 94, 022712.
13. P. Bhatt, T. Sairam, A. Kumar, H. Kumar and C. P. Safvan, Phys. Rev. A, 2017, 96, 022710.
14. R. Thissen, O. Witasse, O. Dutuit, C. S. Wedlund, G. Gronoff and J. Lilensten, Phys. Chem. Chem. Phys., 2011, 13, 18264–18287.
15. O. Dutuit, N. Carrasco, R. Thissen, V. Vuitton, C. Alcaraz, P. Pernot, N. Balucani, P. Casavecchia, A. Canosa, S. Le Picard, J.-C. Loison, Z. Herman, J. Zabka, D. Ascenzi, P. Tosi, P. Franceschi, S. D. Price and P. Lavvas, Astrophys. J. Suppl. Ser., 2013, 204, 20.
16. C. L. Ricketts, D. Schröder, C. Alcaraz and J. Roithová, Chem. – Eur. J., 2008, 14, 4779–4783.
17. E.-L. Zins and D. Schröder, J. Phys. Chem. A, 2010, 114, 5989–5996.
18. J. Roithová and D. Schröder, Chem. – Eur. J., 2007, 13, 2893–2902.
19. J. Roithová and D. Schröder, Phys. Chem. Chem. Phys., 2007, 9, 731–738.
20. L. A. Frank, W. R. Paterson, K. L. Ackerson, V. M. Vasyliunas, F. V. Coroniti and S. J. Bolton, Science, 1996, 274, 394–395.
21. H. Sabzyan, E. Keshavarz and Z. Noorisafa, J. Iran. Chem. Soc., 2014, 11, 871–945.
22. S. Falcinelli, F. Pirani, M. Alagia, L. Schio, R. Richter, S. Stranges, N. Balucani and F. Vecchiocattivi, Atmosphere, 2016, 7, 112.
23. S. Falcinelli, M. Rosi, P. Candori, F. Vecchiocattivi, J. M. Farrar, F. Pirani, N. Balucani, M. Alagia, R. Richter and S. Stranges, Planet. Space Sci., 2014, 99, 149–157.
24. J. Lilensten, C. Simon Wedlund, M. Barthélémy, R. Thissen, D. Ehrenreich, G. Gronoff and O. Witasse, Icarus, 2013, 222, 169–187.
25. M. Alagia, N. Balucani, P. Candori, S. Falcinelli, F. Pirani, R. Richter, M. Rosi, S. Stranges and F. Vecchiocattivi, Rend. Lincei, 2013, 24, 53–65.
26. S. Armenta Butt and S. D. Price, Phys. Chem. Chem. Phys., 2020, 22, 8391–8400.
27. D. F. Mark, F. M. Stuart and M. de Podesta, Geochim. Cosmochim. Acta, 2011, 75, 7494–7501.
28. A. G. W. Cameron, Space Sci. Rev., 1973, 15, 121–146.
29. S. A. Stern, Rev. Geophys., 1999, 37, 453–491.
30. A. O. Nier, W. B. Hanson, A. Seiff, M. B. McElroy, N. W. Spencer, R. J. Duckett, T. C. Knight and W. S. Cook, Science, 1976, 193, 786–788.
31. D. D. Bogard, R. N. Clayton, K. Marti, T. Owen and G. Turner, in Space Science Reviews, ed. R. Kallenbach, J. Geiss and W. K. Hartmann, Springer, Dordrecht, 2001, vol. 12, pp. 425–458.
32. G. Dupeyrat, J. B. Marquette, B. R. Rowe and C. Rebrion, Int. J. Mass Spectrom. Ion Process., 1991, 103, 149–156.
33. W. Lindinger, E. Alge, H. Störi, M. Pahl and R. N. Varney, J. Chem. Phys., 1977, 67, 3495–3499.
34. H. Störi, E. Alge, H. Villinger, F. Egger and W. Lindinger, Int. J. Mass Spectrom. Ion Phys., 1979, 30, 263–270.
35. E. Y. Kamber, P. Jonathan, A. G. Brenton and J. H. Beynon, J. Phys. B: At. Mol. Phys., 1987, 20, 4129–4142.
36. G. C. Shields and T. F. Moran, J. Phys. B: At. Mol. Phys., 1983, 16, 3591–3607.
37. M. A. Parkes, J. F. Lockyear and S. D. Price, Int. J. Mass Spectrom., 2009, 280, 85–92.
38. B. Friedrich and Z. Herman, Chem. Phys. Lett., 1984, 107, 375–380.
39. P. Tosi, R. Correale, W. Lu, S. Falcinelli and D. Bassi, Phys. Rev. Lett., 1999, 82, 450–452.
40. P. Tosi, W. Lu, R. Correale and D. Bassi, Chem. Phys. Lett., 1999, 310, 180–182.
41. W. Lu, P. Tosi and D. Bassi, J. Chem. Phys., 2000, 112, 4648–4651.
42. D. Ascenzi, P. Franceschi, P. Tosi, D. Bassi, M. Kaczorowska and J. N. Harvey, J. Chem. Phys., 2003, 118, 2159–2163.
43. N. Lambert, D. Kearney, N. Kaltsoyannis and S. D. Price, J. Am. Chem. Soc., 2004, 126, 3658–3663.
44. J. F. Lockyear, K. Douglas, S. D. Price, M. Karwowska, K. J. Fijalkowski, W. Grochala, M. Remeš, J. Roithová and D. Schröder, J. Phys. Chem. Lett., 2010, 1, 358–362.
45. H. B. Niemann, S. K. Atreya, J. E. Demick, D. Gautier, J. A. Haberman, D. N. Harpold, W. T. Kasprzak, J. I. Lunine, T. C. Owen and F. Raulin, J. Geophys. Res., 2010, 115, E12006.
46. O. Badr and S. D. Probert, Appl. Energy, 1993, 46, 1–67.
47. E. W. Schwieterman, T. D. Robinson, V. S. Meadows, A. Misra and S. Domagal-Goldman, Astrophys. J., 2015, 810, 57.
48. D. Smith, D. Grief and N. G. Adams, Int. J. Mass Spectrom. Ion Phys., 1979, 30, 271–283.
49. H. M. Holzscheiter and D. A. Church, J. Chem. Phys., 1981, 74, 2313–2318.
50. K. Hu and R. S. Houk, J. Am. Soc. Mass Spectrom, 1993, 4, 28–37.
51. J. S. Becker, G. Seifert, A. I. Saprykin and H.-J. Dietze, J. Anal. At. Spectrom., 1996, 11, 643–648.
52. S. C. Wilschefski and M. R. Baxter, Clin. Biochem. Rev., 2019, 40, 115–133.
53. P. Tosi, R. Correale, W. Lu and D. Bassi, J. Chem. Phys., 1999, 110, 4276–4279.
54. G. D. Flesch and C. Y. Ng, J. Chem. Phys., 1990, 92, 2876–2882.
55. M. W. Wong and L. Radom, J. Phys. Chem., 1989, 93, 6303–6308.
56. G. Frenking, W. Koch, D. Cremer, J. Gauss and J. F. Liebman, J. Phys. Chem., 1989, 93, 3410–3418.
57. W.-P. Hu, S. M. Harper and S. D. Price, Meas. Sci. Technol., 2002, 13, 1512–1522.
58. W.-P. Hu, S. M. Harper and S. D. Price, Mol. Phys., 2005, 103, 1809–1819.
59. S. D. Price, Int. J. Mass Spectrom., 2007, 260, 1–19.
60. K. Yamasaki and S. R. Leone, J. Chem. Phys., 1989, 90, 964–976.
61. Z. Herman, Int. J. Mass Spectrom., 2015, 378, 113–126.
62. M. A. Parkes, J. F. Lockyear and S. D. Price, Int. J. Mass Spectrom., 2014, 365–366, 68–74.
63. S. A. Rogers, S. D. Price and S. R. Leone, J. Chem. Phys., 1993, 98, 280–289.
64. Z. Herman, Int. Rev. Phys. Chem., 1996, 15, 299–324.
65. S. M. Harper, W.-P. Hu and S. D. Price, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, 4409–4423.
66. T. Nakamura, N. Kobayashi and Y. Kaneko, J. Phys. Soc. Jpn., 1985, 54, 2774–2775.
67. J. F. Lockyear, M. A. Parkes and S. D. Price, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 145201.
68. A. Kramida, Y. Ralchenko and J. Reader, NIST ASD Team, NIST Atomic Spectra Database (version 5.6.1), National Institute of Standards and Technology, Gaithersburg, MD, 2020.
69. A. J. Yencha, K. Ellis and G. C. King, J. Electron Spectrosc. Relat. Phenomena, 2014, 195, 160–173.
70. P. Baltzer, M. Larsson, L. Karlsson, B. Wannberg and M. Carlsson Göthe, Phys. Rev. A, 1992, 46, 5545–5553.
71. H. R. Hrodmarsson, R. Thissen, D. Dowek, G. A. Garcia, L. Nahon and T. R. Govers, Front. Chem., 2019, 7, 222.
72. E. M. Bahati, J. J. Jureta, D. S. Belic, H. Cherkani-Hassani, M. O. Abdellahi and P. Defrance, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, 2963–2973.
73. X. Tang, Y. Hou, C. Y. Ng and B. Ruscic, J. Chem. Phys., 2005, 123, 074330.
74. L. Åsbrink and C. Fridh, Phys. Scr., 1974, 9, 338–340.
75. H. R. Koslowski, H. Lebius, V. Staemmler, R. Fink, K. Wiesemann and B. A. Huber, J. Phys. B: At., Mol. Opt. Phys., 1991, 24, 5023–5034.
76. A. Ehbrecht, N. Mustafa, C. Ottinger and Z. Herman, J. Chem. Phys., 1996, 105, 9833–9846.
77. E. Y. Kamber, K. Akgüngör, C. P. Safvan and D. Mathur, Chem. Phys. Lett., 1996, 258, 336–341.
78. L. C. Lee, J. Phys. B: At. Mol. Phys., 1977, 10, 3033–3045.
79. S. R. Langhoff and C. W. Bauschlicher, J. Chem. Phys., 1988, 88, 329–336.
80. A. Lofthus and P. H. Krupenie, J. Phys. Chem. Ref. Data, 1977, 6, 113–307.
81. R. Marx, G. Mauclaire and S. Fenistein, Chem. Phys. Lett., 1975, 33, 357–361.
82. T. R. Govers, C. A. van de Runstraat and F. J. de Heer, Chem. Phys., 1975, 9, 285–299.
83. A. Ehresmann, L. Werner, S. Klumpp, P. V. Demekhin, M. P. Lemeshko, V. L. Sukhorukov, K.-H. Schartner and H. Schmoranzer, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, L119.
84. C. A. van de Runstraat, F. J. de Heer and T. R. Govers, Chem. Phys., 1974, 3, 431–450.
85. S. M. Harper, S. W.-P. Hu and S. D. Price, J. Chem. Phys., 2004, 120, 7245–7248.
86. S. D. Price, M. Manning and S. R. Leone, J. Am. Chem. Soc., 1994, 116, 8673–8680.
87. C. L. Ricketts, D. Schröder, J. Roithová, H. Schwarz, R. Thissen, O. Dutuit, J. Žabka, Z. Herman and S. D. Price, Phys. Chem. Chem. Phys., 2008, 10, 5135–5143.
88. J. H. Eland and E. Duerr, Chem. Phys., 1998, 229, 13–19.
89. S. D. Price, J. Chem. Soc., Faraday Trans., 1997, 93, 2451–2460.
90. T. Aoto, K. Ito, Y. Hikosaka, A. Shibasaki, R. Hirayama, N. Yamamono and E. Miyoshi, J. Chem. Phys., 2006, 124, 234306.
91. Y. Morioka, T. Akahori, T. Hayaishi, T. Namioka, T. Sasaki and M. Nakamura, J. Phys. B: At. Mol. Phys., 1986, 19, 1075–1080.
92. R. J. Van Brunt and L. J. Kieffer, J. Chem. Phys., 1975, 63, 3216–3221.
93. J. C. Lorquet and M. Desouter, Chem. Phys. Lett., 1972, 16, 136–140.
94. C. Nicolas, C. Alcaraz, R. Thissen, M. Vervloet and O. Dutuit, J. Phys. B: At., Mol. Opt. Phys., 2003, 36, 2239–2251.
95. H. Yoshii, T. Tanaka, Y. Morioka, T. Hayaishi and R. I. Hall, J. Mol. Spectrosc., 1997, 186, 155–161.
96. B. Paulus, J. F. Pérez-Torres and C. Stemmle, Phys. Rev. A, 2016, 94, 053423.
97. M. Hochlaf, G. Chambaud and P. Rosmus, J. Phys. B: At., Mol. Opt. Phys., 1997, 30, 4509–4514.
98. R. Locht, J. Schopman, H. Wankenne and J. Momigny, Chem. Phys., 1975, 7, 393–404.
99. L. Deleanu and J. A. D. Stockdale, J. Chem. Phys., 1975, 63, 3898–3906.
100. C. L. Ricketts, S. M. Harper, S. W. P. Hu and S. D. Price, J. Chem. Phys., 2005, 123, 134322.
101. L. Broström, M. Larsson, S. Mannervik and D. Sonnek, J. Chem. Phys., 1991, 94, 2734–2740.
102. K. A. Newson and S. D. Price, Chem. Phys. Lett., 1998, 294, 223–228.
103. K. A. Newson, N. Tafadar and S. D. Price, J. Chem. Soc., Faraday Trans., 1998, 94, 2735–2740.
104. P. W. Burnside and S. D. Price, Int. J. Mass Spectrom., 2006, 249–250, 279–288.
105. D. Kearney and S. D. Price, Phys. Chem. Chem. Phys., 2003, 5, 1575–1583.
106. S. M. Harper, S. W. P. Hu and S. D. Price, J. Chem. Phys., 2004, 121, 3507–3514.
107. J. D. Fletcher, M. A. Parkes and S. D. Price, Int. J. Mass Spectrom., 2015, 377, 101–108.
108. M. A. Parkes, J. F. Lockyear and S. D. Price, Int. J. Mass Spectrom., 2013, 354–355, 39–45.
109. J. D. Fletcher, M. A. Parkes and S. D. Price, Mol. Phys., 2015, 113, 2125–2137.
110. M. Lundqvist, D. Edvardsson, P. Baltzer and B. Wannberg, J. Phys. B: At., Mol. Opt. Phys., 1996, 29, 1489–1499.
111. M. Hochlaf, R. I. Hall, F. Penent, H. Kjeldsen, P. Lablanquie, M. Lavollée and J. H. D. Eland, Chem. Phys., 1996, 207, 159–165.
112. C. Wu, Y. Yang, Z. Wu, B. Chen, H. Dong, X. Liu, Y. Deng, H. Liu, Y. Liu and Q. Gong, Phys. Chem. Chem. Phys., 2011, 13, 18398.
113. N. Saito and I. H. Suzuki, J. Phys. B: At. Mol. Phys., 1987, 20, L785–L790.
114. J. N. Bull, J. W. L. Lee and C. Vallance, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 91, 022704.
115. H. Iwayama, T. Kaneyasu, Y. Hikosaka and E. Shigemasa, J. Chem. Phys., 2016, 145, 034305.
116. W. Eberhardt, E. W. Plummer, I.-W. Lyo, R. Carr and W. K. Ford, Phys. Rev. Lett., 1987, 58, 207–210.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00918d

---