Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
DFT benchmark studies on representative species and poisons of methane steam reforming on Ni(111)†
Sai Sharath
Yadavalli
a,
Glenn
Jones
b and
Michail
Stamatakis
 *a
*a
aThomas Young Centre and Department of Chemical Engineering, University College London, Roberts Building, Torrington Place, London WC1E 7JE, UK. E-mail: m.stamatakis@ucl.ac.uk
bJohnson Matthey Technology Centre, Sonning Common, Reading RG4 9NH, UK
First published on 23rd June 2021
Abstract
Ni catalysts used in methane steam reforming (MSR) are highly susceptible to poisoning by carbon-based species, which poses a major impediment to the productivity of industrial operations. These species encompass graphitic carbon-like formations that are typically modelled as graphene. First principles-based approaches, such as density functional theory (DFT) calculations, can provide valuable insight into the mechanism of graphene growth in the MSR reaction. It is, however, critical that a DFT model of this reaction can accurately describe the interactions of Ni(111) with the MSR intermediates as well as graphene. In this work, a systematic benchmark study has been carried out to identify a suitable DFT functional for the graphene–MSR system. The binding energies of graphene and important MSR species, as well as the reaction energies of methane dissociation and carbon oxidation, were computed on Ni(111) using GGA functionals, DFT-D and van der Waals density functionals (vdW-DF). It is well-established that the GGA functionals are inadequate for describing graphene–Ni(111) interactions. In the case of vdW-DF, the optPBE-vdW functional predicts the binding energies of graphene and several important MSR species with reasonable accuracy; however, it provides poor estimates of CO and O binding energies. Among the DFT-D functionals, PBE-D3 and PBE-dDsC have been found to exhibit acceptable accuracy for graphene and most MSR species (excluding adsorbed CO), and therefore, both functionals are promising for elucidating carbon-based catalytic poisoning in the MSR reaction. Overall, no single DFT functional could estimate the binding energies of all the species with equally high accuracy.
1. Introduction
Methane steam reforming (MSR) is an important industrial process for the production of carbon monoxide and hydrogen (commonly referred to as syngas). These species are crucial in various industrial applications, for instance, in the Fischer–Tropsch process, syngas acts as a feedstock for manufacturing a variety of liquid hydrocarbons.1 Hydrogen is widely used in several industrial operations such as ammonia production, removal of sulphur/nitrogen containing compounds from crude oil, and hydrogenation of unsaturated hydrocarbons.2 It also finds applications as a clean energy source for fuel cell vehicles and electric power generation.3 Typically, hydrogen is produced in the chemical industries using processes such as partial oxidation of methane, dry reforming of methane and MSR.4,5 Among the aforementioned processes, MSR is a major contributor; for instance, in the United States, around 95 percent of hydrogen is produced from the MSR process.3 Currently, MSR is reported to be the most cost-effective and well-established industrial method available for hydrogen production.6Ni is commonly preferred as a catalyst for MSR due to its low price and high activity.5 However, the deactivation of Ni-based catalysts is a major impediment to the productivity of the MSR process. The presence of hydrocarbons and the extreme operating conditions (high temperatures and pressures) of MSR make Ni susceptible to deactivation. The deactivation mechanisms can be broadly classified into three categories: carbon poisoning, sulphur poisoning and Ni particle sintering.7 Among the catalyst deactivation mechanisms, carbon poisoning, commonly referred to as “coking”, severely affects the performance of MSR.8 The coking process mainly involves the nucleation of carbon as graphitic layers (also called whisker carbon) on the support side of the Ni catalyst. Despite numerous efforts, there is a lack of comprehensive molecular-level understanding on the poisoning mechanism of whisker carbon at steam reforming conditions.7
First principles-based methods such as density functional theory (DFT) calculations can provide fundamental insight into the MSR reaction chemistry and whisker carbon formation. The former has been extensively studied using DFT (see e.g. ref. 3, 9, 10 and 11), while there is a limited number of DFT studies on whisker carbon poisoning of MSR. For instance, Helveg et al.12 used high resolution in situ transmission electron microscopy (HRTEM) and DFT calculations to elucidate the mechanism of whisker carbon growth at the molecular scale. The study reports that the carbon atom preferentially binds on the Ni step-edge in the first instance; subsequently, the carbon atom diffuses from the Ni step-edge to the terrace and forms graphene islands. More recently, Abild-Pedersen et al.13 performed DFT calculations to construct the potential energy diagram for the formation of graphene islands on Ni(111). Furthermore, Bengaard et al.9 also proposed a DFT model for graphene formation on Ni(111). These DFT studies conclude that the formation of graphene layers on the terrace is primarily responsible for the deactivation of active sites of Ni (at the molecular scale). Thus, an accurate description of graphene–Ni(111) interactions is of paramount importance to understand whisker carbon poisoning in MSR.
The graphene–Ni(111) system requires a thorough description of local interactions as well as van der Waals forces (non-local correlations).14 The incorporation of van der Waals forces in the exchange–correlation is a major challenge of Kohn–Sham DFT. Some of the standard exchange–correlation functionals, such as those based on the local density approximation (LDA), the generalised gradient approximation (GGA) and hybrid functionals are inaccurate in the description of van der Waals forces.15 Several studies attempted to address this issue by developing dispersion-inclusive DFT functionals such as DFT-D and van der Waals DFT functionals (vdW-DF). The DFT-D approach involves the inclusion of a correction term to the Kohn–Sham DFT energy, which captures the asymptotic behaviour of long-range interactions.15 Some notable DFT-D correction schemes have been developed by Grimme,16 Tkatchenko–Scheffler,17 Steinmann18,19 and Ortmann.20 In the vdW-DF formalism, on the other hand, the non-local correlations are expressed as a functional of electron density; there is no dependence on additional input parameters.15 The first general such functional (vdW-DF) was developed by Dion et al.21 Modified versions of vdW-DF have subsequently been developed, such as the optB86b-vdW, optB88-vdW and optPBE-vdW functionals22,23 as well as the Bayesian error estimation functional (BEEF-vdW24).
Recent studies have extensively tested the applicability of DFT-D3 functionals and vdW-DF for accurately describing the graphene–Ni(111) interactions. Li et al.25 studied the graphene–Ni(111) system using DFT functionals – PBE, PBE-D3 and optB86b-vdW; the authors report that the optB86b-vdW functional gives a reasonable estimate of the graphene–Ni distance and the graphene binding energy. Mittendorfer et al.14 compared the graphene–Ni(111) binding energy predictions of several vdW-DF. In that study, the optB88-vdW functional was found to accurately predict the binding energy of graphene on Ni(111). Furthermore, Janthon et al.26 and Muñoz-Galán et al.27 have carried out comprehensive benchmark studies of graphene–Ni(111) using vdW-DF and DFT-D functionals; these works mainly conclude that the PBE-D3 (Grimme correction) functional has excellent predictive accuracy and the vdW-DF such as optB86b-vdW and optB88-vdW are also promising. In summary, the benchmark studies have successfully identified a few suitable DFT functionals – PBE-D3, optB86b-vdW and optB88-vdW – for capturing the chemical interactions between graphene and Ni(111).
The aforementioned DFT benchmark studies have solely focussed on the graphene–Ni(111) system. However, the MSR reaction network involves several intermediates that bind on Ni(111) mainly via short-range interactions (unlike graphene). In order to develop a reliable DFT model for graphene formation in MSR, it is equally important to capture the chemistry of such intermediates. DFT benchmarks of chemisorbed species/intermediates (bonding mainly via short-range interactions in most cases) are not uncommon in the literature. In this context, Zhu et al.28 used several GGA functionals and DFT-D3 functionals to compute the binding energies of H and H2O on the Ni(111) surface. PBE was able to estimate the binding energy of hydrogen with acceptable accuracy, however, it significantly under-predicts the water binding energy. On the other hand, DFT-D3 functionals (such as PBE-D3 and RPBE-D3) predict the binding energy of water with excellent accuracy but overestimate the hydrogen binding energy. Göltl et al.29 benchmarked the performance of important GGA functionals, DFT-D functionals and vdW-DF for predicting the heat of molecular/dissociative adsorptions of CH4, CH3I, CH3, I and H on Ni(111). The authors conclude that no individual DFT functional has high accuracy for all the species. For instance, the PBE-D3 functional was found to exhibit high predictive accuracy for species such as CH4, CH3 and CH3I, whereas the BEEF-vdW functional gave the best estimate for the binding energies of H and I. Gautier et al.30 computed the binding energies of carbon monoxide, oxygen, hydrogen and several hydrocarbons on Pt(111) using DFT functionals such as PBE, PBE-dDsC and few other vdW-DF. The authors compared the predictions of these functionals with micro-calorimetry data obtained from the literature. In addition, Wellendorff et al.31 carried out a benchmark study for the DFT functionals using experimental data of ten different transition metals. There are other DFT benchmark studies that have tested the applicability of DFT-D functionals and vdW-DF for various systems.32,33 Nevertheless, to the best of our knowledge, a thorough investigation on the performance of GGA functionals, DFT-D functionals and vdW-DF in predicting the binding energies of key intermediates of MSR and graphene on Ni(111) is not available in the literature.
The main objective of this work is to do a systematic comparative study on the predictive accuracy of relevant GGA functionals, DFT-D functionals and vdW-DF for graphene and a few representative MSR elementary reactions. To achieve this goal, the binding energies of graphene and MSR species (CO, C, CH3, H2O, H, O and OH), and the reaction energies of methane dissociation (considered to be the rate-determining step of MSR) and carbon oxidation were computed on the Ni(111) surface. The DFT functionals include PBE,34 RPBE35 and revPBE36 (GGA functionals), PBE-D3, RPBE-D3, revPBE-D3,16 PBE-dDsC18,19 and PBE-TS17 (DFT-D functionals), optB86b-vdW, optB88-vdW, optPBE-vdW22 and BEEF-vdW24 (vdW-DF). The predictions of the aforementioned DFT functionals have been benchmarked against experimental and computational data (from higher-level theory) available in the literature.
The rest of this manuscript is organised as follows. The “Methods” section includes the computational details of the DFT calculations and the relevant formulae used to estimate the DFT binding energy, the zero-point energy (ZPE) correction, the thermal energy contributions and the root mean-square deviation (RMSD). Subsequently, the “Results and discussion” section presents the comparison of DFT predictions of graphene and MSR species to relevant literature data and puts the key findings in the context of practical catalysis. Finally, in the “Conclusions” section, a broad perspective on the performance of GGA functionals, DFT-D functionals and vdW-DF is provided, and some needs and potential opportunities for DFT method development are also discussed.
2. Methods
Spin-polarised DFT calculations have been performed using the Vienna ab initio Simulation Package (VASP). The projector augmented wave (PAW) method was used to model the interactions between core and valence electrons. A plane-wave basis set was employed, and the kinetic energy cut-off was set to 400 eV (refer to Fig. S1(b) and S2(b) of the ESI,† for the plane-wave cut-off convergence plots). The Ni bulk calculations were carried out using a 19 × 19 × 19 k-point grid. In the Ni bulk system, the electron smearing is performed using the tetrahedron method with Blöchl corrections and the smearing width was set to 0.05 eV. The Ni(111) surface was modelled with a six-layer p(4 × 4) slab, where the Ni atoms of the three bottom-most layers were fixed at the optimised lattice constant and others were allowed to fully relax. The periodic images along the z-direction were separated by a vacuum of 12 Å. The first Brillouin zone of Ni(111) was sampled with a 5 × 5 × 1 Monkhorst–Pack k-point grid. The k-point mesh was chosen by performing convergence tests on carbon–Ni(111) and graphene–Ni(111), respectively (refer to Fig. S1(a) and S2(a) of the ESI†). The electronic self-consistency tolerance was set to 10−7 eV, and the geometry optimisation terminated when the Hellmann–Feynman forces acting on the atoms that are allowed to relax reached a value less than 0.01 eV Å−1. The smearing of electrons was carried out using the Methfessel–Paxton method and the smearing width was set to 0.1 eV. In the vibrational calculations, the Hessian matrix was computed using the central finite-difference method. The step size of the displacement was set to 0.02 Å.The binding energy of the adsorbate has been computed using eqn (1), where Eslabtot is the DFT-computed total energy of the clean Ni(111) slab, EA(g)tot indicates the gas phase DFT total energy of the adsorbate, EA+slabtot represents the DFT total energy of the adsorbate–Ni(111) system, and EDFTbind is the DFT-predicted binding energy of the adsorbate on Ni(111). If the adsorbate undergoes dissociative adsorption, eqn (2) is used to estimate the binding energy of the adsorbate, where  is the gas phase DFT total energy of the adsorbate molecule. In an effort to make a reliable comparison to experimental data, the ZPE and thermal energy corrections have been calculated, making it possible to report the internal energy of binding. Eqn (3) and (4) provide the ZPE estimate (within the harmonic approximation) for the species in the gas phase and the bound state, respectively.37,38 In these equations, N denotes the total number of atoms of the molecule, Ntrans the number of translational modes, Nrot then number of rotational modes, vi the frequency of the ith vibrational mode and h Planck's constant.
is the gas phase DFT total energy of the adsorbate molecule. In an effort to make a reliable comparison to experimental data, the ZPE and thermal energy corrections have been calculated, making it possible to report the internal energy of binding. Eqn (3) and (4) provide the ZPE estimate (within the harmonic approximation) for the species in the gas phase and the bound state, respectively.37,38 In these equations, N denotes the total number of atoms of the molecule, Ntrans the number of translational modes, Nrot then number of rotational modes, vi the frequency of the ith vibrational mode and h Planck's constant.
| EDFTbind = Eslabtot + EA(g)tot − EA+slabtot | (1) |
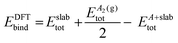 | (2) |
 | (3) |
 | (4) |
When an adsorbate binds to the Ni(111) surface, the translational and rotational motions are reduced to vibrational modes. The thermal energy contribution of the bound state has been computed by using the harmonic approximation.37,38 According to Réocreux et al.,39 the thermal corrections of chemisorbed species obtained under the harmonic approximation have acceptable accuracy (even for low-frequency modes). The bound state vibrational calculation is performed by fixing the positions of the Ni surface atoms (vibrational modes of the Ni surface atoms, commonly referred to as phonons, are assumed to have an insignificant contribution to energies of adsorption or reaction). Eqn (5) and (6) provide the thermal correction for species in the gas phase and the bound state, respectively. In eqn (7), the ZPE and thermal corrections are added to the DFT predicted binding energy.
 | (5) |
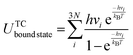 | (6) |
| Utheorybind = EDFTbind + EZPEgas phase + UTCgas phase − EZPEbound state − UTCbound state | (7) |
 | (8) |
The term Utheorybind from eqn (7) is used to make comparisons with experimental data and the root mean square deviation (RMSD) defined by eqn (8) is adopted to obtain a quantitative measure on the overall performance of the DFT functional (in Section 3.2). In eqn (8), Utheorybind,i indicates the DFT predicted binding energy of the ith species and Uexpbind,i represents the experimental binding energy of the ith species.
3. Results and discussion
As discussed in the “Introduction” section, the whisker carbon poisoning of MSR primarily involves the formation of graphene islands on the support side of the Ni catalyst (at the molecular scale). Since graphene binds on Ni(111) under the influence of van der Waals interactions, the DFT model of whisker carbon growth must be able to capture the dispersion forces of graphene–Ni(111) as well as the local interactions of MSR intermediates. Thus motivated, our systematic benchmark study aims at identifying an appropriate DFT functional for the MSR reaction species including graphene. To this end, we employ the computational setup discussed in the “Methods” section to calculate the binding energies of these species on Ni(111) using a range of functionals (GGA, DFT-D, vdW-DF) and assess the performance thereof by comparing the predictions with theoretical and experimental data available in the literature. In the following, we discuss our results in detail, starting with the DFT benchmarks of graphene–Ni(111), subsequently, the graphene–Ni(111) potential energy profiles are presented (Section 3.1), and finally, the DFT benchmarks of MSR species are provided (Section 3.2). Additionally, we tested the predictive accuracy of DFT functionals in reproducing the energies of gas-phase reactions relevant to MSR, as well as graphite formation (refer to Table S2 of the ESI†).3.1 DFT benchmarks of graphene–Ni(111)
For all of our calculations of pure graphene and Ni(111), we have used the DFT-predicted lattice constants which are provided in the ESI,† for each functional (refer to Table S1, ESI†). For the calculations of graphene bound to Ni(111), the Ni lattice constant was adopted. It is known that the LDA, GGA and hybrid functionals fail to capture the van der Waals interactions between graphene and Ni(111),15 and thus, in this benchmark study, the performance of DFT-D and vdW-DF has been tested.The DFT predictions must be compared to reliable experimental or theoretical values; however, there is limited experimental data on the binding energy of graphene on Ni(111). Shelton et al.40 have studied the segregation behaviour of carbon on Ni(111) and concluded that the binding energy of graphene on Ni(111) is around 50 meV greater than the graphite exfoliation energy. Recent experimental works have reported the exfoliation energy of graphite to be in the range of 24.87–66.33 meV per C atom.26,41,42 Based on the findings of Shelton et al.,40 the graphene binding energy on Ni(111) can be deduced to be in the range of 74.62–116.08 meV per C atom.26
As the graphene binding energy estimate is derived using the findings of only a single experimental study (Shelton et al.40), a certain level of caution must be exercised while comparing this value to the DFT predictions. Thus, we also compare our calculated values to theoretical ones, obtained with higher level ab initio methods. A few studies have reported that the random-phase approximation (RPA) method accurately captures the van der Waals interactions.14,43 The RPA prediction of graphene binding energy will therefore be used in assessing the performance of DFT functionals. The RPA predicts two minima for graphene on Ni(111), located at graphene–Ni distances of 2.17 Å and 3.25 Å, respectively.14,44,45 The RPA prediction at the former minimum (referred to as the “first minimum” henceforth) is of importance as it is in close agreement with the experimental graphene–Ni distance of 2.11 ± 0.07 Å.46Fig. 1 compares the DFT-predicted binding energies, RPA prediction14 and experimental value26,40 at the first minimum of graphene–Ni(111). The DFT calculations of graphene–Ni(111) are performed using the top-fcc configuration, which is the most stable configuration (refer to the Fig. S3 of the ESI,† for the different types of graphene–Ni(111) configurations).47,48 In Table 1, the DFT binding energy predictions of this work are compared to the values reported by other theoretical studies available in the literature. The graphene–Ni distance predictions of the DFT functionals are also recorded in Table 1.
 | ||
| Fig. 1 Comparison of the binding energy predictions of the DFT functionals used in this study with the RPA14/experimental value26,40 at the first minimum of graphene–Ni(111). | ||
| Functional | Binding energy (meV per C atom) | Graphene–Ni distance (Å) | Binding energy predictions from literature (meV per C atom) |
|---|---|---|---|
| Ref. 14 uses a five-layer Ni(111) supercell, a 19 × 19 × 1 k-point mesh and a kinetic energy cut-off value of 400 eV. Ref. 24 uses a five-layer p(1 × 1) Ni(111) slab (two bottom layers fixed) and a 20 × 20 × 1 k-point mesh. In ref. 25 a four-layer p(1 × 1) Ni(111) supercell (two bottom layers are fixed), a 20 × 20 × 1 k-point mesh and a plane-wave cut-off energy value of 500 eV was used. Ref. 26 and 27 use a six-layer p(1 × 1) Ni(111) supercell (three bottom layers fixed), a 7 × 7 × 1 k-point grid and a kinetic energy cut-off value of 415 eV. Ref. 44 uses a six-layer p(1 × 1) Ni(111) supercell (three bottom layers are fixed), a k-point mesh of size 25 × 25 × 1 and a plane-wave cut-off energy value of 500 eV.a For the graphene–Ni(111) calculation with the PBE-TS functional, we have used the PBE-D3 optimised Ni lattice constant. On the other hand, if the PBE-TS optimised Ni lattice constant is used for this calculation, the latter does not converge to the first minimum. Further details are provided in the ESI (refer to Table S16 and Fig. S7). | |||
| PBE-D3 | 54.72 | 2.23 | 79.80 (ref. 27), 86.02 (ref. 26), 53 (ref. 44) |
| PBE-dDsC | 42.39 | 2.12 | No values reported |
| PBE-TSa | 178.61 | 2.15 | 51.82 (ref. 26), 128.52 (ref. 27) |
| RPBE-D3 | [No binding] | — | No values reported |
| revPBE-D3 | [No binding] | — | No values reported |
| optB86b-vdW | 105.12 | 2.15 | 68.40 (ref. 26), 102 (ref. 44), 112 (ref. 25) |
| optB88-vdW | 66.82 | 2.22 | 40.42 (ref. 26), 67 (ref. 14) |
| optPBE-vdW | 41.79 | 2.22 | 9.33 (ref. 26) |
| BEEF-vdW | −1.09 (±75.45) | 2.18 | Around −8 (ref. 24), 10 (ref. 44) |
Among the DFT functionals which use the vdW-DF formalism, the binding energy prediction of the optB88-vdW functional is in excellent agreement with the RPA value. The optB88-vdW prediction also agrees closely with the lower bound of the experimental result (refer to Fig. 1). Furthermore, Mittendorfer et al.14 have shown that the optB88-vdW functional predicts the binding energy of graphene with high accuracy. As illustrated in Fig. 1, the optB86b-vdW functional substantially overpredicts the binding energy of graphene with respect to the RPA value, though the predicted value is within the experimental range. Shepard and Smeu44 and Li et al.25 have reported similar binding energy values for graphene using the optB86b-vdW functional. On the contrary, the calculations performed by Janthon et al.26 show that there is close agreement between the optB86b-vdW prediction and the RPA value (refer to Table 1 for the optB86b-vdW predictions obtained from the literature).
As shown in Table 1, the optPBE-vdW functional estimates a binding energy value of 41.79 meV per C atom for graphene–Ni(111), which is in reasonable agreement with the RPA value. Janthon et al.26 report that the optPBE-vdW functional predicts a much weaker adsorption energy for graphene–Ni(111) (9.33 meV per C atom). The authors use a different computational setup compared to our study; this could be the reason for such a substantial difference in the reported optPBE-vdW predictions (key information on the computational setup of the literature studies is provided in the footnote of Table 1). The BEEF-vdW functional was found to predict a weak repulsive interaction between graphene and Ni(111), as also pointed out by Wellendorff et al.24 The computational error estimate of BEFF-vdW is large (obtained by employing an ensemble of 2000 functionals24). Certain caution needs to be exercised while using the BEEF-vdW error estimate which results in a graphene binding energy range from −76.54 meV per C (negative values are qualitatively incorrect with respect to the RPA prediction) to 74.36 meV per C (substantially strong binding affinity between graphene and Ni(111); which closely matches the RPA value). This wide variation also underscores the importance of using the appropriate exchange–correlation approximation to obtain accurate results.
The PBE-TS functional significantly overestimates the graphene binding propensity on the Ni(111) crystal, while the PBE-D3 and PBE-dDsC functionals predict the binding energy of graphene in reasonable agreement with RPA (refer to Fig. 1). However, the predictions of both functionals are substantially lower than the experimental value, though there is quite some uncertainty in the latter, as discussed earlier. The benchmark studies of Muñoz-Galán et al.27 and Janthon et al.26 also conclude that the PBE-D3 functional is an appropriate choice to describe the graphene–Ni(111) interactions. On the other hand, the DFT calculations of RPBE-D3 and revPBE-D3 functionals do not converge to the first minimum of graphene–Ni(111). These functionals show a qualitative disagreement with the RPA prediction at the first minimum of graphene–Ni(111). In an effort to further substantiate these results, the potential energy profiles of graphene–Ni(111) were generated for the DFT-D3 functionals. It is evident from Fig. 2(a) that a shallow minimum at a graphene–Ni distance of 2.23 Å is obtained using the PBE-D3 functional. In contrast, the potential energy profiles of RPBE-D3 and revPBE-D3 functionals predict no such minimum at a graphene–Ni distance range of 2.10–2.50 Å, and thus, both functionals do not give an accurate description of graphene–Ni(111) interactions at the first minimum (refer to Fig. 2(b) and (c)).
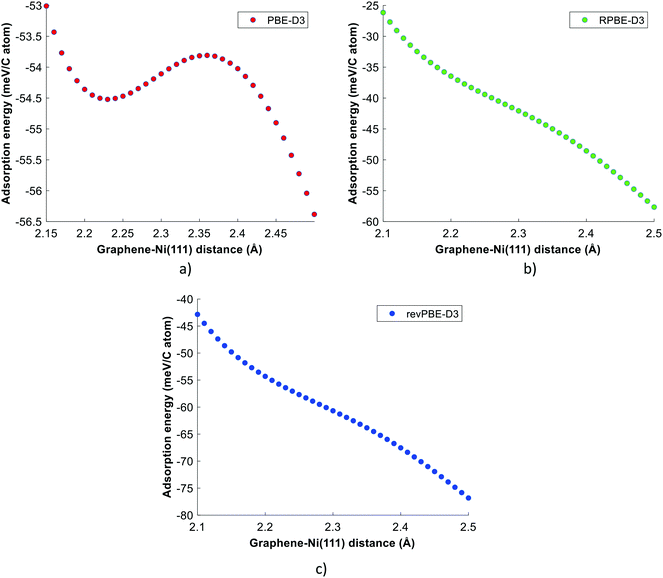 | ||
| Fig. 2 Potential energy profiles of graphene–Ni(111): (a) PBE-D3 functional, (b) RPBE-D3 functional and (c) revPBE-D3 functional. The adsorption energy is equivalent to −EDFTbind (obtained using eqn (1)). The complete graphene–Ni(111) potential energy scans (up to the second minimum) of DFT-D3 functionals are provided in the ESI† (refer to Fig. S6). | ||
At the second minimum of graphene–Ni(111) i.e. the one predicted by RPA (at a graphene–Ni distance of 3.25 Å), the hcp-fcc geometry is reported to be the most stable binding configuration.26 Even though this binding configuration of graphene may be of limited interest, as there is no experimental evidence for it yet, it is instructive to compare the pertinent DFT predictions with the RPA value.44,45 Thus, Fig. 3 shows that the PBE-D3, PBE-dDsC, RPBE-D3, optB86b-dW, optB88-vdW and optPBE-vdW functionals predict the binding energy of the second minimum of graphene in fair agreement with the RPA value.
 | ||
| Fig. 3 Comparison of the binding energy predictions of the DFT functionals used in this study with the RPA value44,45 at the second minimum of graphene–Ni(111). | ||
Taken together, the results of our benchmark studies show that the graphene–Ni(111) interactions are best represented by the optB88-vdW functional. The PBE-D3, PBE-dDsC, and optPBE-vdW functionals also perform reasonably well.
3.2 DFT benchmarks of MSR species
In a second set of benchmark calculations, the DFT functionals were used to estimate the reaction energies of methane dissociative adsorption, carbon oxidation, and the binding energies of representative species of the MSR reaction, in particular: CO, C, CH3, H2O, H, O and OH on Ni(111). The predictions of these functionals have been systematically compared against experimental data, the sources of which are compiled in Table 2. The binding sites of the MSR species are provided in the ESI† (refer to Fig. S4). For each MSR species under study, Table 2 reports the pertinent adsorption reaction, the details of the experiment that we compare against, the simulation setup of the corresponding DFT calculation (this information is provided as a footnote in Table 2), and finally, the value of the experimental binding energy. In Table 2, ML is defined to be the ratio of number of adsorbate atoms/molecules to the number of Ni atoms on the Ni(111) surface. An important caveat to be noted is that the experimental surface coverage of carbon is not clearly known (refer to the second-to-last row of Table 2 for more details), therefore, certain caution is exercised while comparing DFT predictions to the experimental binding energy of carbon.| System | Experimental method | U expbind (eV) |
|---|---|---|
| a The DFT simulation setup as stated in the “Methods” section is used for estimating the binding energy of the adsorbate. The coverage of the adsorbate on the Ni(111) supercell is 0.0625 ML. b The experimental internal energy of adsorption is reported (the heat of adsorption obtained from the experiment is reduced by kBT).57 This value is compared to the DFT prediction Utheorybind. c The Arrhenius activation barrier obtained from flash desorption studies of hydrogen was compared to the ZPE corrected DFT energy prediction (no thermal corrections were included, only eqn (2)–(4) of the “Methods section” were used in this case). d Since the experimental surface coverage is 0.5 ML, a p(2 × 2) Ni(111) supercell (constituting two OH atoms adsorbed on the three-fold hollow sites) has been used and the Brillouin zone integration was done with a 10 × 10 × 1 k-point grid. e The kinetic isotope effects are assumed to be negligible. f By convention, a positive value indicates exothermic reaction, in which case the dissociative adsorption is favourable. A negative value indicates endothermic dissociative adsorption (not favoured). | ||
| CO(g) + * ⇄ CO* | The differential heat of adsorption of CO on Ni(111) is recorded at the limit of zero-coverage using calorimetry. The temperature is maintained at 300 K. | 1.32a,b (±0.03) (ref. 49) |
| D2O(g) + * ⇄ D2O* | The single-crystal adsorption calorimetry (SCAC) method is employed to study the molecular adsorption of D2O on Ni(111). The differential heat of D2O adsorption has been reported at 100 K and zero-coverage limit. | 0.55a,b,e (ref. 50) |
| H2(g) + 2* ⇄ 2H* | The associative desorption of hydrogen is studied using flash desorption spectroscopy. The desorption of H/Ni(111) has been observed to follow second-order kinetics at low coverages. The Arrhenius activation barrier of associative desorption of hydrogen has been estimated. | 0.98a,c (±0.04) (ref. 51) |
| O2(g) + 2* ⇄ 2O* | The dissociative adsorption of O2 on Ni(111) is studied using SCAC at 300 K. The heat of adsorption of oxygen is reported at the zero-coverage limit. | 4.53a,b (±0.2) (ref. 52) |
| OD(g) + * ⇄ OD* | The SCAC method is used to study oxygen assisted D2O dissociation on Ni(111). The heat of adsorption of OD–Ni(111) is derived using thermodynamic cycles (at 0.5 ML coverage). | 3.26b,d,e (ref. 50) |
| CH3(g) + * ⇄ CH3* | The dissociative adsorption of methyl iodide is studied using SCAC at 160 K. The heat of methyl adsorption is obtained via thermodynamic cycles. | 2.25a,b (±0.14) (ref. 53) |
| CH4(g) + 2* ⇄ CH3* + H* | Carey et al.53 estimated the enthalpy of methane dissociation at 160 K by using the experimental heats of adsorption of CH3 and H on Ni(111) (obtained from calorimetric studies), and the heat of formation of CH4 (g). | 0.43a,b,f (ref. 53) |
| C(g) + * ⇄ C* | The isosteric heat of formation of carbon (at 600 K) is derived from the Boudouard equilibrium. The study is conducted using alumina-supported polycrystalline Ni. The carbon coverage is defined to be half of the saturation coverage of CO at 195 K. According to Netzer and Madey,54 the CO adsorbate has a saturation coverage of around 0.57 ML on Ni(111) (at temperatures 220–240 K). Using this information, the carbon coverage might be around 0.29 ML. | 6.84a,b (ref. 55) |
| C* + (½)O2(g) ⇄ CO(g) | The reaction energy of “carbon oxidation” (from carbon on Ni(111) and O2(g)) is derived using the experimental carbon adsorption energy (with respect to C(g)) and the CO gas-phase formation energy (obtained from the atomisation energies dataset of CCSD(T)56). The value is reported at 0 K (the ZPE/thermal contributions of “carbon adsorption” reaction is removed using the PBE functional prediction). | 1.71a,f (ref. 55 and 56) |
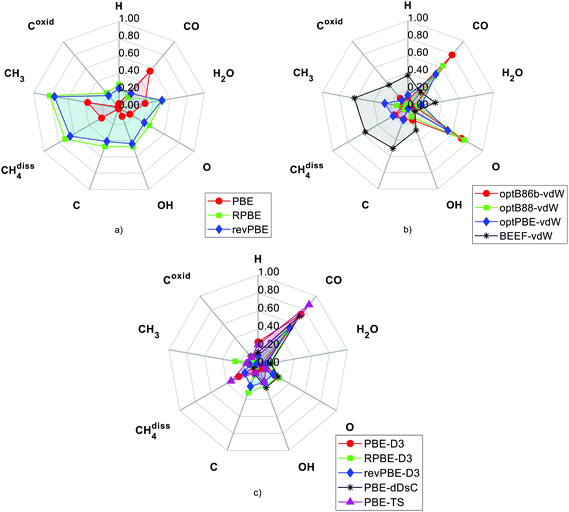
In Table 3, the experimental values and the DFT predictions of MSR species are systematically recorded. The colour code and font style in Table 3 gives an indication on the extent of deviation of the DFT prediction from the corresponding experimental value (the pertinent convention is stated in the heading of Table 3). As shown in Fig. 4, the deviations of the DFT predictions from the experimental values have been presented using radar plots. Furthermore, the RMSD values have been computed to make a quantitative assessment on the overall performance of the DFT functionals (refer to Fig. 5).
| a The vibrational calculations of OH in the gas phase was performed for the DFT functionals revPBE, PBE-D3, revPBE-D3, optB86b-vdW and BEEF-vdW using electronic minimisation tolerance values of 5 × 10−5 eV, 1 × 10−5 eV, 1 × 10−6 eV, 3 × 10−5 eV and 1 × 10−5 eV, respectively. b The geometric optimisation and vibrational analysis of CO in the gas phase were performed by setting the electronic minimisation tolerance value to 5 × 10−6 eV. c The vibrational calculation of H2O in the gas phase was carried out with an electronic minimisation tolerance value of 10−6 eV. d The geometric optimisation and vibrational analysis of O2 in the gas phase were performed by setting the electronic minimisation tolerance value to 10−6 eV. e The geometric optimisation and vibrational calculations of OH in the gas phase were carried out using electronic minimisation tolerance values of 10−6 eV and 10−5 eV, respectively. f The geometric optimisation and vibrational analysis of CH3(g) were performed with an electronic minimisation tolerance value of 10−6 eV. g The OH–Ni(111) DFT calculation was executed with a geometric optimisation tolerance value of 0.02 eV Å−1. h The vibrational analysis of OH gas-phase was performed with an electronic minimisation tolerance value of 10−6 eV. | |||||||||
|---|---|---|---|---|---|---|---|---|---|

|
 | ||
| Fig. 5 RMSD values (obtained using eqn (8)) of the DFT functionals considered in this study. | ||
The oxygen binding energy predictions (reported in Table 3) have been computed with reference to O2 gas-phase DFT energy. It is known that the triplet (ground) state of O2 is poorly captured by DFT calculations; hence, the O2 gas-phase energy thus obtained may exhibit low accuracy. Alternatively, the O2 gas-phase energy can be estimated from the H2O gas-phase formation energy (obtained from the literature),31 H2 gas-phase energy and H2O gas-phase energy (both these energies are calculated using DFT). However, this alternative approach was found to further deteriorate the performance of most of the DFT functionals. The results of the oxygen binding energies obtained using aforementioned approaches are provided in the ESI† (refer to Table S3). Similarly, the O2(g) DFT energy has been used to calculate the reaction energy of carbon oxidation (C* + (½)O2(g) ⇄ CO(g)).
The PBE functional predicts the reaction energy of methane dissociation with reasonable accuracy (it underestimates the experimental value by 0.23 eV). It performs appreciably well for MSR species such as hydrogen, oxygen and hydroxyl. The PBE functional overpredicts the binding energy of carbon monoxide by more than 0.5 eV (as depicted in Fig. 4(a)). In the literature, it is well established that the PBE exchange–correlation approximation fails to accurately predict the binding energy of carbon monoxide.31 The PBE functional underpredicts the binding energy of H2O, as it does not include the dispersive interactions between H2O and Ni(111). Zhu et al.28 also report the same behaviour for the PBE functional. As shown in Table 3 and Fig. 4(a), the PBE functional accurately estimates the carbon binding energy and the reaction energy of carbon oxidation (however, we note again that the experimental value of carbon might be subject to finite coverage effects).
The RPBE and revPBE functionals give a better estimate of the CO binding energy than the other DFT functionals tested in this study (as shown in Fig. 4(a) and Table 3). However, the predictions of these functionals deviate significantly from the experimental binding energies of CH3, O, OH, H2O and C. Furthermore, both functionals predict that the methane dissociation reaction on Ni(111) is an endothermic elementary event (this is qualitatively incorrect as methane dissociates exothermically on Ni(111); refer to Table 3). As shown in Fig. 5, the PBE functional has better overall performance than other GGA functionals. Nonetheless, the GGA functionals do not account for the dispersive interactions of graphene–Ni(111) (as stated in the “Introduction” section), and therefore, they are not suitable to investigate the carbon poisoning mechanism of Ni in the MSR reaction.
It can be inferred from Table 3 and Fig. 4(b) that the performance of functionals within the vdW-DF class is unsatisfactory. Although optB86b-vdW and optB88-vdW functionals predict the reaction energies of methane dissociation and carbon oxidation, and the binding energies of CH3, H2O, H and C with acceptable accuracy, both functionals perform poorly for species such as CO and O (as depicted in Fig. 4(b)). In agreement with the findings of our study, Hensley et al.58 also report that the optB86b-vdW and optB88-vdW functionals do not predict the binding energies of CO with acceptable accuracy. The RMSD values of optB86b-vdW and optB88-vdW functionals are 1.11 eV and 1.00 eV, respectively, which is much higher than most of the other dispersion-inclusive DFT functionals (refer to Fig. 5). Thus, neither of these functionals appear promising for studying graphene formation in the MSR reaction.
The BEEF-vdW functional provides a better prediction of the CO binding energy than other vdW-DF (the deviation from the experimental value is 0.23 eV; Wellendrof et al.31 report a similar result for this functional). Nonetheless, the BEEF-vdW functional exhibits large deviations in estimating the reaction energy of carbon oxidation and the binding energies of MSR species such as H2O, H, C and CH3 (as illustrated in Fig. 4(b)). It predicts the dissociative adsorption of methane on Ni(111) to be an endothermic step (this result is not in qualitative agreement with the experimental value; refer to Table 3). The computational error predictions of the BEEF-vdW functional range from 0.15 to 0.30 eV in most cases, except for O2 dissociative adsorption (at infinite separation), for which the BEEF-vdW gives a computational error of 0.46 eV (as shown in Table 3). The BEEF-vdW functional has the highest RMSD score among all the dispersion-inclusive DFT functionals benchmarked in this study (refer to Fig. 5); which makes it unsuitable for the graphene–MSR system. The optPBE-vdW functional predicts the binding energy of OH with high accuracy. For species such as H2O, H and C, the optPBE-vdW functional produces deviations within an acceptable range (0.14–0.16 eV). It estimates the reaction energy of methane dissociation with reasonable accuracy (the deviation is 0.19 eV). The carbon oxidation reaction energy and the CH3 binding energy predictions of optPBE-vdW deviate from the experimental values by 0.11 eV and −0.27 eV, respectively. In the case of species such as CO and O, the predictions of optPBE-vdW are in poor agreement with experimental data (refer to Table 3 and Fig. 4(b)). Nevertheless, the optPBE-vdW functional has a much better overall performance. The RMSD score of optPBE-vdW functional is 0.85 eV, which is substantially lower than the other vdW-DF (as shown in Fig. 5). Furthermore, as discussed in Section 3.1, the optPBE-vdW functional predicts the first minimum of graphene with reasonable accuracy. Therefore, among the vdW-DF, the optPBE-vdW functional can be considered to study the chemistry of carbon poisoning on Ni(111) (with appropriate corrections to CO and O binding energy values).
In contrast to vdW-DF, the DFT-D functionals perform reasonably well for this system. The deviations of DFT-D functionals are below 0.35 eV for all MSR species except CO (refer to Fig. 4(c)). As depicted in Fig. 5, the RMSD values of RPBE-D3 and revPBE-D3 functionals are lower than the other dispersion-inclusive functionals tested in this study. These two functionals predict with acceptable accuracy the reaction energies of methane dissociation and carbon oxidation, and the binding energies of MSR species (H, H2O, CH3, OH), though, in the case of CO, they exhibit significant deviations from the experimental data (refer to Table 3 and Fig. 4(c)). However, these two functionals do not capture the first minimum of graphene on Ni(111) (as discussed in Section 3.1).
The dispersion-corrected flavours of PBE; namely, PBE-TS, PBE-D3 and PBE-dDsC functionals produce interesting results. It is important to note that the aforementioned functionals significantly overestimate the CO binding energy. This behaviour is expected as the PBE approximation yields a poor description of CO adsorption (the deviation is 0.56 eV), and upon inclusion of dispersion corrections, the deviation from the CO experimental binding energy value is further exacerbated. The PBE-TS functional has high predictive accuracy for species such as H2O, O and C (as illustrated in Fig. 4(c), with deviations that are less than 0.1 eV). It predicts the binding energies of CH3, H and OH with deviations 0.13 eV, 0.23 eV and 0.20 eV, respectively (these deviations are within the acceptable range). Göltl et al.29 have also obtained similar results for CH3 and H using the PBE-TS functional. In the case of CH4 dissociative adsorption, the PBE-TS functional overestimates the reaction energy by 0.35 eV. The inaccurate prediction of CO adsorption and CH4 dissociative adsorption mainly contribute to the high RMSD value of PBE-TS functional. Furthermore, the PBE-TS functional significantly overpredicts the graphene binding energy on Ni(111) (as discussed in Section 3.1). Thus, the PBE-TS functional is not an appropriate choice.
The PBE-D3 functional predicts the binding energies of OH and C with appreciable accuracy. It provides a good description of the H2O–Ni(111) interactions, whereas, the hydrogen binding energy is substantially overestimated; Zhu et al.28 have also made similar observations. According to Table 3, PBE-D3 predicts the CH3 binding energy to be 2.25 eV, which agrees closely with the experimental result. Furthermore, it has been found to predict with reasonable accuracy the reaction energies of methane dissociation and carbon oxidation, as well as the oxygen binding energy (the deviations are less than 0.25 eV; refer to Fig. 4(c)). In a recent study, Göltl et al.29 have reported that the PBE-D3 functional provides accurate estimates of the CH3 binding energy and the reaction energy of CH4 dissociation. The PBE-dDsC functional exhibits excellent predictive accuracy in estimating the reaction energy of methane dissociation. It predicts the reaction energy of carbon oxidation and the binding energies of H, H2O, C and CH3 within a deviation range of 0.10–0.15 eV. In the case of O and OH, the PBE-dDsC predictions deviate from the experimental data by around 0.25 eV (as shown in Fig. 4(c) and Table 3).
The predictions of PBE-D3 and PBE-dDsC functionals agree well with experiments for most MSR species (all the deviations lie well within 0.3 eV excluding CO). Both functionals have similar overall predictive capability for MSR intermediates – the RMSD values of these functionals are around 0.85 eV (as shown in Fig. 5). They also account for the graphene–Ni(111) interactions with acceptable accuracy (refer to Table 1 of Section 3.1). In summary, the PBE-D3 and PBE-dDsC functionals perform better than the other DFT functionals tested in this work, and thus, make suitable choices for understanding the chemistry of graphene formation in the MSR reaction.
Overall, the benchmark studies of graphene and MSR species give us some useful insights into the predictive accuracy of DFT-D and vdW-DF functionals. Comparisons with RPA calculations (which accurately capture the van der Waals interactions) reveal that the optB88-vdW functional predicts the binding energy of graphene with excellent accuracy. The PBE-D3, PBE-dDsC and optPBE-vdW functionals also show reasonable agreement with the RPA prediction of graphene–Ni(111). On the other hand, the BEEF-vdW functional was found to produce a weak repulsive interaction between graphene and Ni(111). Moreover, the RPBE-D3 and revPBE-D3 functionals do not generate the first minimum of the graphene–Ni(111) system. The DFT benchmarks of the MSR species reveal that the “opt” functionals exhibit large deviations for species such as CO and O. Among the vdW-DF, the optPBE-vdW functional has the best overall performance; it can be considered for studying graphene–MSR chemistry on Ni(111) (appropriate corrections need to be made for CO and O intermediates). In the case of DFT-D functionals, the PBE-D3 and PBE-dDsC functionals predict with acceptable accuracy the binding energies of most MSR species (except CO), as well as the reaction energies of dissociative adsorption of methane (an important elementary step of MSR) and carbon oxidation. These functionals also provide a good description of the van der Waals interactions of graphene–Ni(111). Overall, the PBE-D3 and PBE-dDsC functionals are promising for more detailed studies to understand the carbon poisoning chemistry of Ni(111) in the MSR reaction (suitable corrections are required for the CO binding energy predictions of these functionals).
4. Conclusions
Detailed DFT studies of the MSR reaction on Ni can provide valuable mechanistic insight on catalyst poisoning and deactivation phenomena, which have a severe impact on industrial operations. At the molecular scale, the poisoning mechanism primarily involves the formation of graphene islands; thus, the accurate description of graphene–Ni(111) interactions is paramount to develop a reliable carbon poisoning model for MSR. Graphene binds in a commensurate manner to the Ni(111) surface and its accurate description necessitates taking into account local as well as non-local interactions (van der Waals forces) using appropriate DFT functionals. In addition, to ensure the accurate description of the MSR chemistry, including the pathways that lead to poisoning precursors, these functionals should be able to faithfully reproduce the binding of key intermediates within these pathways. GGA functionals fail to capture the dispersion interactions of graphene–Ni(111), however, dispersion-inclusive functionals, such as DFT-D and vdW-DF could be effectively used to this end. Indeed, several studies have shown that some of the DFT-D functionals and vdW-DF are promising for the graphene–Ni(111) system. However, there is little evidence on the accuracy of these functionals in predicting binding energies of important MSR intermediates.In this study, a systematic benchmark analysis has been carried out to assess the performance of DFT-D functionals and vdW-DF in predicting the binding energies of graphene and MSR species, and the reaction energies of methane dissociation and carbon oxidation on Ni(111). The optB88-vdW, optPBE-vdW, PBE-D3 and PBE-dDsC functionals have been found to yield promising results for graphene–Ni(111). The DFT predictions for the binding energies of key MSR species have been compared to experimental data from calorimetric and flash desorption studies available in the literature. The vdW-DF exhibit large RMSD values with respect to experimental data of MSR species. Nonetheless, among the vdW-DF, the optPBE-vdW functional is an appropriate choice for the graphene–MSR system. The DFT-D functionals exhibit a much better performance than the vdW-DF in predicting the binding energies of MSR species. In the case of DFT-D functionals, PBE-D3 and PBE-dDSC functionals appear to be suitable choices for investigations of carbon poisoning of Ni(111) in the MSR reaction.
Our analysis shows that the DFT functionals have moderate predictive accuracy; in particular, none of the DFT functionals considered were found to predict the binding energies of all the key MSR species with equally high accuracy. The RMSD values of DFT functionals fall in the range of 0.6–1.5 eV, which indicates that there is scope for further improving the predictive accuracy of DFT. Although optB88-vdW accurately accounts for the van der Waals interactions of graphene–Ni(111), it significantly overestimates the binding energies of important MSR intermediates such as O and CO. Moreover, the RPBE-D3 and revPBE-D3 functionals do not reproduce the experimentally observed binding configuration of graphene on Ni(111), the “first minimum” at a distance of 2.11 ± 0.07 Å, despite having dispersion correction terms in their formulations. Overall, our analysis can guide the selection of appropriate DFT functionals for future studies of the MSR chemistry.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. S. Y.'s doctoral studies are supported by an Impact Studentship sponsored by the Johnson Matthey Technology Centre. We gratefully acknowledge the use of the UCL High Performance Computing Facility Kathleen@UCL and Grace@UCL in the completion of the simulations of this work. We are grateful to the U.K. Materials and Molecular Modelling Hub, which is partially funded by EPSRC (EP/P020194/1), for computational resources (HPC facilities Thomas and Young). We also thank Dr Konstantinos Papanikolaou, Dr Julia Schumann, and Dr Romain Réocreux for helpful discussions.References
- D. J. Wilhelm, D. R. Simbeck, A. D. Karp and R. L. Dickenson, Fuel Process. Technol., 2001, 71, 139–148 CrossRef CAS.
- R. Ramachandran and R. K. Menon, Int. J. Hydrogen Energy, 1998, 23, 593–598 CrossRef CAS.
- D. W. Blaylock, T. Ogura, W. H. Green and G. J. O. Beran, J. Phys. Chem. C, 2009, 113, 4898–4908 CrossRef CAS.
- L. Dehimi, Y. Benguerba, M. Virginie and H. Hijazi, Int. J. Hydrogen Energy, 2017, 42, 18930–18940 CrossRef CAS.
- H. M. Wang, D. W. Blaylock, A. H. Dam, S. E. Liland, K. R. Rout, Y. A. Zhu, W. H. Green, A. Holmen and D. Chen, Catal. Sci. Technol., 2017, 7, 1713–1725 RSC.
- N. Salhi, A. Boulahouache, C. Petit, A. Kiennemann and C. Rabia, Int. J. Hydrogen Energy, 2011, 36, 11433–11439 CrossRef CAS.
- J. Sehested, Catal. Today, 2006, 111, 103–110 CrossRef CAS.
- J. Xu and M. Saeys, J. Catal., 2006, 242, 217–226 CrossRef CAS.
- H. S. Bengaard, J. K. Norskov, J. Sehested, B. S. Clausen, L. P. Nielsen, A. M. Molenbroek and J. R. Rostrup-Nielsen, J. Catal., 2002, 209, 365–384 CrossRef CAS.
- G. Jones, J. G. Jakobsen, S. S. Shim, J. Kleis, M. P. Andersson, J. Rossmeisl, F. Abild-Pedersen, T. Bligaard, S. Helveg and B. Hinnemann, J. Catal., 2008, 259, 147–160 CrossRef CAS.
- D. W. Blaylock, Y.-A. Zhu and W. H. Green, Top. Catal., 2011, 54, 828 CrossRef CAS.
- S. Helveg, C. López-Cartes, J. Sehested, P. L. Hansen, B. S. Clausen, J. R. Rostrup-Nielsen, F. Abild-Pedersen and J. K. Nørskov, Nature, 2004, 427, 426 CrossRef CAS.
- F. Abild-Pedersen, J. K. Nørskov, J. R. Rostrup-Nielsen, J. Sehested and S. Helveg, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 115419 CrossRef.
- F. Mittendorfer, A. Garhofer, J. Redinger, J. Klimeš, J. Harl and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 201401 CrossRef.
- J. Klimes and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- S. N. Steinmann and C. Corminboeuf, J. Chem. Phys., 2011, 134, 044117 CrossRef PubMed.
- S. N. Steinmann and C. Corminboeuf, J. Chem. Theory Comput., 2011, 7, 3567–3577 CrossRef CAS PubMed.
- F. Ortmann, F. Bechstedt and W. G. Schmidt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205101 CrossRef.
- M. Dion, H. Rydberg, E. Schroder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2009, 22, 022201 CrossRef PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- X. Li, J. Feng, E. Wang, S. Meng, J. Klimeš and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 085425 CrossRef.
- P. Janthon, F. Vines, S. M. Kozlov, J. Limtrakul and F. Illas, J. Chem. Phys., 2013, 138, 244701 CrossRef PubMed.
- H. Muñoz-Galán, F. Viñes, J. Gebhardt, A. Görling and F. Illas, Theor. Chem. Acc., 2016, 135, 165 Search PubMed.
- L. Zhu, C. Liu, X. Wen, Y.-W. Li and H. Jiao, Catal. Sci. Technol., 2019, 9, 199–212 RSC.
- F. Göltl, E. A. Murray, S. A. Tacey, S. Rangarajan and M. Mavrikakis, Surf. Sci., 2020, 700, 121675 CrossRef.
- S. Gautier, S. N. Steinmann, C. Michel, P. Fleurat-Lessard and P. Sautet, Phys. Chem. Chem. Phys., 2015, 17, 28921–28930 RSC.
- J. Wellendorff, T. L. Silbaugh, D. Garcia-Pintos, J. K. Nørskov, T. Bligaard, F. Studt and C. T. Campbell, Surf. Sci., 2015, 640, 36–44 CrossRef CAS.
- P. S. Schmidt and K. S. Thygesen, J. Phys. Chem. C, 2018, 122, 4381–4390 CrossRef CAS.
- M. K. Rana, H. S. Koh, J. Hwang and D. J. Siegel, J. Phys. Chem. C, 2012, 116, 16957–16968 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Norskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- Y. K. Zhang and W. T. Yang, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- Y. A. Zhu, D. Chen, X. G. Zhou and W. K. Yuan, Catal. Today, 2009, 148, 260–267 CrossRef CAS.
- J. Li, E. Croiset and L. Ricardez–Sandoval, Appl. Surf. Sci., 2014, 311, 435–442 CrossRef CAS.
- R. Reocreux, C. Michel, P. Fleurat-Lessard, P. Sautet and S. N. Steinmann, J. Phys. Chem. C, 2019, 123, 28828–28835 CrossRef.
- J. C. Shelton, H. R. Patil and J. M. Blakely, Surf. Sci., 1974, 43, 493–520 CrossRef CAS.
- L. X. Benedict, N. G. Chopra, M. L. Cohen, A. Zettl, S. G. Louie and V. H. Crespi, Chem. Phys. Lett., 1998, 286, 490–496 CrossRef CAS.
- R. Zacharia, H. Ulbricht and T. Hertel, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155406 CrossRef.
- J. Harl and G. Kresse, Phys. Rev. Lett., 2009, 103, 056401 CrossRef PubMed.
- S. Shepard and M. Smeu, J. Chem. Phys., 2019, 150, 154702 CrossRef PubMed.
- T. Olsen, J. Yan, J. J. Mortensen and K. S. Thygesen, Phys. Rev. Lett., 2011, 107, 156401 CrossRef PubMed.
- Y. Gamo, A. Nagashima, M. Wakabayashi, M. Terai and C. Oshima, Surf. Sci., 1997, 374, 61–64 CrossRef CAS.
- F. Bianchini, L. L. Patera, M. Peressi, C. Africh and G. Comelli, J. Phys. Chem. Lett., 2014, 5, 467–473 CrossRef CAS PubMed.
- W. Zhao, S. M. Kozlov, O. Höfert, K. Gotterbarm, M. P. A. Lorenz, F. Vines, C. Papp, A. Görling and H.-P. Steinrück, J. Phys. Chem. Lett., 2011, 2, 759–764 CrossRef CAS.
- J. T. Stuckless, N. Al-Sarraf, C. Wartnaby and D. A. King, J. Chem. Phys., 1993, 99, 2202–2212 CrossRef CAS.
- W. Zhao, S. J. Carey, Z. Mao and C. T. Campbell, ACS Catal., 2018, 8, 1485–1489 CrossRef CAS.
- J. Lapujoulade and K. S. Neil, J. Chem. Phys., 1972, 57, 3535–3545 CrossRef CAS.
- J. T. Stuckless, C. E. Wartnaby, N. Al-Sarraf, S. J. B. Dixon-Warren, M. Kovar and D. A. King, J. Chem. Phys., 1997, 106, 2012–2030 CrossRef CAS.
- S. J. Carey, W. Zhao, A. Frehner, C. T. Campbell and B. Jackson, ACS Catal., 2017, 7, 1286–1294 CrossRef CAS.
- F. P. Netzer and T. E. Madey, J. Chem. Phys., 1982, 76, 710–715 CrossRef CAS.
- A. Takeuchi and H. Wise, J. Phys. Chem., 1983, 87, 5372–5376 CrossRef CAS.
- R. Haunschild and W. Klopper, J. Chem. Phys., 2012, 136, 164102 CrossRef.
- T. L. Silbaugh and C. T. Campbell, J. Phys. Chem. C, 2016, 120, 25161–25172 CrossRef CAS.
- A. J. R. Hensley, K. Ghale, C. Rieg, T. Dang, E. Anderst, F. Studt, C. T. Campbell, J.-S. McEwen and Y. Xu, J. Phys. Chem. C, 2017, 121, 4937–4945 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00862e |
| This journal is © the Owner Societies 2021 |