Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modelling the non-local thermodynamic equilibrium spectra of silylene (SiH2)†
Victoria H. J.
Clark
 * and
Sergei N.
Yurchenko
* and
Sergei N.
Yurchenko
 *
*
Department of Physics and Astronomy, University College London, Gower Street, WC1E 6BT London, UK. E-mail: v.clark.17@ucl.ac.uk; s.yurchenko@ucl.ac.uk
First published on 29th April 2021
Abstract
This paper sets out a robust methodology for modelling spectra of polyatomic molecules produced in reactive or dissociative environments, with vibrational populations outside local thermal equilibrium (LTE). The methodology is based on accurate, extensive ro-vibrational line lists containing transitions with high vibrational excitations and relies on the detailed ro-vibrational assignments. The developed methodology is applied to model non-LTE IR and visible spectra of silylene (SiH2) produced in a decomposition of disilane (Si2H6), a reaction of technological importance. Two approaches for non-LTE vibrational populations of the product SiH2 are introduced: a simplistic 1D approach based on the Harmonic approximation and a full 3D model incorporating accurate vibrational wavefunctions of SiH2 computed variationally with the TROVE (Theoretical ROVibrational Energy) program. We show how their non-LTE spectral signatures can be used to trace different reaction channels of molecular dissociations.
1 Introduction
Normally, molecules are assumed to be in local thermal equilibrium pertaining to a given temperature with the internal degrees of freedom (electronic–rotation–vibration) characterized by the Boltzmann distribution. However many different physical chemical, experimental and technological processes produce molecules that do not satisfy the Boltzmann law and as consequence have unusual, non-local thermal equilibrium (non-LTE) spectroscopic signatures. Molecules produced in reactions do not necessarily obey the Boltzmann thermal equilibrium, at least if the reaction time is shorter than the collision time. Instead, their internal degrees of freedom are populated based on the reaction paths rather than on the temperature of the surrounding environment. These out-of-LTE (i.e. non-LTE) populations encode information about the structural reaction dynamics and can manifest in the molecular spectra. The field of non-LTE spectroscopy has great potential to study these processes as the properties of the molecules producing the non-LTE spectroscopic signatures can shed the light on the dynamics of chemical reactions.1–6 The so-called transition state (TS) spectroscopy is a technique already widely used that employs the high-resolution non-LTE spectra of products to observe reaction processes that are hidden for the conventional spectroscopic methods.7,8 The novel high resolution non-LTE spectroscopic techniques allow decoupling of the vibrational and rotational degrees of freedom of molecules and thus control their vibrational and rotational populations, e.g. with rich vibrational and simplified rotational structures.6,9–13The modern day study of non-LTE spectroscopy can be traced as far back as the 1930s to the original papers of Milne,14 and the many key papers from the decades following.15–24 The non-LTE spectroscopic effects play important role in high-resolution applications and there exist a number of accurate non-LTE spectroscopic and radiative transfer codes, see van der Tak et al.,25 Funke et al.,26 Pannier and Laux27 and references therein. As such, non-LTE spectra are often vital for the modelling of astrophysical problems, including planetary atmospheric properties,28 stellar atmospheres of solar system and exoplanets29–36 and the ISM.25,37,38
The non-local thermodynamic effects of the spectra of molecules has been of interest to chemists and astronomers alike for many years. A notable example of this is the 2011 work by Ferus et al.2 who studied the isomers of HCN within acetonitrile, formamide, and BrCN discharge. Using the features for both the HCN and HNC molecules from these spectra, Ferus et al.2 were able to calculate the ratios of molecules within the reactions and also the reaction path taken by the HNC molecule during the isomerization. In this work we explore this idea to study non-LTE spectral signatures of silylene (SiH2) produced from disilane (Si2H6).
Reaction properties of silylene, silane and disilane such as the rate constants for the formation, destruction and chemical pathways are important for plasma physics aspects such as silicon deposition.39–41 The ease of hydrogen transfer and high barriers in the saturated silicon system, leading to the ready formation of three-centre interactions and consequently the isomerisation reactions of Si2H6, are just as important to study as the elementary reactions.42 Silane containing reactions are also of importance for astrophysics, with the presence of SiH4 in IRC + 10216 discussed by Goldhaber and Betz,43 Kaiser and Osamura.44
The complexity of the silane containing systems has been discussed elsewhere,42,45 with quantitative calculations proving particularly difficult. There were a number of ab initio studies of the structural properties of Si2H6e.g.,46–53 as well as of the formation and reactions involving this molecule.54–58 Agrawal et al.53 produced a global ab initio potential energy surface of disilane and used it to investigate the dissociation dynamics with classical trajectories. Márquez et al.50 reported a force field for Si2H6. The main isomer of Si2H6 has a staggered, ethane-like, structure (see Fig. 1) with a low barrier (1.2 kcal mol−1) to the eclipsed conformation.59 Si2H6 has been shown to have a local minimum as an inverted stable structure with one of the Si–H3 ‘umbrellas’ pointing to the center as well as a transition state with a similar inverted configuration.46,60 These structures are nominally asymmetric (Cs symmetry) but essentially acquiring the C3v symmetry.
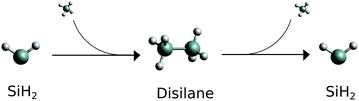 | ||
| Fig. 1 Schematic reaction path for the silylene. Molecular SiH2 is the starting material, fragment SiH2 is the product. | ||
Thermal decomposition of Si2H6 has been extensively studied, both theoretically (mostly using RRKM, Rice–Ramsperger–Kassel–Marcus) and experimentally, with the reaction Si2H6 → SiH2 + SiH4 as the most common53,56,57,61 and important decomposition process of the excited disilane,53,57,62–66 and where Arrhenius parameters and rate constants have been reported (e.g. Bowrey and Purnell,61 Martin et al.,63 Mick et al.,65 Roenigk et al.67). However, it is also possible for the disilane molecule to dissociate homolytically, as was originally thought to be the main pathway owing to disilanes similarities with ethane, and form 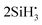 ,53,56,68 or to undergo dehydrogenation to H2Si–SiH2, H3Si–SiH, or H3Si–H2.53,54,57 Disilane can even undergo double dehydrogenation to form Si2H2, however to our knowledge this has only been reported as the main product when undergoing photolysis at 193 nm.69 Yoshida et al.57 notes that the transition state for Si2H6 → SiH2 + SiH4 is 8.48 kcal mol−1 lower than the transition state for Si2H6 → H3SiSiH + H2, at 43.38 kcal mol−1 compared to 51.86 kcal mol−1.
,53,56,68 or to undergo dehydrogenation to H2Si–SiH2, H3Si–SiH, or H3Si–H2.53,54,57 Disilane can even undergo double dehydrogenation to form Si2H2, however to our knowledge this has only been reported as the main product when undergoing photolysis at 193 nm.69 Yoshida et al.57 notes that the transition state for Si2H6 → SiH2 + SiH4 is 8.48 kcal mol−1 lower than the transition state for Si2H6 → H3SiSiH + H2, at 43.38 kcal mol−1 compared to 51.86 kcal mol−1.
The spectroscopy of SiH2 has been used to monitor the SiH2 + SiH4 → Si2H6 and Si2H6 → SiH2 + SiH4 reactions (see Fig. 1) and measure the corresponding rate constants and Arrhenius parameters by spectroscopically tracking electronic (Ö![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) ) transitions of SiH2.39,46,65,70 In these studies, the reconstructions of the amount of SiH2 relied on the assumption of the Boltzmann thermal distribution when estimating the population of the lower state. No account of the possible non-LTE population of SiH2 molecules after dissociation was made, which could potentially hamper the count of the SiH2 molecules and affect the reaction rates estimated. A similar experimental technique was used in Hertl and Jolly71 to monitor SiH2 in SiH4 plasma.
) transitions of SiH2.39,46,65,70 In these studies, the reconstructions of the amount of SiH2 relied on the assumption of the Boltzmann thermal distribution when estimating the population of the lower state. No account of the possible non-LTE population of SiH2 molecules after dissociation was made, which could potentially hamper the count of the SiH2 molecules and affect the reaction rates estimated. A similar experimental technique was used in Hertl and Jolly71 to monitor SiH2 in SiH4 plasma.
It is the second, dissociation, part of the reaction shown in Fig. 1 (Si2H6 → SiH2 + SiH4) we study in this work. More specifically, we show that (i) the (vibrational) populations of the molecules produced in reactions can be very different from the Boltzmann distribution and is important to take into account when interpreting spectroscopic measurements. That (ii) spectral shapes of the dissociated SiH2 can bear strong non-LTE character, very different from the LTE spectrum of an LTE SiH2 sample making it possible to distinguish between different reaction stages and even between different dissociation channels the silylene molecules it is produced from. In this work non-LTE spectra of SiH2 under conditions similar to dissociation processes expected in these experiments are modelled.
Recently we have computed an accurate ro-vibrational line list for SiH2, named CATS.72 It covers a large range of rotational and vibrational excitation, capable of modelling very hot spectra of this molecule (up to T = 2000 K) as part of the ExoMol database.73 The CATS line list was produced using the program TROVE,74,75 which solves the nuclear motion Schrödinger equation variationally. The ro-vibrational energies and corresponding wavefunctions were computed using an accurate, empirically refined potential energy surface (PES) of silane and a high-level ab initio dipole moment surface (DMS). The ro-vibrational probabilities (in the form of Einstein A coefficients) were computed using a high level ab initio dipole moment surface.
The study by Clark et al.72 forms the basis for the present work, where we utilize the CATS line list, wavefunctions, purpose-built numerical basis set, and the CATS computational TROVE setup to model non-LTE spectroscopic properties of SiH2 produced from dissociation of Si2H6 through different reaction channels. Using a simplified 1D Harmonic oscillator wavefunctions (see Pastorek et al.6) and more sophisticated 3D vibrational CATS wavefunctions from accurate variational calculations, the non-LTE ro-vibrational populations of SiH2 are generated and used to produce non-LTE spectroscopic spectra of different dissociation channels of disilane. To this end we investigate reaction topology connecting the global minimum of Si2H6 with the closest saddle points and local minima as well as the corresponding structural properties using a high level ab initio theory cc-pVTZ-F12/CCSD(T)-F12b76,77 employing the program MOLPRO2015.78
Theoretically, the non-LTE properties of dissociating molecules were studied by Band and Freed.79 In the present work we use general approach of Berry80 and Band and Freed,79 which assume no significant structural changes between the reactant and product nuclear configuration, along with the slow vibrational relaxation of the product13 to investigate non-LTE spectroscopic signatures of SiH2 produced from dissociation of Si2H6. In this paper we specifically consider situations where the vibrational relaxations are not achieved during the time of the experiment, so that the molecules still hold the memory of the structure during the reaction or dissociation. The rotation relaxation time however is much shorter and the rotational degrees of freedom can be usually assumed to satisfy the Bolzmann equilibrium.13
We also investigate possible non-LTE impact on the electronic Ã(0,2,0)–![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) (0,0,0) spectrum of SiH2. This is a favorite spectroscopic system for the detection of SiH2 due to the large Franck–Condon factor and the availability of suitable laser.39,70,81–91
(0,0,0) spectrum of SiH2. This is a favorite spectroscopic system for the detection of SiH2 due to the large Franck–Condon factor and the availability of suitable laser.39,70,81–91
The non-LTE absorption spectra of SiH2 are simulated using the (non-LTE) ExoCross program,92 where a new feature of non-Boltzmann populations was added. ExoCross has been previously used to model spectra of molecules in environments that can be characterized using two temperatures, vibrational and rotational.93–96
The paper is structured as follows. In Section 2 we describe the calculations of potential energy surfaces for the disilane and silylene structures. The theory used in this paper is described in Section 3. In Section 4.1 we calculate the 1D harmonic wavefunction population and use them to produce non-LTE spectra of SiH2 corresponding to different dissociation routes. In Section 4.2 we calculate the populations and subsequent non-LTE ro-vibrational spectra of SiH2 using the full 3D wavefunctions and describe the new TROVE methodology. A non-LTE electronic Ã(0,2,0)–![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) (0,0,0) spectrum of SiH2 is presented in Section 4.4. Conclusions are offered in Section 5.
(0,0,0) spectrum of SiH2 is presented in Section 4.4. Conclusions are offered in Section 5.
2 Geometry optimisation and reaction topology of Si2H6
2.1 Disilane isomers
In order to better understand the reaction process of breaking Si2H6, the topology of Si2H6 has been investigated by performing a structural analysis of Si2H6 using a high level ab initio theory. This includes finding the global minimum (GM), local minima (LM), transition states (TS), reaction barriers as well as reaction paths, as detailed below. A reaction slice through the global PES of Si2H6 helps to indicate how likely local minima or transitions states were to be formed based on corresponding topology. These properties of Si2H6 were obtained using the geometry optimization and reaction path finder implemented in MOLPRO201578 using the explicitly correlated coupled cluster method CCSD(T)-F12b76,77 with the F12-optimized correlation consistent basis set, VTZ-F1297 in the frozen core approximation. The calculations employed the diagonal fixed amplitude ansatz 3C(FIX)98 and a Slater geminal exponent value of β = 1.0a0−1.99 The auxiliary basis sets were chosen to be the resolution of the identity OptRI100 basis and the aug-cc-pV5Z/JKFIT101 and cc-awCV5Z/MP2FIT102 basis sets for density fitting. In the following this level of theory will be referenced to as VTZ/CCSD(T)-F12b.We shall refer to different disilane isomers as dGM, dLM and dTS to distinguish them from the SiH2 fragments GM, LM and TS as discussed below.
The global minimum of SiH2 (dGM) has a symmetrical, staggered D3d structure. The closest local minimum (dLM) has an inverted, C3v structure. The lowest transition state, which will be referred to as dTS (TS1 in Becerra et al.46 and TS2 in Tonokura et al.103), has also inverted structure, just a few kJ mol−1 above dLM.46 These structures together with the corresponding optimized parameters for three geometries most relevant to our work are collected in Table 1. Our structural parameters compare well with that from the literature. The structure of the dGM has also been determined spectroscopically, with the equilibrium bond lengths rSi–H = 1.492 Å, rSi–Si = 2.331 Å and bond angles β∠HSiSi = 110.3° and α∠HSiSi = 108.6°.104 The structure of the deuterated isotopologue Si2H5D was reported as rSi–H = 1.4874(17) Å, rSi–Si = 2.3317(15) Å, β∠HSiSi = 110.66(16)°.105
| Isomer | LM | TS | GM | Becerra et al.46 | ||
|---|---|---|---|---|---|---|
| Molecule | LM1 | TS1 | GM | |||
| Si–Si (Å) | 2.467 | 2.489 | 2.341 | 2.470 | 2.485 | 2.346 |
| SiR–HR (Å) | 1.532 | 1.499 | 1.482 | 1.525 | 1.493 | 1.479 |
| SiL–HL (Å) | 1.480 | 1.480 | 1.482 | 1.478 | 1.478 | 1.479 |
| ∠HRSiSi (°) | 55.4 | 64.9 | 110.2 | — | — | 110.24 |
| ∠HLSiSi (°) | 110.7 | 110.0 | 110.2 | 110.7 | 110.2 | 110.24 |
| ∠HRSiHR (°) | 90.9 | 100.6 | 108.6 | 91.4 | 102.6 | — |
| ∠HLSiHL (°) | 108.3 | 109.7 | 108.6 | 108.2 | 108.8 | — |
| ω b (cm−1) | 940 | 940 | 940 | |||
| ω s(L) (cm−1) | 2241.69 | 2245.36 | 2240.10 | |||
| ω s(R) (cm−1) | 2039.12 | 2170.66 | 2240.10 | |||
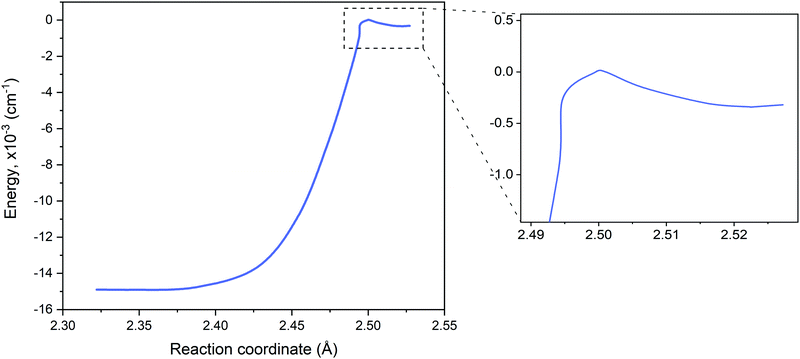
The reaction path connecting the disilane isomers dGM, dLM and dTS is shown in Fig. 2. A zoom of the dLM side is shown as inset. The energies of the global and local minima are 178 kJ mol−1 and 4.1 kJ mol−1 below the transition state, respectively. The energy and geometry information for dLM, dGM, dTS are collected in Table 2. The results calculated compare well with both the results of Becerra et al.46 and Sakai and Nakamura,60 albeit both vary for the dGM structure by 36 kJ mol−1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46 and Sakai and Nakamura60
46 and Sakai and Nakamura60
| Energy, Eh | Rel. energy,d kJ mol−1 | |
|---|---|---|
| a TS2 in Sakai and Nakamura60 is the same as TS1 in Becerra et al.46 b Complex 2 in Sakai and Nakamura60 is the same as LM1 in Becerra et al.46 c Relative to SiH2 + SiH4, kJ mol−1. d Relative to dTS. | ||
| dGM | ||
| Calculated | −581.728134 | −178.00 |
| Becerra | −236.0 | −214.50 |
| Saki | −581.53962 | −214.68715 |
| dTS | ||
| Calculated | −581.660338 | 0.00 |
| Becerra (TS1)a | −48.5 | 0.00 |
| Saki (TS2)a | −581.45785 | 0.00 |
| dLM | ||
| Calculated | −581.661906 | −4.12 |
| Becerra (LM1)b | −51.3 | −3.00 |
| Saki (compl. 2)b | −581.45837 | −1.3652601 |
The dLM isomer of Si2H6 has a shallow potential with a very low barrier to dTS of 344 cm−1. It can be also recovered using lower levels of theory, for example, using MP2/6-311G(d,p)46 and even with the UFF force fields implemented in Avogadro 1.2.0106via the steepest descent method and 4 steps per update.
2.2 The silylene fragments
With the aim to give more quantitative information on the structural and dynamical properties of five SiH2 fragments from Si2H6, the fragments are described as follows. GM is an SiH2 fragment from the global minimum structure (dGM); LM-L is an SiH2 fragment from the left hand side (LHS) of the local minimum structure (dLM) with the Si–H3 umbrella group pointing outside; LM-R is an SiH2 fragment from the right hand side (RHS) of the dLM structure with Si–H3 pointing inside; TS-L is an SiH2 fragment from the LHS of the transition state structure (dTS), Si–H3 umbrella group points outside; and TS-R is an SiH2 fragment from the RHS of the dTS structure, Si–H3 umbrella group pointing inside. The structural parameters and structures are shown in Table 3 and the energies are shown in Table 2. The harmonic frequencies for the disilane molecules were computed with MOLPRO using the TVZ/CCSD(T)-F12b level of theory. The results from the frequency analysis are shown in Table 3 along with a comparison with literature (both experimental, if available, or theoretical data is shown). The symmetry of dGM is D3d whereas the symmetry for the dLM and dTS are both C3v. The columns titled “Theory” were calculated in this work, and the degenerate states have been removed, with an average calculated if there were any differences owing to computational errors associated with the lower symmetry used by MOLPRO. All frequencies of dLM are positive thus confirming that it is a minimum with a stable structure. The ‘negative’ (or imaginary) harmonic frequency of dTS is −551.6 cm−1.| dGM, D3d | dTS, C3v | dLM, C3v | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Calculated | Literature46 | Calculated | Literature46,67 | Calculated | |||||
| Mode | Freq. | Mode | Freq. | Mode | Freq. | Mode | Freq. | Mode | Freq. |
| a Confirmed by the experimental gas phase Raman spectrum of Durig and Church.59 b Although there are three lines of 925 cm−1, there are no triply degenerate states in the C3v symmetry. Roenigk et al.67 assign one 925 cm−1 to ν15, which in the dGM symmetry is an E state degenerate with ν16. The dTS ν16 can be found at 960 cm−1. The other two 925 cm−1 line were assigned to ν9 and ν10 (E). | |||||||||
| E u | 2247.78 | E u | 2179 | E | 2252.06 | A | 2181 | E | 2244.30 |
| A 1g | 2241.03 | A 1g | 2163a | A | 2238.66 | E | 2169 | A | 2239.08 |
| E g | 2239.28 | E u | 2155 | E | 2176.47 | A | 2105 | A | 2050.89 |
| A 1u | 2232.30 | A 1u | 2154 | A | 2161.85 | A | 2087 | E | 2027.35 |
| E u | 962.35 | E g | 941a | E | 995.37 | A | 1585 | E | 1089.15 |
| E g | 948.37 | E u | 940 | E | 966.95 | A | 960 | E | 978.33 |
| A 1g | 931.91 | A 1g | 920a | A | 902.23 | A | 949 | A | 956.33 |
| A 1u | 859.02 | A 1u | 844 | E | 570.16 | A | 927 | A | 667.30 |
| E g | 636.87 | E g | 628a | A | 353.88 | A & Eb | 925 | E | 618.92 |
| A 1g | 438.76 | A 1g | 432a | E | 319.45 | E | 145 | A | 432.13 |
| E u | 372.85 | E u | 379 | A | 316.43 | A | 128 | A | 389.31 |
| A 1u | 136.56 | A 1u | 128 | A | −551.59 | E | 93 | E | 277.91 |
3 Modelling the non-LTE populations of SiH2
We now consider the decomposition reaction Si2H6 → SiH2 + SiH4 shown in Fig. 1 and model the vibrational populations of the product SiH2 assuming that the corresponding relaxation time to LTE is much longer than the time of the spectroscopic experiment. We aim at simulating non-LTE IR spectra of SiH2 using these populations to demonstrate their impact on the spectral shape of dissociated species.In our description of the non-LTE vibrational population of the dissociated molecule we follow the polyatomic Franck–Condon type approximation by Band and Freed79 and Berry80 based on the structural differences between reactant and product assuming no significant change in nuclear configuration of the molecule. In order to connect the product (gas phase SiH2) to an initial structure of Si2H6 through the dissociation process, we assume that the dissociation happens instantaneously, i.e. the initial configuration of the product SiH2 corresponds to the structural parameters (bond lengths Si–H and inter-bond angles ∠HSiH) of SiH2 as a fragment of Si2H6, for which the parameters collected in Table 1 are used. For example, for the dissociation from the dGM structure, the initial configuration of the gas phase SiH2 is assumed to be rSi–H = 1.482 Å, α∠HSiH = 108.6°. Naturally, this is a very deformed geometry comparing to the equilibrium structure of the gas phase SiH2, re = 1.5137 ± 0.003 Å and αe = 92.04 ± 0.05°.107 After being dissociated, in relaxing to be a free molecule, the fragment SiH2 has added vibrational energy and is hence in a situation when it's vibrational populations do not match the LTE distribution for corresponding temperature of the surroundings, at least for the vibrational degrees of freedom.
Experience shows that the rotational equillibration time is usually very short and we can thus safely assume the LTE conditions for the rotational degrees of freedom with the rotational temperature the same as the temperature of the surroundings (see also e.g. Dudás et al.13). The vibrational population however is not in the thermal equilibrium and therefore no sensible vibrational temperature could be associated with the corresponding population.
The non-LTE population NJ,k,ν(T) of a ro-vibrational state |J, k, ν〉 is then given by:6
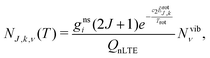 | (1) |
| ẼJ,k,ν = Ẽvibν + ẼrotJ,k, | (2) |
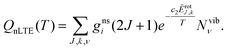 | (3) |
| SiH2 fragment name | Formation & structure |
|---|---|
| GM | From dGM, two equivalent SiH3 |
| TS-R | From dTS, SiH3 pointing inside |
| TS-L | From dTS, SiH3 pointing outside |
| LM-R | From dLM, SiH3 pointing inside |
| LM-L | From dLM, SiH3 pointing outside |
Let us assume that the Si2H6 is LTE and hence is in its ground vibrational state at the moment of dissociation, while the fragment SiH can end up in any vibrationally excited state ≡ (ν1,ν3) with some transition probability giving rise to the vibrational population Nvibν. On top of that we also assume a full separation of the stretching Si–H and bending ∠HSiH modes inside Si2H6 in its ground vibrational state. Possible consequences of deviation from these approximations are discussed below.
Under the assumptions made we define the vibrational population of the SiH2 fragment as a Franck–Condon factor for a vertical transition from the ground vibrational state of disilane Si2H6 to SiH2 + SiH4 with the gas phase (g.ph.) SiH2 transferred to some vibrational state |(g.ph.)〉 = |ν1,ν2,ν3〉. In the approximation of the full separation of the fragment SiH2 from the rest of Si2H6, the population of SiH2 can be represented as an overlap between the ground state wavefunction |ν′′ = 0(fragment)〉 of a fragment SiH2 and that of the corresponding vibrational state |ν′ = (g.ph.)〉 of the gas phase SiH2 as given by
| N = |〈0(fragment)|ν(g.ph.)〉|2. | (4) |
The calculated temperature dependent populations NJ,k,ν(T) in eqn (1) can be then combined with a molecular line list for SiH2 to simulate absorption or emission spectra of this molecule under the non-LTE conditions as defined by NJ,k,ν(T) in eqn (1). Here we use the ExoMol line list CATS by Clark et al.72 as provided by ExoMol (http://www.exomol.com). Technically this is done by incorporating the non-LTE vibrational densities N into the ExoMol States file as described in Section 4 (the ExoMol file formats are discussed extensively elsewhere73). A non-LTE spectrum of SiH2 for given T and P is then calculated using CATS' Einstein A coefficients with the ExoCross program,92 where a new non-LTE option has been implemented as part of this work. The rotational populations are assumed to be in LTE according with eqn (1).
4 Computing vibrational populations of SiH2
Two approaches were used for the calculation of the population densities of the fragment SiH2. One approach – named the decoupled 1D approach – is where the 3D wavefunctions of the fragment as well as of free SiH2 are represented by products of 1D parts with the harmonic oscillators as wavefunctions. This simplified model is mainly used to illustrate the idea of our non-LTE treatment. The second, more accurate approach – named the 3D approach – is based on the full 3D vibrational wavefunctions computed using the variational program TROVE.74 Both approaches are presented in the following in order to assess and compare the accuracy achieved.4.1 The 1D approach
A vibrational state |ν〉 = |ν1,ν2,ν3〉 of SiH2 is characterized by the three (normal mode) quantum numbers ν1, ν2 and ν3 corresponding to the two stretching modes (ν1 and ν3) and one bending mode (ν2) of the SiH2 molecule. The 1D approach considers the stretching Si–H1, Si–H2 and bending ∠HSiH modes, both of the molecular fragment and gas phase SiH2 molecules, as fully independent and described by one dimensional (1D) wavefunctions under the harmonic approximation, as given by: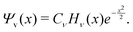 | (5) |
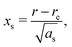 | (6) |
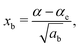 | (7) |
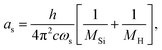 | (8) |
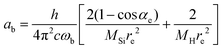 | (9) |
The constants as and ab correspond to inverse masses of the vibrational part of a free three-atomic molecule expressed in terms of the internal coordinates r1, r2, α (see, e.g. Sutcliffe and Tennyson,108 Yurchenko et al.109).
A 1D population for the corresponding mode of the gas phase SiH2 molecule is given by eqn (4) with |ν〉 = Ψv(x). The different disilane fragments have different structural parameters re, αe, ωs and ωb, see Tables 1 and 3, and thus lead to different ground state vibrational 1D wavefunctions |0(fragment)〉 (stretching or bending) and hence result in different vibrational populations Nν of the gas phase SiH2 according with eqn (4).
For each of the three modes (two stretching and one bending), 1D wavefunctions of the gas phase SiH2 for 30 vibrational states from ν0 up to ν29 were calculated. These 1D wavefunctions were then numerically integrated with the corresponding ground state 1D wavefunctions |ν = 0〉 of the fragment in question.
The total vibrational population Nν1,ν2,ν3 in this approximation is then given by a product
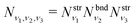 | (10) |
where 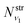 and
and 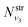 are obtained using the stretching harmonic oscillators wavefunctions |ν1〉 and |ν3〉, while
are obtained using the stretching harmonic oscillators wavefunctions |ν1〉 and |ν3〉, while 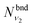 is obtained using the corresponding bending harmonic oscillator wavefunction |ν2〉. The independent treatment of the two stretching populations is partly justified by the local mode character of the vibrational degrees of freedom of SiH2 due to the near 90° bond angle (see, e.g. Jensen110 and Clark et al.72). The asymmetric vibrational modes of SiH2 (B2 in C2v) are non populated in this 1D approximation. This is because for the parallel nature of the Franck–Condon transitions from the ground vibrational state of disilane, which is fully symmetric (A1), only symmetric states of SiH2 give rise to non-zero integrals in eqn (4). For example, the vibrational population of the (2,1,0) state (2 stretching and 1 bending quanta of A1) of the GM fragment is obtained as a product of
is obtained using the corresponding bending harmonic oscillator wavefunction |ν2〉. The independent treatment of the two stretching populations is partly justified by the local mode character of the vibrational degrees of freedom of SiH2 due to the near 90° bond angle (see, e.g. Jensen110 and Clark et al.72). The asymmetric vibrational modes of SiH2 (B2 in C2v) are non populated in this 1D approximation. This is because for the parallel nature of the Franck–Condon transitions from the ground vibrational state of disilane, which is fully symmetric (A1), only symmetric states of SiH2 give rise to non-zero integrals in eqn (4). For example, the vibrational population of the (2,1,0) state (2 stretching and 1 bending quanta of A1) of the GM fragment is obtained as a product of 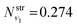 ,
, 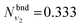 and
and 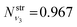 , respectively, resulting in N(ν2,ν1,ν0) = 0.088, while the population of the B2-type (0,0,1) vibratitonal state is assumed to be zero. The populations Nν1,ν2,ν3 are pre-calculated for each vibrational state (ν1,ν2,ν3) of SiH2 and added to the CATS State file to be used in non-LTE simulations (see below, Section 4.3). All the vibrational populations computed and used as part of this work are provided in the ESI.†
, respectively, resulting in N(ν2,ν1,ν0) = 0.088, while the population of the B2-type (0,0,1) vibratitonal state is assumed to be zero. The populations Nν1,ν2,ν3 are pre-calculated for each vibrational state (ν1,ν2,ν3) of SiH2 and added to the CATS State file to be used in non-LTE simulations (see below, Section 4.3). All the vibrational populations computed and used as part of this work are provided in the ESI.†
 | ||
| Fig. 3 The 1D bending mode harmonic wavefunctions for the five SiH2 fragments described in Table 1 as a function of bond angle in degrees. Ground state fragment (black) compared with the LTE |ν = 0〉 (blue), |ν = 1〉 (green), |ν = 2〉 (red). | ||
 | ||
| Fig. 4 The 1D stretching mode harmonic wavefunctions for the five SiH2 fragments described in Table 1 as a function of bond length in Angstrom. Ground state fragment (black) compared with the LTE |ν = 0〉 (blue), |ν = 1〉 (green), |ν = 2〉 (red). | ||
The shapes and positions of the curves in Fig. 3 and 4 match with the parameters from Table 1. The larger ω used for the bending modes manifests itself as wider curves, while the black curves are all centred around the equilibrium bond angles and length listed in Table 1.
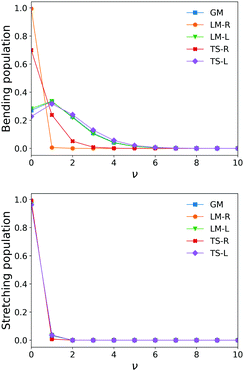
The similarity between the populations of the LM-L, TS-L and GM fragments is expected owing to their similar structural parameters. It is interesting to see the most populated vibrational levels of LM-R and TS-R are always lower than the vibrational levels of LM-L, TS-L and GM.
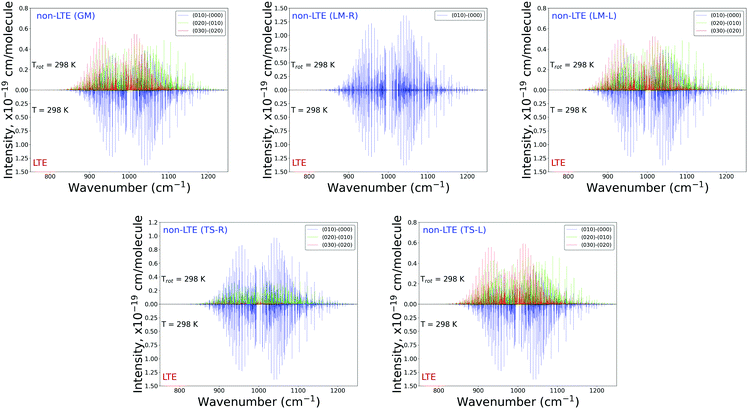
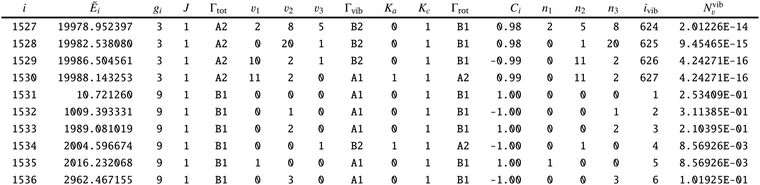
Fig. 6 and 7 show the 1000 cm−1 and 2000 cm−1 (10 μm and 5 μm) bands for the SiH2 absorption spectrum, respectively, simulated using the non-LTE densities from Fig. 5 for all five cases considered and compared to the LTE scenario assuming the (rotational) temperature of T = 296 K and using the CATS line list. The strongest bands are indicated using different colours. Fig. 6 focuses on the 1000 cm−1 band. Most of the non-LTE spectra contain bending hot bands (020)–(010) and (020)–(010), which are stronger than the fundamental band (000)–(000). It can be seen that the P and R branches of the non-LTE spectra are shifted to lower wavenumbers in the GM, LM-L and TS-L spectra. In the TS-R and LM-R spectra the bands are not shifted, with the LM-R spectrum having only the fundamental (010)–(000) band visible.
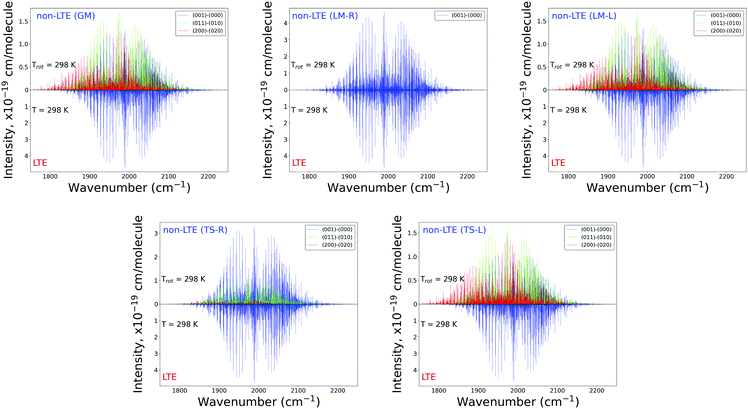
The plots in Fig. 7 show the 2000 cm−1 band in the region of the polyad (100)/(020)/(001) for the five fragments, with the strongest fundamental band (001)–(000). The non-LTE intensities of the hot bands (011)–(010), (200)–(020) are found to be comparable to the intensities of the (001)–(000) band. The Q branch is clearly shifted for the GM, TS-L and LM-L molecules. The band is less shifted for the TS-R and LM-R fragments, but owing to the increased similarity between the fragment and molecular structures with TS-R and LM-R this is to be expected. Only the main polyad system (100)/(020)/(001) is visible for the TS-R spectrum (indicated as (001)–(000) in Fig. 7).
With the equilibrium structures of the TS-R and LM-R fragments being similar to the equilibrium structure of SiH2, their non-LTE spectra are expected to be a similar spectrum to LTE. Indeed, for the 1D harmonic approach their P, Q and R branches maintain the expected LTE intensities for both the 1000 cm−1 and 2000 cm−1 bands.
4.2 The 3D approach for vibrational populations using an accurate variational method
In a full 3D approach, the ground state wavefunction |0,0,0(fragment)〉 represents an SiH2 fragment of an 18D ground state vibrational wavefunction of Si2H6:| ϕSi2H6 = |0,0,0(SiH2)〉 |0,0,0,0,0,0,0,0,0,0,0,0,0,0,0(SiH4)〉. |
The vibrational populations are then modelled using the Franck–Condon integrals as follows:
| Nν1,ν2,ν3 = |〈0,0,0(fragment)|ν1, ν2, ν3(g.ph.)〉|2, | (11) |
In order to simplify the 3D integration in eqn (11), the variational wavefunction |0,0,0(fragment)〉 is obtained using the same vibrational basis set as the variational solution of the gas phase SiH2. By taking advantage of the compatibility of the orthogonality of the basis sets, the Franck–Condon factors are then given by as a sum of products
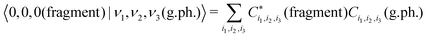 | (12) |
TROVE uses optimized non-standard vibrational basis sets, generated numerically by solving 1D Schrödinger equations for realistic 1D potentials.74 This procedure allows producing compact basis functions optimized for a specific problem. In our case, the PESs of the corresponding five fragments and of the gas phase SiH2 are different and therefore the generated basis sets would be different and even not orthogonal. We therefore implemented a feature in TROVE allowing to read and use externally generated basis functions. Of course all relevant calculation setups must be compatible, including the numerical grids used for the stretching and bending modes and their sizes. Using foreign basis sets certainly degrades their quality. However, since we are only interested in fragments' ground state wavefunctions, this degradation can be mitigated by including enough basis functions. Our typical 1D basis sets contain 12–24 functions (see details below), which should be more than enough to obtain a converged ground state solution even with non-optimized basis sets.
| VSi2H6 = VSiH2(r1, r2, α) + Vrest, |
| VSiH2(r1, r2, α) = fstr(r1) + fstr(r2) + fbnd(α). | (13) |
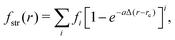 | (14) |
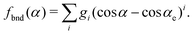 | (15) |
| Parameter | GM | TS-L | TS-R | LM-L | LM- R |
|---|---|---|---|---|---|
| r e, Å | 1.48218 | 1.47971 | 1.49888 | 1.47982 | 1.51611 |
| α e, deg | 108.701 | 108.938 | 103.268 | 108.264 | 92.287 |
| a, Å−1 | 1.29065 | 1.29110 | 1.22364 | 1.27911 | 1.27050 |
| g 1 | 0 | 0 | 0 | 0 | −8132.4642 |
| g 2 | 80964.377 | 90039.635 | 101613.84 | 93608.413 | 168296.56 |
| g 3 | −117331.83 | −126539.98 | −159054.10 | −129420.43 | −299843.15 |
| g 4 | 139212.98 | 168090.27 | 182459.45 | 305247.60 | 324286.87 |
| f 1 | 0 | 0 | 0 | 0 | −793.07685 |
| f 2 | 43617.985 | 43796.459 | 45462.423 | 22217.055 | 19382.230 |
| f 3 | −6594.4391 | −6937.7586 | −8917.729 | −3824.8354 | −2298.2220 |
| f 4 | 2809.6655 | 2714.6696 | 3750.0966 | 1407.7267 | 2233.5205 |
Fig. 8 illustrates the ab initio PESs of different fragments as 1D cuts for the stretching and bending modes compared to the corresponding cuts of the gas phase SiH2 molecule. The bending cuts have especially different shapes with shifts to larger equilibrium angles and much steeper PESs. The differences in the stretching cuts are less pronounced. These features are important for the non-LTE behaviour of the corresponding excited states populations, with the bending degree of freedom to have stronger non-LTE character than stretching.
| P= 2(ν1 + ν3) + ν2 ≤ 24, | (16) |
For the gas phase SiH2 calculations we employed the empirically refined PES by Clark et al.72 For the five SiH2 fragments only the vibrational ground state wavefunctions |0,0,0〉 were computed using the same setup and utilizing the basis functions from the g.ph. calculations as described above, but for the fragments' ab initio PESs from eqn (13).
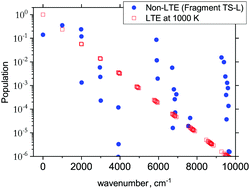
The 3D results generally agree with the 1D case. As an example, Fig. 9 shows the TS-L case: the bending primitive wavefunctions of the gas phase SiH2 are compared to the ν = 0 bending wavefunction generated for the PES of TS-L. Fig. 10 shows the corresponding non-LTE vibrational populations as a function of the corresponding energies for the same TS-L scenario of the 3D vibrational populations. These populations are very different from the Boltzmann distribution, also shown on this figure for the SiH2 vibrational states at T = 1000 K, which exhibits an exponential decay with ν = 0 at its maximum. It nicely demonstrates that it would not be possible to associate a single vibrational temperature for this bell-shaped distribution.
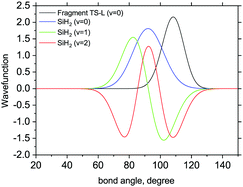 | ||
| Fig. 9 3D Bending primitive wavefunctions of SiH2 compared to the ground state 3D bending wavefunctions for Fragment TS-L. Calculated with TROVE. | ||
4.3 Non-LTE intensity simulations
A non-LTE absorption line intensity Ifi (cm per molecule) can be calculated as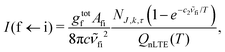 | (17) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) fi is the transition wavenumber (cm−1), QnLTE(T) is the non-LTE partition function defined in eqn (3).
fi is the transition wavenumber (cm−1), QnLTE(T) is the non-LTE partition function defined in eqn (3).
In order to simulate absorption spectra of the gas phase SiH2 assuming a non-LTE vibrational populations Nν1,ν2,ν3, we use the line positions and Einstein A coefficients from the ExoMol CATS line list72 employing the ExoCross program.92 The ExoMol line lists are formatted as two files, a States file and a Transition file. It is described extensively elsewhere73 and in this paper we shall only discuss how the ExoMol format has been adapted for use in non-LTE situations.
To adapt the CATS States file72 for non-LTE applications an additional ‘density’ column Nν1,ν2,ν3 was added as a final column, see an extract from the States file in Table 6. This column contains the weightings to the transition probabilities as populations of the vibrational levels occupied by the gas phase SiH2. The ‘density’ column is specific for the calculation of line lists for non-LTE molecules is not routinely included into the ExoMol States files.
This column is read by ExoCross and used to give the population weighting to each line intensity. Evaluation of the non-LTE population NJ,k,ν(T) given for each ro-vibrational state as in eqn (1) is based on the knowledge of the corresponding vibrational state (ν1,ν2,ν3) as well as the rotational energy contribution ẼrotJ,k. Therefore for this approach to work it is mandatory for all ro-vibrational states to be vibrationally assigned in order to be able to subtract the vibrational contribution Ẽvvib from the total energy according with eqn (2). All vibrational quantum numbers (ν1,ν2,ν3) are not required, only a vibrational index indicating the vibrational state in question. In our model, all asymmetric vibrational states (B2) are not populated due to the zero overlap with the ground state of the A1 symmetry in eqn (11), as part of the completely vertical Franck–Condon approximation.
The stark differences of the non-LTE spectra offer an ability for experiment to distinguish between SiH2 molecules produced from fragmenting Si2H6, and even to indicate dissociation channels involved.
4.4
Ö![[X with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0058_0303.gif) spectrum
spectrum
The visible electronic band Ö![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) of SiH2 has often been used to study different reactions involving leading to silylene.91 Here we used the program RENNER117 to simulate a non-LTE electronic spectrum of SiH2 with the spectroscopic model by Yurchenko et al.118 for the Ã1B1–
of SiH2 has often been used to study different reactions involving leading to silylene.91 Here we used the program RENNER117 to simulate a non-LTE electronic spectrum of SiH2 with the spectroscopic model by Yurchenko et al.118 for the Ã1B1–![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A1 system. The model includes two empirically adjusted PESs, for the à and
1A1 system. The model includes two empirically adjusted PESs, for the à and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) states, respectively, and an ab initio (MRCI) Ö
states, respectively, and an ab initio (MRCI) Ö![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) transition dipole moment surface (TDMS).
transition dipole moment surface (TDMS).
In the RENNER calculations, the size of the basis set originally used in Yurchenko et al.118 was reduced in order to be able to increase the rotational excitations. The main purpose of this exercise is to show a qualitative impact of the non-LTE populations on the spectral shape of the electronic band and not so much the quality of the line positions, and therefore a smaller basis set is justified. We used 18 and 12 bending basis functions for the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) and à electronic states, respectively, for every |k| block (where |k| ≤ J). The
and à electronic states, respectively, for every |k| block (where |k| ≤ J). The ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A1 electronic state basis set included NA = 12 stretching functions of the A1 symmetry and NB = 10 stretching functions of the B2 symmetry. For the Ã1B1 state NA = 10 and NB = 8 stretching functions were used. These stretching functions were constructed from the Morse oscillator functions |n1〉|n3〉 with n1 + n3 ≤ Nstretch = 12.
1A1 electronic state basis set included NA = 12 stretching functions of the A1 symmetry and NB = 10 stretching functions of the B2 symmetry. For the Ã1B1 state NA = 10 and NB = 8 stretching functions were used. These stretching functions were constructed from the Morse oscillator functions |n1〉|n3〉 with n1 + n3 ≤ Nstretch = 12.
A rovibronic line list for the Ã1B1–![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A1 of SiH2 was generated covering the rotational excitations up to Jmax = 15 with the lower state energies (
1A1 of SiH2 was generated covering the rotational excitations up to Jmax = 15 with the lower state energies (![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) ) truncated at hc·25
) truncated at hc·25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and the upper state energies truncated at hc·28
000 cm−1 and the upper state energies truncated at hc·28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1.
000 cm−1.
For the non-LTE simulations we used the 1D vibrational population model with the structural parameters corresponding to TS-L from Table 3. Fig. 12 shows a non-LTE electronic spectrum of SiH2 in the region of the band Ã(0,2,0)←![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) (0,0,0), assuming the rotational temperature Trot = 500 K, compared to an LTE spectrum of T = 500 K. The non-LTE spectrum contains the hot band Ã(0,3,0)←
(0,0,0), assuming the rotational temperature Trot = 500 K, compared to an LTE spectrum of T = 500 K. The non-LTE spectrum contains the hot band Ã(0,3,0)←![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) (0,1,0) which can be used to identify the non-LTE character of the system. The rovibronic line 101←110 belonging to this band used in a number of experimental studies involving SiH2 as a reaction product71,89,90 to estimate reaction rates. It is common for such studies to assume the Boltzmann equilibrium at different stages of the analysis of the measurements. For example, the partition function of SiH2 is required to estimate the number density of SiH2 in its lower, ground electronic state,70,71,119 which is directly affected by the LTE assumption. As our calculations show, the number densities of SiH2 as a reaction product can vary significantly under non-LTE depending on the reaction pathway and impact the experimental rates.
(0,1,0) which can be used to identify the non-LTE character of the system. The rovibronic line 101←110 belonging to this band used in a number of experimental studies involving SiH2 as a reaction product71,89,90 to estimate reaction rates. It is common for such studies to assume the Boltzmann equilibrium at different stages of the analysis of the measurements. For example, the partition function of SiH2 is required to estimate the number density of SiH2 in its lower, ground electronic state,70,71,119 which is directly affected by the LTE assumption. As our calculations show, the number densities of SiH2 as a reaction product can vary significantly under non-LTE depending on the reaction pathway and impact the experimental rates.
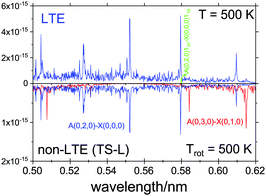 | ||
Fig. 12 An Ã1B1–![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A1 spectra of SiH2, LTE (T = 500 K) and non-LTE Trot = 500 K using the 1D model for Fragment TS-L. The energies and Einstein coefficients are generated using the RENNER program with the spectroscopic model from Yurchenko et al.118 A Gaussian line profile of HWHM = 5 cm−1. The popular ro-vibronic line (0,0,0)101←(0,0,0)110 used in measurements of reaction rates of SiHn species71,89,90 is shown. 1A1 spectra of SiH2, LTE (T = 500 K) and non-LTE Trot = 500 K using the 1D model for Fragment TS-L. The energies and Einstein coefficients are generated using the RENNER program with the spectroscopic model from Yurchenko et al.118 A Gaussian line profile of HWHM = 5 cm−1. The popular ro-vibronic line (0,0,0)101←(0,0,0)110 used in measurements of reaction rates of SiHn species71,89,90 is shown. | ||
5 Conclusion
The focus of this paper is on the new features which have been added to TROVE to allow modelling the non-LTE populations of polyatomic molecules. We have demonstrated this capability by modelling the non-LTE line list of SiH2 calculated with 3D wavefunctions and TROVE, and compared them to non-LTE spectra of SiH2 modelled using a 1D harmonic approach, and the LTE line list calculated previously by ExoMol.There are two stable isomers of disilane, a local minimum structure and a global minimum structure, with a third transition state structure also known. Non-LTE spectra of SiH2 corresponding to dissociation of disilane from different sides of the three disilane isomer were computed. We have shown that the non-LTE spectra of SiH2 are different in most cases. This is important as the spectrum of SiH2 is used to monitor the quantity present in a reaction as a means to track the progress of SiH2 + SiH4 → Si2H6 and Si2H6 → SiH2 + SiH4 when calculating the corresponding rate constant. If Si2H6 is decomposing at a rate slower than it is being formed, then tracking the quantity of SiH2 can give a rate constant that is not reflective of the speed of reaction, and merely an indication of the equilibrium balance of the two species SiH2 and Si2H6.
In two approaches considered, 1D and the 3D, we assume that the rotational degrees of freedom are equillibrated quickly once the dissociation from disilane occurs, hence we use the Boltzmann distribution for the rotational degrees of freedom. We also assume that the SiH2 fragment during the instantaneous dissociation and is fully decoupled from the rest of the Si2H6 molecule, i.e. can be described by a 3D wavefunction in its lowest, relaxed vibrational configuration and has the same structural parameters as the Si2H6 molecule.
We have shown that the non-LTE spectra of SiH2 can be calculated by the new TROVE methodology and existing ExoMol line list, and it compares well to the simpler 1D harmonic approximation published previously. The method could be applied to the non-LTE spectroscopy of other small molecules including SiH4, which has not been explored here.
We have also shown that despite the many approximations used in the 1D approximation (separability of the modes, Harmonic approximate etc.), the results compare well to the results obtained using the full 3D approach. This lends confidence in using the simplified but robust 1D approach in similar non-LTE studies, as e.g. we have used to model the CO non-LTE spectra,6 recently, which are planning to explore in the future.
The methods described here can be used model the intensity distribution of the reaction products and to ascertain from what molecule the SiH2 dissociated from. The equilibrium structured parameters (bond lengths and angles) can be treated as effective parameters to be adjusted to reproduce the experimental spectra.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by UK research councils EPSRC, under grant EP/N509577/1 with COVID extension, and STFC, under grant ST/R000476/1. This work made extensive use of the STFC DiRAC HPC facility supported by BIS National E-infrastructure capital grant ST/J005673/1 and STFC grants ST/H008586/1 and ST/K00333X/1. We thank the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation programme through Advance Grant number 883830. We also thank Thomas Mellor for help with the variational model.References
- H. W. Hermann and S. R. Leone, J. Chem. Phys., 1982, 76, 4766–4774 CrossRef CAS.
- M. Ferus, P. Kubelík, K. Kawaguchi, K. Dryahina, P. Španěl and S. Civiš, J. Phys. Chem. A, 2011, 115, 1885–1899 CrossRef CAS PubMed.
- M. Ferus, R. Michalčíková, V. Shestivská, J. Šponer, J. E. Šponer and S. Civiš, J. Phys. Chem. A, 2014, 118, 719–736 CrossRef CAS PubMed.
- M. Ferus, P. Kubelík, A. Knížek, A. Pastorek, J. Sutherland and S. Civiš, Sci. Rep., 2017, 7, 6275 CrossRef PubMed.
- K. Prozument, J. H. Baraban, P. B. Changala, G. B. Park, R. G. Shaver, J. S. Muenter, S. J. Klippenstein, V. Y. Chernyak and R. W. Field, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 146–151 CrossRef CAS PubMed.
- A. Pastorek, S. Civiš, V. H. J. Clark, S. N. Yurchenko and M. Ferus, J. Quant. Spectrosc. Radiat. Transf., 2021, 262, 107521 CrossRef CAS.
- P. G. Wenthold, D. A. Hrovat, W. T. Borden and W. C. Lineberger, Science, 1996, 272, 1456–1459 CrossRef CAS PubMed.
- W. H. Green Jr, C. B. Moore and W. F. Polik, Annu. Rev. Phys. Chem., 1992, 43, 591–626 CrossRef.
- E. A. Michael, C. J. Keoshian, S. K. Anderson and R. J. Saykally, J. Mol. Spectrosc., 2001, 208, 219–223 CrossRef CAS.
- E. Michael, C. Keoshian, D. Wagner, S. Anderson and R. Saykally, Chem. Phys. Lett., 2001, 338, 277–284 CrossRef CAS.
- G. Bazalgette Courrèges-Lacoste, J. Sprengers, J. Bulthuis, S. Stolte, T. Motylewski and H. Linnartz, Chem. Phys. Lett., 2001, 335, 209–214 CrossRef.
- D. Zhao, K. D. Doney and H. Linnartz, J. Mol. Spectrosc., 2014, 296, 1–8 CrossRef CAS.
- E. Dudás, N. Suas-David, S. Brahmachary, V. Kulkarni, A. Benidar, S. Kassi, C. Charles and R. Georges, J. Chem. Phys., 2020, 152, 134201 CrossRef PubMed.
- E. A. Milne, Handbuch der Astrophysik, Springer, 1930, vol. 3, ch. 2, p. 65 Search PubMed.
- A. Curtis and R. Goody, Proc. Math. Phys. Eng., 1956, 236, 193–206 CAS.
- J. Houghton, Q. J. R. Meteorol. Soc., 1969, 95, 1–20 CrossRef.
- W. R. Kuhn and J. London, J. Atmos. Sci., 1969, 26, 189–204 CrossRef CAS.
- R. E. Dickinson, J. Atmos. Sci., 1972, 29, 1531–1556 CrossRef CAS.
- J. B. Kumer and T. C. James, J. Geophys. Res., 1974, 79, 638–648 CrossRef CAS.
- G. Shved, Soviet Astron., 1975, 18, 499–504 Search PubMed.
- M. López-Puertas, R. Rodrigo, J. López-Moreno and F. Taylor, J. Atmos. Terr. Phys., 1986, 48, 749–764 CrossRef.
- M. López-Puertas, R. Rodrigo, A. Molina and F. Taylor, J. Atmos. Terr. Phys., 1986, 48, 729–748 CrossRef.
- P. P. Wintersteiner, R. H. Picard, R. D. Sharma, J. R. Winick and R. A. Joseph, J. Geophys. Res. - Atmos., 1992, 97, 18083–18117 CrossRef.
- A. P. Williams, PhD thesis, University of Oxford, 1971.
- F. van der Tak, J. Black, F. Schöier, D. Jansen and E. van Dishoeck, Astron. Astrophys., 2007, 468, 627–635 CrossRef.
- B. Funke, M. López-Puertas, M. García-Comas, M. Kaufmann, M. Höpfner and G. Stiller, J. Quant. Spectrosc. Radiat. Transf., 2012, 113, 1771–1817 CrossRef CAS.
- E. Pannier and C. O. Laux, J. Quant. Spectrosc. Radiat. Transf., 2019, 222–223, 12–25 CrossRef CAS.
- M. López-Puertas and F. W. Taylor, Non-LTE radiative transfer in the Atmosphere, World Scientific, 2001, vol. 3 Search PubMed.
- M. Asplund, Annu. Rev. Astron. Astrophys., 2005, 43, 481–530 CrossRef CAS.
- S. Chandrasekhar, Radiative Transfer, Dover Publications, New York, 1960 Search PubMed.
- P. Feautrier, Comptes Rendus Acad. Sci. Paris, 1964, 258, 3189 Search PubMed.
- G. Rybicki, J. Quant. Spectrosc. Radiat. Transf., 1971, 11, 589–595 CrossRef.
- R. G. Athay, Radiation transport in spectral lines, D. Reidel Publishing Co. (Geophysics and Astrophysics Monographs), Dordrecht, Holland, 1972, vol. 1 Search PubMed.
- D. Mihalas, Stellar Atmospheres, WH Freeman and Co, San Francisco, 1978 Search PubMed.
- E. Simonneau and L. Crivellari, Astrophys. J., 1993, 409, 830 CrossRef.
- H. Chen, Z. Zhan, A. Youngblood, E. T. Wolf, A. D. Feinstein and D. E. Horton, Nat. Astron., 2021, 5, 298–310 CrossRef.
- P. F. Goldsmith and W. D. Langer, Astrophys. J., 1999, 517, 209–225 CrossRef CAS.
- F. Lique, F. van der Tak, J. Klos, J. Bulthuis and M. Alexander, Astron. Astrophys., 2009, 493, 557–563 CrossRef CAS.
- J. Jasinski and J. O. Chu, J. Chem. Phys., 1988, 88, 1678–1687 CrossRef CAS.
- J. R. Doyle, D. A. Doughty and A. Gallagher, J. Appl. Phys., 1990, 68, 4375–4384 CrossRef CAS.
- J. Jasinski, B. S. Meyerson and B. A. Scott, Annu. Rev. Phys. Chem., 1987, 38, 109–140 CrossRef CAS.
- M. Ernst, A. Sax and J. Kalcher, Chem. Phys. Lett., 1993, 216, 189–193 CrossRef CAS.
- D. M. Goldhaber and A. L. Betz, Astrophys. J., 1984, 279, L55–L58 CrossRef CAS.
- R. Kaiser and Y. Osamura, Astron. Astrophys., 2005, 432, 559–566 CrossRef CAS.
- P. M. Agrawal, D. L. Thompson and L. M. Raff, J. Chem. Phys., 1988, 89, 741–750 CrossRef CAS.
- R. Becerra, H. M. Frey, B. P. Mason, R. Walsh and M. S. Gordon, J. Chem. Soc., Faraday Trans., 1995, 91, 2723–2732 RSC.
- C. Puzzarini and P. R. Taylor, J. Chem. Phys., 2005, 122, 054315 CrossRef PubMed.
- J. Church, J. Durig, T. A. Mohamed and A. B. Mohamad, Spectrochim. Acta, Part A, 1994, 50, 639–660 CrossRef.
- H. Sun, Macromolecules, 1995, 28, 701–712 CrossRef CAS.
- A. Márquez, J. F. Sanz, M. Gelizé and A. Dargelos, Chem. Phys., 1991, 149, 311–318 CrossRef.
- A. Romero, M. Kiwi and R. Ramrez, Phys. Status Solidi B, 2002, 230, 391–395 CrossRef CAS.
- S. G. Cho, O. K. Rim and G. Park, J. Comput. Chem., 1997, 18, 1523–1533 CrossRef CAS.
- P. M. Agrawal, D. L. Thompson and L. M. Raff, J. Chem. Phys., 1990, 92, 1069–1082 CrossRef CAS.
- S.-W. Hu, Y. Wang, X.-Y. Wang, T.-W. Chu and X.-Q. Liu, J. Phys. Chem. A, 2003, 2954–2963 CrossRef CAS.
- M. M. Law, J. T. Fraser-Smith and C. U. Perotto, Phys. Chem. Chem. Phys., 2012, 14, 6922–6936 RSC.
- W. A. Eger, A. Genest and N. Rösch, Chem. – Eur. J., 2012, 18, 9106–9116 CrossRef CAS PubMed.
- K. Yoshida, K. Matsumoto, T. Oguchi, K. Tonokura and M. Koshi, J. Phys. Chem., 2006, 110, 4726–4731 CrossRef CAS PubMed.
- L. Andrews and X. Wang, J. Phys. Chem. A, 2002, 106, 7696–7702 CrossRef CAS.
- J. R. Durig and J. S. Church, J. Chem. Phys., 1980, 73, 4784–4797 CrossRef CAS.
- S. Sakai and M. Nakamura, J. Phys. Chem., 1993, 97, 4960–4965 CrossRef CAS.
- M. Bowrey and J. Purnell, Proc. Math. Phys. Eng. Sci., 1971, 321, 341–359 CAS.
- G. Olbrich, P. Potzinger, B. Reimann and R. Walsh, Organometallics, 1984, 3, 1267–1272 CrossRef CAS.
- J. G. Martin, H. E. O'Neal and M. A. Ring, Int. J. Chem. Kinet., 1990, 22, 613–631 CrossRef CAS.
- H. K. Moffat, K. F. Jensen and R. W. Carr, J. Phys. Chem., 1992, 96, 7683–7695 CrossRef CAS.
- H.-J. Mick, M. W. Markus, P. Roth and V. N. Smirnov, Ber. Bunsenges. Phys. Chem., 1995, 99, 880–890 CrossRef CAS.
- A. A. Onischuk and V. N. Panfilov, Russ. Chem. Rev., 2001, 70, 321–332 CrossRef CAS.
- K. F. Roenigk, K. F. Jensen and R. W. Carr, J. Phys. Chem., 1987, 91, 5732–5739 CrossRef CAS.
- H. Emeléus and C. Reid, J. Chem. Soc., 1939, 1021–1030 RSC.
- N. Tada, K. Tonokura, K. Matsumoto, M. Koshi, A. Miyoshi and H. Matsui, J. Phys. Chem. A, 1999, 103, 322–329 CrossRef CAS.
- M. W. Markus and P. Roth, J. Quant. Spectrosc. Radiat. Transf., 1994, 52, 783–789 CrossRef CAS.
- M. Hertl and J. Jolly, J. Phys. D: Appl. Phys., 2000, 33, 381–388 CrossRef CAS.
- V. H. J. Clark, A. Owens, J. Tennyson and S. N. Yurchenko, J. Quant. Spectrosc. Radiat. Transf., 2020, 246, 106929 CrossRef CAS.
- J. Tennyson, S. N. Yurchenko, A. F. Al-Refaie, V. H. J. Clark, K. L. Chubb, E. K. Conway, A. Dewan, M. N. Gorman, C. Hill, A. E. Lynas-Gray, T. Mellor, L. K. McKemmish, A. Owens, O. L. Polyansky, M. Semenov, W. Somogyi, G. Tinetti, A. Upadhyay, I. Waldmann, Y. Wang, S. Wright and O. P. Yurchenko, J. Quant. Spectrosc. Radiat. Transf., 2020, 255, 107228 CrossRef CAS.
- S. N. Yurchenko, W. Thiel and P. Jensen, J. Mol. Spectrosc., 2007, 245, 126–140 CrossRef CAS.
- S. N. Yurchenko, A. Yachmenev and R. I. Ovsyannikov, J. Chem. Theory Comput., 2017, 13, 4368–4381 CrossRef CAS PubMed.
- T. B. Adler, G. Knizia and H. J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- Y. B. Band and K. F. Freed, J. Chem. Phys., 1975, 63, 3382–3397 CrossRef CAS.
- M. J. Berry, Chem. Phys. Lett., 1974, 27, 73–77 CrossRef CAS.
- G. Inoue and M. Suzuki, Chem. Phys. Lett., 1984, 105, 641–644 CrossRef CAS.
- J. M. Jasinski, E. A. Whittaker, G. C. Bjorklund, R. W. Dreyfus, R. D. Estes and R. E. Walkup, Appl. Phys. Lett., 1984, 44, 1155–1157 CrossRef CAS.
- G. Inoue and M. Suzuki, Chem. Phys. Lett., 1985, 122, 361–364 CrossRef CAS.
- D. Rayner, R. Steer, P. Hackett, C. Wilson and P. John, Chem. Phys. Lett., 1986, 123, 449–452 CrossRef CAS.
- J. Thoman and J. Steinfeld, Chem. Phys. Lett., 1986, 124, 35–38 CrossRef CAS.
- J. J. O'Brien and G. H. Atkinson, Chem. Phys. Lett., 1986, 130, 321–329 CrossRef.
- J. W. Thoman, J. I. Steinfeld, R. I. McKay and A. E. W. Knight, J. Chem. Phys., 1987, 86, 5909–5917 CrossRef CAS.
- M. Fukushima, S. Mayama and K. Obi, J. Chem. Phys., 1992, 96, 44–52 CrossRef CAS.
- A. Kono, N. Koike, K. Okuda and T. Goto, Jpn. J. Appl. Phys., 1993, 32, L543–L546 CrossRef CAS.
- H. Nomura, K. Akimoto, A. Kono and T. Goto, J. Phys. D: Appl. Phys., 1995, 28, 1977–1982 CrossRef CAS.
- R. Escribano and A. Campargue, J. Chem. Phys., 1998, 108, 6249–6257 CrossRef CAS.
- S. N. Yurchenko, A. F. Al-Refaie and J. Tennyson, Astron. Astrophys., 2018, 614, A131 CrossRef.
- S. N. Yurchenko, I. Szabo, E. Pyatenko and J. Tennyson, Mon. Not. R. Astron. Soc., 2018, 480, 3397–3411 CrossRef CAS.
- H. Y. Li, S. N. Yurchenko and J. Tennyson, Mon. Not. R. Astron. Soc., 2019, 486, 2351–2365 CrossRef CAS.
- A. Y. Adam, P. Jensen, A. Yachmenev and S. N. Yurchenko, J. Mol. Spectrosc., 2019, 362, 77–83 CrossRef CAS.
- A. N. Smirnov, V. G. Solomonik, S. N. Yurchenko and J. Tennyson, Phys. Chem. Chem. Phys., 2019, 21, 22794–22810 RSC.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- S. Ten-No, Chem. Phys. Lett., 2004, 398, 56–61 CrossRef CAS.
- J. G. Hill, K. A. Peterson, G. Knizia and H.-J. Werner, J. Chem. Phys., 2009, 131, 194105 CrossRef PubMed.
- K. E. Yousaf and K. A. Peterson, J. Chem. Phys., 2008, 129, 184108 CrossRef PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291 RSC.
- C. Hättig, Phys. Chem. Chem. Phys., 2005, 7, 59–66 RSC.
- K. Tonokura, T. Murasaki and M. Koshi, J. Phys. Chem. B, 2002, 106, 555–563 CrossRef CAS.
- B. Beagley, A. R. Conrad, J. M. Freeman, J. J. Monaghan, B. G. Norton and G. C. Holywell, J. Mol. Struct., 1972, 11, 371–380 CrossRef CAS.
- J. Duncan, J. Harvie, D. McKean and S. Cradock, J. Mol. Struct., 1986, 145, 225–242 CrossRef CAS.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminformatics, 2012, 4, 17 CrossRef CAS PubMed.
- D. L. Kokkin, T. Ma, T. Steimle and T. J. Sears, J. Chem. Phys., 2016, 144, 244304 CrossRef PubMed.
- B. T. Sutcliffe and J. Tennyson, Int. J. Quantum Chem., 1991, 39, 183–196 CrossRef CAS.
- S. N. Yurchenko, T. M. Mellor, R. S. Freedman and J. Tennyson, Mon. Not. R. Astron. Soc., 2020, 496, 5282–5291 CrossRef.
- P. Jensen, Mol. Phys., 2000, 98, 1253–1285 CrossRef CAS.
- A. Yachmenev and S. N. Yurchenko, J. Chem. Phys., 2015, 143, 014105 CrossRef PubMed.
- S. N. Yurchenko, A. Yachmenev and R. I. Ovsyannikov, J. Chem. Theory Comput., 2017, 13, 4368–4381 CrossRef CAS PubMed.
- J. Tennyson and S. N. Yurchenko, Int. J. Quantum Chem, 2017, 117, 92–103 CrossRef CAS.
- P. R. Bunker and P. Jensen, Molecular Symmetry and Spectroscopy, NRC Research Press, Ottawa, 2nd edn, 1998 Search PubMed.
- B. V. Noumerov, Mon. Not. R. Astron. Soc., 1924, 84, 592–602 CrossRef.
- J. W. Cooley, Math. Comp., 1961, 15, 363–374 Search PubMed.
- P. Jensen, M. Brumm, W. Kraemer and P. Bunker, J. Mol. Spectrosc., 1995, 171, 31–57 CrossRef CAS.
- S. N. Yurchenko, P. R. Bunker, W. P. Kraemer and P. Jensen, Can. J. Chem., 2004, 82, 694–708 CrossRef CAS.
- A. Campargue, D. Romanini and N. Sadeghi, J. Phys. D: Appl. Phys., 1998, 31, 1168–1175 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00839k |
| This journal is © the Owner Societies 2021 |