Open Access Article
Open Access ArticleHydration enthalpies of amorphous sucrose, trehalose and maltodextrins and their relationship with heat capacities†
Ekaterina
Bogdanova
 ab,
Anna
Millqvist Fureby
c and
Vitaly
Kocherbitov
ab,
Anna
Millqvist Fureby
c and
Vitaly
Kocherbitov
 *ab
*ab
aBiomedical Science, Malmö University, SE-20506, Malmö, Sweden. E-mail: vitaly.kocherbitov@mau.se
bBiofilms research center for Biointerfaces, Malmö, Sweden
cRISE Research Institutes of Sweden, Stockholm, Sweden
First published on 4th June 2021
Abstract
The mechanisms of glass transitions and the behavior of small solute molecules in a glassy matrix are some of the most important topics of modern thermodynamics. Water plays an important role in the physical and chemical stability of lyophilized biologics formulations, in which glassy carbohydrates act as cryoprotectants and stabilizers. In this study, sorption calorimetry was used for simultaneous measurements of water activity and the enthalpy of water sorption by amorphous sucrose, trehalose and maltodextrins. Moreover, the heat capacity of these carbohydrates in mixtures with water was measured by DSC in a broad range of water contents. The hydration enthalpies of glassy sucrose, trehalose and maltodextrins are exothermic, and the enthalpy change of water-induced isothermal glass transitions is higher for small molecules. The partial molar enthalpy of mixing of water in slow experiments is about −18 kJ mol−1, but less exothermic in the case of small molecules at fast hydration scan rates. By measuring the heat capacities of disaccharides and maltodextrins as a function of water content, we separated the contributions of carbohydrates and water to the total heat capacities of the mixtures. The combination of these data allowed testing of thermodynamic models describing the hydration-induced glass transitions. The heat capacity changes calculated by the fitting of the hydration enthalpy data for disaccharides are in good agreement with the heat capacity data obtained by DSC, while for maltodextrins, the effect of sub-Tg transitions should be taken into account. Combining the data obtained by different techniques, we found a distinct difference in the behavior of water in glassy polymers compared to that in glassy disaccharides. By understanding the behavior of water in glassy carbohydrates, these results can be used to improve the design of freeze–dried formulations of proteins and probiotics.
1. Introduction
The study of glassy states is one of the key topics of current thermodynamics. Amorphous disaccharides and polysaccharides are of particular interest for pharmaceutical and food industries as these can stabilize proteins, peptides, antibodies and bacteria against degradation during the freeze–drying process and storage.1 One of the important properties of amorphous materials is the glass transition. Polymers and other amorphous materials are fragile and hard at temperatures much lower than the glass transition temperature (glassy state), and soft and flexible at temperatures much higher than the glass transition temperature (rubbery or liquid state). The glass transition parameters are used for predicting the long-term stability of solid formulations2–4 and as a guidance for selecting storage conditions.1,5 Protein degradation increases above the glass transition temperature,3 since the molecular mobility is much higher in the rubbery state. Water is known to decrease the glass transition temperature and increase the molecular mobility, thus acting as a plasticizer. This behavior can be described by the empirical Gordon–Taylor equation6,7 which includes the glass transition temperatures of single components and a parameter individual for a particular binary system. There are, however, opposite examples, indicating that in confinement (and in certain cases in the bulk) water can act as an anti-plasticizer.8–10In the case of amorphous sugars, water sorption changes their physico-chemical properties from rigid amorphous solids to highly viscous liquids and then to solid crystals (if the substance is prone to crystallization) that are dissolved upon further addition of water. The most common technique to study moisture sorption is gravimetric vapor sorption, which measures sorption isotherms, i.e., plots of water activity versus water content at a constant temperature. The water sorption isotherms of amorphous carbohydrates and polymers can be analyzed using either surface adsorption or bulk mixing models. To the first group belong the well-known Langmuir adsorption model, Brunauer–Emmett–Teller (BET) model and Guggenheim–Anderson–de Boer (GAB) model. In this case, the hydration process considers a monolayer or multilayer physical adsorption of adsorbate molecules on a plane surface where all adsorption sites are equivalent, with or without interactions between layers. This approach is successfully used in materials science and catalysis, but biopolymers have important distinguishing features. In particular, water molecules are rather absorbed by the bulk of amorphous sugars than being adsorbed at the surface.11,12 As a result of the mismatch between the assumptions of the adsorption models and the physics of the absorption process, they are unable to account for significant hysteresis between the sorption and desorption isotherms in the case of biopolymers, as the models do not consider the plasticizing effect of water, as well as the swelling of the material. Alternatively, sorption of water can be described using models that assume a mixing in the bulk, rather than adsorption at a surface. In particular, the Flory–Huggins solution theory of polymers shows good agreement with the experimental data for the liquid or rubbery state. However, it is not applicable for the description of polymers in the glassy state. Vrentas and Vrentas13 combined the Flory–Huggins theory with the free volume theory and proposed a model that satisfactorily describes the characteristic shape of water sorption isotherms for polyvinylpyrrolidone (PVP),14 starch,15 and small molecules: glucose and trehalose16 and amorphous mixtures of sugars (trehalose, sucrose) – PVP.17
In addition to water sorption isotherms, fundamental thermodynamic properties of matter such as heat capacity in the glassy state and enthalpy of mixing are used for understanding water–amorphous carbohydrate interactions. Glass is not a thermodynamically stable state, it is less ordered than crystalline state; this has an impact on its thermodynamic properties. It was shown18 that the heat capacity of the amorphous form of sucrose below Tg is significantly higher than that of crystals. Similar data were obtained for other pharmaceutically important glass-forming substances such as sorbitol, trehalose and indomethacin.18 Moreover, the heat capacity of an amorphous material is dependent on the thermal history of the sample. In particular, a lyophilized material has a higher heat capacity than a quench-cooled and then aged material. It has also been shown that the heat capacity of sucrose melt decreases with time.18 Since the amorphous system tends to equilibrium, the heat capacity shifts towards values typical for crystalline materials.19 In general, microscopic molecular motions define the macroscopic thermodynamic properties such as enthalpy and heat capacity. Although heat capacity measurements are routine experiments in adiabatic or scanning calorimetry, a molecular-level interpretation of the experimental heat capacity data of amorphous polymers and their mixtures with water is not a trivial task, but may require statistical thermodynamic calculations.20
One of the examples of a thermodynamic variable that describes mixing process is the enthalpy of solution. The enthalpy of solution is an integral property that describes mixing with water in one step, from the solid state to the liquid state. The experimental data of the heat of solution are available in the literature.21 Due to its integral nature, this parameter is however not suitable for describing the changes that gradually occur in an amorphous material upon hydration. Another thermodynamic property that describes the interactions with water is the partial molar enthalpy of mixing of water (Hmw). It is defined as the change of enthalpy upon the addition of infinitely small amounts of water (normalized per added amount). This is a differential property and is suitable for the characterization of changes that occur upon gradual hydration of a substance. The heat of mixing is the total result of many different interactions between components and gives useful information about complex systems. Due to their technical complexity, calorimetric measurements of water vapor sorption using glassy carbohydrates are rarely found in the literature. As an example, one can mention the work by Lechuga-Ballesteros and coworkers who used a thermal activity monitor to study the interactions between amorphous saccharides and water.12 This methodology allows the measurements of sorption or mixing enthalpy as a function of relative humidity, but water contents in the samples cannot be determined, which presents a substantial limitation.
Another calorimetric approach that does not have these limitations is the method of sorption calorimetry developed by Wadsö and coworkers.22 It is a unique technique for the measurements of the partial molar enthalpy of mixing and the water sorption isotherms in one experiment. It was successfully used for the investigation of interactions of water with biopolymers such as cellulose,11 mucins,23 hyaluronic acid,24 acid-hydrolysed starch25 and lysozymes.26 It was shown that the initial hydration of amorphous biopolymers is exothermic. Water-induced glass transitions can be observed as an endothermic step in the partial molar enthalpy of the mixing curve24,25,27 similar to the heat capacity step in DSC experiments. Crystallization typically produces an exothermic peak in the hydration enthalpy curve;25 however, an endothermic crystallization peak was observed for hyaluronic acid.24
Although the hydration of carbohydrate polymers and sugar-based surfactants27 was studied by sorption calorimetry before, the corresponding studies of low-molecular-weight amorphous carbohydrates have not been, to the best of our knowledge, reported in the literature. Here we present a comparative study of the hydration of amorphous carbohydrates (sucrose, trehalose and maltodextrins) using sorption calorimetry. Moreover, we present the measurements of heat capacities of water–carbohydrate mixtures as a function of water content. Furthermore, using a recently developed theory that describes the enthalpy of water sorption using glassy materials,28 we analyze the relationship between the heat capacities and the hydration enthalpies in the glassy state.
2. Materials and methods
2.1. Materials
Sucrose (CAS 57-50-1) and trehalose dihydrate (CAS 6138-23-4) were purchased from Sigma Aldrich. Glucidex12 and Glucidex9 are corn maltodextrins, with dextrose equivalents (DE) of 12 and 9, respectively, which were kindly provided by Roquette (France). Milli-Q purified water was used for all the experiments (ELGA, Purelab Flex). Glucidex9 and Glucidex12 powders were used as received or dried in a vacuum at room temperature.2.2. Methods
In the case of dry samples, they were placed in 40 μm aluminum pans, hermetically sealed in a nitrogen atmosphere with relative humidity of less than 5% RH. The pans were scanned at different temperature ranges and a heating rate of 10 °C min−1.
We used equilibration or interrupted equilibration of a dried material at various relative humidities in saturated salt solutions such as LiCl (aw = 0.11), MgCl2 (aw = 0.33), Mg(NO3)2 (aw = 0.53), NaCl (aw = 0.75), KCl (aw = 0.84), and K2SO4 (aw = 0.97)29 to obtain different water contents in solid samples. The samples with water contents of more than 30 wt% were prepared in aluminum pans by weighing crystalline sucrose, trehalose dehydrate or maltodextrin powder, adding the required amounts of liquid MQ water (ELGA, Purelab Flex) and sealing the pans.
Heat capacity measurements were performed using the following temperature program: ramp to 25 °C, isothermal 5 min, cooling 10 °C min−1 to −50 °C, isothermal 5 min, and heating 10 °C min−1 to 60 °C (method 1) or to 100 °C (method 2). The first test runs with freeze–dried sucrose were performed up to 100 °C. Since the samples crystallize about 90–100 °C, for further experiments with sucrose, a lower maximum temperature was applied. Method 1 was used for sucrose heat capacity measurements, method 2 for trehalose and both for maltodextrins. The run was performed 4 times for sucrose and trehalose, and once for maltodextrins. The DSC was calibrated with sapphire. From the obtained DSC data, the heat capacity was calculated using MATLAB (MathWorks, Inc).
Two different connecting tubes between the sorption and desorption chambers were used in this work in separate experiments. A narrow tube (diameter 3.6 mm) and a large tube (diameter 9.1 mm) were assembled for slow and fast scan experiments, respectively. The properties of the tube and the corresponding thermal power in maltodextrin experiments are listed in Table 1. The signal at the fast scan rate is ten times higher than that at the slow scan rate, analogous to the difference between the DSC experiments at 10 °C min−1 and 1 °C min−1. Experiments were performed 3 times for sucrose and trehalose with both narrow and large tubes, and once for Glucidex9 and Glucidex12 at the desired scan rate.
3. Results and discussion
3.1. Isothermal sorption calorimetry of sucrose, trehalose and maltodextrin
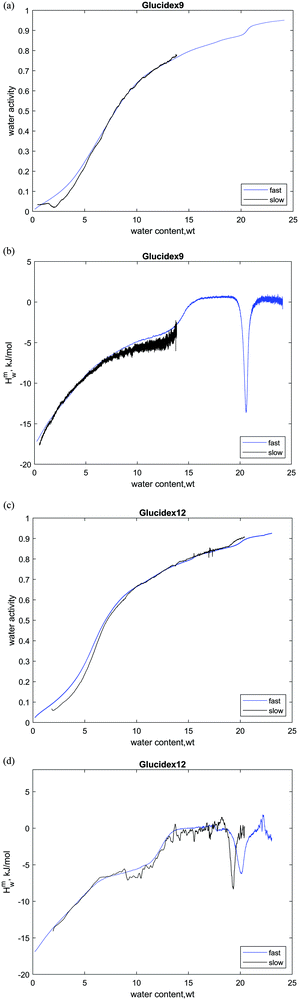
The glassy system is not in a thermodynamically stable equilibrium state, hence it is not surprising that the slow scan rate profile for sucrose has substantial differences compared to the fast one (Fig. 1a and c). First, in the glassy state, the partial molar enthalpy of mixing of water is more exothermic for the slow scan rate (−18 kJ mol−1). Second, the glass transition is shifted to a somewhat lower hydration level, and third, crystallization occurs at much lower water content (5.4 wt% vs. 8 wt%).
This scan rate dependence of the sorption behavior can be understood considering the kinetics of water sorption. For obtaining equilibrium thermodynamic data in sorption calorimetry, it is assumed that the resistance to water diffusion and the gradient of water concentration are present only in the vapor phase (between the vaporization chamber and the sorption chamber), while in the sample, there are no gradients of water activity. In the case of fast experiments when the vapor flow is high, and the water mobility in the glassy state is limited (and dependent on concentration33), this assumption is not fulfilled, and the gradients may appear in the sample. This leads to higher water activity on the surface of the sample in fast experiments, which is one of the reasons for the difference seen in Fig. 1a.
Crystallization of sucrose upon hydration is also dependent on the scan rates. In the fast experiment, one can see some signs of its beginning at aw = 0.4, and at aw = 0.5 it strongly accelerates. In the slow experiment, it starts around aw = 0.35 and in terms of concentration, the scan rate dependence is even more obvious. The literature values for the threshold activity of crystallization are also diverse. For example, Lechuga-Ballesteros and coauthors detected sucrose crystallization using a thermal activity monitor at a water activity of 0.45.12 In an earlier work, it was shown that amorphous sucrose does not crystallize for 3 years at a water activity below 0.17, but at 0.33 crystallization occurs within 24 hours.32 These results can be explained by the fact that crystallization of supercooled (or supersaturated) liquid is a spontaneous and stochastic process that can occur at a random point in time. Since the slow scans take a longer time than the fast ones, there is a higher probability that crystallization occurs at lower water contents.
The initial hydration of amorphous trehalose shows a highly exothermic effect of about −18 kJ mol−1 in the slow scan rate experiment and −12 kJ mol−1 in the fast scan rate experiment. The water-induced glass transition takes place in the range of 6.5–7 wt%, with aw = 0.35–0.4 in both experiments, followed by the hydration of the metastable liquid with the heat effect close to zero. Crystallization occurs below 10 wt% in the slow case and slightly above in the fast case at aw = 0.45–0.5. This crystallization event is consistent with the formation of trehalose dihydrate since the water content in this event is close to that in the trehalose dihydrate (9.52 wt%). This is in good agreement with literature data, for example, crystallization of trehalose dihydrate was observed in ref. 14 in gravimetric water sorption experiments at 30 °C and aw = 0.4.
According to the sorption isotherms of trehalose, the system contains more water at similar water activities in slow experiments, which can be attributed to the slow diffusion of water. As one can see from the comparison of the hydration plots for sucrose and trehalose, the scan rate has a stronger influence on the hydration profile of the former, which is especially clear in the case of crystallization. In this comparison, one should keep in mind that trehalose crystallizes in the form of a dihydrate, while sucrose crystallizes in its anhydrous form, which might influence the kinetics of crystallization.
 was calculated at the point of the water-induced glass transition
was calculated at the point of the water-induced glass transition
| Substance | Scan rate | T g2 (K) | ΔCp2 (J g−1 K−1) | A (K) | ΔHmw (kJ mol−1), eqn (2) | ΔHmw (kJ mol−1), experimentc |
|---|---|---|---|---|---|---|
| a Data provided by the supplier. b Data obtained by linear extrapolation. c The experimental values are taken as a height of the glass transition step on the plot of the partial enthalpy of mixing. | ||||||
| Sucrose | Fast | 343 | 0.620 | 901 | 10 | 9.5 |
| Sucrose | Slow | 343 | 0.620 | 901 | 10 | 11 |
| Trehalose | Fast | 393 | 0.720 | 1034 | 13 | 10 |
| Trehalose | Slow | 393 | 0.720 | 1034 | 13 | 11.5 |
| Glucidex12 | Fast/slow | 473a | 0.225b | 1312 | 5.3 | 5 |
| Glucidex9 | Fast | 498a | 0.224b | 1343 | 5.4 | 5 |
Neither the sorption isotherm of maltodextrin, nor its hydration enthalpy, shows a clear dependence on the humidity scan rate. This behavior is strikingly different compared to that of the sucrose and trehalose cases. We suggest that the primary reason for this is the difference in water diffusion properties. In particular, the water diffusion coefficient for the sucrose–water mixture is 10−16 m2 s−1,33 while the water diffusion coefficient for the maltodextrin–water mixture was estimated to be 10−13 m2 s−1.34 In other words, water molecules in the polymer–water matrix move faster by three orders of magnitude compared to disaccharides and thus are distributed more evenly in the material, hence the absence of the effect of the scan rate for maltodextrins. In the case of sucrose and trehalose, in fast scans, the slow water diffusion can result in the formation of concentration gradients in the solid particles and variation in water uptake.
Water sorption isotherms of amorphous disaccharides, maltodextrins and starch materials have positive slopes. Upon crystallization, water activity changes its behavior and typically, a step on the activity curve is observed. Hence, it is easy to determine the critical water activity of the crystallization from the water sorption isotherm. However, the position of the isothermal water-induced glass transition is not clearly seen on the sorption isotherm. Simultaneous measurements of the sorption isotherm of the sample and the corresponding differential enthalpies of hydration make glass transition and crystallization phenomena clearly visible (Fig. 1 and 2).
3.2. Models describing the enthalpy of sorption
 | (1) |
 is the heat capacity change of the polymer (J g−1 K−1), and A is a positive coefficient characterizing the plasticizing effect of water and defined as Tgm = Tg2 − Aω1. In a more general sense, it is the derivative of the glass transition temperature on the composition which is
is the heat capacity change of the polymer (J g−1 K−1), and A is a positive coefficient characterizing the plasticizing effect of water and defined as Tgm = Tg2 − Aω1. In a more general sense, it is the derivative of the glass transition temperature on the composition which is  . Here and below, we use the following notation: Tg1 – glass transition temperature of pure water, Tg2 – glass transition temperature of the polymer, κ – Gordon–Taylor parameter, Tgm – glass transition temperature of the mixture, w1 – mass fraction of water, and w2 – mass fraction of the polymer.
. Here and below, we use the following notation: Tg1 – glass transition temperature of pure water, Tg2 – glass transition temperature of the polymer, κ – Gordon–Taylor parameter, Tgm – glass transition temperature of the mixture, w1 – mass fraction of water, and w2 – mass fraction of the polymer.
The exothermic contribution to the enthalpy of mixing due to the glassy state is described by the third term of eqn (1):
| ΔHm1 = −M1ΔC0p2A | (2) |
| ΔHm1rg = ΔC0p2(Tg2 − T) | (3) |
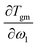 , is calculated from the Gordon–Taylor equation (kappa parameters are listed in Table 3). Despite the assumptions mentioned above, the calculated values are in reasonable agreement with the experimental data. Interestingly, despite the fact that in the dry limit the exothermic heat effect for maltodextrins (Fig. 2c and d) is similar or stronger than that for small sugars (Fig. 1c and d), the step in the enthalpy of mixing at the glass transition point is much smaller.
, is calculated from the Gordon–Taylor equation (kappa parameters are listed in Table 3). Despite the assumptions mentioned above, the calculated values are in reasonable agreement with the experimental data. Interestingly, despite the fact that in the dry limit the exothermic heat effect for maltodextrins (Fig. 2c and d) is similar or stronger than that for small sugars (Fig. 1c and d), the step in the enthalpy of mixing at the glass transition point is much smaller.
| Substance | DSC | Sorption calorimetry | |||||
|---|---|---|---|---|---|---|---|
| T g2, K fixed | κ fixed | ΔCp1 (J g−1 K−1) | ΔCp2 (J g−1 K−1) | Scan rate | ΔCp1 (J g−1 K−1)f | ΔCp2 (J g−1 K−1)f | |
| a Data from ref. 7. b Data from ref. 36. c Data provided by the supplier, obtained from the Gordon–Taylor equation. d Obtained from a linear approximation of difference of heat capacities of liquid and glass at 25 °C. e Correction on sub-Tg according to eqn (8). f The mean values of heat capacity changes obtained by fitting (with the standard deviations). | |||||||
| Sucrose | 343.15 | 0.17a | 3.02 ± 1.0d | 0.73 ± 0.5d | Fast | 2.4 ± 2.0 | 0.69 ± 0.02 |
| Slow | −0.9 ± 1.0 | 0.77 ± 0.02 | |||||
| Trehalose | 393.15 | 0.19b | 1.67 ± 0.5d | 0.81 ± 0.1d | Fast | 2.73 ± 0.06 | 0.762 ± 0.002 |
| Slow | 2.24 ± 0.42 | 0.868 ± 0.008 | |||||
| Glucidex12 | 473.15c | 0.15a | −0.31 ± 0.02e | 0.22 ± 0.03e | Fast | −0.09 ± 0.54 | 0.40 ± 0.02 |
| Slow | 0.04 ± 0.93 | 0.39 ± 0.002 | |||||
| Glucidex9 | 498.15c | 0.13a | −0.35 ± 0.02e | 0.22 ± 0.01e | Fast | −0.09 ± 0.14 | 0.36 ± 0.01 |
| Slow | 0.05 ± 0.22 | 0.361 ± 0.004 | |||||
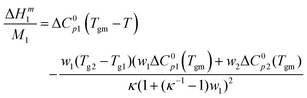 | (4) |
Earlier, the model was tested on starch and cellulose experimental data and gave a satisfactory prediction of the heat capacity change of the dry polymer and the kappa parameter.28 Here, the hydration enthalpy data of the glassy region of sucrose, trehalose, Glucidex12 and Glucidex9 were fitted with eqn (4) using MATLAB (MathWorks, Inc). The fitting results are presented in Table 3.
To check the fitting reproducibility, it was performed 3 times for different concentration ranges for every enthalpy curve. Each curve was split into two parts: low water content and high water content (an example is presented in Fig. 3), where the concentration ranges are 0.01–0.04 and 0.05–0.1, respectively. The concentration ranges were different for each experiment, since the position of the water-induced glass transition varies from sample to sample. The fitting procedure was performed on the two data sets and for the whole glassy region (more data are shown in the ESI,† Tables S1–S7).
 | ||
| Fig. 3 Fitting results of eqn (3) for Glucidex12 for low (a) and high (b) water content range. Black curve – experimental data, blue – data points chosen for fitting, and red – resulted fitting. | ||
The parameters (ΔCp2) obtained in fitting (sorption calorimetry columns in Table 3) for the fast and slow scan rates are similar (about 10% difference), show only few percent standard deviations, and are in good agreement with DSC data. In contrast, the heat capacity increment for water (ΔCp1) obtained in fitting exhibits larger standard deviations reflecting the differences in the thermodynamic parameters of water at different water contents. Moreover, the ΔCp1 shows rather diverse values depending on the material and experimental conditions, which can be a valuable source of information on the properties of the glassy state. In particular, in the case of trehalose, ΔCp1 is positive and shows values comparable to those observed for pure water.38 In the case of sucrose, this parameter is positive for the fast scan rate but negative for the slow experiment. One should, however, note that the fitting quality in the case of sucrose can be lower than that of the other three substances considered in this study due to a very narrow glassy region (see Fig. 1c). The initial disturbance of the calorimetric experiment in the case of fast scan rate might affect the quality of the experimental data. Moreover, the possible residual moisture that could not be fully removed from the freeze–dried samples can have a stronger influence on the results when the glassy region is narrow. The difference between the slow and fast scan rates can also appear due to the enthalpy relaxation. While in DSC experiments the enthalpy relaxation might be seen as a small endothermic peak after the glass transition step on the DSC heating curve,39 in sorption calorimetric experiments, it may influence the Hm1 values in the glassy state.
For both Glucidex9 and Glucidex12, the heat capacity change of water is close to zero, which indicates a different state of water in the glassy maltodextrin compared to that in the sucrose and trehalose.
3.3. The heat capacity and the temperature-induced glass transition
Sucrose is a crystalline substance that needs to undergo a certain treatment in order to be obtained in an amorphous form. Often it is made amorphous by melting and quench-cooling. Below we compare the properties of amorphous sucrose obtained by quench-cooling and freeze–drying. The thermal behaviors of sucrose samples obtained by these two methods are presented in Fig. 4. In the experiment with melting, sucrose crystals were melted in a DSC pan using a temperature ramp of 20 °C min−1 to 186 °C and then quench-cooled by 20 °C min−1 straight after. In the second scan (blue curve), there is a glass transition with Tg (midpoint) = 68.44 °C and ΔCp = 0.645 J g−1 K−1. The freeze–dried amorphous sucrose (black curve) undergoes a glass transition at 70.60 °C with ΔCp = 0.762 J g−1 K−1 followed by a crystallization exotherm at about 110 °C and a broad melting (this part of the curve is not shown). It should be noted that all the DSC curves of the freeze–dried sucrose show crystallization at higher temperatures, while the quench-cooled samples do not. We suggest that the reason for such a behavior is the caramelization of the material during heating. After the second scan, the DSC pan with the melted sugar was opened; the obtained sample was transparent and yellow in color. A similar observation was made previously.40 Since the freeze–dried material was not treated at high temperatures, the pan contained only a white colored material after the first scan and even after the fourth DSC scan. Other factors, for example, higher surface area in the freeze–dried material, which increase the probability of surface-induced nucleation might affect the crystallization kinetics. Still, based on the color-change observation, for further experiments, only freeze–dried sucrose and trehalose were used.
The DSC curves of the freeze–dried sucrose show notable deviation from the baseline prior to the glass transition step, which might be described as an endothermic sub-Tg event. Sub-Tg endotherms (in the form of endothermic peaks) are well-known for carbohydrate polymers, for example, starch-like materials.25 Recently, Johari proposed that sucrose melt has this feature in DSC scans as well.41 The heat capacity of sucrose in the glassy state was reported to be between 1.31 and 1.38 J g−1 K−1 (25 °C),18,19 whereas our measurements provided the values of 1.29 ± 0.15 J g−1 K−1.
The DSC scan of the freeze–dried trehalose shows a glass transition step at 118 °C with ΔCp = 0.770 J g−1 K−1, and the heat capacity of the dry amorphous trehalose was measured to be 1.42 J ± 0.10 g−1 K−1 at 25 °C, which is in perfect agreement with the value from literature data (1.43 J g−1 K−1).18
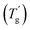 and ice melting events (Fig. S2 in the ESI†).
and ice melting events (Fig. S2 in the ESI†).
 | ||
| Fig. 5 Heat capacities of sucrose–water (a), trehalose–water (b) and Glucidex9–water (c) systems. Different colors correspond to different water contents (in wt%). | ||
The results of the heat capacity measurements of the trehalose–water mixtures are presented in Fig. 5b. The glassy trehalose–water samples with water contents of 3.4–5.1 wt% undergo glass transitions with a small but clear enthalpy relaxation event directly after the glass transition step. The glass transition temperature decreases with the increase of water content. The sample with 1 wt% water content undergoes glass transition at a higher temperature than the presented range. There are some deviations from the baseline (for the sample with 5.1 wt%) prior to the glass transition step that might be a sign of a small sub-Tg event. The heat capacity curves of the samples with water contents higher than 60 wt% exhibit  and ice melting events and are presented in Fig. S3 in the ESI.†
and ice melting events and are presented in Fig. S3 in the ESI.†
The heat capacity measurements of the Glucidex9–water mixtures are presented in Fig. 5c. The heat capacity of the dry sample of Glucidex9 shows no deviation from the baseline in the range of 240–380 K. The glassy Glucidex9–water samples with water contents of 1.8–10.13 wt% show notable deviations from the baseline at about 320–340 K, which corresponds to the sub-Tg transitions in starch-like materials followed by Tg at higher temperatures. The heat capacity dependencies of the samples with water contents higher than 10.13 wt% are presented in the ESI† (Fig. S4 and S5). They exhibit  , ice melting and gelatinization thermal events.
, ice melting and gelatinization thermal events.
For comparison with the sorption calorimetric experiments performed at 25 °C, it is instructive to present the DSC heat capacity data as a function of water content at 25 °C (Fig. 6).
 | ||
| Fig. 6 The heat capacity and heat capacity changes in binary mixtures at 25 °C (unless stated otherwise in the legend). For sucrose, heat capacities in the liquid and glassy states are shown; the data for the glassy state marked as “extr” are obtained by extrapolation of the linear regime of the heat capacity curve before the glass transition; the literature data from the work of Lyle et al.43 are obtained by averaging the data at 20 and 30 °C; the heat capacity change is for the glass transition temperature (a). For trehalose, the heat capacities in the liquid and glassy states are shown; the heat capacity change is for the glass transition temperature (b). For Glucidex9, the heat capacities in the glassy and liquid states, as well as the two-phase regions (B + water, A + B), are shown according to its phase diagram25 (c). For Glucidex9, the heat capacity step is the direct measurements at Tgm; data marked as “corr” are corrected for the sub-Tg endotherm (d). | ||
The height of the heat capacity step at the glass transition temperature, ΔCp(Tgm), in the amorphous sucrose is presented as a function of water content in Fig. 6a (blue triangles). The baselines are taken before the sub-Tg event. The results indicate an increase of the heat capacity step with the increase of water content. All other data points in this figure are obtained at 25 °C. The heat capacities of liquid sucrose solutions (red circles) cover a broad range of concentrations and are in good agreement with literature data (green circles).43 The heat capacities of the glassy mixtures are presented as black squares. Despite the rather narrow range of concentrations, an ascending trend is clearly seen (extrapolated with a black dashed line). A thorough examination of Fig. 5a suggests that this trend can be caused by the endothermic sub-Tg event rather than by the change of the main step size. In order to separate these two events, we calculated the extrapolated values of heat capacities in the glassy state that the system would show in case of the absence of sub-Tg (magenta squares). The extrapolated values were obtained by the linear extrapolation of the baseline measured in the range of 235–265 K to 298.15 K. The results show that the main contribution to the increase in heat capacity in the glassy sucrose–water mixture was due to the sub-Tg event.
The heat capacities at 25 °C and the heat capacity change in the trehalose–water binary mixture are presented in Fig. 6b. All three presented parameters show a clear increase in water content.
The heat capacity of the Glucidex9–water mixture at 25 °C is presented in Fig. 6c. Four different regimes corresponding to different phase compositions of the system are clearly seen. The heat capacity of the glassy mixture (black squares) is in agreement with literature data.42 The second regime in the range of 13–18 wt% corresponds to the liquid state (blue circles). Several points at the beginning of this regime (at 13.8–14 wt%) probably correspond to the transition region between the glass and liquid states. It follows from the fact that the DSC heat capacity curves for these concentrations departed from the glassy baseline below 25 °C but the liquid state was not reached at this temperature. Therefore, the points at 13.8–14 wt% were not taken into account for the calculation of the linear dependence of the liquid. To broaden the concentration range for linear fitting, the heat capacity of the pure liquid water was included in the calculations. Still, due to a very narrow concentration range of the liquid state in the Glucidex–water system, its heat capacity dependence on water content may be less accurate than that of other phases considered here.
Other concentration ranges (red and magenta circles) refer to two-phase regions: water + B and A + B, where A and B are the crystalline phases of maltodextrin according to its phase diagram.25 The heat capacity change in the Glucidex9–water system directly measured at Tgm is presented in Fig. 6d (blue triangles). The heat capacity change corrected for sub-Tg transitions (black triangles) will be discussed at the end of this section.
The presented data of heat capacity and heat capacity change in the two-component systems are approximated by linear fits. To highlight the contributions from the two components, linear equations can be represented in the following form. The heat capacity of the liquid binary mixture at 25 °C is:
| Clp = C0,lp1·w1 + C0,lp2·(1 − w1) | (5) |
| Cgp = C∅,gp1·w1 + C0,gp2·(1 − w1) | (6) |
Subtracting eqn (4) and (5) gives an expression for ΔCp:
| ΔCp = ΔC∅p1·w1 + ΔC0p2·(1 − w1) | (7) |
The ΔC0pi values for sucrose obtained in two different ways (ΔC0pi measured at Tgm and C0,lpi − C0,gpi extr measured at 25 °C) are in reasonable agreement (see Table 4) and the second data set is chosen for comparison with the sorption calorimetry results in Table 3. In the case of trehalose, C0,lpi − C0,gpi values of the heat capacity step were chosen for comparison with the sorption calorimetry results in Table 3.
| Sucrose | Trehalose | |||
|---|---|---|---|---|
| Water (1) | Sucrose (2) | Water (1) | Trehalose (2) | |
| ∅ – apparent values (extrapolated to pure water).a Extrapolated values – the values obtained by linear extrapolation of the baseline in the range of 235–265 K to 298.15 K.b Direct measurement – values evaluated using METTLER TOLEDO software according to ISO standard, baselines were tangent lines before the sub-Tg deviation. These values are measured at the glass transition temperature of the mixture. | ||||
| C 0,l pi liquid | 4.13 | 1.93 | 4.10 | 2.22 |
| C 0,g pi glass | 2.90∅ | 1.29 | 2.42∅ | 1.41 |
| C 0,g pi glass extra | 1.11∅ | 1.20 | — | — |
| C 0,l pi –C0,gpi | 1.23∅ | 0.64 | ![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) ∅ ∅ |
0.81 |
| C 0,l pi –C0,gpi extra | ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) ∅ ∅ |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) |
— | — |
| ΔC0pi at Tgmb | 2.74∅ | 0.62 | 2.42∅ | 0.57 |
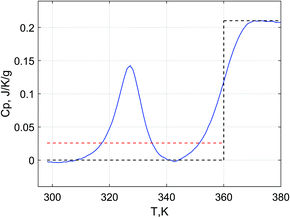
The heat capacity changes of Glucidex9 and Glucidex12 calculated as a difference between the linear approximations for the liquid and glassy states (C0,lpi − C0,gpi at 25 °C in Table 5) show too small values for the dry polymers. The reason for this is the low accuracy for the linear approximation in the liquid state due to a very narrow concentration range. Therefore, the ΔCp data obtained directly at Tgm in a broader concentration range can be considered more appropriate for monitoring the concentration dependence. The apparent values of heat capacity change for water (ΔC∅p1) obtained from these data are much lower compared to ΔC0p1 for pure water. Still, they are not negative (as one could expect from the comparison with the sorption calorimetry data). To explain this discrepancy, we recall that the glass transition in eqn (4) is approximated as a single step, not dependent on temperature. A rigorous equation for the calculation of hydration enthalpy28 includes the integration of heat capacity with respect to temperature rather than the multiplication of heat capacity changes by the temperature differences. In such integration, not only the heat capacity step but also the sub-Tg peak should be taken into account (Fig. 7). Effectively, the presence of the sub-Tg peak corresponds to the increase of the heat capacity in the glassy state (red dashed line in Fig. 7) and therefore the decrease of the heat capacity step.
| Glucidex9 | Glucidex12 | |||
|---|---|---|---|---|
| Water (1) | Glucidex9 (2) | Water (1) | Glucidex12 (2) | |
| ∅ – apparent values.a Direct measurement – values evaluated using METTLER TOLEDO software according to ISO standard, baselines are taken above the sub-Tg.b Correction on sub-Tg according to eqn (8).c Accuracy of these values can be affected by the narrow concentration range in the liquid state. | ||||
| C 0,l pi liquid | 4.06 | 1.16c | 4.00 | 1.12c |
| C 0,g pi glass | 2.37∅ | 1.08 | 2.33∅ | 1.02 |
| C 0,l pi − C0,gpi at 25 °C | 1.70∅ | 0.08c | 1.67∅ | 0.10c |
| ΔC0pi at Tgma | 0.22∅ | 0.20 | 0.24∅ | 0.23 |
| ΔC0pi sub-Tg correctedb | −![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) ∅ ∅ |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) |
−![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) ∅ ∅ |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) |
In order to take this into account, we implemented a correction of the heat capacity change:
 | (8) |
 is the slope of the enthalpy of the sub-Tg peak with respect to w1(S6, S7).
is the slope of the enthalpy of the sub-Tg peak with respect to w1(S6, S7).
The corrected data are shown in Table 5 (last row) and are chosen for comparison with the sorption calorimetry results (Table 3).
3.4. Differences in water sorption behavior between disaccharides and maltodextrins
Based on the results presented in this work, the differences in properties of the two carbohydrates can be illustrated in terms of the thermodynamics of hydration. For a better comparison, we combine the experimental data for sucrose and trehalose, as shown in Fig. 8. In the sorption calorimetry experiments, we observe the water-induced crystallization of sucrose anhydrous crystals as well as trehalose dihydrate. In the case of slow scan rate, the crystallization in the sucrose–water system occurs at the water content of 5.5 wt% and aw = 0.3, whereas in the trehalose–water system, the dihydrate crystallizes at 9.5–10 wt% and aw = 0.45–0.5. Accordingly, the trehalose–water system undergoes water-induced crystallization at higher water content and the glassy state accumulates a higher amount of water prior to crystallization. In this way, the trehalose–water system has higher water sorption capacity or “water stability” with respect to crystallization.
 | ||
| Fig. 8 Water sorption isotherms of sucrose and trehalose (a) and partial molar enthalpies of mixing of water (b). Slow scan rates, 25 °C. | ||
A contrast between the two disaccharides is also seen in the coordinates of the water-induced glass transition at 25 °C. The sucrose–water system undergoes a water-induced glass transition at 2.5–3 wt% (aw = 0.2–0.25), while trehalose at 7 wt% (aw = 0.35). This is due to the fact that the glass transition temperature of the dry sucrose (70 °C) is lower than that of trehalose (120 °C) as mentioned above.
The better water sorption capacity of trehalose can be explained based on the hydration enthalpy data (Fig. 8b). The water activity in the glassy state is dependent on the hydration enthalpy as follows:
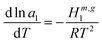 | (9) |
The heat capacity step (ΔCp2) in the case of small sugars is several times higher than that in maltodextrins according to both DSC and sorption calorimetry data (Table 3). Interestingly, the main difference arises from the heat capacity in the liquid state (C0,lp2), where the heat capacities of liquid sucrose and trehalose are higher than those of maltodextrins (see Tables 4 and 5). The difference in heat capacities in the glassy state is less pronounced. In terms of molecular motions, this can be explained by the fact that there are more degrees of freedom in disaccharides than in polymers, and their contributions to heat capacities are more pronounced in the liquid state, while being “frozen” in the glassy state.
In the enthalpy of mixing plot, the glass transition step (ΔHm1) in the case of sugars is higher than that in maltodextrins. This is in good correlation with the heat capacity step of dry substances and matches the predictions of the “constant enthalpy” models.
The glass transition-related heat capacity changes for water (ΔC∅p1) are positive for the disaccharides (Table 3) both in DSC and sorption calorimetry measurements.38 Moreover, the values of heat capacity of glassy water (C∅,gp1) estimated from the long linear extrapolation of the sucrose–water and trehalose–water systems (Table 4) are in reasonable agreement with the heat capacity of glassy water of 2.26 J g−1 K−1 at 300 K calculated by Pyda.20
In the case of maltodextrins, the situation is different. The apparent change of heat capacity of water is negative or close to 0. This can be interpreted as water molecules undergo a glass transition together with the sucrose and trehalose matrices, while in maltodextrins, they remain mobile.
For the calculations of ΔC∅p1 for polymers, an additional factor plays a role. The maltodextrins have a sub-Tg endotherm in the form of a peak that has a substantial area (additional enthalpy) that affects the calculation of the enthalpy using eqn (4). The presence of a peak is equivalent to the increase of the baseline and the decrease of the heat capacity step as illustrated in Fig. 7.
The difference in the thermodynamic properties of water in the glassy matrix of small sugars and polymers also correlated with its dynamical properties. The water diffusion coefficient of the sucrose–water mixtures at a water activity of 0.2 (slightly below glass transition) was measured by the Raman isotope tracer method (10−16 m2 s−1). The water diffusion coefficient of the maltodextrin–water mixtures was estimated to be 10−13 m2 s−1.34 Water molecules move orders of magnitude faster in the polymer–water system than in the sucrose–water system, which supports the idea that in the polymer matrix, water molecules do not exhibit properties typical for the glassy state.
The concept of the water replacement theory is as follows.2,55,56 Upon dehydration, water molecules are replaced by sugar molecules, which form hydrogen bonds with the protein.57 The hydrogen bonds are essential to maintain the three-dimensional structure of the protein, and hence the sugar molecules can support the protein structure by replacing water in these interactions. The basis for the dynamic theory is the restriction of the molecular movements of the protein, as well as the dilution effect of the sugar matrix,58 which reduces the direct protein–protein interactions. Within the frame of this theory, the molecular movements of the protein are “frozen” by incorporation into the glassy matrix.
The physical stability of amorphous formulations is determined by the glass transition temperature. The glass transition temperature is related to the overall molecular motions of the amorphous matrix. In particular, the higher the glass transition temperature, the lower the molecular mobility of the polymer or carbohydrate. The glass transition temperature does, however, not tell the whole story. The heat capacity is almost equally important for understanding the dynamics of the complex binary mixture. The fact that the heat capacity change is twice as high as that in disaccharides compared to polymers shows that the mobility change in smaller molecules is more pronounced at the glass transition temperature. The most interesting observation comes from the fact that the heat capacity change of water in polymers is much lower than that in disaccharides. This indicates that the mobility of water is uncoupled from the mobility of polymers, while in disaccharides, water changes its mobility together with the whole system.
This behavior can be rationalized in terms of free volume approaches. When water molecules penetrate through the glassy matrix during the hydration process, the density of the matrix shows a strong influence on this process. The true density is the mass of a particle divided by its volume, excluding any macroscopic cavities. Based on molecular considerations, the density of a polysaccharide is expected to be higher than the density of a disaccharide. Nevertheless, experimental data for densities in the glassy state do not show a significant difference between the two classes of substances. For example, the true density of the amorphous sucrose was found to be 1.518 g cm−3, trehalose 1.505 g cm−3,59 and maltodextrin with a DE-12 1.5091 g cm−3.60 The evolution of the density of the glassy carbohydrates upon addition of water is, however, different. The density of the maltose–water mixtures decreases upon hydration.61 This correlation is expected since the density of the amorphous disaccharides is higher than that of water. The opposite trend (density increases) was shown for the maltodextrin–water mixture60 at low water content. Even though the density of liquid water is lower than the density of maltodextrin, the addition of small amounts of water increases the density of the system. This suggests that the polymer matrix has a higher free volume, which is filled with water molecules. This also leads to a higher exothermic effect of the enthalpy of mixing with water (Fig. 1 and 2). The free volume in the glassy matrix allows more space for the diffusion of small molecules. As a result, in maltodextrins, water moves three orders of magnitude faster than in disaccharides since there is more available space in the former.
The properties of the glassy matrix affect the penetrant behavior. For best preservation of proteins and probiotics, the selection of carbohydrate excipients should be optimized to provide good interactions with the protein while at the same time providing a physically stable matrix, i.e., has a sufficiently high glass transition temperature. One of the most important parameters to consider here is the behavior of residual water in the glassy matrix. The results presented in this work can help in designing solid-state pharmaceutical formulations with increased stability.
4. Conclusions
Here we present the sorption calorimetry and DSC studies of interactions between water and amorphous sucrose, trehalose and maltodextrins. We conclude that:• The hydration enthalpies of glassy sucrose, trehalose and maltodextrins are exothermic.
• The water-induced glass transition is seen as a step on the enthalpy plot, and the step is higher for small molecules.
• The partial molar enthalpy of mixing of water in slow experiments is about −18 kJ mol−1 for all the studied carbohydrates, but less exothermic in the case for small molecules at fast hydration scan rates.
• For disaccharides, the water-induced glass transition and crystallization at 25 °C shift to lower hydration levels at slow scan rates, while for maltodextrins, this is not observed.
• By measuring the heat capacities of disaccharides and maltodextrins as a function of water content, we separated the contributions of carbohydrates and water to the total heat capacities of the mixtures.
• The heat capacity changes calculated by the fitting of the hydration enthalpy data for disaccharides are in good agreement with the heat capacity data obtained by DSC.
• The heat capacity changes of water in glassy maltodextrins evaluated from the sorption calorimetry data are negative, which can be explained by the effect of sub-Tg transitions in maltodextrins.
• The DSC heat capacity curves of maltodextrin show a sub-Tg transition in the form of a clear peak, amorphous sucrose has a sub-Tg endotherm as a shift of the baseline before the glass transition, and for trehalose no sub-Tg events were observed.
•The relaxation phenomena such as enthalpy relaxation and sub-Tg of the amorphous polymers affect the enthalpy of mixing with water.
• The data described above suggest that in disaccharides, the glass transition of water is more pronounced, while in maltodextrin it is less coupled to the carbohydrate matrix.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research was funded by the Swedish Governmental Agency for Innovation Systems (VINNOVA) and was carried out within the competence center NextBioForm (grant number 2018-04730).References
- L. Chang and M. J. Pikal, Mechanisms of Protein Stabilization in the Solid State, J. Pharm. Sci., 2009, 98(9), 2886–2908 CrossRef CAS PubMed.
- W. Wang, Lyophilization and development of solid protein pharmaceuticals, Int. J. Pharm., 2000, 203(1–2), 1–60 CrossRef CAS.
- S. P. Duddu and P. R. Dal Monte, Effect of Glass Transition Temperature on the Stability of Lyophilized Formulations Containing a Chimeric Therapeutic Monoclonal Antibody., Pharm. Res., 1997, 14, 591–595 CrossRef CAS PubMed.
- B. C. Hancock and G. Zografi, Characteristics and Significance of the Amorphous State in Pharmaceutical Systems, J. Pharm. Sci., 1997, 86(1), 1–12 CrossRef CAS PubMed.
- T. Arakawa, et al., Factors affecting short-term and long-term stabilities of proteins, Adv. Drug Delivery Rev., 2001, 46, 307–326 CrossRef CAS.
- M. Gordon and J. S. Taylor, Ideal copolymers and the second-order transitions of synthetic rubbers. I. non-crystalline copolymers, J. Appl. Chem., 1952, 2(9), 493–500 CrossRef CAS.
- Y. H. Roos and M. Karel, Water and Molecular-Weight Effects on Glass Transitions in Amorphous Carbohydrates and Carbohydrate Solutions, J. Food Sci., 1991, 56(6), 1676–1681 CrossRef CAS.
- K. Elamin, et al., Different behavior of water in confined solutions of high and low solute concentrations, Phys. Chem. Chem. Phys., 2013, 15(42), 18437–18444 RSC.
- J. Swenson, et al., Why is there no clear glass transition of confined water?, Chem. Phys., 2013, 424, 20–25 CrossRef CAS.
- L. Mascia, et al., Antiplasticization of Polymer Materials: Structural Aspects and Effects on Mechanical and Diffusion-Controlled Properties, Polymers, 2020, 12(4), 769 CrossRef CAS.
- V. Kocherbitov, et al., Hydration of microcrystalline cellulose and milled cellulose studied by sorption calorimetry, J. Phys. Chem. B, 2008, 112(12), 3728–3734 CrossRef CAS PubMed.
- D. Lechuga-Ballesteros, A. Bakri and D. P. Miller, Microcalorimetric measurement of the interactions between water vapor and amorphous pharmaceutical solids, Pharm. Res., 2003, 20(2), 308–318 CrossRef CAS PubMed.
- J. S. Vrentas and C. M. Vrentas, Sorption in Glassy-Polymers, Macromolecules, 1991, 24(9), 2404–2412 CrossRef CAS.
- B. C. Hancock and G. Zografi, The Use of Solution Theories for Predicting Water-Vapor Absorption by Amorphous Pharmaceutical Solids - a Test of the Flory–Huggins and Vrentas Models, Pharm. Res., 1993, 10(9), 1262–1267 CrossRef CAS PubMed.
- R. G. M. van der Sman and M. B. J. Meinders, Prediction of the state diagram of starch water mixtures using the Flory–Huggins free volume theory, Soft Matter, 2011, 7, 429–442 RSC.
- J. Zhang and G. Zografi, The Relationship Between “BET”- and “Free Volume”-Derived Parameters for Water Vapor Absorption into Amorphous Solids, J. Pharm. Sci., 2000, 89(8), 1063–1072 CrossRef CAS.
- J. Zhang and G. Zografi, Water Vapor Absorption Into Amorphous Sucrose-Poly(Vinyl Pyrrolidone) and Trehalose-Poly(Vinyl Pyrrolidone) Mixtures, J. Pharm. Sci., 2001, 90(9), 1375–1385 CrossRef CAS PubMed.
- S. L. Shamblin, et al., Characterization of the Time Scales of Molecular Motion in Pharmaceutically Important Glasses, J. Phys. Chem. B, 1999, 103, 4113–4121 CrossRef CAS.
- A. Magon, et al., Heat capacity and transition behavior of sucrose by standard, fast scanning and temperature-modulated calorimetry, Thermochim. Acta, 2014, 589, 183–196 CrossRef CAS.
- M. Pyda, Conformational Contribution to the Heat Capacity of the Starch and Water System, J. Polym. Sci., Part B: Polym. Phys., 2001, 39(23), 3038–3054 CrossRef CAS.
- D. P. Miller and J. J. de Pablo, Calorimetric Solution Properties of Simple Saccharides and Their Significance for the Stabilization of Biological Structure and Function, J. Phys. Chem. B, 2000, 104, 8876–8883 CrossRef CAS.
- L. Wadsö and N. Markova, A method to simultaneously determine sorption isotherms and sorption enthalpies with a double twin microcalorimeter, Rev. Sci. Instrum., 2002, 73(7), 2743–2754 CrossRef.
- Y. Znamenskaya, et al., Effect of hydration on structural and thermodynamic properties of pig gastric and bovine submaxillary gland mucins, J. Phys. Chem. B, 2012, 116(16), 5047–5055 CrossRef CAS PubMed.
- J. E. Cathrine Albèr, P. Falkman and V. Kocherbitov, Hydration of Hyaluronan: Effects on Structural and Thermodynamic Properties, J. Phys. Chem. B, 2015, 119, 4211–4219 CrossRef PubMed.
- J. Carlstedt, J. Wojtasz, P. Fyhr and V. Kocherbitov, Hydration and the phase diagram of acid hydrolyzed potato starch, Carbohydr. Polym., 2014, 112, 569–577 CrossRef CAS PubMed.
- V. Kocherbitov, T. Arnebrant and O. Soderman, Lysozyme-water interactions studied by sorption calorimetry, J. Phys. Chem. B, 2004, 108(49), 19036–19042 CrossRef CAS.
- V. Kocherbitov and O. Soderman, Glassy Crystalline State and Water Sorption of Alkyl Maltosides, Langmuir, 2004, 20, 3056–3061 CrossRef CAS PubMed.
- V. Kocherbitov and I. Argatov, Enthalpy of sorption by glassy polymers, Polymer, 2019, 174, 33–37 CrossRef CAS.
- L. Greenspan, Humidity fixed-points of binary saturated aqueous-solutions, J. Res. Natl. Bur. Stand., Sect. A, 1977, 81(1), 89–96 CrossRef.
- V. Kocherbitov, A new formula for accurate calculation of water activity in sorption calorimetric experiments, Thermochim. Acta, 2004, 414(1), 43–45 CrossRef CAS.
- V. Kocherbitov, On the calculation of thermodynamic parameters in sorption calorimetric experiments, J. Chem. Thermodyn., 2021, 152, 106264 CrossRef CAS.
- B. Makower and W. B. Dye, Equilibrium Moisture Content and Crystallization of Amorphous Sucrose and Glucose, J. Agric. Food Chem., 1956, 4(1), 72–77 CrossRef CAS.
- H. C. Price, et al., Quantifying water diffusion in high-viscosity and glassy aqueous solutions using a Raman isotope tracer method, Atmos. Chem. Phys., 2014, 14(8), 3817–3830 CrossRef.
- M. Räderer, A. Besson and K. Sommer, A thin film dryer approach for the determination of water diffusion coefficients in viscous products, Chem. Eng. J., 2002, 86, 185–191 CrossRef.
- G. P. Johari, G. Astl and E. Mayer, Enthalpy Relaxation of Glassy Water, J. Chem. Phys., 1990, 92(1), 809–810 CrossRef CAS.
- T. Chen, A. Fowler and M. Toner, Literature review: supplemented phase diagram of the trehalose–water binary mixture, Cryobiology, 2000, 40(3), 277–282 CrossRef CAS PubMed.
- J. Swenson, Possible relations between supercooled and glassy confined water and amorphous bulk ice, Phys. Chem. Chem. Phys., 2018, 20(48), 30095–30103 RSC.
- S. Masayasu, S. Hiroshi and S. Syûzô, Calorimetric Study of the Glassy State. IV. Heat Capacities of Glassy Water and Cubic Ice., Bull. Chem. Soc. Jpn., 1968, 41(11), 2591–2599 CrossRef.
- H. J. Thiewes and P. A. M. Steeneken, The glass transition and the sub-T, endotherm of amorphous and native potato starch at low moisture content, Carbohydr. Polym., 1996, 32, 123–130 CrossRef.
- J. W. Lee, L. C. Thomas and S. J. Schmidt, Effects of Heating Conditions on the Glass Transition Parameters of Amorphous Sucrose Produced by Melt-Quenching, J. Agric. Food Chem., 2011, 59(7), 3311–3319 CrossRef CAS PubMed.
- E. Tombari and G. P. Johari, Endothermic Effects on Heating Physically Aged Sucrose Glasses and the Clausius Theorem Violation in Glass Thermodynamics, J. Phys. Chem. B, 2020, 124, 2017–2028 CrossRef CAS PubMed.
- T. R. Noel and S. G. Ring, A study of the heat capacity of starch/water mixtures, Carbohydr. Res., 1992, 227, 203–213 CrossRef CAS.
- O. Lyle, Technology for Sugar Refinery Workers, Chapman & Hall pub, UK, London, 1957 Search PubMed.
- S. Ohtake and Y. J. Wang, Trehalose: Current use and future applications, J. Pharm. Sci., 2011, 100(6), 2020–2053 CrossRef CAS PubMed.
- T. Arakawa, Y. Kita and J. F. Carpenter, Protein–Solvent Interactions in Pharmaceutical Formulations, Pharm. Res., 1991, 8(3), 285–291 CrossRef CAS.
- S. N. Timasheff, Protein Hydration, Thermodynamic Binding, and Preferential Hydration, Biochemistry, 2002, 41(46), 13473–13482 CrossRef CAS PubMed.
- C. Olsson, et al., Mechanism of Trehalose-Induced Protein Stabilization from Neutron Scattering and Modeling. The, J. Phys. Chem. B, 2019, 123(17), 3679–3687 CrossRef CAS.
- L. M. Crowe, D. S. Reid and J. H. Crowe, Is trehalose special for preserving dry biomaterials?, Biophys. J., 1996, 71(4), 2087–2093 CrossRef CAS.
- N. Grasmeijer, et al., Unraveling protein stabilization mechanisms: vitrification and water replacement in a glass transition temperature controlled system, Biochim. Biophys. Acta, 2013, 1834(4), 763–769 CrossRef CAS PubMed.
- F. Librizzi, E. Vitrano and L. Cordone, Dehydration and Crystallization of Trehalose and Sucrose Glasses Containing Carbonmonoxy-Myoglobin, Biophys. J., 1999, 76(5), 2727–2734 CrossRef CAS.
- S. Giuffrida, et al., Proteins in amorphous saccharide matrices: Structural and dynamical insights on bioprotection, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36(7), 79 CrossRef CAS.
- C. Olsson, R. Zangana and J. Swenson, Stabilization of proteins embedded in sugars and water as studied by dielectric spectroscopy, Phys. Chem. Chem. Phys., 2020, 22(37), 21197–21207 RSC.
- T. Starciuc, et al., Trehalose or Sucrose: Which of the Two Should be Used for Stabilizing Proteins in the Solid State? A Dilemma Investigated by In Situ Micro-Raman and Dielectric Relaxation Spectroscopies During and After Freeze-Drying, J. Pharm. Sci., 2020, 109(1), 496–504 CrossRef CAS PubMed.
- V. Kocherbitov and I. Argatov, A thermodynamic theory of sorption in glassy polymers, submitted for publication.
- M. A. Mensink, et al., How sugars protect proteins in the solid state and during drying (review): mechanisms of stabilization in relation to stress conditions, Eur. J. Pharm. Biopharm., 2017, 114, 288–295 CrossRef CAS PubMed.
- F. M. Richards, Protein stability: still an unsolved problem, Cell. Mol. Life Sci., 1997, 53(10), 790–802 CrossRef CAS.
- J. H. Crowe, A. F. A. Hoekstra and L. M. Crowe, Anhydrobiosis., Annu. Rev. Physiol., 1992, 54(1), 579–599 CrossRef CAS.
- R. V. Mannige, Dynamic New World: Refining Our View of Protein Structure, Function and Evolution, Proteomes, 2014, 2(1), 128–153 CrossRef PubMed.
- K. Imamura, et al., True Density Analysis of a Freeze-Dried Amorphous Sugar Matrix, J. Pharm. Sci., 2008, 97(7), 2789–2797 CrossRef CAS PubMed.
- D. Kilburn, et al., Water in glassy carbohydrates: Opening it up at the nanolevel, J. Phys. Chem. B, 2004, 108(33), 12436–12441 CrossRef CAS.
- D. Lourdin, P. Colonna and S. G. Ring, Volumetric behaviour of maltose–water, maltose–glycerol and starch–sorbitol–water systems mixtures in relation to structural relaxation, Carbohydr. Res., 2003, 338(24), 2883–2887 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed fitting results, additional heat capacity data and enthalpies of sub-Tg transitions in Glucidex as a function of water content. See DOI: 10.1039/d1cp00779c |
| This journal is © the Owner Societies 2021 |