Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spectroscopic characterization of a thermodynamically stable doubly charged diatomic molecule: MgAr2+
Dominik
Wehrli
 ,
Matthieu
Génévriez
,
Matthieu
Génévriez
 and
Frédéric
Merkt
and
Frédéric
Merkt
 *
*
Laboratory of Physical Chemistry, ETH Zurich, CH-8093 Zurich, Switzerland. E-mail: merkt@phys.chem.ethz.ch
First published on 30th April 2021
Abstract
Although numerous doubly positively charged diatomic molecules (diatomic dications) are known from investigations using mass spectrometry and ab initio quantum chemistry, only three of them, NO2+, N22+ and DCl2+, have been studied using rotationally resolved optical spectroscopy and only about a dozen by vibrationally resolved double-ionization methods. So far, no thermodynamically stable diatomic dication has been characterized spectroscopically, primarily because of experimental difficulties associated with their synthesis in sufficient densities in the gas phase. Indeed, such molecules typically involve, as constituents, rare-gas, halogen, chalcogen, and metal atoms. We report here on a new approach to characterize molecular dications based on high-resolution photoelectron spectroscopy of the singly charged parent molecular cation and present the first spectroscopic characterization of a thermodynamically stable diatomic dication, MgAr2+. From the fully resolved vibrational and partially resolved rotational structures of the photoelectron spectra of 24MgAr+ and 26MgAr+, we determined the potential-energy function of the electronic ground state of MgAr2+, its dissociation (binding) energy (D0 = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 690(3) cm−1), and its harmonic (ωe(24MgAr2+) = 327.02(11) cm−1) and anharmonic (ωexe(24MgAr2+) = 2.477(15) cm−1) vibrational constants. The analysis enables us to explain quantitatively how the strong bond arises in this dication despite the fact that Ar and Mg2+ both have a full-shell rare-gas electronic configuration.
690(3) cm−1), and its harmonic (ωe(24MgAr2+) = 327.02(11) cm−1) and anharmonic (ωexe(24MgAr2+) = 2.477(15) cm−1) vibrational constants. The analysis enables us to explain quantitatively how the strong bond arises in this dication despite the fact that Ar and Mg2+ both have a full-shell rare-gas electronic configuration.
1 Introduction
Doubly positively charged diatomic molecules BA2+, called diatomic dications (DIDIs) hereafter, are intriguing and elusive chemical species. They are encountered in plasmas and play a role in planetary ionospheres1 and more generally in molecular astrophysics.2 Their structure and reactivity are at the focus of numerous studies.3–12 The qualitative aspects of their stability are well known. The condition for their ground state to be thermodynamically stable is that the dissociation limit associated with the products A + B2+ in their ground states lies energetically below (Fig. 1(d)) or only slightly above (Fig. 1(c)) the dissociation limit associated with the products A+ + B+.4,12,13 This condition requires, in turn, the ionization energy of B+ to be smaller, or only slightly larger, than that of A (see red arrows to the right of Fig. 1(c)–(e)), which is only met if A has an unusually high and B+ has an unusually low ionization energy, as is the case for alkaline-earth–halide and alkaline-earth–rare-gas DIDIs. Falcinelli et al. have listed most candidates of thermodynamically stable DIDIs and identified several of them using mass spectrometry.14 | ||
| Fig. 1 Schematic potential-energy functions for molecules of the type BA2+ corresponding to the situations leading to metastable DIDIs (a and b) and thermodynamically stable DIDIs (c and d). (e) Potential-energy function of the singly charged precursor molecule BA+. Right of panels (c–e): arrows indicating the energetic order of the dissociation limits dependent on the ionization energies of A and B+. Inspired by Fig. 2 of ref. 4. | ||
The large majority of the DIDIs known today are metastable, i.e., their lowest level is located above the dissociation asymptote A+ + B+. Metastability typically arises when the ionization energy of B+ is significantly larger than that of A and results from an avoided crossing between the repulsive potential function dissociating into A+ + B+ and the attractive potential function correlating with A + B2+ (see Fig. 1(b)), or if a potential barrier is formed at short range in the otherwise repulsive Coulomb potential by binding valence interactions13,15–17 (Fig. 1(a)). The best and earliest known case of a DIDI, He22+, belongs to the latter category.15,18,19 Today, the most reliable source of information on the structure and binding of DIDIs is ab initio quantum chemistry, see ref. 20 for a recent example concerning thermodynamically stable DIDIs.
Experimentally, the vast majority of DIDIs has been identified by mass-spectrometric methods, which enable their unambiguous detection but do not provide structural information. Only very few DIDIs have been characterized by spectroscopic methods which provide quantitative information on their structure. High-resolution, rotationally resolved spectra have been obtained for only three DIDIs, N22+,21–25 NO2+,26 and DCl2+,27 and the vibrational structures of about 10 DIDIs have been studied by double-photoionization coincidence methods starting from the ground state of the neutral molecules (see ref. 11 and references therein). All cases for which spectroscopic information is available concern metastable DIDIs and, to our knowledge, no spectroscopic information has ever been obtained on a thermodynamically stable DIDI. One of the reasons for this absence of spectroscopic data is that these dications typically involve rare-gas, halogen, or chalcogen, and metal atoms. It is thus difficult to generate potential precursor neutral or singly-charged molecules BA and BA+ in the gas phase with sufficient densities. Another reason is that the double-ionization thresholds of diatomic molecules lie in the vacuum-ultraviolet (VUV) or soft X-ray ranges and are difficult to reach with table-top laboratory radiation sources.
We present here the first spectroscopic characterization of a thermodynamically stable DIDI, MgAr2+. To obtain high-resolution spectroscopic information on this dication, we have recorded the photoelectron spectrum of MgAr+ using the techniques of pulsed-field-ionization zero-kinetic-energy photoelectron (PFI-ZEKE-PE)28,29 and mass-analyzed threshold ionization (MATI) spectroscopy.30 Until this work, high-resolution photoelectron spectroscopy of molecular cations had been deemed impossible because of (i) the very limited density of ions that can be generated in the gas phase as a result of space-charge effects and (ii) the high ionization energies of cations. We demonstrate here that high-resolution photoelectron spectroscopy can be applied to samples of less than 1000 state-selected cations and that cations can be efficiently ionized despite their high ionization energies by resonant multiphoton excitation.
The photoelectron spectra we obtained were sufficiently resolved (∼2 cm−1) to obtain information on the rotational contours of the successive vibrational bands of the photoelectron spectrum of MgAr+ and to determine isotopic shifts in the spectra of 24MgAr+ and 26MgAr+. From these observations, we could extract an accurate potential-energy function for the electronic ground state of MgAr2+, prove experimentally that it is thermodynamically stable, and analyze the nature of the bond. We found the binding energy to be more than 1.3 eV (125 kJ mol−1), i.e., comparable to a typical covalent bond, despite the fact that both constituents (Mg2+ and Ar) have full-shell rare-gas electron configurations.
MgAr2+ had been observed by mass spectrometry prior to our work.31–35 It appears as an undesirable species in inductively-coupled-plasma mass spectrometry and complicates the chemical analysis of S isotopes.34,35 From the analysis of the density of MgAr2+ at different plasma temperatures, Hattendorf et al. could estimate the ground-state dissociation energy to be in the range between 124 and 130 kJ mol−1.34 In addition, Gardner et al.36 have characterized the electronic and vibrational structure of MgAr2+ in high-level ab initio quantum-chemical calculations. These studies provided very useful and important reference data with which our new results are compared.
Our approach to obtain spectroscopic information on DIDIs relies on the preparation of the precursor singly-charged molecule BA+ by photoionization of the neutral molecule BA. The photoelectron spectra of BA+ are then recorded following resonance-enhanced multiphoton excitation. The scheme used to study MgAr2+ is illustrated in Fig. 2, which depicts the potential-energy functions of all relevant states, as described in more detail in Section 2. It enables us to efficiently ionize MgAr+, despite its high ionization energy of about 13.9 eV, using commercial lasers operating in the UV region of the electromagnetic spectrum. This aspect is of central importance in the present work because of the low densities (typically ∼104 cm−3) and low numbers (typically 200 per experimental cycle at a repetition rate of 25 Hz, i.e., 5000 s−1) of MgAr+ ions generated in our experiments.
 | ||
| Fig. 2 (1 + 1′ + 1′′) three-photon excitation sequence used to photoionize MgAr+ X+(v+) via the A1/2+(v′) and 3dπ1/2+(v′′) intermediate levels. MgAr+ was produced in its X+ ground electronic state by photoionization of metastable MgAr. The MgAr+ potential-energy functions were taken from ref. 39 and that of the ground state of MgAr2+ was taken from ref. 36. | ||
The term symbols and quantum numbers used to designate the different states are cumbersome. To define and simplify the notation of states and transitions, we use the nomenclature summarized in Table 1. For example, 3dπ1/2+(v′′, ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J′′) ← A1/2+(v′,
J′′) ← A1/2+(v′, ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J′) designates the transition between the rovibrational level with vibrational and rotational quantum numbers v′ and J′ of the Ω = 1/2 spin–orbit component of the A+
J′) designates the transition between the rovibrational level with vibrational and rotational quantum numbers v′ and J′ of the Ω = 1/2 spin–orbit component of the A+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2ΠΩ electronic state of MgAr+ and the rovibrational level with quantum numbers v′′ and J′′ of the Ω = 1/2 spin–orbit component of the 3dπΩ+ Rydberg state of MgAr+. More generally, we designate the rotational and vibrational quantum numbers of the a state of MgAr with unprimed letters, those of the X+, AΩ+ and 3dπΩ+ of MgAr+ using letters with a plus (+), a prime (′) and a double-prime (′′) superscript, respectively, and those of the X2+ state of MgAr2+ with letters with a double-plus (2+) superscript. The integer quantum numbers N+ and N2+ used to label the rotational levels of the electronic states of Σ symmetry correspond to the standard notation for states following Hund's angular-momentum coupling case (b) and the quantum numbers J, J′ and J′′ used for the rotational levels of electronic states of Π symmetry correspond to the standard notation for states following Hund's angular-momentum coupling case (a), as described, e.g., in ref. 37 and 38, to which we refer for details.
2ΠΩ electronic state of MgAr+ and the rovibrational level with quantum numbers v′′ and J′′ of the Ω = 1/2 spin–orbit component of the 3dπΩ+ Rydberg state of MgAr+. More generally, we designate the rotational and vibrational quantum numbers of the a state of MgAr with unprimed letters, those of the X+, AΩ+ and 3dπΩ+ of MgAr+ using letters with a plus (+), a prime (′) and a double-prime (′′) superscript, respectively, and those of the X2+ state of MgAr2+ with letters with a double-plus (2+) superscript. The integer quantum numbers N+ and N2+ used to label the rotational levels of the electronic states of Σ symmetry correspond to the standard notation for states following Hund's angular-momentum coupling case (b) and the quantum numbers J, J′ and J′′ used for the rotational levels of electronic states of Π symmetry correspond to the standard notation for states following Hund's angular-momentum coupling case (a), as described, e.g., in ref. 37 and 38, to which we refer for details.
| State label | Molecule | Diss. asymptote | Term symbol | Rovibrational quantum numbers |
|---|---|---|---|---|
| a | MgAr | Mg(3s3p 3P) + Ar(1S0) | 3Π0 |
v,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J J |
| X+ | MgAr+ | Mg+(3s) + Ar(1S0) | 2Σ+ |
v
+,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N+ N+ |
| AΩ+ | MgAr+ | Mg+(3p) + Ar(1S0) | 2ΠΩ |
v′,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J′ J′ |
| 3dπΩ+ | MgAr+ | Mg+(3d) + Ar(1S0) | 2ΠΩ |
v′′,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J′′ J′′ |
| X2+ | MgAr2+ | Mg2+(1S0) + Ar(1S0) | 1Σ+ |
v
2+,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2+ N2+ |
All results presented below are for 24MgAr and its ions, unless stated otherwise.
2 Experimental section
2.1 Materials and sample preparation
The experimental setup has been presented in ref. 40 and 41. Neutral MgAr in the metastable a(v = 0) ground vibrational state was produced by laser ablation of a rod of natural Mg (24Mg (79%), 25Mg (10%), and 26Mg (11%)) in a supersonic expansion of Ar gas. The molecular beam passed through a 3 mm-diameter skimmer located 8 cm downstream of the ablation source before entering the photoexcitation chamber, where it was intersected at right angles by four co-propagating Nd:YAG-pumped dye lasers (25 Hz repetition rate, ∼4 ns pulse duration) that were frequency doubled or tripled in β-barium borate crystals. We refer to these lasers as lasers 1 to 4 below. The laser wavenumbers were calibrated using a commercial wavemeter with a specified accuracy of 0.02 cm−1. Photoexcitation took place within an electrode stack used to apply pulsed electric potentials to field ionize high Rydberg states and extract the produced photoelectrons and photoions into a linear time-of-flight (TOF) spectrometer. MgAr+ was produced in the lowest vibrational levels (v+ ≤ 5) of the X+ electronic ground state by photoionization of metastable MgAr using laser 1 at![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1 = 39
1 = 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 239 cm−1. The particle density of MgAr+ in the X+(v+ = 5) level was estimated to be ∼104 cm−3 based on the signal intensity in the TOF spectrum, corresponding to ∼200 ions in an interaction volume of ∼0.02 cm3 (see also ref. 40). The population of rotational levels in the X+ state is well described by a temperature of ∼4 K, as determined from the analysis of the rotational structure of the spectrum of the AΩ+(v′) ← X+(v+) transition (see below and ref. 42 and 43).
239 cm−1. The particle density of MgAr+ in the X+(v+ = 5) level was estimated to be ∼104 cm−3 based on the signal intensity in the TOF spectrum, corresponding to ∼200 ions in an interaction volume of ∼0.02 cm3 (see also ref. 40). The population of rotational levels in the X+ state is well described by a temperature of ∼4 K, as determined from the analysis of the rotational structure of the spectrum of the AΩ+(v′) ← X+(v+) transition (see below and ref. 42 and 43).
2.2 Photoexcitation sequence
For the photoionization of MgAr+ with lasers 2 to 4, we employed the resonant three-photon excitation sequence depicted in Fig. 2. Lasers 2, 3, and 4 were fired simultaneously ∼10 ns after laser 1. Laser 2 was used to pump rovibronic transitions A1/2+(v′ = 1 and 2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J′) ← X+(v+ = 5,
J′) ← X+(v+ = 5,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N+) at wavenumbers
N+) at wavenumbers ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2 around 31
2 around 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 253 and 31
253 and 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513 cm−1, respectively. Laser 3 further excited to selected rotational levels of the 3dπ1/2+(v′′ = 2, 3, 4) states at wavenumbers
513 cm−1, respectively. Laser 3 further excited to selected rotational levels of the 3dπ1/2+(v′′ = 2, 3, 4) states at wavenumbers ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3 around 35
3 around 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 597, 35
597, 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 843, and 35
843, and 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 cm−1, respectively. The final ionizing transition to the MgAr2+ X2+ state was induced by laser 4, which was tuned in the range
823 cm−1, respectively. The final ionizing transition to the MgAr2+ X2+ state was induced by laser 4, which was tuned in the range ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 4 = 44
4 = 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400–46
400–46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1. All lasers had the same linear polarization and had a beam diameter of ∼1 mm in the interaction region. The pulse energies of lasers 2, 3, and 4 were typically ∼0.6, ∼0.2, and ∼1 mJ, respectively.
500 cm−1. All lasers had the same linear polarization and had a beam diameter of ∼1 mm in the interaction region. The pulse energies of lasers 2, 3, and 4 were typically ∼0.6, ∼0.2, and ∼1 mJ, respectively.
The only electronic states of MgAr+ that had been characterized prior to this work are the X+, AΩ+ and B+ states (see Fig. 2).39,41–46 The resonant excitation sequence thus necessitated the identification and characterization of a suitable intermediate state between the AΩ+ and the X2+ states. In a broad search in the region near the Mg+(3d) + Ar(1S0) dissociation asymptote, we identified the lowest vibrational levels of the 3dπ1/2+ state to be ideal intermediate states because of their long lifetimes (>50 ps) and large Franck–Condon factors.47Fig. 3(a) shows the rotationally resolved spectrum of the A1/2+(v′ = 1, J′) ← X+(v+ = 5,N+) transition recorded by monitoring the yield of Mg+ photodissociation product as a function of the wavenumber ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2 of laser 2.42,43 The sticks indicate the positions and relative intensities of individual rovibronic transitions, calculated for a rotational temperature of 4 K using standard expressions37,38 for transitions between rovibrational levels of 2Σ+ and 2Π1/2 states. The red arrow corresponds to the position of laser 2 which selects the J′ = 3.5, 4.5, and 6.5 rotational levels from which the spectrum of the 3dπ1/2+(v′′ = 3,
2 of laser 2.42,43 The sticks indicate the positions and relative intensities of individual rovibronic transitions, calculated for a rotational temperature of 4 K using standard expressions37,38 for transitions between rovibrational levels of 2Σ+ and 2Π1/2 states. The red arrow corresponds to the position of laser 2 which selects the J′ = 3.5, 4.5, and 6.5 rotational levels from which the spectrum of the 3dπ1/2+(v′′ = 3,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J′′) ← A1/2+(v′ = 1,
J′′) ← A1/2+(v′ = 1,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J′) transition depicted in Fig. 3(b) was measured. This spectrum was recorded by scanning laser 3 and setting laser 4 to 46
J′) transition depicted in Fig. 3(b) was measured. This spectrum was recorded by scanning laser 3 and setting laser 4 to 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 290 cm−1, while monitoring the MgAr2+ signal. It consists of three branches characterized by J′′ − J′ = 0, ±1 and the assignments are grouped and colored according to the selected A1/2+ rotational levels.
290 cm−1, while monitoring the MgAr2+ signal. It consists of three branches characterized by J′′ − J′ = 0, ±1 and the assignments are grouped and colored according to the selected A1/2+ rotational levels.
 | ||
Fig. 3 (a) Rotationally resolved spectrum of the A1/2+(v′ = 1,J′) ← X+(v+ = 5,N+) transition of MgAr+ recorded by monitoring the Mg+ photodissociation yield as a function of the wavenumber ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2 of laser 2.42,43 The sticks indicate the calculated positions and intensities of individual rovibronic transitions. The colors blue, orange, green, and red indicate the rotational branches J′ − N+ = −1.5, −0.5, +0.5, and +1.5, respectively. The arrow marks the position in the spectrum used to select the rovibrational levels of the A1/2+ state with J′ = 3.5, 4.5, and 6.5. (b) Rotationally resolved spectrum of the 3dπ1/2+(v′′ = 3,J′′) ← A1/2+(v′ = 1, J′) transition recorded by monitoring the MgAr2+ signal as a function of the wavenumber 2 of laser 2.42,43 The sticks indicate the calculated positions and intensities of individual rovibronic transitions. The colors blue, orange, green, and red indicate the rotational branches J′ − N+ = −1.5, −0.5, +0.5, and +1.5, respectively. The arrow marks the position in the spectrum used to select the rovibrational levels of the A1/2+ state with J′ = 3.5, 4.5, and 6.5. (b) Rotationally resolved spectrum of the 3dπ1/2+(v′′ = 3,J′′) ← A1/2+(v′ = 1, J′) transition recorded by monitoring the MgAr2+ signal as a function of the wavenumber ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3 of laser 3. The rotational structure reflects the predominantly populated initial rotational levels J′ = 3.5, 4.5, and 6.5 of the A1/2+ state. 3 of laser 3. The rotational structure reflects the predominantly populated initial rotational levels J′ = 3.5, 4.5, and 6.5 of the A1/2+ state. | ||
The band origins  and the rotational constants
and the rotational constants 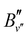 of the 3dπ1/2+ levels were determined from the rotational line positions using the formula for the transition energy,37
of the 3dπ1/2+ levels were determined from the rotational line positions using the formula for the transition energy,37
 | (1) |
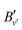 denotes the rotational constant of the A1/2+(v′) state determined in ref. 43. The results relevant for the present article are summarized in Table 2, where the assignment of the vibrational quantum numbers v′′ is based on a standard isotopic-shift analysis.47,48 The relative intensities were calculated using well-known expressions for rotational line intensities.37,38 In order to avoid power broadening and obtain well-resolved spectra, the pulse energies of lasers 2 and 3 had to be reduced by factors between 5 and 10, compared to the numbers given above, which were required to record the spectra of MgAr2+ from the selected 3dπ1/2+(v′′,
denotes the rotational constant of the A1/2+(v′) state determined in ref. 43. The results relevant for the present article are summarized in Table 2, where the assignment of the vibrational quantum numbers v′′ is based on a standard isotopic-shift analysis.47,48 The relative intensities were calculated using well-known expressions for rotational line intensities.37,38 In order to avoid power broadening and obtain well-resolved spectra, the pulse energies of lasers 2 and 3 had to be reduced by factors between 5 and 10, compared to the numbers given above, which were required to record the spectra of MgAr2+ from the selected 3dπ1/2+(v′′,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J′′) levels with a sufficient signal-to-noise ratio.
J′′) levels with a sufficient signal-to-noise ratio.
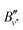 . All values are in units of cm−1 and the numbers in parentheses represent one standard deviation in the unit of the last digit
. All values are in units of cm−1 and the numbers in parentheses represent one standard deviation in the unit of the last digit
2.3 PFI-ZEKE-PE and MATI spectroscopy
Pulsed-field-ionization zero-kinetic-energy photoelectron (PFI-ZEKE-PE) spectroscopy29 and mass-analyzed threshold ionization (MATI) spectroscopy30 are high-resolution variants of threshold photoelectron spectroscopy. Spectra are recorded by monitoring the pulsed-electric-field-ionization yield of very high Rydberg states (principal quantum number n > 100) located just below the ionization thresholds as a function of the frequency of a tunable radiation source. After correction for the shifts of the ionization thresholds induced by the electric fields, the positions of the lines observed in the spectra correspond to energy differences between the levels of the ionized molecule (charge Z) and its precursor (charge Z − 1).The shift ΔEI of the ionization thresholds induced by a single pulsed field of strength F is given in good approximation by49–51
 | (2) |
 | (3) |
The main difference between PFI-ZEKE-PE and MATI spectroscopy is that with the former method one detects the electrons generated by the pulsed field ionization whereas in the latter one detects the ions, which offers the advantage of mass selectivity. This advantage was crucial in the present work to separately record the spectra of 24MgAr2+ and 26MgAr2+ and determine the absolute assignment of the vibrational levels of MgAr2+ from the isotopic shifts. However, the advantage comes at the cost of a reduced resolution because larger electric fields are typically required to distinguish the much heavier ions generated by the successive pulses through their times of flight.
To record the PFI-ZEKE-PE spectra of MgAr+ (Z = 2) we used a four-pulse sequence (typically F1 = +0.34 V cm−1, F2 = −0.52 V cm−1, F3 = −1.12 V cm−1, and F4 = −1.72 V cm−1) and, for each laser scan, we recorded the three spectra corresponding to F2, F3, and F4 simultaneously. We recorded the MATI spectra with optimized pulse sequences, e.g., F1 = −0.86 V cm−1, F2 = −1.72 V cm−1, and F3 = +172.4 V cm−1, the spectra obtained from F2 being the high-resolution ones. Because of the small numbers of state-selected MgAr+ ions (∼200 per laser shot), the pulsed-field-ionization signal was very weak (less than 1 count per laser shot) and the spectra had to be measured several times and averaged to improve the signal-to-noise ratio.
3 Results and discussion
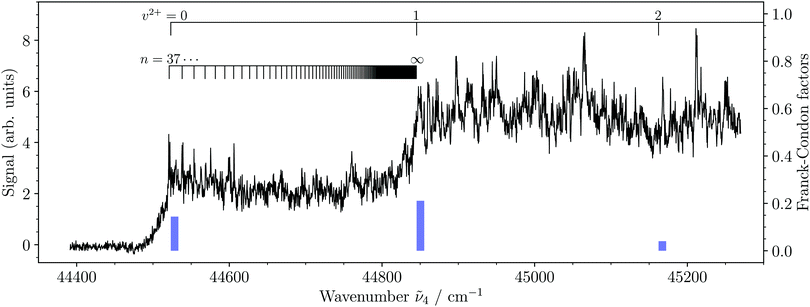
We have measured the spectra of the X2+(v2+ = 0–8) ← 3dπ1/2+(v′′ = 2–4) photoionizing transitions. Our measurements include an overview photoionization spectrum in the vicinity of the v2+ = 0–2 vibrational levels of the X2+ state, PFI-ZEKE-PE spectra of transitions to the X2+(v2+ = 0, 1) levels, and MATI spectra of transitions to the X2+(v2+ = 0–8) levels.Fig. 4 depicts the photoionization spectrum of MgAr+ from its 3dπ1/2+(v′′ = 2) state to the region of the first three vibrational levels of the ground state of MgAr2+. The spectrum shows two distinct steps that indicate the ionization thresholds associated with the v2+ = 0, 1 levels of the X2+ state. Several sharp resonances are also present in the spectrum, which we attribute to autoionizing Rydberg states of MgAr+. Just above the ionization threshold associated with the X2+(v2+ = 0) state, we could assign several of these resonances to Rydberg states of MgAr+ with principal quantum numbers n = 37–40 belonging to series converging to the X2+(v2+ = 1) level of MgAr2+, as indicated along the lower assignment bar. The blue bars represent the Franck–Condon factors of the X2+(v2+ = 0–2) ← 3dπ1/2+(v′′ = 2) transitions calculated using the potential-energy functions shown in Fig. 2. The very weak Franck–Condon factor to the X2+(v2+ = 2) state explains why no step could be detected in the photoionization spectrum at the v2+ = 2 ionization threshold.
High-resolution PFI-ZEKE-PE and MATI spectra of the X2+(v2+ = 0) ← 3dπ1/2+(v′′ = 2) transition are presented in Fig. 5(a) and (b). The red dashed lines depict least-squares fits of Gaussian functions to determine the line positions. The slightly asymmetric base line in Fig. 5(b) is caused by an incomplete separation in the TOF spectrum of the MgAr2+ signals that were produced by the different field-ionization pulses. Fig. 5(c) and (d) show the corresponding MATI spectra of 24MgAr+ and 26MgAr+, respectively, recorded using the two-pulse sequence −0.86, +172.4 V cm−1. We determined the isotopic shift (Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 4 = 9.7 cm−1) of the transition by fitting the error function53 to the high-energy edges of the spectra and extracting the difference in the inflection points shown as black vertical lines. From the isotopic shift of the 3dπ1/2+(v′′ = 2) level (Δ3dπ = 15.1 cm−1, see ref. 47) we determined the isotopic shift of the X2+(v2+ = 0) level to be ΔX2+(0) = Δ3dπ − Δ
4 = 9.7 cm−1) of the transition by fitting the error function53 to the high-energy edges of the spectra and extracting the difference in the inflection points shown as black vertical lines. From the isotopic shift of the 3dπ1/2+(v′′ = 2) level (Δ3dπ = 15.1 cm−1, see ref. 47) we determined the isotopic shift of the X2+(v2+ = 0) level to be ΔX2+(0) = Δ3dπ − Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 4 = 5.4(20) cm−1. A similar measurement of the isotopic shift of the X2+(v2+ = 1) vibrational threshold yielded ΔX2+(1) = 10.9(20) cm−1. These results, together with the vibrational constants determined for 24MgAr2+ (see below), were used to unambiguously establish the vibrational assignment in a standard isotopic shift analysis.48 The fall of the MATI signal below the ionization threshold (Fig. 5(c)) is twice as broad for 24MgAr+ as it is for 26MgAr+ (Fig. 5(d)). This difference has its origin in a different initial population of rotational states caused by the slightly different rotational constants and the multiphoton excitation.
4 = 5.4(20) cm−1. A similar measurement of the isotopic shift of the X2+(v2+ = 1) vibrational threshold yielded ΔX2+(1) = 10.9(20) cm−1. These results, together with the vibrational constants determined for 24MgAr2+ (see below), were used to unambiguously establish the vibrational assignment in a standard isotopic shift analysis.48 The fall of the MATI signal below the ionization threshold (Fig. 5(c)) is twice as broad for 24MgAr+ as it is for 26MgAr+ (Fig. 5(d)). This difference has its origin in a different initial population of rotational states caused by the slightly different rotational constants and the multiphoton excitation.
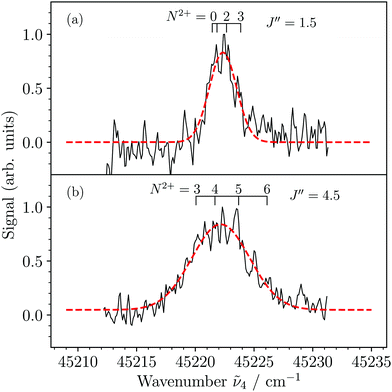
Fig. 6(a) and (b) show MATI spectra of the X2+(v2+ = 3) ← 3dπ1/2+(v′′ = 3) transition recorded using the sequence of field-ionization pulses of +0.26, −1.12, −1.72, and +172.4 V cm−1 and collecting the ionization signal from the −1.72 V cm−1 pulse. Although the resolution was not sufficient to resolve the rotational structure in the spectra, we could observe a broadening of the rotational contour when selecting different rotational levels of the 3dπ1/2+(v′′ = 3) state, i.e., J′′ = 1.5 (Fig. 6(a)) and J′′ = 4.5 (Fig. 6(b)). This effect results from the increasing spread of the rotational transitions at increasing J′′ values, as illustrated by the assignment bars, which indicate the expected dominant transitions to rotational levels of the X2+(v2+ = 3) state corresponding to branches with N2+ − J′′ = −1.5,…,+1.5. From simulations (not shown) of the rotational contour using the rotational constants B3′′ = 0.1813 cm−1 (see Table 2) and B32+ = 0.2017 cm−1 (from ref. 36) of the initial and final states, respectively, we estimated the experimental resolution (full width at half maximum of a single line) to be ∼2 cm−1. The linewidth estimated from the field-ionization pulse is ∼1.5 cm−1 (see eqn (3)) and we attribute this slight discrepancy to power broadening induced by the lasers.
The results of our measurements of the vibrational structure of the X2+ ground state of MgAr2+ are summarized in Table 3, where all values are corrected for the field-induced shifts of the ionization thresholds. The specified uncertainties are all ≲3 cm−1 and represent an improvement in measurement accuracy of approximately two orders of magnitude compared to previous studies of the structure of DIDIs using double-photoionization coincidence methods (see ref. 11 and references therein). The uncertainties of the vibrational term values  are smaller than the uncertainties of the transitions because of the cancellation of systematic errors in the determination of the field-induced shifts of the ionization thresholds and in the frequency calibration. From these results, we determined the harmonic and first anharmonic vibrational constants of the X2+ state to be ωe = 327.02(11) cm−1 and ωexe = 2.477(15) cm−1, respectively, which are very close to the values of ωe = 328.2 cm−1 and ωexe = 2.55 cm−1 calculated ab initio by Gardner et al.36 Using the wavenumbers of the A1/2+(v′ = 1) ← X+(v+ = 0) (31704.6 cm−1, see ref. 41 and 43) and the 3dπ1/2+(v′′ = 2) ← A1/2+(v′ = 1) (35596.2 cm−1, see Table 2) band origins, we further determined the adiabatic ionization energy of MgAr+ to be EI(X+)/(hc) = 111
are smaller than the uncertainties of the transitions because of the cancellation of systematic errors in the determination of the field-induced shifts of the ionization thresholds and in the frequency calibration. From these results, we determined the harmonic and first anharmonic vibrational constants of the X2+ state to be ωe = 327.02(11) cm−1 and ωexe = 2.477(15) cm−1, respectively, which are very close to the values of ωe = 328.2 cm−1 and ωexe = 2.55 cm−1 calculated ab initio by Gardner et al.36 Using the wavenumbers of the A1/2+(v′ = 1) ← X+(v+ = 0) (31704.6 cm−1, see ref. 41 and 43) and the 3dπ1/2+(v′′ = 2) ← A1/2+(v′ = 1) (35596.2 cm−1, see Table 2) band origins, we further determined the adiabatic ionization energy of MgAr+ to be EI(X+)/(hc) = 111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 824(4) cm−1, which, to our knowledge, is the most accurate value for the ionization threshold of a molecular cation obtained to date.
824(4) cm−1, which, to our knowledge, is the most accurate value for the ionization threshold of a molecular cation obtained to date.
| v 2+ | v′′ |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 4
4
|
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
|
|---|---|---|---|---|---|
| a Vibrational term values with respect to the X2+(v2+ = 0) level. b Vibrational term values with respect to the X+(v+ = 0) level. c Vibrational term values calculated using the potential function given in eqn (6) and the parameters listed in Table 4. | |||||
| 0 | 2 | 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 523(3) 523(3) |
0.0(10) | 111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 824(4) 824(4) |
0.8 |
| 1 | 2 | 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 845(3) 845(3) |
322.0(10) | 112![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146(3) 146(3) |
0.1 |
| 2 | 3 | 44916.4(19) | 639.0(10) | 112463.0(24) | −0.4 |
| 3 | 3 | 45228.6(19) | 951.3(10) | 112![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 775(3) 775(3) |
−0.6 |
| 4 | 4 | 45296.3(20) | 1259.3(10) | 113![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 083(3) 083(3) |
0.1 |
| 5 | 3 | 45838.0(18) | 1560.7(10) | 113384.7(24) | −0.6 |
| 6 | 4 | 45894.6(24) | 1857.6(10) | 113![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 682(3) 682(3) |
−0.7 |
| 7 | 4 | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 188(3) 188(3) |
2151.0(10) | 113![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 975(3) 975(3) |
0.8 |
| 8 | 4 | 46474.4(19) | 2437.5(10) | 114261.5(24) | 0.6 |
We determined the dissociation threshold D0 of the X2+ state via the thermodynamic cycle
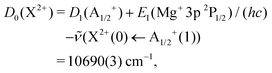 | (4) |
To provide an accurate description of the bond in the MgAr2+ ground state we used a model potential of the form
| V(R) = VMorse(R) + Vlr(R) | (5) |
 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 690(3) cm−1 (127.88(4) kJ mol−1) appears surprisingly large at first sight given the rare-gas electron configurations of Ar and Mg2+. The attractive part of the potential is dominated by the long-range term, with a minor contribution from the Morse term, which highlights the electrostatic nature of the bond. However, considering that both Mg2+ and Ar are chemically hard species, we expected the Morse term to be even less significant. We attribute this weak “chemical” contribution to the binding energy to a charge-transfer interaction with the repulsive MgAr2+ A2+ state (see also the discussions in ref. 36 for charged alkaline-earth-metal–rare-gas DIDIs and in ref. 59 for the isoelectronic alkali-metal–rare-gas cations). The potential-energy function of the A2+ state depicted in Fig. 7 simply corresponds to a repulsive Coulomb potential, which correlates with the dissociation asymptote Mg+(3s) + Ar+(2P3/2). This asymptote lies 5842 cm−1 above the dissociation limit Mg2+ + Ar, corresponding to the difference between the known values of the ionization energies of Ar and Mg+.54 The strong Pauli repulsion between the full-shell constituents Mg2+ and Ar dominates the potential energy at distances below the LeRoy radius60RLeRoy (vertical line in Fig. 7), where the electron clouds of these atoms start to overlap. RLeRoy was calculated in the Hartree–Fock approximation using the program described in ref. 61. The bond of MgAr2+ is thus characterized by the interplay of a strongly attractive electrostatic interaction at long range, a weak charge-transfer contribution, and the Pauli repulsion at short range.
690(3) cm−1 (127.88(4) kJ mol−1) appears surprisingly large at first sight given the rare-gas electron configurations of Ar and Mg2+. The attractive part of the potential is dominated by the long-range term, with a minor contribution from the Morse term, which highlights the electrostatic nature of the bond. However, considering that both Mg2+ and Ar are chemically hard species, we expected the Morse term to be even less significant. We attribute this weak “chemical” contribution to the binding energy to a charge-transfer interaction with the repulsive MgAr2+ A2+ state (see also the discussions in ref. 36 for charged alkaline-earth-metal–rare-gas DIDIs and in ref. 59 for the isoelectronic alkali-metal–rare-gas cations). The potential-energy function of the A2+ state depicted in Fig. 7 simply corresponds to a repulsive Coulomb potential, which correlates with the dissociation asymptote Mg+(3s) + Ar+(2P3/2). This asymptote lies 5842 cm−1 above the dissociation limit Mg2+ + Ar, corresponding to the difference between the known values of the ionization energies of Ar and Mg+.54 The strong Pauli repulsion between the full-shell constituents Mg2+ and Ar dominates the potential energy at distances below the LeRoy radius60RLeRoy (vertical line in Fig. 7), where the electron clouds of these atoms start to overlap. RLeRoy was calculated in the Hartree–Fock approximation using the program described in ref. 61. The bond of MgAr2+ is thus characterized by the interplay of a strongly attractive electrostatic interaction at long range, a weak charge-transfer contribution, and the Pauli repulsion at short range.
 | ||
| Fig. 7 Potential-energy function for the lowest two (X2+ and A2+) electronic states of MgAr2+. The potential-energy function corresponding to the atomic Mg2+ + Ar limit was determined by fitting the potential parameters in eqn (6) to match the measured vibrational levels (shown in blue) and the dissociation threshold (D0). The dashed and dotted lines show the long-range and Morse-type contribution to the potential energy, respectively. The repulsive potential-energy function corresponding to the atomic Mg+ + Ar+ limit (horizontal dashed line at position Drep above the ground rovibronic level) is approximated by a pure Coulomb potential. | ||
4 Conclusions and outlook
In this article, we have reported the first spectroscopic characterization of a thermodynamically stable DIDI. We measured the photoionizing transitions to the first nine vibrational levels (v2+ = 0–8) of the MgAr2+ X2+ ground state using the techniques of PFI-ZEKE-PE and MATI spectroscopy and were able to observe the effect of the rotational structure on the spectra as well as to determine the isotopic shifts of the X2+(v2+ = 0, 1) levels of 24MgAr2+ and 26MgAr2+. From our measurements we could determine accurate values for the ionization energy of MgAr+ and the dissociation energy of the ground state of MgAr2+. We also derived a potential-energy function that accurately describes the interaction between Mg2+ and Ar and unravels the binding mechanisms. The bond is dominated by electrostatic interactions. The double charge of the Mg2+ (Z = 2) constituent leads to a dissociation energy that is comparable to that of a covalent bond. This behavior follows from the Z2 (= 4) dependence of the charge-induced-dipole interaction (see eqn (6)). Compared to the singly-charged isoelectronic species (Z2 = 1) an increase in binding energy of much more than a factor of four is expected because of the reduction of the internuclear separation when increasing Z. From eqn (6) and Fig. 7 one would expect the relation | (7) |
 and Re,NaAr+ = 2.78 Å from ref. 62.
and Re,NaAr+ = 2.78 Å from ref. 62.
25 years have elapsed since Falcinelli et al.14 reported their extensive list of thermodynamically stable DIDIs. In this time, progress in the characterization of their structure and dynamics has been exclusively theoretical (see, e.g., ref. 9, 20 and 36 and references therein). This lack of spectroscopic data may appear surprising at first sight but is explainable by experimental challenges. The spectroscopic methods used to study DIDIs, emission21,26 and photofragment22–25,27 spectroscopy of the doubly charged systems and single-photon or electron-impact double ionization spectroscopy of the neutral parents,11 are all particularly challenging for thermodynamically stable DIDIs. The first electronically excited state in these DIDIs is typically repulsive in the Franck–Condon region of the stable vibrational levels (see Fig. 1(c) and (d)) so that electronic spectra are structureless (continuous). Rotational and vibrational absorption or emission spectra in the electronic ground state are in principle observable, but their detection is severely complicated by the very low densities of BA2+ molecules that can be generated in the gas phase. The parent neutral molecules BA are highly reactive and must be generated in situ, which leads to insufficient concentrations for the detection of single-photon double-ionization coincidence events. In the future, we believe that non-destructive measurements of absorption processes of individual DIDIs in ion traps will offer an attractive route to obtain high-resolution rotational and vibrational spectra of these systems.63
In this article, we have demonstrated the successful use of high-resolution photoelectron spectroscopy of the singly-charged parent ion BA+ as a powerful method to study DIDIs. The advantages are obvious: (i) the measurement of high-resolution photoelectron spectra does not require high-density samples (here 5000 ions per second at 104 cm−3 density) and is ideally suited for the study of charged species, as is well known for anions (see, e.g., ref. 64 and references therein), which can be ionized with commercial VIS and UV lasers. So far its application to cations has been hampered by their high ionization energies. (ii) In the case of thermodynamically stable DIDIs, the ionization energy of BA+ is comparable to that of B+ (EI/(hc) = 121267.64 cm−1 in the case of Mg+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54), which is low as explained in Section 1. The metallic nature of B further guarantees that B+ and therefore also BA+ have low-lying electronic states that can be used as intermediate states to efficiently ionize BA+ in resonant multiphoton processes. (iii) The parent cation BA+ can be produced in selected rovibrational levels by photoexcitation from the ground state of BA using threshold ionization techniques (see ref. 30 and 65), which can be exploited to access a broad range of vibrational levels of BA2+.
54), which is low as explained in Section 1. The metallic nature of B further guarantees that B+ and therefore also BA+ have low-lying electronic states that can be used as intermediate states to efficiently ionize BA+ in resonant multiphoton processes. (iii) The parent cation BA+ can be produced in selected rovibrational levels by photoexcitation from the ground state of BA using threshold ionization techniques (see ref. 30 and 65), which can be exploited to access a broad range of vibrational levels of BA2+.
Photoelectron spectroscopy of singly charged cations can also be used to study metastable DIDIs. The requirements for the efficient photoionization of BA+, however, are more stringent because the energies are higher in this case and adequate multiphoton ionization sequences may be more difficult to find. Nevertheless, the list of metastable DIDIs presented in the review of Sabzyan et al.9 makes one optimistic that several of them can be studied with the method presented here. Studies of He22+, O22+, and CO2+ would be of particular importance for fundamental reasons and also for applications in atmospheric chemistry and astrophysics. In the future, we expect that progress in the development of powerful narrow-band VUV radiation at free-electron laser facilities will offer the possibility of efficiently ionizing molecular cations in single-photon processes and recording their high-resolution single-photon photoelectron spectra.
The experimental method presented here to study molecular dications is not restricted to DIDIs, but can of course be equally well applied to polyatomic systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Hansjürg Schmutz and Josef A. Agner for their technical assistance and Thomas Berglitsch for discussions and experimental help. This work is supported financially by the Swiss National Science Foundation (Grants No. 200020-172620 and 200020B-200478) and the European Research Council through an ERC advanced grant (Grant No. 743121) under the European Union's Horizon 2020 Research and Innovation programme.Notes and references
- R. Thissen, O. Witasse, O. Dutuit, C. S. Wedlund, G. Gronoff and J. Lilensten, Phys. Chem. Chem. Phys., 2011, 13, 18264–18287 RSC.
- M. Larsson, W. D. Geppert and G. Nyman, Rep. Prog. Phys., 2012, 75, 066901 CrossRef CAS PubMed.
- Z. Herman, Int. Rev. Phys. Chem., 1996, 15, 299–324 Search PubMed.
- D. Schröder and H. Schwarz, J. Phys. Chem. A, 1999, 103, 7385–7394 CrossRef.
- A. J. Stace, J. Phys. Chem. A, 2002, 106, 7993–8005 CrossRef CAS.
- D. Mathur, Phys. Rep., 2004, 391, 1–118 CrossRef CAS.
- F. Grandinetti, Eur. J. Mass Spectrom., 2011, 17, 423–463 CrossRef CAS PubMed.
- Z. Herman, Mol. Phys., 2013, 111, 1697–1710 CrossRef CAS.
- H. Sabzyan, E. Keshavarz and Z. Noorisafa, J. Iran. Chem. Soc., 2014, 11, 871–945 CrossRef CAS.
- S. D. Price, J. D. Fletcher, F. E. Gossan and M. A. Parkes, Int. Rev. Phys. Chem., 2017, 36, 145–183 Search PubMed.
- J. H. D. Eland and R. Feifel, Double Photoinisation Spectra of Molecules, Oxford University Press, 2018 Search PubMed.
- S. Falcinelli and M. Rosi, Molecules, 2020, 25, 4157 Search PubMed.
- D. R. Bates and T. R. Carson, Proc. Phys. Soc. A, 1955, 68, 1199–1202 CrossRef.
- S. Falcinelli, F. Fernández-Alonso, K. S. Kalogerakis and R. N. Zare, Mol. Phys., 1996, 88, 663–672 CrossRef CAS.
- L. Pauling, J. Chem. Phys., 1933, 1, 56–59 CrossRef CAS.
- A. C. Hurley and V. W. Maslen, J. Chem. Phys., 1961, 34, 1919–1925 CrossRef CAS.
- A. C. Hurley, J. Mol. Spectrosc., 1962, 9, 18–29 CrossRef CAS.
- J. D. Dunitz and T. K. Ha, J. Chem. Soc., Chem. Commun., 1972, 568–569 RSC.
- M. Guilhaus, A. G. Brenton, J. H. Beynon, M. Rabrenović and P. von Ragué Schleyer, J. Phys. B: At., Mol. Opt. Phys., 1984, 17, L605–L610 CrossRef CAS.
- G. Fernando de Melo and F. R. Ornellas, Comput. Theor. Chem., 2020, 1178, 112792 CrossRef CAS.
- P. K. Carroll and A. C. Hurley, J. Chem. Phys., 1961, 35, 2247–2248 CrossRef CAS.
- P. C. Cosby, R. Möller and H. Helm, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 28, 766–772 CrossRef CAS.
- D. Cossart, F. Launay, J. M. Robbe and G. Gandara, J. Mol. Spectrosc., 1985, 113, 142–158 CrossRef CAS.
- A. S. Mullin, D. M. Szaflarski, K. Yokoyama, G. Gerber and W. C. Lineberger, J. Chem. Phys., 1992, 96, 3636–3648 CrossRef CAS.
- P. A. Martin, F. R. Bennett and J. P. Maier, J. Chem. Phys., 1994, 100, 4766 CrossRef CAS.
- D. Cossart, M. Bonneau and J. M. Robbe, J. Mol. Spectrosc., 1987, 125, 413–427 CrossRef CAS.
- S. G. Cox, A. D. J. Critchley, P. S. Kreynin, I. R. McNab, R. C. Shiell and F. E. Smith, Phys. Chem. Chem. Phys., 2003, 5, 663–676 RSC.
- G. Reiser, W. Habenicht, K. Müller-Dethlefs and E. W. Schlag, Chem. Phys. Lett., 1988, 152, 119–123 CrossRef CAS.
- K. Müller-Dethlefs and E. W. Schlag, Angew. Chem., Int. Ed., 1998, 37, 1346–1374 CrossRef.
- L. Zhu and P. Johnson, J. Chem. Phys., 1991, 94, 5769–5771 CrossRef CAS.
- K. G. Spears and F. C. Fehsenfeld, J. Chem. Phys., 1972, 56, 5698–5705 CrossRef CAS.
- M. Velegrakis and C. Lüder, Chem. Phys. Lett., 1994, 223, 139–142 CrossRef CAS.
- N. R. Walker, G. A. Grieves, J. B. Jaeger, R. S. Walters and M. A. Duncan, Int. J. Mass Spectrom., 2003, 228, 285–295 CrossRef CAS.
- B. Hattendorf, B. Gusmini, L. Dorta, R. S. Houk and D. Günther, ChemPhysChem, 2016, 17, 2640–2644 CrossRef CAS PubMed.
- B. Hattendorf, B. Gusmini, L. Dorta, R. S. Houk and D. Günther, Anal. Chem., 2016, 88, 7281–7288 CrossRef CAS PubMed.
- A. M. Gardner, C. D. Withers, J. B. Graneek, T. G. Wright, L. A. Viehland and W. H. Breckenridge, J. Phys. Chem. A, 2010, 114, 7631–7641 CrossRef CAS PubMed.
- H. Lefebvre-Brion and R. W. Field, The Spectra and Dynamics of Diatomic Molecules, Elsevier, Amsterdam, 2004 Search PubMed.
- R. N. Zare, Angular Momentum, John Wiley & Sons, New York, 1988 Search PubMed.
- D. Wehrli, M. Génévriez, S. Knecht, M. Reiher and F. Merkt, J. Chem. Phys., 2020, 153, 074310 CrossRef CAS PubMed.
- M. Génévriez, D. Wehrli, J. A. Agner and F. Merkt, Int, J. Mass Spectrom., 2019, 435, 209–216 Search PubMed.
- D. Wehrli, M. Génévriez, C. Kreis, J. A. Agner and F. Merkt, J. Phys. Chem. A, 2020, 124, 379–385 CrossRef CAS PubMed.
- M. Génévriez, D. Wehrli and F. Merkt, Mol. Phys., 2020, 118, e1703051 CrossRef.
- M. Génévriez, D. Wehrli and F. Merkt, J. Chem. Phys., 2020, 153, 074311 CrossRef PubMed.
- J. S. Pilgrim, C. S. Yeh and M. A. Duncan, Chem. Phys. Lett., 1993, 210, 322–326 CrossRef CAS.
- J. S. Pilgrim, C. S. Yeh, K. R. Berry and M. A. Duncan, J. Chem. Phys., 1994, 100, 7945–7956 CrossRef CAS.
- C. T. Scurlock, J. S. Pilgrim and M. A. Duncan, J. Chem. Phys., 1995, 103, 3293–3298 CrossRef CAS.
- D. Wehrli, M. Génévriez, S. Knecht, M. Reiher and F. Merkt, to be published.
- G. Herzberg, Molecular Spectra and Molecular Structure, Volume I, Spectra of Diatomic Molecules, Van Nostrand Reinhold Company, New York, 2nd edn, 1950 Search PubMed.
- W. A. Chupka, J. Chem. Phys., 1993, 98, 4520–4530 CrossRef CAS.
- F. Merkt, S. Willitsch and U. Hollenstein, High-Resolution Photoelectron Spectroscopy, in Handbook of High-Resolution Spectroscopy, John Wiley & Sons, Chichester, 2011, vol. 3, pp. 1617–1654 Search PubMed.
- D. Wehrli, U. Hollenstein and F. Merkt, Mol. Phys., 2021, 119, e1900613, DOI:10.1080/00268976.2021.1900613.
- U. Hollenstein, R. Seiler, H. Schmutz, M. Andrist and F. Merkt, J. Chem. Phys., 2001, 115, 5461–5469 CrossRef CAS.
- Handbook of Mathematical Functions, ed. M. Abramowitz and I. A. Stegun, Dover Publications, London, 9th edn, 1970 Search PubMed.
- A. Kramida, Yu. Ralchenko, J. Reader and NIST ASD Team, NIST Atomic Spectra Database (ver. 5.6.1), [Online], Available: https://physics.nist.gov/asd [2020, May 25], National Institute of Standards and Technology, Gaithersburg, MD, 2019.
- C. Gaiser and B. Fellmuth, Phys. Rev. Lett., 2018, 120, 123203 CrossRef CAS PubMed.
- P. E. Siska, J. Chem. Phys., 1986, 85, 7497–7498 CrossRef CAS.
- D. Bellert and W. H. Breckenridge, Chem. Rev., 2002, 102, 1595–1622 CrossRef CAS PubMed.
- R. J. Le Roy, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 179–196 CrossRef CAS.
- W. H. Breckenridge, V. L. Ayles and T. G. Wright, Chem. Phys., 2007, 333, 77–84 CrossRef CAS.
- R. J. Le Roy, Energy Levels of a Diatomic near Dissociation, in Molecular Spectroscopy, The Chemical Society, Burlington House, London, 1973, ch. 3, vol. 1, pp. 113–176 Search PubMed.
- C. Froese Fischer, Comput. Phys. Commun., 1987, 43, 355–365 CrossRef CAS.
- P. Soldán, E. P. F. Lee and T. G. Wright, Mol. Phys., 1999, 97, 139–149 CrossRef.
- Z. Meir, G. Hegi, K. Najafian, M. Sinhal and S. Willitsch, Faraday Discuss., 2019, 217, 561–583 RSC.
- M. L. Weichman and D. M. Neumark, Annu. Rev. Phys. Chem., 2018, 69, 101–124 CrossRef CAS PubMed.
- F. Merkt, S. R. Mackenzie and T. P. Softley, J. Chem. Phys., 1993, 99, 4213–4214 CrossRef CAS.
| This journal is © the Owner Societies 2021 |