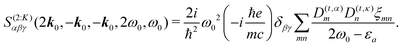Second harmonic generation theory for a helical macromolecule with high sensitivity to structural disorder
Received
15th February 2021
, Accepted 8th May 2021
First published on 25th May 2021
Abstract
Microscopic theory for the second harmonic generation in a helical molecular system is developed in the minimal coupling representation including non-local interaction effects. At the second order to the field we find a compact expression which combines dipolar, quadrupolar and magnetic contributions. A detailed derivation of the response is performed to specifically isolate the quadratic coupling terms, which we denote as the K coupling. Applying the theory to a helical macromolecule we find that the dipolar and quadrupolar contributions reflect the symmetry properties of the system and its homogeneity, while the K coupling contribution reveals inhomogeneities of the system.
1 Introduction
Optical harmonic generation has been extensively used for assessing molecular structures and structures of ordered molecular aggregates since 1960-ties.1–3 The second harmonic generation (SHG) technique4–6 is very efficient for studies of nano-fabricated materials, such as, e.g., hollow gold nano prisms7 or nano-fabricated meta molecules8 and meta materials.9 SHG is symmetry forbidden in centro-symmetric media, therefore symmetry breaking is achieved with molecules deposited on surfaces, or ordered molecular aggregates embedded in 3D matrix, or macroscopically organized biological samples.10–12 The ordered macromolecular aggregates within the biological tissue are routinely visualized with SHG microscopy.13,14 While SHG imaging is widely used in microscopy,15–17 the interpretation of generated signal is not straightforward due to non-resonant excitation conditions, coherent nature of the signal and due to the molecular orientation dependent SHG response.
The efficiency of SHG is characterized by the second order susceptibility tensor, χ(2). Components of the χ(2) are, in general, complex valued, which provides information about retardancy between the different susceptibility tensor components.18 The real and imaginary parts of second order susceptibility tensor components can be directly measured with double Stokes–Mueller polarimetry.19,20 The relative magnitudes between the susceptibility components and retardancies, i.e. the phase shifts between the nonlinear susceptibility components, can be used to extract structural information about the samples.21
The presence of retardancy between susceptibility components requires nonlocal description beyond the dipolar approximation. The quadrupolar and magnetic field interactions are the lowest order sources of retardancy in linear spectroscopy. They are sources of linear polarization rotation, what is denoted as the optical activity.22 These contributions to the response were previously employed for calculating the nonlinear optical properties of molecules.16,23,24 However, at the second order to the response there is an additional component due to square of vector potential magnitude |A|2 in the minimal coupling description or due to magnetic field square B2 in multipolar description.25 Such contributions do not contribute at linear response (as they are originally quadratic) so they can be neglected for linear optical activity, however, they should be studied for nonlinear techniques, e.g. SHG and sum-frequency generation applications.
Intermolecular interactions may affect amplitudes of various susceptibility tensor components. Compact molecular aggregation happens either by self-assembly or by biological replication in e.g. biological systems.26 It is well known that circular dichroism (CD)22 in such samples is due to chiral molecular aggregation.27 Complicated nature of the full interaction Hamiltonian, that is nonlinear with the excitation field,25,28 can introduce additional contributions at second order to the field that are explored in this paper. As the atomistic molecular structures are known, in this paper, we revisit theoretical aspects of SHG generation in the molecular systems and extend it specifically to the case of macromolecules. The non-local description of susceptibility components is employed in minimal coupling Hamiltonian, which directly combines dipolar, quadrupolar and magnetic interactions. A charge-density induced interactions via |A|2 terms are described in detail. Using the tight-binding description of molecular excitation Hamiltonian and local dipolar approximation of each site, we demonstrate that inter-site interactions are responsible for generation of quadrupolar contributions. Specifically it is found that the charge-density induced components via |A|2 terms originate only in the case of symmetry-broken systems and thus are directly amplified by structural inhomogeneities.
The paper is organized as follows: In Section 2 we define the susceptibility tensor for the SHG, in Section 3 we revisit the microscopic nonlinear optical response theory, where all non-vanishing contributions to SHG are derived in the minimal coupling Hamiltonian formulation. In Section 4 we narrow the focus onto the SHG of molecular systems with a single band of excited states and keep terms to the first order in wavevector. This defines the leading non-local terms for the optical response. Developed theory is applied in Section 5 for a helical model macromolecule, which is modeled as an excitonic system of multiple localized oscillators. In Section 6 we discuss relation of our modeling with the multipolar expansion approach, and present the conclusions. The details of how the induced current is related to the induced polarization and magnetization is presented in Appendix A. The selection of dominant contributions to the SHG is described in Appendix B. The article concludes with the SHG of generic excitonic model presented in Appendix C.
2 Second order non-local response function and susceptibility
SHG, which is the lowest order nonlinear optical process, has been implemented as an image contrast mechanism for optical microscopy of biological samples.29 The second harmonic generation can be expressed via second order induced polarization P(2) according to the relation28,30where E is an incident electric field and χ(2) characterizes the second order response of the media. The two basic principles are fundamentally related to generation of SHG: (1) spatial isotropic system cannot generate SHG, as can be demonstrated by performing the space inversion operation, (2) systems described by linear equations of motion cannot evoke the second harmonic generation.
This can be easily demonstrated by using a simple nonlinear oscillator system, for example the Morse oscillator, whose potential is V(x) = De(1 − exp(−ηx))2, where De is the classical ionization energy of the oscillator and η is the width in coordinate space x, which represents the classical dipole moment. Expanding the potential up to cubic terms we can find the classical equation of motion
| | | ẍ + ω02x = α2x2 + F(t). | (2) |
F(
t) is an additional time dependent external force. We denoted the fundamental oscillation frequency
ω02 = 2
η2De, and the quadratic anharmonicity
α2 = 3
η3De. By using the time dependent harmonic force,
F(
t) =
Aω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos(
ωt), with amplitude
Aω and frequency
ω, we can determine various non-linear effects. By denoting the corresponding oscillatory dipole evolution as follows:
| | x(t) = a0 + a1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt) + a2 cos(ωt) + a2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2ωt) + … cos(2ωt) + … | (3) |
we find that the external force induces the linear response
via oscillating dipole with amplitude
a1 =
Aω/(
ω02 −
ω2). The formation of static polarization, represented by a static shift of equilibrium from origin to
a0 ≠ 0 is observed
a0 =
α2a12/(2
ω02), and the second harmonic is generated, with the amplitude
a2 =
α2a12(
ω02− 4
ω2)
−1/2. We can define the SHG susceptibility
viawhich yields
| | 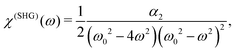 | (5) |
i.e. the SHG susceptibility is purely material property, proportional to the quadratic nonlinearity (cubic anharmonicity of the potential). Two types of resonances could be observed: when
ω ≈
ω0 and when
ω ≈ 2
ω0. In the off-resonant case, the dependence on frequency is weak. Also, the relation
a2 =
a0ω02/(
ω02 − 4
ω2) demonstrates that the SHG amplitude is directly proportional to the difference between the static dipole in the equilibrium state (
a0 = 0 before excitation) and in the excited state (
a0 ≠ 0 after excitation). It is, thus, a direct consequence of the asymmetry of the potential surface.
A dipole approximation is usually accepted for optical response when considering the dominant contributions. The double Stokes–Mueller polarimetry (DSMP) experiments allow to isolate retardancy effects in SHG, i.e., the susceptibility becomes complex with real and imaginary parts,16 therefore nonlocal description of susceptibilities becomes necessary for interpretation of the results. Accordingly, we will use the induced current and the vector potential description in our derivations: the vector potential completely describes electric and magnetic fields of an electromagnetic wave, while the oscillating induced current becomes the source of electromagnetic emitted field according to Maxwell equations.25,31,32 Microscopic nonlocal material properties in this representation are described in Appendix A.
External optical field in the Coulomb gauge is described by a single vector potential, A(r,t), as a function of space r and time t, instead of electric, E(r,t), or magnetic B(r,t), fields. They are related by
| | 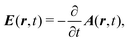 | (6) |
The optical field affects anharmonic material and induces various types of optical response. For spectroscopic detection, induced current is the property of interest (see Appendix A). In accord with the microscopic description, we define the non-local second order response function,
S(2)αβγ, (a tensor) with respect to the induced current
28| | 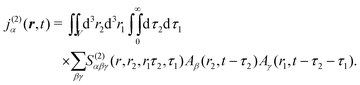 | (8) |
Here
r1,
r2 and
τ1,
τ2 are space and time integration variables, respectively and
α,
β,
γ denote polarization components. Spatial integration involves the sample volume,
V, while the time integration limits denote the causality principle. The integration variables correspond to positions and moments of excitations.
Using Fourier transforms (defined in Appendix A) we have equivalent expression, which additionally relates the incoming field frequencies with the signal frequency suggesting the phase matching condition
| | 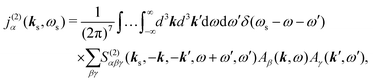 | (9) |
where
k and
ω are the variables of the Fourier (reciprocal) space conjugate to the coordinate
r and momentum
t, respectively.
This expression is self-consistent and cannot be reduced for an arbitrary field. However, a continuous wave (CW) field can be used in the SHG experiment. A focusing of laser beam in SHG microscope setup leads to a broad range of optical modes, which impinge onto the sample. The incident field in this case can be considered from any two waves with the same carrier frequency, but with different wavevectors:
| | 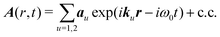 | (10) |
au is the amplitude vector of the
u-th field mode denoting the electric polarization direction (see
eqn (6)). Detection of the second harmonic field with frequency,
ωs = ±2
ω0, will be associated with
α polarization component. By dropping the conjugate part we can isolate the terms with frequency doubling, hence, expressing the second harmonic induced current
| | 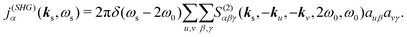 | (11) |
auβ denotes the
β component of vector
au. Notice, that the field is generated only with double frequency,
ωs = 2
ω0, and for the signal wave vector we have |
ks| =
ωs/
c. However, the direction of the wave vector is arbitrary in near-field detection. Accordingly we can have non-collinear measurement. So the signal becomes dependent on incident field polarizations and wavevectors and on the signal wavevector and polarization.
The picture gets simplified in the case of colinear setup. In this case SHG from a single mode can be considered and the field propagation direction is also parallel to the incident field. The SHG susceptibility tensor can thus be defined as:
| | | j(SHG)α(2k,2ω) = χ(SHG)(k)αβγ(ω)aβaγ. | (12) |
Here
k =
kω/
c, hence, the unit vector
k defines the propagation direction of the field,
c being the speed of light. The subscript of
ω0 is dropped from now on for convenience. We then find a simple relation of the susceptibility with the response function.
| | 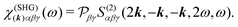 | (13) |
Here
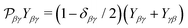
is the permutation operator. In the following Sections 4 and 5 we will consider such collinear setup.
3 Response due to high frequency electronic excitations
In the following we consider the optical field in the region relevant for electronic molecular excitations. Quantum electrodynamics of optical response in this case is described as in the book by Craig and Thirunamachandran.25 In the minimal coupling representation, the Hamiltonian of the material system – a molecule + classical field – is then given by| | 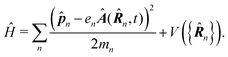 | (14) |
Here ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) n is the n-th particle momentum operator, mn its mass, en – its charge, V({
n is the n-th particle momentum operator, mn its mass, en – its charge, V({![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n}) is the many-particle molecule potential energy depending on the positions of all particles {
n}) is the many-particle molecule potential energy depending on the positions of all particles {![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n} ≡
n} ≡ ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) 1,
1,![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) 2…. Â(
2…. Â(![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n,t) is the vector potential at the position of n-th particle. The first term is the field-affected kinetic energy operator. The second term includes all interactions between charged particles without involving the external field. The kinetic energy (
n,t) is the vector potential at the position of n-th particle. The first term is the field-affected kinetic energy operator. The second term includes all interactions between charged particles without involving the external field. The kinetic energy (![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) − eÂ)2 =
− eÂ)2 = ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) 2 − 2e
2 − 2e![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) ·Â + e2|Â|2 contains the material
·Â + e2|Â|2 contains the material ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) 2 term, related to isolated material system. Together with V({
2 term, related to isolated material system. Together with V({![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n}) this term describes the isolated molecule. The system-field interaction is of two types. The
n}) this term describes the isolated molecule. The system-field interaction is of two types. The ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) ·Â term constitutes the first type of molecule-field interaction due to induced current, while the |Â|2 term is the second type of interaction, related to absolute charge density. Additionally, notice that
·Â term constitutes the first type of molecule-field interaction due to induced current, while the |Â|2 term is the second type of interaction, related to absolute charge density. Additionally, notice that ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) and Â(
and Â(![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) ) in general do not commute due to dependence of vector potential on space, however, to first order in wavevector, permutation of these operators yields a constant shift of the vector potential that does not contribute to system-field interaction. In the commonly used semiclassical description the field is taken to be classical c-number and the complete Hamiltonian is then as followswhere
) in general do not commute due to dependence of vector potential on space, however, to first order in wavevector, permutation of these operators yields a constant shift of the vector potential that does not contribute to system-field interaction. In the commonly used semiclassical description the field is taken to be classical c-number and the complete Hamiltonian is then as followswhere| | 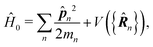 | (16) |
| | 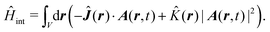 | (17) |
Here| | 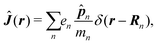 | (18) |
| | 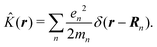 | (19) |
δ(r) = δ(x)δ(y)δ(z) is the three-dimensional Dirac delta function. We thus find the velocity-based excitation current operator Ĵ(r) as a vector field and a scalar field, ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (r), given by absolute charge density. Accordingly, the vector potential A(r,t) is conjugate to Ĵ(r) and the scalar field |A(r,t)|2 is conjugate to
(r), given by absolute charge density. Accordingly, the vector potential A(r,t) is conjugate to Ĵ(r) and the scalar field |A(r,t)|2 is conjugate to ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (r). The scalar field part can be combined with electromagnetic scalar potential,33 however, |A(r,t)|2 should not be neglected in general for nonlinear response. In the following we refer to the two types of coupling as pA type and K-type.
(r). The scalar field part can be combined with electromagnetic scalar potential,33 however, |A(r,t)|2 should not be neglected in general for nonlinear response. In the following we refer to the two types of coupling as pA type and K-type.
The present approach relates the incoming vector field with the momentum of the system, that is the basis for the so-called velocity representation of the interaction Hamiltonian. The other representation of polarization (or length) times electric field is also often adopted. Notice that inequivalence of the velocity and length representations of system-field interaction representation have been demonstrated analytically and computationally (see ref. 34 and references therein). Transformation between representations lead to non unitary shifts of the Hamiltonian, irrespective of whether the transformation can be described as a gauge transformation. It has been shown that the two representations can yield very different results in strong electromagnetic fields35,36 or in chiroptical signals.37,38 For high-order harmonic generation in diatomic molecules at large internuclear separation, a good agreement with the semiclassical three-step mechanism was observed only in velocity gauge.39 As we show in Appendix A the differences must appear at higher than linear order in wavevector.
Usually only the pA term is included while considering the optical response. This is often denoted as the minimal coupling term. Indeed the K-coupling term does not contribute at linear response, where the induced property is linear in A. Additionally K-coupling term does not contribute in impulsive regime when pulse overlap is excluded e.g. in time resolved spectroscopy.40 However, it must contribute to the signal at the second order CW experiment, therefore, in the following we derive the complete optical response function including all interaction contributions.
Accordingly, we rewrite the interaction Hamiltonian as
| | | Ĥint = Ĥ(1)int + Ĥ(2)int. | (20) |
The interaction term
Ĥ(1)int ∼
A is to the first order in the field, while
Ĥ(2)int ∼
A2 is to the second order. The time evolution of the system density matrix in the interaction representation is described by the Liouville equation
28,30| | 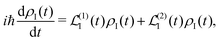 | (21) |
here
ħ is the reduced Planck's constant. Subscript I denotes the interaction representation according to zero-order Hamiltonian
Ĥ0. For an arbitrary operator,
![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif)
, we have:
| | ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) I(t) = eiĤ0t/ħ I(t) = eiĤ0t/ħ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) (t)e−iĤ0t/ħ, (t)e−iĤ0t/ħ, | (22) |
| | 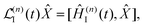 | (23) |
| | | Ĥ(n)I(t) = eiĤ0t/ħĤ(n)int(t)e−iĤ0t/ħ, | (24) |
with
n = 1,2. Now the equation of motion can be formally integrated as
| | 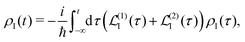 | (25) |
with the boundary condition such that at time
t = −∞ the density matrix is at equilibrium
ρI(−∞) ≡
ρ0, so we find at the first order a single contribution
28| | 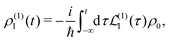 | (26) |
and at the second order we have two contributions
| | 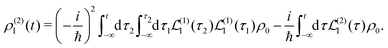 | (27) |
Specific physical observable is related to some specific quantity of interest, defined by the operator Ŷ(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ) and its expectation value by y(r,t). In principle Ŷ(
) and its expectation value by y(r,t). In principle Ŷ(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ) can be an arbitrary operator, related to the detection apparatus. So at the second order to the field we find:
) can be an arbitrary operator, related to the detection apparatus. So at the second order to the field we find:
| | 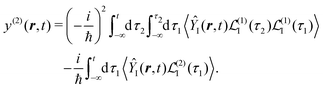 | (28) |
〈…〉 ≡ Tr{…
ρ0} denotes the trace with respect to the equilibrium state. Next, we change the time variables by introducing delays between interactions
t −
t2 =
τ2,
t −
t2 −
t1 =
τ1. Also note that
t ≥
τ2 ≥
τ1. We thus get
| | 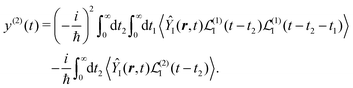 | (29) |
We can write both terms in the same representation with respect to the time integrations using
| | 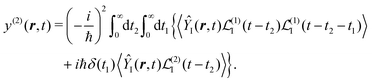 | (30) |
Now we substitute expressions of the superoperators
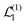
and
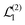
. Using
| | 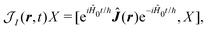 | (31) |
| | 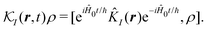 | (32) |
we have a general expression for an observable
y in interaction representation:
| | 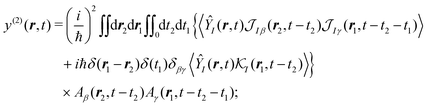 | (33) |
where summation over
β,
γ =
x,
y,
z is implied.
In SHG experiment the detector measures the newly generated field. Its source is the induced current (see Appendix A). So the induced-current related (Ŷ ≡ ĵα) response function tensor, defined in eqn (8) in the interaction representation is given by
| | 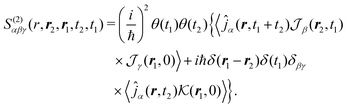 | (34) |
Heaviside functions,
θ(
t), are inserted to guarantee causality. The susceptibility can then be obtained from
eqn (13).
4 SHG susceptibility of a molecular system for non-resonant excitations
Assuming that system Hamiltonian eigenstates with energies εa and wavefunctions ψa are all known, we can expand all operators in the eigenstate representation. Expressions in the eigenstate basis can be represented by Feinman diagrams shown in Fig. 1. Here we assume that ground state is separated from other states by energy gap much larger than thermal energy. States a,b label various system states including the ground state. However, notice that when a = b = g all contributions interfere destructively and the result is zero. Reading each diagram from bottom to top we start from equilibrium ground state population g. Then we have two excitations (either on the left or the right) and last is the detection process, represented by arrow on the left. Diagrams on the first row of Fig. 1 represent pA interaction, while two diagrams on the second row represent K-coupling induced process (Fig. 1c). Notice that in the resonant case only the left-most diagrams would contribute to the signal, as described in Appendix B. In resonant conditions, when the optical field matches a specific molecular transition, we can obtain the frequency dependent SHG spectrum. In the off-resonant case the dependence on frequency is minor.
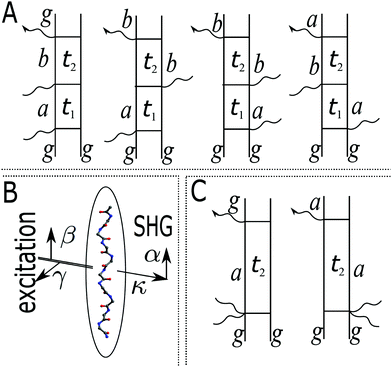 |
| | Fig. 1 (A) Feinman diagrams representing all possible second order interaction pathways induced by pA interaction. g denotes the ground state. a,b are an arbitrary states (including the ground state). t1 and t2 are the time delays between interactions. While all pathways in principle give nonzero contributions in non-resonant measurement, the leading terms originate from the left-most diagram if excited state energies are much larger than the dephasing parameters. (B) Scheme of the SHG experiment. α,β,γ denote field polarization components, κ denotes the field propagation directions. (C) Feinman diagrams representing possible second order interaction pathways induced by K-interaction. In this case t1 = 0 and there is a single delay time t2. | |
Let us first consider only pA excitation. Expanding all superoperators in the Heisenberg representation for operators of eqn (34) (first row) and restricting τ1,τ2 > 0, the four types of contributions induced by pA coupling to the response are as follows:
| | 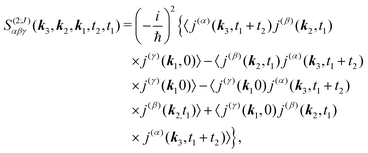 | (35) |
where
j(α) ≡
j·
a indicates
α-th polarization component at the detection step,
β and
γ are polarizations of excitation field (see a scheme in
Fig. 1b);
J in superscript indicates only one part of contributions. This form is very convenient as we can now expand traces in matrix elements as demonstrated in Appendix A.
All terms could in principle contribute to the response in off-resonant regime. The full final expression of the response function is given by eqn (85) together with eqn (88). However, since all terms involve the same transitions, different terms with the same set of transitions can be compared by frequencies in denominators. We then include the dominant contribution, what is sufficient for qualitative evaluation of the effect. Then from pA interaction we obtain the leading contribution from the left-most diagram on Fig. 1a. According to eqn (13) we have
| | 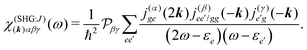 | (36) |
Here
e runs only over the excited states and we denoted diagonal elements as differences
jee/gg(
k) =
jee(
k) −
jgg(
k) while off diagonal elements are the transition moments between states
jee′/gg(
k) ≡
jee′(
k).
εe is the frequency corresponding to excitation energy of state
e. Diagonal terms,
e ≠
e′, in
eqn (36) represent incoherent components, which are induced by excited states independent from each other, while the coherent terms,
e =
e′, involve delocalized collective excited states and transitions between these states.
The terms in eqn (36) are related only to induced current contributions. Next we add contributions from K-coupling. For SHG we obtain (with the same normalization as for pA susceptibility)
| | 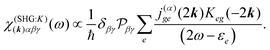 | (37) |
It is thus a diagonal tensor. So the total susceptibility
| | | χ(SHG)(k)αβγ(ω) = χ(SHG:J)(k)αβγ(ω) +χ(SHG:K)(k)αβγ(ω). | (38) |
It becomes important to evaluate and compare the absolute values of eqn (36) and (37). Dimensions of both expressions are the same: notice that J dimension is [charge·distance/time] (in the dipole approximation according to eqn (75), |J| = |ωμ|), while ħωK has dimension [charge·distance/time]2, consequently JJ can be compared to ħωK. If for example we assume a single dipole of 1 D, made up from two charges (e.g. 0.2082 electron charge separated by 1 Å) with charge masses equal to the mass of electron, and being affected by 500 nm wavelength optical field, we find |J| = 0.3768 D ps−1, while at zero order to wavevector 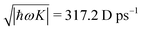 , what seems to be a very significant value. However this value does not contribute to the response (as it is the property of the isolated ground state) and it only shifts the absolute energy. In Appendix A we find expression to first order in wavevector, which indeed contributes to the SHG as we show in Section 5.
, what seems to be a very significant value. However this value does not contribute to the response (as it is the property of the isolated ground state) and it only shifts the absolute energy. In Appendix A we find expression to first order in wavevector, which indeed contributes to the SHG as we show in Section 5.
We can now use eqn (36) to calculate the SHG susceptibility tensor using operator matrix elements in eqn (76). Using Appendix A the SHG susceptibility can be expressed in terms of matrix elements of dipole, quadrupole and magnetic moment operators: dab, q(αβ)ab, mab respectively. In the dipole approximation
| | 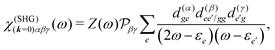 | (39) |
here
k = 0 denotes independence of the wave vector,
Z(
ω) = 2
iω3ħ−2 is a constant amplitude factor at given optical frequency. This expression defines the dominant source of SHG in a wide range of systems and has been utilized in quantum chemistry simulations.
2,25,33,41 However, spatially extended systems allow to include the contributions to the first order in wave vector, where both the
pA and
K induced terms become relevant at the level of magnetic and quadrupole moments:
| | 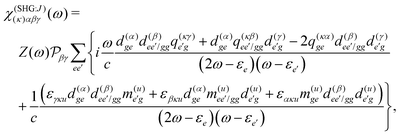 | (40) |
| | 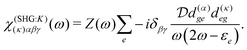 | (41) |
Here we combined universal constants into a single term,
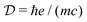
, having the units of dipole moment, equal to 0.0185 D,
κ is the wavevector polarization component.
εuvw is the Levi-Civita symbol, which expresses the cross product. We thus have the expressions in the dipole approximation and beyond the dipole approximation having the same dimensions and thus can be directly used for comparing various contributions.
SHG is often considered for crystals9,11 or partially oriented systems, which are formed on surfaces. It is also used for microscopic imaging of macromolecules that tend to align on surfaces.15,16,18 Here we specifically assume a well defined configuration, therefore we do not include orientational averaging. For example, helical proteins possess one specific axis of symmetry. Such axis we denote by z. Having such geometry we have nine possible independent SHG tensor components (including optical wavevector). Using notation (κ)αβγ we have: (y)xxx, (y)xxz, (y)xzz, (y)zxx, (y)zxz, (y)zzz, (z)xxx, (z)xxy, (z)xyy. In the following we calculate these tensor components for a helical supermolecule.
Notice that we do not have here components like (κ)xyz since in collinear setup such configuration would violate the transversity of the field condition. Such components (on microscopic level in the vicinity of the molecule) require non-collinear configurations of optical fields so that transversity of the field is maintained. However, in that case the notation (κ)αβγ is not sufficient since wavevector directions of all fields should be explicitly stated, e.g. (κακβκγ)αβγ. Here κακβκγ denote wavevector components of the three fields, while αβγ are their polarization components. In this paper we do not consider such components.
5 Application to a helical supermolecule
As a model test system we consider a helical excitonic macromolecule. Such system can be associated with e.g. a single polypeptide backbone excitation. Helical geometry can be characterized by using a linear chain of sites wrapped around a cylinder, a single site representing a peptide unit. The structure is parameterized by diameter of the cylinder dc, pitch of the screw (distance between chains along the cylinder) pc, and the angle ϕc that the nearest neighbor sites make when rotated around the cylinder axis (see Fig. 2). Distance between sites along the chain is given by 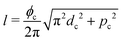 . The following are the excitation parameters of the units. These are the orientations of dipoles (transition and permanent) in the cylinder coordinate system. It is sufficient to define physical parameters of the single site and then all sites will be obtained from that one by applying rotation and translation operations.
. The following are the excitation parameters of the units. These are the orientations of dipoles (transition and permanent) in the cylinder coordinate system. It is sufficient to define physical parameters of the single site and then all sites will be obtained from that one by applying rotation and translation operations.
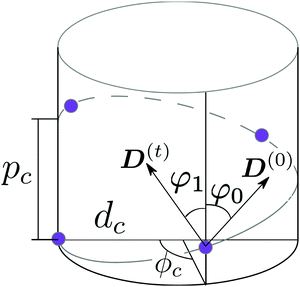 |
| | Fig. 2 Scheme of a cylindrical macromolecule. Geometrical parameters shown are: diameter of the cylinder dc, pitch of the screw pc, and the angle ϕc between the nearest neighbor sites, when rotated around the cylinder axis. φ0 and φ1 are the angles that ground state dipole D(0) and transition dipole D(t) of a single site, respectively, make with the symmetry axis of the cylinder. | |
For a reference the lattice site n = 0 can be used. The molecular frame is taken such that z axis is pointed along the cylinder axis. The rotation matrix around this axis, associated with site n and angle nϕc then is given by ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) n where
n where
| | 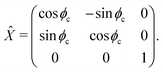 | (42) |
Assuming the homogeneous conditions, where all sites, being twisted around the cylinder, are otherwise identical, and angle
ϕc/(2π) being a rational number, translationally periodic structure emerges and periodic boundary conditions can be easily implemented. Let us assume that the
M-th unit is simply translated by
Ppc along the main helix axis with respect to
n = 0.
P is the number of loops needed to match the 0-th and
M-th sites in
xy plain. The twisting angle thus satisfies
Mϕc = 2π
P.
M and
P must be taken as smallest integers satisfying the relation. Accordingly,
XM = 1 and the chain length, necessary to fulfill the periodic system is
L =
Ml, while the length of the unit-cylinder is
Ppc. For spatial positions taking a point
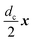
on site
n = 0, the corresponding points of all sites are then expressed by simultaneous rotation and translation operations:
| | 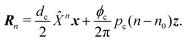 | (43) |
For electronic excitations of the macromolecule we consider the excitonic model (for details see Appendix C). We restrict the model to the nearest-neighbor interactions J and site excitation energy E independent of site position. Since distance between various sites in the helical geometry does not simply decay uniformly, we could have considerable interactions across the winding direction. The nearest neighbor interaction is thus a rough approximation. However, including non-nearest neighbor interactions would not change the results considerably as the excitation wavefunction symmetries would remain the same and in off-resonant regime the exact excitation energy is not that significant.
Eigenstates of the macromolecule (denoted as excitons) are obtained by diagonalizing the zero order system Hamiltonian. For the electronic ground state (all sites are in their ground states), which we label by |g〉, the original system Hamiltonian contains only one state with energy 0. This state is not coupled to all other (excited) states when the optical field is off. Next is the manifold of excited states |e〉. These are obtained from the ground state by promoting one of the sites to its excited state. The number of excited states is thus equal to the number of sites. The excitonic system Hamiltonian of the simple linear chain as described in this section within homogeneous conditions can be easily diagonalized, which yields exciton energies
| | 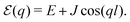 | (44) |
Here
q is the lattice “wavevector” along the chain, wrapping the cylinder. The wavevector
q is discrete: using dimensionless units, it has
M values with the step 2π/
M. The normalized eigenvectors are then given by Bloch wave
| | 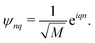 | (45) |
Such situation corresponds to the strong coupling or homogeneous case when J is much larger than fluctuations of the zero order Hamiltonian due to inhomogeneities. In the opposite, for the weak coupling or inhomogeneous case, the eigenstates simply correspond to local excitations with wave functions ψnq = δnq, and energies equal to site energies 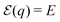 . Both cases will be studied separately.
. Both cases will be studied separately.
The dipole approximation with respect to the single site allows simple definition of excitation parameters relevant for the SHG process. All transition amplitudes will be expressed in terms of dipolar moments of different sites as described in Appendix C. Site-related dipolar moments – the permanent ground state dipole, transition dipole and the permanent excited state dipole – are denoted as D(0)n, D(t)n, D(1)n, respectively. These vectors can be generated from the first site by performing the rotation operation Dn(…) = ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) nD0(…). So we find that for the response of the whole macromolecule the important contributions include: the dipole and quadrupole contributions for the electronic ground state, the transition amplitudes, and the excited state permanent and transition amplitudes.
nD0(…). So we find that for the response of the whole macromolecule the important contributions include: the dipole and quadrupole contributions for the electronic ground state, the transition amplitudes, and the excited state permanent and transition amplitudes.
The eigen vectors enter the matrix elements of the induced current (see Appendix C). Dipole moment matrix elements are obtained by transforming the site dipoles to the macromolecule eigenstate representation, and for the periodic system can be listed explicitly. For the eigenstate matrix elements of the homogeneous model we use superscript (exh), while for the inhomogeneous model we will use (exi). The ground state permanent dipole moment is just a sum of moments of all sites in both homogeneous and inhomogeneous cases. Since the sites are simply rotated around the cylinder, the sum of all site dipoles within the full period yields the dipole parallel to the cylinder symmetry axis, d(exi/h)g,g ≡ MD(0)0zz. Ground-to-excited state transition dipoles, now depend on the type of wavefunction. In the inhomogeneous model for q = n we have d(exi)g,q=n = D(t)n. For the homogenous model 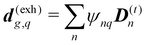 the result splits into two groups. For exciton q = 0 a real-value transition dipole moment is d(exh)g,q=0 = M1/2zD(t)0z, while for condition ql ± ϕc = 0 we find the complex-value perpendicular dipoles
the result splits into two groups. For exciton q = 0 a real-value transition dipole moment is d(exh)g,q=0 = M1/2zD(t)0z, while for condition ql ± ϕc = 0 we find the complex-value perpendicular dipoles
| | 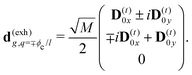 | (46) |
Also notice that states
ql = ±
ϕc have the same energy (are degenerate). So we find two degenerate transitions that are conjugate to each other and are transverse to the cylinder axis, while the single longitudinal transition is oriented along the cylinder axis.
42 Finally the matrix elements for the excited manifold dipoles for both models are given by
| | 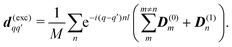 | (47) |
This yields the following nonzero elements: for homogeneous model diagonal
q =
q′ elements
d(exh)qq =
z((
M − 1)
D(0)0z +
D(1)0z), and off-diagonal are nonzero for (
q′ −
q)
l ±
ϕc = 0:
| | 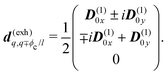 | (48) |
For the inhomogeneous model only diagonal elements are not zero:
d(exi)qq =
z((
M − 1)
D(0)0z +
D(1)0z). The corresponding quadrupole moments are more complicated. They have been calculated numerically for both homogeneous and inhomogeneous models. Having these properties, the susceptibility is calculated from
eqn (40) and (41).
For demonstration, we assume the simplest possible helical system – a three-site transitionary invariant unit, M = 3, ϕc = 2π/3, P = 1. Cylinder diameter and pitch are the scaling parameters, while we assume dc = 5 Å, pc = 3 Å. These are typical parameters for polypeptide backbone in proteins. Orientations and amplitudes of various dipoles lead to very large parameter space. We restrict ourself to the case when all dipoles lie on the cylinder surface. Coordinates of the zero-th site are (x,y,z) = (dc/2,0,0), then we include two angles, φ0 and φ1 as free parameters that define orientations of permanent and transition dipoles of the initial site: D(0)0 = (0,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ0,cos
φ0,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ0) and D(t)0 = (0,sin
φ0) and D(t)0 = (0,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1,cos
φ1,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1), while D(1)0 = 1.1D(0)0. Properties of all other sites are obtained from the zero-th site by translation and rotation operations.
φ1), while D(1)0 = 1.1D(0)0. Properties of all other sites are obtained from the zero-th site by translation and rotation operations.
In Fig. 3 we present the system where all sites are independent. In that case we have four nonzero tensor elements (y)xxz,(y)zxx,(y)zzz, and (z)xxy that originate with the dipole approximation. These elements correspond to incoherent contributions from all independent sites. All contributions beyond dipole approximation vanish since the dipole approximation was assumed for all sites. Eventually since the sites are independent they collectively do not participate in the response and could be considered independently.
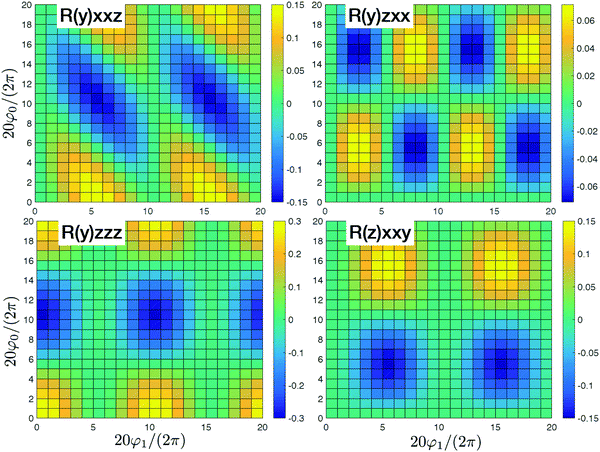 |
| | Fig. 3 SHG tensor amplitude for an ideal helical system of uncoupled sites. Tensor elements are denoted as (κ)αβγ. A grid of 20 × 20 points is used for angles φ0 and φ1 (for definitions see the scheme in Fig. 2). R stands for real parts. All other tensor components in the dipole approximation or beyond dipole approximation vanish. For convenience the constant factors are renormalized: 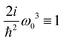 . Note, different ranges of the amplitude values for the color-bars. . Note, different ranges of the amplitude values for the color-bars. | |
By adding couplings between the sites surprisingly the (y)xxz,(y)zxx,(y)zzz, and (z)xxy tensor components do not qualitatively change, as presented in Fig. 4. Amplitudes are slightly smaller by ∼10%, but they do not show qualitative differences. Consequently, these tensor components carry information on the structure, but do not depend on the coupling between sites. However, for the coupled sites we obtain six more tensor components that originate beyond the dipole approximation for the whole macromolecule and are induced by quadrupole components. They have a phase shift (i.e. are imaginary). Since we get (z)xxx ≈ (y)xxy ≈ 4(z)xxy with identical patterns, only four are presented in Fig. 4. Compared to the uncoupled dipole approximation we have additionally two types of novel patterns (y)xzz and (y)zxz that can be employed for structure determination.
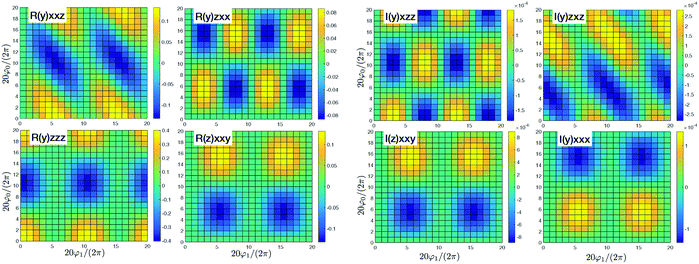 |
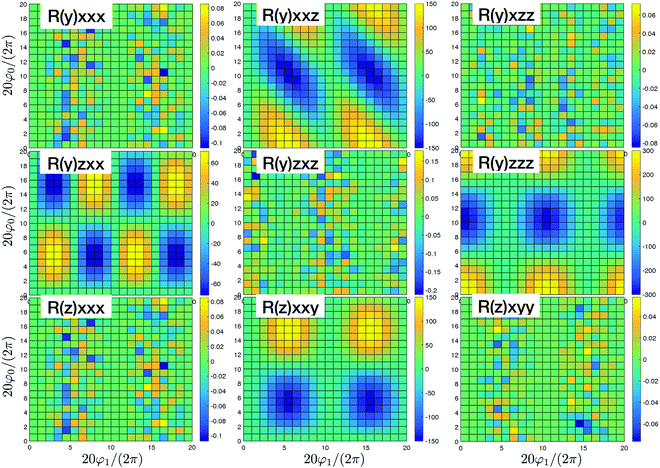
| | Fig. 4 SHG tensor amplitude for an ideal helical system of coupled sites. Tensor elements are denoted as (κ)αβγ. A grid of 20 × 20 points is used for angles φ0 and φ1 (for definitions see the scheme in Fig. 2). R and I stand for real and imaginary parts, correspondingly. Real components originate in the dipole approximations, imaginary components – to first order in optical wavevector. For convenience the constant factors are renormalized: 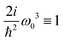 . . | |
We additionally find an unexpected result that due to the structure regularity the K-coupling induced contributions cancel identically for all cases. Consequently, this signifies that K couplings could be sensitive to structural inhomogeneities. To simulate such scenario we assume that excitations are completely local, hence inter-site coupling is not present and site dipolar moments have random contributions to orientations and to amplitudes. Starting from the ideal structure we add independent random vectors (x,y,z) = 0.01(δi,δi+1,δi+2), with δi being a random number from the Normal distribution, to all site dipoles (permanent and transition). To include ensemble averaging we use a helical system with 3000 sites. Also notice, since for each configuration of angles φ0 and φ1 we have to recreate the whole helix, we have also the new randomization.
As a result we obtain the whole spectrum of dipole induced and beyond dipole tensor components that are presented in Fig. 5 and 6. In the dipole approximation we find the same strongest components as in Fig. 4. The other tensor components are ∼1000 times weaker. Additionally we obtain quite strong K-coupling induced tensor components presented in Fig. 6. There are only six possible configurations since we have requirement β = γ and we find (y)xxx = (y)xzz, (y)zzz = (y)zxx, (z)xxx = (y)xzz. As these components are induced purely by the disorder we do not obtain any structure, but the nonzero amplitude signifies explicitly structural inhomogeneities. Additionally notice that for such model all quadrupolar contributions vanish identically as all excitations are purely local. Thus now the imaginary components are all originating from K coupling.
 |
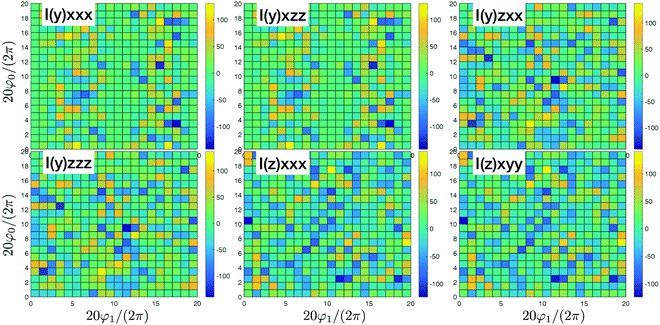
| | Fig. 5 SHG tensor amplitude components in the dipole approximation for a disordered helical system of 3000 uncoupled sites. Tensor elements are denoted as (κ)αβγ. A grid of 20 × 20 points is used for angles φ0 and φ1 (for definitions see the scheme in Fig. 2). R stands for real part. For convenience the constant factors are renormalized: 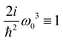 . . | |
 |
| | Fig. 6 SHG tensor amplitude components at first order in wavevector for a disordered helical system of 3000 uncoupled sites. A grid of 20 × 20 points is used for angles φ0 and φ1 (for definitions see the scheme in Fig. 2). I stands for imaginary part. For convenience the constant factors are renormalized: 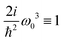 . . | |
6 Discussion and conclusions
The second harmonic theory presented in this paper describes nonlocal second order response theory of cylindrical supermolecules. Such response is employed for second harmonic generation experiments in various polarization configurations. We specifically find tensor components that are induced using the dipole approximation and show that by accounting for quadrupolar contributions additional set of components is induced. Additionally, since the second order response is due to A2 terms we find that non-standard interaction Hamiltonian elements, specifically, due to charge density or K-coupling as we denote it, has to be included in the theory. We first find that this type of coupling is important only beyond dipole approximation. Thus it should be compared to quadrupolar or magnetic contributions. Second, the K-coupling can be ignored in the case of linear optical response. Correspondingly it is not important for well defined circular dichroism spectroscopy and other optical activity experiments. Regarding the higher order nonlinear optical techniques, the K-coupling has to be included when optical fields overlap, like in CW setup. It thus is not important in pulsed laser spectroscopies when pulses do not overlap. However it is important with overlapping pulses, or SHG generated with a single beam pulsed laser.
We thus find that in principle K-coupling is important for SHG amplitude. We find that for the systems with high level of symmetry the K-coupling contribution averages out. This may be related first of all to symmetry properties of separate molecules. Second, the orientational averaging imposes additional symmetries to the system which can also average out the K-contributions. However, these contributions thus become very sensitive to system fluctuations that break the symmetries. As our simulations demonstrate this type of coupling specifically originates due to inhomogeneities and could be observed in microscopy setups with polarimetric SHG microscopy imaging.16
Our theory is used to derive SHG susceptibility in the off resonant regime. In this case we obtain specific expressions which barely depend on system excitation energies. In resonant case we would obtain much fewer contributions, hence the signal expressions would be much simpler, and specific resonances would amplify specific contributions. SHG spectrum, the amplitude as a function of excitation energy, would reveal very delicate information about the systems.
Also, our approach assumes that the molecular excitation energies are much higher than optical field frequency. Other regime could be considered when molecular excitation energies would be with much smaller energy. In that case we could consider molecular vibrational contributions to the SHG.
The other system-field interaction model is obtained by using the gauge independent electric and magnetic fields as basic components. The interaction Hamiltonian becomes especially simple for linear terms. We thus obtain polarization and magnetization terms
| | Ĥint ∼ ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) iEi − iEi − ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) ij∇iEj − ij∇iEj − ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) iBi. iBi. | (49) |
where we have polarization
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif)
, quadrupole
![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif)
and magnetization
![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif)
operators. This Hamiltonian is not complete at higher orders. More complicated
B2 contributions appear
25 that could contribute to
e.g. SHG. Instead of using many terms in interaction Hamiltonian, we choose to use more simple minimal coupling interaction Hamiltonian. Instead of five terms of full interaction Hamiltonian in
PE representation we have only two terms and thus our response function becomes relatively compact. However, even using the Coulomb gauge, the vector potential is still not experimentally observable quantity and retains freedom of the reference. The experimentally measurable quantities are the electric and magnetic fields,
E and
B. They are related to derivatives of the vector potential. An arbitrary constant vector can thus be added to the vector potential and could in principle affect definition of the optical response. In principle this amounts to redefining the material momentum operator, the absolute reference point of the energy and the overall optical response should remain unaffected.
Specific tensor components of the response tensors are often associated with molecular chirality. Macroscopic chirality is addressed in isotropic samples, where full 3D orientational averaging is implied. CD is one example of such approaches: dipolar and magnetic components of the optical response become sources of CD signals. The most important is the property that the dominant type of microscopic chirality determines the sign of various spectral features: inverting the chirality changes the sign of the feature. This can be simply demonstrated by performing space inversion, what changes the sense of chirality: The space inversion inverts coordinates, dipoles and all fields. At second order space inversion changes the polarization, while input, being A2 stays the same. The susceptibility thus changes signs. In this respect the dipolar part of the SHG tensor is thus chirality-dependent. The terms beyond dipole are thus chirality-independent. The same symmetry applies to K-coupling. As it involves two dipoles, the susceptibility is thus non chiral (as linear absorption).
Much richer picture emerges in the case of non-collinear experiment configuration as described in Section 2. In this case the optical response and the susceptibility is not a simple tensor, but depends on all three propagation directions of the two incident fields and on the signal field. In the microscope geometry the incoming beam forms a cone, so the amplitude of SHG field involves a sum over all possible incoming modes. Consequently for specific incoming field polarization from eqn (9) we can write:
| | 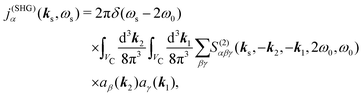 | (50) |
here
C denotes the full volume of the focusing cone.
a(
k) is the polarization vector of the field at the sample as a function of wavevector. Notice that amplitude vector components
aβ(
ku) also depend on the propagation directions: even if the amplitude |
a| is fixed, when
ku rotates, different components of polarization vector change because the field is transverse,
a·
ku = 0. Consequently, summation over
β and
γ includes all three cartesian components. The response function is given by the sum of
eqn (85) and (88) with transition current amplitudes given by
eqn (75) and
K-coupling in
eqn (79). The internal fields can be expressed
via “external” fields, where only polarizations are the quantities of interest. For example, consider the laser beam propagating in
x direction before focusing. Optical polarization
β, for example
y, is perpendicular to beam propagation. After traversing the lense a specific optical mode is bent – the new propagation direction is
κ. Optical polarization is reoriented if
k·
y ≠ 0. It gets
x (longitudinal) component equal to −cos(
ϕ) = −
y·
k; here
ϕ is the angle between vectors
k and
y. The remaining
y component of polarization is equal to sin(
ϕ) = |
y ×
k|. Consequently we can construct susceptibility
| | 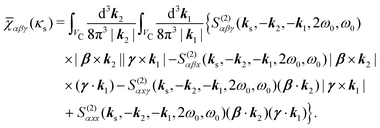 | (51) |
In this case non-collinear polarization tensor components, such as
xyz becomes possible and measurable. Notice that non-collinear field emission in SHG process violates phase matching or momentum conservation,
i.e.
ks =
k1 +
k2 appears only when |
k1| = |
k2| =
ω0/
c and |
ks| = 2
ω0/
c are in collinear configuration. In non-collinear conditions additional momentum should be obtained from system by changing momentum
q of,
e.g., collective vibrational mode or acoustic phonon. We thus have
ks =
k1 +
k2 +
q in 3D. Essentially this is possible only in spacially organized systems such as atomic or molecular crystals and macromolecules.
Additional pecularity is related to the situation when specific orientation of the molecules can be defined in the sample. The fields in the vicinity of the molecule of interest should be defined in the molecular frame. In that case, the susceptibility tensor in the laboratory reference frame χabc can be related to susceptibility tensor χαβγ in the molecular reference frame via rotation matrix:
| | | χabc = TaαTbβTcγχαβγ, | (52) |
where
Taα are the matrix elements of rotation matrix. In rotated molecular coordinate system various susceptibility components contribute to the measured susceptibilities in the laboratory frame. A 2D or 3D complete polarimetry can be performed to obtain complex valued laboratory frame susceptibility components.
18,19,21
Another property that becomes accessible from SHG is the excitation delocalization in spatially extended macromolecules. We show that quadrupolar contributions originate explicitly due to exciton delocalization. For local excitations the quadrupolar components are not generated. This becomes tightly related to inhomogeneities and K-couplings. K couplings do not originate in symmetric system. Inhomogeneities are required to generate K-induced contributions. Additionally, inhomogeneities cause excitation localization. The variation of amplitudes becomes straightforward: as inhomogeneities increase, exciton becomes localized, hence quadrupole contributions decay and K-induced contributions grow up. It should be noticed that noisy signal of aligned macromolecules in the biological structure containing intrinsic disorder has been observed experimentally and could be attributed to K-coupling induced contributions.16
Concluding, we have derived non-local microscopic SHG susceptibility in the off-resonant case by including complete set of interaction Hamiltonian terms. Specifically we obtain contributions from induced current and from K-coupling. The K-coupling yields additional contribution beyond dipole approximation at the same level as quadrupolar and magnetic components. Performed simulations of SHG susceptibility demonstrate that the above-mentioned symmetries hold for the simple model of a helical macromolecule. In the simple excitonic model the quadrupolar components are explicitly generated. Presented theory can be easily extended to the case of off-resonant molecular vibrations and to the resonant sum or difference frequency generation spectroscopy. Additional tensor components of non-collinear field configurations can be directly obtained as well.
Conflicts of interest
There are no conflicts to declare.
A Microscopic material properties
According to classical Maxwell equations in Coulomb gauge,25 a transverse component of the induced current is the source of an optical field. For the vector potential| | 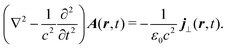 | (53) |
Consequently, considering optical field generation, the material quantity of interest is the induced current.
It is convenient to start with Fourier transform of the full induced current j(r,t). We use the following convention for the inverse transform for an arbitrary function F(r,t)
| | 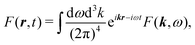 | (54) |
while the direct transform is
| | 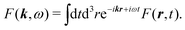 | (55) |
Whether the function is addressed in direct or reciprocal space (and time) is denoted by specifying its arguments.
In the Fourier space we have
| | 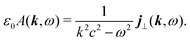 | (56) |
Thus the generated vector potential is directly proportional to the induced current in the material. The condition of non-zero amplitude for the shifted frequency provide non-stationary conditions,
i.e. the generation and decay of the optical field.
The total induced current results from two parts – the induced polarization, 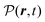 , and the induced magnetization,
, and the induced magnetization, 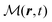 ,
,
| | 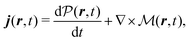 | (57) |
or in Fourier space
| | 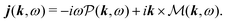 | (58) |
These classical relations can be completely defined using the quantum field representation as follows.
For the system excitation induced by the incoming field we consider the interaction Hamiltonian (eqn (17)). Having the free material Hamiltonian, ĤM, we extend the Hamiltonian by including the free field (so the zero-order Hamiltonian becomes Ĥ0 = ĤM + ĤF; the second term corresponds to the free field), and define the time evolution operator of the material system and of the optical field, U(t) = UM(t)UF(t), according to the zero order Hamiltonian
| | 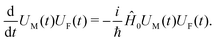 | (59) |
All operators can be defined in the interaction picture with respect to this Hamiltonian: the coordinate operator
Rn(
t) =
UM(−
t)
RnUM(
t) and the velocity operator
![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) n
n(
t) =
UM(−
t)
![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) nUM
nUM(
t) with
| | 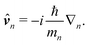 | (60) |
The
jA part of the interaction Hamiltonian is also represented in the interaction picture, where the field is taken as an operator as well
| | 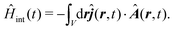 | (61) |
Here
| | 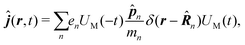 | (62) |
and the vector potential can be expanded in the set of modes
| | 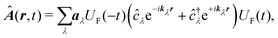 | (63) |
with
aλ the field amplitude of mode
λ, then
kλ and
ωλ are the wavevector and frequency of the mode, while
ĉ†λ and
ĉλ are the mode creation and annihilation operators. Notice that the field operators commute with material momentum and coordinate operators. We can now use
| | 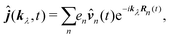 | (64) |
with wavevector corresponding to the specific field mode. In the long wavelength approximation (first order in wavevector) by separating the molecular origin
R0 so that
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n
n =
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n0
n0 +
R0, we find
| | 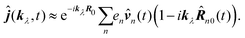 | (65) |
This form can be transformed into the dipole representation by using the Heisenberg relation for the position operator ![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) n(t) = d
n(t) = d![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n0(t)/dt. Using vector decomposition A × B × C = B(A·C) − C(A·B) we obtain
n0(t)/dt. Using vector decomposition A × B × C = B(A·C) − C(A·B) we obtain
| | 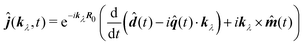 | (66) |
or in Fourier space
| | ĵ(kλ,ω) = e−ikλR0(−iω(![[d with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0064_0302.gif) (ω) − i (ω) − i![[q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0071_0302.gif) (ω)·kλ) + ikλ × (ω)·kλ) + ikλ × ![[m with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006d_0302.gif) (ω)). (ω)). | (67) |
Here we defined
| | 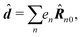 | (68) |
| | 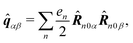 | (69) |
| | 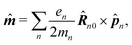 | (70) |
the dipole moment, the quadrupole tensor and the magnetic moment, respectively. The quadrupole moment in this representation is the symmetric tensor. Correspondingly we can write the polarization and magnetization as
| | 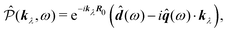 | (71) |
| | 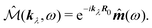 | (72) |
A special care has to be taken when manipulating the matrix elements of the interaction Hamiltonian in quantum description. Inserting the vector potential eqn (63) into the interaction Hamiltonian eqn (61) we have
| | 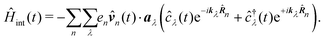 | (73) |
Since the material system and the optical field complement each other to the closed quantum system, the changes in the field state directly correspond to the changes in the material state, since total energy must be conserved. Consequently an arbitrary transition in the system corresponds to emission or absorption of a photon. The frequencies in
eqn (67) can thus be substituted by frequencies of corresponding photon modes. We thus can write
| | ĵ(kλ,ω) = e−ikλR0(−iωλ(![[d with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0064_0302.gif) (ω) − i (ω) − i![[q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0071_0302.gif) (ω)·kλ) + ikλ × (ω)·kλ) + ikλ × ![[m with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006d_0302.gif) (ω)), (ω)), | (74) |
and thus we obtain complete correspondence in the dipole approximation with the multipolar interaction Hamiltonian,
i.e.
j·
A ≡
P·
E.
As we are interested only in transverse component of the induced current, we can consider the projection of the total current onto the polarization vector b, which is perpendicular to k, i.e. a·j ≡ a·j⊥. Additionally let us assume that we know eigenstates of the zero-order Hamiltonian, ψa with eigenvalues εa. In the Schroedinger picture the induced current can be written as
| | | α·jab(kλ) = −e−ikλR0iωλ(α·μab(kλ)), | (75) |
with
| | 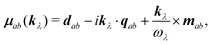 | (76) |
defined as the generalized transition amplitude (vector) containing the dipole, quadrupole and magnetic contributions. Notice that the momentum operator
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif)
entering the magnetic moment is imaginary compared to the coordinate. Thus, the magnetic moment enters at the same level as the quadrupole moment.
Since we have used the Taylor expansion with respect to Rn0·k so R0 must be chosen so that Rn0 are smallest possible.22 A mass center of the molecule for R0 is then the most reasonable choice for the origin point. Additionally, notice that the origin dependent terms cancel in the final signals since they enter at linear order to wave vector and we have the phase matching condition relating the incoming and outgoing field wavevectors, kout + ∑kin = 0.
The second quantity which enters the optical response is the interaction amplitude K(r) related to the charge density (see eqn (19)). After spatial Fourier transform and using the long wavelength approximation we have in Schroedinger representation
| | 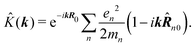 | (77) |
The first term in the brackets is just a constant so it contributes only to diagonal matrix elements
| | 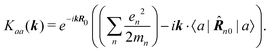 | (78) |
However, this diagonal element does not contribute to the response (see
eqn (37)). The off-diagonal element
Kab gives contributions only at first order in wavevector. Assuming states
a and
b to be electronic, in the Frank Condon approximation disregarding electronic-vibrational couplings, we find that only electrons contribute to the off diagonal amplitude. Then electron charge absolute value and mass are universal constants, and we can write
| | 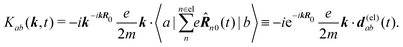 | (79) |
Here
d(el)ab(
t) is the electron-only contribution to the transition dipole moment for the transition between electronic states
a and
b. This quantity is calculated with respect to the mass center of the molecule,
i.e. the same reference as before.
B Derivation of dominant contributions to the SHG
Response function consists of the products of the induced current. One of them can be rewritten by using summation over operator matrix elements:| | 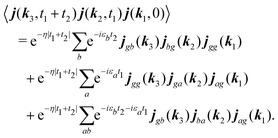 | (80) |
Here decay of correlations is implied with assumption η ≪ εa,ω0. It would come in more complicated form if we include the environment explicitly. The response function includes this correlation function only at positive times t1,t2 > 0. Its contribution to the SHG response function for the fields with frequency ω0 after Fourier transform is| | 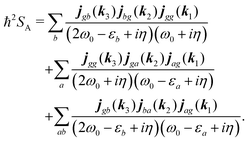 | (81) |
According to eqn (35) the second, third and fourth contributions are| | 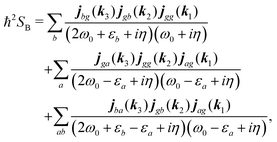 | (82) |
| | 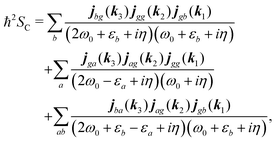 | (83) |
| | 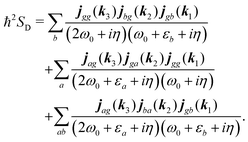 | (84) |
Summations are only over the excited states. By denoting jaa/gg = jaa − jgg as the difference between permanent matrix elements, while jab/gg ≡ jab we can combine terms so that the full pA coupling induced response function is given by| | 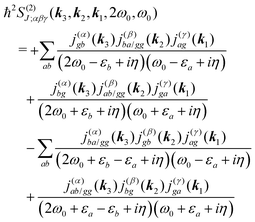 | (85) |
For the non-resonant case in principle all contributions could contribute. However, we still can separate the dominant contributions for specific experiment configuration. First of all dephasing rates η are much smaller than electronic frequencies. In this case all iη can be dropped. Second, it is easy to notice that the four terms contain the same absolute amplitudes. When electronic transition frequency εa and ω0 are of the same order of magnitude (while still off-resonant), we certainly have |ω0 − εa|−1 > |ω0 + εa|−1 and |2ω0 − εa|−1 > (2ω0)−1. Consequently, the first term becomes dominating for the same set of optical transitions.
The response function then takes the form
| | 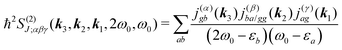 | (86) |
This expression can converted to dipolar form using eqn (75) and (76) in the collinear configuration:
| | 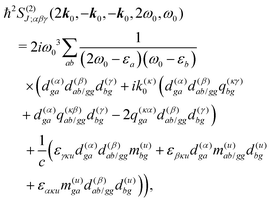 | (87) |
where
εklm is the Levi-Civita tensor and summation over
κ taking values
x,
y,
z is implied.
For the K-coupling terms we similarly take the dominant contribution. Starting from real-space time domain expression eqn (34) after Fourier transform we have
| | 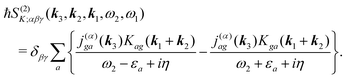 | (88) |
Taking the dominant contribution we have for SHG in collinear configuration
| | 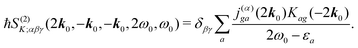 | (89) |
Inserting the expression for
K matrix elements and assuming electronic contributions to the dipole moments we find
| | 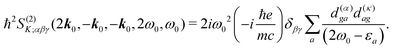 | (90) |
Notice that eqn (85) and (88) are general and hols for all possible tensor components beyond collinear setup.
C SHG of excitonic model
In this section we consider a system, that is partitioned into distinct units, where electron exchange between these units could be neglected. Then electrons can be identified with distinct units and all summs over charges can be grouped accordingly.
An alternative expression for the induced current can be obtained in that case. Starting from eqn (64) we decompose the sum into two sums: one – over molecules and the other over the charges of molecules:
| | 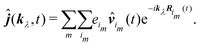 | (91) |
Using the dipole approximation for separate units we obtain
| | 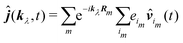 | (92) |
and
| | ĵ(kλ,t) = −iωλe−ikλR0(1 − kλRm0)![[D with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0044_0302.gif) m. m. | (93) |
Comparing to
eqn (75) we find the alternative form of the interaction amplitude
| | | μab(kλ) = Dab − ikλ·Qab | (94) |
with
| | 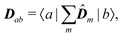 | (95) |
being the sum of dipole operators of different units in the supermolecule and
| | 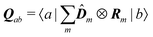 | (96) |
as a non-symmetric quadrupole operator. In this description the magnetic moment is zero. The important parameters thus become the dipole moment matrix elements of various groups.
In the Heitler London approximation excitation characteristics of such macromolecule are described by properties of units and inter-unit interaction. The zero-order system Hamiltonian is then given by
| | 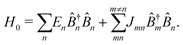 | (97) |
Here
En is the excitation energy of
n-th unit,
Jmn is the inter-unit coupling.
![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) †m
†m and
![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) m
m are excitation creation and annihilation operators (we make an assumption that the unit can be described by a single optical transition). Set of states of such macromolecule consists of the ground state |0〉 and excited states |
e〉, also given in terms of localized excitations of different units:
| | 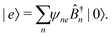 | (98) |
The stationary states are eigenstates of the Hamiltonian: energy of state |0〉 is 0, excited states are defined by
| | 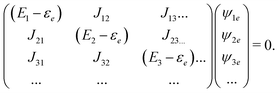 | (99) |
Using the eigenstate basis we find the net ground state dipole moment
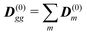
, transition dipoles
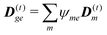
, and net dipoles of the excited state manifold
| | 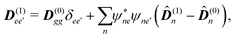 | (100) |
where
D(0)m = 〈0|
![[D with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0044_0302.gif) m
m|0〉 is the ground state dipole of unit
m,
D(t)m = 〈0|
![[D with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0044_0302.gif) m
m![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) †m
†m|0〉 is its transition dipole and
D(1)m = 〈0|
![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) m
m![[D with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0044_0302.gif) m
m![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) †m
†m|0〉 – its excited state permanent dipole. The corresponding quadrupole matrix elements are
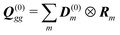
, transition quadrupoles
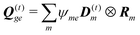
, and the net quadrupoles of the excited state manifold
| | 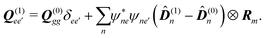 | (101) |
For this model we find very simple expression for the SHG response function
| | 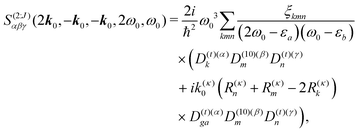 | (102) |
where we denoted
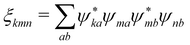
and
D(10)m =
D(1)m −
D(0)m. Independence of the coordinate origin is now clearly expressed as well as importance of excitonic delocalization. For the localized excitations we have
ξkmn =
δkmδmn and quadrupolar contributions vanish due to coordinate cancelation.
The excitonic model for K-induced contribution, following eqn (90) and using 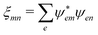 yields
yields
| | 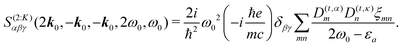 | (103) |
In
K coupling only transition dipole moments matter.
Acknowledgements
This work was supported by the European Regional Development Fund under Measure No. 01.2.2.-LMT-K-718 (project No. 1.2.2.-LMT-K-718-02-0016) under grant agreement with the Research Council of Lithuania (LMT-LT), and Natural Sciences and Engineering Research Council of Canada (NSERC) (RGPIN-2017-06923, DGDND-2017-00099). Numerical calculations were performed on resources at the High Performance Computing Center, HPC Sauletekis, in Vilnius University Faculty of Physics.
References
-
Y. R. Shen, Fundamentals of Sum-Frequency Spectroscopy, Cambridge University Press, 2016 Search PubMed.
-
D. L. Andrews and P. Allcock, Optical Harmonics in Molecular Systems: Quantum Electrodynamical Theory, Wiley-VCH, 2002 Search PubMed.
- D. Tokarz, R. Cisek, M. Garbaczewska, D. Sandkuijl, X. Qiu, B. Stewart, J. D. Levine, U. Fekl and V. Barzda, Carotenoid based bio-compatible labels for third harmonic generation microscopy, Phys. Chem. Chem. Phys., 2012, 14, 10653–10661 RSC.
- N. Bloembergen, R. K. Chang, S. S. Jha and C. H. Lee, Optical second-harmonic generation in reflection from media with inversion symmetry, Phys. Rev., 1968, 174, 813–822 CrossRef CAS.
- N. Kato, Optical second harmonic generation microscopy: application to the sensitive detection of cell membrane damage, Biophys. Rev., 2019, 11, 399–408 CrossRef CAS PubMed.
- J. E. Reeve, H. L. Anderson and K. Clays, Dyes for biological second harmonic generation imaging, Phys. Chem. Chem. Phys., 2010, 12, 13484–13498 RSC.
- B. Hazra, K. Das and M. Chandra, Large second harmonic generation from hollow gold nanoprisms: Role of plasmon hybridization and structural effects, Phys. Chem. Chem. Phys., 2017, 19, 18394–18399 RSC.
- R. Hou, V. Shynkar, C. Lafargue, R. Kolkowski, J. Zyss and F. Lagugné-Labarthet, Second harmonic generation from gold meta-molecules with three-fold symmetry, Phys. Chem. Chem. Phys., 2016, 18, 7956–7965 RSC.
- K. H. Kim, Low-index dielectric metasurfaces supported by metallic substrates for efficient second-harmonic generation in the blue-ultraviolet range, Phys. Chem. Chem. Phys., 2020, 22, 7300–7305 RSC.
- G. Cox, Biological applications of second harmonic imaging, Biophys. Rev., 2011, 3, 131–141 CrossRef PubMed.
- A. Dementjev, D. Rutkauskas, I. Polovy, M. Macernis, D. Abramavicius, L. Valkunas and G. Dovbeshko, Characterization of thymine microcrystals by CARS and SHG microscopy, Sci. Rep., 2020, 10, 17097 CrossRef CAS PubMed.
- C. Greenhalgh, N. Prent, C. Green, R. Cisek, A. Major, B. Stewart and V. Barzda, Influence of semicrystalline order on the second-harmonic generation efficiency in the anisotropic bands of myocytes, Appl. Opt., 2007, 46, 1852 CrossRef PubMed.
- P. Campagnola, Second harmonic generation imaging microscopy: Applications to diseases diagnostics, Anal. Chem., 2011, 83, 3224–3231 CrossRef CAS PubMed.
- P. J. Campagnola and C. Y. Dong, Second harmonic generation microscopy: Principles and applications to disease diagnosis, Laser Photonics Rev., 2011, 5, 13–26 CrossRef CAS.
- X. Chen, O. Nadiarynkh, S. Plotnikov and P. J. Campagnola, Second harmonic generation microscopy for quantitative analysis of collagen fibrillar structure, Nat. Protoc., 2012, 7, 654–669 CrossRef CAS PubMed.
- A. Golaraei, L. Kontenis, K. Mirsanaye, S. Krouglov, M. K. Akens, B. C. Wilson and V. Barzda, Complex Susceptibilities and Chiroptical Effects of Collagen Measured with Polarimetric Second-Harmonic Generation Microscopy, Sci. Rep., 2019, 9, 1–12 CAS.
- M. Rivard, C.-A. Couture, A. K. Miri, M. Laliberté, A. Bertrand-Grenier, L. Mongeau and F. Légaré, Imaging the bipolarity of myosin filaments with Interferometric Second Harmonic Generation microscopy, Biomed. Opt. Express, 2013, 4, 2078 CrossRef PubMed.
- A. Golaraei, K. Mirsanaye, Y. Ro, S. Krouglov, M. K. Akens, B. C. Wilson and V. Barzda, Collagen chirality and three-dimensional orientation studied with polarimetric second-harmonic generation microscopy, J. Biophotonics, 2019, 12, e201800241 CrossRef PubMed.
- M. Samim, S. Krouglov and V. Barzda, Double Stokes Mueller polarimetry of second-harmonic generation in ordered molecular structures, J. Opt. Soc. Am. B, 2015, 32, 451 CrossRef CAS.
- L. Kontenis, M. Samim, A. Karunendiran, S. Krouglov, B. Stewart and V. Barzda, Second harmonic generation double Stokes Mueller polarimetric microscopy of myofilaments, Biomed. Opt. Express, 2016, 7, 559 CrossRef PubMed.
- S. Krouglov and V. Barzda, Three-dimensional nonlinear Stokes-Mueller polarimetry, J. Opt. Soc. Am. B, 2019, 36, 541 CrossRef CAS.
-
L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University Press, 2009 Search PubMed.
- B. M. Bulheller, A. Rodger and J. D. Hirst, Circular and linear dichroism of proteins, Phys. Chem. Chem. Phys., 2007, 9, 2020 RSC.
- D. Abramavicius and S. Mukamel, Chirality-induced signals in coherent multidimensional spectroscopy of excitons, J. Chem. Phys., 2006, 124, 034113 CrossRef PubMed.
-
D. P. Craig and T. Thirunamachandran, Molecular Quantum Electrodynamics: An Introduction to Radiation-molecule Interactions, Academic Press, 1984 Search PubMed.
-
R. E. Blankenship, Molecular Mechanisms of Photosynthesis, Wiley Blackwell, Oxford, UK, Chichester, UK, Hoboken, USA, 2nd edn, 2014, p. 296 Search PubMed.
- G. Garab and H. van Amerongen, Linear dichroism and circular dichroism in photosynthesis research, Photosynth. Res., 2009, 101, 135–146 CrossRef CAS PubMed.
-
S. S. Mukamel, Principles of nonlinear optical spectroscopy, Oxford University Press, New York, 1995 Search PubMed.
-
Second Harmonic Generation Imaging, ed. Pavone, F. S. and Campagnola, P. J., CRC Press, 2016 Search PubMed.
-
N. Bloembergen, Nonlinear Optics, World Scientific Publishing Company, 4th edn, 1996 Search PubMed.
- D. L. Andrews, D. P. Craig and T. Thirunamachandran, Molecular quantum electrodynamics in chemical physics, Int. Rev. Phys. Chem., 1989, 339–383 Search PubMed.
- E. A. Power and T. Thirunamachandran, Circular dichroism: A general theory based on quantum electrodynamics, J. Chem. Phys., 1974, 60, 3695–3701 CrossRef CAS.
- T. Helgaker, S. Coriani, P. Jørgensen, K. Kristensen, J. Olsen and K. Ruud, Recent advances in wave function-based methods of molecular-property calculations, Chem. Rev., 2012, 112, 543–631 CrossRef CAS PubMed.
- R. Dick, Analytic sources of inequivalence of the velocity gauge and length gauge, Phys. Rev. A, 2016, 94, 062118 CrossRef.
- D. Bauer, D. B. Miloevi and W. Becker, Strong-field approximation for intense-laser atom processes: The choice of gauge, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 023415 CrossRef.
- J. Zhang and T. Nakajima, Influence of Coulomb potential for photoionization of H atoms in an elliptically polarized laser field: Velocity gauge versus length gauge, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 043417 CrossRef.
- D. H. Friese and K. Ruud, Three-photon circular dichroism: Towards a generalization of chiroptical non-linear light absorption, Phys. Chem. Chem. Phys., 2016, 18, 4174–4184 RSC.
- M. Kamiński, J. Cukras, M. Pecul, A. Rizzo and S. Coriani, A computational protocol for the study of circularly polarized phosphorescence and circular dichroism in spin-forbidden absorption, Phys. Chem. Chem. Phys., 2015, 17, 19079–19086 RSC.
- C. C. Chirila and M. Lein, Strong-field approximation for harmonic generation in diatomic molecules, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 023410 CrossRef.
- D. Abramavicius, B. Palmieri, D. D. D. V. Voronine, F. Šanda, S. Mukamel, F. Sanda, S. Mukamel, F. Šanda and S. Mukamel, Coherent multidimensional optical spectroscopy of excitons in molecular aggregates; quasiparticle versus supermolecule perspectives, Chem. Rev., 2009, 109, 2350–2408 CrossRef CAS PubMed.
- H. Larsen, J. Olsen, C. Hättig, P. Jørgensen, O. Christiansen and J. Gauss, Polarizabilities and first hyperpolarizabilities of HF, Ne, and BH from full configuration interaction and coupled cluster calculations, J. Chem. Phys., 1999, 111, 1917–1925 CrossRef CAS.
- W. Moffitt, Optical Rotatory Dispersion of Helical Polymers, J. Chem. Phys., 1956, 25, 467–478 CrossRef CAS.
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Serguei
Krouglov
*a,
Serguei
Krouglov
 bc and
Virginijus
Barzda
bc and
Virginijus
Barzda
 bcd
bcd
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt), with amplitude Aω and frequency ω, we can determine various non-linear effects. By denoting the corresponding oscillatory dipole evolution as follows:
cos(ωt), with amplitude Aω and frequency ω, we can determine various non-linear effects. By denoting the corresponding oscillatory dipole evolution as follows:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt) + a2
cos(ωt) + a2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2ωt) + …
cos(2ωt) + …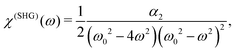
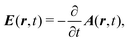
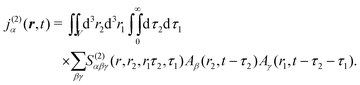
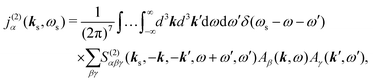
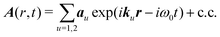
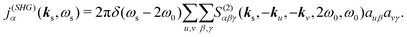
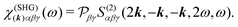
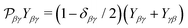 is the permutation operator. In the following Sections 4 and 5 we will consider such collinear setup.
is the permutation operator. In the following Sections 4 and 5 we will consider such collinear setup.
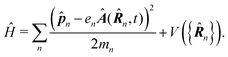
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) n is the n-th particle momentum operator, mn its mass, en – its charge, V({
n is the n-th particle momentum operator, mn its mass, en – its charge, V({![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n}) is the many-particle molecule potential energy depending on the positions of all particles {
n}) is the many-particle molecule potential energy depending on the positions of all particles {![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n} ≡
n} ≡ ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) 1,
1,![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) 2…. Â(
2…. Â(![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n,t) is the vector potential at the position of n-th particle. The first term is the field-affected kinetic energy operator. The second term includes all interactions between charged particles without involving the external field. The kinetic energy (
n,t) is the vector potential at the position of n-th particle. The first term is the field-affected kinetic energy operator. The second term includes all interactions between charged particles without involving the external field. The kinetic energy (![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) − eÂ)2 =
− eÂ)2 = ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) 2 − 2e
2 − 2e![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) ·Â + e2|Â|2 contains the material
·Â + e2|Â|2 contains the material ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) 2 term, related to isolated material system. Together with V({
2 term, related to isolated material system. Together with V({![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n}) this term describes the isolated molecule. The system-field interaction is of two types. The
n}) this term describes the isolated molecule. The system-field interaction is of two types. The ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) ·Â term constitutes the first type of molecule-field interaction due to induced current, while the |Â|2 term is the second type of interaction, related to absolute charge density. Additionally, notice that
·Â term constitutes the first type of molecule-field interaction due to induced current, while the |Â|2 term is the second type of interaction, related to absolute charge density. Additionally, notice that ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) and Â(
and Â(![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) ) in general do not commute due to dependence of vector potential on space, however, to first order in wavevector, permutation of these operators yields a constant shift of the vector potential that does not contribute to system-field interaction. In the commonly used semiclassical description the field is taken to be classical c-number and the complete Hamiltonian is then as follows
) in general do not commute due to dependence of vector potential on space, however, to first order in wavevector, permutation of these operators yields a constant shift of the vector potential that does not contribute to system-field interaction. In the commonly used semiclassical description the field is taken to be classical c-number and the complete Hamiltonian is then as follows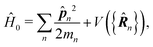
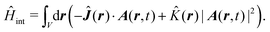
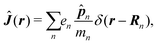
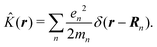
![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (r), given by absolute charge density. Accordingly, the vector potential A(r,t) is conjugate to Ĵ(r) and the scalar field |A(r,t)|2 is conjugate to
(r), given by absolute charge density. Accordingly, the vector potential A(r,t) is conjugate to Ĵ(r) and the scalar field |A(r,t)|2 is conjugate to ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (r). The scalar field part can be combined with electromagnetic scalar potential,33 however, |A(r,t)|2 should not be neglected in general for nonlinear response. In the following we refer to the two types of coupling as pA type and K-type.
(r). The scalar field part can be combined with electromagnetic scalar potential,33 however, |A(r,t)|2 should not be neglected in general for nonlinear response. In the following we refer to the two types of coupling as pA type and K-type.
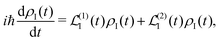
![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) , we have:
, we have:![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) I(t) = eiĤ0t/ħ
I(t) = eiĤ0t/ħ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) (t)e−iĤ0t/ħ,
(t)e−iĤ0t/ħ,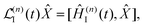
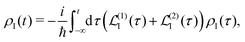
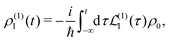
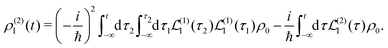
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ) and its expectation value by y(r,t). In principle Ŷ(
) and its expectation value by y(r,t). In principle Ŷ(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ) can be an arbitrary operator, related to the detection apparatus. So at the second order to the field we find:
) can be an arbitrary operator, related to the detection apparatus. So at the second order to the field we find: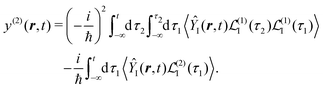
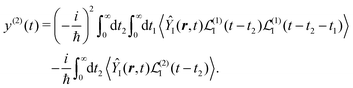
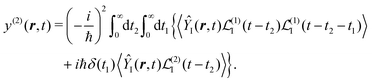
 and
and  . Using
. Using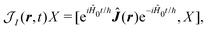
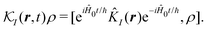
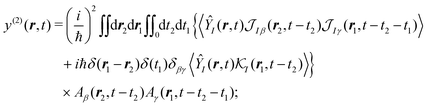
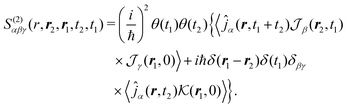
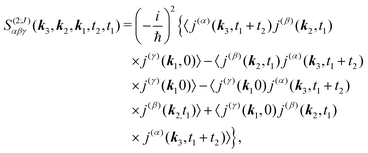
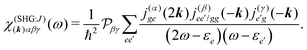
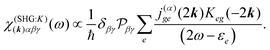
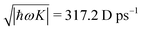 , what seems to be a very significant value. However this value does not contribute to the response (as it is the property of the isolated ground state) and it only shifts the absolute energy. In Appendix A we find expression to first order in wavevector, which indeed contributes to the SHG as we show in Section 5.
, what seems to be a very significant value. However this value does not contribute to the response (as it is the property of the isolated ground state) and it only shifts the absolute energy. In Appendix A we find expression to first order in wavevector, which indeed contributes to the SHG as we show in Section 5.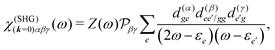
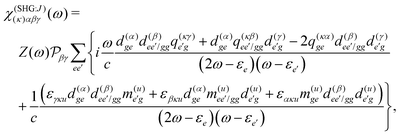
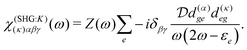
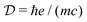 , having the units of dipole moment, equal to 0.0185 D, κ is the wavevector polarization component. εuvw is the Levi-Civita symbol, which expresses the cross product. We thus have the expressions in the dipole approximation and beyond the dipole approximation having the same dimensions and thus can be directly used for comparing various contributions.
, having the units of dipole moment, equal to 0.0185 D, κ is the wavevector polarization component. εuvw is the Levi-Civita symbol, which expresses the cross product. We thus have the expressions in the dipole approximation and beyond the dipole approximation having the same dimensions and thus can be directly used for comparing various contributions.
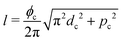 . The following are the excitation parameters of the units. These are the orientations of dipoles (transition and permanent) in the cylinder coordinate system. It is sufficient to define physical parameters of the single site and then all sites will be obtained from that one by applying rotation and translation operations.
. The following are the excitation parameters of the units. These are the orientations of dipoles (transition and permanent) in the cylinder coordinate system. It is sufficient to define physical parameters of the single site and then all sites will be obtained from that one by applying rotation and translation operations.
![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) n where
n where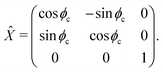
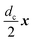 on site n = 0, the corresponding points of all sites are then expressed by simultaneous rotation and translation operations:
on site n = 0, the corresponding points of all sites are then expressed by simultaneous rotation and translation operations: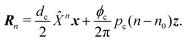
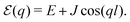
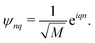
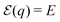 . Both cases will be studied separately.
. Both cases will be studied separately.![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) nD0(…). So we find that for the response of the whole macromolecule the important contributions include: the dipole and quadrupole contributions for the electronic ground state, the transition amplitudes, and the excited state permanent and transition amplitudes.
nD0(…). So we find that for the response of the whole macromolecule the important contributions include: the dipole and quadrupole contributions for the electronic ground state, the transition amplitudes, and the excited state permanent and transition amplitudes.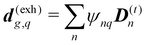 the result splits into two groups. For exciton q = 0 a real-value transition dipole moment is d(exh)g,q=0 = M1/2zD(t)0z, while for condition ql ± ϕc = 0 we find the complex-value perpendicular dipoles
the result splits into two groups. For exciton q = 0 a real-value transition dipole moment is d(exh)g,q=0 = M1/2zD(t)0z, while for condition ql ± ϕc = 0 we find the complex-value perpendicular dipoles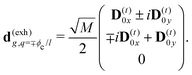
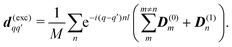
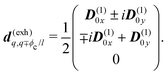
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ0,cos
φ0,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ0) and D(t)0 = (0,sin
φ0) and D(t)0 = (0,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1,cos
φ1,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1), while D(1)0 = 1.1D(0)0. Properties of all other sites are obtained from the zero-th site by translation and rotation operations.
φ1), while D(1)0 = 1.1D(0)0. Properties of all other sites are obtained from the zero-th site by translation and rotation operations.
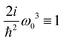 . Note, different ranges of the amplitude values for the color-bars.
. Note, different ranges of the amplitude values for the color-bars.
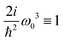 .
.
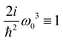 .
.
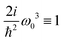 .
.![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) iEi −
iEi − ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) ij∇iEj −
ij∇iEj − ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) iBi.
iBi.![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) , quadrupole
, quadrupole ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) and magnetization
and magnetization ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) operators. This Hamiltonian is not complete at higher orders. More complicated B2 contributions appear25 that could contribute to e.g. SHG. Instead of using many terms in interaction Hamiltonian, we choose to use more simple minimal coupling interaction Hamiltonian. Instead of five terms of full interaction Hamiltonian in PE representation we have only two terms and thus our response function becomes relatively compact. However, even using the Coulomb gauge, the vector potential is still not experimentally observable quantity and retains freedom of the reference. The experimentally measurable quantities are the electric and magnetic fields, E and B. They are related to derivatives of the vector potential. An arbitrary constant vector can thus be added to the vector potential and could in principle affect definition of the optical response. In principle this amounts to redefining the material momentum operator, the absolute reference point of the energy and the overall optical response should remain unaffected.
operators. This Hamiltonian is not complete at higher orders. More complicated B2 contributions appear25 that could contribute to e.g. SHG. Instead of using many terms in interaction Hamiltonian, we choose to use more simple minimal coupling interaction Hamiltonian. Instead of five terms of full interaction Hamiltonian in PE representation we have only two terms and thus our response function becomes relatively compact. However, even using the Coulomb gauge, the vector potential is still not experimentally observable quantity and retains freedom of the reference. The experimentally measurable quantities are the electric and magnetic fields, E and B. They are related to derivatives of the vector potential. An arbitrary constant vector can thus be added to the vector potential and could in principle affect definition of the optical response. In principle this amounts to redefining the material momentum operator, the absolute reference point of the energy and the overall optical response should remain unaffected.
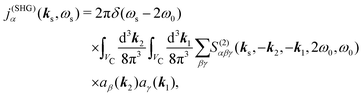
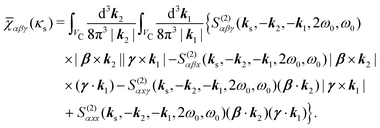
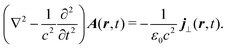
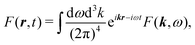
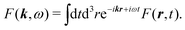
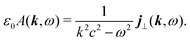
 , and the induced magnetization,
, and the induced magnetization,  ,
,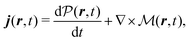
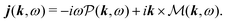
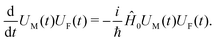
![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) n(t) = UM(−t)
n(t) = UM(−t)![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) nUM(t) with
nUM(t) with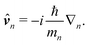
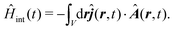
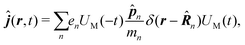
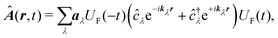
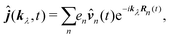
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n =
n = ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n0 + R0, we find
n0 + R0, we find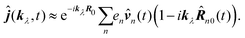
![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) n(t) = d
n(t) = d![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) n0(t)/dt. Using vector decomposition A × B × C = B(A·C) − C(A·B) we obtain
n0(t)/dt. Using vector decomposition A × B × C = B(A·C) − C(A·B) we obtain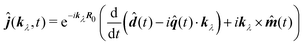
![[d with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0064_0302.gif) (ω) − i
(ω) − i![[q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0071_0302.gif) (ω)·kλ) + ikλ ×
(ω)·kλ) + ikλ × ![[m with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006d_0302.gif) (ω)).
(ω)).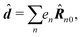
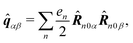
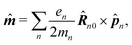
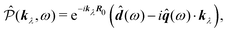
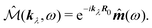
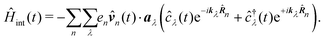
![[d with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0064_0302.gif) (ω) − i
(ω) − i![[q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0071_0302.gif) (ω)·kλ) + ikλ ×
(ω)·kλ) + ikλ × ![[m with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006d_0302.gif) (ω)),
(ω)),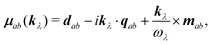
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) entering the magnetic moment is imaginary compared to the coordinate. Thus, the magnetic moment enters at the same level as the quadrupole moment.
entering the magnetic moment is imaginary compared to the coordinate. Thus, the magnetic moment enters at the same level as the quadrupole moment.
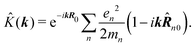
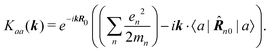
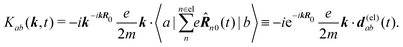
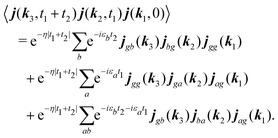
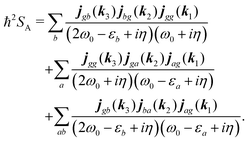
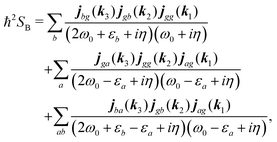
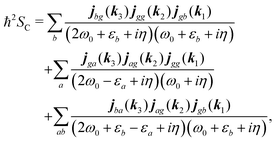
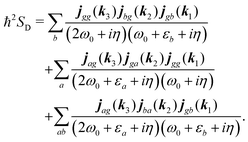
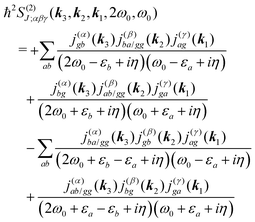
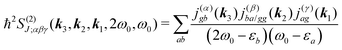
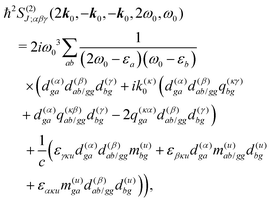
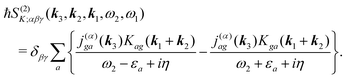
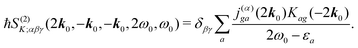
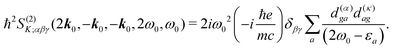
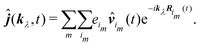
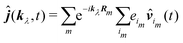
![[D with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0044_0302.gif) m.
m.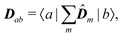
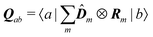
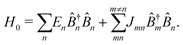
![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) †m and
†m and ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) m are excitation creation and annihilation operators (we make an assumption that the unit can be described by a single optical transition). Set of states of such macromolecule consists of the ground state |0〉 and excited states |e〉, also given in terms of localized excitations of different units:
m are excitation creation and annihilation operators (we make an assumption that the unit can be described by a single optical transition). Set of states of such macromolecule consists of the ground state |0〉 and excited states |e〉, also given in terms of localized excitations of different units: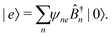
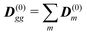 , transition dipoles
, transition dipoles 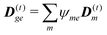 , and net dipoles of the excited state manifold
, and net dipoles of the excited state manifold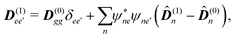
![[D with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0044_0302.gif) m|0〉 is the ground state dipole of unit m, D(t)m = 〈0|
m|0〉 is the ground state dipole of unit m, D(t)m = 〈0|![[D with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0044_0302.gif) m
m![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) †m|0〉 is its transition dipole and D(1)m = 〈0|
†m|0〉 is its transition dipole and D(1)m = 〈0|![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) m
m![[D with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0044_0302.gif) m
m![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) †m|0〉 – its excited state permanent dipole. The corresponding quadrupole matrix elements are
†m|0〉 – its excited state permanent dipole. The corresponding quadrupole matrix elements are 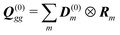 , transition quadrupoles
, transition quadrupoles 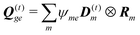 , and the net quadrupoles of the excited state manifold
, and the net quadrupoles of the excited state manifold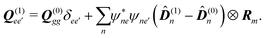
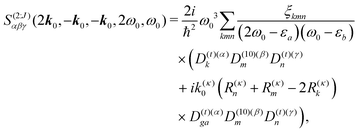
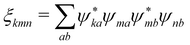 and D(10)m = D(1)m − D(0)m. Independence of the coordinate origin is now clearly expressed as well as importance of excitonic delocalization. For the localized excitations we have ξkmn = δkmδmn and quadrupolar contributions vanish due to coordinate cancelation.
and D(10)m = D(1)m − D(0)m. Independence of the coordinate origin is now clearly expressed as well as importance of excitonic delocalization. For the localized excitations we have ξkmn = δkmδmn and quadrupolar contributions vanish due to coordinate cancelation.
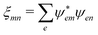 yields
yields