Examination of the short-range structure of molten salts: ThF₄, UF₄, and related alkali actinide fluoride systems

Abstract

The short-range structures of LiF–ThF₄, NaF–AnF₄, KF–AnF₄, and Cs–AnF₄ (An = Th, U), were probed using in situ high temperature Extended X-ray Absorption Fine Structure (EXAFS) spectroscopy. Signally, the EXAFS spectra of pure molten ThF₄ and UF₄ were measured for the first time. The data were interpreted with the aid of Molecular Dynamics (MD) and standard fitting of the EXAFS equation. As in related studies, a speciation distribution dominated by [AnF_x]^4−x (x = 7, 8, 9) coordination complexes was observed. The average coordination number was found to decrease with the increasing size of the alkali cation, and increase with AnF₄ content. An average coordination number close to 6, which had not been detected before in melts of alkali actinide fluorides, was seen when CsF was used as solvent.

---

1 Introduction

Molten salts are a class of ionic liquids which have in recent years been the focus of extensive fundamental research. This can be explained by the fact that they are a versatile class of reaction media, e.g. carbonates, nitrates, fluorides, chlorides, with a variety of melting points, heat capacities, vapor pressures, densities, and other thermophysical properties suited for a variety of industrial applications. The most well-known is perhaps the production of materials as important as aluminum and sulfuric acid, yet thermal energy storage is also a notable application. In the future, molten salts may be used for processes as important as the production of hydrogen¹ and ammonia,² carbon capture and storage,³ nuclear fuel pyroprocessing,⁴ and as nuclear fuels.^5,6

Understanding the speciation and structure of the molten salts, which are closely related to their thermodynamic and transport properties, is crucial for the design and operation of any intended application. Salt systems which have been subject of this type of analysis in the literature include AF–ZrF₄ (A = Li, Na, K),⁷ KF–ThF₄,⁸ LiF–ThF₄⁹ and LiF–ThF₄–UF₄ systems.¹⁰ In these studies, the experimental technique used is in situ high temperature Extended X-ray Absorption Fine Structure (EXAFS) spectroscopy. This element-specific, non-destructive, oxidation state-sensitive technique requires very small masses of sample, making it very powerful and ideally suited for radioactive, corrosive salts at high temperature. It provides detailed information about the local structure such as interatomic distances among nearest neighbors and second-nearest neighbor elements.

However, EXAFS spectroscopy of liquids is less straightforward than that of solids because the standard EXAFS equation¹¹ may be inaccurate to describe the measured experimental data since it relies on a Gaussian distribution of interatomic distances, which liquids do not have. Another approach, known as cumulant expansion, is also inadequate because of a strong correlation between the fitting parameters.^8,12,13 Hence, this work relied on configurations generated from Molecular Dynamics (MD) simulations as the underlying structural models. MD has demonstrated already in numerous studies to be a strikingly valuable tool in its own right for calculating the thermo-physical and thermo-chemical properties of molten salts.^14–17 In other works, our group has presented EXAFS data of the LiF–ThF₄,⁹ LiF–UF₄ (submitted), and NaF–ThF₄⁹ systems. In order to arrive at a comprehensive picture of the local structure of alkali actinide fluoride binary systems as a function of the alkali and actinide ions, this work extends to NaF–UF₄ and focuses on larger alkali ions: KF–ThF₄, KF–UF₄, CsF–UF₄, and CsF–ThF₄. Notably, EXAFS data for pure molten ThF₄ and UF₄ were collected for the first time.

2 Experimental method

EXAFS measurements were performed at the INE beamline¹⁸ of the KARA (Karlsruhe Research Accelerator) synchrotron facility (Karlsruhe, Germany), with 2.5 GeV and 150–170 mA as operating conditions in the storage ring. The beamline uses a Ge(422) double-crystal monochromator (DCM). Rh-coated mirrors before (flat, cylindrically bent) and after (toroidal) the DCM are used to collimate and focus the synchrotron beam, respectively, producing a spot size of 300 mm × 500 mm at the sample surface. Transmission and fluorescence geometries could be measured in unison, and samples were probed at the L₃ edges of Th (16.300 keV) and U (17.166 keV), scanning from ∼16.1 to ∼17.05 keV and ∼17.14 to ∼17.77 keV, respectively.

A dedicated experimental set-up, previously described in detail by Smith et al.⁹ and built to operate at the INE beamline, was used for the measurements. The set-up consists of a specifically designed furnace inside a custom-made glovebox. The salts themselves were sealed in pre-dried boron nitride containment cells loaded into the furnace chamber, which was evacuated under operation down to ∼2 × 10⁻⁵ mbar to avoid reaction of the salts with residual oxygen or water. Once under vacuum, the samples were heated up to (50 ± 10) K above their liquidus temperatures. Quick scans were made during the heating ramp to detect the melting of the material. If the measurement temperature of the sample was less than the melting point of the pure alkali fluoride end-member, the temperature was ramped up to the melting point of the end-member and held for about 15 minutes to ensure complete melting and homogenization. The temperature was subsequently adjusted to a set value (50 ± 20) K above liquidus. In addition, an equilibration time of ∼15–30 min was employed before collecting the X-ray Absorption Spectroscopy (XAS) data to ensure the signal had stabilized. EXAFS data were collected up to ∼12.5 Å, and were Fourier transformed using the Hanning window over the k-range 3–12 Å⁻¹ (dk = 2) for solids, and 3–9 Å⁻¹ (dk = 2) for liquids. A step size of 0.8 eV was used in the X-ray absorption near edge structure (XANES) region.

The samples (8–25 mg) were prepared by mixing and grinding stoichiometric amounts of metal fluorides in the desired stoichiometric ratio, and then pressed in the form of pellets of thickness less than 100 mm by applying a pressure of 10 tons cm⁻². Sodium, potassium, and cesium fluorides were sourced from Alfa Aesar (99.99%, metals basis) and dried at 673 K for 4 h in an open nickel boat under Ar flow. The thorium fluoride was supplied by the Joint Research Center, Karlsruhe, Germany, (0.995 ± 0.005), synthesized as described in ref. 19. The UF₄ was obtained from International Bio-Analytical Industries (0.9999 ± 0.0001 metals basis). All the samples in this work were handled in the inert and dry atmosphere of an argon-filled glovebox (H₂O and O₂ contents below 5 ppm), and in a nitrogen atmosphere when handled in the self-designed glovebox containing the furnace set-up at the KARA-INE beamline.

Each liquid-state scan took close to 30 minutes, and three to four scans were accumulated to be averaged. The energy E₀ of the edge absorption threshold position was identified as the first x-intercept of the second derivative of the signal, which also corresponds to the first inflexion point of the signal. Before averaging, the spectra were aligned with the XANES spectrum of an appropriate reference: a ThO₂–BN pellet in the case of AF–ThF₄ (A = Li, Na, K, Cs) and ThF₄, a metallic yttrium (K edge = 17.0384 keV) plate in the case of AF–UF₄ (A = Na, K, Cs). A UO₂–BN pellet was used as reference for the UF₄ sample at room temperature. The references were located between the second and third ionization chambers and measured simultaneously with the sample. Data treatment of the raw XAS data was done with the ATHENA software,²⁰ version 9.25. The XANES data were analyzed to confirm that the actinide cations remained tetravalent (refer to ESI†).

Fitting of the treated data with the standard EXAFS equation was done with Artemis software,²⁰ version 0.8.012. No third-order cumulant parameter was used. The use of the standard EXAFS equation on liquids has limitations, since liquids are highly disordered and display strong anharmonicity. Moreover, the coordination number and distance to nearest neighbor distributions are lost, replaced by averages. To complement the information obtained with fitting, this work has also relied on MD simulations.

3 Molecular dynamics simulations

MD simulations were performed using the PIMAIM code¹⁴ for all compositions measured by EXAFS at the corresponding experimental temperature: 50 K above the liquidus line. The form of the potential used for the study of these molten salt systems is the Polarizable Ion Model (PIM).²¹ It has been chosen because it has already shown its usefulness in the study of several molten systems such as alkali fluoride mixtures,²¹ LiF–BeF₂,¹⁷,²² AF–ZrF₄ (A = Li, Na, K),⁷ LiF–UF₄,²³ and LiF–ThF₄.¹⁶ The potential has four contributions with functional forms given in eqn (1)–(5): charge–charge (eqn (1)), dispersion (eqn (2)), overlap repulsion (eqn (4)) and polarization (eqn (5)).

• Charge–charge:

where q denotes the ionic formal charges.

• Dispersion:

where C_ij⁶(r_ij) is the dipole–dipole dispersion coefficient and C_ij⁸(r_ij) is the dipole–quadrupole dispersion coefficient, while f_ij⁶(r_ij) and f_ij⁸(r_ij) are Tang-Toennies dispersion damping functions; they are short-range corrections to the asymptotic multipole expansion of dispersions:²⁴

This work only consider dipoles and quadrupoles.

• Overlap repulsion

Here A_ij and a_ij are fitting parameters.

• Polarization

In the equation above, T_α⁽¹⁾ is the charge–dipole interaction tensor, T_αβ⁽²⁾ is the dipole–dipole interaction tensor, α_i is the polarizability of ion i, and μ_i is the set of dipoles, while g_ij(r_ij) is a damping function given by eqn (6):

The parameters were taken from different sources, and are listed in Tables 1, 2 and 3. Aside from LiF–ThF₄, the parameters were not derived ab initio especially for the binary systems in this work, but rather for other fluoride-based ionic systems (e.g. pure alkali fluorides).

Table 1 Parameter values of the pair-wise ionic interactions in the PIM potential used in this work, with values in atomic units

Ion pair	A ij	a ij	C ij ^6	C ij ^8	b ij ^6	b ij ^6	Source
F^−–F^−	282.3	2.44	15	150	1.9	1.9	16
F^−–U^4+	70.623	1.666	38.7	387	1.9	1.9	23
F^−–Th^4+	70.148	1.634	38.7	387	1.9	1.9	16
F^−–Na^+	52.83	1.97	13.25	88.15	1.9	1.9	25
F^−–K^+	138.8	2.043	3.9	38.7	1.9	1.9	25
F^−–Cs^+	151.12	1.874	10.95	109.5	1.9	1.9	21
An^4+–An^4+	1	5	100	1000	1.9	1.9	23
Th^4+–Li^+	1	5	3.16	31.6	1.9	1.9	23
Th^4+–Na^+	1	5	0.001	0.001	1.9	1.9	17, 21 and 26
U^4+–Na^+	1	5	10	100	1.9	1.9	21, 25 and 27
An^4+–A^+ (An = U, Th; A = K, Cs)	1	5	10	100	1.9	1.9	21 and 27
Na^+–Na^+	1	5	11.7	5.18	1.9	1.9	25
K^+–K^+	1	5	1	10	1.9	1.9	25
Cs^+–Cs^+	5000	3	8	80	1.9	1.9	28

---

Table 2 Pair-wise damping terms in the PIM potential used in this work

Interaction	b ^D ij	c ^D ij		Source
a Modified from c^DUF = −0.84905 in ref. 23. b Not defined elsewhere, set arbitrarily.
F^−–U^4+	b ^DFU = b^DUF = 1.7516	c ^DFU = 1.8148	c ^DUF = 0.84905^a	23
F^−–Th^4+	b ^DFU = b^DUF = 1.938	c ^DFU = 2.791	c ^DUF = −0.60906	16
F^−–Na^+	b ^DFNa = b^DNaF = 1.84	c ^DFNa = 2.54	c ^DNaF = −0.19	25
F^−–K^+	b ^DFK = b^DKF = 1.75	c ^DFK = 2.5	c ^DKF = −0.31	25
F^−–Cs^+	b ^DFCs = b^DCsF = 1.93	c ^DFCs = 3.391	c ^DCsF = 0.485	28
An^4+–A^+^b	b ^DAnA = 10.0	c ^DAAn = 0.001	—	—

---

Table 3 Polarizabilities of the ions used in the MD simulations, atomic units

Ion	Polarizability	Ref.
F^−	7.8935	16
U^4+	5.8537	23
Th^4+	7.696	16
Na^+	0.991	25
K^+	5.0	21
Cs^+	14.8	28

---

The systems were equilibrated for 500 ps in the NPT ensemble at 0 GPa and the corresponding temperature 50 K above the liquidus (Table 5), from which the equilibrium volume was taken. This was followed by a 100 ps equilibration and finally a 500 ps production run in the NVT ensemble at the same temperature. Time steps in all runs were set to 0.5 fs, while the relaxation time for both the Nosé–Hoover thermostat and barostat (for the NPT run) was set to 10 ps. The cubic simulation cell contained 600–800 ions in periodic boundary conditions. Cut-offs for the real space part of the Ewald sum and short-range potential were both set to less than half the length of the cell. After the production run, the extracted MD trajectories were used as input for the ab initio code FEFF8.40²⁹ to compute a simulated EXAFS spectrum, to be compared with experimental data. The effect of anharmonic vibrations and Debye–Waller factor were accounted for by accumulating about 25 000 ionic coordinates as input.

4 Results and discussion

4.1 Local structure of uranium and thorium tetrafluoride

4.1.1 Solid vs. liquid states. The suitability of the experimental set-up was originally tested on ThF₄(cr) at room temperature as reported in ref. 9. In a later campaign the EXAFS spectrum of UF₄(cr) was collected and is shown in Fig. 1a and b. Fitting of the latter data (in green) was made using the neutron diffraction refinement by Kern et al.³⁰ as a structural model. The spectra of molten UF₄ (T = 1357 K, also shown in Fig. 1a and b) and ThF₄ (T = 1433 K, Fig. 2) were also collected.

Fig. 1 (a) Experimental (fluorescence, room temperature: □, transmission, T = 1357 K: ■), fitted (green, blue) and simulated (red) k²χ(k) oscillations of UF₄. (b) Fourier transform moduli |χ(R)| of the EXAFS spectra.

Fig. 2 (a) Experimental (transmission, room temperature: □, transmission, T = 1433 K: ■), fitted (green, blue) and simulated (red) k²χ(k) oscillations of ThF₄. (b) Fourier transform moduli |χ(R)| of the EXAFS spectra. Room temperature experimental data and fit taken from Smith et al.⁹

Uranium tetrafluoride is isostructural with thorium tetrafluoride, with space group C2/c. There are two uranium sites, both 8-coordinated, with U–F distances within ∼0.1 Å  of each other (see Table 4). In EXAFS, the threshold above which it is possible to discriminate between neighboring shells depends on the k-range of the spectra, Δk, as ΔR = π/(2Δk). For the solid-state measurement in Fig. 1a, ΔR = 0.17 Å. This means that the resolution in this case is not sufficient to distinguish between more than one U–F first coordination shell and more than one U–U second-nearest neighbor shell, so only one of each was included in the fit. The results are summarized in Table 4 and compared with the structural model used. The bond lengths are within error of each other.

Table 4 Local environment around uranium as derived from the present study using EXAFS spectroscopy (room temperature), compared with neutron data from ref. 30. CN is the coordination number, σ² is the Debye–Waller factor, ΔE₀ = 4.8(4) eV is the energy shift from the L₃ edge, R_f = 0.014 is the goodness of fit. Standard deviations are given in parentheses

Bond	CN	R/Å	σ ^2/Å^2
Neutron data from ref. 30
U1–F6	2	2.256(4)
U1–F4	2	2.268(4)
U1–F7	2	2.280(4)
U1–F3	2	2.328(4)
U2–F5	1	2.237(2)
U2–F1	1	2.247(2)
U2–F7	1	2.273(2)
U2–F6	1	2.281(2)
U2–F3	1	2.286(2)
U2–F5	1	2.288(2)
U2–F2	1	2.308(2)
U2–F4	1	2.313(2)
U1–U2	2	4.516(2)
U2–U2	2	4.510(2)
Averaged neutron data
U–F	8	2.28(2)
U–U	2	4.51(4)
EXAFS data
U–F	8	2.26(3)	0.008(6)
U–U	2	4.50(2)	0.0001(5)

---

In the molten state, the loss of long-range order gives rise to strong damping of the EXAFS signal, as can be seen in Fig. 1. The disorder is also manifest in the Fourier transform (FT) modulus of the signal, where the intensity of the first peak in the liquid state is much diminished with respect to that of the solid. Furthermore, the second shell of U neighbors, displayed by the crystal phase as a peak centered at ∼4.5 Å, can no longer be resolved in the liquid. The same is true in the case of ThF₄: the crystal has its second shell centered around ∼4.6 Å⁹ and in the liquid it is not visible anymore.

4.1.2 Structural models for liquids. Due to the caveats mentioned in the introduction regarding standard fits of the EXAFS equation for disordered states, MD simulations were used to generate atomic positions from which an EXAFS spectrum could be calculated, as described in Section 3. The large number of configurations allows to reproduce non-Gaussian features of the radial distribution function (RDF or g(r)), such as anharmonic vibrations. Despite the caveats, standard fits were included as well, and the MD results help illustrate why this was not an idle exercise. Fig. 3 shows the RDFs of molten UF₄ and ThF₄. It should be noticed that the first peak of the An–F RDFs, although certainly not Gaussian, can be modelled as having this behavior with reasonable accuracy. In contrast, modelling either the remaining peaks in the An–F RDFs or any peaks in the An–An and F–F distributions as Gaussian would be a poor approximation. In short, as long as the fitting of the standard EXAFS equation is limited to the first shell of a pair of species (in this case An–F with A = U, F) with a tail thin enough to resemble a Gaussian, then the fit may contribute useful quantitative information.

Fig. 3 Pairwise radial distribution functions of molten UF₄ and ThF₄ calculated with MD at T = 1357 K and T = 1433 K, respectively.

The EXAFS oscillations in the molten state become considerably noisy at high wavenumbers, but there is a fair agreement between the first three oscillations in the experimental k²χ(k) EXAFS signal, the simulation, and the fit. The MD-generated signals are slightly out of phase with the EXAFS signal, which in many cases translates into an over or underestimation of the radial distance of the maximum of |χ(R)|. The fits using the standard EXAFS equation match the phase and the intensity of the experimental signal more closely. However, the fits themselves were directed by the quantitative information which could be directly extracted from the MD trajectories, namely the coordination numbers (Table 5). These tended to be underestimated by the fitting algorithm, a common problem arising when fitting EXAFS signals of liquids.¹² Hence, if a fitting process is deemed appropriate for a given disordered system, it is good practice to combine it with another suitable structural model, e.g. MD, to gauge the results.

Table 5 Structural information of the first fluoride coordination shell around the actinide ion in different melts as calculated in this work, 50 K above the liquidus line. CN is the coordination number, σ² is the Debye–Waller factor, ΔE is the energy shift from the L₃ edge, R_f is the goodness of fit. Standard deviations are given in parentheses. The amplitude reduction factor was fixed as S₀² = 0.9

System	X(AnF4)^d	CNAn–F	CNAn–F	R An–F	R An–F	E[RAn–F]^b	E[RAn–F]^b	ΔE	σ ^2	R f	K/T^e
		MD	Fit	MD/Å	MD/Å	MD/Å	Fit/Å	Fit/eV	Fit/Å^2	Fit
a Most probable distance. b Expected value. c Bond cut-off = maximum An–F distance. d Standard uncertainty on the composition of starting reagents was u(X(AnF4)) = 0.005. e Standard uncertainty on the temperature is estimated to be u(T) = 20 K.
LiF–ThF4	0.10	7.88		2.21	3.14	2.32	2.34(1)	4(1)	0.020(6)	0.056	1133
	0.25	7.73		2.22	3.15	2.26	2.32(1)	4.59(72)	0.02(2)	0.015	973
	0.50	7.78		2.22	3.15	2.33	2.31(1)	1.31(79)	0.02(3)	0.027	1193
NaF–ThF4	0.33	7.52	7.4(4)	2.21	3.17	2.31	2.30(1)	6.75(43)	0.020(1)	0.016	1073
	0.50	7.89	7.8(8)	2.20	3.18	2.33	2.34(1)	4.08(86)	0.021(2)	0.035	1108
	0.67	7.83	7.9(7)	2.21	3.18	2.33	2.31(1)	2.52(77)	0.019(1)	0.024	1252
NaF–UF4	0.50	7.75	7.2(7)	2.15	3.07	2.27	2.26(1)	1.61(87)	0.020(2)	0.036	1033
	0.67	7.76	7.2(7)	2.16	3.05	2.27	2.23(1)	2.26(57)	0.019(2)	0.025	1153
KF–UF4	0.50	7.42	6.9(4)	2.13	3.09	2.25	2.26(1)	7.07(50)	0.020(1)	0.012	1098
	0.67	7.72	7.8(7)	2.16	3.07	2.27	2.23(1)	2.56(94)	0.02(2)	0.049	1090
KF–ThF4	0.167	7.12	7.0(7)	2.22	3.23	2.28	2.29(1)	3.71(94)	0.018(2)	0.033	1060
	0.33	6.99	6.5(8)	2.19	3.15	2.27	2.30(1)	2(1)	0.017(3)	0.048	1123
	0.50	7.53	7.6(8)	2.18	3.23	2.31	2.31(1)	3.17(92)	0.024(2)	0.040	1209
	0.67	7.70	8.0(4)	2.20	3.20	2.33	2.33(5)	−1(1)	0.020(3)	0.089	1266
CsF–ThF4	0.25	6.24	6.6(7)	2.15	3.16	2.21	2.29(1)	3.65(92)	0.020(2)	0.043	1301
	0.50	6.97	6.9(5)	2.14	3.25	2.27	2.33(1)	4.48(64)	0.016(1)	0.028	1201
CsF–UF4	0.25	6.2	7.0(6)	2.12	3.11	2.17	2.25(1)	7.48(78)	0.018(2)	0.027	1293
	0.50	7.14	7.8(6)	2.12	3.11	2.23	2.26(1)	2.75(71)	0.020(2)	0.019	1058
	0.67	7.46	8.2(8)	2.14	3.08	2.26	2.26(1)	−0.72(99)	0.021(2)	0.048	1191
ThF4	1	7.92	8.0(8)	2.26	3.17	2.34	2.32(1)	2.38(87)	0.020(2)	0.035	1433
UF4	1	7.94	8.0(7)	2.21	3.06	2.28	2.27(1)	3.52(71)	0.030(2)	0.031	1357

---

4.1.3 Features of the radial distribution functions. A key advantage of using MD as a complementary tool is that a more comprehensive picture of the salt structure emerges than with fitting alone. First, the RDFs in Fig. 3, nearly overlapping with each other, readily reveal that UF₄ and ThF₄ are isostructural melts, much like they are isostructural crystals. Second, it is seen that although there is long range order in the molten state, there is a structure of interlocking anionic and cationic coordination shells: three such An–F shells (centered at ∼2.2, ∼4.7, and ∼6.4 Å), are visible for each RDF before stabilizing around the mean value of g(r) = 1 (Fig. 3). There is a small but non-zero probability of having fluorides as first-nearest neighbors (FNN), yet the electric repulsion makes it is so unfavourable for actinides that such probability is zero. There is also a large probability of finding two actinides within a distance r < 2·R_{An–F,cutoff}, which is the basis for quantifying fluoride bridging between actinide centers, as detailed hereafter.

4.1.4 Coordination chemistry of molten thorium and uranium tetrafluorides. The principal coordination shell is the An–F shell which, despite the thermal disorder, is made up of fluorides tightly bound to the actinide cation. Table 5 lists three different distances to characterize the distribution of distances within this shell: a most probable (R_max, corresponding to the maximum of the RDF), a bond cut-off (R_cutoff, corresponding to the first minimum of the RDF), and the expected distance E[R], obtained on the one hand by fitting with the standard EXAFS equation and on the other by computing the expectation value between 0 and R_cutoff:

The spread between R_max,Th–F = 2.26 Å  and R_{cutoff,Th–F} = 3.17 Å  is 0.91 Å, hence more than 6 times greater than in the solid state (0.141 Å), as derived from neutron diffraction data.⁹ In the case of UF₄(l), R_{cutoff,Th–F} − R_max,U–F = (3.06–2.21) Å = 0.85 Å, about 12 times greater than in UF₄(cr) (0.072 Å, see Section 4.1.1 above). In that sense, there is an expansion of the coordination cage, as remarked by Bessada et al.¹⁰ Nevertheless, as Liu et al. suggested after finding R_max to be smaller than the sum of the Shannon radii of Th⁴⁺ and F⁻, there is a concordant strengthening of the local structure. Ocádiz-Flores et al.³¹ reported the same phenomenon by comparing solid phases occurring in the LiF–UF₄ system with the melts at the corresponding mole fractions. On average, the strengthening can be observed because even though longer bond lengths close to R_cutoff become available, shorter bond lengths close to R_max are much more populated, with the result that the average U–F distance in the liquid mixtures is equal to or shorter than in the solids. For ThF₄: E[R] = 2.26 < 2.324(19) Å  in the solid‡. For UF₄: E[R] = 2.28 = 2.28(2) Å  in the solid§.

Bessada et al.¹⁰ calculated average bond lengths in the LiF–ThF₄ melt as a function of coordination number, and the former are seen to consistently decrease as the latter increases. This can be explained mainly by an increased repulsion between the F⁻ ligands with increasing coordination. Decreased shielding from the 2nd shell, evidenced by the absence of an An–An peak in the plots of |χ(R)| (Fig. 1a and 2b), is likely to contribute to the shortening of the An–F distance as well.³² In the liquid phase, the coordination numbers are dominated by CN = 7, 8, 9, with an average close to 8, yet CN = 7 weighs more in the distribution than CN = 9 (see Table 6), allowing for tightening of the cage. It is 8 in the solid state. Finally, in the gas phase, where fluorides are not shared between actinide centers, it is found that E[R_Th–F,gas] = 2.08 Å,³³ and E[R_U–F,gas] = 2.017(5) Å.³⁴

Table 6 Coordination number distribution and expected CN of the EXAFS samples studied in this work

System	X(AnF4)	Anionic fraction [AnFx]^4−x					Expected value
		6	7	8	9	10	CN
LiF–ThF4	0.10	0.008	0.243	0.612	0.134	0.003	7.88
	0.25	0.037	0.322	0.518	0.121	0.004	7.73
	0.50	0.040	0.315	0.476	0.157	0.012	7.78
NaF–ThF4	0.33	0.055	0.432	0.442	0.070	0.002	7.52
	0.50	0.0271	0.271	0.505	0.184	0.0134	7.89
	0.67	0.0367	0.294	0.484	0.171	0.0137	7.83
NaF–UF4	0.5	0.036	0.323	0.503	0.133	0.006	7.75
	0.67	0.038	0.322	0.491	0.141	0.007	7.76
KF–ThF4	0.167	0.836	0.163	0.001	0.0	0	7.12
	0.33	0.233	0.551	0.206	0.010	5.85 × 10^−5	6.99
	0.5	0.089	0.396	0.412	0.098	0.005	7.53
	0.67	0.060	0.343	0.449	0.139	0.010	7.70
KF–UF4	0.5	0.106	0.440	0.388	0.065	0.002	7.42
	0.67	0.041	0.333	0.491	0.129	0.006	7.72
CsF–UF4	0.25	0.806	0.193	0.003	0.00	0.00	6.20
	0.5	0.209	0.475	0.283	0.033	7.48 × 10^−4	7.14
	0.67	0.103	0.422	0.392	0.079	0.003	7.46
CsF–ThF4	0.25	0.771	0.223	0.006	3.31 × 10^−5	0	6.24
	0.5	0.294	0.469	0.212	0.025	7.94 × 10^−4	6.97
ThF4	1	0.034	0.262	0.473	0.210	0.021	7.92
UF4	1	0.023	0.250	0.509	0.201	0.018	7.94

---

4.1.5 Structure beyond the first coordination sphere. Molten ThF₄ was described by Dai et al.³⁵ as a network of predominantly corner (∼69%), edge (∼27%), and face-sharing (<4%) [ThF_n]⁴⁻ (n = 6, 7, 8, 9…) polyhedra. 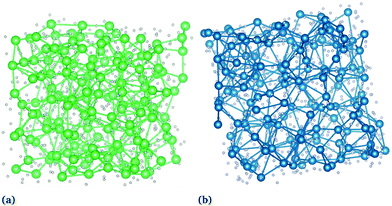In order to characterize the network of UF₄ and ThF₄ in this work, a linkage analysis was performed by defining a bridging fluoride as one which is part of the first coordination shell of two given An⁴⁺, while the distance between the two actinide centers is less than the minimum of their RDF (∼5.1 Å  for both actinides, Fig. 3). The network structure found for molten UF₄ with a distribution of 70% corner-sharing, 27% edge-sharing, and 3% face-sharing is very similar to that of ThF₄, confirming the view of the melt provided by the RDFs. An MD snapshot of the networks, emphasizing An–An connectivity, is shown in Fig. 4.

Fig. 4 (MD) snapshot of (a) molten UF₄ and (b) ThF₄ at the EXAFS measurement temperatures, T = 1357 K and 1433 K, respectively, emphasizing An–An connectivity (U: green, Th: blue). Fluoride ions shown in gray.

4.2 Local structure of the AF–UF₄ and AF–ThF₄ melts

4.2.1 Coordination environment of the alkali cations. As solids, all alkali fluorides crystallize in the rock salt structure (NaCl structure),³⁶ in which the coordination number is 6. In the molten state, alkali fluorides preserve their strong ionic character and local ordering, and on average have a coordination number close to 5,³² as can be seen in Fig. 5a. In mixtures, as the fluoroacidity of the melt increases with AnF₄ (An = Th, U) content, fluoride donation by the alkalis is evidenced by a growing A–F distance (Fig. 5a). The gap between the A–F distance in molten alkali actinide fluorides and pure AF melts grows in the order Li < Na < K < Cs. This growing distance is coupled with a substantial increase in the coordination number of the alkali cation (Fig. 5b). The general trends of the radial distance and coordination number of the alkali cations suggest that uranium molten fluorides are slightly more fluoroacidic than those of thorium, probably due to the actinide contraction.

Fig. 5 (a) Most probable A–F (A = Li, Na, K, Cs) distance and (b) average coordination number around the alkali cations in the (A,An)F_x solutions as a function of composition, calculated with MD in this work. Temperatures are variable; they are indicated in Table 6. For the pure AF melts, T = 1200 K for all except NaF with T = 1270 K (above the melting point).

4.2.2 Coordination environment of the actinide cations. This section presents EXAFS measurements carried out in the molten state for seven different alkali actinide fluoride systems at a few representative compositions. As above, accompanying the experimental data are the simulated EXAFS oscillations, generated as described in Section 3. The Fourier Transform moduli of the signals are shown alongside the EXAFS oscillations (Fig. 6–12). The features of the EXAFS spectra are similar to those of the end-members: damped sinusoidal oscillations, and |χ(R)| signals of which the only discernible peak is that of the An–F first solvation shell. The characteristics of this shell as studied with MD and with standard fitting are summarized in Table 5. The composition LiF : ThF₄ = (0.75 : 0.25) (Fig. 6), which can be singled out because of its importance as Molten Salt Fast Reactor (MSFR) fuel, is compared with data by Bessada et al.¹⁰ Although recorded at different temperatures, the spectra are comparable to each other. The experimental data for all compositions can be found in the ESI.†

Fig. 6 (a) Experimental (■, ref. 9), simulated (red), and fitted (blue) k²χ(k) oscillations of (LiF : ThF₄) = (0.75 : 0.25) (fluorescence, T = 898 K). Dotted green line: experimental data by Bessada et al.¹⁰ at the same composition (absorption, T = 973 K). (b) Fourier transform modulus |χ(R)| of the EXAFS spectra.

Fig. 7 (a) Experimental (■) and calculated (red), and fitted (blue) k²χ(k) oscillations of (NaF : ThF₄) = (0.33 : 0.67) (absorption, T = 1252 K). (b) Fourier transform modulus |χ(R)| of the EXAFS spectra.

Fig. 8 (a) Experimental (■) and calculated (red), and fitted (blue) k²χ(k) oscillations of (NaF : UF₄) = (0.33 : 0.67) (absorption, T = 1153 K). (b) Fourier transform modulus |χ(R)| of the EXAFS spectra.

Fig. 9 (a) Experimental (■), simulated (red), and fitted (blue) k²χ(k) oscillations of (KF : ThF₄) = (0.67 : 0.33) (fluorescence, T = 1123 K). (b) Fourier transform modulus |χ(R)| of the EXAFS spectra.

Fig. 10 (a) Experimental (■), simulated (red), and fitted (blue) k²χ(k) oscillations of (KF : UF₄) = (0.50 : 0.50) (absorption, T = 1098 K). (b) Fourier transform modulus |χ(R)| of the EXAFS spectra.

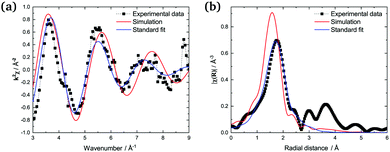Fig. 11 (a) Experimental (■), simulated (red), and fitted (blue) k²χ(k) oscillations of (CsF : UF₄) = (0.75 : 0.25) (absorption, T = 1293 K). (b) Fourier transform modulus |χ(R)| of the EXAFS spectra.

Fig. 12 (a) Experimental (■), simulated (red), and fitted (blue) k²χ(k) oscillations of (CsF : ThF₄) = (0.75 : 0.25) (absorption, T = 1301 K). (b) Fourier transform modulus |χ(R)| of the EXAFS spectra.

Table 6 lists the distribution and expected values of coordination numbers as calculated in this work. They are also plotted in Fig. 13. In agreement with previous studies,^{9,10,16,27,35,37} the distribution ranges between 6 and 10. From the works related to LiF–ThF₄ and LiF–UF₄ melts,^{8,9,16,23,27,31,35} it is clear that the dominant contributions are from CN = 7, 8, and 9 at all temperatures and compositions. Guo et al.,²⁷ who performed MD calculations of dilute solutions of ThF₄ in AF (A = Li, Na, K) systems, observed a bimodal distribution with virtually only [ThF₇]³⁻ and [ThF₈]⁴⁻ complexes present, and very small concentrations of [ThF₉]⁵⁻ (mean values at 1373 K indicated in cyan in Fig. 13). Bessada et al. report the following mean CN in the NaF–ThF₄ system at 1223 K: 7.6 for X(ThF₄) = 0.10, ∼7.8 for X(ThF₄) = 0.45, and ∼8.0 for X(ThF₄) = 0.6.¹⁰ These results correlate well with those in Table 5, where it can be seen that NaF–UF₄ behaves similarly.

Fig. 13 Average coordination number in the (A,An)F_x solutions as a function of temperature, and composition, calculated with MD. Unless otherwise indicated, the data is from this work. Where the temperature is not indicated, it is variable, indicated in Table 5.

In the KF–ThF₄ system it was found previously,³⁷ also with a combined EXAFS-MD approach, that the dominant complexes at X(ThF₄) = 0.25, 1073 K, were [ThF₆]²⁻ (14.5%), [ThF₇]³⁻ (68.7%), and [ThF₇]³⁻ (16.8%), for an expected CN of 7.03.³⁷ In a later work¹⁰ the authors reported a mean coordination of 7.5 in the KF–ThF₄ system at X(ThF₄) = 0.45, T = 1173 K, and slightly higher at T = 1073 K. These values are in excellent agreement with the data collected in this work, i.e. E[CN] = 7.12 at X(ThF₄) = 0.167, T = 1060 K, E[CN] = 6.99 at X(ThF₄) = 0.33, T = 1123 K, and E[CN] = 7.53 at X(ThF₄) = 0.50, T = 1209 K (Table 6).

Finally, there are, to the best of our knowledge, no EXAFS, MD, or otherwise stuctural studies available in the literature on the CsF–AnF₄ (A = U, Th) systems. Like for the other AF–AnF₄ systems, the CN distribution is calculated to be in the 6–10 range, with a small contribution from CN = 9 and a negligible one from CN = 10. The atomic environment for the An⁴⁺ cations in the crystal phases occurring in the CsF–AnF₄ binary systems is mostly a tricapped trigonal prism (CN = 9)³⁸ except for an octa-coordinated site in Cs₂UF₆ (space group Cmcm,³⁹) and an exceptionally rare 1-coordinated site in one of the polymorphs of CsThF₅ (space group P4/nmm⁴⁰). Hence, as discussed earlier for thorium and uranium tetrafluorides, thermal disorder reduces the coordination number in the first solvation shell, as CN = 6 becomes more prevalent than in melts based on other alkali fluorides.

As for the An–F bond length, which was varied freely during the fitting process without constraints based on the MD simulations, the agreement between the fits and the simulations is quite good: in all cases, the average value of the fit falls between the most probable distance and the bond cutoff distance extracted from the MD trajectories, i.e., it is close to the expected value of the simulations.

4.3 Main structural features of the liquid mixtures

4.3.1 General features. The An–F, An–An, and A–F RDFs have been plotted for the three most representative compositions: X(AnF₄) = 0.25 along with 0.33, 0.50, and 0.67 in Fig. 14–16. In a similar way to the pure actinide salts, a structural motif of interlocking shells can be observed: every distribution, with the exception of those for AnF₄ dissolved in CsF at concentration X(AnF₄) = 0.25, displays at least three local maxima before tending to bulk behavior. Hence there is strong ionic ordering, the characteristic range of which is around 3–4 hydrodynamic radii. In the special case of the An–F bond, there is also a degree of covalency, as indicated by the deep first minimum of the RDFs, whereas the broader peaks and shallower minima in the rest of the RDFs indicate more dynamic ion clusters in which a faster exchange of F⁻ ions occurs.⁴¹ The ordering is strong enough so as to guarantee that no An–An or An–A FNN exist, yet weak enough such that A–A and F–F FNN are possible (see ESI,† for An–A, A–A, and F–F RDFs).

Fig. 14 Radial distribution functions: (a) An–F, (b) An–An, and (c) A–F in the AF–AnF₄ melts at composition X(AnF₄) = 0.25 (Li and Cs-based melts) and X(AnF₄) = 0.33 (Na and K-based melts).

Fig. 15 Radial distribution functions: (a) An–F, (b) An–An, and (c) A–F in the AF–AnF₄ melts at composition X(AnF₄) = 0.50.

Fig. 16 Radial distribution functions: (a) An–F, (b) An–An, and (c) A–F in the AF–AnF₄ melts at composition X(AnF₄) = 0.67.

The data available, with varying compositions across systems, allow for three main trends to be observed: (i) trends across composition, (ii) trends as a function of the actinide metal, and (iii) trends as a function of the alkali metal.

4.3.2 Trends as a function of composition. The RDFs in general vary little with increasing AnF₄ content, with the exception of An–An. At X(AnF₄)= 0.25 and 0.33 there is a first maximum centered close to 4 Å  which is of lower intensity than the following one centered between 6 and 7 Å: it is more probable at that composition for An centers to be farther away from each other than second-nearest neighbors (SNN) because it is more favorable for alkali cations to occupy SNN sites. In melts richer in AnF₄ the An number density makes it more likely that actinide pairs will be SNN, so likely indeed that fluoride bridging is still possible, even in the presence of bulky Cs⁺ cations. This change is apparent in the An–F RDFs when going from being dissolved in CsF (X(AnF₄) = 0.25) to AnF₄ being the solvent (X(AnF₄) = 0.67): in the former case only the first shell is distinguishable, while at the other two compositions there is a second shell centered at ∼4.8 Å  where the majority of the fluorides meet the fluoride bridging criteria for r: r < 5.1 Å  ∼ R_An–An,max and r < 6.2 Å  ∼ 2R·_An–F,max.

The An–F bond cutoffs are not very sensitive to composition, a result which agrees with the analysis of Th–F,⁴¹ U–F,³¹ and Zr–F⁷ bond lengths in mixtures with LiF. R_{cutoff,An–F}, however, becomes slightly more populated as the actinide cations start competing with each other for the fluoride counter ions, which results in an increase in the average bond length and the average coordination number. This increase is not monotonic, and actually both quantities were found to go through a minimum between 20 and 30 mol%, (where F:Th ∼7) in isothermal studies of AF–ThF₄ (A = Li, Na, K) mixtures.¹⁰ This effect can be seen in Fig. 13 as well.

4.3.3 Trends as a function of the tetravalent cation. The F–F, A–A, An–A, (see ESI†) and An–An radial distribution functions (Fig. 14b, 15b and 16b) change very little with respect to each other upon replacement from Th⁴⁺ to U⁴⁺. Once again the An–F distribution can be singled out. The subtle structural changes are dominated by the actinide contraction, which the potentials reproduce well: for a given alkali cation, the complete U–F bond distribution shortens with respect to that of Th–F as can be seen from the most probable, the expected, and the bond cutoff lengths (Table 5). If the distributions are further compared with AF–ZrF₄ (A = Li, Na, K) liquid solutions, with an even smaller tetravalent cation for a given coordination number,⁴² the trend is continued, as the bond cutoff distance in that case was identified as R_{Zr−F,cutoff} = 2.8 Å.⁷ Correspondingly, the coordination number distribution shifts from being dominated by 7, 8, and 9, in AF–AnF₄ (A = Li, Na, K, An = Th, U) mixtures, with CN = 6 being a negligible contribution, to being dominated by 6, 7, and 8 in ZrF₄-containing melts. This agrees with the behavior in the solid fluoride compounds: structures with hexa-coordinated An⁴⁺ (An = Th, U) are unknown, but common in the case of Zr⁴⁺.⁴³

4.3.4 Trends as a function of the alkali cation. The substitution of the alkali cation results in pronounced structural changes: all RDFs (Fig. 14a–16c) show a marked evolution when the alkali cation is substituted. The change is dominated by the size of the cation: the RDFs have their maxima ordered from lowest to largest distance in the order Li, Na, K, Cs, except in the case of the An–F distance. The AnF₄ (A = Th, U) salts are Lewis acids, readily accepting fluoride ions from their alkali fluoride solvents or solutes – Lewis bases-to form anionic coordination complexes. As the alkali cation becomes larger, and hence more fluorobasic, the fluorides bind more tightly to their coordinating An⁴⁺ cation, as can be confirmed from the An–F RDFs (Fig. 14a, 15a and 16a): there is a shift to lower bond lengths and they become sharper, with a lower minimum. A measure of the stabilization of the conjugate base was provided by Pauvert et al.,⁷ who calculated the lifetimes of the A–Zr coordination complexes in AF–ZrF₄ (A = Li, Na, K) mixtures, and found them to increase in the order Li < Na < K. The authors suggested that bulkier alkali cations implied larger distances between the complexes, in turn increasing the energy barrier to be overcome for a fluoride ion to leave a cage and incorporate into another. In addition, the stability of the conjugate acid A⁺ itself also increases because the charge can spread over a larger cationic volume. The large stabilization of the conjugate base [AnF_x]^4−x can be most clearly appreciated in Fig. 14a. The RDFs corresponding to the (Cs,An)F_x solutions are characterized by only one very sharp peak, followed by a diffuse layer which slowly approximates bulk behavior.

A second measure of the stabilization of the [AnF_x]^4−x complexes in alkali fluoride melts is given by the negative mixing enthalpies in these systems. The liquid–liquid mixing enthalpies in AF–ZrF₄ (A = Li, Na, K, Rb) mixtures, are convex curves which become more negative in the order Li, Na, K, Rb.⁴⁴ The AF–ThF₄ (A = Li, Na, K) systems^26,45,46 obey the same trend. Moreover, the depth of the curves is greater in ZrF₄-based systems, due to the strength of the shorter Zr–F bond. The progressive tightening of the [AnF_x]^4−x cage down the alkali family corresponds well to the trend in liquid–liquid mixing enthalpies.

Another important conclusion from the study by Pauvert et al.⁷ was that large alkali cations favor lower coordination numbers around zirconium. In NaF and KF-based systems, [ZrF₈]⁴⁻ complexes were only formed when the concentration of ZrF₄ exceeded 40–45 mol%. More recently, Bessada et al.¹⁰ pointed out that shorter AF–AnF₄ (A = Li, Na, K) bond lengths and lower CN are favored as the radius of the alkali cation grows. In the case of CsF-based systems, the trend is accentuated, such that the average CN around the tetravalent actinides is heretofore unseen: as low as 6.2 at X(AnF₄) = 0.25 (Table 5).

4.4 Implications for the transport properties: viscosity and electrical conductivity

Bessada et al.¹⁰ pointed out that the viscosity of LiF–AnF₄ (A = Th, U) mixtures should be greater than that of LiF–ZrF₄ at a the same molar composition, since in the latter system the emergent ionic network is weaker, having instead more stable coordination anions. At a given temperature, a dissociated melt should be less viscous than a molecular one, which in turn should be less viscous than a polymerized one. Nevertheless, it is interesting to consider the role of the alkali cation: the heavier and larger cations stabilize the coordination shell around the tetravalent cation, yet make the network more fragile.^7,47 These two trends should have opposite effects, resulting in a non-monotonic increase of viscosity with AnF₄ concentration. This is what is observed in Fig. 17, adapted from ref. 48. At a temperature of 1230 K, LiF–UF₄, with relatively weak complexes but little ability to disrupt the ionic network, displays a viscosity increasing monotonically with UF₄ concentration. The KF–UF₄ system on the other hand, displays a local maximum in the vicinity of X(UF₄) = 0.33. The MD trajectories of the analogous Th composition KF : ThF₄ = (0.67 : 0.33) reveal a large fraction (∼0.5) of isolated [ThF_x]^4−x complexes. Then, there is a local minimum of the viscosity near X(UF₄) = 0.5. The KF : UF₄ = (0.5 : 0.5) simulation of the EXAFS sample, shows a large extent of network formation, (∼66.5%), but the network appears to be fragile enough that the composition with more long-lived isolated complexes (X(UF₄ ∼ 0.33)) has a greater viscosity. From X(UF₄) = 0.5 onwards, the network becomes more robust as K⁺ is diluted, and the viscosity increases, now monotonically.

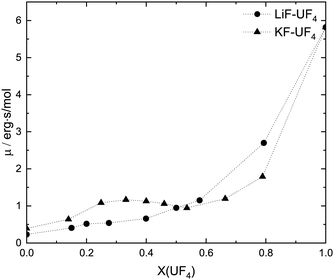Fig. 17 Molar viscosity (erg s mol⁻¹) of AF–UF₄ (A = Li, K) melts at an isotherm of T = 1230 K. Adapted from ref. 48.

While the viscosities of CsF–AnF₄ systems have not been measured, the electrical conductivities of AF–AnF₄ (A = Li, Na, K, Rb, Cs; An = Th, U) are available in the literature,^49–51 and a similar interpretation may be given. For isotherms across AnF₄ mole fraction, the increasing alkali radius is reflected in decreasing electrical conductivities. The conductivities of AF–AnF₄ (A = Li, Na; An = Th, U) do not go through local minima, while those of KF, Rb, and CsF-based melts have minima in the 30–50 mol% region. The reduced ionic mobilities in those areas suggest that the viscosity could go through a local maximum as seen in Fig. 17.

5 Conclusion

Structural studies of alkali fluoride/actinide fluoride salt mixtures in the molten state have been presented, using a combined EXAFS-MD approach which has proven to be a valuable tool to explore the rich chemistry of molten salt systems. Fitting the standard EXAFS equation was done in parallel, and was shown to be an adequate means to extract information about the first coordination shell of thorium and uranium, provided there is another structural model, e.g. obtained from MD, to constrain the fit to physically realistic values. Remarkably, the EXAFS spectra of pure molten ThF₄ and UF₄ were experimentally measured for the first time: the PIM potential parameters derived ab initio by Dewan et al.¹⁶ can approximate them well.

PIM potentials derived for other AF-based systems (A = Na, K, Cs) have shown to have good applicability for the corresponding AF–AnF₄ (An = U, Th) binaries. Fluorides are more loosely bound to alkali cations in mixtures with actinide fluorides than in the pure alkali fluoride melts, while the opposite is true for actinide cations. The observed trends of decreasing average bond length and coordination around the actinide with increasing alkali radius are followed when Cs⁺ is present in the melt; surprisingly, Cs⁺ can even promote an expected coordination number close to 6, something which had not been observed for Li⁺, Na⁺, or K⁺-based systems. The role alkali cations play in stabilizing coordination complexes while destabilizing networks in AF–AnF₄ mixtures, and the opposing effects that might have on the viscosity, was discussed. In future works the role of charge and electronegativity of other families of solvents in molten salt environments will be explored.

6 CRediT author statement

J. A. Ocádiz-Flores: Conceptualization, Methodology, Investigation, Formal analysis, Visualization, Data Curation, Writing – Original Draft preparation A. E. Gheribi: Investigation J. Vlieland: Investigation D. de Haas: Investigation K. Dardenne: Investigation J. Rothe: Investigation R. J. M. Konings: Conceptualization, Supervision, Writing – Review & Editing A. L. Smith: Conceptualization, Methodology, Investigation, Supervision, Funding acquisition, Resources, Project Administration, Writing – Review & Editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Pavel Souček and Ondrej Beneš for providing us with ThF₄ of high purity. We also thank Mathieu Salanne for the use of his Molecular Dynamics code, and fruitful discussions on these systems. We acknowledge the KIT light source for provision of instruments at the INE-Beamline of the Institute for Nuclear Waste Disposal and we would like to thank the Insitute for Beam Physics and Technology (IBPT) for the operation of the storage ring, the Karlsruhe Research Accelerator (KARA). A. L. Smith acknowledges financial support from the Netherlands Organisation for Scientific Research (NWO) (project 722.016.005). J. A. Ocádiz-Flores acknowledges CONACYT-SENER for financial support.

References

1. A. R. Kamali, RSC Adv., 2020, 10, 36020–36030.
2. T. Murakami, T. Nishikiori, T. Nohira and Y. Ito, J. Am. Chem. Soc., 2003, 125, 334–335.
3. W. Weng, L. Tang and W. Xiao, J. Energy Chem., 2019, 28, 128–143.
4. J. J. Laidler, J. Battles, W. Miller, J. Ackerman and E. Carls, Prog. Nucl. Energy, 1997, 31, 131–140.
5. E. S. Bettis, R. W. Schroeder, G. A. Cristy, H. W. Savage, R. G. Affel and L. F. Hemphill, Nucl. Sci. Eng., 1957, 2, 804–825.
6. C. Renault, M. Hron, R. J. M. Konings and D.-E. Holcomb, GIF Symposium, Paris(France), 9–10 September 2009, pp. 191–200.
7. O. Pauvert, M. Salanne, D. Zanghi, C. Simon, S. Reguer, D. Thiaudière, Y. Okamoto, H. Matsuura and C. Bessada, J. Phys. Chem. B, 2011, 115, 9160–9167.
8. C. Bessada, D. Zanghi, O. Pauvert, L. Maksoud, A. Gil-Martin, V. Sarou-Kanian, P. Melin, S. Brassamin, A. Nezu and H. Matsuura, J. Nucl. Mater., 2017, 494, 192–199.
9. A. L. Smith, M. N. Verleg, J. Vlieland, D. D. Haas, J. A. Ocadiz-Flores, P. Martin, J. Rothe, K. Dardenne, M. Salanne and A. E. Gheribi, et al. , J. Synchrotron Radiat., 2019, 26, 124–136.
10. C. Bessada, D. Zanghi, M. Salanne, A. Gil-Martin, M. Gibilaro, P. Chamelot, L. Massot, A. Nezu and H. Matsuura, J. Mol. Liq., 2020, 307, 112927.
11. M. Newville, J. Synchrotron Radiat., 2001, 8, 96–100.
12. A. Filipponi, J. Phys.: Condens. Matter, 2001, 13, R23.
13. Y. Okamoto, Nucl. Instrum. Methods Phys. Res., Sect. A, 2004, 526, 572–583.
14. P. A. Madden and M. Wilson, Chem. Soc. Rev., 1996, 25, 339–350.
15. P. Jemmer, M. Wilson, P. A. Madden and P. W. Fowler, J. Chem. Phys., 1999, 111, 2038–2049.
16. L. C. Dewan, C. Simon, P. A. Madden, L. W. Hobbs and M. Salanne, J. Nucl. Mater., 2013, 434, 322–327.
17. R. J. Heaton, R. Brookes, P. A. Madden, M. Salanne, C. Simon and P. Turq, J. Phys. Chem. B, 2006, 110, 11454–11460.
18. J. Rothe, S. Butorin, K. Dardenne, M. Denecke, B. Kienzler, M. Löble, V. Metz, A. Seibert, M. Steppert and T. Vitova, et al. , Rev. Sci. Instrum., 2012, 83, 043105.
19. P. Souček, O. Beneš, B. Claux, E. Capelli, M. Ougier, V. Tyrpekl, J. Vigier and R. Konings, J. Fluorine Chem., 2017, 200, 33–40.
20. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
21. M. Salanne, B. Rotenberg, S. Jahn, R. Vuilleumier, C. Simon and P. A. Madden, Theor. Chem. Acc., 2012, 131, 1143.
22. M. Salanne, C. Simon, P. Turq, R. J. Heaton and P. A. Madden, J. Phys. Chem. B, 2006, 110, 11461–11467.
23. L. Dewan, PhD thesis, Massachusetts Institute of Technology, 2013.
24. K. Tang and J. Toennies, J. Chem. Phys., 1984, 80, 3726–3741.
25. M. Salanne, C. Simon, P. Turq and P. A. Madden, J. Fluorine Chem., 2009, 130, 38–44.
26. M. Schreuder, MSc thesis, Delft University of Technology, 2019.
27. X. Guo, H. Qian, J. Dai, W. Liu, J. Hu, R. Shen and J. Wang, J. Mol. Liq., 2019, 277, 409–417.
28. O. Beneš, P. Zeller, M. Salanne and R. J. Konings, J. Chem. Phys., 2009, 130, 134716.
29. A. L. Ankudinov, B. Ravel, J. J. Rehr and S. D. Conradson, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7565–7576.
30. S. Kern, J. Hayward, S. Roberts, J. Richardson Jr, F. Rotella, L. Soderholm, B. Cort, M. Tinkle, M. West and D. Hoisington, et al. , J. Chem. Phys., 1994, 101, 9333–9337.
31. J. A. Ocádiz-Flores, A. E. Gheribi, J. Vlieland, K. Dardenne, J. Rothe, R. Konings and A. L. Smith, J. Mol. Liq., 2021, 331, 115820.
32. M. Walz and D. Van der Spoel, Phys. Chem. Chem. Phys., 2019, 21, 18516–18524.
33. G. Girichev, A. Krasnov, N. Giricheva and O. Krasnova, J. Struct. Chem., 1999, 40, 207.
34. R. Konings, A. Booij, A. Kovács, G. Girichev, N. Giricheva and O. Krasnova, J. Mol. Struct., 1996, 378, 121–131.
35. J. Dai, D. Long, P. Huai and Q. Li, J. Mol. Liq., 2015, 211, 747–753.
36. H. Bilz and W. Kress, Phonon Dispersion Relations in Insulators, Springer, 1979, pp. 27–47.
37. C. Bessada, D. Zanghi, O. Pauvert, L. Maksoud, A. Gil-Martin, V. Sarou-Kanian, P. Melin, S. Brassamin, A. Nezu and H. Matsuura, J. Nucl. Mater., 2017, 494, 192–199.
38. P. Villars and K. Cenzual, Crystal Structure Database for Inorganic Compounds, Materials Park (OH), ASM International, 2012, 2009.
39. V. Volkov, I. Suglobova and D. E. Chirkst, Koord. Khim., 1980, 6, 417–422.
40. C. C. Underwood, M. Mann, C. D. McMillen, J. D. Musgraves and J. W. Kolis, Solid State Sci., 2012, 14, 574–579.
41. J.-B. Liu, X. Chen, Y.-H. Qiu, C.-F. Xu, W. E. Schwarz and J. Li, J. Phys. Chem. B, 2014, 118, 13954–13962.
42. R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
43. R. Pennenvan, R. Ryan and A. Rosenzweig, Rare Earths, Springer, 1973, pp. 1–52.
44. G. Hatem, F. Tabaries and M. Gaune-Escard, Thermochim. Acta, 1989, 149, 15–26.
45. E. Capelli, O. Beneš, M. Beilmann and R. J. M. Konings, J. Chem. Thermodyn., 2013, 58, 110–116.
46. J. Ocádiz-Flores, E. Carré, J.-C. Griveau, E. Colineau, E. Capelli, P. Souček, O. Beneš, R. Konings and A. Smith, J. Chem. Thermodyn., 2020, 145, 106069.
47. M. Wilson and P. Madden, Phys. Rev. Lett., 1994, 72, 3033.
48. V. Desyatnik, A. Nechaev and Y. F. Chervinskii, At. Energy, 1979, 46, 408–409.
49. R. Meaker, B. Porter and D. Kesterke, Electrical Conductivity and Density of Fluoride Systems, U.S. Department of Interior, Bureau of Mines, 1971.
50. V. Desyatnik, A. Koverda and N. Kurbatov, At. Energy, 1983, 55, 544–546.
51. V. Desyatnik, A. Koverda and N. Kurbatov, Atomic Energy, 1983, 55, 487–488.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00566a

‡ From neutron diffraction data, ref. 9.

§ Averaged from the crystallographic data in ref. 30.

---