 Open Access Article
Open Access ArticleRoom-temperature diffusion of metal clusters on graphene†
Mohammad
Zarshenas
 *a,
Victor
Gervilla
a,
Davide G.
Sangiovanni
*a,
Victor
Gervilla
a,
Davide G.
Sangiovanni
 b and
Kostas
Sarakinos
b and
Kostas
Sarakinos
 a
a
aNanoscale Engineering Division, Department of Physics, Chemistry and Biology, Linköping University, SE-58183, Linköping, Sweden. E-mail: zarshenas@gmail.com
bTheoretical Physics Division, Department of Physics, Chemistry and Biology, Linköping University, SE-58183, Linköping, Sweden
First published on 24th May 2021
Abstract
We study the diffusion dynamics, the diffusion mechanisms, and the adsorption energetics of Ag, Au, Cu, and Pd dimers, as well as of Ag trimers on single-layer graphene (SLG) by means of ab initio molecular dynamics (AIMD) simulations and density-functional theory (DFT) calculations. The simulations show that Ag, Cu, and Au clusters exhibit a super-diffusive pattern characterized by long jumps, which can be explained by the flat potential energy landscape (PEL) (corrugation of a few tens of meV) encountered by those clusters on SLG. Pd dimers, instead, diffuse in a pattern that is reminiscent of conventional random walk, which is consistent with a significantly rougher PEL of the order of 100 meV. Moreover, our data show that all clusters exhibit diffusion mechanisms that include both concerted translation and rotation. The overall results of the present study provide key insights for modeling the growth of metal layers and nanostructures on graphene and other van der Waals materials, which is a prerequisite for the directed growth of multifunctional metal contacts in a broad range of enabling devices.
1. Introduction
Controlled synthesis of thin films and nanostructures from the vapor phase on two-dimensional (2D) materials is essential for leveraging the unique physical attributes of 2D crystals in a wide array of devices, including photodetectors, catalysts, biosensors, and tunnel field-effect transistors.1–8 Vapor-based film growth is a far-from-equilibrium process in which the resulting film morphology is predominantly governed by the kinetic rates of atomic-scale mechanisms.9–11 One such mechanism is adatom diffusion on the substrate surface, the rate of which determines the competition among island nucleation and growth and, thereby, largely sets the early-stage film morphology.11In classical homo- and heteroepitaxial growth theory, at temperatures that are relevant for thin-film synthesis experiments, diffusion on the substrate is described as a random walk, during which adatoms perform a thermally activated chain of uncorrelated jumps between neighboring adsorption sites.11 We have recently demonstrated, using ab initio and classical molecular dynamics simulations, that the above-described picture is not unconditionally valid during the diffusion of Ag, Au, Pd, Cu, Pt, and Ru adatoms on single-layer graphene (SLG) at room temperature.12 Our results revealed that Ag, Au, Pd, and Cu adatoms experience a markedly flat potential energy landscape (PEL) on the SLG surface, with corrugation of the order of a few tens of meV, which may be significantly modified by vibrational entropy effects. Hence, adatoms follow a super-diffusive pattern known as Lévy walk, in which they move continuously within relatively short-range domains (∼1–4 nm2) without being halted by surface adsorption sites, while they occasionally perform long jumps across multiple surface adsorption sites. In contrast, Pt and Ru adatoms experience PELs with corrugations of the order of a few hundreds of meV (e.g., comparable with PELs encountered by adatoms during epitaxial growth) and perform random walks.
In the present manuscript, we investigate – employing density functional theory (DFT) calculations and ab initio molecular dynamics (AIMD) simulations – the adsorption energetics, and the room-temperature diffusion dynamics and migration mechanisms of Ag, Au, Cu, and Pd dimers, as well as Ag trimers, on SLG. The study is motivated by the fact that, besides adatoms, multiatomic clusters have been shown to be mobile on a number of substrates, including graphite and graphene.13–20 One implication of mobile clusters is that they modify the dynamics governing island nucleation, leading to larger island densities, relative to processes in which adatoms are the only mobile species on the substrate surface.11
Our results show that the diffusion pattern followed by the various adspecies is consistent with their interaction strength with the SLG substrate and the flatness of the PEL they experience. Ag (both dimer and trimers), Au dimers, and Cu dimers interact relatively weakly with SLG, encounter a PEL which is ∼5–40 meV corrugated, and exhibit a super-diffusive behavior. Concurrently, Pd dimers perform a random walk on a considerably rougher PEL with a depth of ∼100 meV. We also establish that diffusion of Ag, Cu, and Au adspecies occurs, primarily, via translation, while they are aligned perpendicularly to SLG, such that only one atom is in contact with the substrate. In contrast, Pd dimers diffuse via in-plane translation and rotation, and they are aligned parallel to SLG with both atoms in the cluster being in constant contact with the substrate. Our overall findings show that cluster diffusion, concerning both dynamics and detailed mechanisms, exhibits non-trivial features that need to be considered when modeling the growth of metals on graphene and other 2D materials.
2. Computational methodology
We perform AIMD simulations to model diffusion of single Ag, Au, Cu, and Pd dimers, as well as Ag trimers, on SLG within the Vienna ab initio simulation package (VASP).21 Core electrons are replaced by the projector augmented wave (PAW) pseudopotentials and the generalized gradient approximation of Perdew, Burke, and Ernzerhof (PBE).22 We use an energy cutoff of 400 eV for the plane waves and Γ-point sampling of the reciprocal space. The SLG substrate is implemented as a hexagonal 6 × 6 supercell containing 72 carbon atoms. A vacuum region of 20 Å separates graphene replicas along the z-direction. We model the van der Waals forces using the DFT-D3 method with Becke–Johnson (BJ) damping,23 which accurately describes the properties of both graphite and diamond.24 Simulations are performed accounting for the electronic-spin degrees of freedom for a total time of 1.2 ns (time step 1 fs) using canonical sampling (Nosé–Hoover thermostat at 300 K) of the configurational space. The simulation output is visualized by the Visual Molecular Dynamics software.25We calculate the lowest energy configuration of the various adspecies on the SGL substrate and we estimate the corrugation of the PEL at 0 K by computing the ground-state adsorption energies E0Kads on the hollow, top, and bridge sites using standard DFT structure relaxations and the following expression:
| E0Kads = E0(Cluster/SLG) − E0(Cluster) − E0(SLG). | (1) |
| Type of cluster | E ads 0K (meV) | |||||||
|---|---|---|---|---|---|---|---|---|
| T (⊥) | B (⊥) | H (⊥) | B–B (‖) | H–H(‖) | B–H (‖) | T–T–2NN (‖) | T–T–3NN (‖) | |
| Ag dimer | 0 | 5 | 60 | 48 | 80 | 67 | 61 | 69 |
| Au dimer | 27 | 0 | 422 | Unstable | 607 | Unstable | Unstable | Unstable |
| Cu dimer | 37 | 0 | 233 | Unstable | 660 | Unstable | Unstable | Unstable |
| Pd dimer | Unstable | Unstable | Unstable | 188 | 61 | 153 | 0 | 147 |
| Ag trimer (Δ) | 31 | 37 | 0 | |||||
| Ag trimer (▽) | 32 | 0 | 35 | |||||
3. Results and discussion
3.1 Diffusion dynamics
We use AIMD simulations to model the migration of single Ag dimers and trimers, Au dimers, Cu dimers, and Pd dimers on the SLG substrate (see Computational methodology section for more details). Fig. 1 displays the diffusion trajectories of the clusters’ center of mass (CM) after a simulation time of 1.2 ns. The data corresponding to the Ag dimer (Fig. 1(a)) reveals that this cluster moves over an area of ∼91 nm2. Closer inspection of the trajectory shows that the dimer remains confined in domains with sizes in the range ∼0.8 to ∼3 nm2 (representative domains are marked with bold lines in Fig. 1(a)) where it diffuses randomly by moving continuously among adsorption sites (see magnified inset in Fig. 1(a), whereby green circles represent the position of carbon atoms in the graphene sheet). Occasionally, it performs directed jumps ∼1.5–5.4 nm long (an example of such jump is marked with a red line in Fig. 1(a)) as it transitions between diffusion domains. The Ag trimer (Fig. 1(b)) exhibits a qualitatively similar trajectory to that of the dimer, with its CM diffusing in a total area of ∼50 nm2 that features ∼0.75 to 2.5 nm2 domains separated by directed jumps ∼1.5–3 nm long. Diffusion patterns consistent with that described for the Ag dimer are also observed for Cu and Au dimers (Fig. 1(c) and (d)), respectively; the corresponding total diffusion areas are provided in each figure). Out of three metals, Au exhibits the shortest diffusion length during 1.2 ns. This is most notably exemplified by the inset in Fig. 1(d), which depicts a typical domain for Au on SLG: diffusion occurs in a smaller area compared to Ag and Cu dimers, but still, the motion of the cluster is not halted by a specific adsorption site.A distinctly different diffusion behavior is obtained for the Pd dimer, as seen in Fig. 1(e). For a total simulation time of 1.2 ns, the CM of this cluster only moves within an area of ∼3.9 nm2 and remains confined in well-defined domains separated by a jump of ∼0.66 nm. Detailed analysis of the cluster trajectory in each of these domains shows that Pd atoms in the dimer mostly lie either on top of the center of adjacent hexagonal rings (i.e., hollow site) or on top of second nearest neighbor carbon atoms, such that the most favorable adsorption site for the CM is the bridge site (see magnified inset in Fig. 1(e)). The analysis also shows that the CM of the Pd dimer resides, on average, for a time of ∼75 ps on each bridge site before transitioning to a neighboring one. This pattern is reminiscent of a random walk, as opposed to the trajectories of the other clusters (Ag, Au, and Cu), which are comprised of correlated jumps across multiple adsorption sites and are, therefore, representative of super-diffusive behavior.
To better understand the diffusion type and dynamics of the various clusters, we calculate from each trajectory displayed in Fig. 1 the time-averaged mean square displacement  of the cluster CM. This is done for observation time scales equal to τ,26–29 according to the expression:30
of the cluster CM. This is done for observation time scales equal to τ,26–29 according to the expression:30
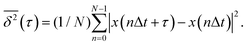 | (2) |
For a simulation time T and an observation time scale τ consisting of NT and Nτ time steps Δt, N = NT − Nτ + 1. We also note that each  value corresponds to an average entailing information of all sub-trajectories with a duration τ. From the latter, it follows that the statistical significance of a given
value corresponds to an average entailing information of all sub-trajectories with a duration τ. From the latter, it follows that the statistical significance of a given  decreases with increasing τ, since longer τ values yield a smaller number of sub-trajectories available for calculating
decreases with increasing τ, since longer τ values yield a smaller number of sub-trajectories available for calculating  . For that reason, following the methodology proposed by Saxton,30 only
. For that reason, following the methodology proposed by Saxton,30 only  points within an interval [0:τcut] are considered. Here, we take τcut = 50 ps, which corresponds to the mean time during which a cluster remains in a diffusion domain.
points within an interval [0:τcut] are considered. Here, we take τcut = 50 ps, which corresponds to the mean time during which a cluster remains in a diffusion domain.
Log–log scale  vs. τ curves extracted from the simulated trajectories for Ag, Au, and Cu clusters in Fig. 1(a) through (d) are displayed in Fig. 2. The data show that the
vs. τ curves extracted from the simulated trajectories for Ag, Au, and Cu clusters in Fig. 1(a) through (d) are displayed in Fig. 2. The data show that the  vs. τ curves exhibit a log–log slope α > 1, i.e.,
vs. τ curves exhibit a log–log slope α > 1, i.e.,  does not exhibit a linear dependence on time. Using the approach proposed by Kepten et al.,31 we compute the most probable value of α by fitting linear functions to the log–log curves in Fig. 2 over multiple time intervals (see Fig. S1 in the ESI† for more details) and find that α ranges between 1.19 and 1.33. The latter quantifies the non-linear correlation among atomic displacement and time, it confirms the super-diffusive nature of the trajectories32–34 in Fig. 1(a)–(d), and it is in agreement with the anomalous nature of diffusion for Ag, Au, Cu, and Pd adatoms on SLG established in a recent study of ours.12 Moreover, based on long (≥30 ns) classical MD simulations of Ag adatom diffusion on graphene12 and Au245 cluster diffusion on graphite,35 we expect that the log–log slope α will approach unity for τ → ∞. This indicates that, at the long-time limit, the motion of adspecies between diffusive domains can be effectively treated as random walk.
does not exhibit a linear dependence on time. Using the approach proposed by Kepten et al.,31 we compute the most probable value of α by fitting linear functions to the log–log curves in Fig. 2 over multiple time intervals (see Fig. S1 in the ESI† for more details) and find that α ranges between 1.19 and 1.33. The latter quantifies the non-linear correlation among atomic displacement and time, it confirms the super-diffusive nature of the trajectories32–34 in Fig. 1(a)–(d), and it is in agreement with the anomalous nature of diffusion for Ag, Au, Cu, and Pd adatoms on SLG established in a recent study of ours.12 Moreover, based on long (≥30 ns) classical MD simulations of Ag adatom diffusion on graphene12 and Au245 cluster diffusion on graphite,35 we expect that the log–log slope α will approach unity for τ → ∞. This indicates that, at the long-time limit, the motion of adspecies between diffusive domains can be effectively treated as random walk.
For the case of the Pd dimer, the cluster remains trapped for ∼75 ps in each adsorption site before diffusing to the next one, i.e., the simulated trajectory of 1.2 ns contains ∼15 diffusive jumps between neighboring sites and one long jump between diffusion domains. This number of migration events represents a rather small statistical sample for extracting  vs. τ curves and computing meaningful values for the exponent α, and hence we choose to analyze the trajectory of the Pd dimer only qualitatively.
vs. τ curves and computing meaningful values for the exponent α, and hence we choose to analyze the trajectory of the Pd dimer only qualitatively.
3.2 Diffusion mechanisms and adsorption energetics
Inspection of the simulation movies shows that the dimers may exhibit two stable configurations on the SLG surface: either both atoms in the cluster are in contact with the substrate (parallel alignment) or one atom only retains contact with the substrate with the second atom being only in contact with the first one (perpendicular alignment). In a first diffusion mechanism (depicted in Fig. 3(a)) the dimer translates across multiple adsorption sites of the SLG by remaining in the perpendicular configuration. This way of surface migration is observed 100% of the simulation time for Cu and Au dimers, and 75% of the time for Ag. In the remaining 25% of the simulation time, the Ag dimer is parallel to the SLG surface and diffuses by translating and occasionally rotating around the axis defined by the substrate surface normal (Fig. 3(b)). The transition between the diffusion modes (perpendicular and parallel) occurs instantly in less than a picosecond, such that this process does not need to be taken into account when calculating the elapsed time for each mechanism. The Pd dimer is aligned parallel to the substrate during the entire simulation time, and diffusion occurs by successive rotations and occasional translations between neighboring bridge sites (see Fig. 3(c)).Owing to the fact that a trimer exhibits a larger number of degrees of freedom for atomic motion relative to a dimer, more diffusion modes are intuitively expected for the former case. Three stable configurations are, predominantly, observed during the simulation of the Ag trimer diffusion. The trimer is aligned perpendicularly with either one or two atoms in contact with the substrate, while in the parallel alignment all three atoms retain contact with the SLG surface. With reference to these configurations, four mechanisms are identified during the diffusion of the Ag trimer on SLG: (i) translation of the trimer with two Ag atoms in contact with the substrate (Fig. 4(a); 87% of the simulation time); (ii) translation along with rotation around the axis defined by the substrate surface normal (Fig. 4(b); 3% of the simulation time); (iii) translation of the trimer with one atom in contact with the substrate, along with partial rotation around an axis parallel to the substrate surface (Fig. 4(c); 9% of the simulation time); and (iv) translation of the trimer with all atoms in contact with the substrate (parallel configuration), along with rotation around defined by the substrate surface normal (Fig. 4(d); 1% of the total simulation time). Once again, the very short transition time between each mechanism can be ignored when calculating the time of each mechanism.
In our previous simulation study on the diffusion of metal adatoms on graphene,12 we demonstrated a correlation among the diffusion type (i.e., normal vs. super-diffusive behavior) and the corrugation of the adatom-SLG PEL. To explore the relevance of this correlation for cluster diffusion investigated in the present work, we calculate (using DFT) the 0 K values of adsorption energy Eads0K of Ag, Au, Cu and Pd dimers, as well as Ag trimer in different possible configurations (see eqn (1) in Section 2). The results are listed in Table 1, where all calculated energies are shifted with respect to the corresponding most stable adsorption site for which we set Eads0K = 0. For dimers, energies are computed for the molecular bond axis perpendicularly (⊥) or parallel (‖) to the SLG substrate. Adsorption states denoted as unstable in Table 1 indicate dimer configurations which spontaneously relax to a different configuration upon slight perturbation from the high-symmetry positions. In the case of the Ag trimer, since it spends almost 99% of the simulation time being perpendicularly aligned to the SLG, only Eads0K values that correspond to the most stable perpendicular configurations (among all possible ones) during diffusion are presented in Table 1.
The static (i.e., 0 K) adsorption energy calculations for dimers are consistent with the trends observed in the dynamic simulations with respect to the cluster alignment: Au and Cu dimers are aligned predominantly perpendicularly to the substrate, Pd remains parallel, while Ag attains both types of alignment. To further understand the correlation among cluster orientation and adsorption energetics, we perform additional AIMD simulations, in which non-favorable cluster alignments are explicitly used as starting configurations, i.e., (i) parallel alignment for Ag trimers, and Cu and Au dimers; and (ii) perpendicular alignment for Pd dimers. Visual inspection of the simulation output shows that all clusters realign to their most common diffusion configuration in less than a few picoseconds after the simulation start. These findings confirm the lowest energy configurations of the clusters established from the Eads0K calculations listed in Table 1.
The data in Table 1 also show that the Ag, Au, and Cu dimers, as well as the Ag-trimer, encounter a PEL with a corrugation (i.e., smallest energy difference between adsorption sites) in the range 5 to 37 meV. This relatively flat PEL is indicative of weak adspecies-substrate interaction and offers transition pathways that can support the super-diffusive behavior observed in Fig. 1(a) through (d). In contrast, the Pd experiences a significantly rougher PEL (corrugation of the order of ∼100 meV), which is indicative of strong adspecies-substrate interaction and can explain the random-walk diffusive behavior. The above-described correlation is consistent with our recent findings with regards to the effect of PEL on the diffusion dynamics of Ag, Au, Pd, Cu, Pt, and Ru adatoms on SLG.12
4. Conclusions
We study via AIMD simulations the diffusion of Ag, Au, Cu, Pd dimers, and Ag trimers on SLG at room temperature. Visualization of the simulation output and quantitative analysis of the simulated trajectories show that Ag, Au, and Cu clusters diffuse by performing correlated jumps over multiple adsorption sites, which is a behavior that can be classified as super-diffusive. In contrast, Pd dimers diffuse between neighboring adsorption sites in a pattern that is reminiscent of random-walk behavior. The differences in the diffusion dynamics can be explained in light of the corrugation of the PEL; Ag, Au, and Cu clusters encounter a flat PEL (corrugation of a few tens of meV), while Pd dimers diffuse on a rougher PEL in which the energy difference between adsorption sites is of the order of ∼100 of meV. Moreover, our results indicate complex diffusion mechanisms for all clusters that involve both translation and rotation. Ag, Cu, and Au adspecies diffuse by being predominantly perpendicularly oriented to the SLG, such their contact and interaction with the substrate is minimized. In contrast, Pd dimers diffuse via in-plane translation and rotation and both atoms in the cluster remain in contact with the substrate.Our results show that differences in metal-cluster mobility may be an important aspect for understanding experimental data with regards to the growth of metal layers and nanostructures on graphene and other van der Waals materials. For instance, Zhou et al. have reported that Au layers exhibit a more pronounced three-dimensional growth morphology on graphene36 as compared to Pd which tends to develop flatter and more uniform layers.37 Similar trends were also found by Gong et al.5 when considering the growth of Ag and Au vs. Pd on MoS2. These differences in the obtained morphology point towards a lower island number density during Ag and Au growth, as compared to Pd. This may, in turn, be explained by the overall larger diffusivity (augmented by their super-diffusive character) of Au and Ag clusters. Furthermore, the present study, in combination with our previous findings on the migration of adatoms on graphene12 show that models of diffusion and initial formation stages of film growth on substrates that exhibit flat PELs cannot be unconditionally based on the conventional random walk theory, but rather on more sophisticated approaches which account for the effect of super-diffusive atomic behavior. Moreover, the data presented herein provide further evidence in favor of the potentially universal relevance of super-diffusive atomic motion for driving self-assembly processes at the nanoscale, including formation of three-dimensional Pb islands on Si(111) and Ni(111) substrates,38–40 and phase separation of Pb on Ge(111).41
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge Linköping University (“LiU Career Contract, Dnr-LiU-2015-01510, 2015-2020”), the Swedish research council (contract VR-2015-04630), the ÅForsk foundation (contract ÅF 19-137), and the Olle Engkvist foundation (contract SOEB 190-312) for financial support. Simulations and data handling were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre (NSC) partially funded by the Swedish Research Council through Grant Agreement No. VR-2015-04630.References
- T. J. Echtermeyer, S. Milana, U. Sassi, A. Eiden, M. Wu, E. Lidorikis and A. C. Ferrari, Surface Plasmon Polariton Graphene Photodetectors, Nano Lett., 2016, 16, 8–20 CrossRef CAS PubMed.
- T. Mueller, F. Xia and P. Avouris, Graphene photodetectors for high-speed optical communications, Nat. Photonics, 2010, 4, 297–301 CrossRef CAS.
- Y. Xu, C. Hsieh, L. Wu and L. K. Ang, Two-dimensional transition metal dichalcogenides mediated long range surface plasmon resonance biosensors, J. Phys. D: Appl. Phys., 2019, 52, 065101 CrossRef.
- X. Liu, Y. Han, J. W. Evans, A. K. Engstfeld, R. J. Behm, M. C. Tringides, M. Hupalo, H. Lin, L. Huang, K. Ho, D. Appy, P. A. Thiel and C. Wang, Growth morphology and properties of metals on graphene, Prog. Surf. Sci., 2015, 90, 397–443 CrossRef CAS.
- C. Gong, C. Huang, J. Miller, L. Cheng, Y. Hao, D. Cobden, J. Kim, R. S. Ruoff, R. M. Wallace, K. Cho, X. Xu and Y. J. Chabal, Metal Contacts on Physical Vapor Deposited Monolayer MoS2, ACS Nano, 2013, 7, 11350–11357 CrossRef CAS PubMed.
- D. Deng, K. S. Novoselov, Q. Fu, N. Zheng, Z. Tian and X. Bao, Catalysis with two-dimensional materials and their heterostructures, Nat. Nanotechnol., 2016, 11, 218–230 CrossRef CAS PubMed.
- Y. Zhu, L. Peng, Z. Fang, C. Yan, X. Zhang and G. Yu, Structural Engineering of 2D Nanomaterials for Energy Storage and Catalysis, Adv. Mater., 2018, 30, 1–19 Search PubMed.
- T. A. Shifa, F. Wang, Y. Liu and J. He, Heterostructures Based on 2D Materials: A Versatile Platform for Efficient Catalysis, Adv. Mater., 2019, 31, 1804828 CrossRef CAS PubMed.
- P. M. Martin, Handbook of Deposition Technologies for Films and Coatings, William Andrew, 2010 Search PubMed.
- I. Petrov, P. B. Barna, L. Hultman and J. E. Greene, Microstructural evolution during film growth, J. Vac. Sci. Technol., A, 2017, 117, S117 Search PubMed.
- J. Michely and T. Krug, Islands, Mounds and Atoms, Springer, Berlin, 2004 Search PubMed.
- V. Gervilla, M. Zarshenas, D. G. Sangiovanni and K. Sarakinos, Anomalous versus Normal Room-Temperature Diffusion of Metal Adatoms on Graphene, J. Phys. Chem. Lett., 2020, 11, 8930–8936 CrossRef CAS PubMed.
- A. Jamnig, D. G. Sangiovanni, G. Abadias and K. Sarakinos, Atomic-scale diffusion rates during growth of thin metal films on weakly-interacting substrates, Sci. Rep., 2019, 9, 6640 CrossRef CAS PubMed.
- S. C. Wang, U. Kürpick and G. Ehrlich, Surface Diffusion of Compact and Other Clusters: Ir x on Ir(111), Phys. Rev. Lett., 1998, 81, 4923–4926 Search PubMed.
- L. Bardotti, A. Hoareau, M. Treilleux, B. Cabaud, A. Perez and F. C. Santos, Diffusion and aggregation of large antimony and gold clusters deposited on graphite, Surf. Sci., 1996, 367, 276–292 CrossRef CAS.
- U. Kürpick, B. Fricke and G. Ehrlich, Diffusion mechanisms of compact surface clusters: Ir7 on Ir(111), Surf. Sci., 2000, 470, L45–L51 CrossRef.
- S. Y. Krylov, Surface Gliding of Large Low-Dimensional Clusters, Phys. Rev. Lett., 1999, 83, 4602–4605 CrossRef CAS.
- I. M. Goldby, L. Kuipers, B. von Issendorff and R. E. Palmer, Diffusion and aggregation of size-selected silver clusters on a graphite surface, Appl. Phys. Lett., 1996, 69, 2819 CrossRef CAS.
- L. J. Lewis, Diffusion of gold nanoclusters on graphite, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 84–90 CrossRef.
- W. D. Luedtke and U. Landman, Slip Diffusion and Lévy Flights of an Adsorbed Gold Nanocluster, Phys. Rev. Lett., 1999, 82, 3835–3838 CrossRef CAS.
- G. Kresse and J. Hafner, Ab. initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- I. Mosyagin, D. Gambino, D. G. Sangiovanni, I. A. Abrikosov and N. M. Caffrey, Effect of dispersion corrections on ab initio predictions of graphite and diamond properties under pressure, Phys. Rev. B, 2018, 98, 174103 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- H. Qian, M. P. Sheetz and E. L. Elson, Single particle tracking Analysis of diffusion and flow in two-dimensional systems, Biophys. J., 1991, 60, 910–921 CrossRef CAS PubMed.
- M. J. Saxton, Anomalous Diffusion Due to Obstacles: A Monte Carlo Study, Biophys. J., 1994, 66, 394–401 CrossRef CAS PubMed.
- M. J. Saxton, Anomalous Diffusion Due to Binding: A Monte Carlo Study, Biophys. J., 1996, 70, 1250–1262 CrossRef CAS PubMed.
- D. V. N. Jr, J. F. Hancock and K. Burrage, Sources of Anomalous Diffusion on Cell Membranes: A Monte Carlo Study, Biophys. J., 2007, 92, 1975–1987 CrossRef PubMed.
- M. J. Saxton, Single-Particle Tracking: The Distribution of Diffusion Coefficients, Biophys. J., 1997, 72, 1744–1753 CrossRef CAS PubMed.
- E. Kepten, A. Weron, G. Sikora, K. Burnecki and Y. Garini, Guidelines for the Fitting of Anomalous Diffusion Mean Square Displacement Graphs from Single Particle Tracking Experiments, PLoS One, 2015, 10, 1–10 CrossRef PubMed.
- R. Metzler and J. Klafter, The random walk's guide to anomalous diffusion: a fractional dynamics approach, Phys. Rep., 2000, 339, 1–77 CrossRef CAS.
- F. Höfling and T. Franosch, Anomalous transport in the crowded world of biological cells, Rep. Prog. Phys., 2013, 76, 046602 CrossRef PubMed.
- E. Barkai, Y. Garini and R. Metzler, Strange kinetics of single molecules in living cells, Phys. Today, 2012, 65, 29 CrossRef CAS.
- Y. Maruyama and J. Murakami, Truncated Lévy walk of a nanocluster bound weakly to an atomically flat surface: Crossover from superdiffusion to normal diffusion, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 1–5 CrossRef.
- H. Zhou, C. Qiu, Z. Liu, H. Yang, L. Hu, J. Liu, H. Yang, C. Gu and L. Sun, Thickness-dependent morphologies of gold on N-layer graphenes, J. Am. Chem. Soc., 2010, 132, 944–946 CrossRef CAS PubMed.
- H. Zhou, F. Yu, H. Yang, C. Qiu, M. Chen, L. Hu, Y. Guo, H. Yang, C. Gu and L. Sun, Layer-dependent morphologies and charge transfer of Pd on n-layer graphenes, Chem. Commun., 2011, 47, 9408–9410 RSC.
- M. Hupalo and M. C. Tringides, Ultrafast kinetics in Pb/Si(111) from the collective spreading of the wetting layer, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 1–7 CrossRef.
- T. R. J. Bollmann, R. Van Gastel, H. J. W. Zandvliet and B. Poelsema, Anomalous decay of electronically stabilized lead mesas on Ni(111), Phys. Rev. Lett., 2011, 107, 1–5 Search PubMed.
- K. L. Man, M. C. Tringides, M. M. T. Loy and M. S. Altman, Superdiffusive motion of the Pb wetting layer on the Si(111) surface, Phys. Rev. Lett., 2013, 110, 1–5 CrossRef PubMed.
- Y. Sato, S. Chiang and N. C. Bartelt, Spontaneous domain switching during phase separation of Pb on Ge(111), Phys. Rev. Lett., 2007, 99, 1–4 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00522g |
| This journal is © the Owner Societies 2021 |





