Open Access Article
Open Access ArticleRoom temperature second sound in cumulene†
Claudio
Melis
 *a,
Giorgia
Fugallo
*a,
Giorgia
Fugallo
 b and
Luciano
Colombo
b and
Luciano
Colombo
 a
a
aDepartment of Physics, University of Cagliari, Cittadella Universitaria, I-09042 Monserrato (CA), Italy. E-mail: claudio.melis@dsf.unica.it
bLTeN, UMR 6607 CNRS PolytechNantes, Université de Nantes, 44306 Nantes, France
First published on 2nd July 2021
Abstract
Second sound is known as the thermal transport regime occurring in a wave-like fashion, usually identified in a limited number of materials only at cryogenic temperatures. Here we show that second sound in a μm-long carbon chain (cumulene) might occur even at room temperature. To this aim, we calibrate a many-body force field on the first principles calculated phonon dispersion relations of cumulene and, through molecular dynamics, we mimic laser-induced transient thermal grating experiments. We provide evidence that by tuning temperature as well as the space modulation of its initial profile we can reversibly drive the system from a wave-like to a diffusive-like thermal transport. By following three different theoretical methodologies (molecular dynamics, the Maxwell–Cattaneo–Vernotte equation, and heat transport microscopic theory) we estimate for cumulene a second sound velocity in the range of 2.4–3.2 km s−1.
1 Introduction
Fourier's law of thermal conduction states that the steady-state heat current is proportional to the local temperature gradient applied; the proportionality constant being the material's intrinsic thermal conductivity.1 Even if there is still no rigorous derivation of this law starting from a microscopic Hamiltonian description,2–4 it has been for 200 years enormously successful in providing a reliable description of heat transport phenomena in bulk, 3D materials. In contrast, its reliability for low-dimensional structures is far from clear and every evidence of its breakdown is seen as a possibility to shed light on its understanding.5–16 On the one hand, the chance to observe divergent thermal conductivity, i.e. infinitely-long ranged ballistic transport, has been experimentally17 and theoretically18–20 reported in combination with the lowering of the system dimensionality. On the other hand, the last five years have been witnessing a revival of interest in second sound, namely the propagation of heat as a wave.21–24In insulating crystals these anomalous behaviours and the different thermal transport regimes can be explained in terms of the dominance of different phonon scattering mechanisms. In particular, the physics of heat conduction is ruled by the intriguing interplay between conserving (Normal) and not conserving (Umklapp, boundary, defects, etc.) crystal-momentum scattering processes. More specifically: (i) a predominant role of the boundary scattering identifies the ballistic regime; (ii) strong Umklapp processes dictate the diffusive regime; (iii) in between, when Normal processes are the strongest, Umklapp the weakest and boundary-scattering the intermediate mechanism, the Poiseuille-hydrodynamic regime appears. In this latter condition, Normal processes preserve the heat flux creating a correlation between phonons and giving rise to collective phonon-excitation which alone will not be able to relax the system into full thermal equilibrium, but at most they will bring it into a drifted Bose–Einstein distribution.25 In other words phonons can develop a nonzero drift velocity when subjected to a temperature gradient, very much like the viscous flow of a fluid driven by a pressure gradient. In analogy, such a heat conduction regime is called hydrodynamics phonon transport. Once this drifting distribution ndrift has accumulated, heat propagates as a wave (second sound) that is eventually dampened on longer timescales by the resistive processes (Umklapp, isotopes, etc.). Poiseuille and second sound can then be considered typical of this hydrodynamic regime, but pioneering experiments in the 70s were able to detect second sound in Bi, NaF and 4He only at cryogenic temperatures in a narrow [1.5–5 K] temperature range,26–29 as in bulk 3D systems very low temperatures are required in order to freeze out Umklapp processes.30,31 These limited temperature conditions made these phenomena fascinating, but not particularly appealing since they were hard to detect experimentally and unsuitable for relevant technological applications.
In this framework, little attention has been paid to this subject for decades; only recently with the theoretical predictions to observe second sound up to 100 K in graphene and other 2D materials21,22 and carbon nanotubes,32 the interest on second sound has risen again, eventually leading to its experimental observation at 100 K in graphite.23 From these studies it is found that the occurrence of Umklapp processes towards low-energy phonons with small phonon wave-vector q is severely reduced. These modes, with a large predominance of Normal scatterings, will then carry the majority of the heat flux.33–35 This is due to the fact that by lowering the dimensionality of the system a softening of the corresponding mode will emerge, and this might effectively reduce the phonon Umklapp scattering phase-space. This result leads to a double gain: first of all, thanks to an extended abundance of Normal processes it is possible to reach extremely high thermal conductivities;‡ secondly, the intrinsic limitation of Umklapp scatterings effectively enlarges the temperature window for the observation of hydrodynamic regime up to temperatures where phonon modes with larger q will be populated, Umklapp processes are eventually activated, and thus the diffusive regime reached. This condition also determines an interesting side effect which misguided some interpretations: in the hydrodynamic regime the main heat carriers are not individual phonons, but rather, collective phonon excitations36–40 with mean free paths which can be orders of magnitude longer than those of individual phonons; accordingly, ballistic regimes can occur up to length scales that can be orders of magnitudes longer than those expected on the basis of a standard comparison between the actual sample size and the individual phonon mean free paths.17 For all these reasons, low dimensional systems are then considered crucibles of possible exotic properties.
From an experimental point of view, the observation of phenomena such as Poiseuille flow and second sound means probing a time scale which falls in between the typical Normal and Umklapp relaxation times.22 This short time scale prevents the use of conventional thermal sensors. In this perspective, time-resolved laser-based measurements are better suited for measuring thermal responses, due to their much higher time resolution. In particular, thermoreflectance-based techniques41 use a time modulated laser to heat the surface of a sample. The variation of the surface temperature leads to a corresponding change in reflectance, which is then measured by a probe laser. By comparing the measured reflectance with theoretical calculations, possible deviations in thermal transport with respect to a diffusive regime can be detected. An alternative method named laser-induced transient thermal gratings (TTG)42 recently allowed the direct observation of second sound in graphite at temperatures above 100 K.23 In this method, two crossing laser pulses are used to create a spatially periodic temperature profile, which is usually set as sinusoidal with a controlled spatial period λ. The transient decay of the amplitude of the imposed sinusoidal temperature profile is then sampled via diffraction by a probe laser beam. Even though the laser-induced TTG technique has recently shown to be very effective to detect wave-like thermal transport features in bulk graphite, there are still many issues that make the use of this technique difficult for studying second-sound features on nanomaterials and/or systems with reduced dimensionality. In this respect, the main issue is the reduced spatial resolution which limits TTG techniques to spatial periods lower than a few μm, thus limiting the overall size of the systems to be analyzed. Moreover, TTG shows a time-resolution in the order of the nanosecond, indeed a feature limiting the frequencies of the detectable second sound signal to just a few GHz. All the above issues are even more severe when dealing with 1D materials, where the limitations in time- and length- resolution (as well as the difficulties in their synthesis) make the experimental detection of second-sound very difficult. In this perspective, the atomistic simulations are an alternative tool to address phenomena occurring at time and length scales which are experimentally hard to address. It is worth stressing that 1D systems are extensively investigated since they represent a convenient playground for both analytical and computer-based investigations; furthermore, the thermal conductivities κ in 1D systems are found to depend on the system length L and will eventually diverge in the thermodynamic limit L → ∞. This issue has captured the attention of the community and 1D systems are considered perfect test cases for better understanding the condition for the non-validity of the Fourier's heat conduction law. The overall momentum conservation appears to be a key factor for the anomalous behaviour,43–49 even with some exceptions such as a 1D coupled rotator system50–52 and the chain with a double-well potential,53 however only a few studies have focused their attention on second sound:32,51 besides ideal single chains described with different model potentials54 and carbon nanotubes,32 no other studies described wave-like transport on these systems.
This state of affairs has motivated us to focus on what could be referred to as the prototypical 1D system, namely cumulene, which has been recently identified as the material with the highest lattice thermal conductivity55 and with a negligible electronic contribution.56 Cumulene is a carbyne isomer,57 showing a simple double bond sequence. It was synthesized in 201558 and its stability has been assessed up to 499 K,59 above which it transforms into the other carbyne isomer, the semiconducting polyyne, where single alternate to triple bonds. Our goal consists in taking this system as a representative/Gedanken experiment to identify all the physical elements necessary for observing second sound. In order to do that, we developed a procedure based on model-potential Molecular Dynamics (MD) that allows to accurately simulate laser-induced TTG by spanning time, length and temperature ranges significantly larger than the experimental ones. Using this procedure, we predict second sound at room temperature for cumulene chains with lengths up to hundreds of microns. We also estimated a second sound velocity vss as large as 2.680 km s−1, in good agreement with the one estimated using the microscopic derivation of Hardy.36
From a theoretical point of view a predictive theory resides on the good description of the harmonic (i.e. the phonon distribution, population and group velocities) and the anharmomic (i.e. phonon lifetimes and scatterings rates) properties of the system under study. By just considering first order anharmonicity and therefore three phonon scatterings, the only possible processes§ are those in which two phonons combine to give a third one and vice versa q1 + q2 ⇆ q3. At the same time, conservation of energy requires E1 + E2 = E3 where q1,2,3 and E1,2,3 are the wave-vectors and the energies of the three individual phonons. As long as q1, q2 and q3 stay all inside the 1st Brillouin Zone (BZ) this process will be called Normal scattering. If, in contrast, q1 and q2 are so large to make their sum q3 lie outside the 1BZ, it will become necessary to add a reciprocal lattice vector G in order to fold q3 back to its equivalent wave-vector within the 1BZ (q1 + q2 = q3 + G). This corresponds to an Umklapp process. On the basis of this definition, it is necessary to accurately reproduce the phonon dispersion over the entire first BZ in order to correctly mimic the good momentum and energy conservation conditions associated with each scattering event.
2 Results and discussion
We developed and implemented in LAMMPS60 a specific Class II force field61 able to reproduce the phonon dispersion curves calculated at the Density Functional Theory (DFT) level (see the ESI† for all the technical details). Fig. 1 shows the comparison between the phonon dispersion curves obtained by the adopted model potential (red lines) and DFT (black lines). For sake of comparison we also report the phonon dispersion previously obtained by a different force field55 showing a much less satisfactory agreement with DFT. Such an unsatisfactory description of the phonon spectrum might lead to an incorrect description of (i) Umkapp/Normal relative proportion, (ii) mean free path lengths of the heat-carriers and (iii) intrinsic thermal conductivity (see the ESI†). We stress that our potential (containing anharmonic and cross-coupling terms) allows us to describe the quadraticity of the degenerate transversal acoustic modes (TA) as well as the Kohn anomaly occurring in the longitudinal acoustic mode (LA), both important features missing in ref. 55. It is then of fundamental importance to accurately describe all the interatomic interactions within the system since thermal transport features (e.g. wave-like/anomalous, diffusive transport) are sensitive to the specific intrinsic and extrinsic source of scattering included.50,51,62,63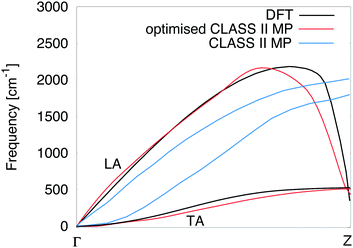 | ||
| Fig. 1 Phonon dispersion curves of cumulene obtained via first principles Density Functional Theory (DFT) calculations (black solid lines), a standard Class II model potential (MP) (blue solid lines)55 and the present optimized Class II MP with the inclusion of cross-coupling terms (red solid lines). | ||
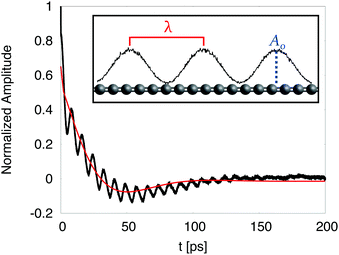
The simulation procedure used to mimic time-resolved optical measurements proceeds through two steps. At first, an initial sinusoidal temperature profile T(x,t) = T0 − A0cos(qx) (where q = 2π/λ, λ the spatial period, A0 = 10 K the initial profile amplitude and T0 the average temperature) was imposed to a single cumulene chain with length Lx. Thermalization was next performed by ideally (i) dividing the system in segments, (ii) exciting all the allowed vibrational modes of each segment at a local value of temperature by means of a white Langevin thermostat, and (iii) periodically varying the local value of temperature along the chain backbone. As a matter of fact, such an initial non-equilibrium condition corresponds to white Langevin thermostatting. The second step consisted in the removal of the Langevin thermostat. The following transient relaxation of the cumulene chain towards a stationary temperature profile was studied in a microcanonical ensemble by monitoring the time evolution of the amplitude A(t) and the temperature profile T(x,t) with a time-resolution as small as 10 ps. All the simulations have been performed by integrating the equation of motions using the velocity-Verlet algorithm with a time step of 0.1 fs. In order to suppress statistical fluctuations, an average over N trajectories (where N varies from 40 up to 1600, depending on the chain length) was performed to obtain the final A(t) profiles. Each simulation corresponding to a specific λ value has been performed using periodic boundary conditions in a simulation box with length Lx = 3λ. In detail, for λ = 0.0409, 0.409, 4.090 and 40.90 μm the corresponding lengths Lx of the simulation box were 0.1228 (103 atoms), 1.228 (104 atoms), 12.28 and (105 atoms) and 122.80 μm (106 atoms) respectively. The corresponding maximum simulation times were 50, 200, 1800 and 15000 ps.
Fig. 2 shows the time evolution of the normalized amplitude A(t)/A0 of the temperature profile along a cumulene chain with length Lx = 1.228 μm. The spatial period of the temperature profile was set as λ= 0.41 μm. Damped oscillations are observed with a sign flip in A(t) after ∼27 ps. As pointed out in ref. 23, this behaviour implies that the spatial phase of the initial sinusoidal temperature profile has shifted by π; or, equivalently, the local maxima converted into minima and vice versa, key feature of wave-like propagation since in principle, in the diffusive regime maxima and minima should not switch simply because the heat moves only from hotter to colder regions. This scenario is fully confirmed in Fig. 3, where we clearly observe that the sinusoidal temperature profile is at first quickly flattened (corresponding to A(t) = 0) during the first ∼27 ps; next, the signal amplitude undergoes a π phase shift reaching its maximum negative amplitude at t∼37 ps. The following profile evolution consists in similar phase oscillations with increasingly damped amplitude. Eventually at t∼200 ps the temperature profile becomes definitely flat.
The heat equation best describing mesoscopic wave-like thermal transport is the phenomenological hyperbolic Maxwell–Cattaneo–Vernotte (MCV) equation:
 | (1) |
 . The MCV 1D solution under periodic boundary conditions is:64A(t) ∼ exp(−t/2τss)cos(qvsst), where q = 2π/λ is the wavevector and vss is the second sound velocity. We observe from Fig. 2 (full red line) that such a solution provides a pretty accurate fit of the amplitude decay generated by the above MD simulations, further confirming the wave-like nature of thermal transport in this case. Moreover, the present fitting procedure allows us to estimate vss and τss for different spatial periods and temperatures (see the ESI†). As mentioned above the occurrence of a wave-like thermal transport is due to the dominance of Normal over border and Umklapp phonon scattering events. By rising the temperature an increase in the occurrence of Umklapp processes is expected with then a corresponding transition towards the diffusive regime. We investigated this phenomenon by studying the time evolution of the amplitude A(t) in a chain with length Lx = 12.280 μm at three different average temperatures 30 K, 300 K, and 450 K. In these simulations we set λ = 4.09 μm.
. The MCV 1D solution under periodic boundary conditions is:64A(t) ∼ exp(−t/2τss)cos(qvsst), where q = 2π/λ is the wavevector and vss is the second sound velocity. We observe from Fig. 2 (full red line) that such a solution provides a pretty accurate fit of the amplitude decay generated by the above MD simulations, further confirming the wave-like nature of thermal transport in this case. Moreover, the present fitting procedure allows us to estimate vss and τss for different spatial periods and temperatures (see the ESI†). As mentioned above the occurrence of a wave-like thermal transport is due to the dominance of Normal over border and Umklapp phonon scattering events. By rising the temperature an increase in the occurrence of Umklapp processes is expected with then a corresponding transition towards the diffusive regime. We investigated this phenomenon by studying the time evolution of the amplitude A(t) in a chain with length Lx = 12.280 μm at three different average temperatures 30 K, 300 K, and 450 K. In these simulations we set λ = 4.09 μm.
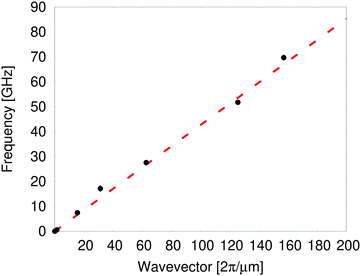
In order to quantitatively analyse the transition from the hydrodynamic to the diffusive transport, we perform the Fourier transform FA(ω) of the time dependent amplitude as shown in Fig. 4. At T = 30 K, we observe a peak at a frequency ∼0.6 GHz in the same range of the “second sound” peaks observed in graphite [23] for similar spatial periods. At T = 300 K this peak is significantly damped, while at T = 450 K it disappears. In the latter case we observe the typical functional form FA(ω) ∼a/(a2 + ω2) corresponding to the Fourier transform of an exponential decay e(at). Other details of the calculated FA(ω) are discussed in the ESI.†
In general, the experimental limitation in time-resolution prevents probing the system response for initial spatial periods lower than a few μm. Instead, by exploiting the extremely high resolution (100 GHz) of our MD simulations, we can address the system response for initial spatial periods spanning 4 orders of magnitude (from 0.04 μm up to 40 μm). The results in Fig. 4 show that second sound occurs in cumulene at T = 300 K provided that a suitably short modulation of the initial temperature profile is set up. More specifically, Fig. 4 shows a clear peak at T = 300 K at a frequency ∼12 GHz for λ = 0.409 μm. For λ = 4.090 μm, we observe a shift of the peak down to ∼0.6 GHz and a corresponding damping of the intensity. Finally, for λ = 40.900 μm, the peak completely disappears. In general, we observe a shift towards lower frequencies by increasing λ as shown in Fig. 5. As reported for graphite[23], we observe a nearly linear dependence ω = ω(q), which allows us to estimate the corresponding second sound velocity vss = 2.680 ± 0.055 km s−1 at T = 30 K in remarkable agreement with the vss = 2.470 ± 0.18 km s−1 obtained at the same temperature by fitting the A(t) time-decay with the approximate solution of the Maxwell–Cattaneo–Vernotte as explained above. Interestingly, this value is also comparable with the one of graphene (1.9–2.0 km s−1) at the same temperature.21,24
As expected, this velocity is much lower with respect to the sound velocity in cumulene, which we estimated from the phonon dispersion curves of Fig. 1 to be as large as 36 km s−1, in very good agreement with the value of 31.5 km s−1 obtained by DFT.65 In order to assess the validity of this procedure, we independently estimate vss according to ref. 36.
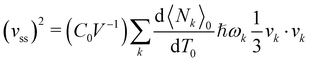 | (2) |
Standard features of wave propagation in nonlinear optical media are higher harmonic generation and sum-frequency generation. At the present stage our simulation procedure does not in principle allow us to detect any nonlinear phononic phenomena due to the fact that the spatial sinusoidal temperature profile is initialized by a white thermalization, i.e. by exciting all the vibrational degrees of freedom. An alternative procedure, which could in principle detect any nonlinear phononic behaviour, should initially thermalize the cumulene chain by selecting a specific phonon mode, e.g. by exciting the displacement pattern of a specific mode, see for example our implementation in ref. 66. Then, by monitoring the time evolution of the spectral energy density, it is in principle possible to detect nonlinear phonic behaviours such as second harmonic generation or sum-frequency generation, see e.g.ref. 67.
3 Conclusions
In conclusion, by means of molecular dynamics we have simulated time-resolved optical measurements aimed at unveiling wave-like features in the transport of heat. We applied this procedure to a single μm-long cumulene chain predicting for such a system second sound even at room temperature. The transition is observed by raising the temperature and activating the Umklapp process connected with the dynamical interactions between CC stretching vibrational coordinates. This behaviour finds complete analogy with the transition from anomalous to normal behavior observed in other 1D chains where by tuning the temperatures it is possible to switch on/off channels of scattering which destroy the momentum conservation.50,51,63 Moreover, we have also been able to prove how, by tuning the length of the initial sinusoidal spatial period λ, it is possible to modulate the transition from the hydrodynamic to the diffusive regime. The present procedure also allows us to estimate via three different theoretical methodologies a cumulene second sound velocity vss in the range of 2.4–3.2 km s−1.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed under the Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme; in particular, GF gratefully acknowledges the computer resources and technical support provided by CINECA.Notes and references
- J.-B. J. Fourier, Encyclopedia Brittannica, 1952.
- F. Bonetto, J. L. Lebowitz and L. Rey-Bellet, Mathematical physics 2000, World Scientific, 2000, pp. 128–150 Search PubMed.
- S. Lepri, R. Livi and A. Politi, Phys. Rep., 2003, 377, 1–80 CrossRef CAS.
- P. L. Garrido, J. Marro and F. de los Santos, AIP Conf. Proc., 2011, 1332, 3–22 CrossRef.
- D. G. Cahill, P. V. Braun, G. Chen, D. R. Clarke, S. Fan, K. E. Goodson, P. Keblinski, W. P. King, G. D. Mahan and A. Majumdar, et al. , Appl. Phys. Rev., 2014, 1, 011305 Search PubMed.
- S. Lepri, R. Livi and A. Politi, EPL, 1998, 43, 271 CrossRef CAS.
- M. Chester, Phys. Rev., 1963, 131, 2013 CrossRef.
- P. I. Hurtado and P. L. Garrido, Sci. Rep., 2016, 6, 38823 CrossRef CAS PubMed.
- A. Dhar, Adv. Phys., 2008, 57, 457–537 CrossRef CAS.
- A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902–907 CrossRef CAS PubMed.
- J. Liu and R. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 104307 CrossRef.
- T.-K. Hsiao, H.-K. Chang, S.-C. Liou, M.-W. Chu, S.-C. Lee and C.-W. Chang, Nat. Nanotechnol., 2013, 8, 534–538 CrossRef CAS PubMed.
- H. Spohn, J. Stat. Phys., 2014, 154, 1191–1227 CrossRef.
- E. R. Smith, P. J. Daivis and B. D. Todd, J. Chem. Phys., 2019, 150, 064103 CrossRef CAS PubMed.
- G. R. Lee-Dadswell, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 012138 CrossRef CAS PubMed.
- S. Liu, P. Hänggi, N. Li, J. Ren and B. Li, Phys. Rev. Lett., 2014, 112, 040601 CrossRef PubMed.
- X. Xu, L. F. Pereira, Y. Wang, J. Wu, K. Zhang, X. Zhao, S. Bae, C. T. Bui, R. Xie and J. T. Thong, et al. , Nat. Commun., 2014, 5, 1–6 Search PubMed.
- L. F. C. Pereira and D. Donadio, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 125424 CrossRef.
- A. Crnjar, C. Melis and L. Colombo, Phys. Rev. Mater., 2018, 2, 015603 CrossRef CAS.
- S. Lepri, R. Livi and A. Politi, Phys. Rep., 2003, 377, 1–80 CrossRef CAS.
- S. Lee, D. Broido, K. Esfarjani and G. Chen, Nat. Commun., 2015, 6, 6290 CrossRef CAS.
- A. Cepellotti, G. Fugallo, L. Paulatto, M. Lazzeri, F. Mauri and N. Marzari, Nat. Commun., 2015, 6, 1–7 Search PubMed.
- S. Huberman, R. A. Duncan, K. Chen, B. Song, V. Chiloyan, Z. Ding, A. A. Maznev, G. Chen and K. A. Nelson, Science, 2019, 364, 375–379 CrossRef CAS.
- P. Scuracchio, K. Michel and F. Peeters, Phys. Rev. B, 2019, 99, 144303 CrossRef CAS.
- J. Callaway, Phys. Rev., 1959, 113, 1046–1051 CrossRef CAS.
- V. Narayanamurti and R. Dynes, Phys. Rev. Lett., 1972, 28, 1461 CrossRef CAS.
- T. McNelly, S. Rogers, D. Channin, R. Rollefson, W. Goubau, G. Schmidt, J. Krumhansl and R. Pohl, Phys. Rev. Lett., 1970, 24, 100 CrossRef CAS.
- C. C. Ackerman, B. Bertman, H. A. Fairbank and R. Guyer, Phys. Rev. Lett., 1966, 16, 789 CrossRef CAS.
- M. Markov, J. Sjakste, G. Barbarino, G. Fugallo, L. Paulatto, M. Lazzeri, F. Mauri and N. Vast, Phys. Rev. Lett., 2018, 120, 075901 CrossRef CAS PubMed.
- R. Peierls, Ann. Phys., 1929, 395, 1055–1101 CrossRef.
- J. Ziman, Electrons and Phonons: The Theory of Transport Phenomena in Solids, Oxford University Press, USA, 2001 Search PubMed.
- S. Lee and L. Lindsay, Phys. Rev. B, 2017, 95, 184304 CrossRef.
- L. Lindsay, D. A. Broido and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115427 CrossRef.
- N. Bonini, J. Garg and N. Marzari, Nano Lett., 2012, 12, 2673–2678 CrossRef CAS PubMed.
- L. Paulatto, F. Mauri and M. Lazzeri, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 214303 CrossRef.
- R. J. Hardy, Phys. Rev. B: Solid State, 1970, 2, 1193 CrossRef.
- G. Fugallo, A. Cepellotti, L. Paulatto, M. Lazzeri, N. Marzari and F. Mauri, Nano Lett., 2014, 14, 6109–6114 CrossRef CAS PubMed.
- A. Cepellotti and N. Marzari, Phys. Rev. X, 2016, 6, 041013 Search PubMed.
- F. X. Alvarez, D. Jou and A. Sellitto, J. Appl. Phys., 2009, 105, 014317 CrossRef.
- A. Cepellotti and N. Marzari, Nano Lett., 2017, 17, 4675–4682 CrossRef CAS PubMed.
- A. J. Schmidt, R. Cheaito and M. Chiesa, Rev. Sci. Instrum., 2009, 80, 094901 CrossRef PubMed.
- H. J. Eichler, P. Günter and D. W. Pohl, Laser-induced dynamic gratings, Springer, 2013, vol. 50 Search PubMed.
- B. Hu, B. Li and H. Zhao, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 2992 CrossRef CAS.
- T. Prosen and D. K. Campbell, Phys. Rev. Lett., 2000, 84, 2857 CrossRef CAS PubMed.
- P. Grassberger, W. Nadler and L. Yang, Phys. Rev. Lett., 2002, 89, 180601 CrossRef PubMed.
- O. Narayan and S. Ramaswamy, Phys. Rev. Lett., 2002, 89, 200601 CrossRef PubMed.
- G. Lee-Dadswell, B. Nickel and C. Gray, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 031202 CrossRef CAS.
- G. Basile, C. Bernardin and S. Olla, Phys. Rev. Lett., 2006, 96, 204303 CrossRef PubMed.
- T. Mai, A. Dhar and O. Narayan, Phys. Rev. Lett., 2007, 98, 184301 CrossRef PubMed.
- C. Giardina, R. Livi, A. Politi and M. Vassalli, Phys. Rev. Lett., 2000, 84, 2144 CrossRef CAS PubMed.
- O. Gendelman and A. Savin, Phys. Rev. Lett., 2000, 84, 2381 CrossRef CAS PubMed.
- E. Pereira and R. Falcao, Phys. Rev. Lett., 2006, 96, 100601 CrossRef PubMed.
- D. Xiong, J. Stat. Mech.: Theory Exp., 2016, 2016, 043208 CrossRef.
- O. V. Gendelman and A. V. Savin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 020103 CrossRef PubMed.
- M. Wang and S. Lin, Sci. Rep., 2015, 5, 18122 CrossRef CAS PubMed.
- H. Zhan and Y. Gu, in Thermal Transport in Carbon-Based Nanomaterials, ed. G. Zhang, Elsevier, 2017, pp. 185–204 Search PubMed.
- R. B. Heimann, S. E. Evsyukov and L. Kavan, Carbyne and Carbynoid Structures, Springer Science & Business Media, 1999, vol. 21 Search PubMed.
- C. B. Cannella and N. Goldman, J. Phys. Chem. C, 2015, 119, 21605–21611 CrossRef CAS.
- X. Liu, G. Zhang and Y.-W. Zhang, J. Phys. Chem. C, 2015, 119, 24156–24164 CrossRef CAS.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, Sandia national labs., albuquerque, nm (united states) technical report, 1993.
- J. R. Maple, M.-J. Hwang, T. P. Stockfisch, U. Dinur, M. Waldman, C. S. Ewig and A. T. Hagler, J. Comput. Chem., 1994, 15, 162–182 CrossRef CAS.
- A. Chaudhuri, A. Kundu, D. Roy, A. Dhar, J. L. Lebowitz and H. Spohn, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 064301 CrossRef.
- D. Roy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 041102 CrossRef PubMed.
- A. M. Krivtsov, 2015, arXiv preprint arXiv:1509.02506.
- I. E. Castelli, P. Salvestrini and N. Manini, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 214110 CrossRef.
- G. Barbarino, G. Fugallo, C. Melis, F. Mauri and L. Colombo, Phys. Rev. B, 2016, 94, 245437 CrossRef.
- A. Bojahr, M. Gohlke, W. Leitenberger, J. Pudell, M. Reinhardt, A. von Reppert, M. Roessle, M. Sander, P. Gaal and M. Bargheer, Phys. Rev. Lett., 2015, 115, 195502 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00501d |
| ‡ Unless the presence of other phonon scattering mechanisms becomes effective in the region of small q. |
| § Conservation of energy forbids the simultaneous creation or annihilation of phonons even though terms to this effect appear in the interaction Hamiltonian. |
| This journal is © the Owner Societies 2021 |