Open Access Article
Open Access ArticleBenchmark ab initio proton affinity of glycine
András B.
Nacsa
and
Gábor
Czakó
 *
*
MTA-SZTE Lendület Computational Reaction Dynamics Research Group, Interdisciplinary Excellence Centre and Department of Physical Chemistry and Materials Science, Institute of Chemistry, University of Szeged, Rerrich Béla tér 1, Szeged H-6720, Hungary. E-mail: gczako@chem.u-szeged.hu
First published on 30th March 2021
Abstract
A systematic conformational search reveals three N- (amino) and eight O- (carbonyl) protonated glycine conformers with benchmark equilibrium(adiabatic) relative energies in the 0.00–7.51(0.00–7.37) and 25.91–31.61(24.45–30.28) kcal mol−1 ranges, respectively. Benchmark ab initio structures of the glycine conformers and its protonated species are obtained at the CCSD(T)-F12b/aug-cc-pVTZ level of theory and the relative energy computations consider basis-set effects up to aug-cc-pVQZ with CCSD(T)-F12b, electron correlation up to CCSDT(Q), core correlation corrections, scalar relativistic effects, and zero-point energy contributions. The best predictions for Boltzmann-averaged 0(298.15) K proton affinities and [298.15 K gas-phase basicities] of glycine are 211.00(212.43)[204.75] and 186.38(187.64)[180.21] kcal mol−1 for N- and O-protonation, respectively, in excellent agreement with experiments.
I. Introduction
Proton affinity of molecules plays an important role in chemistry and biochemistry. The fragmentation pathways of protonated peptides and proteins can be followed by mass spectrometry experiments and the proton affinity (PA) as well as the related gas-phase basicity (GB) values of the protonation sites may control the outcome of these fragmentation processes.1,2 Numerous theoretical and experimental studies investigated the PA and GB of amino acids in the past couple of decades.3–28 However, even for the simplest amino acid, glycine, only the use of low-level electronic structure theories such as density functional theory (DFT) and second-order Møller–Plesset perturbation (MP2) methods with double- and triple-zeta basis sets was feasible in the 1990's and 2000's.3,5,7,9–11,14,17,18,25,27 The highest-level theoretical studies used B3LYP or MP2 with the 6-311++G** basis for geometry optimizations and QCISD(T) or CCSD(T) with 6-311+G** for single-point energy computations.12,13,24 Even in 2008 it was still not viable to perform geometry optimizations using the gold-standard CCSD(T) method with a reasonably large basis set for amino acids; therefore, high-level benchmark ab initio PA studies focused on few-atom systems such as CO,29 NH3,29 and H2CO.30 Thanks to the method and computational hardware developments during the last decade, quantum chemistry has arrived to a stage where high-level explicitly-correlated CCSD(T)-F12 geometry computations are affordable for amino-acid-size molecules.Following recent theoretical work on glycine31–35 and our high-level explicitly-correlated ab initio study on its dehydrogenated radicals,36 here we report benchmark PA and GB values for glycine. The present study aims to move beyond previous work from both qualitative and quantitative points of view. Qualitatively, we plan to perform a comprehensive and systematic conformational search for protonated glycine isomers considering different protonation sites, thereby possibly revealing new conformers, which were not considered in former studies. Quantitatively, we report the first CCSD(T)-F12 structures and vibrational frequencies for protonated glycine conformers and consider energy effects of the large aug-cc-pVQZ basis set, post-CCSD(T) electron correlation up to CCSDT(Q), core-core and core-valence correlation, and scalar relativity for glycine and its protonated species, thus providing benchmark absolute PA and GB values for the simplest amino acid, which may be utilized in mass spectrometry experiments where usually relative PA values can be determined. Besides the benchmark data for glycine, the present study shows the magnitude and assesses the importance of the above-mentioned auxiliary energy corrections, thereby guiding future ab initio investigations for larger systems.
II. Computational details
A. Conformers of protonated glycine isomers
Our first goal is to determine all the conformers of the protonated glycine isomers. First of all, we check the possible protonation sites on the amino acid. One may assume three variations, +H3N–CH2–COOH, H2N–CH2–C+(OH)2, and H2N–CH2–CO(OH2)+, corresponding to the protonation of the amino, carbonyl, and hydroxyl groups, respectively. To test these chemically predicted structures, we take the eight known conformers of the glycine molecule37 and attach one extra proton to the above mentioned sites separately. For the amino group, we arrange the new atom to get an approximately tetrahedral structure around the nitrogen atom and create two sets of inputs – in the second one the NH3+ group is rotated by 60°. There are also two sets of initial structures for the protonation of the carbonyl and the hydroxyl groups. In the former case, the newly formed O–H group can be in cis or trans arrangement relative to the other O–H, while in the latter case, the two O–H bonds are either in the N–C–C plane or not. We optimize these initial structures and compute the harmonic frequencies using the MP2 method38 with the correlation-consistent aug-cc-pVDZ basis set.39 We note in advance that we find that the protonation of the hydroxyl group does not result in stable conformers.To map the complete conformational space of the protonated glycine, we execute a systematical mapping starting from the simplest cases, the N- (amino) and O- (carbonyl) protonated lowest-energy conformer of the amino acid (Ip). For the two isomers we produce different initial geometries based on the description of the torsional motions belonging to the N-protonated {NH3, COOH, OH} groups and the O-protonated {NH2, C(OH)2, and two OH} groups as shown in Fig. 1. The variation of the corresponding torsional angles by 60° steps (six step, since 0°and 360° are equivalent) leads to 63 = 216 and 64 = 1296 N- and O-protonated arrangements, respectively, which may be reduced by recognizing symmetry. For the optimizations we use the MP2/aug-cc-pVDZ level of theory, we assign the results to different conformers and we also perform harmonic frequency computations to determine whether they are minima (all real frequencies) or saddle points (one imaginary frequency).
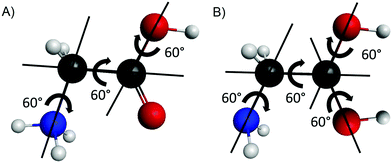 | ||
| Fig. 1 Sketches describing the internal rotations of the N-protonated (A) and O-protonated (B) glycine isomers. | ||
B. Benchmark structures and energies
We further optimize the conformers (minima) of glycine and its protonated counterparts by the explicitly-correlated coupled-cluster singles, doubles, and perturbative triples method (CCSD(T)-F12b)40 using the aug-cc-pVDZ (geometry and frequency), aug-cc-pVTZ (geometry), and aug-cc-pVQZ (energy) basis sets.39 We deal with the following additive energy corrections obtained at the best (CCSD(T)-F12b/aug-cc-pVTZ) geometries:- Coupled-cluster triples41 (δT) and perturbative quadruples42 (δ(Q)) corrections are determined using the 3-21G,43 6-31G,44 and cc-pVDZ39 basis sets and the best estimates are obtained as
| δT = CCSDT/cc-pVDZ − CCSD(T)/cc-pVDZ; | (1) |
| δ(Q) = CCSDT(Q)/cc-pVDZ − CCSDT/cc-pVDZ. | (2) |
- To include all-electron (AE) corrections, AE and frozen-core (FC) energies are computed at the CCSD(T)-F12b/cc-pCVTZ-F12 level of theory40,45 and the core correlation correction is defined as
| Δcore = AE-CCSD(T)-F12b/cc-pCVTZ-F12 − FC-CCSD(T)-F12b/cc-pCVTZ-F12. | (3) |
The standard FC computations only correlate the electrons on the valence shells, whereas AE methods correlate the 1s2 electrons of the C, N, and O atoms as well.
- We also compute second-order Douglas–Kroll (DK)46 relativistic energies using the AE-CCSD(T) method47 with the aug-cc-pwCVTZ-DK basis set48 to determine the scalar relativistic effects:
| Δrel = DK-AE-CCSD(T)/aug-cc-pwCVTZ-DK − AE-CCSD(T)/aug-cc-pwCVTZ. | (4) |
- Zero-point energy corrections (ΔZPE) are based on the CCSD(T)-F12b/aug-cc-pVDZ harmonic frequency results.
Finally, one can obtain the benchmark electronic (equilibrium) and adiabatic (ZPE corrected) energies by the expressions in order:
| Ee = CCSD(T)-F12b/aug-cc-pVQZ + δT + δ(Q) + Δcore + Δrel; | (5) |
| H0 = CCSD(T)-F12b/aug-cc-pVQZ + δT + δ(Q) + Δcore + Δrel + ΔZPE. | (6) |
The MP2, CCSD(T)-F12b, AE-CCSD(T)-F12b, AE-CCSD(T), and DK-AE-CCSD(T) computations are carried out using the MOLPRO program package49 and the CCSD(T) and CCSDT(Q) computations are performed with MRCC50,51 interface to MOLPRO. For CCSD(T)-F12b and AE-CCSD(T)-F12b the default auxiliary basis sets are used as implemented in MOLPRO.
C. Proton affinity and gas-phase basicity computations
Consider the following gas-phase reaction:| BH+(g) → B(g) + H+(g), | (R1) |
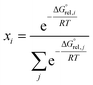 | (7) |
 is the molar standard Gibbs free energy of the i-th conformer relative to the most stable conformer.
is the molar standard Gibbs free energy of the i-th conformer relative to the most stable conformer.
III. Results and discussion
A. Conformers of the protonated glycine
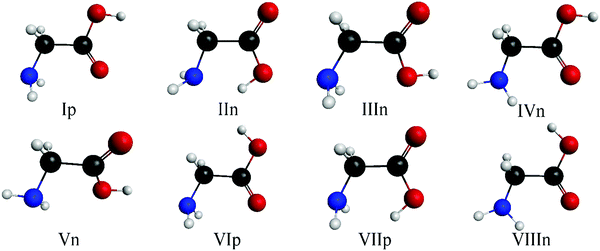
The eight minima of the glycine amino acid are well known at different levels of theory;36,37,52 these can be seen in Fig. 2. The nomenclature follows the traditional notation37 by increasing roman numbers with increasing energies (except for IIIn and IVn) with the p and n letters referring to planar (Cs) (only three of them) and non-planar (C1) symmetry, respectively.By chemical intuition, we predict three possible sites for the protonation of glycine: the amino, the carbonyl, and the hydroxyl group. As mentioned in Section II, we validate this by connecting a proton to these groups of the eight known conformer, one by one, and run geometry optimizations at the MP2/aug-cc-pVDZ level of theory. The investigations show that the protonation of the amino and carbonyl group leads to stable minima and transition states. For the hydroxyl site, the computations, even if there is convergence in 100 steps, end in an amino/carbonyl protonated structure or a cation–water complex with elonged C–O bond,3,18 hence we can categorize the conformers into N- (amino) and O- (carbonyl) protonated ones.
The systematic conformational search based on 216 initial geometries for the N-protonated conformers emerges into 15 cases where there is no convergence (NC), 15 structures that are (three distinct) transition states (TS), which can be produced by simple internal rotations of the minima, and three different conformers with the occuring ratio of 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 69
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 69 (∼2
69 (∼2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) as shown in Fig. 3. The structures of the three N-protonated conformers can be seen in Fig. 4 with the notation of roman numbers increasing with the increase of the CCSD(T)-F12b/aug-cc-pVQZ energies, the p refers to Cs symmetry and subscript-index N means N-protonated conformer. All of them have Cs symmetry and have close relationship with the original glycine minima. The IpN structure, which has the lowest energy, can be derived from the global minimum of the amino acid by simply attaching a proton to the amino group and rotating it 60°, otherwise we achieve a transitional state. This structural change allows the formation of a hydrogen bond between a hydrogen atom and a lone electron pair of the oxygen atom. The situation is the same in the case of the IIIpN and VIp structures. IIpN can be paired with the IIIn minimum, but there is no possibility to form an intramolecular hydrogen bond, thus the amino group is altered by 60° in respect of the previous two conformers.
3) as shown in Fig. 3. The structures of the three N-protonated conformers can be seen in Fig. 4 with the notation of roman numbers increasing with the increase of the CCSD(T)-F12b/aug-cc-pVQZ energies, the p refers to Cs symmetry and subscript-index N means N-protonated conformer. All of them have Cs symmetry and have close relationship with the original glycine minima. The IpN structure, which has the lowest energy, can be derived from the global minimum of the amino acid by simply attaching a proton to the amino group and rotating it 60°, otherwise we achieve a transitional state. This structural change allows the formation of a hydrogen bond between a hydrogen atom and a lone electron pair of the oxygen atom. The situation is the same in the case of the IIIpN and VIp structures. IIpN can be paired with the IIIn minimum, but there is no possibility to form an intramolecular hydrogen bond, thus the amino group is altered by 60° in respect of the previous two conformers.
 | ||
| Fig. 4 The conformers of N-protonated glycine, p denotes planar (Cs) symmetry and N stands for N-protonation. | ||
Approximately half of the 1296 O-protonated initial geometries converges to two of the N-protonated minima (Fig. 3), which indicates that the O-protonated structures have higher energies. The absence of IIpN conformer can be explained by the trans arrangement of the carbonyl and the protonated amino groups in IIpN. 50 geometries end up with no convergence and 20 in four different transition states. We find eight distinct minima obtained 131![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 83
83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132
132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99
99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 times from the 1296 initial geometries as seen Fig. 3. The structures of the eight O-protonated glycine conformers are shown in Fig. 5. The notation of roman numbers inreases with increasing CCSD(T)-F12b/aug-cc-pVQZ energies, p and n refers to planar (Cs) (only two of them) or non-planar (C1) symmetry and subscript O means O-protonated conformer. Four of them (InO, IIpO, IVnO, and VIpO) are resembling the original glycine conformers, and the protonated-carboxylic group is in the main plane of the molecule (N–C–C plane), differing in the relative orientation of the hydroxyl and amino groups. The rotation of the hydroxyl-group by 180° on the side of the amino group would lead to either IpN or IIIpN minimum. The other four structures (IIInO, VnO, VIInO, and VIIInO) have their protonated-carboxylic group tilted (almost) perpendicularly to the N–C–C plane, these are not resembling much to the original amino acid conformers and have smaller occurrences (except VnO) than the others.
29 times from the 1296 initial geometries as seen Fig. 3. The structures of the eight O-protonated glycine conformers are shown in Fig. 5. The notation of roman numbers inreases with increasing CCSD(T)-F12b/aug-cc-pVQZ energies, p and n refers to planar (Cs) (only two of them) or non-planar (C1) symmetry and subscript O means O-protonated conformer. Four of them (InO, IIpO, IVnO, and VIpO) are resembling the original glycine conformers, and the protonated-carboxylic group is in the main plane of the molecule (N–C–C plane), differing in the relative orientation of the hydroxyl and amino groups. The rotation of the hydroxyl-group by 180° on the side of the amino group would lead to either IpN or IIIpN minimum. The other four structures (IIInO, VnO, VIInO, and VIIInO) have their protonated-carboxylic group tilted (almost) perpendicularly to the N–C–C plane, these are not resembling much to the original amino acid conformers and have smaller occurrences (except VnO) than the others.
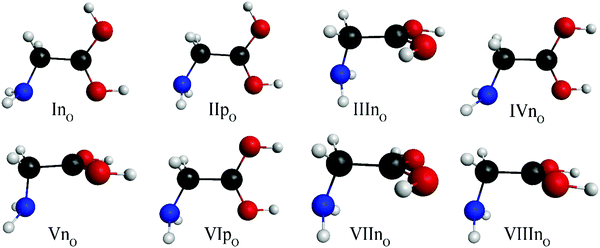 | ||
| Fig. 5 The conformers of O-protonated glycine, p and n denote planar (Cs) and non-planar (C1) symmetry, respectively, and O stands for O-protonation. | ||
B. Benchmark energies
The computed relative energies at different levels of theory can be seen in Table 1 for the conformers of glycine and its protonated analogue forms. Comparing the MP2 and CCSD(T)-F12b methods with same aug-cc-pVDZ basis set one can see an impressive agreement with an average difference of 0.14 kcal mol−1, the only outlier is the IIpN minimum, which has significantly deeper energy (with approximately 0.6 kcal mol−1), according to the MP2 method. Also we can notice, that there are two changes in the energy order with the increasing theoretical level of the methods, see IVnO/VnO and VIpO/VIInO, where the gap between the second pair further increases using larger basis sets. Investigating the convergence of the CCSD(T)-F12b method with different basis sets we can say that the average difference between the aug-cc-pVDZ and aug-cc-pVTZ relative energies is 0.05 kcal mol−1, with the highest value of 0.09 kcal mol−1 in the case of the VIpO conformer. Further increasing the basis to aug-cc-pVQZ results in an average difference of only 0.01–0.02 kcal mol−1 with no outliers, showing the fast basis-set convergence of the explicitly-correlated CCSD(T)-F12b method.| MP2 | CCSD(T)-F12b | δTe | δ(Q)f | Δ core | Δ rel | ΔEei | Δ ZPE | ΔH0k | ΔH298l | ΔG298m | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| aVDZa | aVDZb | aVTZc | aVQZd | ||||||||||
| a MP2/aug-cc-pVDZ relative energies obtained at MP2/aug-cc-pVDZ geometries. b CCSD(T)-F12b/aug-cc-pVDZ relative energies obtained at CCSD(T)-F12b/aug-cc-pVDZ geometries. c CCSD(T)-F12b/aug-cc-pVTZ relative energies obtained at CCSD(T)-F12b/aug-cc-pVTZ geometries. d CCSD(T)-F12b/aug-cc-pVQZ relative energies obtained at CCSD(T)-F12b/aug-cc-pVTZ geometries. e δT correction obtained by CCSDT – CCSD(T) with cc-pVDZ at CCSD(T)-F12b/aug-cc-pVTZ geometries. f δ(Q) correction obtained by CCSDT(Q) – CCSDT with cc-pVDZ at CCSD(T)-F12b/aug-cc-pVTZ geometries. g Core-correlation correction obtained as the difference between AE-CCSD(T)-F12b/cc-pCVTZ-F12 and FC-CCSD(T)-F12b/cc-pCVTZ-F12 relative energies at CCSD(T)-F12b/aug-cc-pVTZ geometries. h Relativistic correction obtained as the difference between Douglas–Kroll AE-CCSD(T)/aug-cc-pwCVTZ-DK and non-relativistic AE-CCSD(T)/aug-cc-pwCVTZ relative energies at CCSD(T)-F12b/aug-cc-pVTZ geometries. i Benchmark relative equilibrium energy obtained by CCSD(T)-F12b/aug-cc-pVQZ + δT + δ(Q) + Δcore + Δrel. j Zero-point energy correction obtained at CCSD(T)-F12b/aug-cc-pVDZ. k Benchmark adiabatic relative energy obtained as ΔEe + ΔZPE. l Relative enthalpy at 298.15 K. m Relative Gibbs free energy at 298.15 K. n The uncertainty of the thermal corrections is above average for these two conformers caused by the accuracy of low-frequency vibrations. | |||||||||||||
| Ip | 0.00 | 0.00 | 0.00 | 0.00 | +0.00 | +0.00 | +0.00 | +0.00 | 0.00 | +0.00 | 0.00 | 0.00 | 0.00 |
| IIn | 0.54 | 0.66 | 0.68 | 0.72 | −0.02 | −0.04 | −0.03 | +0.01 | 0.64 | +0.24 | 0.87 | 0.22n | 1.82n |
| IIIn | 1.59 | 1.73 | 1.73 | 1.73 | +0.00 | −0.01 | +0.01 | +0.00 | 1.73 | +0.04 | 1.77 | 1.77 | 1.20 |
| IVn | 1.25 | 1.23 | 1.23 | 1.24 | +0.00 | +0.00 | −0.01 | +0.00 | 1.24 | −0.02 | 1.22 | 1.17 | 1.43 |
| Vn | 2.43 | 2.59 | 2.62 | 2.65 | +0.00 | −0.01 | +0.01 | +0.00 | 2.65 | +0.08 | 2.74 | 2.66 | 2.90 |
| VIp | 4.86 | 4.79 | 4.80 | 4.81 | −0.03 | +0.00 | +0.02 | +0.00 | 4.80 | −0.17 | 4.63 | 4.68 | 4.65 |
| VIIp | 6.06 | 5.92 | 5.89 | 5.91 | −0.03 | −0.03 | −0.03 | +0.01 | 5.84 | −0.10 | 5.74 | 5.64 | 6.02 |
| VIIIn | 6.25 | 6.05 | 6.06 | 6.08 | −0.03 | +0.00 | +0.00 | +0.00 | 6.06 | −0.14 | 5.93 | 5.90 | 6.16 |
| IpN | 0.00 | 0.00 | 0.00 | 0.00 | +0.00 | +0.00 | +0.00 | +0.00 | 0.00 | +0.00 | 0.00 | 0.00 | 0.00 |
| IIpN | 4.36 | 4.94 | 4.97 | 4.99 | −0.01 | −0.02 | +0.02 | −0.01 | 4.97 | −0.01 | 4.96 | 4.50n | 6.17n |
| IIIpN | 7.55 | 7.49 | 7.51 | 7.52 | −0.03 | −0.01 | +0.02 | +0.00 | 7.51 | −0.13 | 7.37 | 7.31 | 8.08 |
| InO | 0.00 | 0.00 | 0.00 | 0.00 | +0.00 | +0.00 | +0.00 | +0.00 | 0.00 | +0.00 | 0.00 | 0.00 | 0.00 |
| IIpO | 0.62 | 0.70 | 0.67 | 0.67 | +0.00 | +0.00 | +0.00 | +0.00 | 0.67 | +0.02 | 0.69 | 0.58 | 0.88 |
| IIInO | 1.86 | 2.00 | 2.00 | 2.00 | −0.01 | −0.07 | +0.04 | +0.00 | 1.96 | +0.34 | 2.31 | 2.15 | 2.66 |
| IVnO | 3.98 | 3.86 | 3.80 | 3.79 | +0.01 | −0.01 | +0.02 | +0.00 | 3.82 | −0.31 | 3.51 | 3.61 | 3.12 |
| VnO | 3.94 | 3.95 | 3.90 | 3.91 | +0.02 | −0.04 | +0.04 | +0.00 | 3.94 | +0.12 | 4.06 | 4.01 | 4.39 |
| VIpO | 5.20 | 5.15 | 5.06 | 5.06 | +0.01 | −0.01 | +0.02 | +0.00 | 5.08 | −0.25 | 4.83 | 4.75 | 5.03 |
| VIInO | 4.95 | 5.18 | 5.18 | 5.17 | −0.02 | −0.06 | +0.04 | +0.00 | 5.13 | +0.32 | 5.45 | 5.33 | 5.66 |
| VIIInO | 5.67 | 5.78 | 5.72 | 5.72 | +0.01 | −0.09 | +0.06 | −0.01 | 5.70 | +0.13 | 5.82 | 5.68 | 6.28 |
We have also conducted computations for different corrections to get an idea what is the degree of accuracy one can achieve by further increasing the theoretical level and what is the magnitude of error by neglecting various effects. The coupled-cluster post-(T) (full triples and perturbative quadruples) correction with the cc-pVDZ basis set shows that their contributions are between 0.00 and 0.08 kcal mol−1. We cannot say general conclusions about the T terms separately, but the (Q) terms are always negative or 0.00 kcal mol−1 and applying the sum of the two terms results in a smaller relative energy except for IVnO which goes up in energy by 0.01 kcal mol−1, and the relative energy of three conformers (namely IVn, IIpO, VIpO) does not change within 0.00 kcal mol−1 precision. The post-CCSD(T) corrections can be accurately obtained using a small basis, since the effects on the relative energies are usually the same within 0.01 kcal mol−1 utilizing the 3-21G, 6-31G, and cc-pVDZ basis sets (Table 2). The outcome of considering the core electron correlation is a relative energy change by 0.02 kcal mol−1 in average. The sign of this change is mixed for the glycine conformers, but for the protonated forms it is positive in all cases. The second-order Douglas–Kroll relativistic effect has a very negligible improvement, in most of the conformers it is way below 0.01 kcal mol−1. In summary, the computations done on the simplest amino acid show that the sum of these corrections does not go beyond ±0.1 kcal mol−1, in average the cumulative auxiliary correction is 0.03 kcal mol−1, and the most significant value is −0.08 kcal mol−1 for IIn and VIIp. Furthermore, it is comforting that the small corrections do not change the order the conformers, as seen in Table 1. The ZPE corrections have much higher significance than the previous ones, their average is 0.15 kcal mol−1 with varying signs, but they reach over 0.3 kcal mol−1 for several O-protonated forms, although this effect also does not cause a change in the order of the energies (Table 1: ΔH0 values). The neglected anharmonicity, which may be computed by second-order vibrational perturbation theory and/or by hindered rotor analysis for the low-frequency modes as was done in ref. 31–33 for glycine and in ref. 53 for threonine, may have an effect on the ZPE corrections in the range of 0.01–0.10 kcal mol−1.31,53
| δTa | δ(Q)b | δT + δ(Q) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 3-21G | 6-31G | VDZ | 3-21G | 6-31G | VDZ | 3-21G | 6-31G | VDZ | |
| a δT correction obtained by CCSDT – CCSD(T) with the 3-21G, 6-31G, and cc-pVDZ (VDZ) basis sets at CCSD(T)-F12b/aug-cc-pVTZ geometries. b δ(Q) correction obtained by CCSDT(Q) – CCSDT with the 3-21G, 6-31G, and cc-pVDZ (VDZ) basis sets at CCSD(T)-F12b/aug-cc-pVTZ geometries. c Corrections for proton affinities corresponding to N- and O-protonation of glycine obtained by Boltzmann-averaged mixtures of the conformers. | |||||||||
| Ip | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 |
| IIn | −0.03 | −0.03 | −0.02 | −0.03 | −0.03 | −0.04 | −0.06 | −0.05 | −0.06 |
| IIIn | +0.00 | +0.00 | +0.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 |
| IVn | +0.01 | +0.00 | +0.00 | −0.01 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 |
| Vn | +0.01 | +0.01 | +0.00 | −0.01 | −0.01 | −0.01 | +0.00 | +0.00 | −0.01 |
| VIp | −0.04 | −0.04 | −0.03 | +0.00 | +0.00 | +0.00 | −0.03 | −0.04 | −0.03 |
| VIIp | −0.04 | −0.04 | −0.03 | −0.02 | −0.02 | −0.03 | −0.06 | −0.06 | −0.06 |
| VIIIn | −0.03 | −0.04 | −0.03 | −0.01 | +0.00 | +0.00 | −0.04 | −0.04 | −0.03 |
| IpN | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 |
| IIpN | −0.02 | −0.02 | −0.01 | −0.01 | −0.03 | −0.02 | −0.03 | −0.04 | −0.03 |
| IIIpN | −0.04 | −0.04 | −0.03 | −0.01 | +0.00 | −0.01 | −0.04 | −0.05 | −0.04 |
| InO | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 |
| IIpO | −0.01 | +0.00 | +0.00 | +0.00 | +0.00 | +0.00 | −0.01 | +0.00 | +0.00 |
| IIInO | +0.00 | +0.01 | −0.01 | −0.06 | −0.07 | −0.07 | −0.06 | −0.06 | −0.08 |
| IVnO | +0.02 | +0.02 | +0.01 | −0.01 | −0.01 | −0.01 | +0.01 | +0.02 | +0.01 |
| VnO | +0.03 | +0.04 | +0.02 | −0.04 | −0.03 | −0.04 | +0.00 | +0.01 | −0.02 |
| VIpO | +0.00 | +0.01 | +0.01 | −0.01 | −0.01 | −0.01 | +0.00 | +0.01 | +0.00 |
| VIInO | −0.01 | −0.01 | −0.02 | −0.06 | −0.07 | −0.06 | −0.07 | −0.07 | −0.08 |
| VIIInO | +0.02 | +0.03 | +0.01 | −0.08 | −0.09 | −0.09 | −0.07 | −0.06 | −0.08 |
| Ip – IpN | −0.04 | −0.02 | +0.01 | +0.05 | +0.00 | −0.01 | +0.01 | −0.02 | +0.00 |
| Ip – InO | +0.04 | +0.06 | +0.06 | −0.07 | −0.15 | −0.16 | −0.03 | −0.09 | −0.11 |
| Average Nc | −0.04 | −0.02 | +0.01 | +0.05 | +0.01 | −0.01 | +0.01 | −0.02 | +0.00 |
| Average Oc | +0.04 | +0.06 | +0.06 | −0.07 | −0.15 | −0.16 | −0.03 | −0.09 | −0.11 |
To obtain the ΔH298 values we need to calculate the thermal contributions of the internal energies based on statistical thermodynamics. However, the thermal corrections are very sensitive to the low-frequency vibration modes, thereby these computations might not have sub-chemical accuracy. In general, the relative enthalpies at 298.15 K are slightly lower than at 0 K, except for four conformers. Small increase can be observed at VIp (0.04 kcal mol−1) and IVnO (0.1 kcal mol−1), this is caused by the vibrational thermal corrections affected by the uncertainty of the CCSD(T)-F12b/aug-cc-pVDZ low frequencies. IIn and IIpN have much higher (0.5–0.6 kcal mol−1) changes, whereas using the frequencies obtained at the MP2/aug-cc-pVDZ level, the results fit into the trends, with the difference of approximately 0.1 kcal mol−1. The reason behind this is also the uncertainty of the MOLPRO49 low-frequency computations, which may be more problematic at the CCSD(T)-F12b level, where both the first and second differentiations are done numerically.
Upon the calculation of the Gibbs free energy at 298.15 K an extra subtraction of a TS term is needed. The difference between the entropy (S) of the conformers origins from the different rotational and vibrational contributions. The former is due to the variation of the rotational constants and the latter is caused by the different vibrational modes. In general the relative Gibbs free energy values differ by ±(0.2–0.8) kcal mol−1 from the corresponding ΔH298 values, while we again have two outliers, the IIn and IIpN which have a difference of 1.59 and 1.68 kcal mol−1, respectively. Upon calculating the relative Gibbs free energies utilizing the MP2/aug-cc-pVDZ frequencies, these conformers will cease to have outlier values. This finding can be traced back again to the high low-frequency mode sensitivity and uncertainty.
C. Proton affinity and gas-phase basicity
The proton affinity and gas-phase basicity results can be found in Table 3. To employ these quantities in practice, we need to convert the 0 K values to a finite temperature, 298.15 K. We obtained PA and GB values for the protonation of different initial structures into different protonated geometries. The separation of the two protonation sites is a must, since the relative energies of the N-protonated ones are much lower, thus the O-protonation would be neglected via Boltzmann averaging. We pair the global minimum of the glycine and its N- or O-protonated counterpart and we also perform calculations for the mixture of glycine conformers and the mixture of the N- or O-protonated minima, where the population of the structures are calculated by the Boltzmann-distribution. The PA and GB values are also calculated considering the different auxiliary corrections. The post-(T) (full T and (Q)) corrections have the opposite sign in pairs, and for the amino protonation they cancel each other, whereas for the carbonyl protonation the sum retains a value of −0.11 kcal mol−1. As Table 2 shows, here the basis-set dependence is more significant than in the case of the relative energies of the conformers. For N-protonation the 3-21G δT and δ(Q) corrections differ from the 6-31G and cc-pVDZ values by 0.05–0.06 kcal mol−1, whereas the sum of δT and δ(Q) is the same within 0.03 kcal mol−1 using any of the above basis sets. The overall basis-set effect is somewhat larger for O-protonation, since the δT correction is well converged, i.e., {+0.04, +0.06, +0.06} kcal mol−1 with {3-21G, 6-31G, cc-pVDZ}, whereas the δ(Q) effect varies as {−0.07, −0.15, −0.16} kcal mol−1, resulting in a cumulative correction of {−0.03, −0.09, −0.11} kcal mol−1. It is worth noting that the 6-31G basis significantly improves the 3-21G results, providing post-(T) corrections in very good agreement with the cc-pVDZ values at a substantially less computational cost. The core correction terms are positive while the relativistic ones are negative in all cases. In the case of the amino-site protonation (either minima or mixture) the core correction is more relevant, the final value increases by 0.1 kcal mol−1, whereas for the carbonyl-site protonation the absolute relativistic correction is larger and the corrected PA value decreases by 0.02 kcal mol−1 after adding the two effects. The sum of all these small corrections causes a PA change of 0.09 kcal mol−1 for N-protonation and 0.12 kcal mol−1 for O-protonation.| ΔEQZa | δTb | δ(Q)c | Δ core | Δ rel | ΔEef | Δ ZPE | ΔH0hk | ΔH298ik | ΔG298jk | |
|---|---|---|---|---|---|---|---|---|---|---|
| a CCSD(T)-F12b/aug-cc-pVQZ equilibrium proton affinities obtained at CCSD(T)-F12b/aug-cc-pVTZ geometries. b δT correction obtained by CCSDT – CCSD(T) with cc-pVDZ at CCSD(T)-F12b/aug-cc-pVTZ geometries. c δ(Q) correction obtained by CCSDT(Q) – CCSDT with cc-pVDZ at CCSD(T)-F12b/aug-cc-pVTZ geometries. d Core-correlation correction obtained as the difference between AE-CCSD(T)-F12b/cc-pCVTZ-F12 and FC-CCSD(T)-F12b/cc-pCVTZ-F12 proton affinities at CCSD(T)-F12b/aug-cc-pVTZ geometries. e Relativistic correction obtained as the difference between Douglas–Kroll AE-CCSD(T)/aug-cc-pwCVTZ-DK and non-relativistic AE-CCSD(T)/aug-cc-pwCVTZ proton affinities at CCSD(T)-F12b/aug-cc-pVTZ geometries. f Benchmark equilibrium proton affinities obtained by CCSD(T)-F12b/aug-cc-pVQZ + δT + δ(Q) + Δcore + Δrel. g Zero-point energy correction on proton affinities obtained at CCSD(T)-F12b/aug-cc-pVDZ. h Benchmark 0 K proton affinities obtained as ΔEe + ΔZPE. i Benchmark proton affinities at 298.15 K. j Benchmark gas-phase basicities at 298.15 K. k The uncertainty caused by the accuracy of the low-frequency vibrations is much smaller, than for the individual molecules, but it is still present. l The population of the conformers were calculated by Boltzmann-distribution. | ||||||||||
| Ip – IpN | 219.73 | +0.01 | −0.01 | +0.11 | −0.02 | 219.82 | −9.14 | 210.68 | 212.14 | 204.90 |
| Ip – InO | 194.04 | +0.06 | −0.16 | +0.04 | −0.06 | 193.91 | −7.69 | 186.22 | 187.49 | 180.22 |
| Average Nl | 220.04 | +0.01 | −0.01 | +0.11 | −0.02 | 220.13 | −9.13 | 211.00 | 212.43 | 204.75 |
| Average Ol | 194.18 | +0.06 | −0.16 | +0.04 | −0.06 | 194.06 | −7.68 | 186.38 | 187.64 | 180.21 |
The equilibrium PA values (ΔEe) can be obtained by calculation the difference of the benchmark equilibrium energies of the molecule and its protonated form. Further improving the results, adding the ZPE correction gives the enthalpy change of the protonation at 0 K. One can observe a substantial change of about −10 kcal mol−1 for every case. At finite temperature we need to take into account the translational enthalpy of the proton (1.48 kcal mol−1 at 298.15 K), as well as the vibrational and rotational thermal corrections. After considering these corrections, we obtain the proton affinity at 298.15 K, resulting in a ∼1.5 kcal mol−1 increase for the amino site and a ∼1.3 kcal mol−1 increase for the carbonyl site, showing that the vibrational–rotational thermal effects are small besides the enthalpy of the proton. Finally, adding the entropy correction we get the gas-phase basicity (ΔG298) at 298.15 K, and this lowers the PA values by 7.4 kcal mol−1 in average, which effect is close to the difference of the enthalpy and Gibbs free energy of the proton, i.e., 1.48 – (−6.27) = 7.75 kcal mol−1. The computed thermodynamic values for the protonation of the two sites are significantly different. For ΔEe the difference is the highest, 26 kcal mol−1 for both the differences between the two minima and the mixture of minima. The difference for the ΔH0, ΔH298, and ΔG298 thermodynamical values are slightly lower, ∼24.7 kcal mol−1 in average. Calculating with mixtures instead of two minima and taking the population into account increase the ΔEe and the enthalpy (both at 0 K and 298.15 K) by 0.3 kcal mol−1 for the N-protonation and by 0.15 kcal mol−1 for the O-protonation. The exception is the gas-phase basicity where this mixture-effect has negative sign and lower absolute value of 0.15 kcal mol−1 for the amino protonation and 0.01 kcal mol−1 for the carbonyl protonation. These results show that while the global minimum is the most populated energy level, the other ones might not be negligible.
The final proton affinity results (global minima (mixtures)) are 212.14(212.43) kcal mol−1 for the amino protonation and 187.49(187.64) kcal mol−1 for the carbonyl protonation at 298.15 K. For the gas-phase basicities we obtained 204.90(204.75) kcal mol−1 for the N-protonated forms and 180.22(180.21) kcal mol−1 for the O-protonated forms also at 298.15 K. It is important to note, that using the energies and frequencies obtained at MP2/aug-cc-pVDZ level causes a serious error of several kcal mol−1 for the thermodynamic values, whereas calculating with the benchmark energies combined with either the MP2/aug-cc-pVDZ or the CCSD(T)-F12b/aug-cc-pVDZ frequencies results in the same values within 0.10 kcal mol−1 for the PA (both at 0 K and 298.15 K) and 0.50–0.55 kcal mol−1 for the GB of the amino and 0.20–0.25 kcal mol−1 for the GB of the carbonyl site.
In the literature Hunter and Lias4 published a voluminous review and database on the gas-phase basicities and proton affinities for 1700 molecules based on critical evaluation of the literature. For the PA of glycine, their recommended value is 211.9 kcal mol−1, while for the GB it is 203.7 kcal mol−1.4 Two years later, Alfonso et al.6 published an article on measuring the PA of the commonly occurring L-amino acids by using electrospray ionization-ion trap mass spectrometry, resulting in 212.28 ± 0.05 kcal mol−1 for glycine. A more recent article in 2004 was published by Bouchoux and co-workers5 revising the protonation thermochemistry of seven amino acids by carrying out electrospray ionization mass spectrometry and collision-induced dissociation tandem mass spectrometry and evaluating the results by different methods. For the PA value of glycine, they suggested 212.0 kcal mol−1 based on a simple kinetic method, while using an extended kinetic method, the PA is 211.8 ± 0.7 kcal mol−1 and the GB is 204.4 ± 0.9 kcal mol−1. To achieve the most relevant comparison, we should use the results for the amino protonation with conformer mixtures. Our thermodynamic values have an excellent agreement with all of previously mentioned experimental results4–6 with the maximum deviation of 0.5 kcal mol−1 for the PA and 1 kcal mol−1 for the GB (which has the highest uncertainty) while comparing with the most recent experimental PA(GB) results of 211.8 ± 0.7(204.4 ± 0.9) kcal mol−5 obtained with the extended kinetic evaluation method, our computed values, 212.43(204.75) kcal mol−1, are within the experimental error bars.
We should note that previous theoretical studies3,7–14,17–19,24,27 using mostly lower level of theory, i.e., MP2 or DFT methods with small basis sets, for the N-protonation and considering only the global minima or just some of the conformers, resulted in PA values in good agreement with the present high-level benchmark values. It is also interesting to compare the amino and carbonyl PA values with those of ammonia and carbon-monoxide. In 2008 one of the present authors determined these at 298.15 K, for NH3 the PA is 203.78 ± 0.07 kcal mol−1 and it is 141.59 ± 0.05 kcal mol−1 for the CO molecule.29 The difference roughly 10 kcal mol−1 for the amino-ammonia pair and 40 kcal mol−1 for the carbonyl-CO. The reason behind this is that the chemical environment (electrophilicity and partial charge) of the carbonyl group is drastically changed compared to a CO molecule and this effect is much smaller in the case of the amino group.
IV. Summary and conclusions
We have performed a systematic conformational search for protonated glycine revealing 3 N-protonated and 8 O-protonated conformers. The N-protonated conformers were known in the literature,7 in the case of O protonation, we have found 3 new conformers, namely VnO, VIInO, and VIIInO. The N-protonated conformers have Cs symmetry and their benchmark equilibrium(adiabatic) relative energies are 0.00(0.00), 4.97(4.96), and 7.51(7.37) kcal mol−1 for IpN, IIpN, and IIIpN, respectively. The lowest-energy O-protonated glycine conformer is above IpN by 25.91(24.45) kcal mol−1 and the 8 conformers span a roughly 6 kcal mol−1 relative energy range. Our high-level benchmark computations show that the CCSD(T)-F12b/aug-cc-pVQZ relative energies are usually converged within 0.01 kcal mol−1 and the post-CCSD(T), core correlation, and scalar relativistic effects are usually in the range of ±(0.00–0.10) kcal mol−1 and these auxiliary corrections often cancel or partially cancel each other. Thus we estimate that the uncertainty of the present benchmark relative electronic energies is less than 0.05 kcal mol−1. The zero-point energy corrections of ±(0.00–0.34) kcal mol−1 are more significant than the above small corrections. The thermal corrections for relative enthalpy and Gibbs free energy of the conformers are usually ±0.1 and ±(0.3–0.6) kcal mol−1 moving from 0 to 298.15 K. The present benchmark energies are the most accurate predictions for protonated glycine conformers and also for the 8 known conformers of glycine improving and confirming several previous work.36,37,52The above described high-level ab initio energies of the conformers of glycine and protonated glycine provide benchmark proton affinity and gas-phase basicity values for glycine. Considering the Boltzmann population of the conformers, the best 0(298.15) K proton affinity of glycine is 211.00(212.43) kcal mol−1 for N protonation and 186.38(187.64) kcal mol−1 for O protonation. The corresponding gas-phase basicity values are 204.75 and 180.21 kcal mol−1 at 298.15 K, respectively, showing significant entropy effects of around −(7–8) kcal mol−1, whereas the thermal correction for enthalpy is only +(1.2–1.5) kcal mol−1, close to the translational enthalpy of proton (1.48 kcal mol−1), as seen in the case of the proton affinity values. For the proton affinities the CCSD(T)-F12b/aug-cc-pVQZ results are converged within 0.1 kcal mol−1, the post-CCSD(T), core, and relativistic corrections are ±(0.02–0.11) kcal mol−1 resulting in a cumulative correction of +0.09/−0.12 kcal mol−1 for N-/O-protonation. The ZPE corrections are substantial, decreasing the proton affinities of minima(mixtures) by 9.14(9.13)/7.69(7.68) kcal mol−1. We estimate that our benchmark equilibrium proton affinities have small uncertainties around ±0.1 kcal mol−1, the 0 and 298.15 K values have somewhat larger error bars of ±0.3 kcal mol−1 due to the uncertainty of the harmonic ZPE and thermal (vibrational enthalpy) corrections, and the gas-phase basicity is the least accurate with estimated error bars of ±1 kcal mol−1 owing to the large uncertainty of the vibrational entropies caused by the uncertainties of the low frequencies. Thus, we can conclude that anharmonic (hindered rotor) and/or analytical frequency computations may improve the accuracy of the gas-phase basicity values, nevertheless, the present sub-chemically accurate absolute proton affinities may serve as benchmark reference for future theoretical and experimental studies.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank the National Research, Development and Innovation Office – NKFIH, K-125317, the Ministry of Human Capacities, Hungary grant 20391-3/2018/FEKUSTRAT, and the Momentum (Lendület) Program of the Hungarian Academy of Sciences for financial support. Discussions and collaboration with Attila Dékány are gratefully acknowledged.References
- A. R. Dongré, J. L. Jones, Á. Somogyi and V. H. Wysocki, J. Am. Chem. Soc., 1996, 118, 8365 CrossRef.
- B. Paizs and S. Suhai, Mass Spectrom. Rev., 2005, 24, 508 CrossRef CAS PubMed.
- E. Uggerud, Theor. Chem. Acc., 1997, 97, 313 Search PubMed.
- E. P. L. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413 CrossRef CAS.
- G. Bouchoux, D.-A. Buisson, C. Colas and M. Sablier, Eur. J. Mass Spectrom., 2004, 10, 977 CrossRef CAS PubMed.
- C. Afonso, F. Modeste, P. Breton, F. Fournier and J.-C. Tabet, Eur. J. Mass Spectrom., 2000, 6, 443 CrossRef CAS.
- K. Zhang and A. Chung-Phillips, J. Comput. Chem., 1998, 19, 1862 CrossRef CAS.
- Z. B. Maksić and B. Kovačević, Chem. Phys. Lett., 1999, 307, 497 CrossRef.
- C. Bleiholder, S. Suhai and B. Paizs, J. Am. Soc. Mass Spectrom., 2006, 17, 1275 CrossRef CAS PubMed.
- S. Gronert, D. C. Simpson and K. M. Conner, J. Am. Soc. Mass Spectrom., 2009, 20, 2116 CrossRef CAS.
- E. F. Strittmatter and E. R. Williams, Int. J. Mass Spectrom., 1999, 185/186/187, 935 CrossRef CAS.
- I. A. Topol, S. K. Burt, M. Toscano and N. Russo, THEOCHEM, 1998, 430, 41 CrossRef CAS.
- M. Noguera, L. Rodríguez-Santiago, M. Sodupe and J. Bertran, THEOCHEM, 2001, 537, 307 CrossRef CAS.
- T. C. Dinadayalane, G. N. Sastry and J. Leszczynski, Int. J. Quantum Chem., 2006, 106, 2920 CrossRef CAS.
- A. G. Harrison, Mass Spectrom. Rev., 1997, 16, 201 CrossRef CAS.
- A. Baeten, F. De Proft and P. Geerlings, Int. J. Quantum Chem., 1996, 60, 931 CrossRef CAS.
- C. Pepe, S. Rochut, J.-P. Paumard and J.-C. Tabet, Rapid Commun. Mass Spectrom., 2004, 18, 307 CrossRef CAS PubMed.
- S. Bouchonnet and Y. Hoppilliard, Org. Mass Spectrom., 1992, 27, 71 CrossRef CAS.
- G. Bouchoux, S. Huang and B. S. Inda, Phys. Chem. Chem. Phys., 2011, 13, 651 RSC.
- R. Notario, J. Z. Dávalos, R. Guzmán-Mejía and E. Juaristi, J. Phys. Chem. A, 2018, 122, 383 CrossRef CAS PubMed.
- C. J. Cassady, S. R. Carr, K. Zhang and A. Chung-Phillips, J. Org. Chem., 1995, 60, 1704 CrossRef CAS.
- G. Bojesen, J. Am. Chem. Soc., 1987, 109, 5557 CrossRef CAS.
- G. S. Gorman, J. P. Speir, C. A. Turner and I. J. Amster, J. Am. Chem. Soc., 1992, 114, 3986 CrossRef CAS.
- K. Zhang and A. Chung-Phillips, J. Phys. Chem. A, 1998, 102, 3625 CrossRef CAS.
- R. Wu and T. B. McMahon, J. Phys. Chem. B, 2009, 113, 8767 CrossRef CAS PubMed.
- F.-M. Siu and C.-M. Che, J. Phys. Chem. A, 2006, 110, 12348 CrossRef CAS PubMed.
- A. Chung-Phillips, J. Phys. Chem. A, 2005, 109, 5917 CrossRef CAS PubMed.
- A. Moser, K. Range and D. M. York, J. Phys. Chem. B, 2010, 114, 13911 CrossRef CAS PubMed.
- G. Czakó, E. Mátyus, A. C. Simmonett, A. G. Császár, H. F. Schaefer III and W. D. Allen, J. Chem. Theory Comput., 2008, 4, 1220 CrossRef PubMed.
- G. Czakó, B. Nagy, G. Tasi, Á. Somogyi, J. Simunek, J. Noga, B. J. Braams, J. M. Bowman and A. G. Császár, Int. J. Quantum Chem., 2009, 109, 2393 CrossRef.
- V. Barone, M. Biczysko, J. Bloino and C. Puzzarini, Phys. Chem. Chem. Phys., 2013, 15, 10094 RSC.
- V. Barone, M. Biczysko, J. Bloino and C. Puzzarini, Phys. Chem. Chem. Phys., 2013, 15, 1358 RSC.
- V. Barone, M. Biczysko, J. Bloino and C. Puzzarini, J. Chem. Theory Comput., 2013, 9, 1533 CrossRef CAS PubMed.
- C. Puzzarini, J. Bloino, N. Tasinato and V. Barone, Chem. Rev., 2019, 119, 8131 CrossRef CAS PubMed.
- A. Karton, L.-J. Yu, M. K. Kesharwani and J. M. L. Martin, Theor. Chem. Acc., 2014, 133, 1483 Search PubMed.
- E. M. Orján, A. B. Nacsa and G. Czakó, J. Comput. Chem., 2020, 41, 2001 CrossRef PubMed.
- A. G. Császár, J. Am. Chem. Soc., 1992, 114, 9568 CrossRef.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041 CrossRef CAS.
- M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 214105 CrossRef PubMed.
- J. S. Binkley, J. A. Pople and W. J. Hehre, J. Am. Chem. Soc., 1980, 102, 939 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257 CrossRef CAS.
- J. G. Hill, S. Mazumder and K. A. Peterson, J. Chem. Phys., 2010, 132, 054108 CrossRef PubMed.
- M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89 CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
- W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., Molpro, version 2015.1, a package of ab initio programs, see http://www.molpro.net.
- Mrcc, a quantum chemical program suite written by M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy, B. Hégely, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and Á. Ganyecz. See http://www.mrcc.hu.
- M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy, B. Hégely, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and Á. Ganyecz, J. Chem. Phys., 2020, 152, 074107 CrossRef PubMed.
- R. M. Balabin, Chem. Phys. Lett., 2009, 479, 195 CrossRef CAS.
- T. Szidarovszky, G. Czakó and A. G. Császár, Mol. Phys., 2009, 107, 761 CrossRef CAS.
| This journal is © the Owner Societies 2021 |