Protein–ligand free energies of binding from full-protein DFT calculations: convergence and choice of exchange–correlation functional

Abstract

The accurate prediction of protein–ligand binding free energies with tractable computational methods has the potential to revolutionize drug discovery. Modeling the protein–ligand interaction at a quantum mechanical level, instead of relying on empirical classical-mechanics methods, is an important step toward this goal. In this study, we explore the QM-PBSA method to calculate the free energies of binding of seven ligands to the T4-lysozyme L99A/M102Q mutant using linear-scaling density functional theory on the whole protein–ligand complex. By leveraging modern high-performance computing we perform over 2900 full-protein (2600 atoms) DFT calculations providing new insights into the convergence, precision and reproducibility of the QM-PBSA method. We find that even at moderate sampling over 50 snapshots, the convergence of QM-PBSA is similar to traditional MM-PBSA and that the DFT-based energy evaluations are very reproducible. We show that in the QM-PBSA framework, the physically-motivated GGA exchange–correlation functional PBE outperforms the more modern, dispersion-including non-local and meta-GGA-nonlocal functionals VV10 and B97M-rV. Different empirical dispersion corrections perform similarly well but the three-body dispersion term, as included in Grimme's D3 dispersion, is significant and improves results slightly. Inclusion of an entropy correction term sampled over less than 25 snapshots is detrimental while an entropy correction sampled over the same 50 or 100 snapshots as the enthalpies improves the accuracy of the QM-PBSA method. As full-protein DFT calculations can now be performed on modest computational resources our study demonstrates that they can be a useful addition to the toolbox of free energy calculations.

---

1 Introduction

Due to improved methodologies and greater access to computing resources, computational approaches are becoming increasingly valuable in drug discovery and development,^1–4 and the ongoing COVID-19 pandemic illustrates how simulations on supercomputers can rapidly lead to valuable insights into a novel disease.⁵ The ability of a pharmaceutical drug to bind to and interact with a target protein is of central importance and thus, the accurate prediction of protein–ligand binding free energies is one of the grand challenges of computational chemistry. In modeling protein–ligand interactions, the two key challenges are the size and complexity of protein–ligand systems. As a result, protein–ligand binding free energy predictions have traditionally relied on low-cost approximate methods due to limited computing power. Classical mechanics docking and molecular-dynamics based approaches still dominate this field of research. While much progress has been made in addressing challenges like sampling a flexible protein or accurately describing the solvent, the fundamental limitation of force-field based approaches is their inability to explicitly describe important physical effects that influence protein–ligand binding. To account for electron polarization, charge transfer, halogen bonding and many-body effects a quantum mechanical description is essential.^6,7 Force-fields that attempt to incorporate these effects are under development like the polarizable AMOEBA force-field for proteins⁸ as well as charge-transfer including force-fields.^9–15 However, with increasing access to high-performance computing the use of accurate quantum mechanical methods, which innately describe all of the important physical interactions, is becoming viable.

Most proteins consist of many thousands of atoms and thus cheap semi-empirical quantum mechanical (SEQM) methods like AM1 or SCC-DFTB are commonly applied. Despite using these cheaper, more approximate methods, often only the ligand^16–19 or the ligand and surrounding protein-residues^20–23 are treated at a QM level. Merz²³ and Anisimov^24,25 used linear-scaling SEQM methods on the whole protein. Ryde et al.²⁶ used the SEQM methods AM1, RM1 and PM6 to calculated binding energies in three protein–ligand systems using a SEQM-GBSA approach. Most studies using more expensive ab initio density functional theory (DFT) only treat the ligand and surrounding protein sites at this level of theory.^27–32 Fragmentation based approaches like PMISP^33,34 or the fragment molecular orbital (FMO)³⁵ method using QM calculations have been applied to various protein–ligand systems.^36–39 These studies feature either no sampling or very low sampling from molecular-dynamics. Approaches based on sampling at a hybrid QM/MM level have also been developed.⁴⁰

Even on supercomputers, it is prohibitive to perform conventional DFT calculations on entire proteins with thousands of atoms as the computational effort of DFT scales with the third power in the number of atoms. However, such calculations are enabled by the use of linear-scaling DFT approaches.⁴¹ In 2010, Cole et al.⁴² used linear-scaling DFT energy-evaluations with classical molecular-dynamics (MM) sampling on an entire protein–protein complex. In 2012 and 2014, Fox et al.^43,44 extended this approach and evaluated the binding free energies of a full protein–ligand system using ab initio linearly-scaling DFT. The QM-PBSA method combines MM sampling with implicit-solvent full-QM (DFT) energy evaluations. The predicted binding free energies outperformed traditional, classical mechanics based MM-PBSA.⁴⁴

Our goal is to improve the accuracy, transferability and reproducibility of binding free energy calculations in protein–ligand systems by using high-accuracy ab initio DFT. In this study, we push the boundary of DFT-based binding free energy calculations by drastically increasing the number of full-protein DFT calculations to over 2900. This allows us to assess, in-depth, the convergence of the QM-PBSA method. We compare the performance of dispersion-including non-local and meta-GGA-nonlocal exchange–correlation functionals VV10⁴⁵ and B97M-rV^46,47 with the popular GGA functional PBE. In addition to exploring these modern dispersion-including DFT functionals, we compare different empirical dispersion-corrections to the PBE functional and assess the significance of the three-body dispersion term. We demonstrate exceptional reproducibility of DFT energies, determine statistical errors at different levels of sampling and study the entropy correction term. The new general-purpose semi-empirical QM method GFN2-XTB⁴⁸ is also tested. Overall, we lay the foundation for large-scale applications of the QM-PBSA method, comment on best practice and demonstrate that with modern computing capabilities, DFT binding free energy calculations are viable and are a promising avenue of research and industry application.

Section 2.1 outlines the theory of the MM- and QM-PBSA method and some specific aspects of our linear-scaling DFT based approach. Section 2.2 describes the design of this computational study and computational details are summarized in Section 2.3. The results are presented in Section 3, discussing reproducibility (Section 3.1), convergence (Section 3.2), the entropy correction term (Section 3.3), statistical errors (Section 3.4), a comparison of DFT functionals (Section 3.5) and a comparison of different MM-, SEQM- and QM-PBSA methods. Section 4 contains the discussion of the results and we present our conclusions in Section 5.

2 Methods

2.1 The MM- and QM-PBSA methods

MM-PBSA was first proposed by Kollman et al. in 2000⁴⁹ and has become a popular method for estimating binding free energies. The two key assumptions in MM-PBSA are (1) sampling only from the endpoints of the binding process, and (2) treating the solvent implicitly. By sampling only the endpoints of the binding process, the computational cost is reduced greatly. Sampling is usually implemented using molecular-dynamics (MD) or Monte Carlo (MC) methods with an explicit solvent model. A representative ensemble of snapshots is extracted to estimate binding free energies. The binding free energy of a ligand B to a receptor protein A is the difference of the average free energy of the complex and its constituents,

ΔG_bind = 〈G^AB〉 − 〈G^A〉 − 〈G^B〉. (1)

In the three-trajectory approach, 〈G^AB〉 is calculated from the simulation of the bound complex, and 〈G^A〉 and 〈G^B〉 from simulations of the unbound protein and free ligand, respectively. More commonly, a one-trajectory approach is used in which 〈G^A〉 and 〈G^B〉 are computed from the simulation of the complex by deleting, in turn, the protein and ligand from the complex trajectory. The benefits of the one-trajectory method are that only a single simulation of the bound complex is needed and that all intra-molecular energies cancel, reducing noise in the binding free energies. Because the dynamics of the unbound ligand and protein are not sampled, the entropic change due to the restriction of the protein and ligand conformational freedom upon binding is not captured. Furthermore, the fact that the bound and unbound ligand and protein may sample different conformations is also ignored. Given these approximations, single-trajectory MM-PBSA is only suited for the calculation of relative binding free energies and the method implicitly assumes that energetic and entropic changes during the binding process are similar for all ligands and cancel in the computed relative free energies.

In MM-PBSA the mean free energies of the complex, protein and ligand are deconstructed into the following terms,

〈G〉 = 〈E〉 + 〈G_solvation〉 − T〈S〉, (2)

where 〈E〉 is the gas-phase molecular-mechanics energy of the system, averaged over an ensemble of configurations. In traditional force-fields, the gas-phase energy will include terms corresponding to bonds, angles, torsions, van der Waals and electrostatic interactions. 〈G_solvation〉 is the mean free energy of solvation of the snapshots, calculated using an implicit solvent model. This is further split into a polar and non-polar term, 〈G_solvation〉 = 〈G_pol〉 + 〈G_non-pol〉. The polar term is the electrostatic energy upon transfer of a charged molecule from the gas-phase to the solvent. In MM-PBSA it is calculated by solving the generalized Poisson–Boltzmann equation for a two-dielectric continuum electrostatic solvent model. Alternatively, in the related MM-GBSA method, the polar solvation term is calculated using the Generalized Born implicit solvation model.⁵⁰ The non-polar term is associated with the free energy of cavity formation for the solute to be placed into the solvent. This can be further divided into a contribution from the formation of the cavity and a dispersion term from the attractive and repulsive interaction between the solute and solvent molecules.⁵¹ The non-polar term is usually estimated from the solute surface area via the Solvent Accessible Surface Area (SASA). The final term, −T〈S〉, is the configurational entropy of the solute, usually estimated using normal mode analysis.⁵²

Substituting eqn (2) into (1) gives,

ΔG_bind = 〈ΔE〉 + 〈ΔG_solvation〉 − T〈ΔS〉 = 〈ΔH_bind〉 − T〈ΔS〉, (3)

where ΔH = H^AB − H^A − H^B is the total change in enthalpy upon binding and ΔE, ΔG_solvation and ΔS are defined analogously.

The MM-PBSA method is used actively in prospective drug design and lead identification. Recent examples include efforts to identify potential treatments of Covid-19^53,54 and Alszheimer's^55,56 and to better understand Down Syndrome.⁵⁷ A variety of improvements to the original formulation by Kollman et al.⁴⁹ have also been suggested. Duan et al.⁵⁸ have proposed an alternative method, called interaction entropy, of estimating the entropy correction term in MM-PBSA. More involved definitions of the solvent accessible surface area (SASA) like the weighted-SASA⁵⁴ approach have also been developed as well as volume based estimates of the cavitation energy in the non-polar solvation term.⁵⁹ For more background and applications of the MM-PBSA method we recommend the reviews by Genheden,⁶⁰ Wang⁶¹ and Poli.⁶²

In the QM-PBSA method, the gas-phase energies, 〈E〉, and solvation energies, 〈G_solvation〉, are calculated at a QM level. In our implementation of QM-PBSA, we use linear-scaling DFT to calculate QM gas-phase and solvation energies.

While MM-PBSA is a very cheap and approximate method that is outclassed by more sophisticated, thermodynamically rigorous and computationally expensive MM approaches like free energy perturbation (FEP) or thermodynamic integration (TI), its extension to QM is straight forward. The MM- and QM-PBSA methods differ only in how the gas-phase and solvation energy are calculated and thus, a direct comparison between MM and QM is possible. Because of this, we choose QM-PBSA as a stepping stone method, through which we may study the tractability, convergence, errors and other aspects of full-QM protein–ligand binding free energies. We expect, that our findings will aid future developments of QM-variants of more rigorous and involved MM methods.

2.2 Linear-scaling DFT

Due to the cubic scaling of conventional density functional theory, full-protein calculations on many thousands of atoms are not feasible. To study larger systems, linearly-scaling versions of DFT have been developed.⁴¹ The ONETEP code⁶³ is one such linear-scaling DFT implementation and exploits hybrid MPI-OMP parallelization⁶⁴ for efficient and scaleable calculations. The unique characteristic of ONETEP is that even though it is linear-scaling, it is able to retain large basis set accuracy as in conventional cubic-scaling DFT calculations. The implicit solvation model is a minimal-parameter Poisson–Boltzmann (PB) based model which is implemented self-consistently as part of the DFT calculation^65,66 and uses the smeared-ion formalism and electron-density iso-surfaces to construct solute cavities.

2.3 Design of computational study

2.3.1 Sampling. In 2014, Fox et al.⁴⁴ applied the QM-PBSA method to 8 ligands binding to the T4-lysozyme double mutant (L99A/M102Q)⁶⁸ shown in Fig. 1. Sampling was performed at MM-level using the one-trajectory approach and the force-field ff99SB⁶⁹ for the protein and GAFF1 for the ligand in Amber10.^70–72 The MD protocol is described in detail in ref. 44. 20 ns of MD were generated for each ligand from which 1000 configurations were extracted.

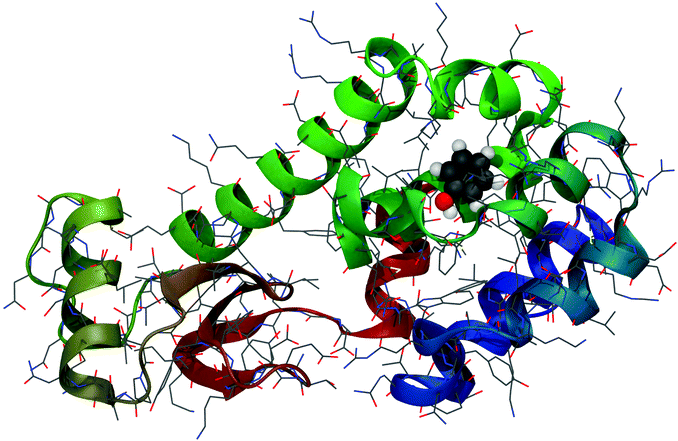Fig. 1 Phenol bound in the buried binding site of the T4-lysozyme double mutant (L99A/M102Q).⁶⁷ PDB Code: 1LI2.

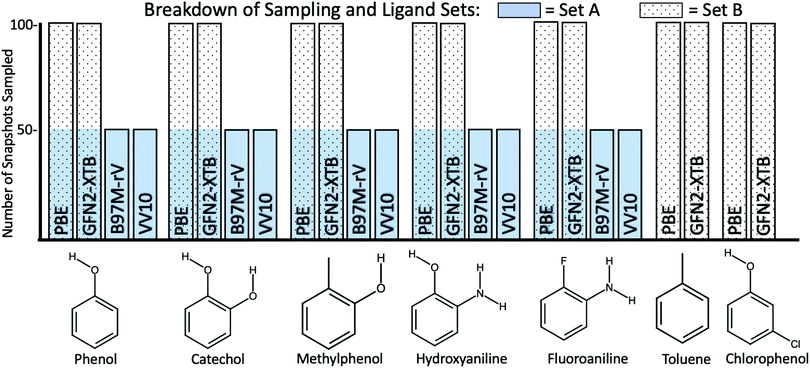
We re-use the identical 1000 MD snapshots for 7 ligands (shown in Fig. 2) in T4-lysozyme in this study. Fox et al. applied the QM-PBSA method to a subset of 50 snapshots, equally spaced within the 1000 extracted from the MD trajectories. Ligand 8, a non-binder, from the 2014 ligand set was excluded from this study as due to its larger size, it is more prone to inducing sidechain motion in the protein upon binding⁷³ which are unlikely to be captured in 20 ns of MD.

Fig. 2 An overview of sampling and methods for each ligand. Ligand set A consists of the first 5 ligands and 50 snapshots of sampling with DFT functionals PBE, VV10 and B97M-rV. Ligand set B consists of all 7 ligands and 100 snapshots for PBE and GFN2-XTB. Structures drawn using Marvin JS on chem-space.com.

2.3.2 Relative binding free energies and treatment of the non-binder. MM-PBSA and related approximate methods are usually employed to calculate relative rather than absolute binding free energies. To compare our calculated results to absolute experimental binding free energies, a normalization to the experimental binding energy of a reference ligand is needed. In 2014, only phenol was considered by Fox et al.⁴⁴ as the reference ligand. To compare the accuracy of the computed relative binding free energies to experimental values, the root mean squared deviation after the removal of the systematic error (mean signed error, MSE) is used as a quality metric in this study. The RMSDtr incorporates all choices of reference ligand and yields a single RMSD value instead of a separate RMSD for each choice or reference ligand, simplifying the comparison of methods.

Hydroxyaniline is a non-binder and thus does not have a well defined experimental binding free energy. The experimental assay used in ref. 74 could identify measurable binders up to a dissociation constant of 10 mMol which corresponds to a binding free energy of −2.7 kcal mol⁻¹ at 300 K. Thus, the lower limit of the non-binder's free energy of binding is −2.7 kcal mol⁻¹ while the theoretical upper limit is 0 kcal mol⁻¹. Going forward, all metrics applied to relative binding energies are calculated for the lower limit, upper limit and under the exclusion of the non-binder.

2.3.3 Exchange–correlation functionals. We selected the exchange–correlation functionals PBE, VV10 and B97M-rV for comparison in this QM-PBSA study.

PBE is a generalized gradient approximation (GGA) functional based on exact constraints and minimal empiricism. Because PBE cannot describe long-range correlation effects, an empirical force-field-like dispersion-correction is added. In this study, we test ONETEP's default dispersion-correction⁶³ and variants of Grimme's D2⁷⁵ and D3^76–78 empirical dispersion-corrections. We chose PBE because it is highly popular and is based on physical considerations with only moderate empiricism.

VV10 was selected because it is a non-local dispersion-including GGA functional. It combines rPW86 exchange, PBE correlation and VV10 dispersion-correlation.⁴⁵ In 2016, Womack et al.⁴⁷ implemented a more numerically efficient version, rVV10, into ONETEP.

Going beyond GGA functionals, meta-GGAs (mGGA) incorporate the electron kinetic energy density as well as the density gradient. This allows for more flexibility in the functional form and in general, mGGAs outperform GGAs but are more computationally demanding. In a benchmarking study by Head-Gordon et al.⁷⁹ the most accurate mGGA was the relatively new empirically-parameterized functional, B97M-rV⁴⁶ which incorporates rVV10 non-local dispersion.

2.3.4 Ligand set A, 50 snapshots: comparison of DFT functionals. To compare DFT functionals, a random subset of 5 ligands, named ligand set A (blue in Fig. 2), was chosen due to the increased computational cost of evaluating multiple DFT exchange–correlation functionals and dispersion-corrections. The binding energies of methylphenol, fluoroaniline, catechol, hydroxyaniline and phenol were calculated (Set A). The energies of 50 equally spaced snapshots, the identical structures as in 2014,⁴⁴ were evaluated at DFT level using functionals PBE,⁸⁰ VV10⁴⁵ and B97M-rV.⁴⁶

2.3.5 Ligand set B, 100 snapshots: convergence, errors and comparison of MM-, SEQM- and QM-PBSA. To investigate the convergence of the QM-PBSA method and to compare it to MM-PBSA, the ligands toluene and chlorophenol were added to ligand set A to form ligand set B (dotted area in Fig. 2) with 7 ligands. Sampling was increased to 100 equally spaced snapshots. These 100 configurations are equally spaced within the 1000 snapshots generated by Fox et al.⁴⁴ and include the 50 snapshots of ligand set A. Only the PBE functional, with dispersion-corrections, was evaluated over the 100 snapshots of ligand set B. The semi-empirical tight-binding method GFN2-XTB by Grimme et al.⁴⁸ was also tested on the 100 snapshots and 7 ligands of set B.

2.4 Computational details

2.4.1 MMPBSA. MM-PBSA post-processing was performed in Amber10 using the force-field ff99SB⁶⁹ for the protein and GAFF1 for the ligand^70–72 with an infinite non-bonded cutoff. Because the choice of solvent model can significantly impact the results,⁸¹ Poisson–Boltzmann solvation, which is available in both Amber and ONETEP, was used for consistency. A dielectric constant of 80.0 was used to represent the solvent water and a dielectric constant of 1 inside the protein.⁸¹

2.4.2 DFT. The linear scaling DFT code ONETEP⁶³ was used for energy evaluation both in this and the 2014 study by Fox et al.⁴⁴ A kinetic energy cutoff of 800 eV was used for all functionals. 4 non-orthogonal generalized Wannier functions (NGWFs) were used for carbon, nitrogen and oxygen and 1 NGWF was used for hydrogen. For sulfur and fluorine 9, NGWFs were used. An NGWF radius of 8.0a₀ was used throughout. ONETEP default parameters for water at room temperature were used. Further details, as well as input and output files are included in Section S1 of the ESI.†

2.4.3 Cavity-correction. The T4-lysozyme (LA99/M102Q) binding site is a buried cavity.⁶⁸ Both the ONETEP and the MM implicit-solvent models incorrectly describe the solvent-accessible surface area (SASA) of buried cavities. Cavity-correction terms appropriate to QM and MM are applied to alleviate this issue. All our QM- and MM-PBSA results, therefore, are cavity-corrected. More detail is provided in Section S1.3 of the ESI† and the mathematical forms of the MM and QM cavity-corrections are derived in ref. 44.

2.4.4 Dispersion. The 2014 binding free energy calculations of Fox et al.⁴⁴ utilized PBE with a DFT+D style dispersion-correction, based on a damping function by Elstner⁸² from 2001 and ONETEP's own parameterization. In this study, Grimme's D2⁷⁵ and variants of the newer D3 dispersion-correction, including a three-body dispersion term (E_ABC), are applied to the PBE functional.^76–78 The dispersion energies for D2 and D3 variants are obtained from Grimme's standalone dftd3 program and manually applied to the DFT(PBE) energies.

2.4.5 GFN2-XTB. The semi-empirical tight-binding method GFN2-XTB⁴⁸ features atom specific parameterization for most of the periodic table, a self-consistent implicit-solvent model and the D4 dispersion-correction.⁸³ It is implemented in the XTB package developed by Grimme et al.^84,85 The default settings for GFN2-XTB single-point implicit-solvent (water) energy evaluations were used. GFN2-XTB uses a GB solvent model⁵⁰ in which the cavitation and dispersion energy is treated with a single parameter, multiplied by the SASA. Thus, the straightforward application of a QM-style cavity-correction is not possible. Results with and without an MM-style cavity-correction are considered.

2.4.6 Entropy. The entropic contribution to binding was calculated using normal mode analysis (NMA)⁵² in the NAB program in Amber16.^71,86 The vibrational, translation and rotational entropies of the complex, host and ligand were evaluated. Before NMA, a two-part energy minimization comprised of a conjugate gradient method, followed by the Newton–Raphson method, was performed on each snapshot with tight convergence criteria using the ff99SB and GAFF1 force-fields. A Hawkins, Cramer, Truhlar (HCT) Generalized Born implicit solvent, with an internal dielectric of 1, was used for the frequency calculations and the energy minimizations with infinite non-bonded cutoff. All 1000 available structures for each ligand were evaluated.

3 Results

3.1 Reproducibility

This study provides a valuable opportunity to demonstrate the reproducibility of DFT-based binding free energy calculations. The calculations by Fox et al.⁴⁴ were performed with a 2012 version (3.1.15.2) of the ONETEP⁶³ code while this study uses version 5.3.2.6 from late 2019. As shown in Table 1, despite 7 years of active code development the average absolute difference between the new and old results using the same structures and functional is 0.1 kcal mol⁻¹. This underlines the robustness and precision of the DFT methodology and the ONETEP code in particular.

Table 1 Total change in enthalpy upon binding, 〈ΔH_bind〉, in kcal mol⁻¹ relative to phenol now and in 2014⁴⁴ over the same 50 snapshots. No entropy correction included

Ligands	PBE	PBE-2014	Delta
Catechol	−8.9	−9.0	0.14
Fluoroaniline	−6.0	−5.9	−0.12
Hydroxyaniline	−6.2	−6.2	0.00
Methylphenol	−8.7	−8.5	−0.16
Toluene	−5.0	−4.8	−0.18
Chlorophenol	−6.9	−6.9	0.01
		Absolute mean	0.10

---

3.2 Convergence

3.2.1 Standard error of the mean. The standard error of the mean (SEM) is a measure of how far the mean of a sample is likely to deviate from the true population mean. The QM-PBSA method averages energy terms over an ensemble of snapshots (population sample). Thus, the SEM provides an estimate of how the calculated energies differ from the true, fully sampled energies (i.e. the population mean). The SEM assumes normality of the energy distributions. Using the Shapiro–Wilks test⁸⁷ we concluded that overall, the use of the SEM is appropriate.

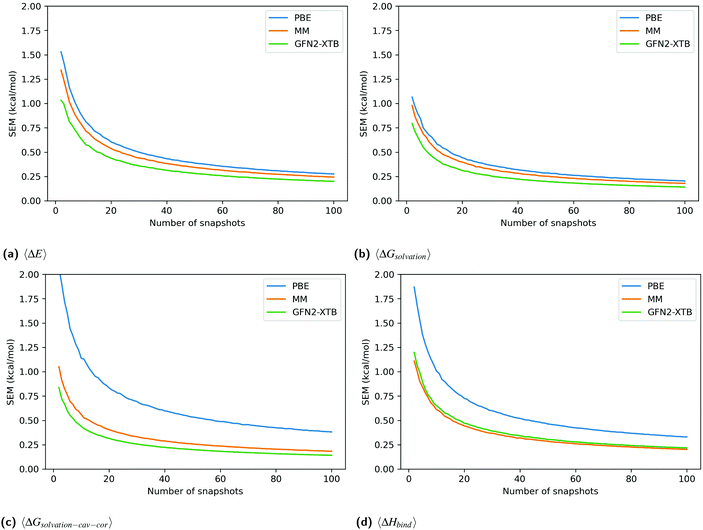
Fig. 3 shows the SEM convergence, calculated by bootstrapping, of each enthalpy component and the total enthalpy for catechol in T4-lysozyme. The enthalpies shown are net enthalpies, as defined in eqn (3). The SEM of the net gas-phase enthalpy, 〈ΔE〉, and the solvation energy, 〈ΔG_solvation〉, in catechol is only slightly higher for PBE than for the other methods. However, the SEM of PBE in the cavity-corrected solvation energy, 〈ΔG_{solvation–cav–cor}〉, is significantly higher. At 100 snapshots the SEM of the cavity-corrected solvation energy is 0.385 kcal mol⁻¹ while the other methods have SEMs below 0.184 kcal mol⁻¹. This leads to the overall higher SEM in the total enthalpy change upon binding, 〈ΔH_bind〉, for the PBE method. The higher SEM of PBE is also reflected in the SEM of functionals VV10 and B97M-rV over ligand set A.

Fig. 3 The standard error of the mean (SEM) calculated by bootstrapping (1000 re-samples) of the change upon binding in the gas-phase energy, 〈ΔE〉, solvation energy, 〈ΔG_solvation〉, cavity-corrected solvation energy, 〈ΔG_{solvation–cav–cor}〉, and total enthalpy, 〈ΔH_bind〉 = 〈ΔE〉 + 〈ΔG_{solvation–cav–cor}〉, for catechol up to 100 snapshots for MM, the DFT functional PBE and the SEQM method GFN2-XTB.

Unlike for PBE, the MM-style cavity-correction term applied to the MM-PBSA results (labeled MM) only minimally increases the solvation energy SEM. GFN2-XTB is shown without cavity-correction and has a similar SEM to MM. The above observations are consistent for all ligands (figures in Section 2.1 of ESI†).

3.2.2 Absolute deviations. Fig. 4 shows the convergence of the mean change in enthalpy upon binding and absolute deviation from 〈ΔH_bind〉 at 100 snapshots for MM and PBE (GFN2-XTB in ESI†). Considering first the mean binding energies, all methods appear surprisingly stable between 25, 50 and 100 snapshots. Especially PBE (and GFN2-XTB) show only small changes in 〈ΔH_bind〉 from 50 to 100 snapshots. The absolute deviation plots show that 〈ΔH_bind〉 fluctuates considerably (≈1 kcal mol⁻¹) for all methods below 25 snapshots. This is most pronounced in PBE and is in-line with the observation of a larger SEM in PBE. MM and GFN2-XTB show comparable levels of fluctuation. Interestingly, for 25 snapshots and beyond, the absolute deviations from the ‘converged’ results at 100 snapshots vary very little and are indistinguishable for PBE and MM. No deviations above 0.5 kcal mol⁻¹ are observed beyond 25 snapshots. Additional analysis using sets of randomly selected snapshots confirmed that beyond 25 snapshots the convergence, with respect to 〈ΔH_bind〉 at 100 snapshots, of MM and PBE is indistinguishable. The corresponding figures are included in Section S2.2 of the ESI.†

Fig. 4 Left: Mean change in total enthalpy upon binding, 〈ΔH_bind〉, of each ligand at different numbers of equally spaced snapshots. Right: Absolute deviation of 〈ΔH_bind〉 at different numbers of equally spaced snapshots from the ‘converged’ mean over 100 snapshots. Methods: MM (a and b), DFT(PBE) (c and d).

3.3 Entropy correction

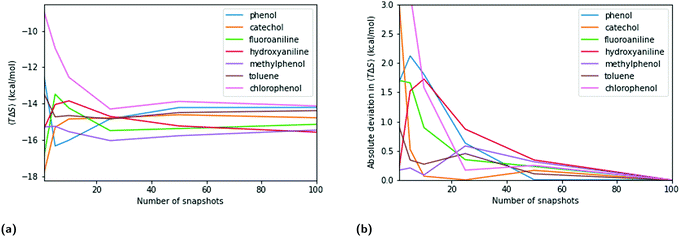
The entropy term in QM- and MM-PBSA is calculated by normal mode analysis as detailed in the methods section. The maximum SEM at low numbers of snapshots is lower than for the enthalpic components, especially the DFT cavity-corrected solvation energies. However, the rate of convergence is also slower. The entropy SEM at 100 snapshots is larger than that of the total enthalpy change upon binding calculated with MM and GFN2-XTB, and is comparable to that of PBE.

Fig. 5 shows a similar analysis for entropy as done for the enthalpic terms. Panels 5a and b show the convergence of the mean net-entropy term and absolute deviation from the mean net-entropy term at 100 snapshots. There are significant fluctuations below 50 snapshots (>1 kcal mol⁻¹). Fluctuations of about 0.5 kcal mol⁻¹ remain even beyond 50 snapshots and, compared to the enthalpic terms, the entropy term appears qualitatively slower in convergence.

Fig. 5 (a) Convergence of mean entropy change upon binding, TΔ〈S〉, over 100 equally spaced snapshots. (b) Absolute deviation of TΔ〈S〉 from “converged” value at 100 snapshots at different numbers of equally spaced snapshots.

The degree of entropy sampling significantly changes the RMSDtr of calculated against experimental relative binding free energies. Fig. 6 shows the RMSDtr over ligand set B at 100 enthalpy snapshots and increasing levels of entropy sampling. Including a small number of entropy snapshots (5, 10, 25) increases the RMSDtr by up to 1.3 kcal mol⁻¹ for MM-PBSA and 0.4 kcal mol⁻¹ for QM-PBSA. At 50 entropy snapshots and beyond the RMSDtr decreases compared to no entropy correction. The lowest RMSDtr is reached at 100 snapshots of entropy, i.e. the same level of sampling as for the enthalpy terms. Beyond this, the sampling of snapshots not included for calculating the enthalpy terms does not further improve accuracy vs. experiment. All three treatments of the non-binder exhibit the increased RMSDtr at low levels of entropy sampling (Figures in ESI†).

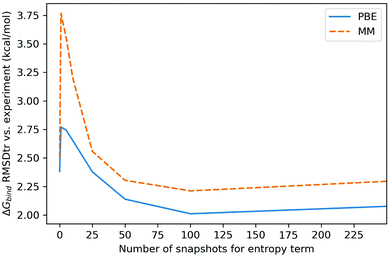Fig. 6 Root mean square deviation from experiment after removal of mean signed error (kcal mol⁻¹) of calculated binding free energies for ligand set B, at different levels of entropy sampling. Enthalpy sampled over 100 snapshots. RMSDtr calculated with upper limit for non-binder (lower limit and binders only in ESI†).

3.4 Statistical error due to incomplete sampling

The calculated absolute binding free energies are the sum of two separate means, the mean enthalpy and mean entropy, sampled over a selection of protein–ligand conformations, i.e. snapshots. By propagation of errors, the SEM of the entropy and enthalpy terms of each ligand and the chosen reference ligand are combined to estimate the total statistical error due to imperfect sampling in the relative binding free energies.

Table 2 shows the maximum statistical error due to incomplete sampling across all choices of reference ligands for each method at different levels of sampling. Enthalpy and entropy terms are evaluated over the same 10, 25, 50 and 100 equally spaced snapshots. The maximum statistical errors for PBE are almost identical to those for VV10 and B97M-rV and hence only PBE is shown. We use these values as estimates of the uncertainty in our calculated binding free energies going forward. This statistical error or uncertainty, due to imperfect sampling, should not be confused with the RMSDtr of calculated against experimental binding free energies, used to quantify the closeness of predicted to experimental results.

Table 2 Maximum statistical errors due to imperfect sampling (SEM) in entropy-corrected relative binding free energies with different methods sampled over 10, 25, 50 and 100 equally spaced snapshots. Enthalpy and entropy terms sampled over same snapshots. Cavity-correction applied for PBE and MM

Snapshots/methods	Max statistical errors (kcal mol^−1)
	10	25	50	100
PBE	1.88	1.22	0.87	0.62
MM	1.63	1.05	0.76	0.54
GFN2-XTB	1.57	1.02	0.73	0.52

---

3.5 Ligand set A: comparing DFT functionals

Table 3 shows the root mean square deviation after removal of the mean signed error of the calculated relative binding free energies with respect to experimental binding free energies^68,74 of ligand set A using 50 enthalpy and 50 entropy snapshots. The RMSDtr is shown for all treatments of the non-binder and the average standard error (SE) is estimated by bootstrapping with 10 000 resamples.

Table 3 Root mean square deviation from experimental binding free energies after removal of the mean signed error (kcal mol⁻¹) for ligand set A with energies and entropies sampled over the same 50 snapshots. RMSDtr values shown with the non-binders energy set to 0 kcal mol⁻¹ (upper limit, [*]), −2.7 kcal mol⁻¹ (lower limit, [‡]) and without the non-binder. Average standard error (SE) in RMSDtr calculated using bootstrapping (10 000 resamples)

Method	RMSD after removal of systematic error (MSE)
	All ligands [*]	All ligands [‡]	Binders only
B97M-rV	2.49	1.86	1.93
VV10	2.68	2.11	2.21
PBE + ONETEP Disp	2.26	1.76	1.93
PBE + D2	2.25	1.71	1.84
PBE + D3(BJ)	2.25	1.79	1.97
PBE + D3(BJ) + ABC	2.17	1.73	1.91
PBE + D3(BJM)	2.22	1.77	1.95
PBE + D3(BJM) + ABC	2.14	1.71	1.90
Average SE	0.26	0.27	0.30

---

Overall, VV10 is the worst performing exchange–correlation functional and has a consistently higher RMSDtr, irrespective of the treatment of the non-binder. The PBE + dispersion methods have slightly lower RMSDtr than B97M-rV when the non-binder is included, either via the upper or lower bound, but given the estimated standard error, this difference is likely not significant. For the subset of binders only, B97M-rV and PBE + dispersion methods achieve the same RMSDtr. All the empirical dispersion corrections to PBE perform well but are indistinguishable given the standard error. The inclusion of the three-body dispersion term (ABC) always slightly reduces RMSDtr but the change is much smaller than the standard error.

3.6 Ligand set B: PBE, GFN2-XTB and MM

We now compare the accuracy vs. experiment of MM, PBE + dispersion and GFN2-XTB on ligand set B at 100 snapshots of enthalpy and entropy. Table 4 shows the RMSDtr of the calculated relative binding free energies against experiment.^68,74 The RMSDtr is shown for all treatments of the non-binder and the average standard error (SE) is estimated by bootstrapping with 10 000 resamples.

Table 4 Root mean square deviation from experimental binding free energies after removal of the mean signed error (kcal mol⁻¹) for ligand set B with energies and entropies sampled over the same 100 snapshots. RMSDtr values shown with the non-binders energy set to 0 kcal mol⁻¹ (upper limit, [*]), −2.7 kcal mol⁻¹ (lower limit, [‡]) and without the non-binder. Average standard error (SE) in RMSDtr calculated using bootstrapping (10 000 resamples)

Method	RMSD after removal of systematic error (MSE)
	All ligands [*]	All ligands [‡]	Binders only
MM	2.21	1.61	1.55
PBE + ONETEP Disp	2.01	1.57	1.65
PBE + D2	2.09	1.63	1.69
PBE + D3(BJ)	2.11	1.73	1.84
PBE + D3(BJ) + ABC	2.03	1.66	1.77
PBE + D3(BJM)	2.11	1.74	1.85
PBE + D3(BJM) + ABC	2.02	1.67	1.79
GFN2-XTB	3.65	3.16	3.12
Average SE	0.15	0.16	0.17

---

Overall, the accuracy against experiment as described by the RMSDtr is comparable for the MM- and QM-PBSA approach. Only the SEQM-PBSA approach using the GFN2-XTB energy method performs significantly worse. The different empirical dispersion corrections are indistinguishable given the standard error. As in ligand set A, the three-body dispersion term does slightly reduce the RMSDtr of both the PBE + D3(BJ) and PBE + D3(BJM) methods but this change is within the estimates standard error.

3.7 Comment on correlation

Correlation to experiment is not included as a quality metric for two main reasons. First, the ligand set is very small. Second, the range of experimental binding free energies is only 1.4 kcal mol⁻¹ and multiple ligands have identical, or near identical, experimental energies. In comparison, the estimated statistical error in the computed relative binding free energies due to incomplete sampling is 0.87 kcal mol⁻¹ at 50 snapshots and 0.62 kcal mol⁻¹ at 100 snapshots for PBE. As a result, the correlation values obtained vary greatly depending on both the choice of reference ligand and the treatment of the non-binder. Furthermore, the 90% confidence intervals calculated by bootstrapping for Pearson r-values exhibit very large ranges of r-value, often above 0.5. Thus, no meaningful comparison between methods is possible. We conclude from this, that both a larger number of ligands and a larger range of experimental binding free energies are key requirements for future protein–ligand system selection.

4 Discussion

4.1 Computational cost

Gathering the results for this study posed a serious computational challenge. Excluding initial testing and exploratory work, 3600 ab initio DFT calculations were completed, 2900 of which were on the entire 2600-atom T4-lysozyme. This was made possible by (1) the linear-scaling of the ONETEP DFT code, (2) the efficient hybrid MPI-OMP parallelization of the ONETEP code and (3) access to three different HPC centers. Running calculations concurrently on three HPC facilities for 6 months, the DFT calculations alone required more than 1 million core-hours. Taking into account the 21 000 normal mode calculations, 15 000 empirical dispersion calculations and 2100 SEQM calculations we estimate a total wall-time of about 30 000 hours or 1250 days.

With full access to the 5632 compute nodes of the tier-0 EU HPC facility HAWK, the entirety of the calculations for this study could be completed in less than 24 hours.

With this study, we have shown that a benchmarking study on the QM-PBSA method comprising of multiple protein systems with up to or beyond 25 ligands is feasible.

4.2 Convergence and errors

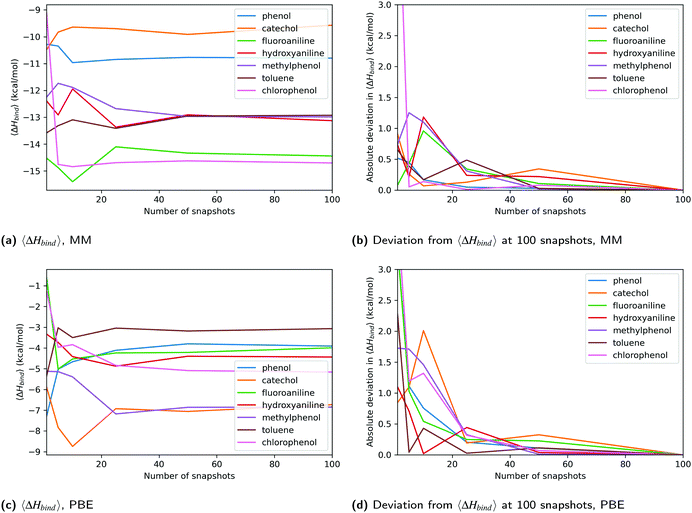
One criticism of QM-PBSA and related methods is that sampling and energy evaluation are performed using different energy functions.⁷ We expected this to lead to poor convergence of the QM energy terms in comparison to the MM energies. While the higher SEM for DFT methods, as compared to MM, initially indicated this to be true, the source of the higher SEM is predominantly the QM cavity-correction. Further investigation showed that the QM non-polar solvation terms calculated in ONETEP have larger variance than the MM non-polar terms. This is exacerbated by the functional form of the QM cavity-correction which combines the host and complex non-polar terms and then scales the result by a factor of 7.116.⁴⁴ This magnifies the effect of the larger variance in the QM non-polar terms on the total binding free energies, leading to a larger overall SEM. The standard deviation of the cavity-corrected solvation energy for PBE ranges from 2.7 to 3.9 kcal mol⁻¹ in ligand set B while the range for MM is 1.3 to 1.9 kcal mol⁻¹. One possible reason for the larger variance in the DFT non-polar term is the more complex definition of the binding cavity via electron-density iso-surfaces. GN2-XTB has similar or lower standard deviations than MM.

Detailed analysis of the convergence of the total enthalpy change upon binding of each ligand showed that beyond 25 snapshots, the QM results appear equally converged as the MM results. Analysis of the absolute deviations from the ‘converged’ enthalpy change upon binding at 100 snapshots using different numbers of equally spaced and randomly selected snapshots also confirmed this. At low numbers of snapshots (<25) the DFT energies fluctuated significantly more than those from MM, reflected by the higher SEM of the QM methods. The SEQM method GFN2-XTB showed similar convergence to MM, even below 25 snapshots. This is likely because the method does not suffer the increased SEM due to the QM cavity-correction.

In terms of precision, the maximum estimated statistical error for PBE in Table 2 is only 0.08 kcal mol⁻¹ higher than for MM at 100 snapshots and 0.11 kcal mol⁻¹ higher at 50 snapshots. This further suggests, that at and beyond 50 snapshots the convergence and precision of MM and DFT methods are comparable. The key finding is that in this system, the QM-PBSA method (irrespective of choice of functional) does not suffer from poorer convergence compared to MM-PBSA.

In this study, snapshots generated from a single MD simulation were used. Sampling snapshots from independent MD simulations may result in large standard errors of the mean and may impact the rate of convergence of both the MM and QM methods.

These results indicate that the MM force-fields (GAFF and ff99SB) used for sampling are well parameterized for this system and produce configurations that overlap well with the true QM ensemble. As a result, the QM calculations converge quickly as no high QM-energy configurations are present in the MM ensemble. In terms of the potential energy landscape, this would mean that the position of energy minima in the MM and QM representation are very similar. The difference in calculated binding free energies is then a result of the different depths and shapes of these energy minima for the different energy functions.

4.3 QM-PBSA: improvements and recommendations

4.3.1 Choice of DFT functional. Between the three DFT exchange–correlation functionals tested over 50 snapshots on ligand set A, PBE + dispersion is the most promising choice, as it outperforms VV10 in terms of RMSDtr and has very similar RMSDtr to B97M-rV, which is computationally twice as expensive. All the empirical dispersion corrections to PBE perform well, but given the estimated standard error, have indistinguishable RMSDtr. The similar performance of the D2 and D3 empirical dispersion-corrections in this large dispersion-dominated system supports the findings by Risthaus et al.⁸⁸ in their 2013 DFT + dispersion benchmarking study.

In the same study, Risthaus et al.⁸⁸ found the D3 three-body dispersion term to contribute 2.3% to 14.6% in large, dispersion-dominated systems. We have confirmed that the three-body dispersion term is significant (about 10% of total dispersion) in protein–ligand systems of this size and tends to improve RMSDtr slightly, however well within the estimated standard error. Given the size of the three-body dispersion term and its tendency to reduce RMDStr, we recommend the use of the D3 empirical dispersion correction due to its ability to include the three-body dispersion term.

Why do the newer and more computationally expensive VV10 and B97M-rV, which explicitly account for dispersion, not improve upon the PBE functional with empirical dispersion in this QM-PBSA study of a large dispersion-dominated system? Application of the non-parametric Kolmogorov–Smirnov test for equality of two one-dimensional distributions showed that the distributions of non-cavity-corrected absolute solvation energies of PBE, VV10 and B97M-rV are very similar. This echoes our past experience using the ONETEP solvent model that showed the solvation energies to be independent of the choice of DFT functional. Based on the Kolmogorov–Smirnov test, the gas-phase energy distributions, which include the dispersion energy, are dissimilar. Both VV10 and B97M-rV use the non-local rVV10 dispersion term. While the dispersion term rVV10 results in different gas-phase energies than the empirical dispersion corrections to PBE, this does not translate to improved accuracy vs. experiment compared to PBE + dispersion in this QM-PBSA study.

Furthermore, the rVV10 non-local dispersion term cannot describe three-body effects, which we found to be significant using the empirical D3-ABC method. Risthaus et al.⁸⁸ have suggested that the three-body dispersion term from D3 could be added, in a post hoc fashion, to dispersion including functionals, however, this was not tested here.

B97M-rV is a meta-GGA functional and thus almost twice as computationally intensive as the GGA functionals PBE and VV10. The data-set used to design and test B97M-rV consisted almost entirely of small molecules.⁴⁶ The only protein–ligand system was a 1686 atom HIV II-protease/indinavir complex split into 21 interaction fragment pair structures. In the 2017 benchmarking study by Head-Gordon et al.,⁷⁹ B97M-rV was the most accurate meta-GGA, however, of the almost 5000 data points tested, there were only 21 protein–ligand fragments (same as above) and 12 protein–DNA complexes with a maximum size of 58 atoms. While we can only comment on the suitability of the functionals to the QM-PBSA method, and not their accuracy on the whole, it is interesting that B97M-rV produced worse or comparable results to PBE + dispersion. A potential explanation is that the accuracy of exchange–correlation functionals on small molecule test sets is not indicative of their applicability to much larger systems. This study serves as an example that moving up the “Jacob's ladder” of functional complexity does not guarantee improved results.

4.3.2 Inclusion of entropy term. The inclusion of an entropy correction term appears to decrease the quality of results when insufficient entropy sampling is performed. For this system, sampling the normal mode entropy term over less than 25 snapshots was found to be inadequate and no entropy sampling should be preferred over poor entropy sampling. This is intuitive as insufficient sampled entropy terms introduce a large statistical error (>1 kcal mol⁻¹) into the binding energies. On the other hand, when the entropy is sampled with more than 25 snapshots, the inclusion of an entropy correction reduces RMSDtr. We found that the best results were obtained when sampling entropy over the same 50 or 100 snapshots used for enthalpy sampling. Sampling beyond this slightly increased errors, possibly due to the sampling of conformations not included in the enthalpy terms. Based on these findings we are concerned about the use of less than 50 NMA calculations in some applications of MM-PBSA.^89–91

4.3.3 Sampling and statistical error. Based on this study we recommend QM energy sampling at 50 snapshots. Sampling at 100 snapshots of enthalpy and entropy reduces the maximum estimated statistical error due to imperfect sampling from 0.87 kcal mol⁻¹ to 0.62 kcal mol⁻¹ but does not, in this system, significantly reduce RMSDtr. Very stable total enthalpies are observed between 50 and 100 snapshots and the absolute deviation of the change in total enthalpy upon binding at 50 and 100 snapshots is lower than 0.5 kcal mol⁻¹ for all ligands.

4.3.4 QM- vs. MM-PBSA. The extent to which PBE + dispersion can consistently improve MM results can not be clearly stated, but the results indicate that in this system the QM-PBSA approach produces relative binding free energies with RMSDtr comparable to MM. None of the methods tested were able to identify hydroxyaniline as a non-binder.

Given the small range of binding energies in the ligand set, the null hypothesis of assigning each ligand the same binding energy yields relatively low errors against experiment. The null hypothesis has a RMSDtr of 0.57 kcal mol⁻¹ if the non-binder is excluded, and 1.00 kcal mol⁻¹ and 1.87 kcal mol⁻¹ when the non-binder is included via the lower and upper bound, respectively. Fundamentally, more ligands with a wider range of binding free energies are needed allow for a comparison between MM- and QM-PBSA and we are actively working on achieving this.

In this study on the T4-lysozyme double mutant (L99A/M102Q) our linear-scaling DFT-based QM-PBSA method achieves a RMSDtr of about 1.7 kcal mol⁻¹ across the 6 binders and MM-PBSA achieves a RMSDtr of 1.6 kcal mol⁻¹. To place our results into context, we briefly outline the results of some other QM- and SEQM-PB(GB)SA studies. For a more in-depth review of QM based biding free energy calculations we recommend the review by Ryde and Söderhjelm.⁷ In 2011, Anisimov et al.^24,25 applied a SEQM-PBSA style method using the PM3 Hamiltonian and a COSMO solvation model to 5 ligands binding to the LcK SH2 domain and 4 binders to BRCA1. They achieved MAD of 0.7 kcal mol⁻¹ and 1.7 kcal mol⁻¹, respectively. In both cases the SEQM approach was more accurate than MM-PBSA. In 2012, Mikulskis et al.²⁶ tested a SEQM-GBSA approach with the AMI, RM1 and PM6 Hamiltonians on three protein–ligand systems. The overall best performing energy function, AM1, achieved an MADtr of 1.8–12.0 kcal mol⁻¹ in avidin, 1.1–1.3 kcal mol⁻¹ in fXa and 0.3–4.9 kcal mol⁻¹ in ferritin, depending on the details of the hydrogen bond correction and choice of dispersion correction. Only in the ferritin system was the best SEQM-GBSA method able to convincingly outperform MM-GBSA and MM-PBSA. In 2010, Söderhjelm et al.³⁴ used the PMISP approach on 7 biotin analogues binding to avidin. They achieved a MADtr of 4.5 kcal mol⁻¹ and the QM approach performed worse than MM-PBSA (3.3 kcal mol⁻¹).

One of the key motivations to extend binding free energy calculations to the quantum mechanical level is that the QM energy evaluations can in principle describe a wider range of physics. In this ligand set and binding site however, the MM force-field is not challenged by high charges, large polarization, charge transfer or similar phenomena that are not well described in traditional empirical force-fields. This may in part explain the similar accuracy of MM- and QM-PBSA in this system. Going forward, we will focus our efforts on protein–ligand systems which explicitly challenge traditional force-fields and where the more involved, quantum mechanical description may be necessary.

4.3.5 GFN2-XTB. Both in ligands set A and B, and irrespective of the treatment of the non-binder, GFN2-XTB has the highest RMSDtr. This may be unsurprising as GFN2-XTB is relatively new, semi-empirical, general-purpose and more than 100 times faster than DFT. As for the B97M-rV functional, the GFN2-XTB method was developed based on small molecule data sets and aimed at systems of roughly 1000 atoms.⁴⁸ To our knowledge, GFN2-XTB has not been used in large-scale protein–ligand binding energy calculations. Lastly, the differences in PBSA solvation in the DFT and MM approaches and GBSA solvation in GFN-XTB may have also contributed to the gap in performance.⁹²

5 Conclusions

In this study, we have shown that in the context of protein–ligand binding studies for drug design applications, thousands of ab initio DFT calculations of full protein–ligand systems are feasible with modest computational effort. In testing the exchange–correlation functionals PBE, VV10 and B97M-rV we find that the computationally cheapest functional, PBE, is the most promising candidate for the application of the QM-PBSA method. Our findings highlight that benchmarking studies focused almost entirely on small systems may not be representative of the performance of the functionals in a QM-PBSA approach applied to much larger systems (2600 atoms in our case). Different empirical dispersion corrections to PBE all perform well but their accuracy against experiment are all within the estimated standard error. The D3 three-body dispersion term is significant in size (≈10%) and tends to improve results slightly. By expanding the QM calculations to 100 snapshots for the PBE functional, we can show that sampling at 50 snapshots is likely sufficient for convergence. While going beyond 50 snapshots reduces statistical error, no improvement in predicted against experimental binding energies is observed. Furthermore, the QM-PBSA and MM-PBSA methods exhibit near indistinguishable convergence beyond 25 snapshots of sampling. This is shown by the similar statistical errors and the convergence of the mean binding energies. In this system, the inclusion of an entropy correction term is only beneficial when sampled over at least 25 snapshots. Entropy terms with less sampling increase RMSDtr. Sampling entropy beyond 100 snapshots does not improve results.

Our study demonstrates that QM-PBSA with full protein calculations is now feasible and can be a useful addition to the toolbox of free energy calculations, especially in cases where force field parameterization may not be sufficiently able to capture effects such as charge transfer and polarisation which are included by default in quantum descriptions. Looking to the future, we believe that the extension of more rigorous classical mechanical binding free energy methods to full-QM, using linear-scaling density functional theory, has significant potential and that the QM-PBSA method is an important stepping stone.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the use of the IRIDIS 5 High Performance Computing Facility, and associated support services at the University of Southampton, in the completion of this work. We are grateful for computational support from the UK Materials and Molecular Modelling Hub, which is partially funded by EPSRC (EP/P020194 and EP/T022213/1). We are also grateful for access to the ARCHER national supercomputer which was obtained via the UKCP consortium, funded by EPSRC grant ref EP/P022030/1. L. G. would also like to thank the CDT for Theory and Modelling in the Chemical Sciences and Boehringer Ingelheim for financial support in the form of a PhD studentship.

Notes and references

1. B. Kuhn, M. Tichý, L. Wang, S. Robinson, R. E. Martin, A. Kuglstatter, J. Benz, M. Giroud, T. Schirmeister, R. Abel, F. Diederich and J. Hert, J. Med. Chem., 2017, 60, 2485–2497.
2. Z. Li, Y. Huang, Y. Wu, J. Chen, D. Wu, C. G. Zhan and H. B. Luo, J. Med. Chem., 2019, 62, 2099–2111.
3. M. Kuhn, S. Firth-Clark, P. Tosco, A. S. Mey, M. MacKey and J. Michel, J. Chem. Inf. Model., 2020, 60, 3120–3130.
4. L. F. Song and K. M. Merz, J. Chem. Inf. Model., 2020, 60, 5308–5318.
5. L. Casalino, A. Dommer, Z. Gaieb, E. P. Barros, T. Sztain, A. Trifan, A. Brace, A. Bogetti, H. Ma, H. Lee, S. Khalid, L. Chong, C. Simmerling, D. J. Hardy, J. D. C. Maia, J. C. Phillips, T. Kurth, A. Stern, L. Huang, J. Mccalpin, T. Gibbs, J. E. Stone, S. Jha, A. Ramanathan and R. E. Amaro, biorxiv, 2020 DOI:10.1101/2020.11.19.390187.
6. C. N. Cavasotto, N. S. Adler and M. G. Aucar, Front. Chem., 2018, 6, 188.
7. U. Ryde and P. Söderhjelm, Chem. Rev., 2016, 116, 5520–5566.
8. Y. Shi, Z. Xia, J. Zhang, R. Best, C. Wu, J. W. Ponder and P. Ren, J. Chem. Theory Comput., 2013, 9, 4046–4063.
9. D. V. Sakharov and C. Lim, J. Am. Chem. Soc., 2005, 127, 4921–4929.
10. M. Soniat and S. W. Rick, J. Chem. Phys., 2014, 140, 184703.
11. M. Soniat and S. W. Rick, J. Chem. Phys., 2012, 137, 6146–6952.
12. M. Soniat, G. Pool, L. Franklin and S. W. Rick, Fluid Phase Equilib., 2015, 407, 31–38.
13. M. Soniat, R. Kumar and S. W. Rick, J. Chem. Phys., 2015, 143, 044702.
14. M. Soniat, L. Hartman and S. W. Rick, J. Chem. Theory Comput., 2015, 11, 1658–1667.
15. A. J. Lee and S. W. Rick, J. Chem. Phys., 2011, 134, 184507.
16. F. Gräter, S. M. Schwarzl, A. Dejaegere, S. Fischer and J. C. Smith, J. Phys. Chem. B, 2005, 109, 10474–10483.
17. M. A. Ibrahim, J. Chem. Inf. Model., 2011, 51, 2549–2559.
18. M. Retegan, A. Milet and H. Jamet, J. Chem. Inf. Model., 2009, 49, 963–971.
19. K. D. Dubey and R. P. Ojha, J. Biol. Phys., 2011, 37, 69–78.
20. Y. T. Wang and Y. C. Chen, Mol. Inf., 2014, 33, 240–249.
21. F. Barbault and F. Maurel, J. Comput. Chem., 2012, 33, 607–616.
22. K. Wichapong, A. Rohe, C. Platzer, I. Slynko, F. Erdmann, M. Schmidt and W. Sippl, J. Chem. Inf. Model., 2014, 54, 881–893.
23. N. Díaz, D. Suárez, K. M. Merz and T. L. Sordo, J. Med. Chem., 2005, 48, 780–791.
24. V. M. Anisimov and C. N. Cavasotto, J. Comput. Chem., 2011, 32, 2254–2263.
25. V. M. Anisimov, A. Ziemys, S. Kizhake, Z. Yuan, A. Natarajan and C. N. Cavasotto, J. Comput.-Aided Mol. Des., 2011, 25, 1071–1084.
26. P. Mikulskis, S. Genheden, K. Wichmann and U. Ryde, J. Comput. Chem., 2012, 33, 1179–1189.
27. M. Kaukonen, P. Söderhjelm, J. Heimdal and U. Ryde, J. Phys. Chem. B, 2008, 112, 12537–12548.
28. X. Chen, X. Zhao, Y. Xiong, J. Liu and C. G. Zhan, J. Phys. Chem. B, 2011, 115, 12208–12219.
29. H. Lu, X. Huang, M. D. M. Abdulhameed and C. G. Zhan, Bioorg. Med. Chem., 2014, 22, 2149–2156.
30. M. Wang and C. F. Wong, J. Chem. Phys., 2007, 126, 026101.
31. S. Manta, A. Xipnitou, C. Kiritsis, A. L. Kantsadi, J. M. Hayes, V. T. Skamnaki, C. Lamprakis, M. Kontou, P. Zoumpoulakis, S. E. Zographos, D. D. Leonidas and D. Komiotis, Chem. Biol. Drug Des., 2012, 79, 663–673.
32. K. E. Tsitsanou, J. M. Hayes, M. Keramioti, M. Mamais, N. G. Oikonomakos, A. Kato, D. D. Leonidas and S. E. Zographos, Food Chem. Toxicol., 2013, 61, 14–27.
33. P. Söderhjelm, J. Kongsted, S. Genheden and U. Ryde, Interdiscip. Sci.: Comput. Life Sci., 2010, 2, 21–37.
34. P. Söderhjelm, J. Kongsted and U. Ryde, J. Chem. Theory Comput., 2010, 6, 1726–1737.
35. D. G. Fedorov, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1322.
36. T. Sawada, D. G. Fedorov and K. Kitaura, J. Am. Chem. Soc., 2010, 132, 16862–16872.
37. R. Kurauchi, C. Watanabe, K. Fukuzawa and S. Tanaka, Comput. Theor. Chem., 2015, 1061, 12–22.
38. U. Tagami, K. Takahashi, S. Igarashi, C. Ejima, T. Yoshida, S. Takeshita, W. Miyanaga, M. Sugiki, M. Tokumasu, T. Hatanaka, T. Kashiwagi, K. Ishikawa, H. Miyano and T. Mizukoshi, ACS Med. Chem. Lett., 2016, 7, 435–439.
39. A. Heifetz, E. I. Chudyk, L. Gleave, M. Aldeghi, V. Cherezov, D. G. Fedorov, P. C. Biggin and M. J. Bodkin, J. Chem. Inf. Model., 2016, 56, 159–172.
40. T. J. Giese and D. M. York, J. Chem. Theory Comput., 2019, 15, 5543–5562.
41. D. R. Bowler and T. Miyazaki, Rep. Prog. Phys., 2012, 75, 036503.
42. D. J. Cole, C. K. Skylaris, E. Rajendra, A. R. Venkitaraman and M. C. Payne, EPL, 2010, 91, 37004.
43. S. J. Fox, PhD thesis, University of Southampton, 2012.
44. S. J. Fox, J. Dziedzic, T. Fox, C. S. Tautermann and C. K. Skylaris, Proteins: Struct., Funct., Bioinf., 2014, 82, 3335–3346.
45. O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103.
46. N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2015, 142, 074111.
47. J. C. Womack, N. Mardirossian, M. Head-Gordon and C. K. Skylaris, J. Chem. Phys., 2016, 145, 204114.
48. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
49. P. A. Kollman, I. Massova, C. Reyes, B. Kuhn, S. Huo, L. Chong, M. Lee, T. Lee, Y. Duan, W. Wang, O. Donini, P. Cieplak, J. Srinivasan, D. A. Case and T. E. Cheatham, Acc. Chem. Res., 2000, 33, 889–897.
50. W. C. Still, A. Tempczyk, R. C. Hawley and T. Hendrickson, J. Am. Chem. Soc., 1990, 112, 6127–6129.
51. C. Wang, D. Greene, L. Xiao, R. Qi and R. Luo, Front. Mol. Biosci., 2018, 4, 87.
52. J. Srinivasan, T. E. Cheatham, P. Cieplak, P. A. Kollman and D. A. Case, J. Am. Chem. Soc., 1998, 120, 9401–9409.
53. V. K. Bhardwaj, R. Singh, J. Sharma, V. Rajendran, R. Purohit and S. Kumar, J. Biomol. Struct. Dyn., 2020, 1–10.
54. J. Wang, J. Chem. Inf. Model., 2020, 60, 3277–3286.
55. R. Singh, V. Bhardwaj, P. Das and R. Purohit, J. Biomol. Struct. Dyn., 2020, 38, 5126–5135.
56. A. Kaur, S. Shuaib, D. Goyal and B. Goyal, Phys. Chem. Chem. Phys., 2020, 22, 1543–1556.
57. V. K. Bhardwaj, R. Singh, J. Sharma, P. Das and R. Purohit, Comput. Methods Progr. Biomed., 2020, 194, 105494.
58. K. Huang, S. Luo, Y. Cong, S. Zhong, J. Z. Zhang and L. Duan, Nanoscale, 2020, 12, 10737–10750.
59. C. Tan, Y. H. Tan and R. Luo, J. Phys. Chem. B, 2007, 111, 12263–12274.
60. S. Genheden and U. Ryde, Expert Opin. Drug Discovery, 2015, 10, 449–461.
61. E. Wang, H. Sun, J. Wang, Z. Wang, H. Liu, J. Z. Zhang and T. Hou, Chem. Rev., 2019, 119, 9478–9508.
62. G. Poli, C. Granchi, F. Rizzolio and T. Tuccinardi, Molecules, 2020, 25, 1971.
63. J. C. Prentice, J. Aarons, J. C. Womack, A. E. Allen, L. Andrinopoulos, L. Anton, R. A. Bell, A. Bhandari, G. A. Bramley, R. J. Charlton, R. J. Clements, D. J. Cole, G. Constantinescu, F. Corsetti, S. M. Dubois, K. K. Duff, J. M. Escartín, A. Greco, Q. Hill, L. P. Lee, E. Linscott, D. D. O'Regan, M. J. Phipps, L. E. Ratcliff, Á. R. Serrano, E. W. Tait, G. Teobaldi, V. Vitale, N. Yeung, T. J. Zuehlsdorff, J. Dziedzic, P. D. Haynes, N. D. Hine, A. A. Mostofi, M. C. Payne and C. K. Skylaris, J. Chem. Phys., 2020, 152, 174111.
64. K. A. Wilkinson, N. D. Hine and C. K. Skylaris, J. Chem. Theory Comput., 2014, 10, 4782–4794.
65. J. Dziedzic, H. H. Helal, C. K. Skylaris, A. A. Mostofi and M. C. Payne, EPL, 2011, 95, 43001.
66. J. C. Womack, L. Anton, J. Dziedzic, P. J. Hasnip, M. I. Probert and C. K. Skylaris, J. Chem. Theory Comput., 2018, 14, 1412–1432.
67. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38.
68. B. Q. Wei, W. A. Baase, L. H. Weaver, B. W. Matthews and B. K. Shoichet, J. Mol. Biol., 2002, 322, 339–355.
69. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Genet., 2006, 65, 712–725.
70. D. Case, T. Darden, T. Cheatham, C. Simmerling, J. Wang, R. Duke, R. Luo, M. Crowley, R. Walker, W. Zhang, K. Merz, B. Wang, S. Hayik, A. Roitberg, G. Seabra, I. Kolossváry, K. Wong, F. Paesani, J. Vanicek, X. Wu, S. Brozell, T. Steinbrecher, H. Gohlke, L. Yang, C. Tan, J. Mongan, V. Hornak, G. Cui, D. Mathews, M. Seetin, C. Sagui, V. Babin and P. Kollman, AMBER 10, 2008.
71. D. A. Case, T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, K. M. Merz, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688.
72. J. W. Ponder and D. A. Case, Adv. Protein Chem., 2003, 66, 27–85.
73. D. L. Mobley and M. K. Gilson, Annu. Rev. Biophys., 2017, 46, 531–558.
74. S. E. Boyce, D. L. Mobley, G. J. Rocklin, A. P. Graves, K. A. Dill and B. K. Shoichet, J. Mol. Biol., 2009, 394, 747–763.
75. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
76. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
77. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
78. D. G. Smith, L. A. Burns, K. Patkowski and C. D. Sherrill, J. Phys. Chem. Lett., 2016, 7, 2197–2203.
79. N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372.
80. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
81. H. Sun, Y. Li, S. Tian, L. Xu and T. Hou, Phys. Chem. Chem. Phys., 2014, 16, 16719–16729.
82. M. Elstner, P. Hobza, T. Frauenheim, S. Suhai and E. Kaxiras, J. Chem. Phys., 2001, 114, 5149–5155.
83. E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112.
84. P. Pracht, E. Caldeweyher, S. Ehlert and S. Grimme, ChemRxiv, 2019, 1–19.
85. S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009.
86. D. Case, R. Betz, D. Cerutti, T. Cheatham, T. Darden, R. Duke, T. Giese, H. Gohlke, A. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. Lee, S. LeGrand, P. Li, C. Lin, T. Luchko, R. Luo, B. Madej, D. Mermelstein, K. Merz, G. Monard, H. Nguyen, H. Nguyen, I. Omelyan, A. Onufriev, D. Roe, A. Roitberg, C. Sagui, C. Simmerling, W. Botello-Smith, J. Swails, R. Walker, J. Wang, R. Wolf, X. Wu, L. Xiao and P. Kollman, Amber 16, 2016.
87. S. S. Shapiro and M. B. Wilk, Biometrika, 1965, 52, 591–611.
88. T. Risthaus and S. Grimme, J. Chem. Theory Comput., 2013, 9, 1580–1591.
89. S. Zhong, K. Huang, Z. Xiao, X. Sheng, Y. Li and L. Duan, J. Phys. Chem. B, 2019, 123, 8704–8716.
90. L. Duan, X. Liu and J. Z. Zhang, J. Am. Chem. Soc., 2016, 138, 5722–5728.
91. P.-C. Su, C.-C. Tsai, S. Mehboob, K. E. Hevener and M. E. Johnson, J. Comput. Chem., 2015, 36, 1859–1873.
92. T. Hou, J. Wang, Y. Li and W. Wang, J. Chem. Inf. Model., 2011, 51, 69–82.

---

Footnote

† Electronic supplementary information (ESI) available: Additional computational details, supplementary figures and directions to all input and output files. See DOI: 10.1039/d1cp00206f

---