Molecular dynamics study of the pore formation in single layer graphene oxide by a thermal reduction process

Abstract

Nanoporous graphene is considered the next-generation material for reverse osmosis water desalination providing both high water permeability and almost complete salt rejection. The main problem with graphene is the difficulty of synthesizing membranes with a consistent subnanometer pore size distribution. A recently proposed solution involves processing as-grown graphene oxide (GO) monolayers via a mild temperature annealing pre-treatment causing GO functional groups to cluster into small oxidized islands. A following harsh thermal reduction process creates pores only in the small oxidized regions. However, a suitable relationship between the area of the GO islands and the pore dimension is still missing. Here, we study in detail the effects of such a thermal reduction process on the graphene oxide sheet by means of molecular dynamics simulations, particularly highlighting and analysing the process parameters affecting the final pore area. Besides proving that epoxides represent the most suitable functional group to induce carbon removal and, thus, pore generation in reduced GO, we find a twofold way to achieve control over the pore size: tuning the dimension and shape of the initial clustered GO areas or changing the harsh reduction process temperature. An accurate balance of these parameters consistently gives rise to targeted pore dimensions in graphene membranes.

---

1 Introduction

Reverse osmosis is considered the most efficient technique for water desalination.¹ Nevertheless, it suffers from significant disadvantages, namely large energy consumption and high capital costs because of water pressure,^2–4 limiting its large-scale employment. Nowadays salt filtration is carried out using polymeric semipermeable membranes which, however, have poor neutral solute rejection or scarce water permeability resulting in an increased energy cost for desalination to be accomplished.⁵ The recently proposed nanoporous graphene membranes have the potential to solve the problem, being superior in terms of permeability by several orders of magnitude, thanks to their small thickness, while preserving, at the same time, an excellent salt rejection rate. Theoretical simulations report that to achieve a high selectivity a pore diameter of 5.5 Å is needed to block the hydrated salt ions while allowing water to pass.⁶ Several following studies proved the effectiveness of graphene membranes^7,8 and analyzed the parameters that influence their performance, stressing in particular on the impact of pore dimensions.^9–12

One of the hardest challenges, that characterizes this material, is to consistently synthesize graphene membranes with a narrow pore size distribution. Many techniques were proposed so far. Ion bombardment was employed to knock off carbon atoms from the sheet using both heavy ions¹³ and noble gases.¹⁴ Alternatively, e-beam lithography¹⁵ was proposed to accurately realize the desired features in the graphene layer. Other approaches are based on ozone treatment¹⁶ or O₂ plasma.¹⁷ Recently, Li-Chiang et al. proposed a new scalable method that consists in the generation of pores starting from a monolayer of graphene oxide (GO). The sheet is exposed to a high temperature process that forms random pores.¹⁸ A promising evolution of the previous method tackles the problem of the random size distribution as a consequence of the high temperature process by applying a two-step thermal process.¹⁹ In the latter method, the starting material is a single layer oxidized graphene with low defect concentration, obtained either by exfoliating a multilayer GO with non-destructive methods^20,21 or by soft oxidation of pristine graphene monolayer.^22,23 The layer is supposed to cover the micrometer sized pores of a polymeric support with its basal plane when used for filtration.²⁴ For brevity, throughout the text we will refer to this structure simply as GO. In the two-step process the GO is, first, heated at controlled low temperature (300–320 K). This step is aimed at favoring the aggregation of GO functional groups into small oxidized areas surrounded by pristine graphene. The oxide cluster size can be tuned by changing the heating time, temperature and initial coverage of the GO. The first two parameters are strictly connected and determine the area of the clusters. The longer the heating time the larger is the average area of the oxidized clusters. A high temperature drastically increases the diffusion of epoxides, reducing the heating time required for the clusterization at the risk of going beyond the targeted average size. Experimentally, these two parameters must be suitably tweaked using a trial-and-error approach to obtain the desired cluster distribution. The initial coverage influences the shape of the clusters. When the coverage is low (), the resulting oxidized islands are mostly circular. As the coverage is increased the clusters become more linear. The treated layer, then, undergoes a high temperature reducing process which not only decreases the concentration of oxygen of the sheet but also causes a localized carbon removal only in the clustered oxidized areas formed in the previous step leaving pores behind. The process ensures a better control over pore size distribution.

Although the technique was proved to work, an extensive characterization of the effects of the reducing thermal process conditions on the clustered GO layers is still missing. A relationship between area of the oxidized domains and final dimension of the pores must be identified. In this work we aim at understanding to which extent parameters like process temperature, local coverage or shape of the oxidized area influence the final pore area in order to guide experimental research for the creation of selective graphene membranes for desalination. The study is carried out by means of molecular dynamics (MD) calculations, able to atomistically describe the reduction of GO sheets under the influence of high temperatures.

2 Method

The simulations were performed using the LAMMPS software package²⁵ with reactive force fields (Reax-FF)²⁶ which, unlike conventional potentials, capture bond formation and breaking. The REAX-FF we chose (ref. 26) is known for its capability to reproduce carbon based materials like graphite,²⁷ 2D graphene,²⁸ laser induced graphene²⁹ and GO.³⁰ Moreover, it was successfully applied to study thermal reducing processes of GO.¹⁸ We tested the capability of the REAX potential to accurately reproduce the heating process on GO by performing ab initio molecular dynamics simulations. The results (see the ESI† for details) indicate that comparable reducing reactions, leading to carbon removal, take place in the classical and ab initio molecular dynamics runs. In our REAX-FF molecular dynamics simulations, a 43 × 45 Ų graphene supercell was realized. We assume that the mild annealing pretreatment already took place, as described in ref. 19, so that the sheet is characterized by oxide clusters surrounded by pristine graphene. Each supercell accommodates a single cluster constituted by either epoxide or hydroxyl groups. Periodic boundary conditions were applied. A vacuum layer of 90 Å was placed in the direction perpendicular to the layer to avoid interactions between replicas and to hold the gas desorbed from GO during annealing. To simulate the effect of a harsh reducing process, we performed calculations at three temperatures, 1000 K, 1500 K and 2500 K. The temperature values are not to be taken quantitatively but as representative of three different intensities of the reductive process. It is common practice in atomistic simulations to increase the temperature to speed up the calculations.¹⁸ Further experimental work will be needed to match the simulation temperatures to the real temperature. Similar matches between simulations and experiments were previously performed for GO.³¹ The thermal process consisted of an initial relaxation of the starting structure, followed by a temperature ramp from 10 K to the target temperature lasting 4 ps. The target temperature was maintained fixed for 500 ps. Finally, the temperature was cooled down to 300 K in 1 ps and held constant for 4 ps (see the ESI† for a representation of the temperature cycle). Temperature control was achieved thanks to a Nose–Hoover thermostat. In our analysis, we explored the effect on the final pore area of different –O–/–OH ratios (0.33 and 3.00), of different local atomic percentages (12.5 at% and 25.3 at%) and of different sizes of the oxidized region (12 Å and 24 Å in diameter). For each cluster dimension, coverage and –O–/–OH ratio, and temperature, ten different annealing samples were simulated.

Additionally, we carried out an analysis of the influence of the initial shape of the oxidized region, considering specific selected structures described below. Ten different initial random velocity distributions, for each combination of temperature and structure, were applied to provide sufficiently large statistics. The different shapes (a single line of epoxides, a double line of epoxides, and a squared and a highly packed configuration) were selected to understand how the linearity of the cluster could affect the pore formation. To estimate the final pore area we considered the steric hindrance of each atom as a sphere whose radius corresponds to the van der Waals radius (1.70 Å for carbon, 1.52 Å for oxygen and 1.20 Å for hydrogen). The pore area was measured considering the largest section shown from a tilted angle of view. We consider the final pore area to be the most appropriate measure of the effect of each factor we analyzed as it can be related to membrane selectivity and permeability in experiments. It is not possible to provide more details about the morphology of the final pores, because of the high stochasticity of the desorption process and the intrinsic random distributions of the functional groups within the oxidized areas.

3 Results and discussion

We start our analysis addressing which functional group is more relevant for pore formation. On the graphene oxide basal plane mainly three functional groups are present: epoxides, ethers and hydroxyls.³² Experimentally it is possible to promote one group over the others by chemical treatments of the sheet after synthesis.^23,32–36 In our analysis, we assume that the sheet we are simulating is the result of a post-synthesis treatment designed to alter the relative ratio of functional groups as previously reported.³⁷ The sheet is supposed then to be exposed to the first of the two-step process proposed in ref. 19, which is aimed at clustering the functional groups in small areas with controlled dimension. To understand the functional groups effect, we simulated the reducing process of a sheet having two different –O–/–OH ratios, 0.33 and 3.00, representative respectively of a hydroxyl or epoxide/ether dominated sheet. The two ratios were selected as test cases to highlight the differences between functionals. For each structure, we monitored the carbon removal and the amount of desorbed species during the reduction process. The functional groups were generated randomly within a circle of 12 Å diameter to reproduce a clustered oxidized area on the graphene surface.

Fig. 1a shows the results of the simulations. In general, there is a strong dependence of the pore area on the heating temperature. Moreover, consistently with what was predicted in ref. 19, pores are only formed within the oxidized regions. Larger pore areas are found if epoxides/ethers are the dominant species, particularly at low process temperatures (1000 K and 1500 K). For higher temperatures (2500 K), the mean pore area is comparable in both epoxide and hydroxyl dominated sheets, although hydroxyls lead to a larger area variance. Even if the final pore area can vary for a considerable amount, especially at higher temperatures, the trends can be clearly identified. The error bars are a consequence of the stochasticity of the desorption process which is characterized by random temperature-activated bond breaking events. From a larger perspective, however, the variability of the process is highly contained in these clustered GO sheets, where the desorption can occur only within the small oxidized area, as opposed to the as-grown GO, where desorption occurs anywhere on the sheet. The presence of the temperature resistant pristine graphene surrounding the GO clusters in treated sheets poses an upper limit to the final dimension of the pores.

Fig. 1 Final pore area (a) and percentage of oxygen atoms covering the sheet that desorbed as gaseous species, indicated along the x axis (b–d), during a thermal reduction process as a function of the –O–/–OH ratio (0.33 or 3.00) and the temperature, 1000 K, 1500 K and 2500 K.

In order to understand why epoxides are more prone to give rise to pores, we plotted the type and number of gas molecules formed for different annealed samples and temperatures. Hydroxyl rich samples mainly form H₂O molecules, which do not involve carbon removal processes. As the treatment temperature increases, both the numbers of H₂O and CO increase, indicating that temperature equally promotes both desorption processes. By contrast, in the epoxide dominated sheet, irrespective of the treatment temperature, a fixed amount of –O– turns into O₂, in agreement with the literature³¹ but a temperature increase strongly boosts the production of CO molecules upon annealing.

The tendency of epoxide groups to form holes is also supported by Density Functional Theory simulations which show that the bond between an oxygen and a graphene carbon is stronger compared to the C–OH bond. Further, the typical barrier for the formation of O₂ from two epoxides is around 1.0 eV while the barrier for water formation from two hydroxyls is only 0.5 eV.^19,38,39 Consequently C–C bond breaking in GO is more probable close to an epoxide rather than close to a hydroxyl group. As such, for pore formation, epoxides are the functional groups that more efficiently give rise to pores. It is, therefore, advised to experimentally obtain an epoxide dominated GO layer, before the reducing process starts, when aiming at pore formation.

We, then, studied the effect of another parameter: the cluster local oxygen atomic percentage. It is important to understand to what extent the functional groups have to be packed in order to consistently give rise to pores. In these calculations the –O–/–OH ratio was set to 3.00 given that epoxides are the most suitable species for pore formation. Functional groups were once again generated randomly within a circle of 12 Å diameter. The local atomic percentage, meaning the ratio between the number of functional groups and carbon atoms within the 12 Å circle, was varied between 12.5 at% and 25.3 at%. Fig. 2a illustrates that a high coverage is needed to consistently form pores. This is in agreement with the mechanism suggested by Larciprete et al.⁴⁰ for which oxygen molecules are formed at lower coverages leaving unmodified the graphene while for high coverages, epoxides evolve into CO or CO₂. Additionally, in ref. 19, it is suggested that, in order to consistently produce pores, a mild annealing pre-treatment is needed to promote the formation of GO clusters in graphene. The formation of clusters is divided into two phases. Initially epoxides diffuse to form small GO islands characterized by a low local atomistic percentage of epoxides. When forming a cluster, epoxides can take many possible relative positions. However, mainly two of them, as we will later discuss, are particularly stable and are characterized by a packed arrangement. In the earlier phase, it is unlikely for the epoxides to occupy these positions. If the mild annealing process is continued, the clusters rearrange to maximize the number of low energy pair arrangements leading to configurations with higher local atomistic percentage. The results in Fig. 2a reveal that the latter stage cannot be skipped. The clusterization process induced by a mild annealing must last for a sufficient time to allow for the rearrangement of the cluster, resulting in a highly packed structure which is more likely to give rise to pores.

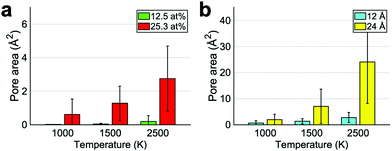Fig. 2 Pore area of a clustered GO sheet with a 12.5 at% and a 25.3 at% (a) or having oxygen containing functional groups localized in a circle of 12 or 24 Å diameter (b).

Literature results on the high temperature process¹⁹ suggest that the size and shape of the clusterized GO area determine the final morphology of the pore. Here we provide a more detailed analysis identifying a precise relationship between clusters and pores. As first test, we generated randomly epoxides and hydroxyls with a ratio of 3.00 within a circle of diameter 12 or 24 Å. As indicated in Fig. 2b, there is a direct relationship between the diameter of the GO cluster and the final pore area. As previously observed, carbon was removed only in the oxidized areas and not in pristine ones. Consequently larger oxidized areas led to wider pores. The proportion between cluster and pore area was found to depend on the treatment temperature. When the heating process was most intense (2500 K), an oxidized area of 113 Ų produced a mean pore area of 2.7 Ų whereas an initial GO cluster of 453 Ų resulted in a 24.1 Ų pore. As a reference, the area of a pore of 5.5 Å diameter like the one optimal for NaCl filtration,¹⁸ is 13.9 Ų estimated with the approach explained in the Methods section. So by either tuning the temperature or the dimension of the oxidized regions, one can achieve the desired pore size to filter different solutes in water.

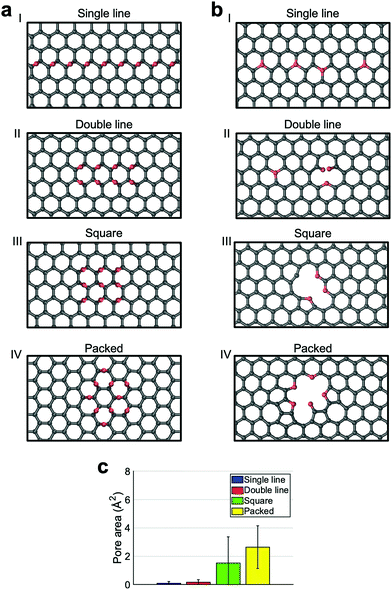
In the following, instead of considering oxidized GO areas with randomly distributed oxygen functional groups, we studied low energy configurations which maximize epoxide pairing. Indeed, it was shown that epoxides tend to arrange in two particular low energy configurations:¹⁹ one has two epoxides lying on one side of a benzene ring (left most couple of epoxides in Fig. 3a panel II) leading to close packed and circular clusters, the other one has two epoxides on a zig-zag geometry (Fig. 3a panel I). The latter configuration is responsible for the linear clusters most frequently observed at high coverages. Typically, a stabilized cluster will be formed by a combination of these two configurations. To comprehend how different cluster shapes affect the final membrane morphology we simulated the reducing processes on selected arrangements: a chain of epoxides located on a zig-zag line (Panel I of Fig. 3a), a double chain on two zig-zag lines (Panel II), a square made of three lines (Panel III) and a packed circular cluster formed by pairs of epoxides lying on the same ring (Panel IV). All these arrangements are made with, at least, one of the two described low energy configurations and they roughly contain the same amount of epoxides.

Fig. 3 Structure of the single line (Panel I), double line (II), square (III) and packed (IV) GO clusters before (a) and after (b) the harsh annealing process. Final pore area of the previously illustrated GO clusters with epoxides (c).

We exposed these structures to a 2500 K thermal treatment, as it is the one that induces the greatest carbon removal. The results show strong dependence on the initial arrangement of the clusters. In particular, a long line of epoxides hardly induces the formation of pores (see Fig. 3b panel I for an example). Oxygen saturates carbon vacancies created during the thermal treatment or it simply leaves the sheet without damages. A similar incorporation of oxygen in graphene was previously reported in the literature for low coverage sheets.³¹ The formation of triple-coordinated oxygen should not be surprising as this configuration was already proven to exist both theoretically and experimentally in graphene.^41,42 When there are two initial zig-zag lines of oxygens, the resulting pore area is minimal (Fig. 3c), although in some cases, very small holes appear as in Panel II of Fig. 3b. A completely different result is obtained in the case of a square or circular cluster (see panel III and IV of Fig. 3b) and a substantial increase in the pore area is reported (from a mean of 0.1 Ų and 0.2 Ų of the single and the double lines to a mean of 1.5 Ų and 2.6 Ų for the square and the packed circular arrangement). The holes originated from the square arrangement are slightly smaller compared to the ones originated from the packed clusters. The analysis, shown in the ESI,† of the number and types of species that desorb, indicates that the two kinds of clusters behave similarly. For both of them mainly 3–4 CO molecules desorb. The reason for the difference, therefore, must be attributed to the different low energy configurations constituting the clusters. The packed configuration is characterized by the presence of three oxygen atoms belonging to the same ring. This arrangement favors the creation of small holes that cannot be easily healed. Conversely, the square configuration reproposes the same zig-zag arrangement of the single or double line clusters. As such, a less probable concerted desorption of many non-aligned oxygen atoms is required to form an unhealable hole. Nevertheless, both square and packed circular arrangements appear to play a relevant role in the consistent generation of pores. To further prove this point, we simulated a cluster consisting of a circular core with a linear tail.

As shown in Fig. 4, the circular core is the part that originates a hole in the graphene while the tail only gives rise to point defects in the sheet. This finding has important consequences for the applicability of the two-step process proposed in ref. 19. One of the constraints of the process was that the initial GO should have a low oxygen coverage (between 5% and 10%), because only in this range clusters, after the mild annealing process, preserved a circular shape. A higher initial coverage (10–15%), typically, leads to mixed circular and linear clusters. Thanks to the result shown in Fig. 3, we understand that higher initial coverages are also suitable for the formation of pores for desalination as only circular clusters will form pores while their linear tail will not tear the GO. This will come at the cost of a mechanically less robust membrane as oxygens will saturate the dangling bonds left by carbon vacancies in the linear tails or small impermeable pores will appear. We also analyzed whether the presence of epoxides on both sides of the sheet would change the trend identified previously (see the ESI†). We found that consistently with the structures having epoxides on the same side, the single and double chain arrangements do not result in pores while the square and the circle do. The analogous trend indicates that there is no significant effect of the sheet side on functional group desorption.

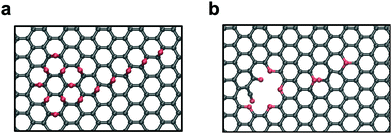Fig. 4 Structure of a cluster consisting of a circular core and a linear tail before (a) and after (b) the reduction treatment.

4 Conclusions

To conclude, we provided indications on the main factors influencing the harsh thermal treatment of clustered GO sheets for pore generation in graphene-based membranes. In particular, we found that epoxides are more likely to produce larger pores than hydroxyls, especially for less intense treatments. We were able to identify that the mild annealing process, required for GO functional groups to cluster before the harsh thermal treatment, must last long enough to ensure that the clusters are stable and highly packed. Only with a high local density of functional groups that weakens C–C bonds and causes the distortion of the sheet, it is possible to induce carbon removal avoiding the sole O₂ formation. Most importantly, the treatment temperature and the initial cluster size (dictated by the mild annealing time and temperature) can be exploited experimentally to tune the pore dimensions. We discovered that the cluster shape heavily influences the final morphology of the sheet: long linear clusters form oxygen impurity defects, and square or circular clusters form pores. Therefore, for the production of pores through application of the two-step process, it is also possible to start from initial higher sheet coverages given that more linear clusters will not tear the layer. Thanks to our results, it will be possible to experimentally synthesize membranes for desalination by means of the highly scalable double-thermal process in a controlled way.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the CINECA award under the ISCRA initiative and HPC@POLITO for the availability of high-performance computing resources and support. This work is part of the “DESAL” project funded by Politecnico di Torino.

Notes and references

1. A. Subramani and J. G. Jacangelo, Water Res., 2015, 75, 164–187.
2. L. F. Greenlee, D. F. Lawler, B. D. Freeman, B. Marrot and P. Moulin, Water Res., 2009, 43, 2317–2348.
3. A. Zhu, A. Rahardianto, P. D. Christofides and Y. Cohen, Desalin. Water Treat., 2010, 15, 256–266.
4. M. Elimelech and W. A. Phillip, Science, 2011, 333, 712–717.
5. A. Boretti, S. Al-Zubaidy, M. Vaclavikova, M. Al-Abri, S. Castelletto and S. Mikhalovsky, NPJ Clean Water, 2018, 1, 5.
6. D. Cohen-Tanugi and J. C. Grossman, Nano Lett., 2012, 12, 3602–3608.
7. D. Jiang, V. R. Cooper and S. Dai, Nano Lett., 2009, 9, 4019–4024.
8. F. Risplendi, F. Raffone, L.-C. Lin, J. C. Grossman and G. Cicero, J. Phys. Chem. C, 2020, 124, 1438–1445.
9. C. Sun, M. S. H. Boutilier, H. Au, P. Poesio, B. Bai, R. Karnik and N. G. Hadjiconstantinou, Langmuir, 2014, 30, 675–682.
10. L. W. Drahushuk and M. S. Strano, Langmuir, 2012, 28, 16671–16678.
11. D. Konatham, J. Yu, T. A. Ho and A. Striolo, Langmuir, 2013, 29, 11884–11897.
12. G. Tronci, F. Raffone and G. Cicero, Appl. Sci., 2018, 8, 1547.
13. M.-C. Clochard, G. Melilli, G. Rizza, B. Madon, M. Alves and J.-E. Wegrowe, et al. , Mater. Lett., 2016, 184, 47–51.
14. C. J. Russo and J. A. Golovchenko, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 5953–5957.
15. M. D. Fischbein and M. Drndicć, Appl. Phys. Lett., 2008, 93, 113107.
16. S. P. Koenig, L. Wang, J. Pellegrino and J. S. Bunch, Nat. Nanotechnol., 2012, 7, 728–732.
17. S. P. Surwade, S. N. Smirnov, I. V. Vlassiouk, R. R. Unocic, G. M. Veith, S. Dai and S. M. Mahurin, Nat. Nanotechnol., 2015, 10, 459–464.
18. L.-C. Lin and J. C. Grossman, Nat. Commun., 2015, 6, 8335.
19. F. Raffone, F. Savazzi and G. Cicero, J. Phys. Chem. Lett., 2019, 10, 7492–7497.
20. W. K. Park, Y. Yoon, Y. H. Song, S. Y. Choi, S. Kim, Y. Do, J. Lee, H. Park, D. H. Yoon and W. S. Yang, Sci. Rep., 2017, 7, 16414.
21. S. Eigler, M. Enzelberger-Heim, S. Grimm, P. Hofmann, W. Kroener, A. Geworski, C. Dotzer, M. Rockert, J. Xiao, C. Papp, O. Lytken, H.-P. Steinruck, P. Muller and A. Hirsch, Adv. Mater., 2013, 25, 3583–3587.
22. K. Vijayarangamuthu, S. Ahn, H. Seo, S. Yoon, C. Park and K. Jeon, Adv. Mater., 2016, 28, 661–667.
23. Y. K. Lee, H. Choi, C. Lee, H. Lee, K. C. Goddeti, S. Y. Moon, W. H. Doh, J. Baik, J.-S. Kim, J. S. Choi, C.-G. Choi and J. Y. Park, Nanoscale, 2016, 8, 11494–11502.
24. C. Castro, M. Cocuzza, A. Lamberti, M. Laurenti, A. Pedico, C. F. Pirri, V. Rocca, E. S. Borello, L. Scaltrito, C. Serazio, D. Viberti and F. Verga, Geofluids, 2018, 7026426.
25. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
26. K. Chenoweth, A. C. van Duin and W. A. Goddard, J. Phys. Chem. A, 2008, 112, 1040–1053.
27. Z. Chen, A. Khajeh, A. Martini and S. H. Kim, ACS Appl. Mater. Interfaces, 2021, 13, 1895.
28. M. S. R. Elapolu and A. Tabarraei, J. Phys. Chem. A, 2020, 124, 7060.
29. F. Rahmani, S. Nouranian and Y. C. Chiew, Ind. Eng. Chem. Res., 2020, 59, 2203.
30. S. G. Srinivasan and A. C. T. van Duin, J. Phys. Chem. A, 2011, 115, 13269–13280.
31. A. Bagri, C. Mattevi, M. Acik, Y. J. Chabal, M. Chhowalla and V. B. Shenoy, Nat. Chem., 2010, 2, 581–587.
32. F. Savazzi, F. Risplendi, G. Mallia, N. M. Harrison and G. Cicero, J. Phys. Chem. Lett., 2018, 9, 1746–1749.
33. C. K. Chua and M. Pumera, Chem. – Eur. J., 2013, 19, 2005–2011.
34. C. Xu, R.-S. Yuan and X. Wang, New Carbon Mater., 2014, 29, 61–66.
35. A. Mathkar, D. Tozier, P. Cox, P. Ong, C. Galande, K. Balakrishnan, A. L. M. Reddy and P. M. Ajayan, J. Phys. Chem. Lett., 2012, 3, 986–991.
36. M. Z. Hossain, J. E. Johns, K. H. Bevan, H. J. Karmel, Y. T. Liang, S. Yoshimoto, K. Mukai, T. Koitaya, J. Yoshinobu, M. Kawai, A. M. Lear, L. L. Kesmodel, S. L. Tait and M. C. Hersam, Nat. Chem., 2012, 4, 305–309.
37. B. Gupta, N. Kumar, K. Panda, V. Kanan, S. Joshi and I. Visoly-Fisher, Sci. Rep., 2017, 7, 45030.
38. S. Zhou and A. Bongiorno, Sci. Rep., 2013, 3, 2484.
39. T. Sun, X. Yao and S. Fabris, J. Phys. Chem. A, 2016, 120, 2607–2613.
40. R. Larciprete, S. Fabris, T. Sun, P. Lacovig, A. Baraldi and S. Lizzit, J. Am. Chem. Soc., 2011, 133, 17315–17321.
41. S. Kurasch, J. C. Meyer, D. Künzel, A. Groß and U. Kaiser, Beilstein J. Nanotechnol., 2011, 2, 394–404.
42. C. Hofer, V. Skakalova, T. Görlich, M. Tripathi, A. Mittelberger, C. Mangler, M. R. A. Monazam, T. Susi, J. Kotakoski and J. C. Meyer, Nat. Commun., 2019, 10, 4570.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00134e

---