Excited state dipole moments and lifetimes of 2-cyanoindole from rotationally resolved electronic Stark spectroscopy

Abstract

The permanent dipole moments of 2-cyanoindole (cyanoindole = CNI) in its ground and lowest excited singlet states have been determined from rotationally resolved electronic Stark spectroscopy under jet-cooled conditions. From the orientation of the transition dipole moment and the geometry changes upon electronic excitation the lowest excited singlet state could be shown to be of L_b-symmetry. The general statement, that the L_a-state has the larger permanent dipole moment of the two lowest excited singlet states, will be challenged in this contribution. On the basis of the different electronic nature of the first excited singlet state the behavior of 2-, 3-, 4- and 5-CNI is discussed. The excited state lifetime of isolated 2-CNI in the gas phase has been determined to be 9.4 ns. This value is compared to the excited state lifetime in ethyl acetate solution of 2.6 ns, which was quantified with a Strickler–Berg analysis. Using water as solvent shortens the 2-CNI lifetime to <40 ps. The reason for this drastic shortening is discussed in detail. Additionally, the rotationally resolved electronic spectrum of 2-CNI(1-d₁) has been measured and analyzed.

---

1 Introduction

Of the three natural fluorescing amino acids, tryptophan, tyrosine, and phenylalanine, the indole chromophore derived tryptophan has the most prominent position, due to its large oscillator strength that makes it an ideal candidate for in vivo spectroscopic and microscopic fluorescence techniques.^1–4 Distance dependent fluorescence techniques like Förster resonance energy transfer (FRET) are used to study conformers of proteins and their time-dependent folding mechanisms. Frequently, synthetic fluorescence probes are used which have large oscillator strength and good photochemical stability. These, however, are often linked to the protein via flexible linkers for sampling reasons, causing additional flexibility, which is not present in the native protein. Therefore, the use of intrinsic fluorescence probes, with only slight modifications has found widespread interest. Recently, cyano-substituted tryptophanes have been proposed as ideal FRET and photo-induced electron transfer (PET) chromophores.⁵ Furthermore, they find increasing interest for fluorescence imaging and microscopy applications.⁶ The photophysical properties of this new class of modified intrinsic fluorophores can be studied, using the isolated chromophore in the gas-phase, and compared with the results of solution data.

A thorough theoretical study of the excited state dynamics of all structural isomers of cyanoindole has been presented by Abou-Hatab and Matsika.⁷ Their calculations predict that “in absorption the L_b-excited state is lower in energy than the L_a-state for all positional isomers in the gas phase and in solution”. The L_a and L_b nomenclature for the close-lying excited singlet ππ*-states goes back to the original proposal by Platt for cata-condensed aromatics^8,9 and has later been extended to the case of indole by Weber.¹⁰ However, if the C₂-axis, present in cata-condensed aromatics is not preserved,‡ the excited states of same multiplicity start to mix and the labeling becomes increasingly difficult. Nonetheless, it seems useful to maintain this nomenclature, because it is widely used in the fluorescence spectroscopy community and can be connected to observables like excited state dipole moments, transition dipole moment orientation, and oscillator strengths. In general, L_a-states have the larger oscillator strengths than the respective L_b-states. This can be traced back to the fact that L_b-states are composed of two orbital contributions (LUMO ← HOMO−1 and LUMO+1 ← HOMO), which are out-of-phase and approximately cancel each other out, while the L_a-state is characterized by a more or less pure LUMO ← HOMO excitation. The fluorescence lifetime of indole and substituted indoles depends on the energy gap between the L_a- and L_b-state. The smaller the gap, the shorter the lifetime.¹¹ It is widely believed that the L_a-state has the larger permanent dipole moment of the two lowest excited singlet states, but we will challenge this general statement in the present contribution.

Gas phase spectroscopy can add important contributions to the photo-physical properties of the CNIs, since it is free from solute–solvent interactions, except for the cases in which definite cluster sizes are used to study the subtle interaction between the chromophore and the first solvating molecule(s). This has up to now been performed for the 3-CNI–water^12–14 and the 5-CNI–water¹⁵ clusters, respectively.

In the present study we analyze the changes of geometry and dipole moments upon electronic excitation of 2-CNI and its N-deuterated isotopologue, using a combination of rotationally resolved fluorescence (Stark) spectroscopy, time-correlated single photon counting (TCSPC) and ab initio calculations on the coupled-cluster level of theory.

2 Experimental section

2.1 Experimental procedures

2.1.1 Rotationally resolved electronic Stark spectroscopy. 2-CNI (≥98%) was purchased from Apollo Scientific, used without further purification, heated to 120 °C and co-expanded with 300 mbar of argon through a 147 μm nozzle into the vacuum. The deuteration was performed as follows: 2-CNI was dissolved in methanol (99.5 atom% D) from Carl Roth and left to rest until the methanol was evaporated. The deuterated isotopologue was measured under the same conditions as the undeuterated sample. After the expansion in the molecular beam machine consisting of three differentially pumped vacuum chambers the molecular beam was formed using two skimmer, with the diameter of 1 mm and 3 mm, linearly aligned inside the machine. The molecular beam was crossed at right angles with the laser beam 360 mm downstream of the nozzle. A single frequency ring dye laser (Sirah Matisse DS), operated with rhodamine 6G, was pumped by 10 W of the 532 nm line of a diode pumped solid state laser (Spectra-Physics Millennia eV) to create the excitation beam. The resulting power of 18 mW during the experiments was reached by the frequency doubling of the fluorescence light of the dye laser in an external folded ring cavity (Spectra Physics Wavetrain). The fluorescence light of the sample was collected perpendicular to the plane defined by laser and molecular beam by a light collecting system consisting of a concave mirror and two planoconvex lenses onto the photocathode of a UV enhanced photomultiplier tube (Thorn Emi 9863QB). For data recording and processing the signal output was discriminated and digitized by a photon counter and transmitted to a PC. The relative frequency was determined using a quasi confocal Fabry–Perot interferometer. By comparing the recorded iodine absorption spectrum to the tabulated lines¹⁶ the absolute frequency was obtained. A detailed description of the experimental setup for rotationally resolved laser induced fluorescence spectroscopy has been given previously.^17,18 The Stark plates consists of a parallel pair of electroformed nickel wire grids (18 mesh per mm, 50 mm diameter) with a transmission of 95% in the UV and an effective distance of 23.49 ± 0.05 mm, calibrated using the accurately known dipole moment of benzonitrile.^19,20 The polarization plane of the incoming laser beam can be rotated by 90° inside the vacuum chamber by means of an achromatic λ/2 plate (Bernhard Halle 240–380 nm), which can be pushed in or pulled out of the laser beam using a linear motion vacuum feedthrough. One can choose between a parallel (selection rules ΔM = 0) and perpendicular (selection rules ΔM = ±1) set-up by changing the plane of polarization.

2.1.2 Time-correlated single photon counting. We performed lifetime measurements in different solvents using time-correlated single photon counting (TCSPC), since the question of excited state lifetimes is important for the discussion of the photophysical properties of the investigated cyanoindoles. TCSPC was performed with a DeltaFlex Ultima spectrometer (HORIBA Jobin Yvon), equipped with a supercontinuum light source SuperK Extreme EXR-20 and frequency doubler SuperK Extend-UV/DUV (both NKT Photonics). The signal was recorded at 328 nm under magic angle conditions, a pulse repetition rate of 19.5 MHz, a sample temperature of 20 °C and with excitation at 299 nm. The instrument response function (IRF, FWHM approximately 60 ps) was recorded at the excitation wavelength, using a scattering solution (Ludox) and used in the fits applying an iterative reconvolution algorithm to minimize χ².²¹

2.2 Quantum chemical calculations

Structure optimizations were performed employing a Dunning's correlation-consistent polarized valence triple zeta (cc-pVTZ) basis set from the Turbomole library.^22,23 The equilibrium geometries of the electronic ground and the lowest excited singlet states were optimized using the approximate coupled cluster singles and doubles model (CC2) employing the resolution-of-the-identity (RI) approximation.^24–26 For the structure optimizations spin-component scaling (SCS) modifications to CC2 were taken into account.²⁷ Vibrational frequencies and zero-point corrections to the adiabatic excitation energies were obtained from numerical second derivatives using the NumForce script.²⁸

2.3 Fits of the rovibronic spectra using evolutionary algorithms

Evolutionary strategies are perfect instruments to automatically fit rotationally resolved electronic spectra, even of large molecules with congested spectra.^29–32 They are powerful tools to handle complex multi-parameter optimizations and to find the global optimum and are inspired by evolutionary processes in nature, which are based on reproduction, mutation and selection. For the analysis of high resolution spectra in the present work, we apply the covariance matrix adaption evolution strategy (CMA-ES), which is described in detail elsewhere.^31,33,34

3 Results

3.1 Computational results

The optimization of the geometry of 2-CNI yields a planar structure in the ground and the lowest excited singlet state both with genuine CC2 as well as with SCS-CC2. The molecular parameters (rotational constants A, B, and C in both electronic states, the inertial defects ΔI, the angle θ of the transition dipole moment with the inertial a-axis, the angle θ_D of the permanent dipole moment with the inertial a-axis, and the zero-point corrected origin frequency ν₀) are compiled in Table 1 and are compared to the experimental results, which are described in detail in Section 3.2. Contrary to the case of 5-CNI, both generic CC2 and its spin-component scaled variant SCS-CC2 reveal that the lowest excited singlet state is the L_b-state.³⁵ However, the L_b- and L_a-states are considerably stronger mixed in the CC2 calculations than in the spin-component scaled variant.

Table 1 SCS-CC2/cc-pVTZ computed and experimental molecular parameters of 2-CNI. Doubly primed parameters belong to the electronic ground and single primed to the excited state. θ_D is the angle of the permanent dipole moment vector with the main inertial a-axis. A positive sign of this angle means an clockwise rotation of the main inertial a-axis onto the dipole moment vector, shown in Fig. 1. θ is the angle of the transition dipole moment vector with the main inertial a-axis. The same convention for its sign is used as for θ_D. For details see text

	Theory SCS-CC2		Theory CC2		Experiment
	S1	S2	S1	S2
A′′/MHz	3850.97		3853.67		3852.31(3)
B′′/MHz	695.28		697.25		698.76(1)
C′′/MHz	588.95		590.42		591.57(1)
ΔI′′/amu Å^2	0.00		0.01		−0.14(2)
μ a′′/D	3.23		3.25		±3.57(1)
μ b′′/D	1.50		1.50		±1.00(1)
μ′′/D	3.56		3.58		3.71(1)
θ D′′/°	−24.94		−24.79		±15.7
A′/MHz	3736.30	3792.22	3777.31	3759.26	3746.10(4)
B′/MHz	687.69	687.32	686.76	691.10	691.84(2)
C′/MHz	580.79	581.86	581.11	583.78	584.14(2)
ΔI′/amu Å^2	0.00	0.00	0.00	0.00	−0.22(3)
μ a′/D	4.52	3.18	5.01	3.22	±5.16(1)
μ b′/D	2.01	1.33	2.12	1.34	±0.71(1)
μ′/D	4.95	3.44	5.44	3.49	5.21(1)
θ D′/°	−24.01	−22.65	−22.94	−22.66	±7.8
ΔA/MHz	−114.67	−58.75	−76.36	−94.41	−106.21(1)
ΔB/MHz	−7.59	−7.96	−10.49	−6.51	−6.91(1)
ΔC/MHz	−8.16	−7.09	−9.31	−6.64	−7.43(1)
ΔνLorentz/MHz	—	—	—	—	16.94(1)
τ/ns	—	—	—	—	9.40(1)
θ/°	+36.4	−15.3	+48.1	−9.4	±45.9(20)
ν 0/cm^−1	34229.35	37812.63	34123.46	37476.13	33422.63(5)

---

A clear indication for the L_b-state as lowest excited singlet state is the orientation of the calculated transition dipole moment with the inertial a-axis (Table 1 and Fig. 1), which is +36.4° (+48.1°) at the SCS-CC2 (CC2) level of theory and which points away from the nitrogen atom. To make a better comparison to indole, the transition dipole moment (TDM) is rotated to the inertial axis-frame of indole. An angle of +13° with the inertial a-axis of indole is obtained.

Fig. 1 (a) Optimized ground state structure, atomic numbering, inertial axes, transition dipole moment (TDM) for excitation to the lowest excited singlet state (red, straight), and the orientation of the permanent dipole moment in the ground (magenta, straight) and first excited state (green, straight) of 2-CNI. The TDM for the excitation to the S₂ state is shown as a blue dotted arrow (only calculated). Positive signs of the angles θ and θ_D refer to a clockwise rotation of the inertial a-axis onto the dipole/TDM vector. (b) Definitions of the axis reorientation angle θ_T and the angle of the TDM θ with the inertial a-axis. The doubly primed axes refer to the ground state, the singly primed to the electronically excited state. A positive sign of θ_T refers to a clockwise rotation of the inertial axis system upon electronic excitation.

Another indication for the L_b-state are the main contributions to the excitation to the lowest excited singlet state at the SCS-CC2 level of theory: 70.3% LUMO ← HOMO−1 + 12.2% LUMO+1 ← HOMO and 8.8% LUMO ← HOMO excitation. The adiabatically second state in contrast is an almost pure LUMO ← HOMO transition (80%), what is typical for an L_a-state. The results are shown in Fig. 2. As mentioned above, the results for the CC2 calculations are much less clear: 47.4% LUMO ← HOMO−1 + 5.4% LUMO+1 ← HOMO and 38.4% LUMO ← HOMO excitation for the S₁-state, pointing to a considerable amount of mixing of the lowest excited singlet states.

Fig. 2 Molecular orbitals of 2-CNI with the percentage of the S₁ (L_b) and S₂ (L_a) excitations according to SCS-CC2/cc-pVTZ calculations.

The zero-point corrected adiabatic excitation energy to the lowest excited singlet state amounts to 34229.35 cm⁻¹ (34123.46 cm⁻¹) at the SCS-CC2 (CC2) level of theory.

The value of the permanent dipole moment is 3.23 D (3.25 D) in the ground state and 4.95 D (5.44 D) in the lowest excited singlet state at the SCS-CC2 (CC2) level of theory with larger amounts of the a-component of the dipole vector. The orientation of the calculated permanent dipole moments with the inertial a-axis stay nearly constant.

3.2 Experimental results

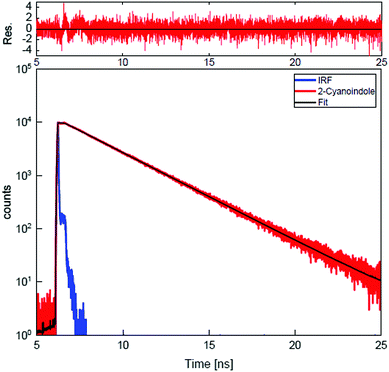
Trace (a) of Fig. 3 shows the rotationally resolved electronic spectrum of the electronic origin of 2-CNI at 33422.63(5) cm⁻¹, which is set to 0 on the scale of the figure. In trace (b) a zoomed part of the spectrum, along with the best fit at zero field is shown. Trace (c) presents the same spectral range at a field strength of 638.90 V/cm. Experimental spectra are shown as black traces, simulations, using the best fit parameters, as red traces. The selection rules ΔM = 0 for the Stark spectrum are held, because the electric field in the chosen set-up is parallel to the polarization of the plane of the exciting light. The spectrum was fit using a CMA-ES and the molecular parameters are compiled in Table 1 and are compared to the results of the SCS-CC2/ccpVTZ calculations. The analysis of the ab-hybrid origin band yields an angle of ±45.9° with the inertial a-axis. By comparison to the ab initio computed value of +36.4° (+48.1°) at the SCS-CC2 (CC2) level of theory the indeterminacy of the TDM orientation can be resolved. A Lorentzian linewidth of 16.94 ± 0.01 MHz to the Voigt line profile using a fixed Gaussian contribution of 18.70 MHz corresponds to an excited state lifetime in the gas phase of 9.40 ± 0.01 ns. The Gaussian contribution was determined from a Voigt fit to a few single rovibronic lines with the boundary condition of equal Gaussian contribution to each line. The lifetime increases to 10.38 ± 0.08 ns upon N-deuteration. A very good agreement between the experimental and the simulated spectrum, using the best fit parameters has been obtained.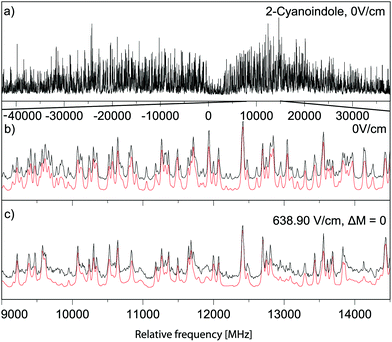

Fig. 3 Rotationally resolved electronic spectrum of the electronic origin of 2-CNI, along with a simulation with the best CMA-ES fit parameters.

The rotationally resolved spectrum of the electronic origin of the deuterated isotopologue 2-CNI(1-d₁) at 33426.61(1) cm⁻¹ is shown in Fig. S1 of the ESI† the molecular parameters, obtained from the CMA-ES fit, are compiled in Table S1 of the ESI.† The angle θ of the TDM in 2-CNI(1-d₁) is slightly smaller than in 2-CNI.

Furthermore, lifetime measurements using TCSPC in ethyl acetate and water as solvents were performed. A single exponential decay with an excited state lifetime of 2.60 ± 0.03 ns is found for ethyl acetate as solvent. The decay curve along with the best fit of a single exponential decay and the residue for 2-CNI in ethyl acetate is shown in Fig. 4. The fluorescence decay in water as solvent is considerably faster (<40 ps). For the deuterated isotopologue the excited state lifetime in ethyl acetate as solvent is also 2.60 ± 0.03 ns and in D₂O <40 ps.

Fig. 4 TCSPC trace of 2-CNI in ethyl acetate solution, along with the instrument response function (IRF) and the best fit to a single exponential decay with excitation at 299 nm. Above, the weighted residuals of the fit vs. experiment are shown.

4 Discussion

4.1 Excited state structure

The planarity in both electronic states is shown by the small negative inertial defects of 2-CNI in the electronic ground state with a value of −0.14 amu Ų and in the lowest electronically excited state with a value of −0.22 amu Ų, what is slightly more negative than in the ground state. A comparison of the inertial defect to those of other cyanoindoles shows a close agreement to that of 5-CNI (Table S2 of the ESI†). Equivalent to the increase of the moment of inertia, all rotational constants decreases upon electronic excitation (Table 1).

The bond lengths changes upon electronic excitation are quite symmetric, with respect to the molecular plane and along the a-axis of the molecule. This is a clear indication for an L_b-state. In contrast to the symmetric changes upon excitation to the L_b-state are the much more irregular changes upon the excitation to the L_a-state. These results were obtained from ref. 36, where the properties of the three lowest singlet electronic states (ground, L_a-and L_b-state) of the chromophore indole have been calculated with second-order approximate coupled-cluster theory (CC2) within the resolution-of-the-identity approximation. The difference in the structural changes upon electronic excitation for the L_a-and the L_b-state and also for the geometry changes upon electronic excitation obtained from the SCS-CC2/cc-pVTZ optimized structure can be seen in Fig. 5. A Kraitchman analysis³⁷ has been performed for a determination of the H-atom position of the pyrrolic NH group using the rotational constants of the ND-deuterated isotopologue in both electronic states. The results, which are described in detail in the ESI,† support the interpretation of the L_b-state as electronically excited state.

Fig. 5 Changes of the bond lengths upon electronic excitation from SCS-CC2/cc-pVTZ calculations. (a) Schematic geometry changes of the parent chromophore indole upon excitation to the L_a-state, adapted from ref. 36. (b) Schematic geometry changes of the parent chromophore indole upon excitation to the L_b-state, adapted from ref. 36. (c) Geometry changes of 2-CNI in pm upon electronic excitation to the lowest excited singlet state, obtained from the SCS-CC2/cc-pVTZ optimized structures. Comparison to trace (a) and (b) show that this must be the L_b-state. For more details see text.

4.2 Excited state lifetime

The excited state lifetime of isolated 2-CNI in the gas phase (9.40 ± 0.01 ns) is shorter than that of the parent indole (16.4 ns).^38–41 Compared to the other cyanoindoles, which were investigated in our group using HRLIF (3-, 4-, 5-CNI), the excited state lifetimes in the gas phase and in solution are the shortest for 2-CNI.^14,21,35

For the N-deuterated isotopologue of 2-CNI, the excited state lifetime is nearly 1 ns (10.38 ± 0.08 ns) longer than for the undeuterated isotopologue. In most cases, deuteration at the chromophore leads to an increase of the excited state lifetime, like for indole. In indole, the excited state lifetime increases slightly from 16.4 ns to 17.2 ns upon N-deuteration.⁴⁰ Another example is isolated 3-CNI, in which an increase from 9.8 ns to 14.8 ns is observed.¹⁴ In contrast to these results, the experimentally determined excited state lifetime for isolated 4-CNI (11.0 ns) is nearly twice as large compared to the three investigated deuterated species, where the lifetime was remarkably independent on the position of deuteration.²¹

The lifetimes of 2-, 3-, 4-, and 5-CNI in solution are in general much shorter than in the gas phase. A single exponential decay with a lifetime of 2.60 ± 0.03 ns is found in the lifetime measurement of 2-CNI in ethyl acetate solution, which shortens to <40 ps in water as solvent.

The pure radiative lifetime of an isolated molecule in the gas phase can be approximated by the following expression:^21,42

where e is the elementary charge, f the dimensionless oscillator strength, ε₀ the vacuum permittivity, m_e the mass of the electron, c the speed of light, and λ the wavelength of the transition. The electronic oscillator strength f is related to oscillator strength f_{υ′υ′′} of the vibronic transition υ′ ← υ′′ by the following expression:

f = f_{υ′υ′′}/q_{υ′υ′′} (2)

where the q_{υ′υ′′} are the Franck–Condon factors 〈υ′|υ′′〉² for the transition from υ′′ to υ′. We determined them for the electronic origin from the vibronically resolved laser induced fluorescence spectrum of 2-CNI, shown in Fig. S3 of the ESI.†

Using eqn (1) and the SCS-CC2/cc-pVTZ calculated oscillator strength and transition wavelength, and the FC factors from eqn (2), we compute a pure radiative lifetime τ_r of 33 ns for isolated 2-CNI after excitation of the vibrationless origin. This value can be converted into an excited state fluorescence lifetime τ_f, if the fluorescence quantum yield Θ_f is known. Unfortunately, the fluorescence quantum yield of 2-CNI in the gas phase is not known, and cannot be determined easily experimentally from molecular beam experiments. From the quotient of the experimental fluorescence lifetime τ^exp_f (9.4 ns) and the calculated radiative lifetime τ_r (33 ns), the fluorescence quantum yield Θ_f of 2-CNI in the gas phase can be approximated to 0.3.

The fluorescence lifetime for emission from the lowest singlet state solutions of ethylacetate (EA) and water are much shorter than for the isolated molecule. A Strickler–Berg (SB) analysis⁴³ has been chosen for quantification of the solution lifetime. The pure radiative lifetime of a fluorescing molecule in a solvent of index of refraction n is approximated by:

where N_A is Avogadro's constant, 〈[small nu, Greek, tilde]_f⁻³〉⁻¹ is the inverse of the expectation value of [small nu, Greek, tilde]_f⁻³. The integral 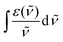has been approximated from a fit of the steady-state absorption spectrum, which was scaled in order to bring it into agreement with discrete values of the molar extinction coefficient ε published in ref. 44. The integral of the lowest energy Gaussian has been used to evaluate the integral in eqn (3). The inverse of the expectation value of [small nu, Greek, tilde]_f⁻³ is approximated by the cube of the wavenumber of maximum fluorescence emission, as proposed by Cohen et al.:⁴⁵where F is the fluorescence emission intensity. Steady state absorption and fluorescence spectrum of 2-CNI in EA are shown in Fig. S4 of the ESI.† The pure radiative lifetime τ^SB_r from the SB analysis for EA amounts to 5.2 ns, which would translate to a quantum yield of 0.5 using the experimental fluorescence lifetime of 2.6 ns.

The steady state fluorescence spectra of 2-CNI in water are too weak to successfully apply the SB analysis. From the TCSPC experiment however, we have the value for the lifetime of <40 ps in water. What makes the lifetime of 2-CNI in water so short? For the isolated binary 3-CNI–water cluster we found a reduction of the lifetime from 9.8 ns to 3.6 ns, already for the first water molecule attached to the chromophore.¹⁴ Of course we tried to measure the 1 : 1 water cluster using rotationally resolved LIF spectroscopy. Although the origin of the cluster was found at 32984.5 cm⁻¹, i.e. red-shifted by 438.1 cm⁻¹ relative to the monomer band in a low resolution LIF spectrum in a free jet (laser bandwidth 0.2 cm⁻¹, Doppler width ≈0.01 cm⁻¹ ≡ 300 MHz) and showed strong fluorescence (cf. Fig. S5 of the ESI†), we failed to record a rovibronically resolved spectrum (laser bandwidth 800 kHz, Doppler width 18.7 MHz). Instead of a well-resolved spectrum like for the monomer, a very broad onset of fluorescence is observed. The respective trace, along with the iodine spectrum and the vibronically resolved spectrum is shown in Fig. S5 of the ESI.† The only reason for this broadening (often encountered before) is a large Lorentz contribution to the line profile from a short lifetime. This additional broadening brings the peak intensity of individual rovibronic transitions below the noise level of our experimental set-up. From a convolution of the experimental spectrum with Lorentz profiles with varying bandwidths, we found this limit to be at 500 MHz equivalent to a lifetime of 300 ps. We suggest that this is the upper limit for the lifetime of the 1 : 1 water cluster of 2-CNI. It thus seems that the short fluorescence lifetime of 2-CNI in water solution is caused already by the first water molecule attached to the chromophore. The effect is similar to the one observed in 3-CNI–water, however it is considerably larger.

The fact that the lifetime of 2-CNI increases upon deuteration at the pyrrolic NH-site, points to a tunneling dominated process, which is responsible for the lifetime. Sobolewski et al.⁴⁶ have shown for indole and phenol that a conical intersection between the primarily excited ππ*-state and the repulsive πσ*-state induces a barrier at the S₁ surface, which is the reason for the strong isotope effect in phenol. The smaller isotope effect in indole and the cyanoindoles is caused by a higher barrier towards dissociation through the ππ*–πσ* conical intersection compared to phenol. Water complexation at the phenolic OH group has the effect of shifting the πσ*-state up in energy and removing the second conical intersection with the ground state. For indole however, the energy πσ*-state decreases considerably along the azine NH coordinate, already for weak electric fields as exerted by a nearby water molecule, resulting in shorter lifetimes for the water cluster.⁴⁷ Our results for the cyanoindoles imply that the relative position of ππ* and πσ*-state is strongly modulated by the position of the cyano group leading to the very different lifetimes of the isolated water clusters as well as the ultrashort lifetimes in water as solvent.

4.3 Dipole moments

4.3.1 Permanent dipole moments. The experimentally determined dipole moment of 2-CNI increases from 3.71 D to 5.21 D upon electronic excitation. The angle of the permanent dipole moment with the inertial a-axis slightly decreases from 15.7 to 7.8° upon excitation. The SCS-CC2/cc-pVTZ calculated values are around 5% smaller, than the experimentally determined values. It is also noticeable, that the experimentally determined a-components are slightly larger and the b-components are smaller in both electronic states, than the expected values of the quantum chemical calculations.

For 3-CNI, a decrease from 5.90 D to 5.35 D upon electronic excitation was observed for the permanent dipole moment.¹⁴ For 4-CNI the experimentally determined dipole moment increases from 6.31 D to 8.92 D²¹ and for 5-CNI from 7.14 D to 8.17 D⁴⁸ upon electronic excitation.

It is commonly believed that the change of the permanent dipole moment upon excitation of the singlet state can be used as a sensitive indicator of the electronic nature of this excited state. L_a-states tend to have larger dipole moments than L_b-states. This would imply that the excited state of 2-CNI is of L_a-character, since the experimentally determined dipole moment agrees well with the one calculated for the S₁, which is larger than for the S₂ state. This has been confirmed both for SCS-CC2 and for CC2 calculations. However, geometry changes, TDM orientation, and orbital contributions clearly indicate that the experimentally observed state is the L_b-state. With special regard to the experimentally determined transition dipole moment orientation, the angle of the reorientation of the inertial axis system upon excitation and the leading contributions to the excitation to the lowest excited singlet state, the lowest excited singlet state for 3-CNI was specified as L_b-, and for 4- and 5-CNI as L_a-character. In these examples, an increase of the permanent dipole moment was observed for excitation to L_a-states, while for the L_b-states the permanent dipole moment in general was equal or even smaller than in the electronic ground state.

Regarding the 5-CNI case, there is a discrepancy between the analysis of Abou-Hatab and Matsika⁷ and our results,³⁵ which shows that an assignment using the original L_a and L_b notation becomes meaningless, when the states mix considerably.§ The assumption of the observed state being L_b is supported by the orbital character of the natural transition orbitals⁷ and the leading contributions of the configurations to the excited state from the SCS-CC2 wavefunctions.³⁵ On the other hand, the orientation of the transition dipole moment, is more “L_a-like”, and the large increase of the permanent dipole moment in 5-CNI upon excitation (more than 1 D) also points to an L_a-state, like the geometry changes from a Franck–Condon analysis.⁴⁹

4.3.2 Transition dipole moments. The angle of the TDM with respect to the inertial a-axis was determined experimentally to be ±45.9(20)°. The assignment of the sign of the TDM was made on the basis of the theoretical value of +36.4° (+48.1°) at the SCS-CC2 (CC2) level of theory. Referring to the uncertainty of 2° the experimentally determined value is in close agreement to the theoretical value of the CC2 level of theory. The experimentally determined TDM orientation is clearly that of the L_b-state relating to the results of indole: in indole the value of the orientation of the TDM vector is known from rotationally resolved electronic spectroscopy for the L_b-state, where the orientation of the TDM vector points also away from the heteroatom of the pyrrole ring.³⁸

As it is well known, the sign of the angle θ between the TDM and the a-axis cannot be determined directly from the experimentally recorded rotationally resolved spectra. From the intensities of the rovibronic transitions of the spectrum it is only possible to obtain the projection of the TDM onto the main inertial axes.

To obtain the sign of this angle in the method of Hougen and Watson the wave functions of the excited state are rotated into the coordinate system of the ground state after diagonalization of the respective Hamiltonian. For planar molecules it is possible to determine the angle of the reorientation of the inertial axis system upon electronic excitation θ_T:⁵⁰

Here, the doubly primed coordinates refer to the principal axis system (PAS) in the electronic ground state and the singly primed quantities to the respective excited state inertial system and the m_i are the atomic masses. Using the SCS-CC2 (CC2) optimized structures for lowest excited singlet state, we obtain an axis reorientation angle θ_T of +0.06° (+1.39°). In general axis reorientation has no effect on the eigenvalues and only a few line intensities are affected by this. To improve this method, only sections of the spectrum have to be included in the fit which show strong intensity variations. Using an axis reorientation Hamiltonian and different combinations of θ_T and θ signs for the fit of the whole rotationally resolved spectrum of the electronic origin of 2-CNI nearly the same result is obtained for ++ (−−) sign combination compared to the fit without axis reorientation (θ_T = 0). However, the fit using +− (−+) combinations is slightly inferior. Thus, we infer that θ_T and θ must have the same sign. Given that θ_T is defined geometrically from the optimized structures in both states, the sign of θ can be deduced. The inertial a-axis calculated in the SCS-CC2 optimized structures rotates clockwise upon excitation, which according to the convention is equivalent to a positive sign. The absolute orientation of the TDM vector θ with the a-axis is therefore +45.9°, cf.Fig. 1. The TDM orientation of excitation to the L_b-state in indole has been determined the same way to be +38.9°.^36,39 It can thus safely be concluded, that the orientation of the TDM vector in 2-CNI represents an L_b excitation. Table 2 compares the TDM orientations of 2-, 3-, 4-, and 5-CNI with that of indole. 2- and 3-CNI have TDM angles of +13° and +35°, while those of 4- and 5-CNI are around −15° (Fig. 6). A (preliminary) conclusion is that substitution in the pyrrole ring leads to the L_b as lowest state, while for substitution in the benzene moiety it is the L_a-state. A confirmation of this supposition can be given, once the missing 6- and 7-CNI have been investigated.

Table 2 Angles θ of the orientation of the transition dipole moment and excited state lifetimes (molecular beam and solution) of indole (In), 2-CNI, 3-CNI, 4-CNI, 5-CNI. In contrast to the θ values presented in Table 1, those shown here, are given with respect to the pseudo C₂-axis of indole

	In	2-CNI	3-CNI	4-CNI	5-CNI
a Ref. 40. b Ref. 14. c Ref. 21. d Ref. 35. e Ref. 44. f Excitation of indole in ethyl acetate (EA) at 284 nm. g Excitation of 3-CNI in EA at 283 nm. h Excitation of 4-CNI in EA at 302 nm. i Excitation of 5-CNI in EA at 295 nm.
θ/°	+38^a	+13	+35^b	−15^c	−12^d
τ/ns	16.4^a	9.4	9.8^b	11.0^c	12^d
τ(EA)^solv/ns	3.1^c^f	2.6	2.6^c^g	4.7^c^h	3.6^c^i
τ(H2O)^solv/ns	4.5^e	<0.04	<0.05^e	9.2^c	0.3^e

---

Fig. 6 Orientation of the TDM of indole (black double arrow), 2-CNI (green double arrow), 3-CNI (magenta double arrow), 4-CNI (blue double arrow) and 5-CNI (red double arrow), relative to the pseudo-C₂ axis of indole (black line).

5 Conclusions

It is commonly believed that L_a-states of substituted indoles tend to have larger dipole moments than the respective L_b-states.^51,52 Apart from the change of the permanent dipole moment, the transition dipole moment orientation, the angle of the reorientation of the inertial axis system upon excitation, and the leading contributions to the excitation to the lowest excited singlet state are used for identification of these states. With regard to these factors the lowest excited singlet state for 3-CNI was specified as being of L_b-character, and for 4- and 5-CNI as L_a-character. The present investigation of 2-CNI concludes that the change of the permanent dipole moment upon excitation of the singlet state can not be used as a sensitive indicator of this excited state in this case, because the results of the experimentally determined dipole moments and the calculated ones would imply that the excited state of 2-CNI has mainly L_a-character. The conclusion that the lowest excited singlet state of 2-CNI is the L_b-state, has been made from the experimentally determined orientation of the transition dipole moment as well as the main molecular orbital contributions to the excitation to the lowest excited singlet state. Also the geometry changes upon electronic excitation could be identified as an L_b-like distortion of 2-CNI. The assignment to the L_b-state as lowest excited singlet state is the same as for 3-CNI, but contrary to 4- and 5-CNI. A confirmation of the conclusion that substitution in the pyrrole ring leads to the L_b-state as lowest excited singlet state is possible, when the missing 6- and 7-CNI will be investigated. Compared to the theoretical analysis of Abou-Hatab and Matsika⁷ there is only discrepancy regarding the 5-CNI case, which shows that an assignment using the original L_a and L_b notation becomes meaningless, when the states mix considerably. Their optimizations of the lowest excited singlet state in the gas phase converged to the L_b minimum for all structural isomers, except for 4-CNI which converged to the L_a. This result is in accordance with our conclusion for the lowest excited singlet state of 4-CNI.²¹ In the 5-CNI case, where their calculations predict an L_b-state as lowest excited singlet state, our experimental data point to an L_a-state: the orientation of the transition dipole moment, which is more “L_a-like”, the large increase of the permanent dipole moment upon excitation and the geometry changes from a Franck–Condon analysis.⁴⁹ In the 2-CNI case there is no discrepancy. Moreover, the fluorescence lifetime could be extracted from the Lorentzian contribution to the Voigt line profile using a fixed Gaussian contribution. The increasing lifetime upon deuteration points to a tunneling process along the NH coordinate. The results from the gas phase were compared to the excited state lifetimes using TCSPC. For quantification of the solution lifetime in ethyl acetate a Strickler–Berg analysis has been chosen. A drastic reduction of the excited state lifetime upon solvation in water has been found, where the steady state spectra of 2-CNI were to weak to apply the Strickler–Berg analysis. The short fluorescence lifetime of 2-CNI in water solution is caused already by the first water molecule attached to the chromophore what is in accord with the broad onset of fluorescence signal instead of a well-resolved spectrum by using high resolution laser induced fluorescence spectroscopy for the 1 : 1 water cluster of 2-CNI. The πσ*-state shifts to lower energies along the azine NH coordinate by the electric field exerted by the first water molecule, resulting in shorter lifetimes for the water cluster.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Peter Gilch for helpful discussions and advice about limitations of the Strickler–Berg relationship. Financial support of the Deutsche Forschungsgemeinschaft via grant SCHM1043/14-1 is gratefully acknowledged. Computational support and infrastructure was provided by the “Center for Information and Media Technology” (ZIM) at the Heinrich-Heine-University Düsseldorf (Germany).

References

1. P. Talukder, S. Chen, B. Roy, P. Yakovchuk, M. M. Spiering, M. Alam, M. M. Madathil, C. Bhattacharya, S. J. Benkovic and S. M. Hecht, Biochemistry, 2015, 54, 7457–7469.
2. B. N. Markiewicz, D. Mukherjee, T. Troxler and F. Gai, J. Phys. Chem. B, 2016, 210, 936–944.
3. M. R. Hilaire, I. A. Ahmed, C.-W. Lin, H. Jo, W. F. DeGrado and F. Gai, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 6005–6009.
4. D. Mukherjee, L. I. O. Rodriguez, M. R. Hilaire, T. Troxler and F. Gai, Phys. Chem. Chem. Phys., 2016, 20, 2527–2535.
5. I. A. Ahmed, J. M. Rodgers, C. Eng, T. Troxler and F. Gai, Phys. Chem. Chem. Phys., 2019, 21, 12843–12849.
6. A. Acharyyaa, I. A. Ahmed and F. Gai, Methods Enzymol., 2020, 639, 191–215.
7. S. Abou-Hatab and S. Matsika, J. Phys. Chem. B, 2019, 123, 7424–7435.
8. J. R. Platt, J. Chem. Phys., 1949, 17, 484–495.
9. J. N. Murrell, The Theory of the Electronic Spectra of Organic Molecules, Chapman and Hall, London, 1971.
10. G. Weber, Biochem. J., 1960, 75, 335–345.
11. A. A. Sukhodola, J. Appl. Spectrosc., 2008, 75, 527–531.
12. A. Ahn, A. Min, C. J. Moon, J. H. Lee and M. Y. Choi, Chem. Phys. Lett., 2014, 616–617, 55–60.
13. A. Min, A. Ahn, C. J. Moon, J. H. Lee, M. Y. Choi and S. K. Kim, Chem. Phys. Lett., 2014, 614, 263–268.
14. M. Schneider, M.-L. Hebestreit, M. M. Lindic, H. Parsian, A. Y. Torres-Boy, L. Alvarez-Valtierra, W. L. Meerts, R. Kühnemuth and M. Schmitt, Phys. Chem. Chem. Phys., 2018, 20, 23441–23452.
15. A. Min, C. J. Moon, A. Ahn, J. H. Lee, S. K. Kim and M. Y. Choi, Chem. Phys. Lett., 2016, 658, 63–70.
16. S. Gerstenkorn and P. Luc, Atlas du spectre d'absorption de la molécule d'iode 14800-20000 cm⁻¹, CNRS, Paris, 1986.
17. M. Schmitt, Habilitation, Heinrich-Heine-Universität, Math. Nat. Fakultät, Düsseldorf, 2000.
18. M. Schmitt, J. Küpper, D. Spangenberg and A. Westphal, Chem. Phys., 2000, 254, 349–361.
19. J. Wilke, M. Wilke, W. L. Meerts and M. Schmitt, J. Chem. Phys., 2016, 144, 044201.
20. K. Wohlfart, M. Schnell, J. U. Grabow and J. Küpper, J. Mol. Spectrosc., 2014, 247, 119–121.
21. M.-L. Hebestreit, H. Lartian, M. Schneider, R. Kühnemuth, A. Y. Torres-Boy, S. Romero-Servin, J. A. Ruiz-Santoyo, L. Alvarez-Valtierra, W. L. Meerts and M. Schmitt, J. Mol. Struct., 2020, 1210, 127992.
22. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
23. J. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
24. C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161.
25. C. Hättig and A. Köhn, J. Chem. Phys., 2002, 117, 6939–6951.
26. C. Hättig, J. Chem. Phys., 2002, 118, 7751–7761.
27. A. Hellweg, S. Grün and C. Hättig, Phys. Chem. Chem. Phys., 2008, 10, 1159–1169.
28. P. Deglmann, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2002, 362, 511–518.
29. W. L. Meerts, M. Schmitt and G. Groenenboom, Can. J. Chem., 2004, 82, 804–819.
30. W. L. Meerts and M. Schmitt, Phys. Scr., 2005, 73, C47–C52.
31. W. L. Meerts and M. Schmitt, Int. Rev. Phys. Chem., 2006, 25, 353–406.
32. M. Schmitt and W. L. Meerts, in Handbook of High Resolution Spectroscopy, ed. M. Quack and F. Merkt, John Wiley and Sons, 2011.
33. A. Ostenmeier, A. Gawelcyk and N. Hansen, in Parallel Problem Solving from Nature, PPSN III, ed. Y. Davidor, H.-P. Schwefel and R. Männer, Springer, Berlin/Heidelberg, 1994.
34. N. Hansen and A. Ostermeier, Evol. Comput., 2001, 9, 159–195.
35. O. Oeltermann, C. Brand, B. Engels, J. Tatchen and M. Schmitt, Phys. Chem. Chem. Phys., 2012, 14, 10266–10270.
36. C. Brand, J. Küpper, D. W. Pratt, W. L. Meerts, D. Krügler, J. Tatchen and M. Schmitt, Phys. Chem. Chem. Phys., 2010, 12, 4968–4997.
37. J. Kraitchman, Am. J. Phys., 1953, 21, 17.
38. G. Berden, W. L. Meerts and E. Jalviste, J. Chem. Phys., 1995, 103, 9596–9606.
39. J. Küpper, D. W. Pratt, W. L. Meerts, C. Brand, J. Tatchen and M. Schmitt, Phys. Chem. Chem. Phys., 2010, 12, 4980–4988.
40. G. A. Bickel, D. R. Demmer, E. A. Outhouse and S. C. Wallace, J. Chem. Phys., 1989, 91, 6013.
41. J. W. Hager and S. C. Wallace, J. Phys. Chem., 1983, 87, 2121.
42. R. S. F. Peter and W. Atkins, Molecular Quantum Mechanics, Oxford University Press, New York, 2011.
43. S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814–822.
44. M. R. Hilaire, D. Mukherjee, T. Troxler and F. Gai, Chem. Phys. Lett., 2017, 685, 133–138.
45. B. Cohen, C. E. Crespo-Hernández and B. Kohler, Faraday Discuss., 2004, 127, 137–147.
46. A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093–1100.
47. C. Dedonder-Lardeux, C. Jouvet, S. Perun and A. Sobolewski, Phys. Chem. Chem. Phys., 2003, 5, 5118.
48. J. Wilke, M. Wilke, C. Brand, W. L. Meerts and M. Schmitt, ChemPhysChem, 2016, 17, 2736–2743.
49. B. Stuhlmann, A. Gräßle and M. Schmitt, Phys. Chem. Chem. Phys., 2014, 16, 899–905.
50. J. T. Hougen and J. K. G. Watson, Can. J. Phys., 1965, 43, 298–320.
51. E. H. Strickland, J. Horwitz, E. Kay, L. M. Shannon, M. Wilchek and C. Billups, Biochem. J., 1970, 9, 4914–4921.
52. D. Brisker-Klaiman and A. Dreuw, ChemPhysChem, 2015, 16, 1695–1702.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00097g

‡ In indole a pseudo-C₂-axis can be defined, which runs through C(2) and bisects the C(5)–C(6) bond. This pseudo-symmetry axis nearly coincides with the inertial a-axis of indole, with the deviation to be attributed to the mass difference of N(1)–H and C(3)–H.

§ The leading contributions of the configurations to the excited states shows that the adiabatically lowest S₁ state is characterized by 0.56 (LUMO ← HOMO) − 0.51 (LUMO ← HOMO−1) + 0.44 (LUMO+1 ← HOMO−1) + 0.42 (LUMO+1 ← HOMO) excitation. The S₂-state is comprised of 0.77 (LUMO ← HOMO) + 0.44 (LUMO ← HOMO−1) − 0.29 (LUMO+1 ← HOMO) − 0.26 (LUMO ← HOMO−2). A pure L_a-state would show as pure HOMO–LUMO excitation.

---