 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Measurement and modelling solubility of amino acids and peptides in aqueous 2-propanol solutions†
Hoang Tam
Do
 ,
Patrick
Franke
,
Sophia
Volpert
,
Marcel
Klinksiek
,
Max
Thome
and
Christoph
Held
,
Patrick
Franke
,
Sophia
Volpert
,
Marcel
Klinksiek
,
Max
Thome
and
Christoph
Held
 *
*
Laboratory of Thermodynamics, TU Dortmund University, Emil-Figge-Str. 70, 44227 Dortmund, Germany. E-mail: christoph.held@tu-dortmund.de
First published on 8th April 2021
Abstract
Amino acids and peptides are essential components in the biochemical industry. The final products are employed in a wide range of applications and are often synthesized by fermentation and purified in a complex downstream process. One possible separation step is using an additional solvent to lower the solubility of the desired product and, thus, promote the crystallization of the particular component. Therefore, it is crucial to have accurate knowledge of the solubility of these components. In this work, the solubilities of 20 proteinogenic amino acids and 21 peptides in aqueous 2-propanol solutions were gravimetrically determined. Additionally, the pH values of the saturated liquid phases were measured and the crystal structures of solid crystals were analysed using X-ray diffraction. The anti-solvent 2-propanol caused a decrease in the solubilities of the amino acids and peptides upon increasing its mass fraction. Exceptions were found for amino acids with aromatic substituents, L-phenylalanine and L-tyrosine. The solubility of 15 amino acids and 18 peptides was successfully modelled using the equation of state PC-SAFT that used recently determined melting properties of the amino acids and peptides as input data.
Introduction
Amino acids and peptides are not only essential biomolecules in the body, but also attract increasing attention in the chemical industry and biotechnology.1,2 This is mainly due to the wide range of applications of amino acids and their derived products. The three most important markets comprise production of pharmaceuticals, including nutritional supplements, cosmetics, and animal nutrition from amino acids.3,4In general, one possible method for separating amino acids or peptides from other biomolecules or industrial residues is the so-called anti-solvent crystallization. Here, an additional solvent, like ethanol or 2-propanol, can be utilized to lower the total solubility to promote the crystallization of the particular component.5 This technique is favourable because extreme process conditions (e.g., high or low temperature, high shear forces, or high pressures) can be avoided, and the biomolecules can be purified more gently.
Unfortunately, the data situation in this field of research is less developed than expected. Several aqueous solubility data can be found based on different aliphatic alcohols (methanol, ethanol, 1-propanol and 2-propanol) at one or different temperatures. Ferreira et al. measured the solubility of glycine, DL -alanine,6L-serine, L-threonine and L-isoleucine.7 Orealla and Kirwan8 measured the solubility of glycine, L-alanine, L-isoleucine, L-phenylalanine and L-asparagine monohydrates. Needham et al.9 measured the solubility of glycine, L-alanine, L-valine and L-phenylalanine in mixed10 and pure9 alcohol solvents. Ji et al. measured the solubility of glycine, DL-valine, DL-serine, L-alanine and L-leucine. Fuchs et al. measured the solubility of DL-methionine. Bowden et al. measured the solubility of amino acids and amino acid mixtures.11 Ferreira et al. also measured the solubility of glycine and DL-alanine. Nozaki and Tanford measured the solubility of several amino acids (glycine, alanine, leucine, phenylalanine, tryptophan, methionine, threonine, tyrosine, histidine, asparagine, and glutamine) and also that of the peptides diglycine and triglycine in aqueous guanidine hydrochloride solutions12 and in ethanol and dioxane solutions.13 Ghosh et al. measured the solubility of DL-phenylalanine and DL-serine in aqueous ethylene glycol solutions.14
However, often data are missing in terms of pH measurements and analysis of the crystal structure between the solid phase in saturated solution and its pure component, which allows detecting whether a new polymorph was formed upon anti-solvent addition. Furthermore, solutions containing biologically active components usually reveal strong deviations from ideal solutions. These substances strongly vary in ionic strength and state of dissociation, and they often occur together with copious amounts of electrolytes in solution. Thus, it is necessary to enlarge the data to allow for better design of technologies concerning anti-solvent crystallization. In order to reduce the experimental efforts when establishing an industrial process, it is highly necessary to find a precise modelling framework. The perturbed-chain statistical associating fluid theory (PC-SAFT) equation of state (EOS) was used to model the amino-acid/peptide solubility in water-2-propanol systems. This EOS has previously been shown to predict the thermodynamic data of biomolecules successfully.15–17
In the current study the solubility of ternary systems of 20 proteinogenic amino acids and 21 peptides in aqueous 2-propanol systems was determined using a gravimetric method. Within the thermodynamic framework of PC-SAFT, a solid–liquid equilibrium was used to model the solubility in aqueous 2-propanol systems. This requires melting properties as input, which were available for amino acids18–20 and peptides17,21 from our previous studies. For a pure solid phase the solubility xLi is calculated according to the study by Prausnitz22 with the following equation:
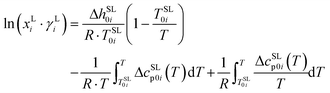 | (1) |
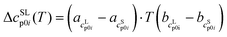 | (2) |
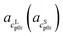 and
and 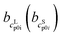 as the slope and the intercept of the heat capacities, respectively.
as the slope and the intercept of the heat capacities, respectively.
Solubility calculation according to eqn (1) is based on the physical properties such as melting enthalpy, temperature and heat capacity differences. The influence of the molecular interactions between the solute component and solvent in the liquid phase is accounted for by the activity coefficient γLi. Eqn (1) is only applicable to the neutral form of the molecule, which was confirmed from pH measurements of the saturated solutions and crystal structure analysis of the solid phase by powder X-ray diffractometry (PXRD).
Methodology
Materials and reagents
20 proteinogenic amino acids and 21 peptides investigated in this work are listed in Table S1 in the ESI.† All components were of commercial grade and used without additional purification. The Millipore-Q grade water for the solubility measurements was directly obtained from the lab.Measurement of solubility
All amino acid and peptide solubilities in aqueous 2-propanol solutions were measured using the gravimetric method by preparing first the isothermal supersaturated solutions. Therefore, excess amounts of the amino acid or peptide were added to 1.5 mL (5 mL) Eppendorf tubes. Then, 500 μL (2 mL) of 10 wt%, 20% wt%, and 30 wt% 2-propanol in water solutions were added. At each concentration, three independent samples were prepared. The solutions were shaken (24 h) and equilibrated isothermally (48 h) at T = 298.15 K in a ThermoMixer from Eppendorf with an accuracy of ±0.01 K to ensure that the solid–liquid equilibrium was reached.After this step, 100 μL of the saturated liquid phase was withdrawn and transferred to another 1.5 mL Eppendorf tube. The initial weight of the liquid phase was determined using a precision scale (Mettler Toledo, XS-205, ± 0.0001 g). The sample solution was placed in a drying chamber and then in a vacuum chamber to ensure total evaporation of the solvents. The remaining solid was weighed again; thus, the solubility was determined by weight-difference measurements. The final results were averaged from three independent samples. Additionally, the pH values of the saturated solutions were measured with a standard uncertainty of ±0.01 and the crystal-structure analysis of the solid phase was performed using PXRD (Miniflex 600, Rigaku, Japan, operating temperature (T = 295.15 K) and pressure (p = 1 atm), scan speed of 5° min−1 from 2° to 35° in 0.02° steps, voltage of 40 kV, current of 15 mA, and type of radiation Cu Kα anode), respectively. Information on the crystal structure is required since eqn (1) is valid only if the pure component (from the supplier) and the solid component in the equilibrium state are of equal form.
Solubility modelling with PC-SAFT
The successful modelling of amino-acid/peptide solubility in aqueous 2-propanol solutions using eqn (1) requires the corresponding activity coefficient at saturation concentration at the respective temperature. The activity coefficient is calculated using the fugacity coefficient ϕLi at the solubility mole fraction divided by the fugacity coefficient ϕL0i of the pure component. In the current study PC-SAFT was used to calculate the fugacity coefficient by: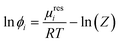 | (3) |
| ares = ahc + adisp + aassoc | (4) |
The Helmholtz energy contributions ahc, adisp and aassoc are due to “hard chain” repulsion, and “dispersion” and “association” attraction, respectively. All the required contributions have been already implemented in PC-SAFT by Gross and Sadowski.23 For mixtures (here water + 2-propanol + amino acid/peptide), the conventional Berthelot–Lorentz combining rules were applied to describe the interactions between two components i and j
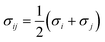 | (5) |
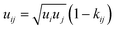 | (6) |
In the current work the amino acids/peptides were considered as associating fluids, and each one association site was assigned for the amine group and for the carboxylic group, respectively. In the case of specific side chains, additional association sites were added depending on a proton donator or proton acceptor. The association contribution aassoc describes the self-associating and cross-associating interactions (e.g., hydrogen bonds) between molecules in a mixture. To evaluate this contribution, two more parameters must be introduced: the association energy εAiBj and the association volume κAiBj. Analogous to the dispersive contribution, interaction parameters are defined using thermodynamically well-established mixing rules. In this case, the mixture parameters are obtained by applying the combining rules suggested by Wolbach and Sandler.25
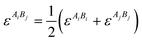 | (7) |
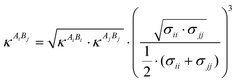 | (8) |
These equations can be utilized without any additional adjustable parameters.
Modelling fugacity coefficients and thus, activity coefficients, allows using eqn (1) to calculate the solubility of the neutral solute. The Henderson–Hasselbalch equation to model pH-dependent solubility requires pKa values (Table S2 in ESI†) as input into the formalism (Table S3 in the ESI†). The PC-SAFT pure-component parameters of all amino acids18,19 and peptides21 have already been published in previous work; they were utilized in the current work without modification. Water was modelled with the 2B association scheme with a temperature-dependent segment diameter as it was used already in our previous work.18 The 2-propanol parameters as well as the binary interaction parameter have already been published.24 The PC-SAFT pure-component parameters as well as binary interaction parameters according to eqn (6) used in this work are listed in Table S4 in the ESI.†
Results
Experimental solubility determination
The solubility of 20 proteinogenic amino acids and 21 peptides in unbuffered aqueous 2-propanol solutions (10, 20, and 30 wt% 2-propanol) was measured at T = 298.15 K and p = 1 atm. Melting temperatures are given in Table S5 in the ESI,† and the solubility data at liquidus equilibrium temperature are listed in Table S6 in the ESI.† These data are valid at the measured pH values. In general, a decrease of solubility with addition of 2-propanol was observed. Exceptions were observed for Phe and Trp, for which the solubility increased upon 2-propanol addition reaching a plateau value. The effect of 2-propanol on solubility will be discussed separately in the Discussion section.pH measurements of the saturated solutions
The pH measurements were carried out for the binary system solute-water as well as for ternary systems solute and 10 wt%, 20 wt% and 30 wt% of 2-propanol in water. The results are listed in Table S6 in the ESI.† The measured pH values are in good agreement with the isoelectric points (pI values) from the platform Chemicalize®. In the literature, the dissociation constants of amino acids in aqueous 2-propanol solutions have already been investigated by Dey et al.26 They found that the negative logarithm of dissociation constants (pKa values) were shifted to higher values by adding 2-propanol to water. The dissociation constant shift of the carboxyl group seemed to be more affected than the dissociation constant shift of the amine group as can be seen in Table S2 in the ESI.† Slightly increased dissociation constants are accompanied by higher values for the pI. This is also consistent with the results from the pH measurements in the current work (cf. Table S6 in the ESI†). Slightly higher pH values were measured in the presence of 2-propanol in water. Nevertheless, these changes were not significant, as the species distribution still showed that >99% of the neutral molecules were in the liquid phase for most components. Exceptions were found for Glu, Asp, Cys (>80%), and Lys (>70%). While for Glu and Asp the amount of neutrally charged species was considered to be sufficient for solubility modelling, this could not be assumed for Lys. The species contributions of each amino acid based on different dissociation constants are shown in Fig. S1 in the ESI.† It has to be mentioned that only for some amino acids experimental dissociation constants were found in the literature. Since dissociation constants in aqueous 2-propanol solutions were not found for any of the considered peptides, the dissociation constants in pure water were used as obtained from the platform Chemicalize®.PXRD measurements
X-ray powder diffraction was used to detect possible changes in the crystal structure of the measured component. The diffractograms were compared to the available data from the Cambridge Crystallographic Data Centre (CCDC). The designation whether it is in α-, β-, or γ-form, and polymorph I, II or III is inconsistent in the database; nevertheless, we were able to find the diffractograms in the CCDC and the designations were taken directly.Precipitation of amino acid hydrates has been reported in the literature.27–32 For a couple of amino acids, such transformations in solutions are reported, for example Ser,33 Lys,34 Asn,19 and Pro19 which form hydrates in aqueous solutions. Another example is cysteine, which is shown to dimerize to cystine in solution and in contact with oxygen.35,36 This is due to the very reactive terminal sulphur group. Furthermore, glutamic acid has the ability to form pyroglutamic acid, especially at elevated temperatures.37,38 Most of the components measured in this work remain the same when dissolved in aqueous 2-propanol. In this work 2-propanol addition induced a crystal structure change for five amino acids (Gly, Ser, Asn, Lys, and Cys) and five peptides (Gly–Pro, Ala–Pro, Pro–Gly, Ala–Gly–Ala and Ala–Ala–Ala).
For Gly the crystal structure shows inconsistency resulting in both polymorphs (α- and γ-forms) for 10 and 20 wt% solutions within the three independently prepared solutions. For the 30 wt% solution only the α-form was observed for all three solutions. In previous work we investigated the amino-acid solubility in water and especially only found hydrate formation for Pro, Ser and Asn. It seems that 2-propanol up to 30 wt% has no effect on the formation of Ser and Asn hydrates. For Pro and Lys the hydrate formation was observed in aqueous solutions free of 2-propanol. For aqueous 2-propanol solutions Pro still forms a hydrate, while Lys transforms from monohydrate (in pure water) to hemihydrate (in 10 wt% and 20 wt% 2-propanol) and to the crystal form of the pure component (in 30 wt% 2-propanol). For Cys the crystal structure changes only in pure water, which is similar to polymorph II from CCDC.
For Pro–Gly the formation of monohydrate was observed in pure water, but not with the addition of 2-propanol. For Gly–Pro no crystal structure change was observed in pure water but with the addition of 2-propanol. For Ala–Pro, Ala–Gly–Ala and Ala–Ala–Ala a crystal structure change was observed for pure water as well as for the addition of 2-propanol. The diffractograms of all amino acids and peptides are shown in Fig. S2 in the ESI.†
Solubility modelling with PC-SAFT
The solubility of 15 amino acids and 18 peptides was modelled with PC-SAFT. PC-SAFT pure-component parameters were obtained from the literature. The deviations between PC-SAFT modelled solubility and the respective experimental data were quantified with the absolute relative deviations (ARDs) according to eqn (9)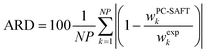 | (9) |
Discussion
Solubility in aqueous organic solvent solutions
In general, adding 2-propanol to aqueous amino-acid solutions leads to a decrease of the amino-acid solubility. This is also consistent with the solubility data found in the literature. This confirms that 2-propanol acts as an anti-solvent. The decrease in the solubility can be explained with a change in the polarity of the solvent. An important value that provides information on the polarity of a component is the relative dielectric constant εr as shown in Fig. 1.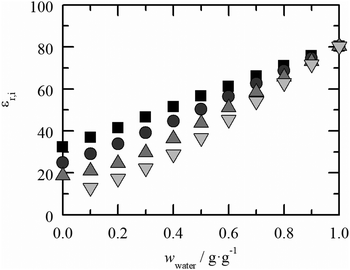 | ||
Fig. 1 Dielectric constants of the aqueous solvent systems with different weight fractions in the literature. ■: water–methanol,  : water–ethanol, : water–ethanol,  : water-2-propanol and : water-2-propanol and  : water-t-butanol at T = 293.15 K and p = 1 atm. The values were determined by measuring the capacity resistances of the solvents. The overall uncertainty is specified to be not greater than 0.1%.39 : water-t-butanol at T = 293.15 K and p = 1 atm. The values were determined by measuring the capacity resistances of the solvents. The overall uncertainty is specified to be not greater than 0.1%.39 | ||
ε r decreases linearly with the increasing weight fraction of the organic solvents (methanol, ethanol, 2-propanol and t-butanol), which is in accordance with the general decrease of solubility for the amino acids/peptides under study. It includes information on the strength of dipole moments of the solvent system. The higher the dielectric constant, the higher the polarity of the solvent and the higher the solubility of an ionic species39. Besides the various other influencing factors such as hydrogen bonding or steric effects, the polarity seems to have a dominating impact on solvent-dependent interactions.
In the following section, solubility of amino acids and peptides will be discussed. Since the pI of several amino acids (acidic and basic amino acids) is far from pH = 7, the solubility of the amino acids will be discussed at the saturation pH values. In contrast, the pI of the peptides under study is close to pH = 7, and the solubility of all the peptides was shifted to pH = 7 using the Henderson–Hasselbalch equation as shown in Table S3 in the ESI.†
Solubility of amino acids in aqueous 2-propanol solutions at saturation pH
In this section, the experimentally determined solubility data of the different amino acids in aqueous 2-propanol solutions are discussed. Amino acids are grouped according to the functional groups of their side chains. An adequate scheme of the general classification of amino acids can be found in the work of Dwyer.40 The solubilities of amino acids are presented in Fig. 2.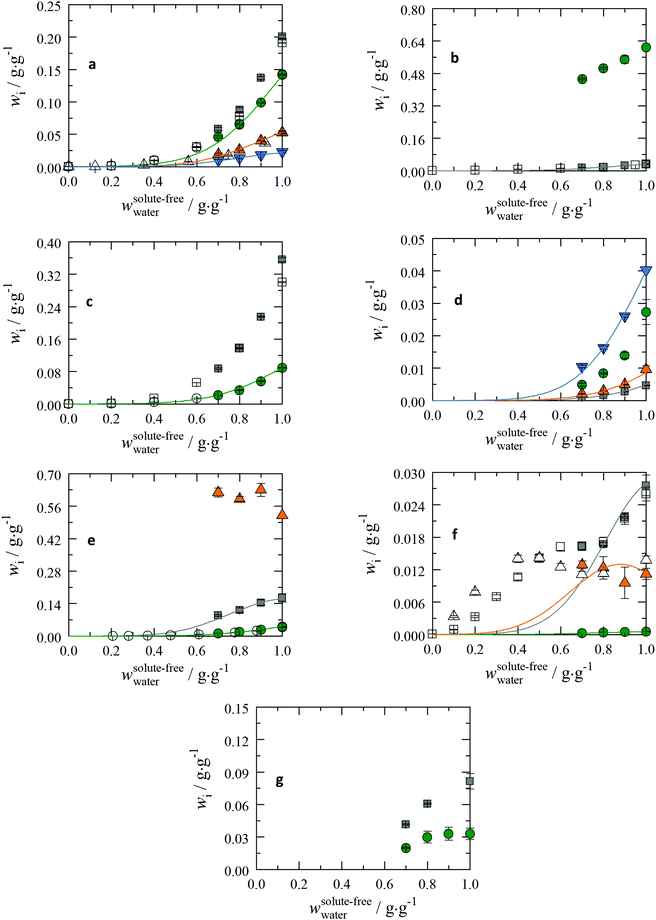 | ||
Fig. 2 The amino-acid solubilities dependent on the 2-propanol weight fraction at T = 298.15 K and p = 1 atm in unbuffered solutions; pH = pI in a pseudo-binary plot. On the x-axis the solute-free weight fraction of water for aqueous 2-propanol solutions is shown. On the y-axis the solubility in the ternary system of the amino acid is shown. Lines: PC-SAFT. Solubility data at wwater = 1 are taken from previous work;19 all other data are from this work except where otherwise stated. Note that PC-SAFT was only applied to conditions without solid state transformation. (a) Amino acids with non-polar substituents (1/2): Gly:  this work □: Ferreira et al.;6 Ala: this work □: Ferreira et al.;6 Ala:  : this work ○: Ferreira et al.;6 Val: : this work ○: Ferreira et al.;6 Val:  : this work ○: Ferreira et al.;6 Leu: : this work ○: Ferreira et al.;6 Leu:  . (b) Amino acids with non-polar substituents(2/2): Ile: . (b) Amino acids with non-polar substituents(2/2): Ile:  : this work □: Ferreira et al.;6 Pro: : this work □: Ferreira et al.;6 Pro:  . (c) Amino acids with polar substituents: Ser: . (c) Amino acids with polar substituents: Ser:  : this work □: Ferreira et al.;7 Thr: : this work □: Ferreira et al.;7 Thr:  : this work ○: Ferreira et al.7 (d) Amino acids with acidic substituents: Asp: : this work ○: Ferreira et al.7 (d) Amino acids with acidic substituents: Asp:  ; Asn: ; Asn:  ; Glu: ; Glu:  ; Gln: ; Gln:  . (e): Amino acids with basic substituents: Arg: . (e): Amino acids with basic substituents: Arg:  ; His: ; His:  : this work ○: Liu;41 Lys: : this work ○: Liu;41 Lys:  . (f) Amino acids with aromatic substituents: Phe: . (f) Amino acids with aromatic substituents: Phe:  : this work □: Orella;8 Tyr: : this work □: Orella;8 Tyr:  ; Trp: ; Trp:  : this work △: in ethanol, Nozaki and Tanford.42 (g): Amino acids with sulfur containing substituents: Cys: : this work △: in ethanol, Nozaki and Tanford.42 (g): Amino acids with sulfur containing substituents: Cys:  (wwater = 1): Bowden43 and (wwater = 1): Bowden43 and  : this work; Met: : this work; Met:  . . | ||
Amino acids with non-polar substituents
The solubility of the amino acids with non-polar substituents decreases with the increasing number of methylene groups in the side chain resulting in the solubility order Gly > Ala > Val > Ile > Leu as shown in Fig. 2(a) and (b). This also coincides with the melting properties measured in previous work. For Gly the α- and γ-forms were detected with addition of 2-propanol (Fig. S2 in ESI†). At 10 wt% and 20 wt% of 2-propanol the crystal forms could not be exactly identified. At 30 wt% of 2-propanol, only the α-form was present in all three independently prepared samples. The solubilities of the α- and γ-forms differ only slightly, while the β-form should lead to an increase of solubility.44 Anyway, having polymorphs in solution hinders the application of any thermodynamic model based on eqn (1). For Ala, Val, Leu and Ile, a change in crystal structure was not observed. The PC-SAFT modelled solubility was in good agreement with the experimental data from this work and from the literature.6 Furthermore, Pro is often classified as an amino acid with a hydrophobic side chain. However, the pyrrolidine side chain causes an extremely high solubility, the highest among all amino acids (cf.Fig. 2(b)). Pro undergoes hydrate formation in aqueous solutions, and the hydrate remains stable up to addition of 30 wt% of 2-propanol. PC-SAFT modelling was not applied. 2-Propanol (even at a weight fraction of 30 wt%) does not reduce the solubility of Pro to less than 0.4 g g−1. This emphasizes that the secondary amine in the side chain strongly favours intermolecular interactions with water molecules in solution.Amino acids with polar substituents
The solubility of Ser is higher than that of Thr (cf.Fig. 2(c)). This is caused by the additional methyl group substituent within Thr. Ser tends to form a hydrate in aqueous solutions (Fig. S2 in the ESI†); PC-SAFT modelling was not applied for Ser. For Thr the PC-SAFT modelled solubility is in good agreement with the experimental data from this work and from the literature.7Amino acids with acidic substituents
This group comprises the amino acids Asp, Asn, Glu and Gln (cf.Fig. 2(d)). All components of this group show a characteristic decrease of solubility with increasing 2-propanol wt%. Glu and Gln show a lower reduction in solubility than Asp and Asn. Characteristically, the isoelectric points of these acidic amino acids can be found at low pH-values (pIAsp= 2.77, pIAsn= 5.41, pIGlu= 3.22, and pIGln= 5.65). At pIs of these amino acids the dominating species are still the zwitterions but at a significantly lower fraction (>80%) compared to other amino acids. Asn and Gln are the amides of the corresponding acidic components. They have an amine residue instead of the hydroxyl group. In contrast to Asp and Glu the zwitterions occur here at a fraction greater than 99% at pIs. In general, it can be annotated that the amides show a higher solubility than their acidic pendants. The components with a greater number of carbons in the molecules within these two subgroups exhibit higher solubility (Glu > Asp; Gln > Asn). This is particularly unusual as long aliphatic chains are considered to be less soluble as discussed for amino acids with non-polar substituents. Probably, self-association is stronger for Asp and Asn than for Glu and Gln, and the melting temperature of Glu is less than that of Asp. Asn was found to form a hydrate in aqueous solutions; PC-SAFT modelling was not applied. For Asp, Glu and Gln the modelled solubilities agree well with the experimental data.Amino acids with basic substituents
Arg, His, and Lys form the class of basic amino acids. Arg contains the guanidino group, His contains the imidazole side chain and Lys contains an additional primary amine group. Analogous to the amino acids with acidic substituents, the basic amino acids are not entirely dissociated from zwitterions at their pIs: Arg (>80%), His (>80%) and Lys (>80%). The solubility of the three components varies broadly. The highest solubility is observed for Lys. Arg and His are distinctly less soluble in water (cf.Fig. 2(e)).With the increase of 2-propanol, the solubility data of Arg and His show the expected drop that has been discussed previously. Arg and His reveal a similar decrease in solubility upon 2-propanol addition. One possible explanation of the similar intermolecular interactions could be the secondary amino group, which is present in both molecules. This could result from the possibility of a primary amine group to establish two hydrogen bonds. Interestingly, an increase of solubility with respect to the addition of 2-propanol was observed for Lys. However, these results have to be considered with care: during the evaporation step, Lys tended to encrust in the tube; the crust that separated the remaining solid phase had to be pierced several times with a needle. During this process, some solid substance could have been lost. For Arg and His the modelled solubilities correspond well with the experimental data; for Lys PC-SAFT was not applied.
Amino acids with aromatic substituents
Three amino acids are considered to be aromatic as they all contain a phenyl ring in their side chain. These are Phe, Tyr and Trp. Tyr has an additional hydroxyl group attached to the phenyl ring, while Trp has an indole group besides the aromatic ring structure. Phe shows the highest solubility in water within this series; the same is observed for aqueous 2-propanol solutions, followed by Trp (cf.Fig. 2(f)). The most insoluble amino acid among all amino acids is Tyr. The only difference between Phe and Tyr is the additional hydroxyl group. As a result, this group is the reason for the massively decreased solubility. The slopes of the solubility curves with increasing 2-propanol wt% differ significantly among these amino acids. Phe experiences the most pronounced solubility decrease in the presence of 2-propanol. Trp behaves broadly differently. Apparently, the solubility decreases at small wt% of 2-propanol and then increases again. Here, the decrease down to 70 wt% of 2-propanol is distinctly lower than that of Phe. Lastly, Tyr shows a monotonic decrease in solubility in the investigated range. A further characteristic behaviour of the aromatic amino acids can be obtained from additional solubility data that cover the whole range of weight fractions of the alcoholic co-solvent. These data are taken from the literature and are presented in Fig. 2(f) for Phe8 in 2-propanol and Trp in ethanol,42 respectively. Interestingly, the solubility data in 2-propanol and ethanol do not differ much.These data reveal that Phe and Trp show a region with a slight increase or a plateau in solubility. Researchers who also observed this effect suggest that the behaviour is due to the arrangement of water and alcoholic molecules around the amino acid in a lattice. The lattice structure can only be maintained at a specific composition of the solvent. If the water fraction is too high or too low, the structure gets disrupted.11 The results support the theory that the solute–solvent interactions are enhanced at a specific composition of the solvent system. As the hydroxyl group is the only difference between Phe and Tyr, it must be concluded that this functional group leads to increased interactions between the Tyr molecules in solution. This lowers the interactions in the solvent system and the solubility. In contrast, the indole group in Trp is considered to improve the solute–solvent interactions.
It is also possible that the dissociation constants in aromatic rings behave differently compared to those in the carboxyl and amine groups. The pH measurements have seen a slight decreasing trend and not the expected increase of the pI due to the increase of the dissociation constant (Table S6 in the ESI†). Unfortunately, only one source was found that measured the dissociation constants of Phe as a function of 2-propanol.26 However, this in turn indicates an increase in the dissociation constant with addition of 2-propanol, which is in contradiction to the decrease of the measured pH values in solution. For Tyr and Trp no literature data are available to our knowledge. As shown in Fig. 2(f) the modelled solubility cannot describe the plateau or the increase of Phe and Trp, respectively. For Tyr the modelled solubility is in good agreement with the experimental data.
Amino acids with sulphuric substituents
Cys contains a thiol group within the molecule, while Met carries an S-methyl thioether. Considering the effect of 2-propanol addition, it can be observed that all solubility values of these solutes decrease with increasing 2-propanol concentrations (cf.Fig. 2(f)). Cys shows higher solubility compared to Met; however, Cys is more affected upon 2-propanol addition resulting in a higher solubility drop. The solubility of Met is almost independent of 2-propanol at low wt% of 2-propanol. For Cys a different crystal form was observed in pure water. With addition of 2-propanol the same crystal structure as the pure solid was observed. PC-SAFT modelling was not applied due to this crystal change. For Met no crystal change during the solubility measurements was detected. Unfortunately no melting properties could be determined in previous work.19 Therefore PC-SAFT modelling was not applied either.Solubility of peptides in aqueous 2-propanol solutions at pH = 7
As mentioned in the beginning of the Discussion section, the solubility of the peptides will be discussed at pH = 7. For this purpose, the Henderson–Hasselbalch equation in Table S3 in the ESI† was used to shift the solubility data from their saturation pH values to pH = 7. To distinguish and efficiently identify the impact of different functional groups, steric effects, and peptide arrangements on the overall solubility, the peptides are grouped within their functional groups as shown in Fig. 3.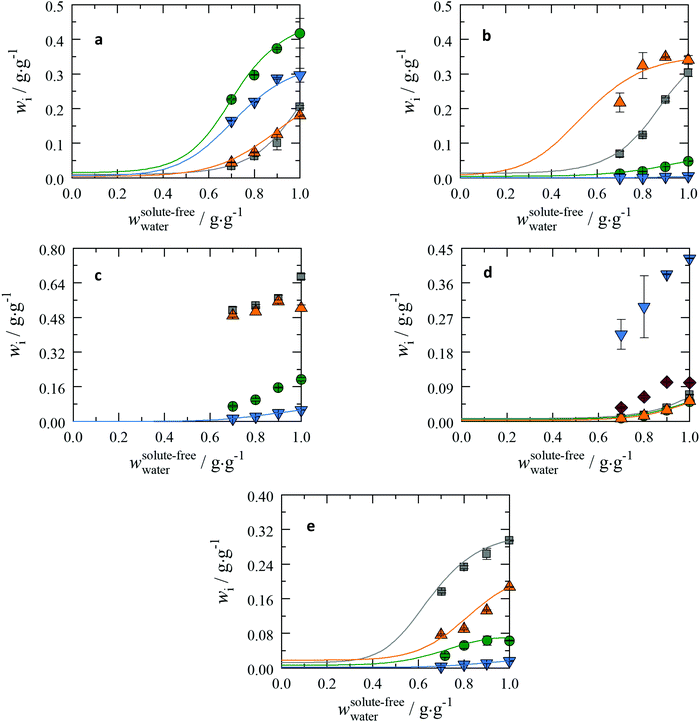 | ||
Fig. 3 The peptide solubilities dependent on the 2-propanol fraction at T = 298.15 K and p = 1 atm in aqueous solutions in a pseudo-binary plot and shifted to pH = 7 using the Henderson–Hasselbalch equation in Table S3 in the ESI.† On the x-axis the initial weight fraction between 2-propanol and water is shown. On the y-axis the solubility of the peptide is shown. Lines: PC-SAFT. Solubility data at wwater = 1 are taken from previous work;19 all other data are from this work. Note, that PC-SAFT was only applied to conditions without solid state transformation. (a) Dipeptides based on Gly and Ala: Gly–Gly:  , Gly–Ala: , Gly–Ala:  , Ala–Gly: , Ala–Gly:  , and Ala–Ala: , and Ala–Ala:  . (b) Dipeptides based on Gly, Ala and Ser: Gly–Ser: . (b) Dipeptides based on Gly, Ala and Ser: Gly–Ser:  , Ser–Gly: , Ser–Gly:  , Ala–Ser: , Ala–Ser:  , and Ser–Ala: , and Ser–Ala:  . (c) Dipeptides based on Gly, Ala and Pro: Gly–Pro: . (c) Dipeptides based on Gly, Ala and Pro: Gly–Pro:  , Pro–Gly: , Pro–Gly:  , Ala–Pro: , Ala–Pro:  , and Pro–Ala: , and Pro–Ala:  . (d) Tripeptides based on Gly and Ala: Gly–Gly–Gly: . (d) Tripeptides based on Gly and Ala: Gly–Gly–Gly:  , Gly–Gly–Ala: , Gly–Gly–Ala:  , Gly–Ala–Gly: , Gly–Ala–Gly:  , Ala–Gly–Ala: , Ala–Gly–Ala:  , and Ala–Ala–Ala: , and Ala–Ala–Ala:  . (e) Tripeptides based on Gly, Ala and Leu: Leu–Gly–Gly: . (e) Tripeptides based on Gly, Ala and Leu: Leu–Gly–Gly:  , Gly–Leu–Gly: , Gly–Leu–Gly:  , Gly–Gly–Leu: , Gly–Gly–Leu:  , and Gly–Ala–Leu: , and Gly–Ala–Leu:  . . | ||
In general, all the peptides show the characteristic non-linear decrease in solubility with increasing 2-propanol wt%. However, it can be seen that the solubility is affected to a different extent depending on the sequence of the primary structure of the peptides.
Dipeptides based on Gly and Ala
The order of solubility in pure water is Gly–Ala > Ala–Ala > Gly–Gly > Ala–Gly as shown in Fig. 3(a). However, the solubilities of Gly–Ala and Gly–Gly decreases more pronounced compared to Ala–Ala and Ala–Gly upon addition of 2-propanol. As the solubilities of Gly–Gly and Ala–Gly in pure water are similar, the solubility order in aqueous 2-propanol solutions is reversed. Using PXRD analysis changes in the crystal during the solubility measurement were not detected. Thus, PC-SAFT modelling was applied resulting in good agreement with the experimentally determined solubilities.Dipeptides based on Gly, Ala and Ser
In Fig. 3(b) the solubility sequence is Ala–Ser > Gly–Ser > Ser–Gly > Ser–Ala; this series is valid in water and remains unchanged upon the addition of 2-propanol. Peptides with Gly or Ala in the first place within the primary structure comprise a much higher solubility compared to their corresponding isomeric peptides. Even more, Ala–Ser is not prone to solubility changes upon adding small wt% of 2-propanol; only addition of higher amount (30 wt% of 2-propanol) causes a significant decrease of the solubility of Ala–Ser. This is very different from the behaviour of Gly–Ser, for which a strong reduction in solubility upon addition of 2-propanol can be seen even at very low 2-propanol wt%. In contrast, the solubility of Ser–Gly and Ser–Ala does not change much upon 2-propanol addition. The solubility behaviour of these peptides could be modelled well compared with the experimental data; slightly higher ARD values were observed for Ala–Ser.Dipeptides based on Gly, Ala and Pro
The same observation as in the previous section can also be made here: Gly–Pro and Ala–Pro show higher solubilities than their isomeric pendants Pro–Gly and Pro–Ala (cf.Fig. 3(c)). The effect of 2-propanol on the solubility is of different strength: for Gly–Pro a significant decrease of solubility can be observed with addition of 10 wt% of 2-propanol, while further addition of 2-propanol leads to a less decrease of solubility. The solubilities with 2-propanol are in the same magnitude as Ala-Pro. A crystal structure change was detected with addition of 2-propanol for Gly–Pro, which might explain the solubility drop. For Ala–Pro the crystal structure changed; the pure substance is different from the crystal in saturated solution (in pure water as well as in the water-2-propanol mixtures); this prevents the application of the PC-SAFT modelling. In this group only for Pro-Ala the application of PC-SAFT was valid and shows good results with the experimental data.Tripeptides based on Gly and Ala
First of all, the tripeptide Ala–Gly–Ala exhibits the highest solubility in this group (cf.Fig. 3(d)), followed by Ala–Ala–Ala; the solubilities of Gly–Gly–Ala and Gly–Ala–Gly differ less than 1% from each other in aqueous 2-propanol solutions. The solubility of Gly–Gly–Ala is found to be marginally higher than that of Gly–Ala–Gly. The solubilities of Gly–Gly–Gly, Gly–Gly–Ala, and Gly–Ala–Gly approach the same values with increasing wt% of 2-propanol. Overall, if Ala is in the first position, the solubility tends to be higher than of the peptides with Gly in the first place. Furthermore, it seems that it barely matters whether Ala or Gly is in the second place or if there is any Ala in the molecule when Gly is in the first position. This is especially true for increasing 2-propanol fractions. This is the case for all measured points in this work. Particularly interesting is Ala–Ala–Ala because Ala–Ala–Ala is expected to be less soluble in water than Gly–Gly–Gly, due to the additional hydrophobic methylene groups within Ala–Ala–Ala; this can only be explained by the melting properties, which contribute strongly to the solubility. For Gly–Gly–Gly, Gly–Gly–Ala and Gly–Ala–Gly the PC-SAFT modelled solubility agrees well with the experimental data.Tripeptides based on Gly, Ala and Leu
In this section, the tripeptides under study are Leu–Gly–Gly, Gly–Leu–Gly, Gly–Gly–Leu and Gly–Ala–Leu. The impact of the position of Leu within these molecules in the primary structure can be investigated. The solubility order is Leu–Gly–Gly > Gly–Gly–Leu > Gly–Leu–Gly > Gly–Ala–Leu but the influence of 2-propanol is different (cf.Fig. 3(e)). While Leu–Gly–Gly and Gly–Gly–Leu show a similar decrease of solubility upon addition of 2-propanol, Gly–Leu–Gly has a constant solubility up to 10 wt% 2-propanol; this can be explained by the accessibility of the Leu residue to 2-propanol. Replacing Gly with Ala in the second place within this series leads to (i) a decrease in solubility in general and (ii) a direct decrease with small amounts of 2-propanol. For all tripeptides in this group crystal changes were not observed during the solubility measurements, which allowed the application of the PC-SAFT model. The modelled solubility corresponds well with the experimental data.The present case emphasizes that peptides are more soluble if the most hydrophobic amino acid is in the first position. This effect is also observed with the tripeptides containing Gly and Ala as well as for most dipeptides.
The influence of activity coefficients on the amino-acid/peptide solubility
In this work the activity coefficients were modelled at constant temperature of T = 298.15 K with 0–30% by weight of 2-propanol in aqueous solutions. Based on the available melting properties from FSC measurements published in previous work and using solubility data, ‘experimental’ activity coefficients were quantified using a reordered eqn (1); the activity coefficients were modelled with PC-SAFT and the results are shown in Fig. 4.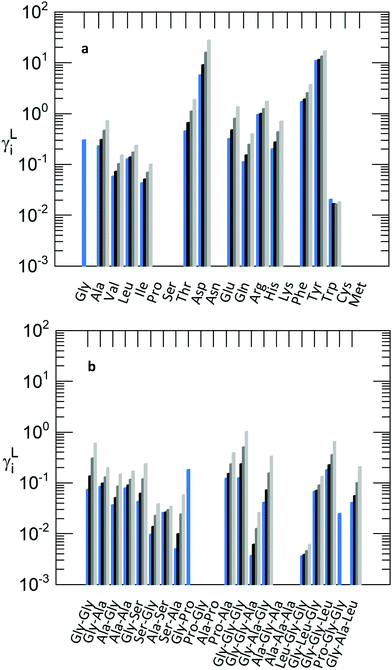 | ||
| Fig. 4 PC-SAFT modelled activity coefficients of amino acids (a) and of peptides (b) at the respective solubility concentration in aqueous 2-propanol solutions at T = 298.15 K and p = 1 atm. Modelling using the pure-component parameters (Table S4 in the ESI†), the binary parameters (Table S4 in the ESI†), and the melting properties from previous work (Table S5 in the ESI†). Colours represent the solute-free composition of the solvent water-2-propanol: Blue: pure water, black: w2-propanol = 0.1 g g−1, dark grey: w2-propanol = 0.2 g g−1, and bright grey: w2-propanol = 0.3 g g−1. | ||
It can be seen that most of the activity coefficients are lower than one (except those of Asp, Phe and Tyr are greater than one). The importance of the activity coefficient can be seen by their range: 0.003 < γ < 20. Thus, the activity coefficients strongly influence the solubility in aqueous 2-propanol solutions by factors of up to 300 and down to 0.05 compared to the ideal mixture (γ = 1). The decrease in solubility with the addition of 2-propanol in aqueous solutions can only be explained by different interactions between the solutes (amino acids/peptides) and the solvents (water and 2-propanol). In the case γ < 1 the attractive interactions (solute–water and solute-2-propanol) are stronger than those in the pure-component state. The activity coefficient of the solute increases to higher values with an increasing fraction of 2-propanol. Higher activity coefficients result in lower solubility based on eqn (1). Considering first a high solubility in pure water, the attractive interactions between the solute and water must be higher compared to those of the pure solute. With an increasing 2-propanol fraction, these interactions are repressed by less attractive forces between the solute (amino acids/peptides) molecules that become more dominant with higher weight fractions of 2-propanol.45 In general, for most of the solutes the solubility decreases upon addition of 2-propanol, which is caused by an increase of the activity coefficient. Exceptions can be observed for Phe and Trp. As discussed in the previous sections, the solubility of amino acids and peptides decreases upon 2-propanol addition with different strengths. The relative decrease of Gly solubility is much higher than that of Leu. This behaviour is uniquely determined by the activity coefficient. However, low (high) solubility does not necessarily mean a high (low) activity coefficient, as the solid (the melting properties) also contributes to solubility. This can be seen for Gly–Pro which shows the overall highest solubility in this work but does not show the lowest activity coefficient. Asp, Tyr and Ser–Ala show the lowest solubility in this work. While for Asp and Tyr, high activity coefficients were also observed, the activity coefficients of Ser–Ala are low. A similar effect can be observed using the series of Gly-based peptides. The solubility of Gly and Gly–Gly is slightly different, while the solubility of Gly–Gly–Gly is much lower. However, the activity coefficients follows the order γGly > γGly–Gly–Gly > γGly–Gly and are not in the same series as the solubility (Gly > Gly–Gly > Gly–Gly–Gly). The deviation between the order of the solubility data and activity coefficients elucidates that solubility not only depends on the solute–solvent interactions but also on the melting properties of the pure solid. The impact of the melting properties in eqn (1) might overcompensate for the intermolecular interactions expressed by the activity coefficient. Hence, it can be noted that it is not possible to estimate the behaviour of activity coefficients just from the solubility of the solute or vice versa. This phenomenon can only be explained by the synergy of the activity coefficients and melting properties based on eqn (1). Very similar solids concerning their chemical structure can dissolve broadly differently due to different melting properties, while having similar interactions, and thus similar activity coefficients.
Further discussion
Finally, we carried out two additional studies. First, to compare the results with less complex models such as the gE models Wilson, NRTL, and UNIQUAC. These results are listed in the ESI† in Section S9 (Fig. S3 and Tables S7, S8, ESI†). To summarize these results, the same treatment of the models shows that PC-SAFT is superior for modelling solubility of biomolecules such as amino acids and peptides in broad temperature ranges and/or upon co-solvent addition. Among the gE models only UNIQUAC allowed a reasonable modelling result; Wilson and NRTL models are not suitable at all for modelling the solubility of amino acids in the presence of 2-propanol. We are actually working on this in a detailed follow-up study.Second, modelling with eqn (1) requires that the stable form of the solid is an anhydrate, i.e. in solubility experiments the liquid phase is in equilibrium with the solid anhydrate. Unfortunately, several amino acids and peptides in this work are stable as hydrates. An example can be found for Ser, which forms a monohydrate as the stable form at room temperature. Modelling of the hydrates (or other polymorphic transitions) requires a different approach, the so-called solubility-product method, which describes the dissolution of the solid hydrate into anhydrate solute and water in aqueous solution. The activity-based formalism of the respective law-of-mass action constant (the solubility product KSP) for monohydrates (n = 1) is expressed as
| KSP(T,p) = xSer·γSer·(xwater·γwater)n=1 | (10) |
Based on the PC-SAFT parameters in Table S4 (ESI†) four solubility products (0, 10, 20 and 30 wt% 2-propanol in solute-free solutions) were modelled. As a result, the KSP values were found to be constant (KSP (298 K, 1 bar) = 0.010 ± 0.0015), while solubility significantly decreased. Deeper studies on this are suggested in future.
Conclusions
In this work, the solubilities of 20 proteinogenic α-amino acids and 20 peptides at T = 298.15 K and p = 1 atm in aqueous solutions with 10, 20, and 30 wt% 2-propanol were gravimetrically measured. The pH values of the supersaturated solutions were measured and are in accordance with the literature data of Dey et al.26 Also possible structural transformations were investigated using PXRD and found for several amino acids (Gly, Ser, Asn, Lys, and Cys) and peptides (Gly–Pro, Ala–Pro, Pro–Gly, Ala–Gly–Ala and Ala–Ala–Ala). For these components PC-SAFT modelling was not used.In general, for all amino acids and peptides a decreasing solubility with increasing weight fraction of 2-propanol is observed. Here, the slope of the decrease in solubility is solely determined by intermolecular interactions of the solute and the solvent. The amino acids Phe and Trp that contain hydrophobic aromatic side chains present an exception from these observations. The solubility of Phe and Trp increases upon 2-propanol addition and reaches a maximum value. This effect can be affiliated to the phenyl ring within the chemical structure, which attracts 2-propanol stronger than water.
The results of the peptides underline the importance of the position of a particular amino acid in the molecule. The position seems to have a more considerable impact on the total solubility and the decrease in solubility in aqueous 2-propanol, than the nature of the amino acid itself. This was evaluated by studying the structural isomers of dipeptides and tripeptides. Frequently, the molecule is more soluble if the morehydrophobic amino acid is in the first position.
The modelling with PC-SAFT was successful for most amino acids and peptides. Nevertheless, one binary interaction parameter between solute and 2-propanol, k13, was found to be required to quantitatively match the experimentally determined data.
It could be shown that amino acids and peptides have broadly varying solubilities in water and aqueous 2-propanol solutions. This is mainly affected by their characteristic side chains. By studying the solubilities and the corresponding activity coefficients, the impact of the melting properties and the intermolecular interactions on the overall solubility was analysed. Melting properties can overcompensate for hydrophobic effects of the side chain within the amino acid or peptide. The synergy between physical properties (melting properties) and intermolecular interactions (activity coefficients) is the key to describe successfully the solubility of amino acids and peptides.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding from the German Research Foundation (DFG) with Grants HE 7165/6-1.References
- Q. Hou, R. Bourgeas, F. Pucci and M. Rooman, Sci. Rep., 2018, 8, 1 CrossRef PubMed.
- A. A. Warraich, A. R. Mohammed, Y. Perrie, M. Hussain, H. Gibson and A. Rahman, Sci. Rep., 2020, 10, 1 CrossRef PubMed.
- M. J. Jones and J. Ulrich, Chem. Ing. Tech., 2005, 77(10), 1527 CrossRef CAS.
- A. Yokota and M. Ikeda, Amino Acid Fermentation: Advances in Biochemical Engineering/Biotechnology, Springer, Tokyo, Japan, 2017, 159 Search PubMed.
- G. Hofmann, Kristallisation in der industriellen Praxis, Wiley, 2006 Search PubMed.
- L. A. Ferreira, E. A. Macedo and S. P. Pinho, Chem. Eng. Sci., 2004, 59(15), 3117 CrossRef CAS.
- L. A. Ferreira, S. P. Pinho and E. A. Macedo, Fluid Phase Equilib., 2008, 270, 1 CrossRef CAS.
- C. J. Orella and D. J. Kirwan, Ind. Eng. Chem. Res., 1991, 30, 1040–1045 CrossRef CAS.
- T. E. Needham Jr., A. N. Paruta and R. J. Gerraughty, J. Pharm. Sci., 1971, 60, 565 CrossRef CAS PubMed.
- T. E. Needham Jr., A. N. Paruta and R. J. Gerraughty, J. Pharm. Sci., 1971, 60, 258 CrossRef CAS PubMed.
- N. A. Bowden, J. P. M. Sanders and M. E. Bruins, J. Chem. Eng. Data, 2018, 63(3), 488 CrossRef CAS PubMed.
- Y. Nozaki and C. Tanford, J. Biol. Chem., 1970, 245(7), 1648 CrossRef CAS.
- Y. Nozaki and C. Tanford, J. Biol. Chem., 1971, 246, 2211 CrossRef CAS.
- S. Ghosh, S. Mondal, S. Roy, S. Saha, D. Subba and B. K. Dolui, J. Mol. Liq., 2018, 249, 659 CrossRef CAS.
- C. Held, T. Reschke, R. Müller, W. Kunz and G. Sadowski, J. Chem. Thermodyn., 2014, 68, 1 CrossRef CAS.
- C. Held, L. F. Cameretti and G. Sadowski, Ind. Eng. Chem. Res., 2011, 50(1), 131 CrossRef CAS.
- H. T. Do, Y. Z. Chua, J. Habicht, M. Klinksiek, M. Hallermann, D. Zaitsau, C. Schick and C. Held, RSC Adv., 2019, 9(56), 32722 RSC.
- Y. Z. Chua, H. T. Do, C. Schick, D. Zaitsau and C. Held, RSC Adv., 2018, 8(12), 6365 RSC.
- H. T. Do, Y. Z. Chua, A. Kumar, D. Pabsch, M. Hallermann, D. Zaitsau, C. Schick and C. Held, RSC Adv., 2020, 10, 44205 RSC.
- A. Roda, F. Santos, Y. Z. Chua, A. Kumar, H. T. Do, A. Paiva, A. R. C. Duarte and C. Held, Phys. Chem. Chem. Phys., 2021, 23, 1706 RSC.
- H. T. Do, Y. Z. Chua, J. Habicht, M. Klinksiek, S. Volpert, D. Pabsch, M. Hallermann, M. Thome, D. Zaitsau, C. Schick and C. Held, Ind. Eng. Chem. Res., 2021, 60(12), 4693–4704 CrossRef CAS.
- J. M. Prausnitz and R. N. Lichtenthaler, Molecular thermodynamics of fluid-phase equilibria, 1969 Search PubMed.
- J. Gross and G. Sadowski, Ind. Eng. Chem. Res., 2001, 40(4), 1244 CrossRef CAS.
- D. Fuchs, J. Fischer, F. Tumakaka and G. Sadowski, Ind. Eng. Chem. Res., 2006, 45(19), 6578 CrossRef CAS.
- J. P. Wolbach and S. I. Sandler, Ind. Eng. Chem. Res., 1998, 37(8), 2917 CrossRef CAS.
- B. P. Dey, S. Dutta and S. C. Lahiri, Indones. J. Chem., 1982, 21, 886 Search PubMed.
- S. Goto and T. Isemura, Annual Meeting of the Chemical Society of Japan, 1964, vol. 37, issue 11, p. 1697.
- I. S. Pominov, D. R. Sidorova and B. P. Khalepp, UDC, 1971, 13, 1084 Search PubMed.
- D. I. Kotova, V. S. D. S. Beiline and O. A. Shepeleva, J. Pharm. Chem., 2001, 35, 44 Search PubMed.
- J. M. Goodfellow, Proc. Natl. Acad. Sci. U. S. A., 1982, 79, 4977 CrossRef CAS PubMed.
- T. K. Kim and M. S. Jhon, J. Mol. Liq., 1994, 59, 179 CrossRef CAS.
- M. M. Vorobev, A. A. Baranov, V. M. Belikov and Y. I. Khurgin, Russ. Chem. Bull., 1996, 45, 577 CrossRef.
- C.-W. J. Luk and R. W. Rousseau, Cryst. Growth Des., 2006, 6(8), 1808 CrossRef CAS.
- P. A. Williams, C. E. Hughes, J. Martin, E. Courvoisier, A. B. M. Buanz, S. Gaisford and K. D. M. Harris, J. Phys. Chem. C, 2016, 120(17), 9385 CrossRef CAS.
- G. Bulaj, T. Kortemme and D. P. Goldenberg, Biochemistry, 1998, 37(25), 8965 CrossRef CAS PubMed.
- E. Oshimura and K. Sakamoto, Amino Acids, Peptides, and Proteins, in Cosmetic science and technology: Theoretical principles and applications, ed. K. Sakamoto, H. I. Maibach, R. Y. Lochhead and Y. Yamashita, Elsevier, Amsterdam, Netherlands, 2017, pp. 285–303 Search PubMed.
- C. B. Airaudo, A. Gayte-Sorbier and P. Armand, J. Food Sci., 1987, 52(6), 1750 CrossRef CAS.
- A. Kumar and A. K. Bachhawat, Curr. Sci., 2012, 102, 288 CAS.
- G. Akerlof, J. Am. Chem. Soc., 1932, 54(11), 4125 CrossRef CAS.
- D. S. Dwyer, Amino Acids: Chemical Properties, in Wiley Encyclopedia of Chemical Biology, ed. T. P. Begley, John Wiley & Sons, Inc, Hoboken, NJ, USA, 2007. p. 1075 Search PubMed.
- Y. Liu, Y. Wang, Y. Liu, S. Xu, M. Chen, S. Du and J. Gong, J. Chem. Thermodyn., 2017, 105, 1 CrossRef CAS.
- Y. Nozaki and C. Tanford, J. Biol. Chem., 1971, 246(7), 2211 CrossRef CAS.
- N. A. Bowden, D. M. Sevillano, J. P. M. Sanders and M. E. Bruins, Fluid Phase Equilib., 2018, 459, 158 CrossRef CAS.
- A. Bouchard, G. W. Hofland and G.-J. Witkamp, J. Chem. Eng. Data, 2007, 52(5), 1626 CrossRef CAS.
- L. Cameretti, Modeling of Thermodynamic Properties in Biological Solutions, Cuvillier Verlag, Göttingen, 1st edn, 2009 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00005e |
| This journal is © the Owner Societies 2021 |
