Anion–anion and anion–neutral triel bonds

Abstract

The ability of a TrCl₄⁻ anion (Tr = Al, Ga, In, Tl) to engage in a triel bond with both a neutral NH₃ and CN⁻ anion is assessed by ab initio quantum calculations in both the gas phase and in aqueous medium. Despite the absence of a positive σ or π-hole on the Lewis acid, strong triel bonds can be formed with either base. The complexation involves an internal restructuring of the tetrahedral TrCl₄⁻ monomer into a trigonal bipyramid shape, where the base can occupy either an axial or equatorial position. Although this rearrangement requires a substantial investment of energy, it aids the complexation by imparting a much more positive MEP to the site that is to be occupied by the base. Complexation with the neutral base is exothermic in the gas phase and even more so in water where interaction energies can exceed 30 kcal mol⁻¹. Despite the long-range coulombic repulsion between any pair of anions, CN⁻ can also engage in a strong triel bond with TrCl₄⁻. In the gas phase, complexation is endothermic, but dissociation of the metastable dimer is obstructed by an energy barrier. The situation is entirely different in solution, with large negative interaction energies of as much as −50 kcal mol⁻¹. The complexation remains an exothermic process even after the large monomer deformation energy is factored in.

---

1. Introduction

The chemistry of noncovalent interactions has a long and venerable history, in which the hydrogen bond occupies a special place.^1–7 Years of study have revealed that this interaction is based mainly on electrostatic forces with an important admixture of polarization, charge transfer and dispersion.^6,8–14 The ubiquitous role of hydrogen bonds in such critical areas as, for example pairing of DNA strands, undoubtedly catalyzed and accelerated inquiry into this stabilizing force. At this point, emphasis has begun to shift to other closely related noncovalent interactions, in particular the extensive group of σ- and π-hole interactions.^15–20

The principles of these families of bonds are derived in large measure from the anisotropic electronic density distribution around the bridging atom that replaces the central H of hydrogen bonds, which is accentuated by highly electron-withdrawing substituents.^21–25 The asymmetry of the charge surrounding the bridging X atom arises from the formation of the R–X covalent bond that tends to thin the electron density along the extension of the R–X bond. This positively-charged region has come to be known in common parlance as a σ-hole,²⁶ whereas π-holes occur above the plane of the entire molecule.²⁷

TrR₃ molecules (where Tr refers to a triel atom as a member of the 13th group of the periodic table) are typically planar, and this sort of π-hole commonly occurs above the Tr atom, allowing them to come into close contact with Lewis bases in what is termed a triel bond (TrB). Increased electron-withdrawing power of the R substituents intensifies the π-hole and thereby strengthens the TrB.^{18,23,26–31} The TrB designation was originally introduced by Grabowski^32,33 and is defined in terms of the contact between Tr atoms, from boron to thallium, and electron-rich donors such as electron pair(s) or π-electron systems.³⁴ Beside the Coulombic stabilization, the attraction is also derived from charge transfer from the lone pair orbital(s) of the Lewis base to the empty p orbital of Tr. Past research has been concerned with various facets of the TrB: its structural, vibrational and electronic properties,³⁵ potential for tuning the anion–π interactions,³⁶ hypo- and hypervalence bonding of Tr atoms in complexes of boron trihalides^32,37 or the behavior of the intermolecular TrB in the presence of an intramolecular TrB in naphthalene derivatives.³⁸ The TrB has also been explored with regard to its contribution to the process of molecular hydrogen release³⁹ and is a subject of investigations linked with hydrogen storage material.⁴⁰

Along another line, there have been a number of recent studies concerning stable pairing of one anion with another^41–47 despite the obvious repulsive forces that need to be overcome for such a complexation to occur. Such anion–anion complexes are held together by both hydrogen and halogen bonds.^43,48–54 A recent work from our own group⁵⁵ has expanded this list, documenting that metastable complexes occur when MCl₃⁻ (M = Be, Mg, Ca, Sr, Ba) anions are paired with CN⁻. Even though the formation of each such complex from individual monomers is endothermic in the gas phase, the dissociation process is hindered by an energy barrier of some 20 kcal mol⁻¹. When immersed in aqueous solvent, on the other hand, the association process is highly exothermic by as much as 20 kcal mol⁻¹. Further work showed a similar sort of situation for MCl₃⁻ when the group 2A alkaline earth metal M atom is replaced by group 2B atoms Zn, Cd, or Hg.⁵⁶ These sorts of complexes extend into the pnicogen family as well: ZCl₄⁻ (Z = P, As, Sb) also engages in metastable complexes with CN⁻ anion.⁵⁷ For all of these systems, the complexation process in water is a facile, energetically downhill process.

Given the above, it is natural to wonder if triel bonds could also be formed between an anionic Tr-containing Lewis acid and an anionic base. There has been no prior study of such an anion–anion triel bond so this issue remains an open question. There is some reason to believe such an interaction may occur based on a survey of the CSD (Cambridge Structural Database) which identified 401 crystalline structures containing TrX₄⁻, where Tr refers to Al, Ga, In or Tl, and X denotes a halogen atom. Five structures were identified which suggest the presence of a triel bond motif, as illustrated in Fig. S1 (ESI†). However, simple elucidation of crystal structural parameters is unable to unambiguously prove the interaction is attractive, quantify its strength, nor can it probe the underlying sources of stability. In any case, it would be highly desirable to better understand the properties of any such interaction, in the absence of perturbing crystal packing forces.

By a suitable choice of model systems, quantum chemical calculations are used to probe this question. Formation of a TrB relies to some extent on a positive σ or π-hole on the Lewis acid which can attract a nucleophile. So the first question is whether a TrX₄⁻ anion with a full negative charge can engage in a triel bond of any sort. And secondly, would such an anionic Lewis acid be able to overcome coulombic repulsion with an anionic base so as to engage in a TrB? Would such an anion–anion complex represent a metastable equilibrium in the gas phase, higher in energy than its constituent monomers, stabilized by an energy barrier to separation? When placed in aqueous solvent, could this same anion–anion complex form, and would the association be a barrier-free exothermic process? Does the association process require the presence of a positively charged π-hole on the Lewis acid, and if so how intense must this hole be? It is expected that the approach of a nucleophile toward the Tr atom would induce geometric changes within the TrX₄⁻ unit. How large a role does this deformation play in the entire process?

The TrCl₄⁻ (Tr = Al, Ga, In, Tl) anions are taken as model anionic Lewis acids. They thus encompass the full set of triel atoms (with the exception of B which does not engage in any of the TrBs described below, probably due to a particularly negative σ-hole). NH₃ is chosen as a small but powerful neutral base. Its small size mitigates against secondary interactions which might otherwise complicate the analysis, and its common usage as model base permits comparison with other sorts of noncovalent bonds in the literature. For purposes of consistency with earlier work, CN⁻ serves as model anionic base. As in the case of NH₃, its small size facilitates the analysis and avoids unwanted secondary interactions.

2. Systems and methods

Geometries of isolated monomers and complexes were optimized at the MP2/aug-cc-pVDZ level of theory.^58–60 The pseudopotential aug-cc-pVDZ-PP^61–65 basis set was used to model In and Tl atoms so as to integrate relativistic effects. For purposes of comparison and verification, energies were also computed at the CCSD(T) level^66,67 using MP2 geometries. The interaction energy (E_int) of each dimer is defined as the difference in total electronic energy between the fully optimized complex and the sum of its constituent monomers in the geometry adopted within the complex; the binding energy (E_b) takes as its reference the monomers in their fully optimized isolated structures. These two quantities differ by the deformation energy caused by the restructuring of each monomer as it melds into the complex. Both E_int and E_b were corrected for basis set superposition error (BSSE) via the standard counterpoise formalism.⁶⁸ Harmonic frequency analysis verified that the stationary points were true minima by the absence of any imaginary frequencies. Calculations were performed in both the gas phase and aqueous medium; in the latter case simulation of water solvent was provided by the PCM (polarizable continuum model).⁶⁹

Calculations made use of the Gaussian 16 set of codes.⁷⁰ AIM analysis was utilized to elucidate bond paths through analysis of the electron density topology by AIMAll⁷¹ software. Decomposition of the interaction energies into components was carried out through the Morokuma–Ziegler scheme embedded in the ADF software at the BLYP-D3/ZORA/TZ2P level of theory using MP2 optimized geometries.^72–74 Energy barriers for dissociation made use of the QST2 method of the Synchronous Transit-Guided Quasi-Newton (STQN) procedure.⁷⁵ The MultiWFN and VMD programs^76–78 were applied to examine the molecular electrostatic potential (MEP) of each monomer, and identification of its extrema on the 0.001 a.u. isodensity surface.

3. Results

3.1. Monomers

The isolated TrCl₄⁻ monomers all adopt a tetrahedral geometry in both the gas and aqueous phases. The r(Tr–Cl) bonds elongate from 2.197 to 2.474 as the triel atom grows in size from Al to Tl and in the gas phase; they are very slightly shorter in water. The molecular electrostatic potential (MEP) of the all TrCl₄⁻ monomers have the same characteristics. Within the context of a tetrahedral geometry of each monoanion with its overall negative MEP lies a maximum that lies directly opposite each Tr–Cl bond, that can be described as a σ-hole although its sign is negative. The magnitude of this hole is reported as V_s,max is listed in Table 1 and becomes progressively less negative as the triel atom enlarges, from −80.4 kcal mol⁻¹ for Al to −63.1 kcal mol⁻¹ for Tl. These quantities are slightly more negative in aqueous solution, and obey the same trend. Of most concern for the bases is the most negative segment of their MEP. The minimum, V_s,min, for neutral NH₃ is aligned with its lone pair along its C₃ axis. The CN⁻ anion contains several minima of roughly equal magnitude: two along the C–N bond axis near either the N or C atom, while a third lies in the equatorial region that encircles the CN bond. V_s,min is of course much more negative for the anion than for the neutral base.

Table 1 Molecular electrostatic potential maxima (kcal mol⁻¹) on the 0.001 a.u. isodensity surface of TrCl₄⁻ and minima (kcal mol⁻¹) of base monomers

Isolated species	Gas phase	Aqueous solution
V s,max (Tr–Cl) σ-hole
AlCl4^−	−80.4	−83.1
GaCl4^−	−79.1	−81.7
InCl4^−	−61.4	−61.8
TlCl4^−	−63.1	−63.2
	V s,min
NH3	−37.7	−42.2
CN^−	−137.7 (N) π	−139.6
	−136.6 (N)	−138.6
	−135.5 (C)	−137.2

---

3.2. Complexes

3.2.1. Complexes with NH₃. The approach of the neutral NH₃ to TrCl₄⁻ leads to two stable minima, pictured in Fig. 1. Geometry A is a clear trigonal bipyramid, with NH₃ occupying one of the two axial sites. The other axial Cl is labeled Cl_a and Cl_e is used for the three equatorial atoms. Structure E is also a trigonal bipyramid, albeit a more distorted one. There are two Cl atoms (Cl_a) at the vertices, and two more (Cl_e) at equatorial positions, with the NH₃ occupying the third equatorial site, leading to the E designation of the complex. It might be noted that NH₃ lies directly opposite a Cl atom in A, so can take advantage of the σ-hole generated by it. Its equatorial position in E is not optimally positioned as it does not oppose any particular Tr–Cl bond. In the gas phase, A is the only minimum, whereas A and E coexist in aqueous solution. A has an energetic advantage of between 1 and 4 kcal mol⁻¹, as reported in Table S2 (ESI†).

Fig. 1 The structures of H₃N⋯TrCl₄⁻ complexes.

The geometric parameters of the two sorts of complexes are compiled in Tables 2 and 3. Focusing first on structure A, the equilibrium Tr⋯N distance elongates from 2.16 to 2.49 Å which parallels the growth in the size of the Tr atom. The r(TrCl) bonds are a bit longer than r(N⋯Tr), commensurate with the larger size of Cl as compared to N. The equatorial Cl atoms are slightly further from the central Tr than Cl_a. The three equatorial atoms are bent up a bit toward the NH₃, with θ(N⋯Tr–Cl_e) angles somewhat less than 90°. Perturbations of these geometries introduced by immersion in water include contraction of r(N⋯Tr) and r(Tr–Cl_e), coupled with elongation of r(Tr–Cl_a); there is also a trend toward more perpendicular equatorial atom positions. Restructuring this complex to place the NH₃ in an equatorial position in E leads to a closer approach to Tr. The axial Cl atoms are pushed further away, with little change in the r(Tr–Cl_e) distances. There is a bit of asymmetry in that the two equatorial Cl atoms are not necessarily the same 120° angle away from N.

Table 2 Structural parameters (distances in Å, angles in deg.) for A complexes of H₃N⋯TrCl₄⁻

	r(N⋯Tr)	r(Tr–Cla)	r(Tr–Cle)	θ(N⋯Tr–Cle)
	Gas
H3N⋯AlCl4^−	2.159	2.247	2.263	82.4
H3N⋯GaCl4^−	2.233	2.277	2.286	81.9
H3N⋯InCl4^−	2.393	2.447	2.467	79.9
H3N⋯TlCl4^−	2.486	2.504	2.525	79.9
	Aqueous
H3N⋯AlCl4^−	2.084	2.316	2.253	86.3
H3N⋯GaCl4^−	2.131	2.352	2.278	86.3
H3N⋯InCl4^−	2.305	2.507	2.460	85.6
H3N⋯TlCl4^−	2.369	2.567	2.518	85.5

---

Table 3 Structural parameters (distances in Å, angles in degs) for E complexes of H₃N⋯TrCl₄⁻ in aqueous phase

	r(N⋯Tr)	r(Tr–Cla)	r(Tr–Cle)	θ(N⋯Tr–Cla)	θ(N⋯Tr–Cle)
H3N⋯AlCl4^−	2.020	2.366	2.223	84.4	116.5
			2.231		124.5
H3N⋯GaCl4^−	2.043	2.409	2.246	84.3	117.8
			2.251		122.9
H3N⋯InCl4^−	2.248	2.539	2.444	82.6	121.0
				83.9
H3N⋯TlCl4^−	2.304	2.604	2.496	81.8	121.3
				82.7

---

The energetic aspects of the dimers are presented in Table 4. The interaction energies in the first two columns refer to the monomers in the geometries they adopt within the complex. These quantities are quite negative, particularly within the aqueous phase where they can exceed 35 kcal mol⁻¹. The interaction energies are most negative for the smallest Al triel atom, and least negative for Tl, although the pattern is not so consistent for the intermediate-sized Ga and In. There is also a clear pattern that the E interaction energies are larger than those for the A structures by between 6 and 12 kcal mol⁻¹. The binding energies in the last two columns are considerably less negative, and some even positive. This difference between E_b and E_int results from the use of optimized monomer geometries for the former, so these two quantities differ by the energy required to distort the pair of monomers into the geometries within the dimer. It is important to note that raising the level of inclusion of electron correlation to CCSD(T) has only a minor effect on the energetics, making each reaction a little bit less exothermic, and doing so uniformly so that all of the MP2 trends remain intact.

Table 4 Interaction E_int and binding energy E_b of H₃N⋯TrCl₄⁻ complexes, all in kcal mol⁻¹

	E int		E b
	MP2	CCSD(T)	MP2	CCSD(T)
	A gas phase
H3N⋯AlCl4^−	−13.45	−11.91	−0.38	0.83
H3N⋯GaCl4^−	−8.92	−7.26	2.39	3.64
H3N⋯InCl4^−	−11.43	−10.05	−4.95	−3.88
H3N⋯TlCl4^−	−8.24	−6.73	−2.63	−1.53
	A aqueous
H3N⋯AlCl4^−	−25.22	−23.58	−7.65	−6.34
H3N⋯GaCl4^−	−20.52	−18.62	−4.22	−2.79
H3N⋯InCl4^−	−21.50	−23.01	−11.67	−10.42
H3N⋯TlCl4^−	−16.04	−14.16	−8.07	−6.67
	E aqueous
H3N⋯AlCl4^−	−36.95	−35.20	−3.73	−2.32
H3N⋯GaCl4^−	−33.51	−31.37	−1.18	0.38
H3N⋯InCl4^−	−28.52	−26.87	−9.28	−7.87
H3N⋯TlCl4^−	−22.07	−19.95	−6.01	−4.43

---

When immersed in aqueous solvent, it is reasonable to wonder whether the NH₃ ligand might be displaced by a water molecule. In order to answer this question, parallel calculations were carried out with H₂O replacing NH₃, again within the context of aqueous medium. The structures of the resulting complexes are illustrated in Fig. S2 (ESI†) to be of type A. The interaction and binding energies can be seen in Table S3 (ESI†) to obey similar trends to the corresponding NH₃ dimers, with interaction energies dropping as the Tr atom grows in size. However, these quantities are considerably less negative than for NH₃. Moreover, the binding energies are also much less exothermic than the quantities in Table 4. The optimized geometries in Table S4 (ESI†) are consistent with the energetics, with longer intermolecular R(O⋯Tr) distances. Altogether the data affirms that the more basic NH₃ engages in a much more tightly bound complex with the TrCl₄⁻ anions than does H₂O, so that the former would not easily be displaced by the latter.

The individual deformation energies described in Table S5 (ESI†) show that it is the TrCl₄⁻ that bears the brunt of this distortion. And these deformation energies become progressively smaller as the central Tr atom grows larger. In the case of the A configuration, the transformation of the originally tetrahedral TrCl₄⁻ unit to a trigonal pyramid requires some 5–13 kcal mol⁻¹ (slightly more in solution). The E dimer requires TrCl₄⁻ to adopt a see-saw geometry, which is more energetically costly, requiring between 16 and 33 kcal mol⁻¹.

Due to these substantive deformation energies, the strongly exothermic interaction energies of the A structures in the gas phase become much smaller, and even endothermic in some cases. There are similar reductions in exothermicity on going from E_int to E_b in water, but the latter remain clearly negative due to the large negative interaction energies in this phase. With respect to the E dimers, these structures engendered the largest negative interaction energies, but are also subject to the highest deformation energies. The net result is that the binding energies for the E structures are slightly less exothermic than those of the A configurations, both lying in the overall 1–12 kcal mol⁻¹ range. It is also interesting to note that the order of binding energies is the same for either A or E, and for both gas and aqueous phase, increasing in the order Ga < Al < Tl < In, i.e. quite different than atomic size. This pattern is quite different than the interaction energies which are largest for the smallest Al atom and generally diminish with growing Tr size. As another point of comparison, whereas the E structures have a larger interaction energy than A, it is the latter that is favored by E_b after deformation energies are factored in.

3.2.2. Analysis of wave functions. It is instructive to partition each interaction energy into separate components that each bear a physical significance. Such a partitioning for the A complexes is described in Table 5 where it may be seen that the Pauli repulsion term is opposed by the three attractive elements of electrostatic, orbital interaction, and dispersion energies. The first of these accounts for something more than half of the total attractive force, roughly 2/3. Another 30% derives from the orbital interactions, followed by a much smaller dispersion component of about 5%.

Table 5 EDA/BLYP-D3/ZORA/TZ2P decomposition of the interaction energy of A complexes into Pauli repulsion (E_Pauli), electrostatic (E_elec), orbital interaction (E_oi) and dispersion (E_disp) components. All energies in kcal mol⁻¹

	E Pauli	E elec	%^a	E oi	%^a	E disp	%^a	E int
a Percentage contributions to total attractive interactions (Eelec + Eorb + Edisp).
H3N⋯AlCl4^−	90.77	−65.72	64	−32.19	31	−4.71	5	−11.86
H3N⋯GaCl4^−	91.10	−61.61	64	−29.77	31	−4.86	5	−5.13
H3N⋯InCl4^−	76.05	−56.24	67	−23.38	28	−4.68	6	−8.25
H3N⋯TlCl4^−	72.79	−51.52	66	−22.53	29	−4.50	6	−5.76

---

Measures of bond strength other than energetic arise in connection with analysis of the wave functions. QTAIM focuses on the topology of the total electron density. The molecular diagrams of these complexes are displayed in Fig. S3 (ESI†) where bond paths indicated by black lines confirm that each complex is held together by a single Tr⋯N bond, with no indication of secondary stabilizing interactions such as H-bonds. The most important properties of the various bond critical points are listed in Table 6. The electron densities of the Tr⋯N BCPs vary from 0.039 to 0.066 a.u. for the A structures, and as high as 0.080 a.u. for the E configurations. These quantities are indicative of a strong noncovalent bond, bordering on covalent.

Table 6 AIM descriptors of the H₃N⋯TrCl₄⁻ complexes. Bond critical point (BCP) properties: electron density ρ, Laplacian of electron density ∇²ρ and total electron energy H, all in atomic units

	Interaction	A gas phase
		ρ	∇^2ρ	H
H3N⋯AlCl4^−	Al–N	0.039	+0.195	+0.000
	Al–Cla	0.050	+0.227	−0.004
	Al–Cle	0.047	+0.220	−0.003
H3N⋯GaCl4^−	Ga–N	0.053	+0.160	−0.012
	Ga–Cla	0.070	+0.181	−0.022
	Ga–Cle	0.069	+0.180	−0.021
H3N⋯InCl4^−	In–N	0.048	+0.180	−0.004
	In–Cla	0.061	+0.204	−0.009
	In–Cle	0.058	+0.197	−0.008
H3N⋯TlCl4^−	Tl–N	0.048	+0.167	−0.002
	Tl–Cla	0.064	+0.194	−0.009
	Tl–Cle	0.061	+0.190	−0.008
		A aqueous
H3N⋯AlCl4^−	Al–N	0.047	+0.255	+0.001
	Al–Cla	0.043	+0.183	−0.003
	Al–Cle	0.048	+0.229	−0.003
H3N⋯GaCl4^−	Ga–N	0.066	+0.224	−0.016
	Ga–Cla	0.060	+0.147	−0.018
	Ga–Cle	0.070	+0.185	−0.021
H3N⋯InCl4^−	In–N	0.059	+0.233	−0.005
	In–Cla	0.054	+0.177	−0.007
	In–Cle	0.059	+0.201	−0.008
H3N⋯TlCl4^−	Tl–N	0.061	+0.225	−0.006
	Tl–Cla	0.056	+0.173	−0.006
	Tl–Cle	0.062	+0.194	−0.009
		E aqueous
H3N⋯AlCl4^−	Al–N	0.053	+0.317	+0.002
	Al–Cla	0.039	+0.158	−0.003
	Al–Cle	0.051	+0.250	−0.003
H3N⋯GaCl4^−	Ga–N	0.080	+0.305	−0.019
	Ga–Cla	0.054	+0.129	−0.015
	Ga–Cle	0.074	+0.201	−0.023
H3N⋯InCl4^−	In–N	0.066	+0.275	−0.007
	In–Cla	0.051	+0.165	−0.006
	In–Cle	0.061	+0.208	−0.009
H3N⋯TlCl4^−	Tl–N	0.070	+0.264	−0.008
	Tl–Cla	0.052	+0.163	−0.005
	Tl–Cle	0.064	+0.200	−0.010

---

Indeed, the A N⋯Tr critical point densities are only slightly smaller than those characterizing the Tr–Cl bonds in the gas phase. Immersion in solvent causes an increase of ρ_BCP for the Tr⋯N bonds while those of Tr–Cl_a are reduced. The rise in the former is likely due to a lessening of the electrostatic repulsion between the partial negative charge on the NH₃ lone pair and the full negative charge of the anion due to the influence of the polarizable medium. This bond strengthening then induces a compensating weakening of the TrCl_a bond lying directly opposite. The positive values of the Laplacian of the electron density are indicative of their largely noncovalent nature. The total electron energy density (H) values are negative and quite small. As may be seen by the data in the lowermost section of Table 6, the switch from A to E geometry causes a small increase in the Tr⋯N critical point density, consistent with the larger interaction energies of the latter structure type and the shorter r(Tr⋯N). There is also a small weakening of the Tr–Cl_a bonds, coupled with a strengthening of Tr–Cl_e, both of which are consistent with their respective bond stretches and contractions on going from A to E.

3.2.3. Complexes with CN⁻. When paired with the CN⁻ anion, TrCl₄⁻ forms four different complexes. The global minimum E resembles the E geometry of the NH₃ complexes in that CN⁻ sits in one of the three equatorial sites. The next most stable is labeled A in which it is an axial site where the CN⁻ is located. In both E and A, it is the C atom of CN⁻ that approaches the triel atom. This situation is reversed in geometries E′ and A′ where the Tr atom makes contact with N instead of C, axial in A′ and equatorial in E′. As reported in Table S6 (ESI†), A is only slightly less stable than E, whereas E′ and A′ lie higher in energy by 2–10 kcal mol⁻¹. The calculations thus focused on E and A as the more stable pair, comparable in energy to one another, both of which are displayed in Fig. 2 along with the atomic labeling.

Fig. 2 Most stable structures of NC⁻⋯TrCl₄⁻.

As may be seen by the geometrical parameters listed in Table 7, the CN⁻ anion comes a bit closer to the central Tr atom than does the N of NH₃, particularly for the larger Tr atoms. The r(Tr⋯C) distances are in the range between 2.01 and 2.27 Å, and the equatorial (E) distances of the anion are a bit shorter than the axial (A) distances. There is a certain amount of “bunching” in that the distances for the two smaller Al and Ga are roughly the same, about 0.2 Å shorter than for the two larger Tr atoms. Placement in water shortens this bond distance a bit. Along with the closer approach of the CN⁻ to the Tr comes some small degree of lengthening of the Tr–Cl bonds.

Table 7 Structural parameters (distances in Å, angles in deg.) for the most stable complexes of CN⁻ with TrCl₄⁻

	r(C⋯Tr)	r(Tr–Cla)	r(Tr–Cle)	θ(C⋯Tr–Cla)	θ(C⋯Tr–Cle)
a Parameters for aqueous solution in parentheses.
E
NC^−⋯AlCl4^−	2.039 (2.020)^a	2.411 (2.401)	2.268 (2.242)	87.7 (87.4)	121.1 (121.3)
NC^−⋯GaCl4^−	2.026 (2.005)	2.467 (2.461)	2.284 (2.261)	88.1 (88.0)	121.2 (121.5)
NC^−⋯InCl4^−	2.230 (2.203)	2.591 (2.581)	2.485 (2.460)	88.8 (88.8)	120.6 (121.7)
NC^−⋯TlCl4^−	2.237 (2.120)	2.672 (2.673)	2.534 (2.507)	89.1 (89.4)	121.5 (123.7)
A
NC^−⋯AlCl4^−	2.093 (2.079)	2.372 (2.365)	2.300 (2.274)	179.9 (180.0)	89.3 (89.4)
NC^−⋯GaCl4^−	2.091 (2.081)	2.396 (2.404)	2.337 (2.308)	179.9 (180.0)	89.8 (90.1)
NC^−⋯InCl4^−	2.269 (2.255)	2.544 (2.546)	2.520 (2.490)	180.0 (179.8)	89.6 (90.2)
NC^−⋯TlCl4^−	2.265 (2.250)	2.573 (2.582)	2.602 (2.570)	180.0 (179.9)	90.0 (90.8)

---

In contrast to the NH₃ cases, Table 8 shows that complexation reactions involving CN⁻ anion are endothermic in the gas phase, with E_int and E_b turning negative only within aqueous medium. E_b is in fact very positive, between 37 and 51 kcal mol⁻¹, and is particularly endothermic for the smaller Tr atoms. Interaction energies are also positive, but less so than E_b, especially for structure E where E_int is close to zero. Immersion in water has a profound effect, leading to clearly exothermic quantities. The interaction energies are quite negative, up to as much as −50 kcal mol⁻¹. Whereas the E interaction energies are much larger than those for A, there is a much smaller difference between the two geometries in terms of E_b. The binding energies become increasingly more exothermic in the order Ga < Al < Tl < In. As in the case of the NH₃ complexes, the CCSD(T) data are slightly more endothermic than MP2 but maintain the same trends.

Table 8 Interaction E_int and binding energy E_b of NC⁻⋯TrCl₄⁻ complexes, all in kcal mol⁻¹

	Gas phase				Aqueous solution
	E int		E b		E int		E b
	MP2	CCSD(T)	MP2	CCSD(T)	MP2	CCSD(T)	MP2	CCSD(T)
E
NC^−⋯AlCl4^−	1.49	4.68	48.78	50.99	−49.53	−46.48	−9.11	−6.63
NC^−⋯GaCl4^−	1.88	5.70	49.10	51.53	−49.78	−46.13	−8.54	−5.80
NC^−⋯InCl4^−	0.71	3.93	36.98	39.13	−44.54	−41.61	−17.06	−14.59
NC^−⋯TlCl4^−	4.98	8.94	37.78	40.23	−42.10	−38.23	−15.61	−12.72
A
NC^−⋯AlCl4^−	16.80	19.78	48.85	50.98	−34.46	−31.58	−8.81	−6.47
NC^−⋯GaCl4^−	18.48	21.95	50.59	52.89	−32.38	−29.05	−6.45	−3.92
NC^−⋯InCl4^−	11.98	15.00	37.28	39.31	−33.63	−30.83	−16.01	−13.64
NC^−⋯TlCl4^−	14.18	17.94	38.13	40.44	−30.81	−27.20	−13.85	−11.22

---

Table S6 (ESI†) contains the deformation energies required for each monomer to attain its structure within the complex. As was the case for NH₃, nearly all of the deformation energy is concentrated in the Lewis acid as it transitions from tetrahedral to see-saw (E) or trigonal pyramid (A). The former requires some 33–47 kcal mol⁻¹, as compared to only 24–32 kcal mol⁻¹ for the latter. It is largely this higher deformation energy within the E complexes that keeps their binding energies similar to those of A, despite their much lesser positive interaction energies. It might be noted also that the deformation energies connected to NH₃ complexation are considerably smaller than required for CN⁻.

Decomposition of the total interaction energy of the most stable E complexes in Table 9 reveal a qualitative difference with the NH₃ complexes. Whereas the former were held together in large measure by electrostatics, which accounted for some 65% of the total attraction, the coulombic force is considerably smaller for the CN⁻ complexes, reduced to only 35–46%. The difference is made up by orbital interactions which raise to more than half of the total; dispersion remains negligible. Despite its smaller contribution to the total, the electrostatic term is quite substantial, between 38 and 63 kcal mol⁻¹.

Table 9 EDA/BLYP-D3/ZORA/TZ2P decomposition of the interaction energy of E complexes of CN⁻⋯TrCl₄⁻ into Pauli repulsion (E_Pauli), electrostatic (E_elec), orbital interaction (E_oi) and dispersion (E_disp) components. All energies in kcal mol⁻¹

	E Pauli	E elec	%^a	E oi	%^a	E disp	%^a	E int
a Percentage contributions of total attractive interactions (Eelec + Eorb + Edisp).
NC^−⋯AlCl4^−	108.95	−38.01	35	−66.10	62	−3.13	3	1.70
NC^−⋯GaCl4^−	149.50	−56.94	40	−80.90	57	−3.27	2	8.39
NC^−⋯InCl4^−	119.34	−49.00	43	−61.07	54	−2.92	3	6.35
NC^−⋯TlCl4^−	148.80	−63.01	46	−69.55	51	−2.96	2	13.27

---

The AIM diagrams for anion–anion complexes are displayed in Fig. S4 (ESI†), which again confirm the Tr⋯C triel bond as the only stabilizing intermolecular noncovalent bond. These analyses are summarized numerically in Table 10. The ρ_BCP values suggest that the Tr⋯C bond is systematically slightly stronger for E than A, consistent with the less endothermic E_int for E in Table 8. This density varies in the order Al < In < Tl < Ga for E which is only slightly different for A. But this order bears little resemblance to the interaction energies. These triel bond densities are considerably larger for CN⁻ than for NH₃, consistent with the shorter intermolecular distances in the former.

Table 10 AIM descriptors of the NC⁻⋯TrCl₄⁻ complexes. Bond critical point (BCP) properties: electron density ρ, Laplacian of electron density ∇²ρ and total electron energy H, all in atomic units

	Interaction	Gas phase			Aqueous solution
		ρ	∇^2ρ	H	ρ	∇^2ρ	H
E
NC^−⋯AlCl4^−	Al–C	0.058	+0.300	−0.003	0.061	+0.319	−0.003
	Al–Cla	0.036	+0.133	−0.004	0.036	+0.140	−0.003
	Al–Cle	0.047	+0.214	−0.003	0.049	+0.234	−0.003
NC^−⋯GaCl4^−	Ga–C	0.091	+0.246	−0.033	0.094	+0.263	−0.034
	Ga–Cla	0.048	+0.110	−0.012	0.048	+0.115	−0.012
	Ga–Cle	0.069	+0.177	−0.021	0.072	+0.193	−0.022
NC^−⋯InCl4^−	In–C	0.074	+0.238	−0.016	0.078	+0.253	−0.018
	In–Cla	0.046	+0.142	−0.005	0.046	+0.148	−0.005
	In–Cle	0.056	+0.186	−0.007	0.059	+0.200	−0.008
NC^−⋯TlCl4^−	Tl–C	0.085	+0.229	−0.023	0.091	+0.242	−0.028
	Tl–Cla	0.046	+0.139	−0.003	0.045	+0.142	−0.003
	Tl–Cle	0.060	+0.184	−0.008	0.063	+0.196	−0.009
A
NC^−⋯AlCl4^−	Al–C	0.053	+0.254	−0.003	0.054	+0.267	−0.003
	Al–Cla	0.039	+0.149	−0.004	0.039	+0.155	−0.003
	Al–Cle	0.043	+0.193	−0.003	0.046	+0.213	−0.046
NC^−⋯GaCl4^−	Ga–C	0.080	+0.205	−0.027	0.081	+0.22	−0.028
	Ga–Cla	0.055	+0.126	−0.016	0.054	+0.127	−0.015
	Ga–Cle	0.061	+0.154	−0.018	0.065	+0.170	−0.020
NC^−⋯InCl4^−	In–C	0.069	+0.217	−0.013	0.070	+0.228	−0.014
	In–Cla	0.050	+0.157	−0.006	0.050	+0.159	−0.006
	In–Cle	0.052	+0.172	−0.006	0.056	+0.187	−0.007
NC^−⋯TlCl4^−	Tl–C	0.081	+0.217	−0.020	0.083	+0.230	−0.022
	Tl–Cla	0.052	+0.162	−0.005	0.055	+0.165	+0.006
	Tl–Cle	0.052	+0.162	−0.005	0.056	+0.176	−0.006

---

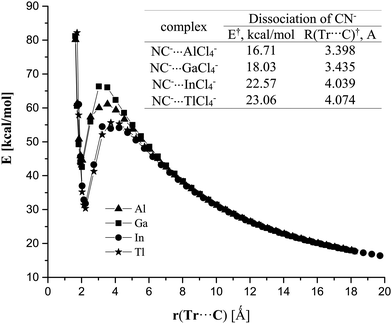
Given the strongly endothermic binding energies for the CN⁻⋯TrCl₄⁻ in the gas phase, it is perhaps surprising that there is even a minimum in the potential energy surface; one might expect an energetically facile dissociation into a pair of separate monomers. However, such a separation is opposed by an energy barrier, as exhibited in Fig. 3. This barrier varies between 17 and 23 kcal mol⁻¹, so is easily high enough to maintain each of these complexes as a metastable minimum. When placed in aqueous solution, however, the situation reverses entirely. The binding energies are substantially negative, between 6 and 17 kcal mol⁻¹; the complexation process is exothermic, proceeding steadily downhill from the individual monomers.

Fig. 3 Association profiles of NC⁻⋯TrCl₄⁻ complexes in gas phase. Zero of energy is taken as the fully separated pair of monomers in each case. Inset provides quantitative measures of the barrier height and location.

4. Discussion

The idea that a distinctly endothermic process like the gas-phase association of the CN⁻ and TrCl₄⁻ anions may represent a metastable equilibrium, with a substantial energy barrier separating the complex from the much more stable isolated anions, might seem a bit surprising at first. Yet this behavior seems to be a common feature of the dissociation of other anion–anion complexes including H-bonds,^{46,49,50,79–81} halogen bonds,^82–86 pnicogen bonds,⁸⁷ those involving metal atoms from both groups IIA and IIB⁸⁸ as well as other sorts of species.⁸⁹ Regarding the height of the energy barrier, it is typically below 10 kcal mol⁻¹ or so for H-bonded complexes between ions of like charge,^90–93 a bit higher at 15 kcal mol⁻¹ for the (H₂PO₄⁻)₂ dimer⁹⁴ or for a pair of anions terminating in carboxyl groups.⁸⁰ These barriers climb up above 20 kcal mol⁻¹ for CN⁻⋯MCl₃⁻ complexes with M a member of group 2A of the periodic table, i.e. Be, Mg, etc.⁹⁵ and higher still,⁸⁸ more than 25 kcal mol⁻¹ when M is a transition metal from group 2B: Zn, Cd, and Hg. The barriers increase further, up near 30 kcal mol⁻¹ for the pnicogen bonded complexes⁸⁷ and certain others.⁴⁶ So the barriers in the 16–23 kcal mol⁻¹ range computed here for the triel-bonded complexes fit nicely into this historical context.

One can think of this phenomenon in the following way. As the two anions begin to approach one another from long distance, they are initially repelled by their like charges so the energy climbs. But once they have come closer together, noncovalent attractive forces begin to kick in and slowly overcome the long-distance Coulomb repulsion, and the energy drops as they continue their approach. At the same time, this approach forces the Lewis acid to rearrange from its initial tetrahedral shape into a trigonal bipyramid, so imposes an energy cost on the complexation reaction.

As the CN⁻ and TrCl₄⁻ anions both bear a negative charge, one might intuitively expect an electrostatic repulsion that only gets larger and larger as they approach one another. Yet a glance at Table 9 reveals a very substantial negative attractive electrostatic component. There are two elements in unraveling this paradox. In the first place, the mutual approach of the two anions causes a rather dramatic rearrangement of the Lewis acid's internal geometry. In the case of the more stable E geometry, TrCl₄⁻ shifts from tetrahedral to a see-saw geometry. This deformation has a drastic effect on the surrounding MEP, substantially enhancing its σ-holes opposite the two equatorial Cl atoms. Due to this rearrangement, V_s,max grows by some 50–80 kcal mol⁻¹, and achieves the values reported in the first column of Table 11. Note that despite the fact that this species remains an anion, the MEP is only slightly negative, and even positive for Al and In. On the other hand, the CN⁻ species does not situate itself precisely at the σ-hole positions which lie directly opposite the two Cl_e atoms, but instead directly between them. So it might be more appropriate to examine the MEP at the site of the C atom. As indicated in Table 11, the MEP here is more negative than at the two σ-holes, but remains far less negative than the σ-holes of the undistorted tetrahedral TrCl₄⁻ monomer, by between 42 and 68 kcal mol⁻¹. In either case the internal rearrangement of the acid is a major factor in allowing for an attractive electrostatic interaction.

Table 11 Values of MEP in TrCl₄⁻ anions (kcal mol⁻¹) when in the geometry adopted within E complexes with CN⁻, and distances of indicated points from the central Tr atom (Å)

	ρ = 0.001 a.u.		At C atom position
	V s,max	R	V	R
AlCl4^−	0.3	1.897	−12.7	2.039
GaCl4^−	−10.2	1.938	−17.3	2.026
InCl4^−	3.7	2.018	−12.3	2.230
TlCl4^−	−13.2	2.108	−20.7	2.237

---

As a second issue, one should recall that a simple point-point representation of the interaction between these two anions quickly breaks down as the two approach one another, where the full electron densities must be considered, as well as charge penetration effects. Indeed, attractive coulombic terms have been noted earlier in other anion–anion interactions for this same reason. The electrostatic component was fairly small and of variable sign in complexes of CN⁻ with MCl₃⁻ (M = Be, Mg, Ca, Sr, Ba), with a maximum attractive component of 6.5 kcal mol⁻¹ in NC⁻⋯BeCl₃⁻,⁹⁵ but is much larger in magnitude, up to 97 kcal mol⁻¹ when NC⁻ approaches MCl₃⁻ (M = Zn, Cd, Hg),⁸⁸ and climbs above 100 kcal mol⁻¹ for interactions with main group ZCl₄⁻ (Z = P, As, Sb).⁸⁷ Comparable and even larger attractive components have been recorded in other related ion–ion systems.^87,96 The attractive electrostatic components of 38–63 kcal mol⁻¹ in the triel-bonding interactions here of CN⁻ with TrCl₄⁻ lie comfortably within the range of these earlier calculations.

The dissociation profile for the CN⁻⋯TrCl₄⁻ complexes undergoes a dramatic change upon immersion in aqueous solvent. A highly endothermic association in the gas phase, stabilized by an energy barrier, transforms into an energetically downhill exothermic process. This metamorphosis is not without precedent, noted for a range of different types of system,^{41,42,44,51,85–88,95,97} so should probably be thought of as a general feature of ion–ion complexes.

It is interesting to compare the energetics of the anion–anion TrB with its anion–neutral counterpart. First with respect to the interaction energies, these quantities are all negative, between 8 and 13 kcal mol⁻¹ in the gas phase for the NH₃ complexes, raised up to the 16–37 kcal mol⁻¹ range in water. The anion–anion interaction energies are all positive, some approaching +20 kcal mol⁻¹, in the gas phase. But they reverse completely in solution and become strongly negative, even larger in magnitude than is the case for the anion–neutral systems, up to as much as −50 kcal mol⁻¹. In the context of binding energies, gas phase values for the anion–neutral are small, and generally negative, whereas the anion–anion E_b are very positive, surpassing 50 kcal mol⁻¹. Placing the anion–neutral pairs in water make them more negative by some 7–16 kcal mol⁻¹ so that they are all negative. The solvation of the anion–anion complexes dramatically change E_b from strongly positive to quite negative. Indeed, the aqueous binding energies of the anion–anion complexes are more negative than the equivalent quantities for the anion-neutral pairs.

More complete thermodynamic data for the complexation reactions are supplied in Tables S8 and S9 (ESI†). As a dimerization reaction, the ΔS quantities are all negative, with a magnitude of some 30–40 cal K⁻¹ mol⁻¹. When combined with the enthalpies, the Gibbs free energies of the reactions of NH₃ with the TrCl₄⁻ anions are roughly thermoneutral, more positive in the gas phase. ΔG for the dimerization reactions of CN⁻ in the gas phase are quite positive, but become negative when in aqueous solvent. Positive values of ΔG have been noted in the literature for σ-hole interactions.⁹⁸

Another question arises in connection with the use of pseudopotentials. Interaction energies were recomputed at the M06-2X/def2tzvpp level of theory. As reported in Table S10 (ESI†), the switch to an all-electron basis set does not alter any of the patterns noted above with pseudopotentials for the heavier atoms.

There are numerous instances of neutral trivalent triel species engaging in exothermic complexes with a host of Lewis bases.^{32,33,37,38,99–104} Tr⋯N triel bonds in triel trihalide adducts with NH₃, HCN, and N₂ were described by Grabowski.³²E_int of the studied dimers were as high as 26 kcal mol⁻¹ for Tr = B, diminishing as the triel atom grew in size. The lowest value of ρ_BCP(Tr⋯N) was found for Tr = Al, which disagreed with the E_int trend.³² Work by our own group focused on complexes of TrR₃ (R = H, F, Cl, Br, CH₃) with pyrazine, which demonstrated that the triel bond strength depends on the electron-withdrawing power of substituents.¹⁰² Triel bonds with delocalized π-electron systems as base were also studied for benzene¹⁰³ where its complexes with BH₃ and AlH₃ were classified as weak to medium strength. The dissociation energies were calculated to be about 3–5 kcal mol⁻¹ for B complexes and 10–15 kcal mol⁻¹ for Al.¹⁰³ The π–hole–π electrons complexes, of TrH₃ and TrX₃ (Z = B, Al, X = F, Cl, Br) with acetylene and ethylene were analysed. Based on the QTAIM results, the Al complexes engaged in stronger interactions than the B analogues and both of them exhibit features of covalent or partial covalent bond.¹⁰⁴ Very recently Grabowski presented a study on triel trihydrides and trihalides with small bases: N₂, HCN and NH₃.⁹⁹ These neutral complexes are characterised by a broad spectrum of interactions, from −1.5 kcal mol⁻¹ for BCl₃⋯N₂ to −50.4 kcal mol⁻¹ for BCl₃⋯NH₃. The deformation energies for the neutral complexes rose along with the total interaction energy.⁹⁹ The influence of solvent (heptane and DMSO) on the triel bond has been investigated in RTrH₂⋯NH₃ (R = CH, CH₂, CH₃; Tr = B and Al) complexes.¹⁰⁰ It was observed that solvents are able to change the nature of the Al⋯N triel bond. The fluorine substituent on the triel donor enhances the TrB, depending on the specific substitution position. The authors concluded that in solvent the Tr⋯N bonds were shortened and strengthened and charge transfer was increased. These changes grow along with increase of solvent polarity.¹⁰⁰ With respect to triel bonds of charged species, in our recent work the complexation between naphthalene derivatives C₁₀H₇TrF₂ and C₁₀H₆NH₂TrF₂ (Tr = B, Al, Ga, In, Tl) and their complexes with the anionic ligand CN⁻ were examined.³⁸ This anion-neutral triel bond was quite strong, reaching 70 kcal mol⁻¹. The presence of a strong external TrB was found to weaken the intramolecular Tr⋯N bond.

5. Conclusions

TrCl₄⁻ anions can engage in fairly strong triel bonds with both neutral NH₃ and the CN⁻ anion, even though these Lewis acids do not possess a positively charged σ or π-hole. The complexation involves an internal restructuring of the tetrahedral TrCl₄⁻ monomer into a trigonal bipyramid shape, where the base can occupy either an axial or equatorial position. This rearrangement aids the complexation by imparting a much more positive MEP to the site that is to be occupied by the base. Interaction energies with the neutral base are negative (exothermic) in the gas phase and even more so when the system is immersed in aqueous solvent. The same is true of binding energies although the energy required to deform the monomer into its shape within the dimer makes the entire complexation process less exothermic. Despite the long-range coulombic repulsion between a pair of anions, CN⁻ can also engage in a strong triel bond with TrCl₄⁻. The interaction energies are positive in the gas phase, and binding energies even more so, but the metastable dimer is held together by an energy barrier opposing its dissociation. The situation is entirely different in solution, with large negative interaction energies and a potential that progresses smoothly and steadily downhill as the two monomers approach one another.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financed in part by a statutory activity subsidy from the Polish Ministry of Science and Higher Education for the Faculty of Chemistry of Wroclaw University of Science and Technology and by the US National Science Foundation under Grant No. 1954310. A generous allotment of computer time from the Wroclaw Supercomputer and Networking Center is acknowledged.

References

1. L. Sobczyk, S. J. Grabowski and T. M. Krygowski, Chem. Rev., 2005, 105, 3513–3560.
2. P. M. J. Szell, G. Cavallo, G. Terraneo, P. Metrangolo, B. Gabidullin and D. L. Bryce, Chem. – Eur. J., 2018, 24, 11364–11376.
3. P. Schuster, Hydrogen Bonds, Springer-Verlag, Berlin, 1984.
4. The Hydrogen Bond. Recent Developments in Theory and Experiments, ed. P. Schuster, G. Zundel and C. Sandorfy, North-Holland Publishing Co., Amsterdam, 1976.
5. H. Umeyama and K. Morokuma, J. Am. Chem. Soc., 1977, 99, 1316–1332.
6. G. Zundel, C. Sandorfy and P. Schuster, The hydrogen bond: recent developments in theory and experiments 2, North-Holland, Amsterdam, Oxford, 1976.
7. S. Scheiner, Hydrogen Bonding: A Theoretical Perspective, Oxford University Press, New York, 1997.
8. K. Kendall and A. D. Roberts, Philos. Trans. R. Soc., B, 2015, 370, 20140078.
9. K. Müller-Dethlefs and P. Hobza, Chem. Rev., 2000, 100, 143–168.
10. S. Grabowski, Hydrogen Bonding – New Insights, Springer, Netherlands, Berlin, 1st edn, 2006.
11. G. R. Desiraju and T. Steiner, The weak hydrogen bond: in structural chemistry and biology, Oxford University Press, Oxford, 2001.
12. G. Gilli and P. Gilli, The Strength of the H-Bond: Definitions and Thermodynamics. The Nature of the Hydrogen Bond, Oxford, 2009, 222–244.
13. G. Gilli and P. Gilli, The nature of the hydrogen bond: outline of a comprehensive hydrogen bond theory, Oxford University Press, Oxford, 2013.
14. S. Scheiner, Hydrogen Bonding: A Theoretical Perspective, Oxford University Press, 1997.
15. T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296.
16. J. S. Murray, P. Lane, T. Clark and P. Politzer, J. Mol. Model., 2007, 13, 1033–1038.
17. J. S. Murray, P. Lane and P. Politzer, Int. J. Quantum Chem., 2007, 107, 2286–2292.
18. P. Politzer, P. Lane, M. C. Concha, Y. G. Ma and J. S. Murray, J. Mol. Model., 2007, 13, 305–311.
19. P. Politzer, J. S. Murray and M. C. Concha, J. Mol. Model., 2007, 13, 643–650.
20. P. Politzer, J. S. Murray and P. Lane, Int. J. Quantum Chem., 2007, 107, 3046–3052.
21. J. S. Murray and P. Politzer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e13260.
22. P. Politzer and J. S. Murray, Crystals, 2017, 7, 212.
23. P. Politzer, J. S. Murray, T. Clark and G. Resnati, Phys. Chem. Chem. Phys., 2017, 19, 32166–32178.
24. P. Politzer and J. S. Murray, Crystals, 2018, 8, 42.
25. J. S. Murray and P. Politzer, J. Mol. Model., 2019, 25, 101.
26. P. Politzer and J. S. Murray, Crystals, 2019, 9, 165.
27. P. Politzer and J. S. Murray, J. Comput. Chem., 2018, 39, 464–471.
28. K. E. Riley, J. S. Murray, J. Fanfrlik, J. Rezac, R. J. Sola, M. C. Concha, F. M. Ramos and P. Politzer, J. Mol. Model., 2011, 17, 3309–3318.
29. P. Politzer and J. S. Murray, ChemPhysChem, 2013, 14, 278–294.
30. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189.
31. A. Bundhun, P. Ramasami, J. S. Murray and P. Politzer, J. Mol. Model., 2013, 19, 2739–2746.
32. S. J. Grabowski, ChemPhysChem, 2014, 15, 2985–2993.
33. S. J. Grabowski, ChemPhysChem, 2015, 16, 1470–1479.
34. A. Bauza, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496–2517.
35. T. A. Ford, J. Mol. Struct., 2020, 1210, 128020.
36. M. D. Esrafili and P. Mousavian, Mol. Phys., 2018, 116, 388–398.
37. S. J. Grabowski, J. Comput. Chem., 2018, 39, 472–480.
38. W. Zierkiewicz, M. Michalczyk and S. Scheiner, Molecules, 2020, 25(3), 635.
39. S. Bhunya, T. Malakar, G. Ganguly and A. Paul, ACS Catal., 2016, 6, 7907–7934.
40. C. W. Hamilton, R. T. Baker, A. Staubitz and I. Manners, Chem. Soc. Rev., 2009, 38, 279–293.
41. I. Mata, I. Alkorta, E. Molins and E. Espinosa, Chem. Phys. Lett., 2013, 555, 106–109.
42. A. Shokri, M. Ramezani, A. Fattahi and S. R. Kass, J. Phys. Chem. A, 2013, 117, 9252–9258.
43. Y. Yang, Z. Xu, Z. Zhang, Z. Yang, Y. Liu, J. Wang, T. Cai, S. Li, K. Chen, J. Shi and W. Zhu, J. Phys. Chem. B, 2015, 119, 11988–11997.
44. L. M. Azofra, J. Elguero and I. Alkorta, J. Phys. Chem. A, 2020, 124, 2207–2214.
45. I. Mata, E. Molins, I. Alkorta and E. Espinosa, J. Phys. Chem. A, 2015, 119, 183–194.
46. M. O. Miranda, D. J. R. Duarte and I. Alkorta, ChemPhysChem, 2020, 21, 1052–1059.
47. D. Quiñonero, I. Alkorta and J. Elguero, ChemPhysChem, 2020, 21, 1597–1607.
48. J. Vondrášek, P. E. Mason, J. Heyda, K. D. Collins and P. Jungwirth, J. Phys. Chem. B, 2009, 113, 9041–9045.
49. I. Mata, E. Molins, I. Alkorta and E. Espinosa, J. Phys. Chem. A, 2014, 119, 183–194.
50. I. Alkorta, I. Mata, E. Molins and E. Espinosa, Chem. – Eur. J., 2016, 22, 9226–9234.
51. Í. Iribarren, M. M. Montero-Campillo, I. Alkorta, J. Elguero and D. Quiñonero, Phys. Chem. Chem. Phys., 2019, 21, 5796–5802.
52. T. Niemann, P. Stange, A. Strate and R. Ludwig, Phys. Chem. Chem. Phys., 2019, 21, 8215–8220.
53. S. G. Dash and T. S. Thakur, Phys. Chem. Chem. Phys., 2019, 21, 20647–20660.
54. A. E. Khudozhitkov, J. Neumann, T. Niemann, D. Zaitsau, P. Stange, D. Paschek, A. G. Stepanov, D. I. Kolokolov and R. Ludwig, Angew. Chem., Int. Ed., 2019, 58, 17863–17871.
55. W. Zierkiewicz, R. Wysokinski, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 870–877.
56. R. Wysokiński, W. Zierkiewicz, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 1119–1125.
57. S. Scheiner, R. Wysokinski, M. Michalczyk and W. Zierkiewicz, J. Phys. Chem. A, 2020, 124, 4998–5006.
58. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
59. C. Moller and M. S. Plesset, Phys. Rev., 1934, 46, 0618–0622.
60. D. E. Woon and T. H. D. Jr., J. Chem. Phys., 1995, 103, 4572–4585.
61. B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibsom and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820.
62. K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052.
63. K. A. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296.
64. D. Figgen, G. Rauhut, M. Dolg and H. Stoll, J. Chem. Phys., 2005, 311, 227–244.
65. D. Feller, J. Comput. Chem., 1996, 17, 1571–1586.
66. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Headgordon, Chem. Phys. Lett., 1989, 157, 479–483.
67. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975.
68. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
69. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
70. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. C.01, Wallingford, CT, 2016.
71. A. T. Keith, AIMAll, version 14.11.23, TK Gristmill Software, Overland Park KS, USA, 2014, aim.tkgristmill.com.
72. ADF2014, SCM, Theoretical Chemistry, Amsterdam, The Netherlands, 2014.
73. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
74. O. A. Stasyuk, R. Sedlak, C. F. Guerra and P. Hobza, J. Chem. Theory Comput., 2018, 14, 3440–3450.
75. C. Peng and H. Bernhard Schlegel, Isr. J. Chem., 1993, 33, 449–454.
76. T. Lu and F. Chen, J. Mol. Graphics Modell., 2012, 38, 314–323.
77. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
78. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38.
79. L. M. Azofra, J. Elguero and I. Alkorta, Phys. Chem. Chem. Phys., 2020, 22, 11348–11353.
80. R. Barbas, R. Prohens, A. Bauzá, A. Franconetti and A. Frontera, Chem. Commun., 2019, 55, 115–118.
81. F. Weinhold, Angew. Chem., Int. Ed., 2017, 56, 14577–14581.
82. J. M. Holthoff, E. Engelage, R. Weiss and S. M. Huber, Angew. Chem., Int. Ed., 2020, 59, 11150–11157.
83. C. Wang, Y. Fu, L. Zhang, D. Danovich, S. Shaik and Y. Mo, J. Comput. Chem., 2018, 39, 481–487.
84. S. M. Chalanchi, I. Alkorta, J. Elguero and D. Quiñonero, ChemPhysChem, 2017, 18, 3462–3468.
85. G. Wang, Z. Chen, Z. Xu, J. Wang, Y. Yang, T. Cai, J. Shi and W. Zhu, J. Phys. Chem. B, 2016, 120, 610–620.
86. D. Quinonero, I. Alkorta and J. Elguero, Phys. Chem. Chem. Phys., 2016, 18, 27939–27950.
87. S. Scheiner, R. Wysokiński, M. Michalczyk and W. Zierkiewicz, J. Phys. Chem. A, 2020, 124, 4998–5006.
88. R. Wysokiński, W. Zierkiewicz, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 1119–1125.
89. D. Quiñonero, I. Alkorta and J. Elguero, ChemPhysChem, 2020, 21, 1597–1607.
90. S. R. Kass, J. Am. Chem. Soc., 2005, 127, 13098–13099.
91. I. Mata, E. Molins, I. Alkorta and E. Espinosa, J. Phys. Chem. A, 2015, 119, 183–194.
92. R. Prohens, A. Portell, M. Font-Bardia, A. Bauzá and A. Frontera, Chem. Commun., 2018, 54, 1841–1844.
93. F. Weinhold, Inorg. Chem., 2018, 57, 2035–2044.
94. I. Mata, I. Alkorta, E. Molins and E. Espinosa, ChemPhysChem, 2012, 13, 1421–1424.
95. W. Zierkiewicz, R. Wysokiński, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 870–877.
96. P. R. Horn, Y. Mao and M. Head-Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067–23079.
97. Z. Zhu, G. Wang, Z. Xu, Z. Chen, J. Wang, J. Shi and W. Zhu, Phys. Chem. Chem. Phys., 2019, 21, 15106–15119.
98. G. R. Desiraju, P. Shing Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713.
99. S. J. Grabowski, Molecules, 2020, 25(11), 2703.
100. Z. F. Xu and Y. Li, J. Mol. Model., 2019, 25, 219.
101. J. R. Zhang, W. Z. Li, J. B. Cheng, Z. B. Liu and Q. Z. Li, RSC Adv., 2018, 8, 26580–26588.
102. M. Michalczyk, W. Zierkiewicz and S. Scheiner, ChemPhysChem, 2018, 19, 3122–3133.
103. S. J. Grabowski, Struct. Chem., 2017, 28, 1163–1171.
104. S. J. Grabowski, Molecules, 2015, 20, 11297–11316.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp06547a

---