Bridging experiment and theory: enhancing the electrical conductivities of soft-templated niobium-doped mesoporous titania films

Abstract

Theoretical calculations suggest a strong dependence of electrical conductivity and doping concentration in transition-metal doped titania. Herein, we present a combined theoretical and experimental approach for the prediction of relative phase stability and electrical conductivity in niobium-doped titania as model system. Our method paves the way towards the development of materials with improved electrical properties.

---

1. Introduction

The optical and electronic properties of various transition metal oxides have been investigated for decades due to their broad applicability in photo-,^1,2 electro-catalysis,^3–5 photovoltaics⁶ and, amongst others, sensing.⁷ The oxides of titanium, primarily TiO₂, are of particular importance as a result of their excellent efficiencies in photocatalytic processes, e.g. water splitting,⁸ water purification⁹ or as support materials in electro-catalytic reactions.¹⁰ For TiO₂, the rutile phase is the most stable modification under atmospheric conditions.¹¹ Different ways to obtain TiO₂ materials in the thermodynamically less stable anatase or brookite phase have been developed and shown to have superior photocatalytic properties compared to rutile, for instance.^12–14

The semiconducting properties of bare TiO₂ limit its application as support material in electro-catalytic reactions.¹⁰ Aliovalent doping is an important concept to significantly enhance the conductivity of a material. In the case of TiO₂, both n- and p-type doping have been reported in literature.^15,16 The impact of different dopant atoms and concentrations on the photocatalytic activity were theoretically simulated.^15,16 Niobium-doped TiO₂ was shown to exhibit higher activities compared to bare rutile TiO₂ or other transition-metal-doped TiO₂ photo-catalysts.^11,17 By photoemission spectroscopic techniques, the oxidation states of the transition metals were analyzed and correlations with the electrical conductivity of the oxide materials were found.^18,19 Moreover, there is a clear correlation between electrical conductivity and electrochemical activity due to improved charge carrier kinetics lowering the activation barriers of redox reactions at an electrode.¹⁰

Beside a high electrical conductivity, many applications, e.g. as support materials²⁰ or energy storage materials,²¹ demand for nanostructured materials with large surface areas. Mesoporous materials offer high surface-to-volume ratios²² and are able to promote mass transfer kinetics.²³ Mesoporous doped TiO₂ materials show superior activities as a consequence of their enhanced surface areas and nanostructure.^24,25 Importantly, a fully accessible, interconnected pore network is desirable for catalytic applications. The evaporation-induced self-assembly (EISA) process using an appropriate soft template, e.g. a block-copolymer, is a well-established method to produce mesoporous transition metal oxide films of varying thicknesses from several nanometers to micrometers with excellent reproducibility and stoichiometric control.²⁶ Liu et al.¹⁹ synthesized mesoporous Nb-doped TiO₂ films from the assembly of pre-formed nanoparticles. Such inexpensive nanostructured transparent conductive oxides (TCO) were previously shown to improve the photovoltaic performance when applied as photo-anode in dye-sensitized solar cells (DSSCs).²⁷ Advantageously, an improved electrical conductivity combined with a controlled mesoporosity not only affects the application of titania-based electrodes in photovoltaics,²⁷ but also in photo-,²⁸ electro-catalysis²⁹ and charge storage.^30,31

Our theoretical studies suggest Nb to be the most promising dopant for improving the electrical conductivity of TiO₂. Even though there are several reports about the synthesis of high surface area Nb-doped TiO₂ nanomaterials with enhanced conductivities to date, inconsistent results regarding the exact influence of the dopant ion concentration on phase and electrical conductivity can be found.^31,32

Herein, we elucidate structure–property relationships based on calculated and experimental results to highlight the correlation between Nb-dopant fraction and electrical conductivity. Scheme 1 provides an overview on the proposed combined experimental and computational approach. In order to establish a model system with systematically varied properties, a composition series of Nb_xTi_1−xO₂ with Nb-fraction between 0 and 50 mol% was defined. The respective materials were synthesized via dip-coating because of its high reproducibility, control of layer thickness and atmosphere during deposition based on evaporation-induced self-assembly. Using such model-type oxides allows the deduction of structure–activity correlations, e.g. the impact of electrical conductivity on the electrocatalytic performance in the oxygen evolution reaction,^33,34 as well as fundamental phase formation and transition processes.³⁵ Herein, we modified a previously reported synthesis route²⁶ to obtain Nb-doped titania with controlled nanostructure. As precursors, TiCl₄ and NbCl₅ were dissolved in EtOH, leading to the formation of the corresponding metal ethoxides. A commercially available tri-block-copolymer, PEO–PPO–PEO (Pluronic F127), was used as soft-template for the introduction of mesoporosity after oxidative removal via calcination at 600 °C. The materials were analyzed via electron microscopy (SEM, TEM, EDX), X-ray diffraction (GI-XRD), Raman and impedance spectroscopy to derive physicochemical and electrical properties, in particular the formed crystal phases and the electrical conductivity. For the prediction of phase stability and electrical conductivity via DFT calculations, rutile and anatase supercells were proposed, in which Ti atoms were partially replaced by defined numbers of Nb atoms. As explained in the section Theoretical Calculations in the SI, the relative phase stabilities were calculated using VASP,^36–38 a high energy cut-off of 900 eV and the SCAN³⁹ functional. The electrical properties were calculated applying a self-consistent hybrid approach using CRYSTAL17^40,41 with pob-TZVP-rev2 basis sets^42,43 and the PW1PW⁴⁴ functional (see section Sheet conductivity in the SI for further explanations). Finally, experimental and theoretical values were compared. The maximum conductivity of the synthesized mesoporous films amounts to 0.0014 S cm⁻¹ at 25 °C for 35 mol% Nb in Nb_xTi_1−xO₂ after calcination of a stabilized mesophase at 600 °C in air. Theoretical calculations suggest a maximum in conductivity for 33 mol% Nb.

Scheme 1 Combined experimental and computational approach for the analysis of stable phases and electrical conductivity in model-type doped metal oxide systems. Synthesis route for mesoporous Nb_xTi_1−xO₂ films via dip-coating in a controlled atmosphere. The deposited micelle-structured mesophase is converted to a mesoporous Nb_xTi_1−xO₂ film after calcination and concomitant removal of the soft-template for 30 min at 600 °C in air. The computation method relies on two different approaches. Relative phase stabilities were calculated using VASP/900 eV/SCAN. For the calculation of the electrical properties, a self-consistent hybrid approach with CRYSTAL17/pob-TZVP-rev2/sc-PW1PW was used.

2. Results and discussion

2.1. Synthesis of mesoporous Nb_xTi_1−xO₂ films

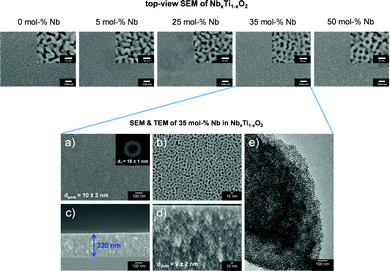
The synthesis route schematically illustrated in Scheme 1 affords mp. Nb_xTi_1−xO₂ materials with macroscopically crack-free, templated porosity extending throughout the entire film volume. Fig. 1 illustrates scanning electron microscopy (SEM) images of a concentration series of mp. Nb_xTi_1−xO₂ films. The dopant ion concentration can be precisely adjusted by the ratio of the metal precursors. Cross-sectional SEM images (see SI-1) reveal the formation of an interconnected pore network and layer thickness between 280 and 320 nm. There is no collapse of the micelle-templated mesoporous structure prior to the crystallization of the oxide materials. The organic block-copolymer template can be successfully removed via calcination for 30 min at 600 °C. Energy-dispersive X-ray spectroscopy (EDX) revealed the successful synthesis of mp. Nb_xTi_1−xO₂ materials with different Nb fractions (see SI-2). Notably, the incorporation of Nb atoms into the titania lattice stabilizes the morphology of the templated oxide films.

Fig. 1 Top: Electron microscopy of mesoporous Nb_xTi_1−xO₂ films. Bottom: Electron microscopy of a selected mesoporous film containing 35 mol% Nb; (a and b) Top-view SEM images at different magnifications with corresponding FFT (inset, a). (c and d) Cross-sectional SEM images at different magnifications. A film thickness of 320 nm was evaluated using ImageJ software (c). (e) TEM image clearly indicating the mesoporous structure.

As representative example, electron microscopic analysis of 35 mol% Nb in Nb_xTi_1−xO₂ is shown in more detail in Fig. 1. The average pore diameter amounts to 10 ± 2 nm (Fig. 1a) with a local order indicated by a periodic distance of 15 ± 1 nm (fast Fourier transform (FFT); inset Fig. 1a). Cross-section SEM (Fig. 1c and d) indicates a layer thickness of approximately 320 nm and the formation of a homogeneous mesoporous structure which is further corroborated by TEM images (Fig. 1e).

2.2. Relative phase stability rutile vs. anatase

Experimental results indicate a higher relative phase stability of the rutile phase for increasing Nb fractions >25 mol%, which is evidenced by gracing-incidence X-ray diffraction (GI-XRD) and Raman spectroscopy (see Fig. 2a and b). Due to the polycrystallinity and small crystallite size, broad reflexes were obtained for all Nb_xTi_1−xO₂ films (cf.Fig. 2a). For bare TiO₂, the metastable anatase phase is found in experiment. The diffraction pattern corresponds well to that for anatase TiO₂ and no reflections of rutile TiO₂ can be observed (Fig. 2a). With an increase in Nb fraction, the B_1g bands of the anatase phase shift to lower wavenumbers, as already observed by Yue et al.²¹ This can be explained by the formation of Nb–O–Ti bonds.^21,45 For Nb fractions ≥25 mol%, both Raman and GI-XRD indicate the coexistence of anatase and rutile phases, which is in excellent accordance with theory. For 35 mol%, the rutile phase becomes predominant (cf.Fig. 2a and b). A further increase in Nb fraction to 50 mol% leads to a significant decrease in crystallinity, as shown in the corresponding GI-XRD pattern. Raman spectroscopy suggests the predominance of the rutile phase, which, accordingly, is X-ray amorphous. X-ray photoelectron spectroscopy (XPS) was used to investigate the surface composition of the synthesized Nb_xTi_1−xO₂ materials. As shown in the results in SI-3, Nb atoms tend to segregate toward the surface of the nanocrystalline Nb_xTi_1−xO₂ materials. This surface-segregation is particularly pronounced for 35 mol% Nb in Nb_xTi_1−xO₂ and leads to an increase in the relative fraction of Ti³⁺ species compared to the other Nb_xTi_1−xO₂ materials. The stable phases predicted by the computation strongly depend on the dopant fraction, as shown in Fig. 2c. For small fractions <25 mol% Nb, the metastable anatase phase is favored, whereas for increasing Nb fractions, the rutile phase starts to emerge. For a fraction of 33 mol% Nb, the rutile phase is favored by 2.02 kJ mol⁻¹ over the anatase phase. Fig. 2d illustrates an overview over the obtained experimental and calculated results regarding phase stability in dependency of dopant fraction. Therein, a very high consistency between experiment and theory is indicated, validating our simplified theoretical DFT approach via VASP and SCAN functional (further information given in the Experimental section in the ESI†).

Fig. 2 Experimental GI-XRD patterns (a) and Raman spectra (b) of synthesized templated Nb_xTi_1−xO₂ films in dependency of Nb fraction. Calculated relative phase stabilities of rutile and anatase phase in dependency of Nb fraction (c). Clear indications for an ongoing phase transition from anatase to rutile for Nb >25 mol% in Nb_xTi_1−xO₂ are given in both experimental and theoretical data in (a–c). In (b), calculated active Raman modes for the rutile (orange) and anatase (grey) phase are illustrated as vertical bars (absolute values are given in SI-5). The dotted grey line in (c) represents a guideline to the eye. In (d), an overview over experimentally observed and theoretically calculated phases is given, revealing good consistency of experiment and theory (A = anatase, R = rutile, A/R = mixed phase of anatase and rutile, am. = X-ray amorphous).

2.3. Impact of Nb fraction on electrical properties of Nb_xTi_1−xO₂

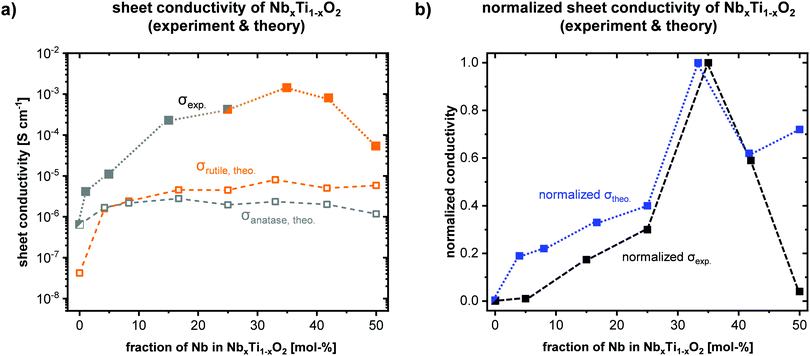
Significant variations in the electronic properties are expected considering the distinct structural differences for an increasing fraction of Nb. Both theoretical and experimental results show a strong correlation of phase and electrical conductivity of the doped transition metal oxides. A clear trend can be deduced from the data shown in Fig. 3. Bare TiO₂ shows the lowest electrical sheet conductivity (Fig. 3a). Up to a fraction of 35 mol% Nb in Nb_xTi_1−xO₂, an increase in conductivity of more than three orders of magnitude was experimentally determined, which is in agreement with theoretical calculations based on a substitutional incorporation of Nb ions into the titania lattice. A detailed discussion for the general trend from a theoretical point of view is given in SI-9. Mulliken population analyses reveal an increasing occupation of Ti 3d-orbitals, in particular 3d_z², 3d_x²−y² and 3d_xy, for increasing Nb-fraction (cf.SI-9). For a high fraction of 50 mol% Nb, a decreased sheet conductivity was observed, which can be explained by the lower crystallinity and the formation of a solid solution rather than a doped titanium oxide (cf.Fig. 2a; SI-4). Accordingly, the crystal phase shows a pronounced impact on the electronic properties and a high material's crystallinity is of pivotal importance for high electrical conductivities.

Fig. 3 Calculated and experimental electrical sheet conductivities in dependency of Nb fraction in mp. Nb_xTi_1−xO₂ films (filled squares: experimentally determined sheet conductivities via impedance spectroscopy, open grey squares: calculated values for anatase, open orange squares: calculated values for rutile) (a); normalized calculated and experimental conductivities as function of Nb fraction (b). All values in (a) are given in S cm⁻¹. To ensure comparability between theory and experiment, the calculated conductivity of the bare anatase was set to the experimentally determined sheet conductivity of 6.40·10⁻⁷ S cm⁻¹ and all calculated conductivities are stated relative to this value. The absolute values of the calculated conductivities are given in SI-6. The color code for the experimental data in (a) represents an indication of the respective phase.

Notably, the mesoporous structure is kept intact at high temperatures up to 600 °C, i.e. the incorporation of Nb ions into the titania lattice has a beneficial impact on the morphological stability of the porous network. For bare titania, crystallite growth and sintering effects become pronounced at high temperatures, leading to a loss of templated pore structure. Comparing the experimentally determined values with the theoretical data calculated applying a self-consistent hybrid approach (for further details see section Sheet conductivity in the SI), the impact of Nb fraction on conductivity is well in line. A maximum conductivity is predicted for a fraction of 33 mol% Nb and rutile phase. The correlation between high crystallinity and electrical conductivity becomes evident for high fractions of 50 mol% Nb. Experimental results show a significantly reduced conductivity compared to theoretical calculations assuming high crystallinity at high Nb fractions up to 50 mol%. In this context, the deviation between experiment and theory for large Nb fractions of 50 mol% (cf.Fig. 3a and b) can be explained by the differences in crystallinity. For fractions ≤42 mol% Nb, consistent results between experimental and theoretical conductivities were obtained.

The herein obtained values of more than 10⁻³ S cm⁻¹ for mp. Nb_xTi_1−xO₂ with 35 mol% Nb are, to the best of our knowledge, the highest electrical sheet conductivities for mesoporous early-transition-metal doped TiO₂ films. It has to be noted that grain boundaries and the mesoporous structure decrease the electrical conductivity of a material. Similar observations were previously reported by Liu et al.¹⁹ who assembled pre-synthesized nanoparticles into mesoporous films via dip-coating. Compared to their study showing a maximum in sheet conductivity of 3 × 10⁻⁴ S cm⁻¹ for a fraction of 20 mol%, our results suggest a maximum electrical conductivity for a higher Nb fraction of 35 mol%. Liu et al. found decreased conductivity values for Nb fractions of more than 20 mol%. Importantly, no observations of an emerging rutile phase for higher Nb fractions were reported. A more detailed discussion and comparison with previous reports in literature can be found in SI-3 in the ESI.† Even though the herein presented DFT results exclusively refer to the bulk properties of the doped oxides, the theoretical calculations coincide well with the observed trends in both relative conductivity and relative phase stability without any consideration of (meso-)porosity in the theoretical models. The high crystallinity of the oxides, the independence of the pore size and the interface with insulating air filling the pores underline the dominance of bulk properties (for further explanations see SI-10). The herein presented system enables a systematic investigation of structure–property relations. For small fractions of Nb dopants (<10 mol%), theoretical calculations suggest a stronger increase in electrical conductivity (cf.Fig. 3b), yet, the general trend is in good agreement. Particularly, the theoretically predicted maximum in conductivity was corroborated by our experimental data and our calculations provide reasonable explanations for the observed behavior, e.g. the highest electrical conductivity resulting from a combination of increasing electron density while avoiding Nb–Nb interactions, which can be deduced from quantum chemical calculations (see SI-9).

3. Conclusions

The herein presented combined experimental and computational approach for the analysis of stable phases and electrical conductivity in model-type doped metal oxide systems synthesized via template-assisted dip-coating highlights the most relevant factors to tune the electrical properties of a semiconducting material. As a model system, the impact of Nb fraction on the phase, crystallinity and electrical conductivity of mesoporous titanium oxide films was experimentally and theoretically investigated. Advantageously, the herein presented synthesis concept enables a detailed investigation by the variation of a single parameter, i.e. doping concentration. A profound understanding of the correlations between doping concentration, phase stability and electronic properties lead to the synthesis of a high surface area support material which can find promising applications in electro- or photo-catalysis, in which high electrical conductivities and stability are key factors for achieving a superior performance. Importantly, our model system is not limited to Nb-doped titania, but can also be extended to other dopants such as Y³⁺, for instance. As such, a new highly effective screening method is presented which may help to identify suitable materials for applications in electro- or photo-(electro-)catalysis.

Author contributions

M. Frisch* and J. Laun* contributed equally to this work. M. F. contributed to all experimental aspects of data analysis and interpretation. J. L. contributed to all theoretical aspects, simulations and interpretation of the calculated data. M. F. & J. L. contributed to the writing and editing of the manuscript. J. M. performed Raman spectroscopic measurements and evaluated the data. A. A., D. B. and M. B. aided in the design of synthesis protocols of the templated mesoporous films. A. A. contributed to GI-XRD analyses. K. B. contributed to the calculations of relative phase stability and Raman spectra. T. B. & R. K. conceived the study, contributed to the writing and editing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank ZELMI (TU Berlin) for access to TEM and SAED analyses and gratefully acknowledge financial support by BMBF (Bundesministerium für Bildung und Forschung) ATO-KAT: Atomar dünn beschichtete poröse Elektroden als neuartige Katalysatoren für die Wasser-Elektrolyse (03EK3052A). Jörg Radnik (BAM, Berlin) is thankfully acknowledged for XPS analyses. The authors acknowledge also preliminary tests by Paulina Kalle at TU Berlin and the support of Benjamin Paul (TU Berlin) in the building of a setup for impedance spectroscopy measurements of thin films in the dark.

Notes and references

1. A. Fujishima, X. Zhang and D. Tryk, Surf. Sci. Rep., 2008, 63, 515–582.
2. S.-Y. Lee and S.-J. Park, J. Ind. Eng. Chem., 2013, 19, 1761–1769.
3. J. M. Macak, P. J. Barczuk, H. Tsuchiya, M. Z. Nowakowska, A. Ghicov, M. Chojak, S. Bauer, S. Virtanen, P. J. Kulesza and P. Schmuki, Electrochem. Commun., 2005, 7, 1417–1422.
4. S. Shanmugam and A. Gedanken, Small, 2007, 3, 1189–1193.
5. H.-J. Kim, D.-Y. Kim, H. Han and Y.-G. Shul, J. Power Sources, 2006, 159, 484–490.
6. W. M. Campbell, A. K. Burrell, D. L. Officer and K. W. Jolley, Coord. Chem. Rev., 2004, 248, 1363–1379.
7. H.-M. Lin, C.-H. Keng and C.-Y. Tung, Nanostruct. Mater., 1997, 9, 747–750.
8. M. Ni, M. K. H. Leung, D. Y. C. Leung and K. Sumathy, Renewable Sustainable Energy Rev., 2007, 11, 401–425.
9. R. W. Matthews, Sol. Energy, 1987, 38, 405–413.
10. Z.-X. Lu, Y. Shi, C.-F. Yan, C.-Q. Guo and Z.-D. Wang, Int. J. Hydrogen Energy, 2017, 42, 3572–3578.
11. W. Yan and X. Liu, Inorg. Chem., 2019, 58, 3090–3098.
12. S. C. Pillai, P. Periyat, R. George, D. E. McCormack, M. K. Seery, H. Hayden, J. Colreavy, D. Corr and S. J. Hinder, J. Phys. Chem. C, 2007, 111, 1605–1611.
13. K. Lv, J. Yu, L. Cui, S. Chen and M. Li, J. Alloys Compd., 2011, 509, 4557–4562.
14. A. Di Paola, M. Bellardita and L. Palmisano, Catalysts, 2013, 3, 36–73.
15. M. V. Dozzi and E. Selli, J. Photochem. Photobiol., C, 2013, 14, 13–28.
16. G. Liu, Y. Zhao, C. Sun, F. Li, G. Q. Lu and H.-M. Cheng, Angew. Chem., Int. Ed., 2008, 47, 4516–4520.
17. L. Kong, C. Wang, H. Zheng, X. Zhang and Y. Liu, J. Phys. Chem. C, 2015, 119, 16623–16632.
18. M. S. Dabney, M. F. A. M. van Hest, C. W. Teplin, S. P. Arenkiel, J. D. Perkins and D. S. Ginley, Thin Solid Films, 2008, 516, 4133–4138.
19. Y. Liu, J. M. Szeifert, J. M. Feckl, B. Mandlmeier, J. Rathousky, O. Hayden, D. Fattakhova-Rohlfing and T. Bein, ACS Nano, 2010, 4, 5373–5381.
20. F. Hu, F. Ding, S. Song and P. K. Shen, J. Power Sources, 2006, 163, 415–419.
21. J. Yue, C. Suchomski, P. Voepel, R. Ellinghaus, M. Rohnke, T. Leichtweiss, M. T. Elm and B. M. Smarsly, J. Mater. Chem. A, 2017, 5, 1978–1988.
22. M. Vallet-Regí, F. Balas and D. Arcos, Angew. Chem., Int. Ed., 2007, 46, 7548–7558.
23. J. Kärger and D. Freude, Chem. Eng. Technol., 2002, 25, 769–778.
24. X. Fan, X. Chen, S. Zhu, Z. Li, T. Yu, J. Ye and Z. Zou, J. Mol. Catal. A: Chem., 2008, 284, 155–160.
25. J. B. Yin and X. P. Zhao, Chem. Mater., 2002, 14, 4633–4640.
26. E. Ortel, A. Fischer, L. Chuenchom, J. Polte, F. Emmerling, B. Smarsly and R. Kraehnert, Small, 2012, 8, 298–309.
27. X. Lü, X. Mou, J. Wu, D. Zhang, L. Zhang, F. Huang, F. Xu and S. Huang, Adv. Funct. Mater., 2010, 20, 509–515.
28. H. Liu, H. Gong, M. Zou, H. Jiang, R. S. Abolaji, A. K. Tareen, B. V. Hakala and M. Yang, Mater. Res. Bull., 2017, 96, 10–17.
29. L. Chevallier, A. Bauer, S. Cavaliere, R. Hui, J. Rozière and D. J. Jones, ACS Appl. Mater. Interfaces, 2012, 4, 1752–1759.
30. Y. Tanaka, H. Usui, Y. Domi, M. Ohtani, K. Kobiro and H. Sakaguchi, ACS Appl. Energy Mater., 2019, 2, 636–643.
31. Y. Wang, B. M. Smarsly and I. Djerdj, Chem. Mater., 2010, 22, 6624–6631.
32. C. Hao, H. Lv, C. Mi, Y. Song and J. Ma, ACS Sustainable Chem. Eng., 2016, 4, 746–756.
33. M. Bernicke, D. Bernsmeier, B. Paul, R. Schmack, A. Bergmann, P. Strasser, E. Ortel and R. Kraehnert, J. Catal., 2019, 376, 209–218.
34. M. Bernicke, E. Ortel, T. Reier, A. Bergmann, J. Ferreira de Araujo, P. Strasser and R. Kraehnert, ChemSusChem, 2015, 8, 1908–1915.
35. K. Schulz, R. Schmack, H. W. Klemm, A. Kabelitz, T. Schmidt, F. Emmerling and R. Kraehnert, Chem. Mater., 2017, 29, 1724–1734.
36. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
37. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
38. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
39. J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
40. R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 1360.
41. S. C. R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D’Arco, M. Llunell, M. Causà, Y. Noël, L. Maschio, A. Erba and M. Rerat, CRYSTAL17 User's Manual, University of Torino, 2017.
42. D. Vilela Oliveira, J. Laun, M. F. Peintinger and T. Bredow, J. Comput. Chem., 2019, 40, 2364–2376.
43. J. Laun, D. Vilela Oliveira and T. Bredow, J. Comput. Chem., 2018, 39, 1285–1290.
44. T. Bredow and A. R. Gerson, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 5194–5201.
45. L. De Trizio, R. Buonsanti, A. M. Schimpf, A. Llordes, D. R. Gamelin, R. Simonutti and D. J. Milliron, Chem. Mater., 2013, 25, 3383–3390.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp06544g

‡ M. Frisch and J. Laun contributed equally to this work.

---