Cooperativity in micellar solubilization
Received
15th December 2020
, Accepted 12th March 2021
First published on 30th March 2021
Abstract
Sudden onset of solubilization is observed widely around or below the critical micelle concentration (CMC) of surfactants. It has also been reported that micellization is induced by the solutes even below CMC and the solubilized solute increases the aggregation number of the surfactant. These observations suggest enhanced cooperativity in micellization upon solubilization. Recently, we have developed a rigorous statistical thermodynamic theory of cooperative solubilization. Its application to hydrotropy revealed the mechanism of cooperative hydrotropy: hydrotrope self-association enhanced by solutes. Here we generalize our previous cooperative solubilization theory to surfactants. We have shown that the well-known experimental observations, such as the reduction of CMC in the presence of the solutes and the increase of aggregation number, are the manifestations of cooperative solubilization. Thus, the surfactant self-association enhanced by a solute is the driving force of cooperativity and a part of a universal cooperative solubilization mechanism common to hydrotropes and surfactants at low concentrations.
1. Introduction
Low solubility is a major hindrance to formulation processes.1 Adding cosolvents, hydrotropes2–4 and surfactants4–11 can dramatically increase solubility. Traditionally, solubilization by hydrotropes, which are mainly short amphiphilic molecules that do not form micelles, was attributed to hydrotrope self-association based on an analogy between the minimum hydrotrope concentration (MHC, the onset of solubilization) and the critical micelle concentration (CMC).12,13 However, our rigorous statistical thermodynamic approach has shown that bulk-phase hydrotrope self-association reduces solubilization efficiency, contrary to the traditional hypothesis.14,15 The non-specific accumulation of hydrotropes around a solute was identified as the driving force for solubilization,4,14–16 and the enhancement of hydrotrope association around a solute as the origin of MHC.11,17–19 This mechanism has been confirmed directly by experiments.20
This new view of hydrotropy necessitates a renewed look at solubilization by surfactants. Since our statistical thermodynamic approach to hydrotropy made no assumptions other than the basic principles of statistical thermodynamics,21–24 it should apply to surfactants as well. However, micellar solubilization uses a different theoretical framework, such as the molar solubilization ratio and micelle-water partition coefficient,8,10 to quantify solubilization. A statistical thermodynamic interpretation of these quantities has been established.25,26 However, despite our previous attempts,4,11,25–27 there is still a significant gap between the two different approaches.
The remaining gap is the mechanism of cooperative solubilization by surfactants. Here, cooperative solubilization refers to the effects of solubilized solutes to enhance the cooperativity in micellization, such as the solute-induced micellization below CMC and the increase of the aggregation number. Sudden, sharp onset of solubilization at CMC has been observed very commonly,5,7,8,10,28 yet no statistical thermodynamic approach to cooperative solubilization was available before ours.4,11,17–19 This article aims to reveal the mechanisms of cooperative solubilization by surfactants, namely, the interactions that give rise to the initial onset of solubility increase at low surfactant concentrations.
Previously, we have identified the following solubilization mechanisms for hydrotropes:4,11,17,19,27
(1) the accumulation of solubilizer around a solute and
(2) solubilizer self-association enhanced by a solute at the onset of solubilization.
In this paper, we will show that (1) and (2) manifest also in micellar solubilization through the following scenarios:
I. association of solutes with micelles;
II. increase in surfactant aggregation number;
III. induced micellization by solutes below CMC
All I–III have been reported widely in the surfactant literature.5,7,8 They will be shown to drive cooperative solubilization as the micellar counterpart of (1) and (2) for hydrotropes.
Although we describe a universal mechanism for the solubilization phenomena around CMC, we are not suggesting that its application is universal. For example, our focus on equilibrium (phase) solubility means that the pathways of the solubilization process in a kinetic sense29–33 are out of the scope of this paper. And we make no attempt here to describe the complexities of the phenomena relating to microemulsions with their large solubilization capacities that are associated with especially low interfacial tensions and complex curvature behaviour in domains of formulation space above a larger critical microemulsion concentration (or the second CMC)34–36 and, typically, in the presence of larger amounts of solutes/oils.37–43
Rather the contrast is with other approaches in the conventional domain around CMC, such as continuum44,45 or activity models.46 Although these models can successfully predict the micelle-water partition coefficient of solutes,47 neither can capture the change of solution structure responsible for solubilization. Our aim, therefore, is to understand the cooperative solubilization on a molecular basis, taking advantage of the assumption-free, model-free and rigorous foundation.
2. Fluctuation theory for solubilization by surfactants
Let us first generalize our statistical thermodynamics of solubilization, which was limited previously to dilute solutes,4,14–16,48 to any solute concentrations. Consider a mixture consisting of water (species 1) and solubilizer (species 2). The “solubilizer” includes cosolvents, hydrotropes, and surfactants. Our central question is twofold: (i) how the solubility cu of solute (species u) depends on solubilizer concentration, c2, and (ii) what the mechanism of solubilization is on a microscopic basis. From the principles of classical statistical thermodynamics alone, the following relationship can be derived for any solute concentrations (Appendix A) under phase equilibrium for solutes| | 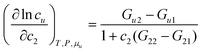 | (2.1a) |
where Gij is Kirkwood–Buff integral14–16 between the species i and j defined in terms of the correlation between Ni (the number of species i) and Nj (of species j), as| | 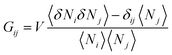 | (2.1b) |
where V is the volume and 〈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉 signifies an ensemble average and the deviation δNi = Ni − 〈Ni〉 was introduced. Note that the right-hand side of eqn (2.1a) was previously derived at cu → 0,14–16 which has now been generalized to finite solute concentrations in Appendices A and B. This means our previous analyses of hydrotropy4,14–16,48 and the entrainer effect in supercritical CO249 were limited to dilute solutes simply because G21 and G22 were calculated using the physical properties of binary solutions.
〉 signifies an ensemble average and the deviation δNi = Ni − 〈Ni〉 was introduced. Note that the right-hand side of eqn (2.1a) was previously derived at cu → 0,14–16 which has now been generalized to finite solute concentrations in Appendices A and B. This means our previous analyses of hydrotropy4,14–16,48 and the entrainer effect in supercritical CO249 were limited to dilute solutes simply because G21 and G22 were calculated using the physical properties of binary solutions.
Based on our eqn (2.1), we can generalize our previous conclusion: solubilization is driven by the preferential solute-solubilizer interaction (over solute–water interaction), Gu2 − Gu1, but its efficacy is reduced by the self-association of solubilizer, G22 − G21. Here, G22 − G21 in a ternary mixture (water-solubilizer-solute) must be used, rather than that in the bulk solvent.4,14–16,48 (Note: see Appendix B for the difference between G22 and Gu,22, the driving force of cooperative solubilization.11,17,19)
Now we apply eqn (2.1) to surfactants. The focus of this paper is to understand the onset of solubilization at low surfactant concentration around the CMC, which has been commonly observed.5,7,8,10,28 Previously, the efficacy reduction for surfactants was shown to be negligible based on the order of magnitude analysis, namely, 1 + c2(G22 − G21) ≃ 1; the magnitude of micelle–micelle co-volume, which makes G22 large and negative, cannot override the low micelle concentration c2 in eqn (2.1a).11 This is equivalent to the common practice of adopting the dilute ideal activity coefficient for surfactants.8,50,51 Furthermore, Gu1 in eqn (2.1a), which can be calculated from the partial molar volume of the solute, is shown to be negligible compared to Gu2.11 Combining all above, we obtain
| | 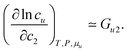 | (2.2) |
Here, it is useful to have several different perspectives at hand to interpret experiments by eqn (2.1). In addition to the Kirkwood–Buff integrals,14–16 the excess number and number correlation will also be useful in surfactant solubilization, through which eqn (2.2) can be rewritten as
| |  | (2.3a) |
where
Nij is the excess number of
j around
i. There are two equivalent definitions of the excess number, both of which will be useful. The first is the solute–surfactant number correlation, defined in terms of
Nu (the number of solutes) and
N2 (of surfactants), as
| | 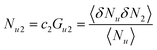 | (2.3b) |
The excess number is thus the solute–surfactant number correlation per solute, 〈
δNuδN2〉/〈
Nu〉. The second definition of
Nu2,
via the inhomogeneous solvation theory,
11,52,53 is the increment of surfactant number induced by a probe solute,
| | 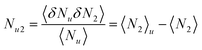 | (2.3c) |
namely, the excess number
Nu2 is the difference between 〈
N2〉
u (the number of surfactants in the presence of a solute molecule fixed at the origin) and 〈
N2〉 (the number of surfactants in the bulk with the same volume).
11,17,19 (Note that there may be more solutes in the system other than the probe solute.) Such an increment in the number of surfactants comes from the vicinity of the probe solute.
54 Therefore, a local subsystem around a probe solute, which is large enough to contain all the surfactant number increment, is a convenient tool.
54 Therefore,
| | | Nu2 = 〈N2〉u − 〈N2〉 = 〈n2〉u − 〈n2〉 | (2.3d) |
where
n2 is the number of surfactants in the local subsystem. Thus, we have established a link between solubilization and solute–surfactant correlation (or the excess number of surfactants)
viaeqn (2.3d). We emphasize that the solute–solute correlation is absent in
eqn (2.3a), because of the equilibrium condition for solute dissolution (
i.e., under constant
μu). See Appendix A for details.
The theory of solubilization presented here is based directly on the principles of statistical thermodynamics and involves no model assumptions. It is valid at any solute concentrations. Indeed, the statistical thermodynamic foundation presented in our previous papers for a dilute solute in a two-component mixture11,17,19,55 can be generalized without any modifications, except for changing a “two-component mixture” to a “three-component mixture” in specifying the ensemble, as shown in Appendix C. We have introduced the solute–surfactant number correlation and the surfactant number increment in a local subsystem around a probe solute as the tools to interpret experimental data.
3. Mechanism of micellar solubilization around CMC
Here we analyze the conventional measures of solubilization by surfactants based on our general statistical thermodynamic theory. The molar solubilization ratio, κ,7,8,10 defined as| | | cu = c0u + κ(c2 − ccmc2) | (3.1a) |
where cu is the solubility of the solute and c0u is that at CMC (ccmc2).10,56,57 The solute's partition coefficient between micelle and water, KM, has been introduced in the context of rewriting eqn (3.1a) as4,25| |  | (3.1b) |
We have already enumerated the problems arising from interpreting KM as though it were a partition coefficient between bulk water and the micelle pseudo phase, especially in light of the multiplicity of solubilization location.4,58 The true microscopic interpretation of KM can be obtained by the help of statistical thermodynamics. Combining eqn (2.3) and (3.1b), we obtain25| |  | (3.2a) |
Eqn (3.2) establishes a link between KM and solute–surfactant excess number. Assuming KM as a constant, we obtain the following clear interpretation for KM:However, note that the values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KM vary between 1 to 7,47,59,60 hence, at typical c2 used for solubilization (i.e., ∼101 mM) neither KM(c2 − ccmc2) nor 1 is negligible in the denominator of eqn (3.2a). Combining eqn (3.2a) with eqn (2.3c), we obtain,
KM vary between 1 to 7,47,59,60 hence, at typical c2 used for solubilization (i.e., ∼101 mM) neither KM(c2 − ccmc2) nor 1 is negligible in the denominator of eqn (3.2a). Combining eqn (3.2a) with eqn (2.3c), we obtain,| | 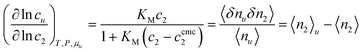 | (3.3) |
which will be used as the basis of our discussion.
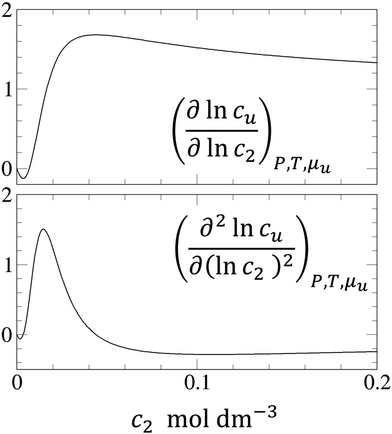
In principle, a substance added to water can either increase or decrease the solubility of the solute. These cases correspond to the signs of KM. and Nu2. Here, the added substance is called “solubilizer” when it facilitates the dissolution of the solute with KM > 0 and Nu2 > 0. It was noted in Appendix A of ref. 26 that KM can be considered a partition coefficient when KM > 0 and the spatial integral constituting Nu2 or Gu2 converges within the region occupied by the micellar aggregates. If the solubilizer does not form distinct aggregates, the pseudophase model cannot be adopted for KM. Still, eqn (3.2) is an exact expression and is applicable even when the formation of distinct aggregates is not observed or further when KM < 0, which, in fact, means that the dissolution of the solute is suppressed by the added substance. What eqn (3.3) signifies can be illustrated in Fig. 1, which shows the change of naphthalene solubility (cu) with the concentration of sodium cholate (c2) measured by Mukerjee and Cardinal.61 Note that there is an onset of solubilization. We have calculated its gradient, 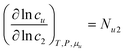 , by fitting the experimental data to a function (see Appendix D). Fig. 2 shows a drastic increase in Nu2 is seen at low c2. The larger the Nu2 value, the more significant the solubilization.
, by fitting the experimental data to a function (see Appendix D). Fig. 2 shows a drastic increase in Nu2 is seen at low c2. The larger the Nu2 value, the more significant the solubilization.
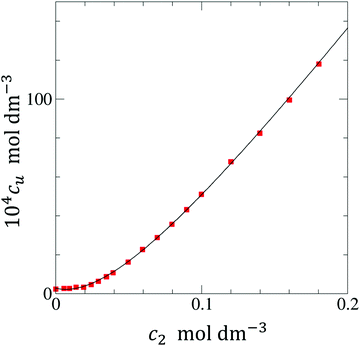 |
| | Fig. 1 The experimental solubility (red square) of naphthalene (104cu) against sodium cholate concentration (c2) taken from Mukerjee and Cardinal.61 The fitting function and parameters are given in Appendix D. | |
 |
| | Fig. 2
 (top) and (top) and 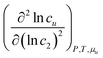 (bottom) calculated from the fitting function (Appendix D) of naphthalene solubilization by sodium cholate shown in Fig. 1.61 (bottom) calculated from the fitting function (Appendix D) of naphthalene solubilization by sodium cholate shown in Fig. 1.61 | |
Now we clarify the factors contributing to micellar solubilization based on eqn (3.3). Regardless of the location of solutes, solutes and surfactants associate.5,8,50,62 This can be viewed as the increment in the number of surfactants in the local subsystem 〈n2〉u compared to the bulk 〈n2〉 or as a strong number correlation between solute and surfactants 〈δnuδn2〉 in eqn (3.3). The latter perspective is particularly useful in view of multiple solutes being contained within a micelle.59,60
When the local subsystem is introduced for the micellar region, n2 corresponds to the aggregation number. Consequently, the positive Nu2 or KM means that the aggregation number is increased around the fixed solute. According to eqn (3.3), a sudden increase of cu at a certain c2 is related to the enhancement of the aggregation number or micellar size at that c2. It has long been known that a solute, or often called a solubilizate, “usually increases the sizes of micelles not only by the incorporation of the solubilizate itself but also by causing an increase in the average number of surfactant molecules in the micelles”.5 Indeed, the sphere-to-rod transition is often induced by solutes,5,62,63 and the solubilization of the molecules promotes the axial growth of the micelles,7 with a subsequent doubling in solubilization power.64,65 These classical observations agree, for example, with a static light scattering of the solubilized bis-diazo dye by TTAB;66 a 30- to 50-fold increase in the TTAB aggregation number was observed when the dye was solubilized,66 consistent with increased viscosity.5,66 Indomethacin, when solubilized by polysorbate 80 in water-sorbitol mixtures, increased micellar weight due not only to indomethacin inclusion but also to increased aggregation number.67
Solubilization of aliphatic hydrocarbon by rod-like micelles, in particular, has been challenging to understand in relation to the change of micellar size and shape.68 A shortening of the rod with a minor change in aggregation number has been observed at low solute concentration.43,69,70 In this case, the location of hydrocarbon solutes at the micellar core43,68–71 gives rise to a large solute–surfactant correlation function, leading to a large Gu2 and leads viaeqn (2.3b) to solubilization.
Thus, the solute-induced increase in micellar size, viewed with our statistical thermodynamic foundation, is an important factor for solubilization. This is consistent with greater stability of larger micelles when solutes are incorporated into micelles5,72 and also with increased solubilization, in the presence of salts, by ionic surfactants, in which an increase of micelle size is observed with the enhanced solubilization effect.8,10 Our statistical thermodynamic theory can also rationalize the solubilization of aliphatic solutes by rod-like micelles. Statistical thermodynamics has identified the mechanism of solubilization: micelle-solute interaction and the change of micellar size and stability caused by solutes.
4. Cooperative solubilization and CMC reduction by solutes
A sharp increase in the solubility of hydrophobic solutes has been observed frequently around CMC5,7,8,10 and sometimes below CMC.5,73,74 Such cooperative solubilization has been considered to be related to the micellization process.5 This kind of cooperativity is usually treated in connection to the equilibrium of association (micellization). A more general framework needs to be established, though, to examine the hydrotropic actions in a unified manner, including those that do not exhibit sharp transitions to association states. We have recently established a rigorous statistical thermodynamic theory of cooperative solubilization11,17 and also developed a model to reproduce a sigmoidal solubility curve.18 We have applied these theories successfully to hydrotropic solubilization, yet the theory, being general, is not restricted to hydrotropes; it can be applied to micelles as well. Here we show that the enhanced micellization by solutes, which has long been observed,5,7,73,75–77 is closely connected to the cooperative solubilization by micelles.
To this end, how solute-solubilizer correlation depends on solubilizer activity plays a key role.11,17 Using only the fundamental principles of statistical thermodynamics,11,17 the following formula, derived previously at cu → 0, can be generalized to any solute concentrations (Appendix B):
| | 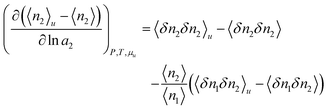 | (4.1) |
Now we simplify eqn (4.1) using surfactant-specific experimental conditions. Firstly, surfactant concentration is much lower than water, i.e., 〈n2〉 ≪ 〈n1〉, which means that the second term of eqn (4.1) is negligible. Secondly, due to the dilute ideal solution condition for surfactants,8 which has been justified also from the fluctuation theory,11 we can replace the derivative by ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a2 with ln
a2 with ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c2. Under these conditions, eqn (2.3) and (4.1) can be combined to yield
c2. Under these conditions, eqn (2.3) and (4.1) can be combined to yield
| | 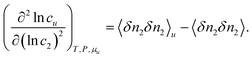 | (4.2a) |
where the right-hand side of
eqn (4.2a) signifies the increase of surfactant-surfactant correlation which accompanies the introduction of a fixed probe solute molecule, namely from the value in the bulk solution 〈
δn2δn2〉 to that in the inhomogeneous solution 〈
δn2δn2〉
u. Using the relationship between inhomogeneous and homogeneous ensemble averages,

, where
X is a physical quantity,
52,53,78 we can express
eqn (4.2a) also as
| | 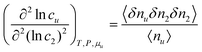 | (4.2b) |
where 〈
δnuδn2δn2〉 is the solute–surfactant–surfactant number correlation.
The interpretation of eqn (4.2) can be illustrated again by the solubilization of naphthalene by sodium cholate.61 Around the sudden onset of solubilization, a peak of the second-order derivative, 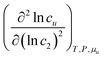 , is observed in Fig. 2. According to eqn (4.2), this peak is caused by the enhanced surfactant-surfactant number fluctuation in the presence of a solute 〈δn2δn2〉u compared to that in the bulk phase 〈δn2δn2〉. Even though the precise location of the peak is dependent sensitively on the fitting function, the peak at c2 = 1.5 × 10−2 M is consistent with one of the “apparent CMC” values (1.6 × 10−2 M) estimated by Mukerjee and Cardinal from the same solubilization data as in Fig. 1.61
, is observed in Fig. 2. According to eqn (4.2), this peak is caused by the enhanced surfactant-surfactant number fluctuation in the presence of a solute 〈δn2δn2〉u compared to that in the bulk phase 〈δn2δn2〉. Even though the precise location of the peak is dependent sensitively on the fitting function, the peak at c2 = 1.5 × 10−2 M is consistent with one of the “apparent CMC” values (1.6 × 10−2 M) estimated by Mukerjee and Cardinal from the same solubilization data as in Fig. 1.61
The physical meaning of eqn (4.2) becomes clearer viaeqn (2.1b), applied to both inhomogeneous and homogeneous local subsystems,11,17,54 as
| |  | (4.3) |
where
Gu,22 is the surfactant-surfactant Kirkwood–Buff integral in the presence of a probe solute and
v is the volume of the local subsystem.
11,17,54 The right-hand side of
eqn (4.3) signifies the increase in the self-association of the species 2 (in this case, surfactant) induced by a probe solute.
11,17,54 Thus, a sharp peak of

indicates the enhancement of surfactant self-association and micellization.
This statistical thermodynamic scenario is consistent with the well-known observations in surfactant science since the 1940s. The CMCs measured via solubilized probe dyes tend to be lower than the values from other methods.75 Such a discrepancy was attributed to micelle formation below CMC induced by the probe dye,73 which has been confirmed in many systems.5,7,76,77,79 This is equivalent to the onset of solubilization lower than the bulk-phase CMC74 from a perspective of the cooperative solubilization theory (eqn (4.2) and (4.3)). In a wider context, hydrophobic molecules, when added to surfactants, are observed to reduce CMC.8,80–82 How CMC depends on solute concentration has been measured and compiled.79 Assisted by thermodynamics, such a measurement has become one of the standard approaches to calculating the micelle-water partition coefficient.7,79 Thus, the evidence abounds for the enhancement of micellization by solutes being the driving force for the cooperative onset of solubilization at CMC.
The enhancement of solubilizer self-association by solutes is a mechanism common to solubilization by hydrotropes and surfactants alike. The sub-CMC solubilization of hydrophobic solutes by surfactants83,84 also exhibits a sudden onset of solubilization with the appearance of large aggregates,83,84 consistent with the cooperative hydrotropy theory.11,17–19 Note that “enhancement” does not exclude the possibility of surfactant-surfactant interaction in pre-existing micelles; the key is its enhancement around a solute molecule. Thus, the enhancement of aggregation by solutes seems to be a universal statistical thermodynamic mechanism of cooperative solubilization onset at low concentrations.
5. Connection to micellization models
Here we present simple thermodynamic approaches to illustrate how the experimental observations, such as an increase of micellar size around a solute (Section 3) and the reduction of CMC or the “induced micellization”5,73 (Section 4), contribute to cooperative solubilization. The theory presented in Sections 2–4 is general and rigorous and without any assumptions. Here, in contrast, we introduce some model assumptions, such as (i) monomer–micelle equilibrium and (ii) micellization as complex formation. Note that these assumptions are introduced at the cost of the Kirkwood–Buff integrals with the exceptions of the simplest cases.
Monomer–micelle equilibrium
We assume that a surfactant takes two different states: monomeric and micellar states,8,51,85–88 denoted here by mon and mic. Under the equilibrium condition μmon2 = μmic2 = μ2, the molarity-based equilibrium constant,  , can be introduced statistical thermodynamically89 without any assumptions on the activity coefficient (Appendix E). This model can be applied in two different ways. The first case considers the effect of surfactants on phase solubility, i.e., dμu = 0. Under this condition, the surfactant-surfactant Kirkwood–Buff integrals in the monomeric and micellar states, Gmon22 and Gmic22 can be introduced (Appendix E). How solubility depends on surfactant chemical potential, μ2, can then be expressed as
, can be introduced statistical thermodynamically89 without any assumptions on the activity coefficient (Appendix E). This model can be applied in two different ways. The first case considers the effect of surfactants on phase solubility, i.e., dμu = 0. Under this condition, the surfactant-surfactant Kirkwood–Buff integrals in the monomeric and micellar states, Gmon22 and Gmic22 can be introduced (Appendix E). How solubility depends on surfactant chemical potential, μ2, can then be expressed as| | 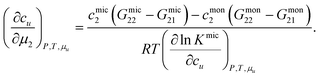 | (5.1) |
Noting that since μ2 increases with surfactant concentration, the solubility cu increases with the surfactant concentration when (i) the self-association in the micellar state is stronger than in the monomeric state, i.e., cmic2(Gmic22 − Gmic21) > cmon2(Gmon22 − Gmon21), and simultaneously that (ii) solute induces micellization, i.e.,  .
.
The second case considers when a small quantity of solutes is added to the surfactant solution (without the phase equilibrium for solutes). In this case, we can introduce the change of solute–surfactant Kirkwood–Buff integral accompanying micellization, ΔG2u, shown in Appendix E, as
| |  | (5.2) |
The enhancement of micellization by solute addition,
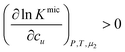
, reported in experimental literature as the lowering of CMC,
8,80–82 is linked to Δ
G2u > 0, signifying a stronger solute–surfactant interaction in the micellar state than in the monomer state.
Micellization as complex formation
Here we model micelle formation as the complexation of m surfactant and n solute molecules, with the equilibrium condition,where μm and μmon2 are the chemical potentials of the micelle and the monomeric (unassociated) surfactant molecule, respectively. We keep m and n constant. Because of the statistical thermodynamic approach,89 there is no need to introduce any assumptions on activity coefficients as the mass action models (Appendix E).86–88 However, introducing the equilibrium condition (eqn (5.3)) involving the species u and 2 makes it impossible to determine the Kirkwood–Buff integrals between the species. Since the equilibrium condition (eqn (5.3)) is assumed to be satisfied at any cu, its cu-derivative, under the phase equilibrium dμu = 0, leads to the following result (Appendix E):| | 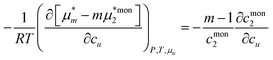 | (5.4) |
The contribution that stabilize a micelle over m surfactants is identified in eqn (5.4) as the solute-induced changes in the reduction of unassociated monomer concentration,  . This contribution is in agreement with the discussion in Section 3 for micellization enhancement in the presence of solutes. They contribute to stabilizing the micelle (i.e., a complex involving m surfactant molecules) over the surfactant monomers. This corresponds to the enhancement of surfactant-surfactant interaction by solutes.
. This contribution is in agreement with the discussion in Section 3 for micellization enhancement in the presence of solutes. They contribute to stabilizing the micelle (i.e., a complex involving m surfactant molecules) over the surfactant monomers. This corresponds to the enhancement of surfactant-surfactant interaction by solutes.
Thus, the simple thermodynamic models for micellization have captured the factors that lead to cooperative solubilization. They have shown that the enhancement of micellar stability, as well as surfactant self-association, leads to solubilization. This approach, based on combining thermodynamic models with a general statistical thermodynamic framework, can be extended by adopting more precise models of micellization9,76,85,90,91 for a more precise description of the cooperative solubilization mechanism.
Higher surfactant and solute concentrations
This paper has focused on the cooperative onset of solubility at low surfactant and solute concentrations around the CMC. Here we comment briefly on solubilization at higher concentrations. An apparent disagreement with the theory here comes from the observation of a decrease in aggregation size after a specific solute concentration.43,71 However, the driving force for solubilization is not the aggregation size but is the solute–surfactant distribution function being large enough to make the Kirkwood–Buff integral positive (eqn (2.2)), which is possible even when the aggregation size is smaller.
Eqn (2.1) is a rigorous statistical thermodynamic relationship for three component systems valid at any concentrations of solute and surfactant.34–36,41 However, as we go to more complex systems above the critical microemulsion concentration (second CMC), extra terms to describe the multiple surfactants, co-surfactants, and salts8,40,92 become necessary, for which the multiple component version of eqn (2.1) must be used.4,54,55,93 Because of the notable success of model-based approaches,94–96 especially the HLD-NAC by Acosta and coworkers.29,38,39,97 it seems likely that to capture the fluctuating nature of molecular interactions, the models and the rigorous theory can be combined. Such an approach has been demonstrated to be fruitful in the study of other complex solutions.49,98–100
6. Conclusion
We have established a universal mechanism for cooperative solubilization: enhanced self-association of solubilizers in the presence of a solute. This mechanism, originally proposed for hydrotropes,11,17–19 is at work also for surfactants. We have arrived at this conclusion through a generalization of our solubilization theory4,11,14,15,17–19,48 beyond dilute solutes and combining it with experimental evidence from surfactant literature. We have shown that the experimental reports on (i) the incorporation of solutes into micelles, (ii) enlargement of micelles, and (iii) the reduction of CMC by solutes are the evidence for this universal mechanism. The hydrophobic solubilization at sub-CMC concentrations also exhibits enhanced surfactant self-association. Thus, a universal statistical thermodynamic framework governs the initial onset of solubilization by cosolvents, hydrotropes, and surfactants at their low concentrations.
Conflicts of interest
There are no conflicts to declare.
Appendix A
Here we derive eqn (2.1a) under constant temperature and pressure. The chemical potential of a solute, 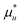 , whose centre-of-mass is fixed at origin, can be expressed as
, whose centre-of-mass is fixed at origin, can be expressed as| | 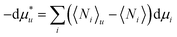 | (A.1) |
where μi is the chemical potential of the species i. 〈Ni〉u and 〈Ni〉 express the ensemble average of the numbers of the species i in the presence and absence of a fixed solute, respectively.11 Using the definition of the Kirkwood–Buff integral (eqn (2.1b)), eqn (A.1) is rewritten as| | 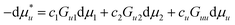 | (A.2) |
where ci = 〈Nj〉/V is the bulk number density of the species i.
To express how the solvation free energy of a solute, 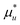 , is affected by the addition of surfactants, we use the Gibbs–Duhem equation11,55
, is affected by the addition of surfactants, we use the Gibbs–Duhem equation11,55
| | | cudμu + c1dμ1 + c2dμ2 = 0 | (A.3) |
to eliminate d
μ1 from
eqn (A.2) using
eqn (A.3), which yields
| |  | (A.4) |
We then consider an equilibrium between a solute in its pure phase
μou and in solution
μu. Since
μou only depends on
T and
P,
μu =
μou is a constant. Therefore,
Because of eqn (A.5), the solute–solute correlation (i.e., the last term of eqn (A.4)) does not affect solubilization. Note that the solute–solute correlations affect  indirectly by modifying Gu1 and Gu2. We also use the well-known relationship between
indirectly by modifying Gu1 and Gu2. We also use the well-known relationship between  and μu,55
and μu,55
| | 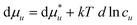 | (A.6) |
Combining
eqn (A.4)–
(A.6), we obtain
| | kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cu = c2(Gu2 − Gu1)dμ2 cu = c2(Gu2 − Gu1)dμ2 | (A.7) |
which leads to
eqn (2.1), when combined with
14,21,23
(see Appendix B).
Appendix B
Our first task here is to prove| | 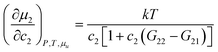 | (B.1) |
under a finite solute concentration cu, as long as the equilibrium condition, dμu = 0 (eqn (A.5)), is satisfied. Under constant temperature and pressure, analogous to eqn (A.2), we can derive the following equation for  :
:| | 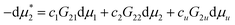 | (B.2) |
together with the relationship equivalent to eqn (A.6)| |  | (B.3) |
Because of the equilibrium condition for the solute, dμu = 0. Under this condition, combining eqn (B.2) and (B.3) yields| | 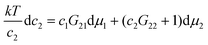 | (B.4) |
Using the Gibbs–Duhem equation (eqn (A.3)) under the equilibrium condition, dμu = 0, eqn (B.4) can be rewritten as| | 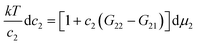 | (B.5) |
Eqn (B.1) can be derived straightforwardly from eqn (B.5).
Note that G22 is different from Gu,22, which is the driving force of cooperative solubilization. This can be best illustrated by calculating the Kirkwood–Buff integral from a distance distribution from a probe solubilizer. G22 is calculated regardless of the presence of solutes in the vicinity of the probe surfactant, whereas in the case of Gu,22, a probe surfactant is in the vicinity of a solute. Gu,22 converges to G22 far from the solute.
Our second task is to justify eqn (4.1). This is the generalization of our previous result (eqn (35) of ref. 11), derived under cu → 0, to finite cu. We start from the following grand canonical expression (see Appendix B of ref. 11, which can be generalized straightforwardly to any three component mixtures in Appendix C of this paper) valid for homogeneous and inhomogeneous systems:
| | 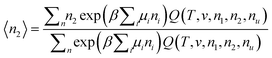 | (B.6) |
where
β = 1/
kT in which
k is the Boltzmann constant. Differentiating
eqn (B.6) for the homogeneous and inhomogeneous systems yields
| | 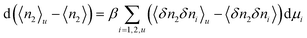 | (B.7) |
Eqn (B.7) is a generalization of our previous discussion (eqn (B.9) of
ref. 11). The difference is the presence of the
i =
u term in
eqn (B.7). This term, however, is zero because of the phase equilibrium condition, d
μu = 0 (
eqn (A.5)). We therefore obtain
| |  | (B.8) |
This can be used in conjunction with the combination of
eqn (A.3) and (A.5),
| |  | (B.9) |
to derive
eqn (4.1).
Appendix C
Here we derive the following relationship between the grand partition functions and the pseudo chemical potential (i.e., the chemical potential of a solute whose centre-of-mass position is fixed),  :
:| |  | (C.1) |
where Ξ(T,V,μu,μ1,μ2) is the grand partition function of a three-component solution consisting of species 1, 2, and u, and Ξu(T,V,μu,μ1,μ2) is the grand partition function of an inhomogeneous solution, which contains a solute with its centre-of-mass position fixed, in addition to the homogeneous solution. Our derivation is parallel to Section 3.1 of ref. 101.
By the definition of μu*, i.e.,  in the grand canonical ensemble,101 our goal, eqn (C.1), can be rewritten as
in the grand canonical ensemble,101 our goal, eqn (C.1), can be rewritten as
| |  | (C.2) |
where
Λu is the momentum partition function of the species
u. To prove
eqn (C.2), let us start from the definition of the grand partition function,
102| |  | (C.3) |
where
Q is the canonical partition function and
λi =
eβμi is the fugacity of the species
i. The key to derivation is to calculate 〈
Nu〉 which appears in
eqn (C.2), as
| | 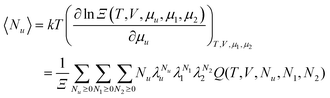 | (C.4) |
The next step is to relate eqn (C.4) to fix one of the solute molecules. We denote the resulting partition function by the subscript u. As a preparation, we write down the canonical partition function explicitly as the product of the momentum and coordinate partition functions, P(T,Nu,N1,N2) and Z(T,V,Nu,N1,N2), as
| | | Q(T,V,Nu,N1,N2) = P(T,Nu,N1,N2)Z(T,V,Nu,N1,N2) | (C.5) |
where
| | | P(T,Nu,N1,N2) =Λu−3NuΛ1−3N1Λ2−3N2 | (C.6a) |
| | 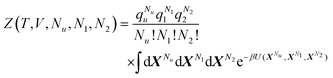 | (C.6b) |
with
qi, the intramolecular partition function of the species
i,
U, the potential function of the system, and
X, the configuration of each molecule. Fixing a solute molecule leads to losing
Λu−3, namely,
| | | Pu(T,Nu − 1,N1,N2) =Λu3P(T,Nu,N1,N2) | (C.7a) |
and to the loss of particle identity and volume integral for the fixed solute, as
101| |  | (C.7b) |
Substituting
eqn (C.5) and (C.7) into
eqn (C.4) yields
| | 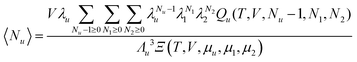 | (C.8) |
The right-hand side of
eqn (C.8) can be simplified as
| |  | (C.9) |
By the definition of fugacity,
eqn (C.9) is identical to
eqn (C.2), which we intended to prove.
We emphasize that the concentration of the solute in eqn (C.1) is finite. In our previous papers, our formalism was limited to the homogenous solution containing the species 1 and 2 only, with a fixed solute incorporated into the inhomogeneous solution.11,17,19 However, this Appendix has shown that our previous results can be generalized straightway to the system with solutes with any concentrations.
Appendix D
Here we detail the calculation procedures for Fig. 1. Firstly, the experimental data on the surfactant concentration (c2, in molar) dependence of naphthalene solubility (104cu, in molar) was fitted to a function| | 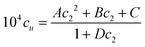 | (D.1) |
where A = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 787, B = −149.2, C = 2.85 and D = 12.74 were obtained via regression. Substituting eqn (D.1) into eqn (2.3a), we obtain
787, B = −149.2, C = 2.85 and D = 12.74 were obtained via regression. Substituting eqn (D.1) into eqn (2.3a), we obtain| |  | (D.2) |
Further differentiation of eqn (D.2) yields| | 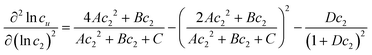 | (D.3) |
Appendix E
Here we employ thermodynamic models to investigate the mechanism of cooperative solubilization by micelles. Our first model is based on an equilibrium of a surfactant molecule between a micellar state and a monomer state, μmon2 = μmic2 = μ2. Both chemical potentials are linked to the pseudo-chemical potentials,  and
and  , as89
, as89| |  | (E.1) |
Combining eqn (E.1) with the equilibrium condition, we obtain the following expression for the transfer free energy of a surfactant from the monomeric state to the micellar state,  , as89
, as89| |  | (E.2) |
Using the pseudo-chemical potentials makes it unnecessary to consider the activity coefficients of the monomer and micelle based on self-association.86 Now we consider how free energy change, 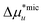 , depend on concentrations.24,103,104 To do so, let us start from eqn (A.4) with the exchange of indexes u and 2 as our starting point, namely,
, depend on concentrations.24,103,104 To do so, let us start from eqn (A.4) with the exchange of indexes u and 2 as our starting point, namely,
| |  | (E.3) |
Eqn (E.3) applies to both states,
mic and
mon.
We will use eqn (E.3) for the two different experimental conditions. The first is under the phase solubility equilibrium, dμu = 0, which yields
| |  | (E.4) |
From
eqn (E.4), we obtain
| | 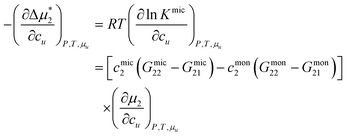 | (E.5) |
From
eqn (E.5), the following form was used as
eqn (5.1) in the main text.
| |  | (E.6) |
The second application of eqn (E.3) is with dμ2 = 0. Under this condition, we obtain
| | 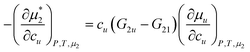 | (E.7) |
Under the dilute ideal solution condition for the solute, eqn (E.7) can be simplified as
| |  | (E.8) |
Applying eqn (E.8) for the monomer and micellar states of a surfactant, we obtain,
| |  | (E.9) |
Here, the contribution from Δ
G21 can be neglected, because the volume change of micellization, which is linked to Δ
G21via Δ
V2 = −Δ
G21,
24 is negligibly small, evidenced by a weak pressure dependence of CMC.
105Eqn (E.9) was used as eqn (5.2) in the main text.
Our second model is the complexation of m surfactants and n solutes, with eqn (5.3) as the equilibrium condition. Both m and n are constants. Under the phase solubility equilibrium dμu = 0, the cu-derivative of eqn (5.3) yields
| | 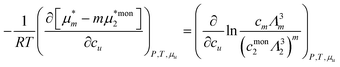 | (E.10) |
To derive
eqn (E.10) from
(5.3), we have introduced the pseudo-chemical potentials,
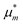
and

,
via| |  | (E.11) |
where
cm and
cmon2 are the molar concentrations and
Λm and
Λ2 are the thermal de Broglie wavelengths of the micelle and surfactant monomer, respectively.
89 We aim to quantify the effect of solute addition on micellar stability. The concentration of micelles,
cm, is expressed as
where
c2 is the total surfactant concentration. Let us evaluate the first term in the right-hand side of
eqn (E.10) around
c2 =
ccmc2, which yields
| |  | (E.13) |
where
mccmcm=
cmon2 at CMC was used. Combining
eqn (E.11) and (E.13) yields
| | 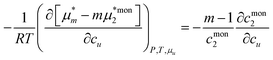 | (E.14) |
which was used as
eqn (5.3) in the main text.
Note added after first publication
This article replaces the version published on 30 Mar 2021, which contained proofing errors in eqn (D.2), eqn (E.14) and the definition below eqn (E.13).
Acknowledgements
We thank Steven Abbott for stimulating discussions, encouragements, and a careful reading of our manuscript at various stages. This paper is dedicated to him on the occasion of his 70th birthday. N. M. is grateful to the Grant-in-Aid for Scientific Research (No. JP19H04206) from the Japan Society for the Promotion of Science and by the Elements Strategy Initiative for Catalysts and Batteries (No. JPMXP0112101003) and the Fugaku Supercomputing Project from the Ministry of Education, Culture, Sports, Science, and Technology.
References
- S. Shimizu, Formulating rationally via statistical thermodynamics, Curr. Opin. Colloid Interface Sci., 2020, 48, 53–64 CrossRef CAS.
- S. E. Friberg, Hydrotropes, Curr. Opin. Colloid Interface Sci., 1997, 2, 490–494 CrossRef CAS.
- W. Kunz, K. Holmberg and T. Zemb, Hydrotropes, Curr. Opin. Colloid Interface Sci., 2016, 22, 99–107 CrossRef CAS.
- S. Shimizu and N. Matubayasi, Unifying hydrotropy under Gibbs phase rule, Phys. Chem. Chem. Phys., 2017, 19, 23597–23605 RSC.
- P. Mukerjee, Solubilization in micellar systems, Pure Appl. Chem., 1980, 52, 1317–1321 CAS.
-
S. D. Christian and J. F. Scamehorn, Solubilization in Surfactant Aggregates, Taylor & Francis, Boca Raton, Fl, 1995 Search PubMed.
- R. Nagarajan, Solubilization in aqueous solutions of amphiphiles, Curr. Opin. Colloid Interface Sci., 1996, 1, 391–401 CrossRef CAS.
-
M. J. Rosen and J. T. Kunjappu, Surfactants and Interfacial Phenomena: Fourth Edition, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2012 Search PubMed.
-
J. Israelachvili, Intermolecular and Surface Forces, Elsevier, Amsterdam, 2011 Search PubMed.
- C. De Oliveira, R. Yagui, A. Lineu Prestes, C. O. Rangel-Yagui, A. Pessoa-Jr and L. C. Tavares, Micellar solubilization of drugs, J. Pharm. Pharm. Sci., 2005, 8, 147–163 Search PubMed.
- S. Shimizu and N. Matubayasi, Hydrotropy: Monomer–micelle equilibrium and minimum hydrotrope concentration, J. Phys. Chem. B, 2014, 118, 10515–10524 CrossRef CAS PubMed.
- P. Bauduin, A. Renoncourt, A. Kopf, D. Touraud and W. Kunz, Unified concept of solubilization in water by hydrotropes and cosolvents, Langmuir, 2005, 21, 6769–6775 CrossRef CAS PubMed.
- M. L. Klossek, D. Touraud and W. Kunz, Eco-solvents--cluster-formation, surfactantless microemulsions and facilitated hydrotropy, Phys. Chem. Chem. Phys., 2013, 15, 10971–10977 RSC.
- J. J. Booth, S. Abbott and S. Shimizu, Mechanism of hydrophobic drug solubilization by small molecule hydrotropes, J. Phys. Chem. B, 2012, 116, 14915–14921 CrossRef CAS PubMed.
- J. J. Booth, M. Omar, S. Abbott and S. Shimizu, Hydrotrope accumulation around the drug: the driving force for solubilization and minimum hydrotrope concentration for nicotinamide and urea, Phys. Chem. Chem. Phys., 2015, 17, 8028–8037 RSC.
- S. Abbott, J. J. Booth and S. Shimizu, Practical molecular thermodynamics for greener solution chemistry, Green Chem., 2017, 19, 68–75 RSC.
- T. W. J. Nicol, N. Matubayasi and S. Shimizu, Origin of non-linearity in phase solubility: solubilisation by cyclodextrin beyond stoichiometric complexation, Phys. Chem. Chem. Phys., 2016, 18, 15205–15217 RSC.
- S. Shimizu and N. Matubayasi, The origin of cooperative solubilisation by hydrotropes, Phys. Chem. Chem. Phys., 2016, 18, 25621–25628 RSC.
- S. Shimizu and N. Matubayasi, Hydrotropy and scattering: pre-ouzo as an extended near-spinodal region, Phys. Chem. Chem. Phys., 2017, 19, 26734–26742 RSC.
- D. O. Abranches, J. Benfica, B. P. Soares, A. Leal-Duaso, T. E. Sintra, E. Pires, S. P. Pinho, S. Shimizu and J. A. P. Coutinho, Unveiling the mechanism of hydrotropy: Evidence for water-mediated aggregation of hydrotropes around the solute, Chem. Commun., 2020, 56, 7143–7146 RSC.
- J. G. Kirkwood and F. P. Buff, The statistical mechanical theory of solutions, J. Chem. Phys., 1951, 19, 774–777 CrossRef CAS.
- D. G. Hall, Kirkwood-Buff theory of solutions. An alternative derivation of part of it and some applications, Trans. Faraday Soc., 1971, 67, 2516–2524 RSC.
- A. Ben-Naim, Inversion of the Kirkwood–Buff theory of solutions: Application to the water–ethanol system, J. Chem. Phys., 1977, 67, 4884–4890 CrossRef CAS.
- S. Shimizu, Estimating hydration changes upon biomolecular reactions from osmotic stress, high pressure, and preferential hydration experiments, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 1195–1199 CrossRef CAS PubMed.
- N. Matubayasi, K. K. Liang and M. Nakahara, Free-energy analysis of solubilization in micelle, J. Chem. Phys., 2006, 124, 154908 CrossRef PubMed.
- N. Matubayasi, W. Shinoda and M. Nakahara, Free-energy analysis of the molecular binding into lipid membrane with the method of energy representation, J. Chem. Phys., 2008, 128, 195107 CrossRef PubMed.
- S. Shimizu and N. Matubayasi, Statistical thermodynamic foundation for mesoscale aggregation in ternary mixtures, Phys. Chem. Chem. Phys., 2018, 20, 13777–13784 RSC.
- K. Matsuoka, R. Yamashita, M. Ichinose, M. Kondo and T. Yoshimura, Solubilization of naphthalene and octafluoronaphthalene in ionic hydrocarbon and fluorocarbon surfactants, Colloids Surf., A, 2014, 456, 83–91 CrossRef CAS.
- E. J. Acosta, M. A. Le, J. H. Harwell and D. A. Sabatini, Coalescence and solubilization kinetics in linker-modified microemulsions and related systems, Langmuir, 2003, 19, 566–574 CrossRef CAS.
- P. D. Todorov, G. S. Marinov, P. A. Kralchevsky, N. D. Denkov, P. Durbut, G. Broze and A. Mehreteab, Kinetics of triglyceride solubilization by micellar solutions of nonionic surfactant and triblock copolymer. 3. Experiments with single drops, Langmuir, 2002, 18, 7896–7905 CrossRef CAS.
- B. Shekunov, Theoretical analysis of drug dissolution in micellar media, J. Pharm. Sci., 2017, 106, 248–257 CrossRef CAS PubMed.
- K. Peddireddy, P. Kumar, S. Thutupalli, S. Herminghaus and C. Bahr, Solubilization of thermotropic liquid crystal compounds in aqueous surfactant solutions, Langmuir, 2012, 28, 12426–12431 CrossRef CAS PubMed.
- S. Herminghaus, C. C. Maass, C. Krüger, S. Thutupalli, L. Goehring and C. Bahr, Interfacial mechanisms in active emulsions, Soft Matter, 2014, 10, 7008–7022 RSC.
- M. Miura and M. Kodama, The second CMC of the aqueous solution of sodium dodecyl sulfate. I. Conductivity, Bull. Chem. Soc. Jpn., 1972, 45, 428–431 CrossRef CAS.
- M. Kodama and M. Miura, The second CMC of the aqueous solution of sodium dodecyl sulfate. II. Viscosity and density, Bull. Chem. Soc. Jpn., 1972, 45, 2265–2269 CrossRef CAS.
- L. Magnus, Bergström, Second CMC in surfactant micellar systems, Curr. Opin. Colloid Interface Sci., 2016, 22, 46–50 CrossRef.
- B. P. Binks, P. D. I. Fletcher and D. I. Horsup, Effect of microemulsified surfactant in destabilising water-in-oil emulsions containing C12E4, Colloids Surf., 1991, 61, 291–315 CrossRef CAS.
- E. J. Acosta, J. H. Harwell and D. A. Sabatini, Self-assembly in linker-modified microemulsions, J. Colloid Interface Sci., 2004, 274, 652–664 CrossRef CAS PubMed.
- A. B. Troncoso and E. Acosta, Integrated Free Energy Model (IFEM) for microemulsions, J. Colloid Interface Sci., 2016, 466, 400–412 CrossRef PubMed.
- E. Acosta, Engineering cosmetics using the Net-Average-Curvature (NAC) model, Curr. Opin. Colloid Interface Sci., 2020, 48, 149–167 CrossRef CAS.
- L. M. Bergström, A theoretical investigation of the influence of the second critical micelle concentration on the solubilization capacity of surfactant micelles, AIP Adv., 2018, 8, 55136 CrossRef.
- P. Lianos, J. Lang, C. Strazielle and R. Zana, Fluorescence probe study of oil-in-water microemulsions. 1. Effect of pentanol and dodecane or toluene on some properties of sodium dodecyl sulfate micelles, J. Phys. Chem., 1982, 86, 1019–1025 CrossRef CAS.
- H. Hoffmann and W. Ulbricht, Transition of rodlike to globular micelles by the solubilization of additives, J. Colloid Interface Sci., 1989, 129, 388–405 CrossRef CAS.
- A. Klamt, Conductor-like screening model for real solvents: A new approach to the quantitative calculation of solvation phenomena, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt, The COSMO and COSMO-RS solvation models, Wiley
Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1338 Search PubMed.
-
J. M. Prausnitz, R. N. Lichtenthaler and E. G. de Azevedo, Molecular Thermodynamics of Fluid-Phase Equilibria, Prentice Hall, Upper Saddle River, NJ, 1986 Search PubMed.
- L. Mokrushina, M. Buggert, I. Smirnova, W. Arlt and R. Schomäcker, COSMO-RS and UNIFAC in prediction of micelle/water partition coefficients, Ind. Eng. Chem. Res., 2007, 46, 6501–6509 CrossRef CAS.
- S. Shimizu, J. J. Booth and S. Abbott, Hydrotropy: binding models vs. statistical thermodynamics, Phys. Chem. Chem. Phys., 2013, 15, 20625–20632 RSC.
- S. Shimizu and S. Abbott, How entrainers enhance solubility in supercritical carbon dioxide, J. Phys. Chem. B, 2016, 120, 3713–3723 CrossRef CAS PubMed.
-
H.-J. Butt, K. Graf and M. Kappl, Physics and Chemistry of Interfaces, Wiley-VCH, Weinheim, 2013 Search PubMed.
-
A. W. Adamson and A. P. Gast, Physical Chemistry of Surfaces, Wiley, New York, 1997 Search PubMed.
-
D. Henderson, Fundamentals of Inhomogeneous Fluids, Marcel Dekker, New York, 1992 Search PubMed.
- T. Lazaridis, Inhomogeneous fluid approach to solvation thermodynamics. 1. Theory, J. Phys. Chem. B, 1998, 102, 3531–3541 CrossRef CAS.
- S. Shimizu and N. Matubayasi, Intensive nature of fluctuations: reconceptualizing Kirkwood-Buff theory via elementary algebra, J. Mol. Liq., 2020, 318, 114225 CrossRef CAS.
- S. Shimizu and N. Matubayasi, A unified perspective on preferential solvation and adsorption based on inhomogeneous solvation theory, Phys. A, 2018, 492, 1988–1996 CrossRef CAS.
-
D. Attwood and A. T. Florence, Surfactant Systems, Springer, Netherlands, Dordrecht, 1983, pp. 229–292 Search PubMed.
- F. A. Alvarez-Núñez and S. H. Yalkowsky, Relationship between Polysorbate 80 solubilization descriptors and octanol-water partition coefficients of drugs, Int. J. Pharm., 2000, 200, 217–222 CrossRef.
- R. Nagarajan, M. A. Chaiko and E. Ruckenstein, Locus of solubilization of benzene in surfactant micelles, J. Phys. Chem., 1984, 88, 2916–2922 CrossRef CAS.
- A. A. Dar, G. M. Rather and A. R. Das, Mixed micelle formation and solubilization behavior toward polycyclic aromatic hydrocarbons of binary and ternary cationic-nonionic surfactant mixtures, J. Phys. Chem. B, 2007, 111, 3122–3132 CrossRef CAS PubMed.
- P. A. Bhat, G. M. Rather and A. A. Dar, Effect of surfactant mixing on partitioning of model hydrophobic drug, Naproxen, between aqueous and micellar phases, J. Phys. Chem. B, 2009, 113, 997–1006 CrossRef CAS PubMed.
- P. Mukerjee, and J. R. Cardinal, Solubilization as a method for studying self-association: Solubility of naphthalene in the bile salt sodium cholate and the complex pattern of its aggregation, J. Pharm. Sci., 1976, 65, 882–886 CrossRef CAS PubMed.
- Y. Chevalier and T. Zemb, The structure of micelles and microemulsions, Rep. Prog. Phys., 1990, 53, 279–371 CrossRef CAS.
- H. Høiland, A. M. Blokhus, O. J. Kvammen and S. Backlund, Solubilization of 1-hexanol in hexadecyltrimethylammonium bromide, sodium dodecyl sulfate, and sodium decanoate, J. Colloid Interface Sci., 1985, 107, 576–578 CrossRef.
- S. Ozeki and S. Ikeda, The difference in solubilization power between spherical and rodlike micelles of dodecyldimethylammonium chloride in aqueous solutions, J. Phys. Chem., 1985, 89, 5088–5093 CrossRef CAS.
- T. Imae, A. Abe, Y. Taguchi and S. Ikeda, Solubilization of a water-insoluble dye in aqueous solutions of dodecyltrimethylammonium halides, and its relation to micelle size and shape, J. Colloid Interface Sci., 1986, 109, 567–575 CrossRef CAS.
- B. Herzog, K. Huber and A. R. Rennie, Characterization of worm-like micelles containing solubilized dye-molecules by light scattering techniques, J. Colloid Interface Sci., 1994, 164, 370–381 CrossRef CAS.
- D. Attwood, G. Ktistis, Y. McCormick and M. J. Story, Solubilization of indomethacin by polysorbate 80 in mixed water-sorbitol solvents, J. Pharm. Pharmacol., 1989, 41, 83–86 CrossRef CAS PubMed.
-
P. Mukerjee, Solution Chemistry of Surfactants, Springer, New York, 1979, pp. 153–174 Search PubMed.
- O. Bayer, H. Hoffmann, H. Ulbricht and H. Thurn, The influence of solubilized additives on surfactant solutions with rodlike micelles, Adv. Colloid Interface Sci., 1986, 26, 177–203 CrossRef CAS.
- G. X. Zhao and X. G. Li, Solubilization of n-octane and n-octanol by a mixed aqueous solution of cationic-anionic surfactants, J. Colloid Interface Sci., 1991, 144, 185–190 CrossRef CAS.
- M. Törnblom and U. Henriksson, Effect of solubilization of aliphatic hydrocarbons on size and shape of rodlike C16TABr micelles studied by 2H NMR relaxation, J. Phys. Chem. B, 1997, 101, 6028–6035 CrossRef.
- K. J. Mysels, The effect of tracer dyes on the size distribution and transport properties of micelles, J. Colloid Interface Sci., 1967, 23, 474–477 CrossRef CAS.
- P. Mukerjee and K. J. Mysels, A Re-evaluation of the Spectral Change Method of Determining Critical Micelle Concentration, J. Am. Chem. Soc., 1955, 77, 2937–2943 CrossRef CAS.
- J. H. Li, B. X. Zhou and W. M. Cai, The solubility behavior of bisphenol A in the presence of surfactants, J. Chem. Eng. Data, 2007, 52, 2511–2513 CrossRef CAS.
- H. B. Klevens, The effects of temperature upon the critical concentrations of anionic and cationic detergents, J. Phys. Colloid Chem., 1947, 51, 1143–1154 CrossRef CAS PubMed.
- S. Göktürk and R. Y. Talman, Effect of temperature on the binding and distribution characteristics of thionine in sodium dodecylsulfate micelles, J. Solution Chem., 2008, 37, 1709–1723 CrossRef.
- M. De Vijlder, Influence of solubilized azo dyes on the C.M.C. value of cetyl-trimethylammonium bromide, Z. Phys. Chem., 2003, 217, 653–665 CrossRef CAS.
- R. M. Levy, D. Cui, B. W. Zhang and N. Matubayasi, Relationship between solvation thermodynamics from IST and DFT perspectives, J. Phys. Chem. B, 2017, 121, 3825–3841 CrossRef CAS PubMed.
-
C. Treiner, in Solubilization in surfactant aggregates, ed. S. D. Christian and J. F. Scamehorn, Taylor & Francis, Boca Raton, Fl, 1995, pp. 384–428 Search PubMed.
- S. Miyagishi, The Effect of organic additives on the thermodynamic parameters of micellization, Bull. Chem. Soc. Jpn., 1976, 49, 34–37 CrossRef CAS.
- M. J. Schick and F. M. Fowkes, Foam stabilizing additives for synthetic detergents. Interaction of additives and detergents in mixed micelles, J. Phys. Chem., 1957, 61, 1062–1068 CrossRef CAS.
- N. Nishikido, Y. Moroi, H. Uehara and R. Matuura, Effect of alcohols on the micelle formation of nonionic surfactants in aqueous solutions, Bull. Chem. Soc. Jpn., 1974, 47, 2634–2638 CrossRef CAS.
- H. Zhong, L. Yang, G. Zeng, M. L. Brusseau, Y. Wang, Y. Li, Z. Liu, X. Yuan and F. Tan, Aggregate-based sub-CMC solubilization of hexadecane by surfactants, RSC Adv., 2015, 5, 78142–78149 RSC.
- H. Zhong, X. Yang, F. Tan, M. L. Brusseau, L. Yang, Z. Liu, G. Zeng and X. Yuan, Aggregate-based sub-CMC solubilization of n-alkanes by monorhamnolipid biosurfactant, New J. Chem., 2016, 40, 2028–2035 RSC.
- K. Shinoda and E. Hutchinson, Pseudo-phase separation model for thermodynamic calculations on micellar solutions, J. Phys. Chem., 1961, 66, 577–582 CrossRef.
- P. Mukerjee, The nature of the association equilibria and hydrophobic bonding in aqueous solutions of association colloids, Adv. Colloid Interface Sci., 1967, 1, 242–275 CrossRef.
- Y. Moroi, R. Sugii and R. Matuura, Examination of micelle formation by phase rule, J. Colloid Interface Sci., 1984, 98, 184–191 CrossRef CAS.
- M. J. Blandamer, P. M. Cullis, L. G. Soldi, J. B. F. N. Engberts, A. Kacperska, N. M. Van Os and M. C. S. Subha, Thermodynamics of micellar systems: Comparison of mass action and phase equilibrium models for the calculation of standard Gibbs energies of micelle formation, Adv. Colloid Interface Sci., 1995, 58, 171–209 CrossRef CAS PubMed.
-
A. Ben-Naim, Molecular Theory of Solutions, Oxford University Press, Oxford, 2006 Search PubMed.
- C. Tanford, Thermodynamics of micelle formation: prediction of micelle size and size distribution, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 1811–1815 CrossRef CAS PubMed.
- R. Nagarajan and E. Ruckenstein, Theory of surfactant self-assembly: A predictive molecular thermodynamic approach, Langmuir, 1991, 7, 2934–2969 CrossRef CAS.
- D. P. Acharya and P. G. Hartley, Progress in microemulsion characterization, Curr. Opin. Colloid Interface Sci., 2012, 17, 274–280 CrossRef CAS.
- S. Shimizu and N. Matubayasi, Implicit function theorem and Jacobians in solvation and adsorption, Phys. A, 2021, 570, 125801 CrossRef.
- B. C. Stephenson, C. O. Rangel-Yagui, A. Pessoa, L. C. Tavares, K. Beers and D. Blankschtein, Experimental and theoretical investigation of the micellar-assisted solubilization of ibuprofen in aqueous media, Langmuir, 2006, 22, 1514–1525 CrossRef CAS PubMed.
- A. Goldsipe and D. Blankschtein, Molecular-thermodynamic theory of micellization of multicomponent surfactant mixtures: 1. Conventional (pH-insensitive) surfactants, Langmuir, 2007, 23, 5942–5952 CrossRef CAS PubMed.
- S. May and A. Ben-Shaul, Molecular theory of the sphere-to-rod transition and the second CMC in aqueous micellar solutions, J. Phys. Chem. B, 2001, 105, 630–640 CrossRef CAS.
- A. Boza Troncoso and E. Acosta, Formulating nonionic detergents via the integrated free energy model, J. Surf. Deterg., 2019, 22, 1023–1037 CAS.
- S. Shimizu, Caffeine dimerization: effects of sugar, salts, and water structure, Food Funct., 2015, 6, 3228–3235 RSC.
- S. Shimizu, S. Abbott and N. Matubayasi, Quantifying non-specific interactions between flavour and food biomolecules, Food Funct., 2017, 8, 2999–3009 RSC.
- S. Shimizu, S. Abbott, K. Adamska and A. Voelkel, Quantifying non-specific interactions: via liquid chromatography, Analyst, 2019, 144, 1632–1641 RSC.
-
A. Ben-Naim, Solvation Thermodynamics, Springer US, 1987 Search PubMed.
-
T. L. Hill, Statistical Mechanics. Principles and Selected Applications, McGraw-Hill, New York, 1956 Search PubMed.
- S. Shimizu and N. Matubayasi, Preferential solvation: Dividing surface vs excess numbers, J. Phys. Chem. B, 2014, 118, 3922–3930 CrossRef CAS PubMed.
- S. Shimizu, R. Stenner and N. Matubayasi, Gastrophysics: Statistical thermodynamics of biomolecular denaturation and gelation from the Kirkwood-Buff theory towards the understanding of tofu, Food Hydrocoll., 2017, 62, 128–139 CrossRef CAS.
- M. Lesemann, K. Thirumoorthy, Y. J. Kim, J. Jonas and M. E. Paulaitis, Pressure dependence of the critical micelle concentration of a nonionic surfactant in water studied by 1H-NMR, Langmuir, 1998, 14, 5339–5341 CrossRef CAS.
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
Nobuyuki
Matubayasi
*a and
Nobuyuki
Matubayasi
 b
b
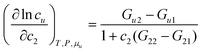
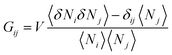
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉 signifies an ensemble average and the deviation δNi = Ni − 〈Ni〉 was introduced. Note that the right-hand side of eqn (2.1a) was previously derived at cu → 0,14–16 which has now been generalized to finite solute concentrations in Appendices A and B. This means our previous analyses of hydrotropy4,14–16,48 and the entrainer effect in supercritical CO249 were limited to dilute solutes simply because G21 and G22 were calculated using the physical properties of binary solutions.
〉 signifies an ensemble average and the deviation δNi = Ni − 〈Ni〉 was introduced. Note that the right-hand side of eqn (2.1a) was previously derived at cu → 0,14–16 which has now been generalized to finite solute concentrations in Appendices A and B. This means our previous analyses of hydrotropy4,14–16,48 and the entrainer effect in supercritical CO249 were limited to dilute solutes simply because G21 and G22 were calculated using the physical properties of binary solutions.
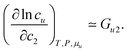

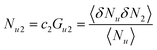
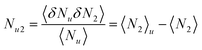


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KM vary between 1 to 7,47,59,60 hence, at typical c2 used for solubilization (i.e., ∼101 mM) neither KM(c2 − ccmc2) nor 1 is negligible in the denominator of eqn (3.2a). Combining eqn (3.2a) with eqn (2.3c), we obtain,
KM vary between 1 to 7,47,59,60 hence, at typical c2 used for solubilization (i.e., ∼101 mM) neither KM(c2 − ccmc2) nor 1 is negligible in the denominator of eqn (3.2a). Combining eqn (3.2a) with eqn (2.3c), we obtain,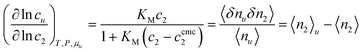
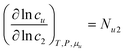 , by fitting the experimental data to a function (see Appendix D). Fig. 2 shows a drastic increase in Nu2 is seen at low c2. The larger the Nu2 value, the more significant the solubilization.
, by fitting the experimental data to a function (see Appendix D). Fig. 2 shows a drastic increase in Nu2 is seen at low c2. The larger the Nu2 value, the more significant the solubilization.

 (top) and
(top) and 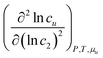 (bottom) calculated from the fitting function (Appendix D) of naphthalene solubilization by sodium cholate shown in Fig. 1.61
(bottom) calculated from the fitting function (Appendix D) of naphthalene solubilization by sodium cholate shown in Fig. 1.61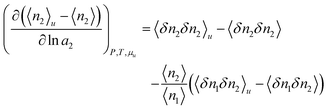
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a2 with ln
a2 with ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c2. Under these conditions, eqn (2.3) and (4.1) can be combined to yield
c2. Under these conditions, eqn (2.3) and (4.1) can be combined to yield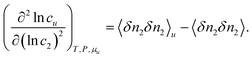
 , where X is a physical quantity,52,53,78 we can express eqn (4.2a) also as
, where X is a physical quantity,52,53,78 we can express eqn (4.2a) also as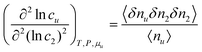
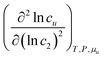 , is observed in Fig. 2. According to eqn (4.2), this peak is caused by the enhanced surfactant-surfactant number fluctuation in the presence of a solute 〈δn2δn2〉u compared to that in the bulk phase 〈δn2δn2〉. Even though the precise location of the peak is dependent sensitively on the fitting function, the peak at c2 = 1.5 × 10−2 M is consistent with one of the “apparent CMC” values (1.6 × 10−2 M) estimated by Mukerjee and Cardinal from the same solubilization data as in Fig. 1.61
, is observed in Fig. 2. According to eqn (4.2), this peak is caused by the enhanced surfactant-surfactant number fluctuation in the presence of a solute 〈δn2δn2〉u compared to that in the bulk phase 〈δn2δn2〉. Even though the precise location of the peak is dependent sensitively on the fitting function, the peak at c2 = 1.5 × 10−2 M is consistent with one of the “apparent CMC” values (1.6 × 10−2 M) estimated by Mukerjee and Cardinal from the same solubilization data as in Fig. 1.61
 indicates the enhancement of surfactant self-association and micellization.
indicates the enhancement of surfactant self-association and micellization.
 , can be introduced statistical thermodynamically89 without any assumptions on the activity coefficient (Appendix E). This model can be applied in two different ways. The first case considers the effect of surfactants on phase solubility, i.e., dμu = 0. Under this condition, the surfactant-surfactant Kirkwood–Buff integrals in the monomeric and micellar states, Gmon22 and Gmic22 can be introduced (Appendix E). How solubility depends on surfactant chemical potential, μ2, can then be expressed as
, can be introduced statistical thermodynamically89 without any assumptions on the activity coefficient (Appendix E). This model can be applied in two different ways. The first case considers the effect of surfactants on phase solubility, i.e., dμu = 0. Under this condition, the surfactant-surfactant Kirkwood–Buff integrals in the monomeric and micellar states, Gmon22 and Gmic22 can be introduced (Appendix E). How solubility depends on surfactant chemical potential, μ2, can then be expressed as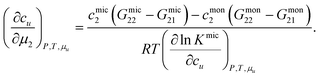
 .
.

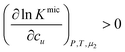 , reported in experimental literature as the lowering of CMC,8,80–82 is linked to ΔG2u > 0, signifying a stronger solute–surfactant interaction in the micellar state than in the monomer state.
, reported in experimental literature as the lowering of CMC,8,80–82 is linked to ΔG2u > 0, signifying a stronger solute–surfactant interaction in the micellar state than in the monomer state.

 . This contribution is in agreement with the discussion in Section 3 for micellization enhancement in the presence of solutes. They contribute to stabilizing the micelle (i.e., a complex involving m surfactant molecules) over the surfactant monomers. This corresponds to the enhancement of surfactant-surfactant interaction by solutes.
. This contribution is in agreement with the discussion in Section 3 for micellization enhancement in the presence of solutes. They contribute to stabilizing the micelle (i.e., a complex involving m surfactant molecules) over the surfactant monomers. This corresponds to the enhancement of surfactant-surfactant interaction by solutes.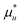 , whose centre-of-mass is fixed at origin, can be expressed as
, whose centre-of-mass is fixed at origin, can be expressed as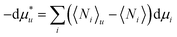
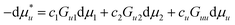
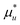 , is affected by the addition of surfactants, we use the Gibbs–Duhem equation11,55
, is affected by the addition of surfactants, we use the Gibbs–Duhem equation11,55
 indirectly by modifying Gu1 and Gu2. We also use the well-known relationship between
indirectly by modifying Gu1 and Gu2. We also use the well-known relationship between  and μu,55
and μu,55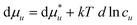
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d
d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cu = c2(Gu2 − Gu1)dμ2
cu = c2(Gu2 − Gu1)dμ2 (see Appendix B).
(see Appendix B).
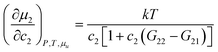
 :
: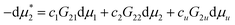

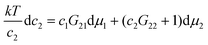
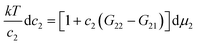
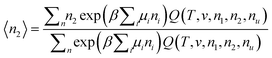
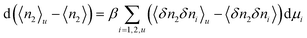


 :
:
 in the grand canonical ensemble,101 our goal, eqn (C.1), can be rewritten as
in the grand canonical ensemble,101 our goal, eqn (C.1), can be rewritten as

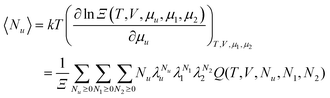
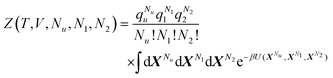

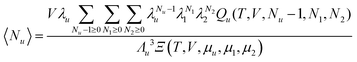

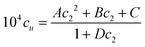
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 787, B = −149.2, C = 2.85 and D = 12.74 were obtained via regression. Substituting eqn (D.1) into eqn (2.3a), we obtain
787, B = −149.2, C = 2.85 and D = 12.74 were obtained via regression. Substituting eqn (D.1) into eqn (2.3a), we obtain
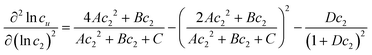
 and
and  , as89
, as89
 , as89
, as89
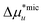 , depend on concentrations.24,103,104 To do so, let us start from eqn (A.4) with the exchange of indexes u and 2 as our starting point, namely,
, depend on concentrations.24,103,104 To do so, let us start from eqn (A.4) with the exchange of indexes u and 2 as our starting point, namely,

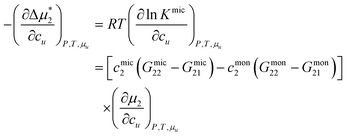

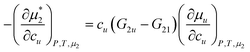


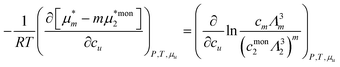
 and
and  , via
, via


