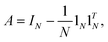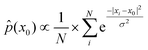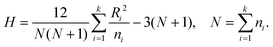Comprehensive characterization of oligosaccharide conformational ensembles with conformer classification by free-energy landscape via reproductive kernel Hilbert space

Abstract

Oligosaccharides play versatile roles in various biological systems but are difficult to characterize from a structural viewpoint due to their remarkable degrees of freedom in internal motion. Therefore, molecular dynamics simulations have been widely used to delineate the dynamic conformations of oligosaccharides. However, hardly any methods have thus far been available for the comprehensive characterization of simulation-derived conformational ensembles of oligosaccharides. In this research, we attempted to develop a non-linear multivariate analysis by employing a kernel method using two homologous high-mannose-type oligosaccharides composed of ten and eleven residues as model molecules. These oligosaccharides’ conformers derived from simulations were mapped into reproductive kernel Hilbert space with a positive definite function in which all required non-redundant variables for describing the oligosaccharide conformations can be treated in a non-biased manner. By applying Gaussian mixture model clustering, the oligosaccharide conformers were successfully classified by different funnels in the free-energy landscape, enabling a systematic comparison of conformational ensembles of the homologous oligosaccharides. The results shed light on the contributions of intraresidue conformational factors such as the hydroxyl group orientation and/or ring puckering state to their global conformational dynamics. Our methodology will open opportunities to explore oligosaccharides' conformational spaces, and more generally, molecules with high degrees of motional freedom.

---

Introduction

Oligosaccharides modify proteins and lipids and play essential roles in various biological processes, including cell adhesion, cell growth regulation, and cancer cell metastasis.^1,2 Viral and bacterial infections and defensive immune functions are also mediated by specific oligosaccharides on cell surfaces.^3–5 These oligosaccharide functions are evolved by a series of enzymes that create specific covalent structures of oligosaccharides and are promoted through interactions with various oligosaccharide-binding proteins collectively termed lectins. These enzymes and lectins recognize specific covalent structures, or more precisely, specific conformations of oligosaccharides. Therefore, the determination of oligosaccharide structures is crucial for a better understanding of the molecular mechanisms underlying physiological oligosaccharide functions and drug design targeting of the oligosaccharide recognition systems of pathological interest.

Oligosaccharide conformations in solution have been experimentally characterized primarily by nuclear magnetic resonance (NMR) spectroscopy.^6–8 However, since oligosaccharides generally possess considerable degrees of freedom in internal motion, their three-dimensional structures fluctuate dynamically and are difficult to delineate simply by experimental approaches. Therefore, dynamic conformations of oligosaccharides have been depicted by employing computational approaches typified by molecular dynamics (MD) simulations.^9–12 In this context, we have developed a method to explore conformational spaces occupied by oligosaccharides in solution using replica-exchange MD simulation validated with paramagnetism-assisted NMR data.^13–15 Our approach has provided the basis for comparison of conformational spaces among structurally homologous but functionally distinct oligosaccharides.

Traditionally, the comparison of oligosaccharide conformational ensembles has been performed based on Ramachandran-type plots for individual glycosidic linkages.^15,16 This approach is useful for comparing oligosaccharides' local conformational features, which, however, are difficult to integrate into overall conformational differences. In contrast, the global conformations of oligosaccharides have been represented simply with end-to-end distances or collision cross sections, although these can provide no conformational details.^13,17 Hence, methodological development is needed to highlight the features of dynamic conformational ensembles of oligosaccharides with the integration of local structural characters, including ring puckering and hydroxyl orientation as well as glycosidic linkage conformation. In this study, we attempted to address this issue by developing a non-linear multivariate analysis using a kernel method in conjunction with graph theoretical techniques.

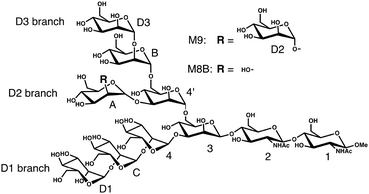
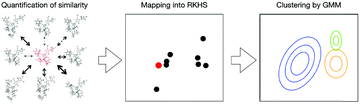
Our test molecules are tri-antennary oligosaccharides composed of eight or nine mannose (Man) and two N-acetyl glucosamine (GlcNAc) residues, which operate as quality control tags of glycoproteins in the early secretory pathway (Fig. 1). These high-mannose-type deca- and undeca-saccharides have 91 and 100 degrees of freedom in internal motion, respectively (vide infra). The kernel method can deal with such multivariate systems because the cost of calculation is independent of the number of variables.¹⁸ Here we develop a kernel methodology in which all non-redundant variables needed to describe the oligosaccharide conformations can be treated equally (Fig. 2). First, using an appropriate positive definite kernel function that takes a complete set of the non-redundant variables, the conformational ensembles of oligosaccharides are mapped into reproductive kernel Hilbert space (RKHS). Second, a clustering method based on the Gaussian mixture model (GMM) is applied to the images in RKHS, which detects the numbers of clusters based on the Bayesian information criterion (BIC).^19,20 Through the clustering process, the images are classified by different funnels (corresponding to individual clusters) in the free-energy landscape to which the preimage conformers belong. Finally, each cluster is characterized by a statistical approach to reveal the unique conformational features of the target oligosaccharides.

Fig. 1 Chemical structures of the high-mannose-type oligosaccharides M9 and M8B.

Fig. 2 Scheme of our proposed approach for non-linear multivariate analysis of oligosaccharide conformational ensembles. The structural similarity among individual conformers extracted from MD data is evaluated by employing a kernel function considering all the independent conformational variables equally. Individual conformers are mapped into an RKHS, where the relative positions of the points reflect the similarity between the corresponding conformers. To explore the conformational free-energy landscape, a cluster analysis is performed with consideration of the Gaussian distribution of the data in the RKHS.

Methods

General

In this paper, CPPTRAJ in AmberTools 16 was used to analyze the conformers.^21,22 The calculation for the mapping and clustering was performed with R software.²³ The conformers were visualized by VMD.²⁴

MD simulation

We analyze MD ensembles of the triantennary undecasaccharide containing nine mannose residues, i.e., Manα1-2Manα1-6(Manα1-2Manα1-3)Manα1-6(Manα1-2Manα1-2Manα1-3)-Manβ1-4GlcNAcβ1-4GlcNAcβ-OMe (termed M9) and its derivative (termed M8B), which lacks the non-reducing-terminal mannose residue (D2) at the central branch (termed the D2 branch; Fig. 1). The MD simulations of M9 and M8B were performed in the previous study.¹³ Briefly, NVT ensembles were calculated by replica-exchange MD simulation using 64 replicas and the simulation time is 52 ns with 2 fs time-steps for each replica. From 26 000 snapshots extracted at equal intervals in the MD trajectory at the lowest temperature (300 K), we randomly sampled 10 000 snapshots used as a conformational ensemble in this study.

In this paper, we denote the conformational ensemble derived from the MD simulation trajectories as X = (x₁,x₂,…x_n). X consists of N conformers constituted from snapshots x_i (i = 1, 2,…,N), and each x_i represents a single f-dimensional instance. Note that f is the degree of freedom of the conformation of the molecule.

Definition of the kernel function

A kernel function uniquely determines the RKHS by measuring the “similarity” between arguments. We designed the positive definite kernel k, a variation of the Gaussian kernel to consider all the non-redundant variables equally.

In the description of the oligosaccharide, one possible set of all non-redundant variables is composed of Cremer–Pople variables (Q,φ,θ), glycosidic linkage dihedrals (ϕ,ψ,ω) and dihedrals, which define the orientation of the hydroxyl group and the acetyl group (designated as γ in this paper).

Thus, vector τ_i corresponding to x_i is expressed by the following equation:

with the imaginary unit j, reflecting all information about the conformation of the oligosaccharide at a moment.

Here, θ, Q and φ denote 1 × p vectors whose elements are Cremer–Pople torsion parameters,²⁵ total puckering amplitude, and generalized spherical coordinate variables, respectively. ϕ and ψ are 1 × q vectors whose elements are values of dihedrals, which define the glycosidic linkage conformations as O₅–C₁–O–C_X′ and C₁–O–C_X′–C_X−1′, respectively. ω are 1 × r vectors whose elements are values of dihedrals defined as O–C₆′–C₅′–C₄′. γ are the 1 × s vectors whose elements are dihedrals defined as C_x−1–C_x–O_x–H_xO (γ_x(x=2,3,4,6)), C₄–C₅–C₆–O₆ (γ₅), C₁–C₂–N₂–C₂N (γ_N) or C₂–N₂–C₂N–O₂N (γ_o).

p, q, and r are the numbers of 6-membered rings, glycosidic linkages, and α1-6 glycosidic linkages in the oligosaccharide, respectively. s is the number of γ dihedrals. The actual values of p, q, r, and s are 11, 10, 2, and 45 for M9 and 10, 9, 2, and 41 for M8B, respectively. Therefore, the degree of freedom is shown as f = 3p+ 2q + r + s, i.e., 100 and 91 for M9 and M8B, respectively.

The parameters σ_θ, σ_φ, σ_ϕ, σ_ψ, σ_ω, and σ_γ are vectors of parameters for “scaling” each variable and are chosen so that the contribution of all variables to “similarity” shall be equal. Their values were estimated to be the median value of |v_l − v_m| for all l and m (l,m = 1,2,…,N) where v_l denotes a single component of τ_l.

The kernel function k used in this paper is expressed by:

where σ is the hyperparameter. The value of the hyperparameter is chosen as an estimate of the median value of |τ_l − τ_m| for all l and m to minimize the calculation error. To estimate the median of |v_l − v_m| or |τ_l − τ_m|, 100 conformers were extracted randomly from the ensemble 100 times. Then we calculated the mean of the medians among all.

Mapping into reproductive kernel Hilbert space

The conformational ensemble data sampled from the MD simulation trajectory was projected into RKHS H̃ defined by the positive definite kernel function k, which satisfies x, x′ ∈ X,

k(x,x′) = 〈[capital Phi, Greek, tilde](x),[capital Phi, Greek, tilde](x′)〉, k: X × X → R,

where [capital Phi, Greek, tilde](·) is mapping into H̃, and 〈·,·〉 is an inner product in H̃.¹⁸ Due to kernel trick, images in H̃ can be obtained from the centralized gram matrix G̃ expressed by:

G̃ = (AGA),

G = (k(x_i,x_j))_{i,j=1,2,…,N},

where G is a gram matrix, I_N is N-dimensional identity matrix, 1_N is an N × 1 vector with elements (1,1,…,1)^T, and ·^T is a transpose operator.

A principal component analysis was performed for H̃, which initially has N-dimensional space. We reduced its dimension to the least number of dimension d* whose cumulative variance ratio is over 0.90 to obtain an RKHS, H*. We denote ξ_i as an element of H* corresponding to an element of preimage x_i throughout this paper. To characterize the conformational ensembles of each oligosaccharide, a mapping from the ensemble X of M9 or M8B into H* was performed. For comparison of conformational ensembles between M9 and M8B, the ensemble data of their common structures, i.e., the whole M8B structure and the partial M9 structure without the ManD2 residue (designated as M9*), were projected into the same feature space.

Gaussian mixture model clustering

The empirical distribution in conformational space directly reflects the conformational free-energy landscape.^26,27 Let p(x) denote the probability density on X, and f_c be the conformational free-energy. The relationship between them can be calculated as follows:

f_c = −k_BT ln p(x_i) + C₁,

where k_B is the Boltzmann constant, T is the absolute temperature, and C₁ is a constant. Hence, considering the above equation, we can say directly with a constant C₂,

Furthermore, empirical distribution in RKHS also reflects the empirical distribution in conformational space because a consistent estimate of the density function value at the fixed point x₀ in X can be expressed as²⁸

Thus, we may say that local maxima in the empirical distribution in RKHS represent its corresponding local minima in the conformational free-energy landscape.

The GMM clustering was performed for the above mentioned RKHS, to explore the conformational free-energy landscape. In this model, data points are assumed to be generated from a mixture of C component Gaussian distribution, in which p(ξ_i) represents the density function of c-th component, where θ_c is the parameter which is estimated for cluster c (c = 1, 2,…,C). The probability density is

where α_c is the mixing proportion of the components. m_c and S_c are the mean and the covariance matrix of component c, respectively. |·| is the determinant operator.

The models are estimated by EM algorithm initialized by hierarchical, ellipsoidal, varying volume, shape, and orientation model-based agglomerative clustering.²⁹ The optimal model is then selected according to the BIC shown as

BIC = b ln N − 2 ln L,

where b is the number of the estimated parameters and L is the estimated likelihood
[small straight theta, Greek, circumflex] is an estimated parameter that maximizes the likelihood function. Through this model estimating process, we obtain the most likely estimated parameter [small straight theta, Greek, circumflex] including m̂_c for m_c and ŝ_c for S_c. This calculation was performed with the R package Mclust.²⁹

Maximum mean discrepancy among the centers of clusters

The maximum mean discrepancy (MMD) is a robust measure that determines how much the two distributions differ.³⁰ Let P,Q be the probability distributions on X, and H be an RKHS defined by a universal kernel k, including Gaussian kernel. Then P is embedded into H as:

Then MMD between two distributions P and Q is shown as

MMD(P,Q) = ||μ_P − μ_Q||_H,

where ||·|| is a norm in H.

By the GMM clustering mentioned above, the images in H* are classified by the funnels in the free-energy landscape to which the corresponding conformers belong. Hence, each clusters’ estimate of the mean point in RKHS corresponds to the embedding of the empirical distribution on conformers in each free-energy funnel.

Now we examine whether a cluster of M9* has its “equivalent” among those of M8B (or vice versa) by calculating the Euclidean distance between their mean points. The estimated mean points of the clusters of M9* and those of M8B are used in the calculation. When one mean point of a cluster of M9* is always greater than a threshold away from the mean points of M8B clusters, the cluster was judged as an M9* characteristic cluster containing M9* characteristic conformers, and vice versa. We set the threshold to the MMD value between the ensembles of M9* and M8B, to 0.100.

Kruskal–Wallis test

The Kruskal–Wallis test was used to characterize the clusters in the feature space H* mentioned above. We performed the Kruskal–Wallis test for the distribution of each variable in τ between one cluster and the whole ensemble. When the p-value was less than the significance level of 0.01, we considered the tested variable characterizing the cluster.

The null hypothesis of the Kruskal–Wallis test is that the dependent variable's distribution is the same in the different populations that are to be compared with one another.³¹ Let k (k ≥ 2) denote the number of populations to be compared. The Kruskal–Wallis test starts by substituting the rank in the overall data set for each measurement value. The sum of the ranks R_i is calculated for each group i (i = 1,2,…,k) of size n_i, then the test statistic H is calculated as follows:

H follows approximately χ² distribution, with the degrees of freedom equal to k − 1.

Results and discussion

Characterizing conformational ensembles of M9 and M8B

We attempted to perform a non-linear multivariate analysis based on the conformational ensembles of M9 and M8B previously obtained from the experimentally validated replica-exchange MD simulations (Fig. S1, ESI†).¹³ These simulations have underscored their differences in the incidence of fold-back conformations in which the outer mannose residues gain access to the reducing terminus, although major conformers of these oligosaccharides adopt extended structures. This is best exemplified by the distance between the outer ManA and reducing-terminal GlcNAc1 residues in the fold-back conformations. M9 exhibits a local maximal value of the fold-back conformational population at the distance of ∼8 Å. In contrast, M8B has no obvious extreme value of the population but adopts the fold-back conformations with shorter distances of <7 Å. In this study, we attempted to provide a comprehensive understanding of these oligosaccharides’ conformational features by our developed kernel methodology in conjunction with GMM clustering. Our approach will be able to complement a previously reported Markov modeling approach, which uses a kernel method for characterizing a biomolecular conformational space on the basis of a limited time scale of the MD simulation.³²

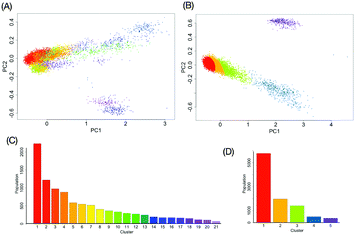
We performed a mapping from the ensemble X of M9 or M8B into RKHS H̃ with the kernel function k, which considers all information of the global conformation of oligosaccharides equally (Fig. S2, ESI†). The values of parameters in the kernel function were estimated as listed in Table S1 (ESI†). To reduce the computational cost, we performed principal component analysis on H̃. Consequently, the obtained RKHS H* (Fig. S3, ESI†) for M9 and M8B with the least number of dimension (d*) of 4 and 2, respectively. To characterize the conformational ensemble X in the feature space H* in connection to the conformational free-energy landscape, clustering with GMM was performed on the images ξ_i(∈H*) mapped from the ensemble of M9 or M8B. The scatterplots in H* are shown in Fig. 3A and B. Twenty-one and five clusters were identified for M9 and M8B, respectively. The population of each cluster is shown in Fig. 3C and D. The relationship between the number of clusters and negative BIC is shown in Fig. S4 (ESI†). Because the mixing proportions of the components are proportional to each cluster's population, they represent the depth of the funnels in the free-energy landscape. These results suggested that M9 and M8B have 21 and 5 meta-stable conformational clusters, respectively.

Fig. 3 Gaussian mixture model clustering in RKHS. (A and B) The scatter plots of the first two kernel principal components projected from the conformational ensemble data of (A) M9 and (B) M8B. The dots correspond to individual conformers. The GMM clustering analysis identified 21 and 5 clusters for M9 and M8B, respectively, which are differently colored. (C and D) The population of individual clusters of (C) M9 and (D) M8B are shown.

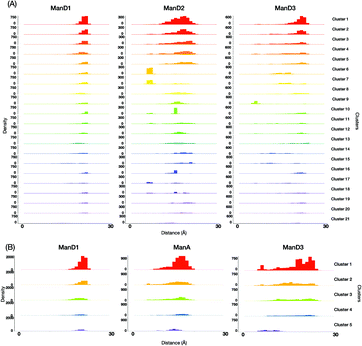
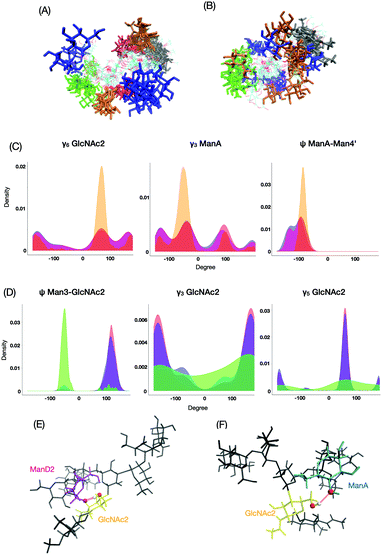
By the Kruskal–Wallis test, we revealed the variables characterizing each cluster. The characteristic variables differ from one cluster to another and their locations in the 3D structure of the oligosaccharides are not always close to each other (Fig. 4). The results implied that not only glycosidic linkage dynamics but also intraresidue conformational factors, including the orientation of each hydroxyl group and the ring puckering state, make non-negligible contributions to the dynamics of the global conformations of oligosaccharides.

Fig. 4 The result of the Kruskal–Wallis test to reveal the variables characterizing each cluster of (A) M9 or (B) M8B. The cells (p < 0.01) are colored in navy blue.

For a more intuitive visualization of the difference among conformational spaces occupied by each cluster, we made scatter plot matrices using end-to-end distances between the reducing-terminal GlcNAc1 residue and each outer mannose residue of M9 and M8B (Fig. 5). In our analysis, 10 clusters of M9 (No. 1, 2, 3, 4, 5, 8, 12, 13, 19, and 20), which occupy approximately 70% in total, commonly exhibited extended structures with the GlcNAc1–ManD2 distance at ∼18 Å and the GlcNAc1–ManD3 distance at ∼23 Å (Fig. S5, ESI†). This is consistent with the previous studies showing that M9 mainly forms extended structures as stable conformers.^33–35 However, it should be noted that these clusters differ in some orientation of hydroxyl groups, e.g., γ₅ in Man4, or ring puckering states, e.g., φ in GlcNAc1 (Fig. S6, ESI†). On the other hand, the unique clusters commonly exhibiting the GlcNAc1–ManA distance at ∼8 Å (e.g., No. 6, 7, and 17), which are therefore characterized as the fold-back conformations, could be unambiguously extracted from the M9 ensembles. Again, these clusters are different in the hydroxyl group orientations and/or ring puckering.

Fig. 5 Analysis of the conformational spaces occupied by each cluster. Histograms of the distances between the anomeric carbons of the reducing-terminal GlcNAc1 residue and that of each outer mannose residue of (A) M9 and (B) M8B, where different colors represent the individual clusters.

This implies that our methodology could successfully classify the conformers with the previously known features, taking account of implicit information, i.e. alteration in the hydroxyl group orientation and/or ring puckering state. They may be coupled with rearrangements of the hydrogen bond networks of residues associated with global conformational dynamics.

Comparing the conformational ensembles between M8B and M9

Despite their distinct functions in cells, M9 and M8B share almost identical covalent structures that differ only in the presence or absence of the non-reducing-terminal mannose residue at the central branch, i.e., ManD2. As mentioned earlier, the conformational distributions in the fold-back states are significantly different between these oligosaccharides. To characterize the difference in their dynamical structures in a more systematic manner, we performed a mapping from the conformational ensembles for M8B and its corresponding parts of M9 (M9*) to a common RKHS H̃ with the kernel function k. The values of scaling parameters in the kernel function are presented in Table S1 (ESI†). By reducing the dimensions with principal component analysis, we gained 3-dimensional feature space H* commonly shared by M9* and M8B. The cumulative variance ratio is shown in Fig. S7 (ESI†).

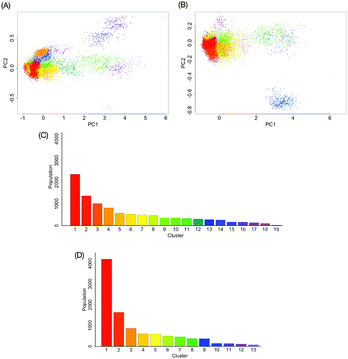
Clustering with GMM was performed on ξ_i ∈ H* to gain 19 and 13 clusters for M9* and M8B, respectively (Fig. 6). The population of each cluster is shown in Fig. 6C and D. The scatterplot in H* colored by the clusters is shown in Fig. 6A and B. The relationship between the number of clusters and negative BIC is shown in Fig. S8 (ESI†). Among these clusters, we identified the conformationally distinct clusters between M9* and M8B by the MMD analysis (Fig. S9, ESI†). We found that the eleven (No. 4, 6, 7, 8, 12, 14, 15, 16, 17, 18 and 19) and six (No. 3, 4, 9, 10, 11, and 13) clusters are distinctive for M9* and M8B, respectively (Fig. S10, ESI†).

Fig. 6 Gaussian mixture model clustering for M9* and M8B in the common RKHS. The scatter plots of the first two kernel principal components projected from the conformational common ensemble data of (A) M9* and (B) M8B. Note that the axes between the two plots are common. Each GMM clustering analysis identified 19 and 13 clusters for M9 and M8B, respectively. The individual clusters are color-coded. The population of individual clusters of (C) M9 and (D) M8B are shown.

These distinctive clusters shed light on significant differences in the distribution of end-to-end distance (Fig. S11, ESI†), demonstrating our methodology's utility, which enables unambiguous classification of M9*- and M8B-characteristic conformers. The M9* ensembles exhibited the second maximum in the GlcNAc1–ManA distance distribution at ∼8 Å, while the M8B ensemble has no prominent secondary peak but exhibits a trailing for shorter distances.

The most major cluster among the M9*-characteristic clusters was cluster No. 4 (Fig. 7A), in which ManD2 is in close spatial proximity to GlcNAc1 with characteristic distributions such as ψ between ManA and Man4′ and γ₆ in GlcNAc2 (Fig. 7C). The conformers in this cluster are frequently stabilized through the hydrogen bonding network involving ManD2 (O2) and GlcNAc2 (H6O–O6) (Fig. 7E). This hydrogen bond is seen in 50% of conformers in the cluster while only 8% in the whole ensemble of M9*. On the other hand, the M8B ensemble is primarily characterized by cluster No. 3 (Fig. 7B). This cluster exhibits characteristic distributions of hydroxyl group orientations as exemplified by γ₃ and γ₅ in GlcNAc2 and glycosidic linkage dihedrals exemplified by ψ between Man3 and GlcNAc2 (Fig. 7D), suggesting that rearrangements of the hydrogen bonding network are coupled with the formation of this M8B-characteristic cluster. Indeed, the hydrogen bond between ManA (O2) and GlcNAc2 (H6O–O6) can be seen more than 10 times more frequently among the conformers in this cluster than in the whole ensemble (5.2% in M8B cluster No. 3 and 0.5% in the whole ensemble). Since M9 possesses the ManD2 residue, which is linked to the C2–OH of ManA, it precludes the formation of its hydrogen bonding (Fig. 7F), rendering this cluster-specific for M8B.

Fig. 7 The structural characterization of M9*-characteristic and M8B-characteristic clusters. The superimposition of each 10 structure extracted from the major (A) M9*-characteristic cluster No. 4 and (B) M8B-characteristic cluster No. 3. The ManD1, ManD2, MaD3, ManA, and GlcNAc1 residues are colored in green, red, blue, yellow, and black, respectively. The characteristic distributions of the orientation of hydroxyl groups and glycosidic linkages in M9* cluster No. 4 and M8B cluster No. 3. (C) The distribution profiles for cluster No. 4, all M9* clusters without No. 4, and all M8B clusters are represented by orange, red, and blue, respectively. (D) The distribution profiles for cluster No. 3, all M8B clusters without No. 3, and all M9* clusters are represented by green, blue and orange, respectively. Close up views of a representative 3D structure of (E) M9* cluster No. 4 and (F) M8B cluster No. 3. The ManD2, ManA, and GlcNAc2 residues are colored in purple, cyan, and yellow, respectively. Dotted lines represent the hydrogen bonds.

Conclusions

In this research, we established a non-linear multivariate analysis of oligosaccharide conformational ensembles using the positive definite kernel function designed for mapping into RKHS by treating all non-redundant variables in a non-biased manner. Using our developed method, we successfully classified conformers of oligosaccharide in association with its conformational free-energy landscape. Our results obtained from the M9 and M8B ensembles indicate that not only glycosidic linkage dihedrals but also intraresidue conformational parameters, i.e., hydroxyl group orientation and/or ring puckering state, should be considered for characterizing the dynamic conformational ensembles. The kernel method proposed in this study will be applicable to nonlinear correlation analyses for quantifying the correlation among the conformational variables, thereby extracting key variables relevant for the formation of specific conformational clusters. Thus, our methodology will open opportunities for exploring the conformational spaces of oligosaccharides, and more generally, molecules with high degrees of motional freedom.

Author contributions

Conceptualization, T. W. and K. K.; data curation, T. W., H. Y., T. Y. and S. Y.; formal analysis, T. W. and T. Y.; funding acquisition, H. Y., T. Y., S. Y., and K. K.; investigation, T. W. and T. Y.; project administration, T. Y., and H. Y.; methodology, T. W. and T. Y.; resources, T. Y.; supervision, K. K.; validation, T. W., H. Y., T. Y., and S. Y.; visualization, T. W., T. Y., and H. Y.; writing – original draft, T. W., H. Y., T. Y., and S. Y.; writing – review and editing, K. K.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partly supported by the Ministry of Education, Culture, Sports, Science and Technology/the Japan Society for the Promotion of Science (MEXT/JSPS) Grants in Aid for Scientific Research (JP19H04569 to T. Y., JP20K15981 to S. Y., and JP19H01017 to K. K.), the Japan Agency for Medical Research and Development, AMED (Project for utilizing glycans in the development of innovative drug discovery technologies), and Joint Research supported by Exploratory Research Center on Life and Living Systems (ExCELLS) (19-302 and 20-304 to T. Y.).

Notes and references

1. U. Häcker, K. Nybakken and N. Perrimon, Nat. Rev. Mol. Cell Biol., 2005, 6, 530–541.
2. M. M. Fuster and J. D. Esko, Nat. Rev. Cancer, 2005, 5, 526–542.
3. Y. Watanabe, T. A. Bowden, I. A. Wilson and M. Crispin, Biochim. Biophys. Acta, Gen. Subj., 2019, 1863, 1480–1497.
4. R. J. Sugrue, Glycovirology Protocols, 2007, pp. 1–13.
5. S. Shanker, L. Hu, S. Ramani, R. L. Atmar, M. K. Estes and B. V. Venkataram Prasad, Curr. Opin. Struct. Biol., 2017, 44, 211–218.
6. K. Kato and T. Peters, NMR in Glycoscience and Glycotechnology, Royal Society of Chemistry, Cambridge, 2017.
7. Y. Yu and M. Delbianco, Chem. – Eur. J., 2020, 26, 9814–9825.
8. A. Gimeno, P. Valverde, A. Ardá and J. Jiménez-Barbero, Curr. Opin. Struct. Biol., 2020, 62, 22–30.
9. E. Fadda and R. J. Woods, Drug Discovery Today, 2010, 15, 596–609.
10. S. Re, Y. Yamaguchi and Y. Sugita, Trends Glycosci. Glycotechnol., 2020, 32, E113–E118.
11. A. Imberty and S. Pérez, Chem. Rev., 2000, 100, 4567–4588.
12. O. Guvench, S. S. Mallajosyula, E. P. Raman, E. Hatcher, K. Vanommeslaeghe, T. J. Foster, F. W. Jamison and A. D. MacKerell, J. Chem. Theory Comput., 2011, 7, 3162–3180.
13. T. Yamaguchi, Y. Sakae, Y. Zhang, S. Yamamoto, Y. Okamoto and K. Kato, Angew. Chem., Int. Ed., 2014, 53, 10941–10944.
14. T. Suzuki, M. Kajino, S. Yanaka, T. Zhu, H. Yagi, T. Satoh, T. Yamaguchi and K. Kato, ChemBioChem, 2017, 18, 396–401.
15. Y. Zhang, T. Yamaguchi, T. Satoh, M. Yagi-Utsumi, Y. Kamiya, Y. Sakae, Y. Okamoto and K. Kato, Adv. Exp. Med. Biol., 2015, 842, 217–230.
16. M. R. Wormald, A. J. Petrescu, Y. L. Pao, A. Glithero, T. Elliott and R. A. Dwek, Chem. Rev., 2002, 102, 371–386.
17. S. Re, S. Watabe, W. Nishima, E. Muneyuki, Y. Yamaguchi, A. D. MacKerell and Y. Sugita, Sci. Rep., 2018, 8, 1644.
18. T. Hofmann, B. Schölkopf and A. J. Smola, Ann. Stat., 2008, 36, 1171–1220.
19. G. W. Brier, Mon. Weather Rev., 1950, 78, 1–3.
20. T. Gneiting and A. E. Raftery, J. Am. Stat. Assoc., 2007, 102, 359–378.
21. D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095.
22. D. A. Case, R. M. Betz, D. S. Cerutti, T. E. Cheatham III, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, C. Lin, T. Luchko, R. Luo, B. Madej, D. Mermelstein, K. M. Merz, G. Monard, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. Roitberg, C. Sagui, C. L. Simmerling, W. M. Botello-Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, L. Xiao and P. A. Kollman, AMBER2016, 2016.
23. R. Ihaka and R. Gentleman, J. Comput. Graph. Stat., 1996, 5, 299–314.
24. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
25. D. Cremer and J. A. Pople, J. Am. Chem. Soc., 1975, 97, 1354–1358.
26. A. Turupcu and C. Oostenbrink, J. Chem. Inf. Model., 2017, 57, 2222–2236.
27. A. M. Westerlund, T. J. Harpole, C. Blau and L. Delemotte, J. Chem. Theory Comput., 2018, 14, 63–71.
28. M. Kanagawa and K. Fukumizu, J. Mach. Learn. Res., 2014, 33, 457–465.
29. L. Scrucca, M. Fop, T. B. Murphy and A. E. Raftery, Mclust 5: Clustering, classification and density estimation using Gaussian finite mixture models, The R Journal, 2016, 8, 289–317.
30. B. K. Sriperumbudur, A. Gretton, K. Fukumizu, B. Schölkopf and G. R. G. Lanckriet, J. Mach. Learn. Res., 2010, 11, 1517–1561.
31. Comprehending Behavioral Statistics|Higher Education.
32. S. Klus, A. Bittracher, I. Schuster and C. Schütte, J. Chem. Phys., 2018, 149, 244109.
33. T. Yamaguchi, Trends Glycosci. Glycotechnol., 2020, 32, E93–E98.
34. E. W. Wooten, R. Bazzo, C. J. Edge, S. Zamze, R. A. Dwek and T. W. Rademacher, Eur. Biophys. J., 1988, 313–319.
35. R. J. Woods, A. Pathiaseril, M. R. Wormald, C. J. Edge and R. A. Dwek, Eur. J. Biochem., 1998, 258, 372–386.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp06448c

---