Shock wave and modelling study of the dissociation kinetics of C2F5I†
Received
11th December 2020
, Accepted 4th February 2021
First published on 4th February 2021
Abstract
The thermal dissociation of C2F5I was studied in shock waves monitoring UV absorption signals from the reactant C2F5I and later formed reaction products such as CF, CF2, and C2F4. Temperatures of 950–1500 K, bath gas concentrations of [Ar] = 3 × 10−5–2 × 10−4 mol cm−3, and reactant concentrations of 100–500 ppm C2F5I in Ar were employed. Absorption-time profiles were recorded at selected wavelengths in the range 200–280 nm. It was found that the dissociation of C2F5I → C2F5 + I was followed by the dissociation C2F5 → CF2 + CF3, before the dimerization reactions 2CF2 → C2F4 and 2CF3 → C2F6 and a reaction CF2 + CF3 → CF + CF4 set in. The combination of iodine atoms with C2F5 and CF3 had also to be considered. The rate constant of the primary dissociation of C2F5I was analyzed in the framework of statistical unimolecular rate theory accompanied by a quantum-chemical characterization of molecular parameters. Rates of secondary reactions were modelled as well. Experimental rate constants for the dissociations of C2F5I and C2F5 agreed well with the modelling results. The comparably slow dimerization 2CF2 → C2F4 could be followed both by monitoring reactant CF2 and product C2F4 absorption signals, while CF3 dimerization was too fast to be detected. A competition between the dimerization reactions of CF2 and CF3, the recombination of CF2 and CF3 forming C2F5, and CF-forming processes like CF2 + CF3 → CF + CF4 finally was discussed.
Introduction
The unimolecular dissociation of perfluoroethyl iodide| |  | (1) |
is of interest for several reasons. On the one hand, like other perfluoroalkyl iodides, C2F5I may be of technical use replacing chlorine- and bromine-containing halons, the latter leading to ozone depletion (e.g., ref. 1–4;  values in the present article are taken from ref. 5 and 6, except for C2F5I and C2F4I whose values are estimated by quantum-chemical calculations). On the other hand, it has interesting kinetic aspects. These are the issue of the present article.
values in the present article are taken from ref. 5 and 6, except for C2F5I and C2F4I whose values are estimated by quantum-chemical calculations). On the other hand, it has interesting kinetic aspects. These are the issue of the present article.
There is, at first, the rate of the unimolecular dissociation of C2F5I. Next, like the thermal dissociation of (C2F5)3N leading to 3C2F5 + N,7reaction (1) is a precursor for C2F5 which dissociates by the reaction
| |  | (2) |
Under typical shock tube conditions, the products CF2 and CF3 of reaction (2) decompose much more slowly than C2F5I and C2F5, see below. Instead of dissociating, they dimerize by the reactions
| |  | (3) |
| |  | (4) |
CF radicals could be formed in reactions like
| |  | (5) |
which would lead to the stable product CF
4; CF might dimerize as well, forming the thermally stable C
2F
2 (or C
2F + F), see below. The rate constants of the various steps in the decomposition mechanism of C
2F
5I play a central role for the understanding of halon dissociation in general (see,
e.g.,
ref. 8). It, therefore, appears worthwhile to study C
2F
5I decomposition in detail.
While the unimolecular dissociations of CF3I and C3F7I have been investigated extensively (see, e.g., the shock wave and modelling studies of ref. 3, 9, and 10 for CF3I and of ref. 4 for C3F7I), such work is lacking for C2F5I. There have been indirect isothermal, steady-state,11,12 and CO2-laser induced11 pyrolysis experiments at moderate temperatures. To our knowledge, however, only a single high-temperature shock wave study has been performed for C2F5I.13 This used the chemiluminescence process I + I → I2 + hν to conclude on reaction (1). Because high reactant concentrations (0.2–1% of C2F5I in Ar) were employed, secondary reactions such as
| |  | (6) |
or
| |  | (7) |
(
reaction (6) followed by the fast dissociation of C
2F
4I to C
2F
4 + I and
reaction (7) followed by the dissociation of I
2) were suggested to form the I atoms which then were used for detection. Other secondary reactions could not be identified, partly because the also recorded UV absorptions of the parent molecules and reaction products were found to be superimposed. As we have studied UV absorptions of possible reaction products separately before, we started a new approach to C
2F
5I dissociation in shock waves, analyzing superimposed absorption signals from reactants and products in the UV. In comparison to
ref. 13, we were able to reduce the reactant concentrations in the shock waves down to 100 ppm in Ar, such that mechanistic aspects of the decomposition could be further investigated under simpler conditions.
The present work should also be seen in relation to dissociation studies of C2F5I using other excitation techniques. The UV photolysis of C2F5I, e.g., has attracted attention as a fast, direct, dissociation process with high yields of excited 2P1/2 iodine atoms (e.g., ref. 14–17). The latter was considered useful for the construction of iodine photodissociation lasers (e.g., ref. 18 and 19). The fast dissociation of C2F4I to C2F4 + I, which had been suggested to follow reaction (6),13 has also been accessible.20 UV laser flash photolysis and IR multiphoton excitation studies of C2F5I led to information21,22 on the reverse of reaction (1) near room temperature, i.e. to the recombination
| |  | (8) |
It was the aim of the present work to shed more light on the mechanism of C2F5I decomposition under high-temperature and low reactant concentration conditions. A theoretical modelling of the falloff curves for the unimolecular dissociation of C2F5I and its reverse reaction (8) was considered helpful for an analysis of the experimental results. As the present work uses UV absorption spectroscopy of the parent molecules and reaction products, quantitative knowledge of several high-temperature absorption coefficients was required. Such information was available from earlier publications referred to later. More information on absorption coefficients of C2F5I has been described recently.23 As reaction (5) may lead to the formation of CF, the dimerization of this species, forming C2F2 (or leading to C2F + F), was also modelled. Likewise, rate constants of other possible secondary reactions such as reactions (6) and (7) were inspected.
Experimental technique and results
Mixtures of 100 and 500 ppm of C2F5I in Ar were heated in shock waves. The mixtures (C2F5I from abcr with 99% purity and Ar from Air Liquide with 99.9999% purity) were prepared in vessels outside the shock tube before being introduced into the tube. The used tube (length of the test section 4.15 m and inner diameter 9.4 cm) has been described before (e.g.ref. 5, 10, and 23–34). The progress of the reaction was followed through windows placed into the wall of the tube, 5 cm in front of the reflecting end plate. Absorption measurements were made with a high pressure Xe arc lamp (Osram XBO 150 W/4), quartz monochromator (Zeiss M3), photomultiplier, and data acquisition arrangement. Absorption-time profiles were recorded behind incident and reflected waves. The available time for measurements behind the reflected shock was about 1.5 ms. As the observed spectra were all continuous or quasi-continuous, broad spectral widths of about ±1 nm could be used. Selected wavelengths from the range 200–280 nm were monitored. Temperatures for kinetic measurements were between 950 and 1500 K, bath gas concentrations [Ar] between 3 × 10−5 and 2 × 10−4 mol cm−3.
The experiments led to a diversity of absorption-time profiles. Representative examples are shown in Fig. 1–5. The analysis of the signals used high-temperature absorption cross sections for C2F5I and C2F5 from ref. 23, for C2F4 from ref. 24, for CF3I (formed by combination of CF3 with I) from ref. 10 and 25, for CF3 from ref. 23 and 26, for CF2 from ref. 24 and 27, and for CF from ref. 28 (representative absorption cross sections at a typical temperature of 1200 K, for orientation, are given in Table 1). In addition, modelled rate constants such as summarized in Table 2 (for their determination, see the following sections and the ESI†) facilitated the analysis. Besides the dissociation reactions, their reverse recombination processes had also to be included. All dissociation and recombination reactions were in their falloff ranges such that suitable falloff expressions of the rate constants (with the parameters given in Table 2) had to be used. Without the mentioned spectroscopic and kinetic input parameters, an interpretation of the signals would have been considerably more difficult.
 |
| | Fig. 1 Absorption-time profile recorded at 268.5 nm in the decomposition of C2F5I (reflected shock wave: T = 1195 K, 500 ppm of C2F5I in Ar, [Ar] = 1.3 × 10−4 mol cm−3; OD5 = ln(I0/I) with light intensity I and path length x = 9.4 cm, see text;  : modelled points with data from Tables 1–3, k5 fitted as k5 ≈ 2 × k−2,∞ where k−2,∞ = k2,∞/K2,c, see text). : modelled points with data from Tables 1–3, k5 fitted as k5 ≈ 2 × k−2,∞ where k−2,∞ = k2,∞/K2,c, see text). | |
 |
| | Fig. 2 As Fig. 1, but recorded at 248 nm (reflected shock wave: T = 1213 K, 530 ppm of C2F5I in Ar, [Ar] = 1.3 × 10−4 mol cm−3;  : modelled points with data from Tables 1–3, k5 fitted as k5 ≈ 1.5 × k−2,∞ where k−2,∞ = k2,∞/K2,c, see text). : modelled points with data from Tables 1–3, k5 fitted as k5 ≈ 1.5 × k−2,∞ where k−2,∞ = k2,∞/K2,c, see text). | |
 |
| | Fig. 3 As Fig. 1, but recorded at 248 nm (reflected shock wave: T = 1117 K, 108 ppm of C2F5I in Ar, and [Ar] = 1.4 × 10−4 mol cm−3;  : modelled points with data from Tables 1–3, k3 increased by a factor of 2 and k5 fitted as k5 ≈ 10 × k−2,∞ where k−2,∞ = k2,∞/K2,c, see text). : modelled points with data from Tables 1–3, k3 increased by a factor of 2 and k5 fitted as k5 ≈ 10 × k−2,∞ where k−2,∞ = k2,∞/K2,c, see text). | |
 |
| | Fig. 4 As Fig. 1, but recorded at 200 nm (reflected shock wave at t = 0.18 ms: T = 1255 K, 533 ppm of C2F5I in Ar, and [Ar] = 1.2 × 10−4 mol cm−3). | |
 |
| | Fig. 5 As Fig. 1, but recorded at 280 nm (reflected shock wave: T = 970 K, 497 ppm of C2F5I in Ar, [Ar] = 1.6 × 10−4 mol cm−3;  : modelled points with data from Tables 1–3, k1 and K1,c decreased by a factor of exp(−600 K/T), see text). : modelled points with data from Tables 1–3, k1 and K1,c decreased by a factor of exp(−600 K/T), see text). | |
Table 1 Selected absorption cross sections σ near T = 1200 K, used for the analysis of Fig. 1–5, see text (* upper limits, estimated for 2000 K)
| Species |
Wavelength (nm) |
σ (cm2) |
Ref. |
| C2F5I |
280 |
4.1 × 10−19 |
23
|
|
|
268.5 |
3.3 × 10−19 |
|
| C2F4 |
200 |
4.5 × 10−18 |
24
|
| CF2 |
280 |
4.2 × 10−19 |
27
|
|
|
268.5 |
2.0 × 10−18 |
|
|
|
248 |
6.8 × 10−18 |
|
|
|
200 |
3.3 × 10−23 |
|
| CF |
248 |
1.0 × 10−17 |
28* |
|
|
200 |
7.0 × 10−17 |
|
Table 2 Modelled rate constants for dissociation reactions and their equilibrium constants (limiting high pressure dissociation rate constants k∞ in s−1, limiting low pressure dissociation rate constants k0/[Ar] in cm3 mol−1 s−1, and weak collision center broadening factors Fcent = Fsccent × 0.64 to be used in falloff expressions from ref. 39–41, equilibrium constants Kc = kdis/krec in mol cm−3, *: experimental adjustment of k1,∞, k1,0, and K1,c possible by adding a factor of exp(−600 K/T), see text)
| Reaction |
Modelled values |
Ref. |
| (1) C2F5I (+Ar) → C2F5 + I (+Ar) |
k
1,∞ = 6.15 × 1015(T/1000 K)−0.90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−28 exp(−28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675 K/T), k1,0 = [Ar]8.70 × 1024(T/1000 K)−11.92 675 K/T), k1,0 = [Ar]8.70 × 1024(T/1000 K)−11.92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−33 exp(−33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 775 K/T), Fcent = 0.059(1000 K), 0.079(1500 K), K1,c = 6.15 × 102(T/1000 K)−1.36 775 K/T), Fcent = 0.059(1000 K), 0.079(1500 K), K1,c = 6.15 × 102(T/1000 K)−1.36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−28 exp(−28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675 K/T) 675 K/T) |
Present* |
|
|
| (2) C2F5 (+Ar) → CF2 + CF3 (+Ar) |
k
2,∞ = 7.88 × 1014![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−27 exp(−27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 181 K/T), k2,0 = [Ar]2.281024(T/1000 K)−14.89 181 K/T), k2,0 = [Ar]2.281024(T/1000 K)−14.89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−35 exp(−35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 119 K/T), Fcent = 0.054(1000 K), 0.051(1500 K), K2,c = 5.75 × 102(T/1000 K)−0.24 119 K/T), Fcent = 0.054(1000 K), 0.051(1500 K), K2,c = 5.75 × 102(T/1000 K)−0.24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−27 exp(−27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 181 K/T) 181 K/T) |
ESI of 5 |
|
|
| (3) C2F4 (+Ar) → 2CF2 (+Ar) |
k
3,∞ = 6.0 × 1015(T/1000 K)−0.87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−35 exp(−35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 K/T), k3,0 = [Ar]1.07 × 1023(T/1000 K)−9.7 050 K/T), k3,0 = [Ar]1.07 × 1023(T/1000 K)−9.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−36 exp(−36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660 K/T), Fcent = 0.083(1000 K), 0.079(1500 K), K3,c = 4.20 × 104(T/1000 K)−2.4 660 K/T), Fcent = 0.083(1000 K), 0.079(1500 K), K3,c = 4.20 × 104(T/1000 K)−2.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−35 exp(−35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 K/T) 050 K/T) |
27 and 29 |
|
|
| (4) C2F6 (+Ar) → 2CF3 (+Ar) |
k
4,∞ = 1.2 × 1018(T/1000 K)−0.52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−49 exp(−49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 316 K/T), k4,0 = [Ar]2.61 × 1027(T/1000 K)−13.8 316 K/T), k4,0 = [Ar]2.61 × 1027(T/1000 K)−13.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−52 exp(−52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289 K/T), Fcent = 0.052(1000 K), 0.041(1500 K), K4,c = 5.94 × 104(T/1000 K)−1.29 289 K/T), Fcent = 0.052(1000 K), 0.041(1500 K), K4,c = 5.94 × 104(T/1000 K)−1.29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−49 exp(−49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 316 K/T) 316 K/T) |
30
|
|
|
| (17) C2F2 (+Ar) → 2CF (+Ar) |
k
17,∞ = 3.90 × 1016(T/1000 K)−0.59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−58 exp(−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 K/T), k17,0 = [Ar]1.22 × 1022(T/1000 K)−7.10 130 K/T), k17,0 = [Ar]1.22 × 1022(T/1000 K)−7.10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−59 exp(−59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 K/T), Fcent = 0.19(1000 K), 0.15(1500 K), K17,c = 3.60 × 104(T/1000 K)−2.15 020 K/T), Fcent = 0.19(1000 K), 0.15(1500 K), K17,c = 3.60 × 104(T/1000 K)−2.15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−58 exp(−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230 K/T) 230 K/T) |
Present |
|
|
| (18) CF3I (+Ar) → CF3 + I (+Ar) |
k
18,∞ = 5.94 × 1015(T/1000 K)−2.20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−28 exp(−28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 928 K/T), k18,0 = [Ar]5.44 × 1021(T/1000 K)−10.46 928 K/T), k18,0 = [Ar]5.44 × 1021(T/1000 K)−10.46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−31 exp(−31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 358 K/T), Fcent = 0.14(1000 K), 0.13(1500 K), K18,c = 8.80 × 102 (T/1000 K)−2.72 358 K/T), Fcent = 0.14(1000 K), 0.13(1500 K), K18,c = 8.80 × 102 (T/1000 K)−2.72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−28 exp(−28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 928 K/T) 928 K/T) |
10
|
Fig. 1, first, shows a signal recorded at 268.5 nm, i.e. at the maximum of the room temperature spectrum of C2F5I.14,35,36 The absorption steps at the arrival of the incident and reflected shocks (behind the two Schlieren peaks) allow one23 to derive the absorption coefficients of C2F5I at 691 K (incident shock) and 1195 K (reflected shock; for a quantitative analysis, one has also to account for the absorption in front of the incident shock, using the known room temperature absorption coefficient). At the temperature of the reflected shock, obviously not only the disappearance of C2F5I but the appearance of a more strongly absorbing reaction product is observed which then disappears on a longer time scale. The identification of this absorber can be made using the rate constants characterized in Table 2. As k1 (close to 105 s−1) for Fig. 1 is markedly larger than k2 (close to 2 × 104 s−1), the decay of C2F5I is too fast to be resolved and the rising signal behind the reflected shock must be attributed to CF2 from reaction (2) (the maximum of CF2 absorption of is located at 248 nm,24,27 but the absorption of the broad quasi-continuum with increasing temperature increasingly extends to longer wavelengths, i.e. also to 268.5 nm).
Fig. 2 shows a signal recorded at 248 nm. Under the assumption that each decomposing C2F5I by reactions (1) and (2) leads to one CF2, the initial rate of increase of the absorption behind the reflected shock in Fig. 2 allows one to derive an experimental value of k2. The detailed analysis (accounting for the Schlieren signal) indeed leads to the modelled value following from Table 2, see below. Besides the initial increase of the signal due to the formation of CF2, the decay of the signal behind the reflected shock must be explained. One finds that the decay of the CF2 signal can mostly be attributed to the known dimerization of CF2 (with rate constants following from Table 2). One, furthermore, observes that the maximum of the signal is markedly smaller than expected for a simple mechanism of reactions (1) and (2) alone. This is attributed to a contribution from reaction (5) which converts CF2 into less reactive species, see below.
A dependence of the CF2 signal on the reactant concentration is documented in Fig. 3 where the initial C2F5I concentration has been decreased by about a factor of 5 in comparison to Fig. 1 and 2. The initial rate of CF2 formation again is well explained by that of C2F5 dissociation (k2 ≈ 2 × 104 s−1). The decay of the CF2 signal on the other hand is markedly slower than that of Fig. 1 and 2, indicating a more complicated kinetics of CF2 disappearance than explained by dimerization alone, see below.
While a contribution from the parent C2F5I to the signal behind the reflected shock at 248 nm is only of minor importance and can be accounted for, one may also look for absorptions from other species. For this reason, we inspected signals at shorter wavelengths. Fig. 4 shows an example recorded at 200 nm. At this wavelength, a contribution of CF2 to the signal can safely be neglected.24 Instead, the absorption from stronger absorbers, forming during the reaction here dominates. One of these can be identified as C2F4.24 First, the rise time of the signal corresponds to the dimerization of CF2 by reaction (3).27,29 Second, at higher temperatures where C2F4 thermally decomposes, the final signals are consistent with the temperature dependence of the C2F4 ⇔ 2CF2 equilibrium.27 Third, the absolute values and the wavelength dependence of the signals agree with the known results for C2F4.24 A second contribution to the signal may arise from the even stronger absorber CF formed by reactions like reaction (5).28 Unfortunately the present work could not provide more insight into the kinetics of CF radicals. It was, therefore, also not clear whether “irregularities” of the signals at late time in Fig. 2 and 4 (after about 1 ms) were due to such reactions, or simply marked the end of the observation time in the shock wave experiments.
In order to record signals with contributions mostly from C2F5I, we finally inspected absorption-time profiles at 280 nm, i.e. on the long-wavelength tails of the C2F5I and CF2 absorption continua. Fig. 5 shows a signal recorded for a temperature lower than those used in Fig. 1–4. Here, CF2 formation is too slow to disturb the absorption signal from C2F5I to a major extent, but the decay of C2F5I becomes visible.
The overall mechanism of C2F5I dissociation, even at reactant concentrations as low as 100 ppm in Ar, apparently was not only determined by the primary first-order dissociation of C2F5I, but by several secondary first- and second- order reaction steps and their reverse reactions (equilibrium constants are included in Table 2). A modelling of the corresponding rate constants appeared helpful for a start of the analysis of signals like Fig. 1–5. This modelling is described in the following section (as well as in the ESI†).
Modelling of rate constants for the unimolecular dissociation of C2F5I
Our quantum-chemical characterization of the potential energy surface for C2F5I dissociation (1) closely followed the procedure outlined for CF3I dissociation in ref. 10 (and its ESI) and needs not to be repeated here. The derived electronic potential for the C2F5–I bond is illustrated in Fig. S1 of the present ESI.† The potential can be approximated by a Morse potential with a Morse parameter β = 1.51 Å−1 (for C2F5–I distances larger than 2.2 Å) or β = 1.76 Å−1 (for C2F5–I distances larger than 3.25 Å). The quanta of the bending modes of C2F5I, which disappear during bond-breaking, decrease exponentially with increasing C2F5–I bond length (with decay parameters α = 0.53(±0.01) Å−1, see Fig. S2 of the ESI†). The decrease of the rotational constant (B + C)/2 of the decomposing C2F5I is also fitted such as illustrated in Fig. S3 of the ESI.† The latter is required for the determination of the centrifugal barriers which can be represented by E0(J) ≈ E0(J = 0) + Cν[J(J + 1)]ν with Cν = hc·1.14 × 10−3 cm−1 and ν = 1.17. Neglecting the anisotropy of the potential, i.e. using phase space theory (PST), high pressure recombination rate constants for reaction (8) of kPSTrec,∞ = (4–6) × 1013 cm3 mol−1 s−1 are obtained between 750 and 2000 K (see the modelling results in Table 2). The anisotropy of the potential introduces “rigidity” and reduces krec,∞ to values below kPSTrec,∞. The classical trajectory version of the statistical adiabatic channel model (SACM/CT) of ref. 37 provides a simple approach to express this reduction as a function of the ratio α/β, here shown to be about 0.3 (one notes that this ratio in the present case is somewhat below the “standard value” 0.5,38i.e. it corresponds to a comparably rigid potential). Table 3 shows the results for krec,∞ which can be approximated by| | | krec,∞ ≈ 1.0 × 1013 (T/1000 K)0.46 cm3 mol−1 s−1 | (9) |
Table 3 Modelled rate constants for dissociation and recombination of C2F5I, kdis = k1 and krec = k8 (kPSTrec,∞ = krec from Phase Space Theory (PST); kPSTrec,∞ and krec,∞ in cm3 mol−1 s−1; kdis,∞ in s−1; kdis,0/[Ar] in cm3 mol−1 s−1; Fcent: weak collision center broadening factors; [Ar]cent in mol cm−3: centers of the falloff curves, see text)
|
T/K |
k
PSTrec,∞
|
k
rec,∞
|
k
dis,∞
|
k
dis,0/[Ar] |
F
cent
|
[Ar]cent |
| 750 |
4.40 × 1013 |
8.89 × 1012 |
1.99 × 10−1 |
4.20 × 107 |
0.063 |
4.7 × 10−9 |
| 1000 |
4.76 × 1013 |
1.00 × 1013 |
2.16 × 103 |
1.86 × 1010 |
0.059 |
1.2 × 10−7 |
| 1500 |
5.46 × 1013 |
1.22 × 1013 |
2.14 × 107 |
1.02 × 1012 |
0.079 |
2.1 × 10−5 |
| 2000 |
6.01 × 1013 |
1.39 × 1013 |
1.95 × 109 |
1.62 × 1012 |
0.12 |
1.2 × 10−3 |
The corresponding dissociation rate constants kdis,∞ in Table 2 are represented by
| | kdis,∞ ≈ 6.15 × 1015(T/1000 K)−0.90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−28 exp(−28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675 K/T) s−1 675 K/T) s−1 | (10) |
It appears worthwhile to compare the modelled high-pressure recombination rate constants for 300 K, i.e. krec,∞(300 K) ≈ 5.5(±3) × 1012 cm3 mol−1 s−1, with the measurements from ref. 21 and 22 which led to a value of 1.2(±0.4) × 1013 cm3 mol−1 s−1. Within the estimated uncertainties of either approach, the results appear sufficiently close.
The calculation of the limiting low-pressure rate constant kdis,0 followed the procedure described in ref. 39 with the required parameters Cν, ν, and E0(J) for the centrifugal barriers as given above (for other parameters, see the ESI†). Collision efficiencies and the corresponding average (total) energies transferred per collision 〈ΔE〉 as usual had to be estimated. Like in previous work, we used a value of 〈ΔE〉/hc ≈ −100 cm−1 for a start. This led to
| | kdis,0 ≈ [Ar]8.7 × 1024(T/1000 K)−11.92 exp(−33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 775 K/T) cm3 mol−1 s−1 775 K/T) cm3 mol−1 s−1 | (11) |
Falloff expressions for the transition of k1 from kdis,0 to kdis,∞ were expressed in the form proposed in ref. 39–42. The required weak collision “center broadening factors” Fcent = Fsccent × 0.64 were estimated with the method of ref. 39–41. Values of Fcent ≈ 0.063, 0.059, 0.079, and 0.12 were derived for T/K = 750, 1000, 1500, and 2000, respectively. The finally obtained falloff curves are shown in Fig. 6. The figure well documents the shift of the falloff curves with temperature. At a bath gas concentration [Ar] = 10−4 mol cm−3 and T ≤ 750 K, the reaction is close to the high-pressure limit, while it is closer to the low-pressure limit at T ≥ 1500 K. Intermediate falloff effects thus are important for all conditions of the present work. Modelled dissociation and recombination rate constants are summarized in Table 3. Values for krec,∞ are compared with kPSTrec,∞, illustrating the effects of the anisotropy of the potential. Furthermore, the positions of the “centers of the falloff curves” [Ar]cent are given, i.e. the values of [Ar] for which kdis,0≈ kdis,∞. The increase of [Ar]cent with increasing T quantifies the shift of the falloff curves with temperature. It also appears important to estimate the uncertainty of kdis,∞ caused by the uncertainty of the reaction enthalpy. The modelling of the signal of Fig. 5 and of the rate constants k1(T) described below suggests an increase of  by about 5 kJ mol−1 which adds a factor of about exp(−600 K/T) to eqn (10) and (11) as well as K1,c in Table 2. Finally, it appears of interest to compare the present modelling results for k1 with values obtained from the iodine chemiluminescence experiments of ref. 13. The values for k1 from the latter work at 1100 K are about a factor of two larger than the present modelling whereas they nearly agree near 1300 K.
by about 5 kJ mol−1 which adds a factor of about exp(−600 K/T) to eqn (10) and (11) as well as K1,c in Table 2. Finally, it appears of interest to compare the present modelling results for k1 with values obtained from the iodine chemiluminescence experiments of ref. 13. The values for k1 from the latter work at 1100 K are about a factor of two larger than the present modelling whereas they nearly agree near 1300 K.
 |
| | Fig. 6 Modelled falloff curves for the unimolecular dissociation of C2F5I in Ar (calculations for 750, 1000, 1500, and 2000 K from bottom to top; see text and ESI†). | |
Modelling of rate constants for secondary reactions
In this section we describe modelling results for reactions which may play a role as secondary processes in the decomposition mechanism of C2F5I. As the falloff curves for the dissociation reactions of C2F4, C2F5, C2F6, and CF3I and their reverse recombination (or dimerization) reactions had been characterized before, they need not to be described here again (see their parameters in Table 2). We only performed a further modelling of C2F2 dissociation and the reverse CF dimerization rates. These data are needed in case that CF is formed by some secondary reactions (details of this modelling are described in the ESI† and the results are included in Table 2). CF is a particularly strong absorber over the wavelength range 200–280 nm studied in the present work, such that eventual contributions from CF to the recorded signals had to be carefully considered. CF, e.g., could be formed by reaction (5); high-energy dissociation channels of C2F4, C2F5, and C2F6, however, could also play some role. For this reason, we determined minimum-energy path (MEP) potentials of the corresponding processes using the quantum-chemical techniques mentioned above. Fig. 7 shows the results for reaction (5) and the dissociation of C2F5. The calculations first show that the MEP pathway from CF2 + CF3 through bound C2F5 to CF + CF4 involves a high energy barrier (TS) of 224.6 kJ mol−1. This would rule out reaction (5) as a pathway for CF formation. However, one may imagine that the exothermic reaction proceeds as a roaming radical process (analogous to processes described in ref. 43–45), skirting “outside” along the barrier of the TS and avoiding the passage of the C2F5 intermediate. While this looks like an attractive possibility, its confirmation by trajectory calculations on a full potential for C2F5 is not within the scope of the present article.
 |
| | Fig. 7 Schematic energy diagram for reactions (2) and (5) (energies in kJ mol−1; from ab initio composite G4 model and Intrinsic Reaction Coordinate (IRC) calculations; see text and ESI†). | |
A high-energy pathway of C2F4 dissociation forming CF under the present conditions apparently is too endothermic (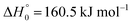 , see the MEP potential of Fig. S13 of the ESI†). On the other hand, the exothermic pathway
, see the MEP potential of Fig. S13 of the ESI†). On the other hand, the exothermic pathway  , followed by reaction (5)i.e. by
, followed by reaction (5)i.e. by  , could also lead to CF (see the MEP potential for CF3 + CF3 in the ESI,† Fig. S14). The formation of some CF in the decomposition mechanism thus also appears possible. It should finally be mentioned that absorption-time profiles like Fig. 4 were also observed in the study of the decomposition of CF3I (see Fig. 6 of ref. 10); these signals were tentatively attributed to the formation of IF. However, an interpretation analogous to that from the present work presents a more attractive alternative. If CF is formed, besides the dimerization 2CF → C2F2 a reaction 2CF → C2F + F should also be considered (see details in ESI†-III).
, could also lead to CF (see the MEP potential for CF3 + CF3 in the ESI,† Fig. S14). The formation of some CF in the decomposition mechanism thus also appears possible. It should finally be mentioned that absorption-time profiles like Fig. 4 were also observed in the study of the decomposition of CF3I (see Fig. 6 of ref. 10); these signals were tentatively attributed to the formation of IF. However, an interpretation analogous to that from the present work presents a more attractive alternative. If CF is formed, besides the dimerization 2CF → C2F2 a reaction 2CF → C2F + F should also be considered (see details in ESI†-III).
Besides pathways for CF formation and rates for CF dimerization, we also modelled the bimolecular reactions (6) and (7) between the parent C2F5I and its dissociation products C2F5 and I. These reactions could be important for higher reactant concentrations and they were used for the observation of the C2F5I decomposition reaction by detection of I2 in ref. 13, see above. Reaction (6) could proceed on the two exothermic pathways
| |  | (12) |
| |  | (13) |
but in both cases high energy barriers TS are involved. The calculations described in the ESI
† led to activation enthalpies of 164.8 kJ mol
−1 for reaction
(12) and 181.1 kJ mol
−1 for
reaction (13). TST calculations of the rate constants were represented by
| | k12 ≈ 2.7 × 1010(T/1000 K)3.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1985 K/T) cm3 mol−1 s−1 exp(−1985 K/T) cm3 mol−1 s−1 | (14) |
| | k13 ≈ 1.2 × 1011(T/1000 K)3.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−21850 K/T) cm3 mol−1 s−1 exp(−21850 K/T) cm3 mol−1 s−1 | (15) |
corresponding to
k12 = 6.5 × 10
1 cm
3 mol
−1 s
−1 and
k13 = 4.0 × 10
1 cm
3 mol
−1 s
−1 at
T = 1000 K. In contrast to these reactions, for
reaction (7) between I and C
2F
5I no activation barrier was found beyond the endothermicity. This is consistent with the experiments of
ref. 11,
12, and
46 which determined an activation energy close to zero for the reverse reaction I
2 + C
2F
5 → I + C
2F
5I. Converting the experimental results for this reaction with the equilibrium constants led to
| | k7 ≈ 3.6 × 1013![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−7460 K/T) cm3 mol−1 s−1 exp(−7460 K/T) cm3 mol−1 s−1 | (16) |
corresponding to
k7 ≈ 2 × 10
10 cm
3 mol
−1 s
−1 at
T = 1000 K. Clearly
reaction (6) thus can be neglected, while
reaction (7) must be accounted for in experiments using larger concentrations than those of the present work.
Analysis of experimental absorption profiles
As emphasized before, the analysis of experimental absorption-time profiles is greatly facilitated by the modelling results described in the two previous sections. In the following this will be demonstrated for the shown examples of experimental signals. As the considered dissociation and the reverse recombination reactions are all in their falloff ranges, the falloff expressions from ref. 39–41 for the [Ar]-dependence of the rate constants were used. The required falloff parameters and equilibrium constants Ki,c were taken from Tables 2 and 3.
For the lowest temperatures of the present study (and the given [Ar]), k1 exceeds k2 (e.g., k1 = 6.7 × 102 s−1vs. k2 = 2.0 × 102 s−1 for Fig. 5). The signal of Fig. 5 at 280 nm, therefore, is dominated by the faster decay of C2F5I and not by the much slower formation of CF2. Fig. 5 includes a modelled absorption-time profile, accounting for the contributions from C2F5I and CF2. In spite of the superposition of the two absorptions, signals like Fig. 5 can be used to derive experimental values of k1 independent of the precise value of k2. One should note, however, that in later stages of the reaction one must account for the onset of the recombination reaction (8), i.e. of C2F5 + I → C2F5I. This can be done with the help of the equilibrium constant K1,c given in Table 2. Within the relatively large experimental uncertainty (because of the superposition of the two absorptions estimated to be about a factor of two), the derived values of k1 agree with the [Ar]-dependent modelling results such as illustrated by the Arrhenius plot of Fig. 8. An improved fit was obtained (both in Fig. 5 and 8) if  was increased from the value calculated in the present work (see the ESI†) by about 5 kJ mol−1. One should mention one further complication: according to the equilibrium constants from Table 2, one would have expected a dissociation of only a few percent of C2F5I until equilibrium in Fig. 5 is reached whereas the signal decays to smaller values. This observation, however, is explained by the onset of reactions (2) and (5), and possibly some contribution from reaction (6).
was increased from the value calculated in the present work (see the ESI†) by about 5 kJ mol−1. One should mention one further complication: according to the equilibrium constants from Table 2, one would have expected a dissociation of only a few percent of C2F5I until equilibrium in Fig. 5 is reached whereas the signal decays to smaller values. This observation, however, is explained by the onset of reactions (2) and (5), and possibly some contribution from reaction (6).
 |
| | Fig. 8 Pseudo-first order rate constants k1 of the unimolecular dissociation of C2F5I at [Ar] = 1.4 × 10−4 mol cm−3 (full line: modelling results from Tables 1–3, curve a for  , curve b for , curve b for  ; symbols: examples of experimental results from the present work with estimated error bars, see text). ; symbols: examples of experimental results from the present work with estimated error bars, see text). | |
Observations at 268.5 nm, such as illustrated in Fig. 1, like in Fig. 5 are characterized by the superposition of absorptions from C2F5I and CF2. As the absorption cross sections of both species are known (see Table 1), the signals nevertheless can be simulated. With the modelled values for k1 and k2 (as well as the other rate constants from Table 1, in particular k3), results such as included in Fig. 1 are obtained, validating the given interpretation of the signals.
At 248 nm the absorption cross section of CF2 by far exceeds that of C2F5I. As C2F5I decomposes much more rapidly than CF2, the formation and consumption of the latter species can well be studied without interference from C2F5I. Assuming that one C2F5 is produced per one dissociating C2F5I, the initial rise of the CF2 signal can be attributed to CF2 formation by reaction (2) alone. The modelling of the complete mechanism also allows one to predict the maximum of the signal. With reactions (1)–(4) one predicts a larger signal than observed. This can be attributed to reaction (5) which efficiently converts CF2 and CF3 into the less active species CF and CF4. The reduction of the maximum of the signals allows one to fit k5. One obtains values of the order of the limiting high pressure rate constant for the recombination of CF2 and CF3 forming C2F5 (e.g., for Fig. 2, k5 ≈ 2 × k−2,∞ where k−2,∞= k2,∞/K2,c; unfortunately the fit of k5 is markedly influenced by uncertainties in k1, k2, k3, and k4, such that more precise determinations have to wait for studies in simpler reaction systems; so far the uncertainty of k5 is estimated to be about a factor of 4).
The contribution of reaction (5) weakens when the reactant concentration is further decreased. Fig. 3 shows an example with a reactant concentration as low as about 100 ppm. The mechanism here indeed is dominated by reactions (1)–(4). Measurements at 248 nm were also performed behind incident shock waves, such that [Ar] could be varied between 2 × 10−5 and 2 × 10−4 mol cm−3. The comparison between experimental and modelled rate constants in the falloff range of reaction (2) is illustrated in Fig. 9 for low and high [Ar]. An agreement with the modelled rate constants within about a factor of 2 was obtained, similar to that of Fig. 8.
 |
| | Fig. 9 Pseudo-first order rate constants k2 of the unimolecular dissociation of C2F5 (2) (full line: modelling results for [Ar] = 1.5 × 10−4 mol cm−3, dashed line: modelling results for [Ar] = 2.8 × 10−5 mol cm−3, see Table 2 and ref. 7; symbols: experimental results from the present work with estimated error bars, see text; open circles for [Ar] = 2.8 × 10−5 mol cm−3, filled circles for [Ar] = 1.5 × 10−4 mol cm−3). | |
While the signals of Fig. 1, 3 and 5 could well be modelled with the data from Tables 1–3 and fitted values of k5, the modelling of Fig. 4 met with difficulties. Although the time dependence of the increasing signal at 200 nm corresponds well to the formation of C2F4 by the dimerization reaction (3), the signal is larger than explained by C2F4 formation alone. Obviously, there is an important, additional, contribution to the signal from the strong absorber CF formed by reaction (5). As only upper limits of the absorption cross section of CF at 200 nm are available (for temperatures near 2000 K) and more precise values of k5 are needed, a modelling of the signal of Fig. 4 does not yet appear warranted. This also concerns the “irregularities” of the signal after about 1 ms (mentioned for Fig. 2 above; one should also mention that the step of the signal at the arrival of the reflected shock wave is due to C2F5I from an absorption band located at wavelengths below 200 nm23). Because of these complications, the present reaction system did not appear suitable for further studies of CF reactions.
Conclusions
The described UV absorption study has provided insight into the dissociation mechanism of C2F5I. It has allowed us to analyze the absorption-time profiles of the dissociating C2F5I and of reaction products like CF, CF2 and C2F4. As the absorptions of these species are all superimposed, modelled rate constants and separately determined absorption cross sections facilitated the analysis of the recorded signals. The diversity of the signals allowed for a validation of the modelled rate constants and the decomposition mechanism. The detection of iodine atoms by ARAS (atomic resonance absorption spectroscopy) like in ref. 3 and 4 (studying the dissociations of CF3I and C3F7I), would have allowed to work with even lower reactant concentrations than the present UV absorption technique and provided a more direct access to the unimolecular dissociation of C2F5I. However, monitoring UV absorption signals of other species at higher reactant concentrations has provided insight into the decomposition mechanism and its secondary reactions.
A number of points deserve particular mention: (i) even under the low concentration conditions of the present work, the reverse of all dissociation reactions had to be included; (ii) falloff effects of all dissociation and recombination reactions had to be accounted for; (iii) the dominant absorption contributions came from C2F5I, CF2, C2F4, and CF, however, with relative importance varying with wavelength and temperature; (iv) CF probably was formed by a roaming radical process CF2 + CF3 → CF + CF4 (5) bypassing the bound C2F5 intermediate (with a rate constant of the order of, but somewhat larger than, the limiting high pressure rate constant for the recombination of CF2 and CF3 forming C2F5); (v) CF apparently dimerizes to C2F2. (vi) besides I atoms, the most stable end products of the decomposition under the conditions of the described work probably are CF4 and C2F2.
The present study illustrates again the benefit of combining kinetic measurements with rate constant modellings. Experimentally determined rate constants for the dissociations of C2F5I and C2F5 were shown to agree well with modelled values which then validates the use of the modelled rate constants for extrapolation into unexplored ranges.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Financial support of this work by the Deutsche Forschungsgemeinschaft (Project TR 69/21-3) is gratefully acknowledged. Open Access funding provided by the Max Planck Society.
References
- S. Solomon, J. B. Burkholder, A. R. Ravishankara and R. R. Garcia, Ozone Depletion and Global Warming Potentials of CF3I, J. Geophys. Res., 1994, 99, 20.929–20.935 CrossRef.
- Yu. N. Shebeko, V. V. Azatyan, I. A. Bolodian, V. Y. Navzenya, S. N. Koyplov, D. Y. Shebeko and E. D. Zamishevski, The Influence of Fluorinated Hydrocarbons on the Combustion of Gaseous Mixtures in a Closed Vessel, Combust. Flame, 2000, 121, 542–547 CrossRef CAS.
- N. S. Bystrov, A. V. Emelianov, A. V. Eremin and P. I. Yatsenko, Direct Measurements of Rate Coefficients for Thermal Decomposition of CF3I using Shock-Tube ARAS technique, J. Phys. D: Appl. Phys., 2018, 51, 1–8 CrossRef.
- N. S. Bystrov, A. V. Emelianov, A. V. Eremin, B. Loukhovitski, A. Sharipov and P. I. Yatsenko, Direct Measurements of C3F7I Dissociation Rate Constant using a Shock-Tube ARAS technique, Int. J. Chem. Kinet., 2019, 51, 206–214 CrossRef CAS.
-
E. Goos, A. Burcat and B. Ruscic, Extended Third Millenium Ideal Gas and Condensed Phase Thermochemical Database for Combustion with Updates from Active Thermochemical Tables. http://burcat.technion.ac.il/div September 2005, January 2015.
-
J. B. Burkholder, J. P. D. Abbatt, R. E. Huie, M. J. Kurylo, D. M. Wilmouth, S. P. Sander, J. R. Barker, C. E. Kolb, V. L. Orkin and P. H. Wine, Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies Evaluation Number 18, JPL Publication 15 – 10 2015, Jet Propulsion Laboratory, Pasadena.
- C. J. Cobos, K. Hintzer, L. Sölter, E. Tellbach, A. Thaler and J. Troe, Shock Wave and Modelling Study of the Dissociation Pathways of (C2F5)3N, Phys. Chem. Chem. Phys., 2019, 21, 9785–9792 RSC.
- K. Li, E. M. Kennedy and B. Z. Dlugogorski, Experimental and Computational Studies of the Pyrolysis of CBrF3, and the Reaction of CBrF3 with CH4, Chem. Eng. Sci., 2000, 55, 4067–4078 CrossRef CAS.
- S. S. Kumaran, M.-C. Su, K. P. Lim and J. V. Michael, Thermal Decomposition of CF3I using I-atom Absorption, Chem. Phys. Lett., 1995, 243, 59–63 CrossRef CAS.
- C. J. Cobos, L. Sölter, E. Tellbach and J. Troe, Falloff Curves and Mechanism of Thermal Decomposition of CF3I in Shock Waves, Phys. Chem. Chem. Phys., 2019, 21, 23892–23899 Search PubMed.
- S. L. Dobychin, V. I. Mashendzhinov, V. I. Mishin, V. N. Semenov and V. S. Shpak, Kinetics of Thermal Decomposition of Perfluoroalkyl Iodides and D(R-I) Binding Energy, R = CF3, C2F5, n-C3F7, iso-C3F7, n-C4F9, tert-C4F9, Dokl. Akad. Nauk SSSR, 1990, 312, 1166–1168 CAS.
- G. A. Skorobogatov, B. P. Dymov and V. K. Khripun, Determination of Rate Constants and Equilibrium Constants of RI ↔ R + I and I + RI ↔ I2 + R for R = CF3, C2F5, or C4F9, Kinet. Katal., 1991, 32, 252–259 CAS.
- I. S. Zaslonko, Yu. K. Mukoseev, G. A. Skorobogatov, V. N. Smirnov and V. K. Khripun, Rate Constant of Thermal Dissociation of Gaseous C2F5I, Kinet. Katal., 1991, 32, 468–473 Search PubMed.
- W. H. Pence, S. L. Baughcum and S. R. Leone, Laser UV Photofragmentation of Halogenated Molecules. Selective Bond Dissociation and Wavelength-Specific Quantum Yields for Excited I(2P1/2) and Br(2P1/2) Atoms, J. Phys. Chem., 1981, 85, 3844–3851 CrossRef CAS.
- D. Krajnovich, L. J. Butler and Y. T. Lee, UV Photodissociation of C2F5Br, C2F5I, and 1,2-C2F4BrI, J. Phys. Chem., 1984, 81, 3031–3047 CrossRef CAS.
- A. V. Baklanov, M. Aldener, B. Lindgren and U. Sassenberg, R2PI Detection of the Quantum Yields of I(2P1/2) and I(2P3/2) in the Photodissociation of C2F5I, n-C3F7I, i-C3F7I and CH3I, Chem. Phys. Lett., 2000, 325, 399–404 CrossRef CAS.
- A. V. Baklanov, G. A. Bogdanchikov, M. Aldener, U. Sassenberg and A. Persson, Nanosecond and Femtosecond Probing of the Dynamics of the UV-photodissociation of Perfluoroethyliodide C2F5I, J. Chem. Phys., 2001, 115, 11157–11165 CrossRef CAS.
-
K. Hohla and K. L. Kompa, in Handbook of Chemical Lasers, ed. R. W. F. Gross and J. F. Bott, Wiley, New York, 1976 Search PubMed.
- G. A. Skorobogatov, Chemical Processes in Active Volume of Photodissociative Iodine Laser, Czech. J. Phys., 1991, 41, 1189–1203 CrossRef CAS.
- D. Zhong and A. H. Zewail, Femtosecond Real-Time Probing of Reactions. 23. Studies of Temporal, Velocity, Angular, and State Dynamics from Transition States to Final Products by Femtosecond-Resolved Mass Spectrometry, J. Phys. Chem. A, 1998, 102, 4031–4058 CrossRef CAS.
- A. M. Velichko, E. B. Gordon, A. A. Nadeikin, A. I. Nikitin and V. L. Tal’roze, Multiphoton Dissociation and Fragmentation of C2F5I, High Energ. Chem., 1986, 20, 468–471 CAS.
- G. A. Skorobogatov, V. G. Seleznev and O. N. Slesar, Method of Overlapping Relaxations Measurement of the Absolute Rate Constants of Competing Reactions of a CnF2n+1 Radical and I(2P1/2), I(2P3/2) Atoms in the Gas Phase, Dokl. Phys. Chem., 1976, 231, 1292–1295 Search PubMed.
- C. J. Cobos, K. Hintzer, L. Sölter, E. Tellbach, A. Thaler and J. Troe, Shock Wave and Modelling Study of the UV Spectra of Perfluorocarbon Iodide and Perfluorocarbon Radicals, Combust. Flame, 2021, 224, 177–182 CrossRef CAS.
- C. J. Cobos, G. Knight, L. Sölter, E. Tellbach and J. Troe, Kinetic and Spectroscopic Studies of the Reaction of CF2 with H2 in Shock Waves, J. Phys. Chem. A, 2017, 121, 7827–7834 CrossRef CAS.
- L. Brouwer and J. Troe, Shock Wave Study of the UV Spectrum of CF3I, Chem. Phys. Lett., 1981, 82, 1–4 CrossRef CAS.
- K. Glänzer, M. Maier and J. Troe, Shock-Wave Study of the High-Temperature UV Absorption and the Recombination of CF3 Radicals, J. Phys. Chem., 1980, 84, 1681–1686 CrossRef.
- C. J. Cobos, A. E. Croce, K. Luther, L. Sölter, E. Tellbach and J. Troe, Experimental and Modeling Study of the Reaction C2F4(+M) ↔ CF2 + CF2(+M), J. Phys. Chem. A, 2013, 117, 11420–11429 CrossRef CAS.
- C. J. Cobos, G. Knight, L. Sölter, E. Tellbach and J. Troe, Experimental and Modeling Study of the Multichannel Thermal Decomposition of CH3F and CH2F, Phys. Chem. Chem. Phys., 2018, 20, 2627–2636 RSC.
- C. J. Cobos, L. Sölter, E. Tellbach and J. Troe, Shock Wave Study of the Thermal Dissociations of C3F6 and c-C3F6. II. Dissociation of Hexafluorocyclopropane and Dimerization of CF2, J. Phys. Chem. A, 2014, 118, 4873–4879 CrossRef CAS.
- C. J. Cobos, A. E. Croce, K. Luther and J. Troe, Temperature and Pressure Dependence of the Reaction 2 CF3(+M) ↔ C2F6(+M), J. Phys. Chem. A, 2010, 114, 4748–4754 CrossRef CAS.
- C. J. Cobos, A. E. Croce, K. Luther and J. Troe, Experimental and Modelling Study of the Unimolecular Thermal Dissociation of CHF3, Z. Phys. Chem., 2011, 225, 1019–1028 CrossRef CAS.
- C. J. Cobos, A. E. Croce, K. Luther and J. Troe, Shock Wave Study of the Thermal Decomposition of CF3 and CF2 Radicals, J. Phys. Chem. A, 2010, 114, 4755–4761 CrossRef CAS.
- C. J. Cobos, G. Knight, L. Sölter, E. Tellbach and J. Troe, Falloff Curves of the Reaction CF3(+M) → CF2 + F(+M), J. Phys. Chem. A, 2020, 124(7), 1235–1239 CrossRef CAS.
- G. Knight, L. Sölter, E. Tellbach and J. Troe, Shock Wave and Modeling Study of the Reaction CF4(+M) ↔ CF3 + F(+M), Phys. Chem. Chem. Phys., 2016, 18, 17592–17596 RSC.
- R. N. Hazeldine, Studies in Spectroscopy. Part III. the Ultra-violet Absorption Spectra of Halogen-containing aliphatic Iodo-compounds, and the Relative Stability of Free Halogen-containing Alkyl Radicals, J. Chem. Soc., 1953, 1764–1771 RSC.
- L. Zhang, W. Fuss and K. L. Kompa, Bond-Selective Photodissociation of CX (X = Br, I) in XC2H4C2F4X, Chem. Phys., 1990, 144, 289–297 CrossRef CAS.
- A. I. Maergoiz, E. E. Nikitin, J. Troe and V. G. Ushakov, Classical Trajectory and Statistical Adiabatic Channel Study of the Dynamics of Capture and Unimolecular Bond Fission. V. Valence Interactions between Atoms and Linear Rotors, J. Chem. Phys., 1998, 108, 9987–9998 CrossRef CAS.
- C. J. Cobos and J. Troe, Theory of Thermal Unimolecular Reactions at High Pressures. II. Analysis of Experimental Results, J. Chem. Phys., 1985, 83, 1010–1015 CrossRef CAS.
- J. Troe, Predictive Possibilities of Unimolecular Rate Theory, J. Phys. Chem., 1979, 83, 114–126 CrossRef CAS.
- J. Troe and V. G. Ushakov, Revisiting Falloff Curves of Thermal Unimolecular Reactions, J. Chem. Phys., 2011, 135(054304), 1–10 Search PubMed.
- J. Troe and V. G. Ushakov, Representation of “Broad” Falloff Curves for Dissociation and Recombination Reactions, Z. Phys. Chem., 2014, 228, 1–10 CAS.
- J. Troe, Theory of Thermal Unimolecular Reactions in the Falloff Range. I. Strong Collision Rate Constants, Ber. Bunsenges. Phys. Chem, 1983, 87, 161–169 CrossRef CAS.
- N. Herath and A. G. Suits, Roaming Radical Reactions, J. Phys. Chem. Lett., 2011, 2, 642–647 CrossRef CAS.
- J. M. Bowman and B. C. Shepler, Roaming Radicals, Annu. Rev. Phys. Chem., 2011, 62, 531–553 CrossRef CAS.
- B. Joalland, Y. Shi, A. Kamasah, A. G. Suits and A. M. Mebel, Roaming Dynamics in Radical Addition-Elimination Reactions, Nat. Commun., 2014, 5(4064), 1–6 Search PubMed.
- E.-C. Wu and R. S. Rodgers, Kinetics of the Gas Phase Reaction of Pentafluoroethyl iodide with Hydrogen Iodide. Enthalpy of Formation of the Pentafluoroethyl Radical and the π Bond Dissociation Energy in Tetrafluoroethylene, J. Am. Chem. Soc., 1976, 98, 6112–6115 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp06414a |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *bc
*bc

 values in the present article are taken from ref. 5 and 6, except for C2F5I and C2F4I whose values are estimated by quantum-chemical calculations). On the other hand, it has interesting kinetic aspects. These are the issue of the present article.
values in the present article are taken from ref. 5 and 6, except for C2F5I and C2F4I whose values are estimated by quantum-chemical calculations). On the other hand, it has interesting kinetic aspects. These are the issue of the present article.








 : modelled points with data from Tables 1–3, k5 fitted as k5 ≈ 2 × k−2,∞ where k−2,∞ = k2,∞/K2,c, see text).
: modelled points with data from Tables 1–3, k5 fitted as k5 ≈ 2 × k−2,∞ where k−2,∞ = k2,∞/K2,c, see text).
 : modelled points with data from Tables 1–3, k5 fitted as k5 ≈ 1.5 × k−2,∞ where k−2,∞ = k2,∞/K2,c, see text).
: modelled points with data from Tables 1–3, k5 fitted as k5 ≈ 1.5 × k−2,∞ where k−2,∞ = k2,∞/K2,c, see text).
 : modelled points with data from Tables 1–3, k3 increased by a factor of 2 and k5 fitted as k5 ≈ 10 × k−2,∞ where k−2,∞ = k2,∞/K2,c, see text).
: modelled points with data from Tables 1–3, k3 increased by a factor of 2 and k5 fitted as k5 ≈ 10 × k−2,∞ where k−2,∞ = k2,∞/K2,c, see text).

 : modelled points with data from Tables 1–3, k1 and K1,c decreased by a factor of exp(−600 K/T), see text).
: modelled points with data from Tables 1–3, k1 and K1,c decreased by a factor of exp(−600 K/T), see text).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−28
exp(−28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675 K/T), k1,0 = [Ar]8.70 × 1024(T/1000 K)−11.92
675 K/T), k1,0 = [Ar]8.70 × 1024(T/1000 K)−11.92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−33
exp(−33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 775 K/T), Fcent = 0.059(1000 K), 0.079(1500 K), K1,c = 6.15 × 102(T/1000 K)−1.36
775 K/T), Fcent = 0.059(1000 K), 0.079(1500 K), K1,c = 6.15 × 102(T/1000 K)−1.36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−28
exp(−28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675 K/T)
675 K/T)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−27
exp(−27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 181 K/T), k2,0 = [Ar]2.281024(T/1000 K)−14.89
181 K/T), k2,0 = [Ar]2.281024(T/1000 K)−14.89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−35
exp(−35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 119 K/T), Fcent = 0.054(1000 K), 0.051(1500 K), K2,c = 5.75 × 102(T/1000 K)−0.24
119 K/T), Fcent = 0.054(1000 K), 0.051(1500 K), K2,c = 5.75 × 102(T/1000 K)−0.24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−27
exp(−27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 181 K/T)
181 K/T)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−35
exp(−35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 K/T), k3,0 = [Ar]1.07 × 1023(T/1000 K)−9.7
050 K/T), k3,0 = [Ar]1.07 × 1023(T/1000 K)−9.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−36
exp(−36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660 K/T), Fcent = 0.083(1000 K), 0.079(1500 K), K3,c = 4.20 × 104(T/1000 K)−2.4
660 K/T), Fcent = 0.083(1000 K), 0.079(1500 K), K3,c = 4.20 × 104(T/1000 K)−2.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−35
exp(−35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 K/T)
050 K/T)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−49
exp(−49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 316 K/T), k4,0 = [Ar]2.61 × 1027(T/1000 K)−13.8
316 K/T), k4,0 = [Ar]2.61 × 1027(T/1000 K)−13.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−52
exp(−52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289 K/T), Fcent = 0.052(1000 K), 0.041(1500 K), K4,c = 5.94 × 104(T/1000 K)−1.29
289 K/T), Fcent = 0.052(1000 K), 0.041(1500 K), K4,c = 5.94 × 104(T/1000 K)−1.29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−49
exp(−49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 316 K/T)
316 K/T)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−58
exp(−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 K/T), k17,0 = [Ar]1.22 × 1022(T/1000 K)−7.10
130 K/T), k17,0 = [Ar]1.22 × 1022(T/1000 K)−7.10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−59
exp(−59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 K/T), Fcent = 0.19(1000 K), 0.15(1500 K), K17,c = 3.60 × 104(T/1000 K)−2.15
020 K/T), Fcent = 0.19(1000 K), 0.15(1500 K), K17,c = 3.60 × 104(T/1000 K)−2.15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−58
exp(−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230 K/T)
230 K/T)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−28
exp(−28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 928 K/T), k18,0 = [Ar]5.44 × 1021(T/1000 K)−10.46
928 K/T), k18,0 = [Ar]5.44 × 1021(T/1000 K)−10.46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−31
exp(−31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 358 K/T), Fcent = 0.14(1000 K), 0.13(1500 K), K18,c = 8.80 × 102 (T/1000 K)−2.72
358 K/T), Fcent = 0.14(1000 K), 0.13(1500 K), K18,c = 8.80 × 102 (T/1000 K)−2.72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−28
exp(−28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 928 K/T)
928 K/T)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−28
exp(−28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675 K/T) s−1
675 K/T) s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 775 K/T) cm3 mol−1 s−1
775 K/T) cm3 mol−1 s−1 by about 5 kJ mol−1 which adds a factor of about exp(−600 K/T) to eqn (10) and (11) as well as K1,c in Table 2. Finally, it appears of interest to compare the present modelling results for k1 with values obtained from the iodine chemiluminescence experiments of ref. 13. The values for k1 from the latter work at 1100 K are about a factor of two larger than the present modelling whereas they nearly agree near 1300 K.
by about 5 kJ mol−1 which adds a factor of about exp(−600 K/T) to eqn (10) and (11) as well as K1,c in Table 2. Finally, it appears of interest to compare the present modelling results for k1 with values obtained from the iodine chemiluminescence experiments of ref. 13. The values for k1 from the latter work at 1100 K are about a factor of two larger than the present modelling whereas they nearly agree near 1300 K.

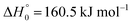 , see the MEP potential of Fig. S13 of the ESI†). On the other hand, the exothermic pathway
, see the MEP potential of Fig. S13 of the ESI†). On the other hand, the exothermic pathway  , followed by reaction (5)i.e. by
, followed by reaction (5)i.e. by  , could also lead to CF (see the MEP potential for CF3 + CF3 in the ESI,† Fig. S14). The formation of some CF in the decomposition mechanism thus also appears possible. It should finally be mentioned that absorption-time profiles like Fig. 4 were also observed in the study of the decomposition of CF3I (see Fig. 6 of ref. 10); these signals were tentatively attributed to the formation of IF. However, an interpretation analogous to that from the present work presents a more attractive alternative. If CF is formed, besides the dimerization 2CF → C2F2 a reaction 2CF → C2F + F should also be considered (see details in ESI†-III).
, could also lead to CF (see the MEP potential for CF3 + CF3 in the ESI,† Fig. S14). The formation of some CF in the decomposition mechanism thus also appears possible. It should finally be mentioned that absorption-time profiles like Fig. 4 were also observed in the study of the decomposition of CF3I (see Fig. 6 of ref. 10); these signals were tentatively attributed to the formation of IF. However, an interpretation analogous to that from the present work presents a more attractive alternative. If CF is formed, besides the dimerization 2CF → C2F2 a reaction 2CF → C2F + F should also be considered (see details in ESI†-III).

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1985 K/T) cm3 mol−1 s−1
exp(−1985 K/T) cm3 mol−1 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−21850 K/T) cm3 mol−1 s−1
exp(−21850 K/T) cm3 mol−1 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−7460 K/T) cm3 mol−1 s−1
exp(−7460 K/T) cm3 mol−1 s−1 was increased from the value calculated in the present work (see the ESI†) by about 5 kJ mol−1. One should mention one further complication: according to the equilibrium constants from Table 2, one would have expected a dissociation of only a few percent of C2F5I until equilibrium in Fig. 5 is reached whereas the signal decays to smaller values. This observation, however, is explained by the onset of reactions (2) and (5), and possibly some contribution from reaction (6).
was increased from the value calculated in the present work (see the ESI†) by about 5 kJ mol−1. One should mention one further complication: according to the equilibrium constants from Table 2, one would have expected a dissociation of only a few percent of C2F5I until equilibrium in Fig. 5 is reached whereas the signal decays to smaller values. This observation, however, is explained by the onset of reactions (2) and (5), and possibly some contribution from reaction (6).
 , curve b for
, curve b for  ; symbols: examples of experimental results from the present work with estimated error bars, see text).
; symbols: examples of experimental results from the present work with estimated error bars, see text).
