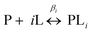Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A general model to optimise CuII labelling efficiency of double-histidine motifs for pulse dipolar EPR applications†
Joshua L.
Wort
a,
Katrin
Ackermann
 a,
David G.
Norman
a,
David G.
Norman
 b and
Bela E.
Bode
b and
Bela E.
Bode
 *a
*a
aEaStCHEM School of Chemistry, Biomedical Sciences Research Complex, and Centre of Magnetic Resonance, University of St Andrews North Haugh, St Andrews KY16 9ST, UK. E-mail: beb2@st-andrews.ac.uk
bSchool of Life Sciences, University of Dundee, Medical Sciences Institute, Dundee, DD1 5EH, UK
First published on 27th January 2021
Abstract
Electron paramagnetic resonance (EPR) distance measurements are making increasingly important contributions to studies of biomolecules underpinning health and disease by providing highly accurate and precise geometric constraints. Combining double-histidine (dH) motifs with CuII spin labels shows promise for further increasing the precision of distance measurements, and for investigating subtle conformational changes. However, non-covalent coordination-based spin labelling is vulnerable to low binding affinity. Dissociation constants of dH motifs for CuII–nitrilotriacetic acid were previously investigated via relaxation induced dipolar modulation enhancement (RIDME), and demonstrated the feasibility of exploiting the dH motif for EPR applications at sub-μM protein concentrations. Herein, the feasibility of using modulation depth quantitation in CuII–CuII RIDME to simultaneously estimate a pair of non-identical independent KD values in such a tetra-histidine model protein is addressed. Furthermore, we develop a general speciation model to optimise CuII labelling efficiency, depending upon pairs of identical or disparate KD values and total CuII label concentration. We find the dissociation constant estimates are in excellent agreement with previously determined values, and empirical modulation depths support the proposed model.
Introduction
Pulse dipolar electron paramagnetic resonance (PDEPR) spectroscopy is an attractive methodology to supplement crystallography, FRET, cryo-EM, or NMR data with nanometre distance constraints in the range 1.5–16 nm.1–6 The approach is solution-based, and accesses structural and dynamic information in biomolecules such as proteins7–12 and nucleic acids.13–16 PDEPR has contributed to conformational studies,17–19 disentangling competing structural models,20,21 and provided mechanistic insights into complex biomolecular apparatus.22–24 Furthermore, PDEPR has been used to monitor complexation,25–27 determine solution-state protein–ligand binding equilibria,28–30 and study oligomerisation-degree.31–34 Commonly, pairs of paramagnetic moieties, such as nitroxide radicals, are covalently introduced and conjugated with thiol side-chains of cysteine residues inserted at strategic positions via site-directed mutagenesis.35,36This covalent attachment of nitroxide radicals through sulfhydryl moieties is convenient and robust,35,37–39 however it results in the labelling of all accessible cysteine residues and so is often intractable in systems which contain essential structural or functional cysteines. This has precipitated interest in alternative labelling chemistries and strategies, such as incorporation of genetically-encoded spin-labels as artificial amino-acids,40–42 and exogenously-introduced transition metal,43–45 or lanthanide metal centres.46–49 One especially promising spin-labelling approach is the co-ordination-based introduction of exogenous CuII–chelates at double-histidine residue (dH) motif sites.50 Typically, histidine residues are arrayed in α-helical and β-sheet secondary structural elements, at positions i to i + 4 and i to i + 2, respectively, and CuII chelated by iminodiacetic acid (CuII–IDA)51 or nitrilotriacetic acid (CuII–NTA)52 self-assemble at these sites. However, because the labelling is non-covalent, it is governed by an equilibrium determined by both the free concentrations of macromolecule and label. It was recently shown that CuII–NTA has low-micromolar affinities for dH sites, under cryogenic conditions.28
These CuII–chelate spin-labels also yield exquisite precision in the distance domain owing to the bipedal mode of attachment, and the rigidity of the co-ordinating imidazole moieties with respect to the protein backbone.50,53 The lack of a flexible linker means dH CuII-labelling is appealing for structural studies in systems with subtle conformational changes54 or nuanced conformational equilibria.55 Furthermore, use of CuII–NTA in conjunction with the commercially available methanethiosulfonate spin label MTSL, in the 5-pulse dead-time free Relaxation Induced Dipolar Modulation Enhancement (RIDME) experiment56 yields superb concentration sensitivity, down to hundreds of nM.28,57 Taken together, this makes dH CuII-labelling a powerful tool for future applications in PDEPR spectroscopy.
However, considering the simple case of a tetra-histidine (double dH) protein labelled with CuII spin-label, optimisation of labelling efficiency for PDEPR applications can become non-trivial.58 Under conditions of partial loading, all CuII species whether dH bound or not can be detected, but not all species will contribute to dipolar modulation of the detected echo. This has obvious implications for measurement sensitivity, being further exacerbated if each site coordinates CuII spin-label with differential affinity and must therefore be treated as non-identical and independent. To achieve widespread use of dH CuII-labelling, there must be a means to optimise labelling efficiency in any given double dH system. The situation will further complicate for more than 2 dH sites.
This problem has been approached previously using a probabilistic method to approximate double dH loading,51 in which the affinities of CuII–IDA and CuII–NTA for each dH co-ordination site were treated individually. However, the approximation of independent sites not depleting the free ligand concentration is not always satisfied. Thus, a model to explicitly treat two independent dH coordination sites simultaneously in a single macromolecule is currently lacking.
Here, we give a general derivation for a multi-site binding polynomial, treating a pair of binding sites with differential affinities. Numerical simulations are used to predict the optimal labelling efficiency depending upon KD values, and the mathematical model is validated experimentally in a protein system. The methodology is evaluated in two aspects: (i) benchmarking the theoretical treatment of modelling speciation against experiment, and (ii) empirical considerations and limitations associated with the approach.
Theoretical background
Multi-site speciation model
Let us begin by considering the general case of a protein (P) ligand (L) reaction scheme, written as:where βi is the macroscopic association constant and is given as (square brackets giving concentrations):
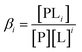 | (1) |
The binding polynomial, Z, can be defined as the partition function of the system, and is therefore the sum of all n species with respect to the concentration of the free macromolecule, [P] as a reference-state:59
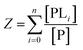 | (2) |
Now consider insertion of βi into the expression for Z above, we have (where for i = 0, β = 1):
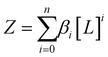 | (3) |
For a protein system containing s identical binding sites, one can convert from macroscopic association constants, βi to microscopic association constant, K:59
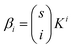 | (4) |
Therefore, in the case of s identical ligand binding sites, we can define Z in terms of the microscopic association constant as:
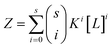 | (5) |
By virtue of the symmetry of Pascal's triangle of binomial coefficients this equals:
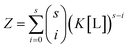 | (6) |
Using the binomial identity, Z can be defined as a sth order polynomial in product of free ligand concentration and microscopic association constant:
| Z = (1 + K[L])s | (7) |
Since Z is a partition function, the fractional population of each species is given as:
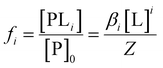 | (8) |
Consider that in the case of non-identical independent binding, that is if K1 ≠ K2:
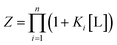 | (9) |
We see for two-site non-identical independent binding, this gives the following definition of Z:
| Z = (1 + K1[L])s × (1 + K2[L])t | (10) |
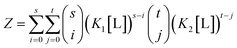 | (11) |
This is equivalent to the form given for 2 non-identical independent binding sites.59 Indeed, in the case of s identical sites, t is 0, so this binomial term reduces to unity, and yields the familiar expression given above in (eqn 7).
It should be recognised that to calculate fractional speciation via this approach, one must have a closed-form expression of the ligand concentration at equilibrium. While analytical solutions exist for polynomials with degree 4, the corresponding roots are no longer unique, and otherwise require numerical simulation. Therefore, it is necessary to approximate all sites as belonging to two classes; considered here as high- and low-affinity, respectively. This allows calculation of [L], from a polynomial with degree 3, trigonometrically via Vietta's substitution.60
More explicitly, [L] is cubic in [L]0 for a two-site system, precluding cooperativity considerations. Let us derive an expression for concentration of protein–ligand complex for a one-site system:
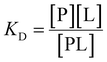 | (12) |
| [P] = [P]0 − [PL] | (13) |
Substituting eqn (13) into eqn (12), we can write:
| KD[PL] = ([P]0 − [PL])[L] | (14) |
Isolating total protein concentration yields:
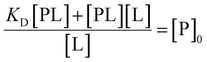 | (15) |
Finally, this can be rearranged to yield an expression for protein–ligand complex, as the familiar one-site Langmuir isotherm:
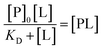 | (16) |
Extending this to a multi-site Langmuir isotherm yields an expression for the concentration of bound ligand, [L]B, where from mass law, and in analogy to (eqn 13):
| [L]B = ([L]0 − [L]) | (17) |
Thus:
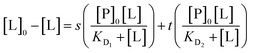 | (18) |
| ([L]0 − [L])(KD1 + [L])(KD2 + [L]) = (KD2 + [L])s[P]0[L] + (KD1 + [L])t[P]0[L] | (19) |
| [L]3 + a[L]2 + b[L] − c = 0 | (20) |
| a = ((s + t)[P]0 + KD1 + KD2 − [L]0) | (21) |
| b = (t[P]0KD1 + s[P]0KD2 + KD1KD2+ (KD1 + KD2)[L]0) | (22) |
| c = KD1KD2[L]0 | (23) |
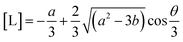 | (24) |
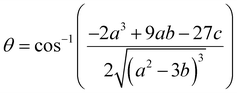 | (25) |
RIDME experiment
The fraction of CuII-labels in doubly labelled protein will be inferred from the modulation depths (Δ) of RIDME experiments. This provides a proxy for the labelling efficiency, which can be optimised by determining the maximum RIDME modulation depth as a function of total CuII-label concentration.Briefly, the 5-pulse RIDME experiment (pulse sequence in ESI†) relies on intrinsic longitudinal relaxation (characterised by the phenomenological relaxation times T1) of homo or hetero spin-pairs; detected (A) spins are perturbed by the change in local magnetic field induced by longitudinal relaxation (Δms) of (B) spins during the interval Tmix, and this manifests as a modulation of the detected refocused electron spin-echo by the dipolar coupling, ωAB. The corresponding inter-spin distance (rAB) is related to the frequency of this modulation61,62 by:
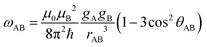 | (26) |
Modulation depth build-up depends on both the length of the interval Tmix, and T1. Under the approximation of mono-exponential T1 behaviour, the asymptotic modulation depth (ΔTmix) for a given ratio of Tmix and T1, is given as:
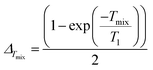 | (27) |
It should be recognised that in the limiting case where: Δ = ΔTmix, the fraction of bound CuII–chelate is unity. One can then define the fraction of CuII–chelate that is doubly bound to the macromolecule (Qexp), given as:
| Δ × ΔTmix−1 = Qexp | (28) |
This equivalence is used interchangeably from this point onwards.
Experimental procedures
Protein purification and EPR sample preparation:
All Streptococcus sp. group G protein G, B1 domain (GB1) protein constructs (I6H/N8H/K28H/Q32H, I6R1/K28H/Q32H and I6H/N8H/K28R1) were produced, expressed, purified and spin labelled as previously reported.28,50 CuII–chelate spin labels were prepared and quantified as previously reported.28,63 All samples were exchanged into deuterated buffer (42.4 mM Na2HPO4, 7.6 mM KH2PO4, 150 mM NaCl, pH 7.4) by freeze-drying and redissolving in D2O. Addition of 50% (v/v) ethylene glycol (EG) d-6 (Deutero GmbH) ensured formation of a glassy frozen solution, after addition of CuII nitrilotriacetic acid (CuII–NTA) label, to a total volume of 70 μL, unless otherwise stated. All EPR samples were immediately flash-frozen in N2(l) by direct immersion, following preparation. The experimental details for EPR spectroscopy and analysis are given in the ESI.† All errors are given as 2σ confidence intervals.Results and discussion
Simulation of I6H/N8H/K28H/Q32H GB1 speciation and modulation depth profile
In the case of orthogonal spin-labels as in CuII–nitroxide RIDME, isotherms can be measured at plateau because modulation depth increases asymptotically, and CuII–chelate can be added to saturation. However, in the case of CuII–CuII RIDME, the titrant will contribute to the signal. The implication is that the sensitivity optimum of CuII–CuII RIDME is a point-solution on the curve, rather than a plateau, which yields a hyperbolic single site saturation function as excess CuII–NTA does not contribute to the detected nitroxide echo.28 For a CuII homo spin-pair (S = 1/2) this means the detected echo will be the weighted contributions of unbound, singly-bound, and doubly-bound (macromolecules with both dH-motifs occupied) CuII spin-label. However, only the doubly-bound macromolecule will modulate the detected echo signal with the dipolar frequency; therefore, to good approximation, the observed modulation depth is the relative quotient of CuII spins which are doubly-bound, against all CuII spins present in the sample, [L]0. This can be succinctly expressed as: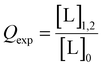 | (29) |
| [L]1,2 = 2θ1,2[P]0 | (30) |
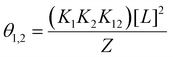 | (31) |
Therefore, using the model elaborated in the theory section, a modulation depth profile is simulated for various concentrations of I6H/N8H/K28H/Q32H GB1 in presence of CuII–NTA, shown in Fig. 1; the dissociation constants used in the simulation (KD1 = 1.4 × 10−7 and KD2 = 1.4 × 10−6) are estimates from previous work.28 Panels (c) and (d) show that dH loading is >90% under these simulated conditions, and a sensitivity optimum is anticipated at approximately a protein-to-CuII–NTA ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.
2.
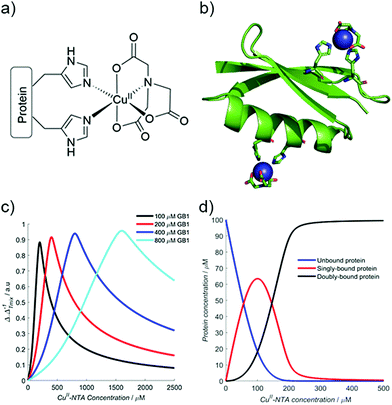 | ||
| Fig. 1 (a) The structure of the CuII–NTA spin label, coordinated to the δ-nitrogen atoms of the imidazole rings of a protein dH site. (b) Double dH (I6H/N8H/K28H/Q32H GB1) construct in cartoon representation (PDB: 4WH4),50 with the CuII–NTA spin labels and co-ordinating dH sites in stick representation and CuII ions as blue spheres. (c) A simulation of modulation depth quotient as a function of increasing CuII–NTA concentration for 100 (black), 200 (red), 400 (blue) and 800 (cyan) μM I6H/N8H/K28H/Q32H GB1, with KD1 = 140 nM and KD2 = 1.40 μM, estimated from previous work.28 (d) A simulated speciation plot for 100 μM protein showing the concentrations of unbound (blue), singly bound (red), and doubly bound (black) protein as a function of CuII–NTA concentration, assuming KD1 = 140 nM and KD2 = 1.40 μM. The axis is truncated to 500 μM, to better resolve each curve. Panels (a) and (b) are taken from Fig. 1 of ref. 28. | ||
The ‘breadth’ of this sensitivity optimum is determined by both KD values, and the protein concentration; at higher protein concentrations, for a fixed KD pair, the profile maximum is broader (see Fig. 1c). The sensitivity optimum will tend towards unity for increasing protein concentrations, for any value of KD. However, in practice, it may be more useful to measure at lower protein concentration, while maintaining high sensitivity in a concentration regime several orders of magnitude greater than the predicted KD values (see ESI†).
Double-dH pseudo-titration with CuII–NTA
To investigate the validity and robustness of the speciation model developed above, a pseudo-titration series of 100 μM I6H/N8H/K28H/Q32H GB1 in presence of 50, 70, 100, 170, 500 and 1000 μM CuII–NTA was prepared. For a homo-spin pair there is a trade-off between measurement sensitivity and the accuracy of the observed modulation depth quotients (Qexp), depending on the error in the approximated T1 value. Importantly, the largest source of error will likely manifest as deviations from the mono-exponential approximation (see ESI†). RIDME measurements were performed with 3 experimental mixing times, since the observed modulation depth is a function of both dH loading and ΔTmix. Mixing times between 0.7 and 1.9 × T1 were used to determine the consistency of the modulation depth quotients.The RIDME data recorded with a ratio of ∼0.7 between mixing time and T1 are shown in Fig. 2. Quantitatively, the trend in modulation depth is consistent with expectation. This is best seen in panel (b) upon comparison of the empirical modulation depths which first increase towards 20% before reducing as excess CuII–NTA is added. Panel (c) of Fig. 2 demonstrates that at low dH CuII-labelling, the reliability of the distance distributions is substantially reduced compared to optimal labelling conditions. Furthermore, the additional distance peaks observed for the 1000 μM CuII–NTA sample may correspond to non-specific interactions away from the dH sites. Nevertheless, in all cases reliable modulation depth information could still be extracted (see ESI†). This further emphasizes the utility of being able to identify optimal labelling conditions for a given system, in the purview of extracting reliable, meaningful distances for CuII–CuII RIDME.
The dipolar spectra are shown in panel (d), the sample measured in presence of 170 μM CuII–NTA gives a spectrum closely resembling a Pake pattern and indicating minimal effects from orientational correlation. However, other points in the series yield spectra with low signal-to-noise (as seen for the 50 and 70 μM CuII–NTA samples) or with additional singularities (as seen for the 1000 μM CuII–NTA sample). An advantage of the 5-pulse RIDME experiment is a reduced susceptibility to orientation selection arising from broadband B-spin excitation only limited by relaxation anisotropy rather than pulse excitation bandwidth as in pulsed electron-electron double resonance (PELDOR).66–69 Orientation selection has previously been demonstrated for double dH CuII–CuII PELDOR at Q-band frequencies,70 although it has not been observed at X-band frequencies attributed to a broad distribution of the g‖ component, and the relative orientations of the g-tensors of the two CuII centres.71 This mechanism of orientational selectivity suppression at X-band has also been observed in other CuII-based spin labels.72
It was observed that the raw 5-pulse RIDME traces contained an additional feature at ∼900 ns in the dipolar evolution functions; it is most prominent in the 70 and 100 μM CuII–NTA samples but persists to varying degrees in all cases. This was attributed to a standing echo artefact that can likely be suppressed through use of an extended 32-step phase-cycle.73 Here, an 8-step phase-cycle was retained for the sake of simplicity as the presence of the artefact did not affect the downstream data analysis. For further discussion and measurements performed using the extended phase-cycle see ESI.† Initial concern that for low signal-to-noise ratio samples, the presence of the artefact would artificially inflate the white-noise estimation in the error analysis did not manifest (see ESI†).
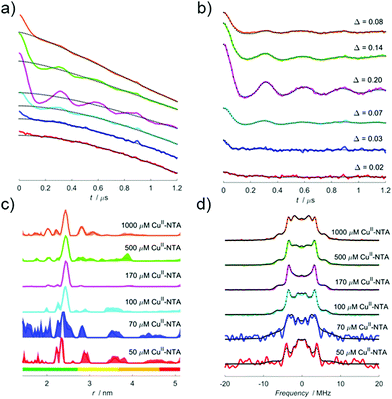
Bivariate fitting of dissociation constants
The pseudo-titration series (treated with a stretched exponential background function) for all ratios of Tmix and T1 are shown in Fig. 3, and pairs of dissociation constants are fitted to experimental modulation depth quotients (Qexp) and are given in the figure legend.Importantly, the fit demonstrates that both sites differ by an order of magnitude in affinity, in good agreement with isothermal titration calorimetry (ITC) data and CuII–NTA nitroxide RIDME pseudo-titrations.28 CuII–nitroxide RIDME pseudo-titrations suggested KD values of 140 nM and 1.4 μM for the α-helical and β-sheet dH motifs, respectively. Fig. 3d shows the error surface corresponding to all CuII–CuII RIDME pseudo-titration data fitted simultaneously. There are two correlated troughs, with the diagonal ridge indicating the affinities are different, though all fitted solutions fall within these broad ridges. The determined affinities from the CuII–CuII RIDME pseudo-titration are in the low μM concentration regime (one site will be <10 μM, and the other will be an order of magnitude lower).
However, the error in the absolute KD estimation will be large, since measurements at protein concentrations in the same range as the KD value afford higher measurement accuracy.74–76 Owing to sensitivity limitations associated with detection of small modulation depth changes in intentionally under-labelled samples, an empirical protein concentration of 100 μM was chosen. In the limiting case of high affinity, the simulated profiles are largely identical, and the discerning feature becomes the maximum modulation depth quotient (see ESI†). In this case, moving into a lower protein concentration regime would be desirable, and would improve precision of KD determination.
The fitted KD estimates are within the troughs of the error surface for all mixing time ratios. Comparison with values previously determined by ITC extrapolated to 239 K (220 and 750 nM) indicate they are at the periphery of the ridge, likely because the current protein concentration does not facilitate precise determination of KDs significantly below the low μM concentration regime. The ITC data showed exothermic binding, predicting higher affinity at lower temperature. The EPR data of samples snap-frozen in liquid nitrogen was consistent with the binding equilibrium freezing out at 235–240 K.28 Comparison of the KDs determined by CuII–nitroxide RIDME further supports this assumption, being consistent with the error surface troughs. Recent UV-vis data suggested an arithmetic average KD across both dH sites of 6 μM in phosphate buffer,58 comparing favourably with previous ITC measurements extrapolated to 281 K (16 and 2 μM for β-sheet and α-helical dH motif, respectively), which is consistent with the upper limits of the CuII–CuII RIDME error surface troughs (∼10 μM and ∼1 μM), see Fig. 3d.
The lack of exact numerical agreement between the CuII–CuII RIDME and UV-vis data is unsurprising since measurements were performed with different temperatures and cryoprotectant. As expected from the temperature dependence of the binding equilibrium, the KD estimates from UV-vis and ITC at 281 K represent the upper-bound of the CuII–CuII RIDME estimates. The agreement between the CuII–nitroxide and CuII–CuII RIDME is greater, likely because the KD values are reflective of similar temperature regimes, and buffer composition was nominally identical. The buffer conditions can have a significant effect on affinity.58 Furthermore, the cooling rate would be expected to influence the measured KD value, as the equilibrium will freeze out somewhere between room-temperature and the glass transition temperature. Using freeze-quench techniques or alteration of the matrix composition are potential avenues of investigation in future work, to provide snapshots of the equilibrium at different temperatures using this approach.
All data shown in Fig. 3 were also fitted globally (for all ratios of Tmix and T1) and KD values were consistent, particularly with the Tmix to T1 ratio of 1.9 (see ESI†). The global fitting approach of both CuII–CuII and low concentration CuII–nitroxide RIDME shows an improved agreement with ITC predictions (see ESI†). Taken together, this suggests that accurate information regarding binding equilibria can be extracted from double dH systems, in a single measurement series. However, where available CuII–nitroxide and CuII–CuII RIDME pseudo-titrations can be combined, to independently validate binding affinities. It should also be noted that CuII–CuII RIDME pseudo-titrations are likely to be of greater diagnostic value in systems where binding sites differ by an order of magnitude or greater in their respective affinities.
The error associated with modulation depth quotients (Qexp) quantified via CuII–CuII RIDME will tend to be larger than those quantified via CuII–nitroxide RIDME. However, the error in modulation depths (Δ) was more comparable with CuII–nitroxide RIDME, within ±0.03. Additionally, the relative error in the modulation depth quotients generally reduces at longer mixing time and was found to be ±25% for a Tmix and T1 ratio of 1.9. Only for the series recorded with the highest ratio (Fig. 3c) do all experimental data points lie on the fitted curve (within error), and the original simulated modulation depth profile, indicating it is the most consistent with previous ITC and CuII–nitroxide RIDME data. The fit quality improves at longer mixing times.
The series measured with a ratio of 0.7 overestimates Δ, and so yields the highest affinity estimates and gives a bad fit of points away from the curve. These manifest because a fast component in T1 is not treated by the mono-exponential approximation. While all mixing time ratios reproduce the trend in KD estimates, the longer mixing times provide greater accuracy because deviations of T1 from mono-exponential behaviour will not manifest as severely. Indeed, analysis of the RIDME modulation depths using a bi-exponential approximation of T1 behaviour results in KD estimates that are more stable for different Tmix and T1 ratios (see ESI†).
Interestingly, the error surface also reveals that the shape of the modulation depth profile is highly sensitive to the magnitude of the individual KD values, and not simply their product. Indeed, simulation with KD values of (i) 100 nM and 1 μM, and (ii) 10 nM and 10 μM (where individual KD values are increased and decreased respectively, by an order of magnitude, but their product remains unchanged) show that the agreement between simulation and experiment is poorer in the latter case (see ESI†). However, this approach cannot assign the KD values to each disparate site without additional information.
The observation that the KD values are not ‘compensatory’ has important implications for the robustness of the model. It allows one to ‘compartmentalise’ the profile into the initial flank, maximum and the region to the right of the maximum, in discussions regarding the higher- and lower-affinity KD values. The region to the right of the maximum is independent of either KD and only dependent upon the ratio of double dH protein and total CuII chelate concentrations, since in this regime all additional ligand will be unbound, and thus dilute the bound component which contributes to modulation depth. Therefore, this region of the profile can be used as an internal control, to assess the concentration accuracy of the pseudo-titration series (see ESI†).
Considerations for accurate CuII–CuII RIDME modulation depth quantitation
One consideration of using a coordination-based spin labelling method, is that relaxation behaviour may differ between the free and bound components. This means that under conditions of partial loading, the relative contributions of free and dH-bound CuII–chelate to the detected echo will be different. Differences in Tm between free and dH bound CuII–NTA were found to be negligible, while Tm of free and dH bound CuII–IDA varied by approximately 2-fold (see ESI†). More significant is differential longitudinal relaxation behaviour.25 This is partially addressed by varying mixing time length with respect to T1, although sensitivity becomes limiting at sufficiently long mixing time intervals. Nevertheless, for all mixing times the trend in Δ was found to be consistent, without further treatment.If bound and free CuII–NTA differ in their EPR spectra, their contribution might not reflect their stoichiometry. Indeed, for CuII–nitroxide PELDOR measurements, the modulation depth varied when selecting different spectral positions corresponding to the CuII–chelate for the echo forming pulses. This is attributed to different spectra and maxima of the two species. Since CuII–CuII RIDME also relies on detection of a CuII–chelate species, this could be problematic because measurement at two distinct field positions could yield different affinity estimates, and therefore not be robust. However, all RIDME measurements in this work were performed using the maximum of the CuII–chelate spectrum as the detection position, which would commonly be the most desirable position (ignoring effects from angular correlations and orientation selection) to ensure a high SNR. Furthermore, we find that the affinities estimated from the CuII–CuII RIDME measurements closely align with previous estimates stated above. In our hands, detecting at the maximum of the CuII–chelate spectrum does not cause significant deviations in the apparent KD, however this is not necessarily satisfied for all field positions.
Perhaps the furthest reaching implication of determining KDvia pulse EPR is that it allows the coupling of structural and binding equilibria information. Therefore, the aim should be to find a compromise wherein both modulation depth information and structural information can be reliably extracted. Here, using longer mixing times (i.e., 1.9 × T1 as Tmix) yielded the best agreement of KD estimates with previous CuII–nitroxide RIDME measurements, while still allowing reliable extraction of distance information. Taken together, this suggests that CuII–CuII RIDME measurements with longer mixing times (in the regime ∼2 × T1 as Tmix) allow for greater accuracy in KD determination, despite the associated loss of a factor 2 in measurement sensitivity, and without compromising the reliability of the distance information extracted.
Conclusions
Our findings demonstrate that modulation depth quantitation in a CuII homo-spin system via 5-pulse RIDME is feasible; binding equilibria information can be reliably obtained, and empirical observation agrees nicely with theoretical prediction from the general multi-site binding model developed herein. Results indicate that while there is a reasonable uncertainty in the absolute affinities, their relative difference is pronounced, even at protein concentrations >2 orders of magnitude above KD. Furthermore, the previously benchmarked method of KD determination via 5-pulse RIDME can be extended to an analytical two-site independent binding model. Potential empirical considerations for modulation depth quantitation in double dH constructs have also been discussed. Even so, for future work a systematic treatment of how to optimise modulation depth quantitation and KD determination from CuII–nitroxide and CuII–CuII 5-pulse RIDME pseudo-titrations is desirable.One exciting prospect is that PDEPR allows intimate coupling of both structural and thermodynamic information. Furthermore, the sensitivity of PDEPR is significantly higher than for other techniques used to study thermodynamic parameters, such as ITC, and so could be used in concert with these techniques. It is also recognised that through orthogonal labelling routines or using spectroscopically orthogonal spin centres, it may become feasible to investigate complicated protein–ligand binding equilibria via modulation depth quantitation between different subsets of spins, simultaneously. This is particularly appealing in comparison to ITC since calorimetric methods have historically struggled to disentangle non-specific or multiple sequential binding events.
Additionally, the results presented herein also showcase that dissociation constants can be investigated and derived for systems which are not amenable to thiol-based site-directed spin labelling with an organic radical spin label. This is significant because it expands the utility of this approach to proteins containing essential cysteine residues. However, it should be acknowledged that this approach cannot assign affinities to individual sites. Nonetheless, the further confirmation of high nM and low μM affinities of α-helical and β-sheet dH motif sites for CuII–NTA, respectively, holds promise for their future widespread application in the field of PDEPR. Finally, the mathematical model derived above can be appropriated to solve sensitivity optima and maximise labelling efficiency for coordination-based spin labelling strategies, governed by binding equilibria. This may be especially useful in cases where binding affinity or protein concentration is limiting.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Hassane El Mkami for help with EPR. JLW is supported by the BBSRC DTP Eastbio. We thank the Leverhulme Trust for support (RPG-2018-397). This work was supported by equipment funding through the Wellcome Trust (099149/Z/12/Z) and BBSRC (BB/R013780/1). We gratefully acknowledge ISSF support to the University of St Andrews from the Wellcome Trust. The research data supporting this publication can be accessed at https://doi.org/10.17630/d591aa48-7239-40b0-afef-9f63dac86e9c [ref. 77]Notes and references
- A. D. Milov, K. M. Salikhov and M. D. Schirov, Fiz. Tverd. Tela., 1981, 23, 975 CAS.
- A. D. Milov, A. B. Ponomarev and Y. D. Tsvetkov, Chem. Phys. Lett., 1984, 110, 67 CrossRef CAS.
- T. Schmidt, M. A. Walti, J. L. Baber, E. J. Hustedt and G. M. Clore, Angew. Chem., Int. Ed., 2016, 55, 15905 CrossRef CAS.
- G. Jeschke, Emerging Top. Life Sci., 2018, 2, 9 CrossRef CAS.
- H. Sanabria, D. Rodnin, K. Hemmen, T. Peulen, S. Felekyan, M. R. Fleissner, M. Dimura, F. Koberling, R. Kuhnemuth, W. Hubbel, H. Gohlke and C. A. M. Seidel, Nat. Commun., 2020, 11, 1231 CrossRef CAS.
- O. Duss, M. Yulikov, F. H. T. Allain and G. Jeschke, Methods Enzymol., 2015, 558, 279 CAS.
- E. H. Yardeni, T. Bahrenberg, R. A. Stein, S. Mishra, E. Zomot, B. Graham, K. L. Tuck, T. Huber, E. Bibi, H. S. Mchaourab and D. Goldfarb, Sci. Rep., 2019, 9, 12528 CrossRef.
- T. Strohaker, B. C. Jung, S. Liou, C. O. Fernandez, D. Riedel, S. Becker, G. M. Halliday, M. Bennati, W. S. Kim, S. Lee and M. Zweckstetter, Nat. Commun., 2019, 10, 5535 CrossRef.
- S. Chuo, S. Liou, L. Wang, R. D. Britt, T. L. Poulos, I. F. Sevrioukova and D. B. Goodin, Biochemistry, 2019, 58, 3903 CrossRef CAS.
- M. Kim, S. A. Vishivetskiy, N. V. Eps, N. S. Alexander, W. M. Cleghorn, X. Zhan, S. M. Hanson, T. Morizumi, O. P. Ernst, J. Meiler, V. V. Gurevich and W. L. Hubbell, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18407 CrossRef CAS.
- D. T. Edwards, T. Huber, S. Hussain, K. M. Stone, M. Kinnebrew, I. Kaminker, E. Matalon, M. S. Sherwin, D. Goldfarb and S. Han, Structure, 2014, 22, 1677 CrossRef CAS.
- B. Verhalen, R. Dastvan, S. Thangapandian, Y. Peskova, H. A. Koteiche, R. K. Nakamoto, E. Tajkho and H. S. Mchaourab, Nature, 2017, 543, 738 CrossRef CAS.
- O. Schiemann, N. Piton, Y. Mu, G. Stock, J. W. Engels and T. F. Prisner, J. Am. Chem. Soc., 2004, 126, 5722 CrossRef CAS.
- C. Wuebben, S. Blume, D. Abdullin, D. Brajtenbach, F. Haege, S. Kath-Schorr and O. Schiemann, Molecules, 2019, 24, 4482 CrossRef CAS.
- O. Duss, M. Yulikov, G. Jeschke and F. H. T. Allain, Nat. Commun., 2014, 5, 3669 CrossRef CAS.
- E. S. Babaylova, A. A. Malygin, A. A. Lomzov, D. V. Pyshnyi, M. Yulikov, G. Jeschke, O. A. Krumkacheva, M. V. Fedin, G. G. Karpova and E. G. Bagryanskaya, Nucleic Acids Res., 2016, 44, 7935 CrossRef CAS.
- H. Sameach, A. Narunsky, S. Azoulay-Ginsberg, L. Gevorkyan-Aiapetov, Y. Zehavi, Y. Moskovitz, T. Juven-Gershon, N. Ben-Tal and S. Ruthstein, Structure, 2017, 25, 988 CrossRef CAS.
- A. Dalaloyan, A. Martorana, Y. Barak, D. Gataulin, E. Reuveny, A. Howe, M. Elbaum, S. Albeck, T. Unger, V. Frydman, E. H. Abdelkader, G. Otting and D. Goldfarb, ChemPhysChem, 2019, 20, 1860 CrossRef CAS.
- B. Joseph, A. Sikora and D. S. Cafiso, J. Am. Chem. Soc., 2016, 138, 1844 CrossRef CAS.
- F. X. Theillet, A. Binolfi, B. Bekei, A. Martorana, H. M. Rose, M. Stuiver, S. Versini, D. Lorenz, M. van Rossum, D. Goldfarb and P. Selenko, Nature, 2016, 530, 45 CrossRef CAS.
- P. S. Kerry, H. L. Turkington, K. Ackermann, S. A. Jamieson and B. E. Bode, J. Phys. Chem. B, 2014, 118, 10882 CrossRef CAS.
- C. A. J. Hutter, M. Hadi-Timachi, L. M. Hurlimann, I. Zimmerman, P. Egloff, H. Goddeke, S. Kucher, S. Stefanic, M. Kartunnen, L. V. Schafer, E. Bordignon and M. A. Seeger, Nat. Commun., 2019, 10, 2260 CrossRef CAS.
- C. Kapsalis, B. Wang, H. El Mkami, S. J. Pitt, J. R. Schnell, T. K. Smith, J. D. Lippiat, B. E. Bode and C. Pliotas, Nat. Commun., 2019, 10, 4619 CrossRef.
- D. Constantinescu-Aruxandei, B. Petrovic-Stojanovska, O. Schiemann, J. H. Naismith and M. F. White, Nucleic Acids Res., 2016, 44, 954 CrossRef CAS.
- A. Giannoulis, M. Oranges and B. E. Bode, ChemPhysChem, 2017, 18, 2318 CrossRef CAS.
- K. Ackermann, A. Giannoulis, D. B. Cordes, A. M. Z. Slawin and B. E. Bode, Chem. Commun., 2015, 51, 5257 RSC.
- A. Giannoulis, K. Ackermann, P. Spindler, C. Higgins, D. B. Cordes, A. M. Z. Slawin, T. F. Prisner and B. E. Bode, Phys. Chem. Chem. Phys., 2018, 20, 11196 RSC.
- J. L. Wort, K. Ackermann, A. Giannoulis, A. J. Stewart, D. G. Norman and B. E. Bode, Angew. Chem., Int. Ed., 2019, 58, 11681 CrossRef CAS.
- J. Glaenzer, M. F. Peter, G. H. Thomas and G. Hagelueken, Biophys. J., 2017, 112, 109 CrossRef CAS.
- A. Collauto, H. A. DeBerg, R. Kaufmann, W. N. Zagotta, S. Stoll and D. Goldfarb, Phys. Chem. Chem. Phys., 2017, 19, 15324 RSC.
- E. A. Riederer, P. J. Focke, E. R. Georgieva, N. Akyuz, K. Matulef, P. P. Borbat, J. H. Freed, S. C. Blanchard, O. Boudker and F. I. Valiyaveetil, eLife, 2018, 7, e36478 CrossRef.
- A. Giannoulis, R. Ward, E. Branigan, J. H. Naismith and B. E. Bode, Mol. Phys., 2013, 111, 2845 CrossRef CAS.
- G. Hagelueken, W. J. Ingledew, H. Huang, B. Petrovic-Stojanovska, C. Whitfield, H. E. Mkami, O. Schiemann and J. H. Naismith, Angew. Chem., Int. Ed., 2009, 48, 2904 CrossRef CAS.
- T. Schmidt, R. Ghirlando, J. Barber and G. M. Clore, ChemPhysChem, 2016, 17, 2987 CrossRef CAS.
- W. L. Hubbell and C. Altenbach, Curr. Opin. Struct. Biol., 1994, 4, 566 CrossRef CAS.
- T. Braun, M. Drescher and D. Summerer, Int. J. Mol. Sci., 2019, 20, 373 CrossRef.
- S. Kim, Y. Jang, S. Ha, J. Ahn, E. Kim, J. H. Lim, C. Cho, Y. S. Ryu, S. K. Lee, S. Y. Lee and K. Kim, Nat. Commun., 2015, 6, 8410 CrossRef CAS.
- P. Khanal, Z. Jia and X. Yang, Sci. Rep., 2018, 8, 3485 CrossRef.
- D. W. Bak, M. D. Pizzagalli and E. Weerapana, ACS Chem. Biol., 2017, 12, 947 CrossRef CAS.
- G. E. Merz, P. P. Borbat, A. R. Muok, M. Srivastava, D. N. Bunck, J. H. Freed and B. R. Crane, J. Phys. Chem. B, 2018, 122, 9443 CrossRef CAS.
- E. G. B. Evans and G. L. Millhauser, Methods Enzymol., 2015, 563, 503 CAS.
- M. J. Schmidt, J. Borbas, M. Drescher and D. Summerer, J. Am. Chem. Soc., 2014, 136, 1238 CrossRef CAS.
- E. Narr, A. Godt and G. Jeschke, Angew. Chem., Int. Ed., 2002, 114, 4063 CrossRef.
- B. E. Bode, J. Plackmeyer, T. F. Prisner and O. Schiemann, J. Phys. Chem. A, 2008, 112, 5064 CrossRef CAS.
- Z. Wu, A. Feintuch, A. Collauto, L. A. Adams, L. Aurelio, B. Graham, G. Otting and D. Goldfarb, J. Phys. Chem. Lett., 2017, 8, 5277 CrossRef CAS.
- L. Garbuio, E. Bordignon, E. K. Brooks, W. L. Hubbell, G. Jeschke and M. Yulikov, J. Phys. Chem. B, 2013, 117, 3145 CrossRef CAS.
- A. Shah, A. Roux, M. Starck, J. A. Mosely, M. Stevens, D. G. Norman, R. I. Hunter, H. El Mkami, G. Smith, D. Parker and J. E. Lovett, Inorg. Chem., 2019, 58, 3015 CrossRef CAS.
- G. Prokopiou, M. D. Lee, A. Collauto, E. H. Abdelkader, T. Bahrenberg, A. Feintuch, M. Ramirez-Cohen, J. Clayton, J. D. Swarbrick, B. Graham, G. Otting and D. Goldfarb, Inorg. Chem., 2018, 57, 5048 CrossRef CAS.
- D. Barthelmes, M. Granz, K. Barthelmes, K. N. Allen, B. Imperiali, T. F. Prisner and H. Schwalbe, J. Biomol. NMR, 2015, 63, 275 CrossRef CAS.
- T. F. Cunningham, M. R. Putterman, A. Desai, W. S. Horne and S. Saxena, Angew. Chem., Int. Ed., 2015, 54, 6330 CrossRef CAS.
- M. J. Lawless, S. Ghosh, T. F. Cunningham, A. Shimshi and S. Saxena, Phys. Chem. Chem. Phys., 2017, 19, 20959 RSC.
- S. Ghosh, M. J. Lawless, G. S. Rule and S. Saxena, J. Magn. Reson., 2018, 286, 163 CrossRef CAS.
- S. Ghosh, S. Saxena and G. Jeschke, Appl. Magn. Reson., 2018, 49, 1281 CrossRef CAS.
- H. Sameach, S. Ghosh, L. Gevorkyan-Airapetov, S. Saxena and S. Ruthstein, Angew. Chem., Int. Ed., 2019, 10, 3053 CrossRef.
- M. J. Lawless, J. R. Petterson, G. S. Rule, F. Lanni and S. Saxena, Biophys. J., 2018, 114, 592 CrossRef CAS.
- S. Milikisyants, F. Scarpelli, M. G. Finiguerra, M. Ubbink and M. Huber, J. Magn. Reson., 2009, 201, 48 CrossRef CAS.
- K. Ackermann, J. L. Wort and B. E. Bode, Nanomolar Pulse Dipolar EPR Spectroscopy in Proteins Using Commercial Labels and Hardware, ChemRxiv, 2020 DOI:10.26434/chemrxiv.13370924.v1.
- A. Gamble Jarvi, J. Casto and S. Saxena, J. Magn. Reson., 2020, 320, 106848 CrossRef CAS.
- E. Freire, A. Schön and A. Velazquez-Campoy, Methods Enzymol., 2009, 455, 127 CAS.
- Z. X. Wang and R. F. Jiang, FEBS Lett., 1996, 392, 245 CrossRef CAS.
- A. D. Milov, A. G. Marysov and Y. D. Tsvetkov, Appl. Magn. Reson., 1998, 15, 107 CrossRef CAS.
- S. Valera and B. E. Bode, Molecules, 2014, 19, 20227 CrossRef.
- J. Gao, F. Xing, Y. Bai and S. Zhu, Dalton Trans., 2014, 43, 7964 RSC.
- J. J. Wyman, Adv. Protein Chem., 1964, 19, 223 CrossRef CAS.
- D. F. Senear and M. Brenowitz, J. Biol. Chem., 1991, 266, 13661 CrossRef CAS.
- D. Abdullin, F. Duthie, A. Meyer, E. S. Muller, G. Hagelueken and O. Schiemann, J. Phys. Chem. B, 2015, 119, 13534 CrossRef CAS.
- D. Abdullin, H. Matsuoka, M. Yulikov, N. Fleck, C. Klein, S. Spicher, G. Hagelueken, S. Grimme, A. Lutzen and O. Schiemann, Chem. – Eur. J., 2019, 25, 8820 CAS.
- S. Razzaghi, M. Qi, A. I. Nalepa, A. Godt, G. Jeschke, A. Savitsky and M. Yulikov, J. Phys. Chem. Lett., 2014, 5, 3970 CrossRef CAS.
- A. Giannoulis, C. L. Motion, M. Oranges, M. Buhl, G. M. Smith and B. E. Bode, Phys. Chem. Chem. Phys., 2018, 20, 2151 RSC.
- A. G. Jarvi, K. Ranguelova, S. Ghosh, R. T. Weber and S. Saxena, J. Phys. Chem. B, 2018, 122, 10669 CrossRef.
- X. Bogetti, S. Ghosh, A. G. Jarvi, J. Wang and S. Saxena, J. Phys. Chem. B, 2020, 124, 2788 CrossRef CAS.
- A. G. Jarvi, A. Sargun, X. Bogetti, J. Wang, C. Achim and S. Saxena, J. Phys. Chem. B, 2020, 124, 7544 CrossRef.
- I. Ritsch, H. Hintz, G. Jeschke, A. Godt and M. Yulikov, Phys. Chem. Chem. Phys., 2019, 21, 9810 RSC.
- J. R. Horn, D. Russell, E. A. Lewis and K. P. Murphy, Biochemistry, 2001, 40, 1774 CrossRef CAS.
- L. Baranauskiene, V. Petrikaite, J. Matuliene and D. Matulis, Int. J. Mol. Sci., 2009, 10, 2752 CrossRef CAS.
- S. A. Kantonen, N. M. Henriksen and M. K. Gilson, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861, 485 CrossRef CAS.
- J. Wort, K. Ackermann, D. Norman and B. E. Bode, 2020 A General Model to Optimise Copper(II) Labelling Efficiency of Double-Histidine Motifs for Pulse Dipolar EPR Applications (Dataset). Dataset. University of St Andrews Research Portal. https://doi.org/10.17630/d591aa48-7239-40b0-afef-9f63dac86e9c Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp06196d |
| This journal is © the Owner Societies 2021 |