Open Access Article
Open Access ArticleThe crystallization enthalpy and entropy of protein solutions: microcalorimetry, van't Hoff determination and linearized Poisson–Boltzmann model of tetragonal lysozyme crystals
Lorena
Hentschel
a,
Jan
Hansen
 a,
Stefan U.
Egelhaaf
a,
Stefan U.
Egelhaaf
 a and
Florian
Platten
a and
Florian
Platten
 *ab
*ab
aCondensed Matter Physics Laboratory, Heinrich Heine University, Universitätsstraße 1, 40225 Düsseldorf, Germany. E-mail: florian.platten@hhu.de
bInstitute of Biological Information Processing (IBI-4: Biomacromolecular Systems and Processes), Forschungszentrum Jülich, Wilhelm-Johnen-Straße, 52428 Jülich, Germany
First published on 15th January 2021
Abstract
During a first-order phase transition, a thermodynamic system releases or absorbs latent heat. Despite their fundamental importance, the heat or enthalpy change occurring during protein crystallization has been directly measured only in a few cases, and the associated entropy change can only be determined indirectly. This work provides an experimental determination and theoretical analysis of the dependence of the molar crystallization enthalpy of lysozyme solutions, ΔHxtal, on the physicochemical solution parameters. Its value is determined directly by isothermal microcalorimetry and indirectly by a van't Hoff analysis of solubility data, which quantitatively agree. This suggests a two-state crystallization process, in which oligomeric intermediates play a minor role. ΔHxtal is found to be negative on the order of few tens of the thermal energy per molecule. It is independent of protein concentration and stirring speed, but weakly depends on salt (NaCl) concentration and solution pH. Assuming that crystals are electrostatically neutral, these trends are explained by a linearized Poisson–Boltzmann theory. In addition, the molar crystallization entropy, ΔSxtal, is analyzed. The dependence of the van't Hoff entropy on salt concentration and pH is captured by the model, complementing the analysis of crystallization thermodynamics.
1 Introduction
The crystallization of proteins is relevant to many fields of science and technology, ranging from structural biology, pharmacy, to medicine, and inspiring to physics.1 In modern structural biology, the functions of proteins are related to their three-dimensional molecular structure. An important technique to determine the protein structure is X-ray crystallography, for which high-quality crystals are required and hence identifying conditions under which crystals grow represents a major bottleneck.2 In biotechnology, crystallization is used for batch purification in order to improve storage and stability of enzymes.3 The slow dissolution of protein crystals is exploited in protein-based therapeutics for controlled high-dose delivery with sustained release, which allows for treatments of acute and chronic diseases.4 In addition, protein crystallization occurs under both native and abnormal conditions in vivo.5 Native in cellulo crystallization is a rare process, but occurs in all kingdoms of life. It is related to specific functions, such as storage, protection and catalysis.6 Non-native crystallization can be induced by small environmental changes or point mutations. It is often associated with pathological conditions, e.g., those relevant for lens opacification7 and anemia,8 but also occurs due to recombinant gene expression in host cells. Concepts developed in colloid physics have successfully been applied to rationalize certain aspects of protein crystallizations,9 including the DLVO theory to describe inter-protein interactions,10–14 the colloidal phase behavior of proteins with short-range attractions15–19 and the “crystallization slot” to characterize conditions favoring nucleation based on two-body interactions.20–24 Moreover, the study of protein crystallization has opened up new vistas on soft-matter concepts, such as the phase behavior of patchy particles9,25 and non-classical crystallization pathways.26–29 However, despite these efforts, many aspects of protein crystallization are still not fully understood. For example, screening for optimum crystallization conditions often remains a trial-and-error process.30 Hence, further attempts to rationalize aspects of protein crystallization are highly desired.Protein crystallization depends on both thermodynamic and kinetic factors that govern the equilibrium state as well as the path toward equilibrium, that is nucleation and growth, respectively.31 Equilibrium properties, such as the (molar) protein solubility ceq as well as the change of enthalpy ΔHxtal and entropy ΔSxtal upon crystallization, are used to describe the thermodynamics of protein crystallization and reflect the quantities that stabilize protein crystals. Many experimental efforts have been undertaken to explore the dependence of protein solubility on physicochemical parameters, such as pH and temperature,32–36 as well as type and concentration of precipitant.37,38 In particular, a correlation between solubility (or crystallization boundary) and second virial coefficient has been observed.12,39–41 However, direct experimental determinations of ΔHxtal are rare, as noted previously,42,43 and its dependence on the solution parameters has as yet not been systematically explored. This is likely due to experimental difficulties associated with the kinetics and thermodynamics of protein crystallization. On the one hand, to be reliably captured by microcalorimetry, the onset and offset of the crystallization process may neither be too fast compared to the initial thermalization of the sample and instrument nor too slow to allow for a significant signal. On the other hand, the absolute value of ΔHxtal is typically less than 100 kJ mol−1,42,44 and thus difficult to measure. The value of ΔHxtal is expected to largely reflect hydrophobic and hydrogen bonding interactions as well as electrostatic protein–protein and protein–salt interactions. The enthalpic (and entropic) contributions of hydrophobic and hydrogen bonding interactions differ in sign45–49 and thus partially compensate each other. As a consequence, depending on the specific protein studied, ΔHxtal can be moderately negative or positive or close to zero.42
The few studies in which ΔHxtal was examined do not lead to a conclusive picture. Calorimetric and van't Hoff enthalpies are equivalent for simple two-state transitions,50 which in some cases has been found for biomolecular ion binding reactions.51 However, whether complex processes, such as crystallization, can be effectively modelled as two-state transitions is controversial. For two specific conditions, the directly determined values of ΔHxtal were shown to agree with the van't Hoff enthalpy,52 but arguments raised against van't Hoff analysis of protein solubility data34 have still not been dispelled. Moreover, in order to obtain molar quantities which allow for thermodynamic inferences, the calorimetric enthalpy has to be related to the crystallized protein fraction, which needs to be obtained from independent measurements. Yet, this aspect has been ignored in a previous study.53 Furthermore, the magnitude of ΔHxtal was found to increase with salt concentration,52 whereas the opposite trend was predicted theoretically.49
Microcalorimetry represents a powerful method to study the thermodynamic properties of individual proteins,44,54 such as unfolding,55 protein–ligand56 or protein–ion binding.57,58 However, it has been only scarcely used for studying protein condensation, due to the difficulties mentioned above. Nevertheless, some calorimetric experiments have been performed to study amyloid fibril formation59–62 and protein crystallization,52,53,63,64 where the latter focussed on lysozyme as a model protein.
Here, we directly measure ΔHxtal of lysozyme solutions by combining microcalorimetry with UV-vis spectroscopy to determine the fraction of protein crystallized. The results are found to agree with the van't Hoff enthalpy as determined based on solubility data. We quantitatively and systematically study the dependence of ΔHxtal on the physicochemical solution parameters, such as protein and salt concentrations, pH value, and stirring speed, and explain the observed trends theoretically. We furthermore determine and theoretically explain the salt and pH dependences of the van't Hoff entropy. This work thus aims for a comprehensive picture of the crystallization thermodynamics of protein solutions and a resolution of the controversial results of previous studies.
2 Experimental methods
2.1 Sample preparation
Hen egg-white lysozyme powder (Roche Diagnostics, prod. no. 10837059001, purity ≥95%), sodium chloride (NaCl; Fisher Chemical, prod. no. S/3160/60, purity ≥99.5%), and sodium acetate (NaAc; Merck, prod. no. 1.06268, p.a.) were used without further purification. Ultrapure water with a minimum resistivity of 18 MΩ cm was used to prepare buffer solutions. The protein powder was dissolved in 50 mM NaAc buffer solutions, which were adjusted to pH 4.0, 4.5, 5.0 and 5.4 by adding small amounts of hydrochloric acid. Solution conditions resemble those of our previous work12,23 and allow for a comparison with theory.49 Protein stock solutions with an initial protein mass concentration ρp ≈ 80 mg mL−1 were filtered through an Acrodisc syringe filter with low protein binding (pore size: 0.1 μm; Pall, prod. no. 4611) in order to remove impurities and undissolved proteins. The final protein concentration (typically 65 mg mL−1) was determined by UV-vis absorption spectroscopy and/or refractometry.65 For some experiments, higher protein concentrations (up to 150 mg mL−1) were needed, which were achieved by ultrafiltration, as described previously.65 Samples were prepared by mixing appropriate amounts of lysozyme, buffer and salt stock solutions. Sample preparation was conducted at room temperature (21 ± 2) °C, above the solution cloud-points.66,67 Due to the high salt content, the samples were prone to crystallize and hence injected into the calorimeter immediately after preparation. Most solution conditions were studied three to five times in order to allow for a statistical analysis.2.2 Microcalorimetry
A VP ITC (isothermal titration calorimeter) instrument (MicroCal) consisting of a pair of identical cells was used to monitor the heat signal of crystallizing protein solutions at 20.0 °C. The reference cell was filled with ultrapure water. Before each measurement, the adiabatic shield was cooled 0.5 °C below the working temperature in order to compensate for the injection heat and thus to allow for reaching the working temperature fast. The freshly prepared sample solution was injected into the sample cell (volume V = 1.4129 mL, according to the producer) of the calorimeter. The syringe was not used to titrate any ligands into the solution, but to seal the calorimeter and to stir the solution at 270 rpm, as recommended by the manufacturer to homogeneously dissipate heat and obtain a stable baseline. For a few conditions, explicitly mentioned below, different stirring speeds have been chosen. The instrument started to record the heat signal, once the working temperature was reached a few minutes after sample preparation. While the reference cell was continuously supplied with a small power of 5 μcal s−1, the instrument measured the differential power ΔP between the two cells necessary to hold both cells at the same temperature as a function of time. The instrument was operated in the passive feedback mode, allowing for highest sensitivity, as recommended for slow thermal processes. As the sample solution crystallized, heat was released, such that less power had to be provided; i.e., ΔP became negative and showed an exothermic peak. When the differential power signal reached the baseline again, which typically occurred one or two days after sample preparation, the exothermic reaction was assumed to be completed and the measurement stopped. Subsequently, the crystal-free supernatant was carefully removed from the sample cell and its protein mass concentration ρf determined spectrophotometrically. As equilibrium and hence the molar protein solubility ceq is only reached after months,68 typically, ρf ≫ ceqM with the molecular weight of lysozyme M = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 320 g mol−1. In addition, the UV-vis spectra were inspected for the presence of oligomers or aggregates. Even if small amounts of such species were present in the supernatant, they would scatter light much stronger than the monomers, reducing the transmission and augmenting the measured absorbance. With increasing wavelength, the amount of scattered light diminishes and thus the increase in absorbance becomes weaker, leading to a gradual decrease of the measured UV-vis absorbance with wavelength.69 The UV-vis spectra did not indicate the presence of aggregates or oligomers. Afterwards, the crystallized protein sample was removed from the sample cell, usually containing visually observable small crystals. For very similar solution conditions (without stirring), optical microscopy studies revealed the occurrence of (tetragonal) lysozyme crystals.66 In the vicinity of the binodal, spherulitic needle-like crystals have been observed as a polymorph.18,70 After each microcalorimetric experiment, the sample cell was meticulously cleaned with ethanol, acetone and ultrapure water to completely remove any residuals. ITC experiments with a drifting baseline and those that did not show the characteristic minimum in ΔP due to an extended period necessary to reach the working temperature were discarded. The instrumental response, especially regarding the accuracy of the power signal, has been validated by measuring the chelation reaction of calcium with ethylenediaminetetraacetic acid (EDTA).
320 g mol−1. In addition, the UV-vis spectra were inspected for the presence of oligomers or aggregates. Even if small amounts of such species were present in the supernatant, they would scatter light much stronger than the monomers, reducing the transmission and augmenting the measured absorbance. With increasing wavelength, the amount of scattered light diminishes and thus the increase in absorbance becomes weaker, leading to a gradual decrease of the measured UV-vis absorbance with wavelength.69 The UV-vis spectra did not indicate the presence of aggregates or oligomers. Afterwards, the crystallized protein sample was removed from the sample cell, usually containing visually observable small crystals. For very similar solution conditions (without stirring), optical microscopy studies revealed the occurrence of (tetragonal) lysozyme crystals.66 In the vicinity of the binodal, spherulitic needle-like crystals have been observed as a polymorph.18,70 After each microcalorimetric experiment, the sample cell was meticulously cleaned with ethanol, acetone and ultrapure water to completely remove any residuals. ITC experiments with a drifting baseline and those that did not show the characteristic minimum in ΔP due to an extended period necessary to reach the working temperature were discarded. The instrumental response, especially regarding the accuracy of the power signal, has been validated by measuring the chelation reaction of calcium with ethylenediaminetetraacetic acid (EDTA).
3 Results and discussion
At first, the solution conditions that we want to study are localized in the protein state diagram. In a second step, the different methods used to determine the crystallization enthalpy ΔHxtal and entropy ΔSxtal are discussed and illustrated with examples. Finally, data on the independence of ΔHxtal on protein concentration and stirring speed as well as the weak, but systematic dependence of ΔHxtal and ΔSxtal on salt concentration and pH value are presented and discussed. Directly and indirectly determined values of ΔHxtal quantitatively agree with each other, and the dependence of ΔHxtal and ΔSxtal on solution conditions is rationalized theoretically.3.1 Crystallization conditions in the state diagram of lysozyme solutions
The state of a protein solution depends on, e.g., molar protein and salt concentrations, cp = ρp/M and cs, respectively. For a systematic microcalorimetric study of isothermal protein crystallization, solution conditions have to be identified (i) under which crystals form and (ii) microcalorimetric experiments can be successfully performed.As previous theoretical studies indicate that ΔHxtal exhibits only a weak temperature dependence,49,71 isothermal crystallization is studied at 20.0 °C, which is a common temperature for protein crystallization experiments.68 We focus on acidic pH values ranging from 4.0 to 5.4, covering the conditions where the solubility as well as number and size of tetragonal lysozyme crystals are maximized, respectively.72–74 In addition, theoretical calculations predict a systematic variation of the crystallization enthalpy over this pH range.49
As pointed out by George and Wilson,20 optimum conditions for protein crystallization are met when the (net) attractions between the proteins are neither too weak nor too strong. In this case, the second virial coefficient, B2, of the solution is in the range
| −10 ≲ B2/BHS2 ≲ −1, | (1) |
The second condition, the feasibility of microcalorimetric experiments, is met if protein concentrations are chosen that lead to moderate supersaturations. At hight supersaturation, nucleation starts within minutes, while it can take days to months at low supersaturation levels.1 Neither of these cases can be reasonably studied by microcalorimetry.53 In the former case, crystallization is faster than thermostatting after sample loading, which, however, is essential due to the weak heat signal associated with protein crystallization (on the order of microwatts52) in order to avoid spurious effects due to thermal offsets. In the latter case, the instrument and its surroundings have to be thermally stable over a long time period.
Fig. 1 shows the state diagram of lysozyme solutions in the cpvs. cs plane at pH 4.5 and 20.0 °C and indicates the conditions studied in this work. The state diagram contains data on solubility (black filled circles36) and metastable liquid–liquid phase separation (LLPS, gray filled squares), where the latter have been extrapolated from cloud-point measurements at fixed protein or salt concentration.65,67 With increasing cs both the solubility and the binodal (solid) lines occur at lower values of cp, reflecting the enhanced (net) attractions. In the present work, protein crystallization has been studied by microcalorimetry for the solution compositions marked with an ×, corresponding to supersaturations cp/ceq ≳ 10. Experiments with smaller cs or cp than indicated were not successful. The solutions are investigated under continuous gentle stirring, inducing convection and local shear effects. This might accelerate the crystallization process,75,76 break large protein clusters,53 and displace the phase coexistence curve,77 but does not alter the solubility. For some conditions (denoted by a circle symbol), the supernatant was found to be cloudy when removed at the end of the experiment. We speculate that the cloudiness is directly or indirectly related to phase separation. It is, for example, conceivable that the LLPS line is shifted to lower salt concentrations, due to stirring, as observed for colloidal suspensions under shear.77 As phase separation is much faster (on the order of seconds78,79) than crystallization, it is expected to occur during the initial equilibration period of the calorimeter (if induced by stirring) and thus to not noticeably affect the microcalorimetric crystallization experiment. In addition, those conditions for which the effects of pH or stirring speed vstir have been examined are labelled with a blue and green rectangle, respectively.
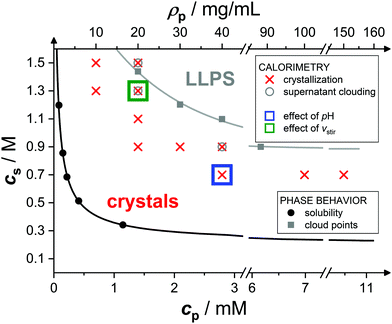 | ||
| Fig. 1 State diagram of lysozyme solutions at pH 4.5 and 20.0 °C in the salt concentration csvs. molar protein concentration cp (or, equivalently, mass protein concentration ρp) plane: solubility (black filled circles36) and cloud-point data (gray filled squares65,67). Lines are guides to the eye. Microcalorimetric crystallization experiments from the present work, conducted under constant stirring, are marked by an ×. Open circles denote that the supernatant was cloudy when removed from the calorimeter and open squares that further solution conditions (as indicated) were investigated. | ||
3.2 Determination of the crystallization enthalpy ΔHxtal and entropy ΔSxtal
The value of ΔHxtal can be experimentally determined directly by a combination of microcalorimetry with a spectrophotometric measurement of the protein concentration of the supernatant and indirectly based on a van't Hoff analysis of solubility data. In addition, it can be calculated based on theoretical approaches. The value of ΔSxtal is obtained from van't Hoff fits and the model. These different ways will be described and discussed in turn.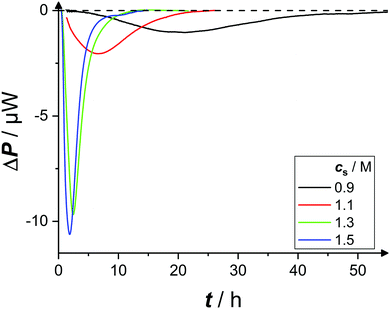 | ||
| Fig. 2 Exemplary time-dependent microcalorimetric power signals of protein solutions (ρp = 20 mg mL−1, pH 4.5) with various salt concentrations cs, as indicated. | ||
The heat Q released upon crystallization is given by the integral of the differential microcalorimetric power signal ΔP(t), which is limited by ti and tf to minimize noise effects:
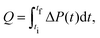 | (2) |
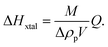 | (3) |
The uncertainty of ΔHxtal, δ(ΔHxtal), depends on the uncertainties of the various quantities in eqn (3). The relative uncertainty of Δρp was calculated, in most cases reaching δ(Δρp)/Δρp = 0.1, which comprise pipetting and dilution uncertainties of two protein solutions, and that of Q estimated with a typical value δQ/Q = 0.05. Since the relative uncertainties in M and V are at least an order of magnitude smaller, δ(ΔHxtal)/ΔHxtal ≈ 0.1.
For some solution conditions, in particular at large supersaturations (e.g., cs = 1.1 M in Fig. 2), the first data point recorded by the instrument might already lie below the baseline. In these cases, the initial part of the recorded signal is extrapolated to the baseline and the associated error in Q estimated to be on the order of the additional area (typically, δQ/Q = 0.15, and sometimes even larger), such that δ(ΔHxtal)/ΔHxtal ≈ 0.2. The instrument would allow to record the ΔP signal before the working temperature was reached. However, in this case, the temperature of the sample would be offset, leading to a systematic error in Q, which is often neglected in other studies.
| ΔGxtal = ΔHxtal − TΔSxtal, | (4) |
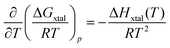 | (5) |
The equilibrium constant Kxtal for the transfer of a molecule from solution to the crystal is defined as
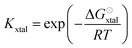 | (6) |
Based on eqn (4) and (6), the logarithm of Kxtal is expected to be a linear function in inverse temperature T−1:
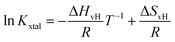 | (7) |
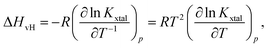 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kxtal plotted as a function of T−1, shows a linear behavior, its temperature-independent slope is related to the van't Hoff enthalpy ΔHvH and the heat capacity of the solution does not change between initial and final state.44
Kxtal plotted as a function of T−1, shows a linear behavior, its temperature-independent slope is related to the van't Hoff enthalpy ΔHvH and the heat capacity of the solution does not change between initial and final state.44
The value of Kxtal can be determined via
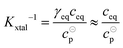 | (9) |
Despite the amount of protein (typically grams) and time (few months) required for common solubility measurements from batch crystallization, solubility data for tetragonal lysozyme crystals are available in literature for a wide range of temperatures, pH values and salt concentrations.33–36,70 Here, van't Hoff enthalpies are determined based on the comprehensive dataset provided in ref. 36 containing solubility data with two or three significant digits, corresponding to uncertainties ranging from 0.1 mg mL−1 to 1 mg mL−1, for a temperature range (with a temperature control of 0.1 K) which covers the temperature used in our calorimetric experiments.
Fig. 3 shows an exemplary van't Hoff plot of the solubility data (open symbols36) of lysozyme solutions at pH 4.5 for various salt concentrations (2, 3, 4, 5, and 7% (w/v), corresponding to cs = 0.34, 0.51, 0.68, 0.86, and 1.2 M). For the temperature range available, 1.8 ≤ T/°C ≤ 22.7, the natural logarithm of the equilibrium constant exhibits a linear increase with the inverse temperature, and the slopes retrieved from fitting (lines) provide the van't Hoff enthalpy ΔHvH according to eqn (8). As expected, ΔHvH is negative. The magnitude of the slope and, correspondingly, the value of ΔHvH decreases slightly with cs. Further details are discussed in Section 3.3.
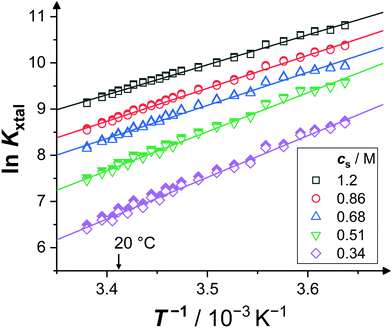 | ||
| Fig. 3 Exemplary van't Hoff plots: dependence of the equilibrium constant Kxtal on inverse temperature T−1 (open symbols; calculated using eqn (9) with solubility data from ref. 36) and corresponding van't Hoff fits (lines), according to eqn (7), for various salt concentrations cs, as indicated. Values of the equilibrium constant taking corrections due to non-ideality into account are shown as filled symbols. | ||
In addition, the van't Hoff entropy ΔSvH can be inferred from the intercept of a linear fit to the van't Hoff plot according to eqn (7).80 (Note that the value of ΔSvH depends on the choice of c⊖p.) The negative intercept of the van't Hoff fit according to eqn (7) in Fig. 3 increases with cs and, accordingly, |ΔSvH| decreases.
For lysozyme in brine, temperature-dependent virial coefficients are known14 and hence activity coefficients can be estimated.81,82 As crystallization will only occur if B2 < 0, Kxtal will generally exhibit smaller values if non-ideality is accounted for by the second virial coefficient.83 However, since B2 and ceq are correlated with each other,39i.e., the smaller (more negative) B2, the smaller ceq, their effects to non-ideality, to some degree, compensate each other. For the solution conditions considered, the value of Kxtal taking non-ideality into account via B2 (filled symbols) increases by a few percent, ranging from 0.14% (at high cs and low T) up to 1.5% (at low cs and high T), compared to the value of Kxtal that assumes ideal solutions (open symbols). However, due to the temperature dependence of the virial coefficients, i.e., B2 becomes less negative with increasing T within the relevant range, there is only little effect on the slope of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kxtal: the magnitude of ΔHvH (fits not shown) is only very slightly decreased, at most by 2.2% (at the lowest cs) and at least by 0.6% (at the highest). This small effect is neglected here.
Kxtal: the magnitude of ΔHvH (fits not shown) is only very slightly decreased, at most by 2.2% (at the lowest cs) and at least by 0.6% (at the highest). This small effect is neglected here.
Within this model, the stability of protein crystals is governed by four terms: (i) electrostatic inter-protein repulsion and, more important, counterion sequestration into the crystal, (ii) nonelectrostatic protein–protein contact interactions due to the hydrophobic effect and hydrogen bonding, as well as the (iii) translational entropy of the proteins and (iv) that of counterions. The two latter (entropic) contributions, (iii) and (iv), oppose crystallization, whereas the two former contributions, (i) and (ii), are enthalpic and favor crystallization. Thus the crystallization enthalpy and entropy read
| ΔHxtal(Z,cs) = ΔH0 + ΔHES(Z,cs), | (10) |
| ΔSxtal(Z,cs) = ΔS0 + ΔSES(Z,cs) | (11) |
The electrostatic contribution ΔHES(Z,cs) can be determined by solving the nonlinear Poisson–Boltzmann equation with appropriate boundary conditions.49 Using the linearized (Debye–Hückel) approximation, an analytical expression for the electrostatic enthalpy change has been derived:
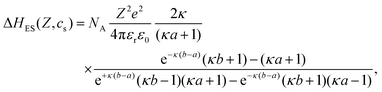 | (12) |
Despite the high charge density of the proteins, both the linear and the non-linear treatment lead to qualitatively similar behavior as a function of pH49 with the main difference being an almost constant offset, i.e., a slightly smaller magnitude of ΔHES(Z,cs) in the non-linear case, which could largely be accounted for by readjusting ΔH0. This might, in parts, be ascribed to the relatively high salt concentrations considered here. For simplicity, the analytical expression is used here. To determine the protein net charge Z for a given pH value, titration data84 obtained in the presence of 1 M salt have been interpolated. It is important to note that experimental titration curves84,85 are slightly smaller (by about 2e) at pH 4.0 than the calculated values in ref. 49, which affects ΔHES. Eqn (10) and (12) provide a theoretical description of ΔHxtal(Z,cs) that will be compared with experimental results in the next section.
The electrostatic term ΔSES(Z,cs) is determined by the different ions surrounding the protein in the concentric spherical shell. If the protein was uncharged, the total number of ions would be: n = csNAVsh with the shell volume 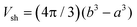 . The co- and counterion enrichment numbers read:
. The co- and counterion enrichment numbers read:
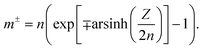 | (13) |
Thus, ΔSES(Z,cs) implicitly depends on Z and cs:
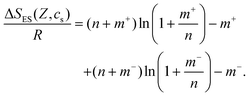 | (14) |
3.3 Dependence of ΔHxtal and ΔSxtal on physicochemical solution parameters
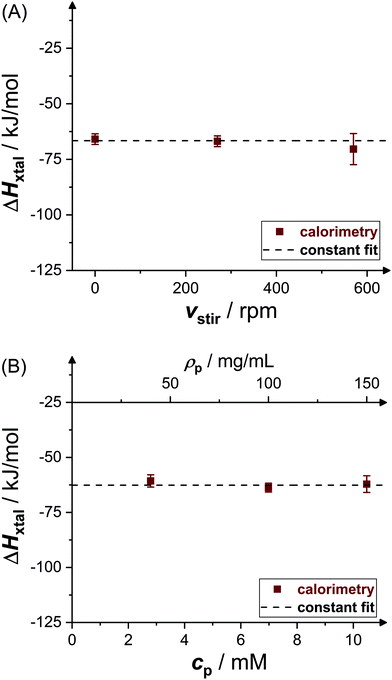
Fig. 4 shows experimental data (symbols) on the crystallization enthalpy for solution conditions differing in stirring speed vstir and protein concentration cp. The values reported represent weighted averages of the values determined in, typically, three to five individual experiments with independently prepared samples. For the conditions considered, ΔHxtal is, within experimental uncertainty, constant (indicated by the dashed lines) at the different stirring speeds and protein concentrations. From a thermodynamic point of view, this is expected, both stirring and protein concentration affect the crystallization kinetics only (not shown). As a consequence of the independence of ΔHxtal on vstir, the following experiments have been performed under constant stirring with vstir = 270 rpm to obtain a reliable measurement. In addition, the enthalpy change upon crystallization determined for solutions with different protein concentrations is averaged taking uncertainties into account.Fig. 5 shows the resulting dependence of the crystallization enthalpy on salt concentration and pH. Data obtained from direct microcalorimetric measurements (brown filled squares), indirect van't Hoff determinations (blue crosses), literature data (green open symbols,52,53,63,64 as indicated) as well as theoretical calculations based on the Schmit–Dill model (red solid lines) are presented. Direct and indirect determinations as well as theoretical predictions yield a consistent picture: within the experimental uncertainties, directly determined and van't Hoff enthalpies quantitatively agree with each other and with the model. The magnitude of ΔHxtal tends to slightly decrease with increasing salt concentration and pH value. According to the theoretical description, this decrease is due to screening of electrostatic inter-protein repulsions at increased cs or reduced ion sequestration owing to the lower net charge at higher pH. It is important to note that the theoretical model is not a fit to our data, but calculated without any free parameters. The quantitative agreement with the experimental data is therefore particularly significant.
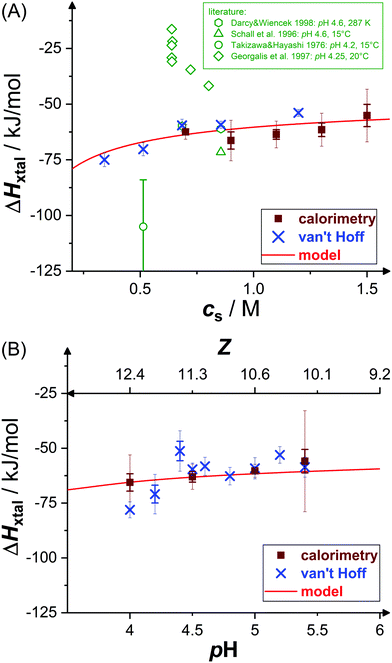 | ||
| Fig. 5 Effects of (A) salt concentration cs (at pH 4.5) and (B) pH value (or net charge Z, at cs = 0.7 M) on crystallization enthalpy ΔHxtal: calorimetric experiments (brown filled squares), van't Hoff enthalpies as calculated from solubility data36 (blue crosses), theoretical model49 (red solid line; based on eqn (10) and (12)); calorimetric literature data52,53,63,64 (green open symbols). Note that some literature data53 (green diamonds) were normalized by ρp instead of Δρp. Thin error bars indicate 95% confidence intervals. | ||
van't Hoff enthalpy data slightly scatter around the microcalorimetric data and the model calculation. Taking inter-protein interactions into account in the van't Hoff analysis (see Fig. 3, filled symbols) or restricting the temperature interval of the van't Hoff analysis symmetrically around T = 20 °C leads to slightly less negative van't Hoff enthalpies, especially at low cs or low pH, and hence an even better agreement (not shown). However, for these solution conditions, either direct measurements have not been successful (low cs) or the solubility data show larger uncertainties and scatter more about the van't Hoff fit (low pH), thus not allowing for a detailed analysis.
Microcalorimetric literature data grossly scatter around our data. Some values (green hexagons and triangle) follow our trends.52,64 In an early experiment (green circle),63 a value of ΔHxtal with a larger magnitude than observed here was reported. We note that individual experimental runs scatter a lot; both the value and the uncertainty do agree with single runs of our measurement series. In another experiment (green diamonds),53 the heat effect of the solution was considered; i.e., these values have not been normalized by the crystallized fraction of the sample but by the whole solute concentration and, accordingly, have smaller magnitudes. Moreover, their dependence on cp (at fixed cs) or cs is difficult to compare with our data. Overall, the few previous direct measurements of lysozyme crystallization experiments are well in line with our data or their different results can be rationalized.
Fig. 6 shows the dependence of the entropic contributions to the Gibbs free energy, −TΔSxtal, at a temperature of T = 20 °C on salt concentration and solution pH value, including indirect van't Hoff determinations (blue crosses) and model calculations (red solid lines). The van't Hoff values range from 31 kJ mol−1 to 59 kJ mol−1 and, again, slightly scatter around the model calculation. The salt and pH dependences of −TΔSvH are captured by the model. This indicates contributions to the entropy by the translational entropy of the proteins and ions as well as a constant non-electrostatic contribution. Furthermore, according to the model, the standard change of the Gibbs free energy upon crystallization (not shown) ranges from −17 kJ mol−1 to −22 kJ mol−1 (i.e., from −7 RT to −9 RT) at T = 20 °C for the conditions studied, which agrees with values computed from solubility data (cf.Fig. 3) using eqn (6).
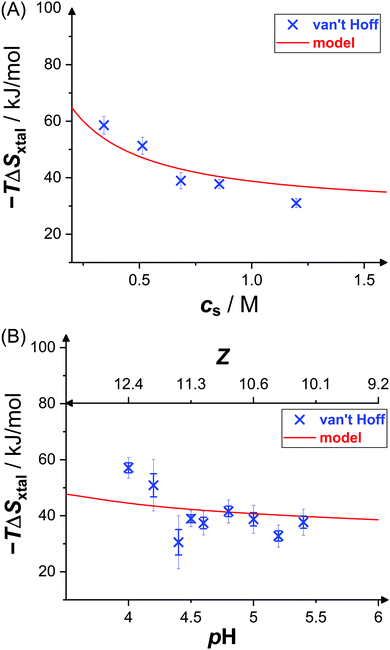 | ||
| Fig. 6 Effects of (A) salt concentration cs (at pH 4.5) and (B) pH value (or net charge Z, at cs = 0.7 M) on crystallization entropy ΔSxtal, shown as its contribution to the Gibbs free energy −TΔSxtal with T = 20 °C: van't Hoff entropies as calculated from solubility data36 (blue crosses) and theoretical model49 (red solid line; based on eqn (11) and (14)). Thin error bars indicate 95% confidence intervals. | ||
3.4 Discussion
We have carried out and analyzed a number of microcalorimetric lysozyme crystallization experiments, performed a van't Hoff analysis of solubility data and described the experimental observations by a theoretical model. Experimental, van't Hoff and theoretical enthalpy and entropy values semi-quantitatively agree. The analysis of the microcalorimetric experiments reveals that the enthalpy of tetragonal lysozyme crystallization is about −65 kJ mol−1. ΔHxtal was neither observed to depend on stirring speed nor on protein concentration, as expected for thermodynamic consistency. According to the model,49 ΔHxtal and ΔSxtal are dominated by hydrophobic and hydrogen bonding interactions as well as electrostatics. They weakly, but systematically vary with salt content and pH value. The decrease of the magnitude of ΔHxtal with salt concentration is in contrast to a previous study,52 in which the opposite trend was reported. Their claim was based on a van't Hoff analysis of solubility data33 that were measured at few temperatures and with lower precision, whereas our van't Hoff analysis (blue crosses in Fig. 5) of the more comprehensive and accurate data set36 revealed the opposite trend in accordance with the direct microcalorimetric experiments. Nevertheless, for the two solution conditions microcalorimetrically probed in ref. 52 (cs = 0.86 M, pH 4.6 (green triangle in Fig. 5(A)); cs = 0.51 M, pH 5.2; both at 15 °C), a coincidence of microcalorimetric and van't Hoff enthalpies was observed. The agreement of different independent methods in this work provides confidence that the controversial observations regarding the weak salt-dependence of ΔHxtal are resolved and underlines the importance of accurate solubility measurements to reach reliable thermodynamic conclusions. The agreement between the van't Hoff and model entropies provides further support.Here, the agreement between direct and van't Hoff values as well as theoretical predictions has been observed for a broad range of solution conditions and is thus unlikely to be incidental, despite concerns previously raised against van't Hoff analysis of protein solubility data34 that have so far not been clarified. The coincidence of direct and van't Hoff enthalpies suggests that the tetragonal lysozyme crystallization process can be effectively described as a two-state transition. Some experiments,86 in particular atomic-force microscopy observations,87 have suggested that tetragonal lysozyme crystals grow by addition of oligomers, especially tetramers, preformed in the bulk solution. However, comprehensive light scattering experiments did not indicate any evidence for prenucleation aggregate formation.88,89 Moreover, the dependence of the growth rate of protein crystals on solution conditions showed best agreement with a model assuming monomer adhesion as mechanism, which includes non-productive binding in wrong orientations to describe the growth rate at high supersaturations.24 Furthermore, in our experiments, the UV-vis analysis of the supernatant removed after the microcalorimetric experiments did not indicate the presence of oligomers or aggregates, but of soluble monomers only. In view of these previous and the present results, it is plausible to assume that the initial state of our two-state description of lysozyme crystallization is composed of protein monomers and, as a consequence, tetragonal crystal growth is likely to proceed via the integration of monomers into crystals.
Cacioppo et al.34 argue further that, due to a lack of knowledge about or uncertainties in the composition of the solvent within the crystalline phase, the chemical potential of the protein in the crystal might not be constant. However, after their publication the sequestration of ions into the crystal has been accurately measured90 and the solvent content can be inferred from crystallographic modelling.91 At equilibrium, thermodynamics requires the chemical potential of the protein in the solution to be the same as that of the protein in the crystal in agreement with experiments and theory. After long enough equilibration, the supernatant concentration of crystallizing solutions and solutions with dissolving crystals were found to be equal.68 Coarse-grained colloidal descriptions, in which the solvent was modelled as a continuum, semi-quantitatively reproduced experimental protein solubility data.9,40,49 In view of these findings, the chemical potential of the protein in the crystal appears to be constant for fixed solution conditions. Thus, the arguments previously raised against the van't Hoff analysis of protein solubility34 do no longer appear compelling.
4 Conclusion
We have measured the heat-power peaks of crystallizing lysozyme solutions and determined the molar crystallization enthalpy, ΔHxtal, for solutions differing in protein and salt composition as well as pH value. The experimental results quantitatively agree with van't Hoff enthalpies inferred from solubility data. This indicates that the crystallization process can be effectively considered as a two-state transition. The dependence of ΔHxtal and ΔSxtal on salt concentration and pH is captured by a theoretical model based on charge neutrality of the protein crystals and a linearized Poisson–Boltzmann treatment for the electrostatic contribution to the enthalpy and entropy. These consistent experimental and theoretical findings provide a detailed description of tetragonal lysozyme crystallization thermodynamics. This contributes to our understanding of protein crystallization and can aid the search for optimum conditions for protein crystal growth.Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. P. thanks the Strategic Research Fund of the Heinrich Heine University (F 2016/1054-5) and the German Research Foundation (PL 869/2-1) for funding.Notes and references
- S. D. Durbin and G. Feher, Annu. Rev. Phys. Chem., 1996, 47, 171–204 CrossRef CAS.
- N. E. Chayen and E. Saridakis, Nat. Methods, 2008, 5, 147–153 CrossRef CAS.
- C. P. Govardhan, Curr. Opin. Biotechnol., 1999, 10, 331–335 CrossRef CAS.
- S. K. Basu, C. P. Govardhan, C. W. Jung and A. L. Margolin, Expert Opin. Biol. Ther., 2004, 4, 301–317 CrossRef CAS.
- J. P. Doye and W. C. K. Poon, Curr. Opin. Colloid Interface Sci., 2006, 11, 40–46 CrossRef CAS.
- R. Schönherr, J. M. Rudolph and L. Redecke, Biol. Chem., 2018, 399, 751–772 Search PubMed.
- A. Pande, J. Pande, N. Asherie, A. Lomakin, O. Ogun, J. King and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 6116–6120 CrossRef CAS.
- P. G. Vekilov, A. R. Feeling-Taylor, D. N. Petsev, O. Galkin, R. L. Nagel and R. E. Hirsch, Biophys. J., 2002, 83, 1147–1156 CrossRef CAS.
- D. Fusco and P. Charbonneau, Colloids Surf., B, 2016, 137, 22–31 CrossRef CAS.
- M. Muschol and F. Rosenberger, J. Chem. Phys., 1995, 103, 10424–10432 CrossRef CAS.
- R. Piazza, J. Cryst. Growth, 1999, 196, 415–423 CrossRef CAS.
- H. Sedgwick, J. E. Cameron, W. C. K. Poon and S. U. Egelhaaf, J. Chem. Phys., 2007, 127, 125102 CrossRef CAS.
- G. Pellicane, J. Phys. Chem. B, 2012, 116, 2114–2120 CrossRef CAS.
- F. Platten, J. Hansen, J. Milius, D. Wagner and S. U. Egelhaaf, J. Phys. Chem. Lett., 2016, 7, 4008–4014 CrossRef CAS.
- D. Rosenbaum, P. C. Zamora and C. F. Zukoski, Phys. Rev. Lett., 1996, 76, 150–153 CrossRef CAS.
- N. Asherie, A. Lomakin and G. B. Benedek, Phys. Rev. Lett., 1996, 77, 4832–4835 CrossRef CAS.
- W. C. K. Poon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1997, 55, 3762–3764 CrossRef CAS.
- M. Muschol and F. Rosenberger, J. Chem. Phys., 1997, 107, 1953–1962 CrossRef CAS.
- F. Platten, N. E. Valadez-Pérez, R. Castañeda-Priego and S. U. Egelhaaf, J. Chem. Phys., 2015, 142, 174905 CrossRef.
- A. George and W. W. Wilson, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1994, 50, 361–365 CrossRef CAS.
- A. George, Y. Chiang, B. Guo, A. Arabshahi, Z. Cai and W. Wilson, Methods Enzymol., 1997, 276, 100–110 CAS.
- D. F. Rosenbaum, A. Kulkarni, S. Ramakrishnan and C. F. Zukoski, J. Chem. Phys., 1999, 111, 9882–9890 CrossRef CAS.
- W. C. K. Poon, S. U. Egelhaaf, P. A. Beales, A. Salonen and L. Sawyer, J. Phys.: Condens. Matter, 2000, 12, L569 CrossRef CAS.
- J. D. Schmit and K. Dill, J. Am. Chem. Soc., 2012, 134, 3934–3937 CrossRef CAS.
- J. J. McManus, P. Charbonneau, E. Zaccarelli and N. Asherie, Curr. Opin. Colloid Interface Sci., 2016, 22, 73–79 CrossRef CAS.
- M. Sleutel and A. E. S. Van Driessche, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E546–E553 CrossRef CAS.
- A. Sauter, F. Roosen-Runge, F. Zhang, G. Lotze, R. M. J. Jacobs and F. Schreiber, J. Am. Chem. Soc., 2015, 137, 1485–1491 CrossRef CAS.
- M. A. Vorontsova, D. Maes and P. G. Vekilov, Faraday Discuss., 2015, 179, 27–40 RSC.
- F. Zhang, J. Phys.: Condens. Matter, 2017, 29, 443002 CrossRef.
- A. McPherson and J. A. Gavira, Acta Crystallogr., 2014, F70, 2–20 Search PubMed.
- P. G. Vekilov and A. A. Chernov, Solid State Phys., 2003, 57, 1–147 Search PubMed.
- T. Arakawa and S. N. Timasheff, Methods Enzymol., 1985, 114, 49–77 CAS.
- S. B. Howard, P. J. Twigg, J. K. Baird and E. J. Meehan, J. Cryst. Growth, 1988, 90, 94–104 CrossRef CAS.
- E. Cacioppo and M. L. Pusey, J. Cryst. Growth, 1991, 114, 286–292 CrossRef CAS.
- F. Rosenberger, S. Howard, J. Sowers and T. Nyce, J. Cryst. Growth, 1993, 129, 1–12 CrossRef CAS.
- E. L. Forsythe, R. A. Judge and M. L. Pusey, J. Chem. Eng. Data, 1999, 44, 637–640 CrossRef CAS.
- M. M. Ries-Kautt and A. F. Ducruix, J. Biol. Chem., 1989, 264, 745–748 CrossRef CAS.
- J.-P. Guilloteau, M. M. Riès-Kautt and A. F. Ducruix, J. Cryst. Growth, 1992, 122, 223–230 CrossRef CAS.
- B. Guo, S. Kao, H. McDonald, A. Asanov, L. Combs and W. W. Wilson, J. Cryst. Growth, 1999, 196, 424–433 CrossRef CAS.
- C. Haas, J. Drenth and W. W. Wilson, J. Phys. Chem. B, 1999, 103, 2808–2811 CrossRef CAS.
- S. Ruppert, S. I. Sandler and A. M. Lenhoff, Biotechnol. Prog., 2001, 17, 182–187 CrossRef CAS.
- P. G. Vekilov, in Handbook of Crystal Growth, ed. T. Nishinaga, Elsevier, Boston, 2nd edn, 2015, ch. 19, pp. 795–871 Search PubMed.
- Z. S. Derewenda and A. Godzik, in Protein Crystallography, ed. A. Wlodawer, Z. Dauter and M. Jaskolski, Humana Press, New York, 2017, ch. 4, pp. 77–115 Search PubMed.
- P. L. Privalov, Microcalorimetry of Macromolecules: The Physical Basis of Biological Structures, Wiley, Hoboken, 6th edn, 2012 Search PubMed.
- G. I. Makhatadze and P. L. Privalov, Biophys. Chem., 1994, 51, 291–309 CrossRef CAS.
- P. Ross and M. Rekharsky, Biophys. J., 1996, 71, 2144–2154 CrossRef CAS.
- J. M. Richardson and G. I. Makhatadze, J. Mol. Biol., 2004, 335, 1029–1037 CrossRef CAS.
- R. L. Baldwin, J. Mol. Biol., 2007, 371, 283–301 CrossRef CAS.
- J. D. Schmit and K. A. Dill, J. Phys. Chem. B, 2010, 114, 4020–4027 CrossRef CAS.
- K. A. Dill and S. Bromberg, Molecular Driving Forces: Statistical Thermodynamics in Biology, Chemistry, Physics, and Nanoscience, Taylor & Francis, New York, 2010 Search PubMed.
- J. R. Horn, D. Russell, E. A. Lewis and K. P. Murphy, Biochemistry, 2001, 40, 1774–1778 CrossRef CAS.
- C. A. Schall, E. Arnold and J. M. Wiencek, J. Cryst. Growth, 1996, 165, 293–298 CrossRef CAS.
- Y. Georgalis, P. Umbach, A. Zielenkiewicz, E. Utzig, W. Zielenkiewicz, P. Zielenkiewicz and W. Saenger, J. Am. Chem. Soc., 1997, 119, 11959–11965 CrossRef CAS.
- S. Leavitt and E. Freire, Curr. Opin. Struct. Biol., 2001, 11, 560–566 CrossRef CAS.
- M. Senske, D. Constantinescu-Aruxandei, M. Havenith, C. Herrmann, H. Weingärtner and S. Ebbinghaus, Phys. Chem. Chem. Phys., 2016, 18, 29698–29708 RSC.
- P. C. Weber and F. R. Salemme, Curr. Opin. Struct. Biol., 2003, 13, 115–121 CrossRef CAS.
- M. Bončina, J. Lah, J. Reščič and V. Vlachy, J. Phys. Chem. B, 2010, 114, 4313–4319 CrossRef.
- O. Matsarskaia, F. Roosen-Runge, G. Lotze, J. Möller, A. Mariani, F. Zhang and F. Schreiber, Phys. Chem. Chem. Phys., 2018, 20, 27214–27225 RSC.
- J. Kardos, K. Yamamoto, K. Hasegawa, H. Naiki and Y. Goto, J. Biol. Chem., 2004, 279, 55308–55314 CrossRef CAS.
- M. D. Jeppesen, K. Hein, P. Nissen, P. Westh and D. E. Otzen, Biophys. Chem., 2010, 149, 40–46 CrossRef CAS.
- A. K. Buell, C. M. Dobson and T. P. Knowles, Essays Biochem., 2014, 56, 11–39 CrossRef.
- T. Ikenoue, Y.-H. Lee, J. Kardos, H. Yagi, T. Ikegami, H. Naiki and Y. Goto, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 6654–6659 CrossRef CAS.
- T. Takizawa and S. Hayashi, J. Phys. Soc. Jpn., 1976, 40, 299–300 CrossRef CAS.
- P. A. Darcy and J. M. Wiencek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1998, 54, 1387–1394 CrossRef CAS.
- F. Platten, J. Hansen, J. Milius, D. Wagner and S. U. Egelhaaf, J. Phys. Chem. B, 2015, 119, 14986–14993 CrossRef CAS.
- H. Sedgwick, K. Kroy, A. Salonen, M. B. Robertson, S. U. Egelhaaf and W. C. K. Poon, Eur. Phys. J. E: Soft Matter Biol. Phys., 2005, 16, 77–80 CrossRef CAS.
- C. Gögelein, D. Wagner, F. Cardinaux, G. Nägele and S. U. Egelhaaf, J. Chem. Phys., 2012, 136, 015102 CrossRef.
- G. Feher and Z. Kam, Methods Enzymol., 1985, 114, 77–112 CAS.
- S. M. Kelly, T. J. Jess and N. C. Price, Biochim. Biophys. Acta, 2005, 1751, 119–139 CrossRef CAS.
- Y. Liu, X. Wang and C. B. Ching, Cryst. Growth Des., 2010, 10, 548–558 CrossRef CAS.
- D. N. Petsev, X. Wu, O. Galkin and P. G. Vekilov, J. Phys. Chem. B, 2003, 107, 3921–3926 CrossRef CAS.
- M. Ataka and S. Tanaka, J. Phys. Soc. Jpn., 1978, 45, 1779–1780 CrossRef CAS.
- M. Ataka and S. Tanaka, Biopolymers, 1986, 25, 337–350 CrossRef CAS.
- R. A. Judge, R. S. Jacobs, T. Frazier, E. H. Snell and M. L. Pusey, Biophys. J., 1999, 77, 1585–1593 CrossRef CAS.
- A. Onuki, J. Phys.: Condens. Matter, 1997, 9, 6119–6157 CrossRef CAS.
- J. J. Cerdà, T. Sintes, C. Holm, C. M. Sorensen and A. Chakrabarti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031403 CrossRef.
- J. K. G. Dhont, Phys. Rev. Lett., 1996, 76, 4269–4272 CrossRef CAS.
- M. Shah, O. Galkin and P. G. Vekilov, J. Chem. Phys., 2004, 121, 7505–7512 CrossRef CAS.
- S. Da Vela, M. K. Braun, A. Dörr, A. Greco, J. Möller, Z. Fu, F. Zhang and F. Schreiber, Soft Matter, 2016, 12, 9334–9341 RSC.
- P. G. Vekilov, A. R. Feeling-Taylor, S.-T. Yau and D. Petsev, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2002, 58, 1611–1616 CrossRef.
- W. G. McMillan and J. E. Mayer, J. Chem. Phys., 1945, 13, 276–305 CrossRef CAS.
- T. L. Hill, Thermodynamics of small systems, Benjamin, New York, 1963 Search PubMed.
- M. Grant, J. Cryst. Growth, 2000, 209, 130–137 CrossRef CAS.
- C. Tanford and R. Roxby, Biochemistry, 1972, 11, 2192–2198 CrossRef CAS.
- D. E. Kuehner, J. Engmann, F. Fergg, M. Wernick, H. W. Blanch and J. M. Prausnitz, J. Phys. Chem. B, 1999, 103, 1368–1374 CrossRef CAS.
- M. L. Pusey and A. Nadarajah, Cryst. Growth Des., 2002, 2, 475–483 CrossRef CAS.
- H. Li, A. Nadarajah and M. L. Pusey, Acta Crystallogr., 1999, D55, 1036–1045 CrossRef CAS.
- M. Muschol and F. Rosenberger, J. Cryst. Growth, 1996, 167, 738–747 CrossRef CAS.
- F. Rosenberger, P. Vekilov, M. Muschol and B. Thomas, J. Cryst. Growth, 1996, 168, 1–27 CrossRef CAS.
- P. G. Vekilov, L. A. Monaco, B. R. Thomas, V. Stojanoff and F. Rosenberger, Acta Crystallogr., 1996, D52, 785–798 CrossRef CAS.
- M. C. Vaney, S. Maignan, M. Riès-Kautt and A. Ducruix, Acta Crystallogr., 1996, D52, 505–517 CrossRef CAS.
| This journal is © the Owner Societies 2021 |