Microsolvation of Zn cations: infrared multiple photon dissociation spectroscopy of Zn⁺(H₂O)_n (n = 2–35)

Abstract

The structures, along with solvation evolution, of size-selected Zn⁺(H₂O)_n (n = 2–35) complexes have been determined by combining infrared multiple photon photodissociation (IRMPD) spectroscopy and density functional theory. The infrared spectra were recorded in the O–H stretching region, revealing varying shifts in band position due to different water binding motifs. Concordant with previous studies, a coordination number of 3 is observed, determined by the sudden appearance of a broad, red-shifted band in the hydrogen bonding region for clusters n > 3. The coordination number of 3 seems to be retained even for the larger clusters, due to incoming ligands experiencing significant repulsion from the Zn⁺ valence 4s electron. Evidence of spectrally distinct single- and double-acceptor sites are presented for medium-sized clusters, 4 ≤ n ≤ 7, however for larger clusters, n ≥ 8, the hydrogen bonding region is dominated by a broad, unresolved band, indicative of the increased number of second and third coordination sphere ligands. No evidence of a solvated, six-fold coordinated Zn²⁺ ion/solvated electron pair is present in the spectra.

---

Introduction

Ion solvation is a ubiquitous process relevant in chemistry, biology, and geochemistry.¹ Gas-phase metal ion–water complexes provide a model system to study fundamental solvation behaviour at the molecular level.^2–7 In particular, gas-phase hydrated metal ions represent a well-defined system in which to study fundamental chemical processes, including hydrogen production and corrosion mechanisms, bridging the gap from small metal–water complexes to bulk aqueous solution.^8–15

Many spectroscopic studies on isolated, gas-phase metal ion–water complexes have been carried out employing electronic spectroscopy techniques.^16,17 Early experiments by Duncan and co-workers investigated small Mg⁺(H₂O)_n and Ca⁺(H₂O)_n complexes,^18,19 as these metals, in their cationic form, have a single valence electron and a relatively simple electronic structure. Recently, our group also studied the electronic spectra of Mg⁺(H₂O)_n clusters in the n = 1–5 and n = 20–70 size regime.^20,21 The electronic spectra of transition metal ion–water complexes were also studied by Metz and co-workers, investigating the Ni⁺(H₂O) and Co⁺(H₂O) complex,^22,23 and Abate et al., studying the Zn⁺(H₂O) complex.²⁴

Structural trends and solvation evolution can be determined by employing infrared (IR) spectroscopy, and has been used extensively by many groups to investigate the structural isomers of metal ion–water complexes as a function of cluster size.^25–42 When combined with quantum chemical calculations, IR spectroscopy is a powerful technique used to investigate vibrational frequency shifts of metal ion–water complexes, along with structural isomers and coordination numbers. For example, studies by Walters et al. on Ni⁺(H₂O)_n complexes indicate a coordination number of four,³⁰ whilst Furukawa et al. present a coordination number of three for Co⁺(H₂O)_n complexes.⁴⁰ Infrared spectroscopy of doubly-charged Zn²⁺(H₂O)_n complexes by Williams and co-workers reveal a coordination number of 5.⁴² Duncan and co-workers found a coordination number of 3 in their study of small Zn⁺(H₂O)_n–Ar complexes (n = 1–4).⁴³

In reactivity studies of Zn⁺(H₂O)_n with HCl, elimination of atomic hydrogen was observed upon uptake of two HCl molecules.⁴⁴ A fairly efficient uptake of O₂ was observed by Zn⁺(H₂O)_n, while CO₂ and N₂O were unreactive.⁸¹ No H/D exchange was found in reactions with D₂O.⁴⁵ An intriguing chemistry was found with NO, where HNO and ZnOH⁺(H₂O)_m is formed following the initial uptake of one NO molecule, i.e. the reaction or the evaporation of HNO is delayed and occurs preferentially for n ≈ 15–20 water molecules.⁴⁶ Oxidation of Zn⁺(H₂O)_n to ZnOH⁺(H₂O)_m is also observed in the reactions with acetonitrile.⁴⁷ With 1-iodopropane, Zn⁺(H₂O)_n reacts efficiently to ZnI⁺(H₂O)_m, again with oxidation of the Zn centre.⁴⁸ These studies showed that hydrated monovalent zinc ions can be oxidized by suitable reactants, but the details of the reactions and their cluster size-dependence can be quite complex. The question arises whether hydrated electrons are formed in sufficiently large clusters, similar to Mg⁺(H₂O)_n,²¹ however an insertion to form HZnOH⁺ does not seem plausible, given the lack of H/D exchange in the D₂O experiment.⁴⁵

To shed more light on these reactions, the structural properties of Zn⁺(H₂O)_n, with n ≤ 35, are probed by infrared spectroscopy. This study goes significantly beyond previous work by Duncan and co-workers, which was limited to n ≤ 4 and performed with Ar tagging. Starting with n = 2, the small clusters are investigated without Ar tagging, which provides interesting insight into the effect of temperature on the structural motifs and probes the clusters in a state that is closer to the reactivity studies mentioned above. The focus of this study is to establish how the water molecule binding motifs evolve from the small clusters, where we expect low coordination (3 water molecules), to larger clusters. Clusters explored in this study range from the small (n = 2–4), medium (n = 5–10), to large (n = 12–35). This goes far beyond the size range studied previously, and we expect relevant insight into the evolution of the hydration environment of the Zn⁺ ion. The substantially enlarged hydration shell may induce a change of coordination number, as well as formation of a solvated electron. We recently reported evidence of a six-fold coordinated Mg²⁺ ion and a solvated electron in Mg⁺(H₂O)_n (n = 20–70) complexes, measured in the ultraviolet (UV) region.²¹ One can speculate that the presence of a Zn²⁺/e⁻ pair in the cluster would lead to significant broadening of the water absorption band to the red, due to the strongly polarizing effect of the compact Zn²⁺ ion, thus the spectra of the largest clusters up to n = 35 water molecules may reveal evidence for or against the presence of the Zn²⁺ ion. The evolution of the IR spectra with cluster size leads to an enhanced understanding of solvation for Zn⁺(H₂O)_n complexes.

Experimental and computational details

Experimental measurements were performed on a modified 4.7 Tesla Bruker/Spectrospin CMS47X FT-ICR mass spectrometer^49–53 equipped with a Bruker infinity cell⁵⁴ and laser vaporisation source.^55,56 Briefly, a frequency-doubled Litron Nano S 60-30 Nd:YAG laser (532 nm, 5 mJ per pulse, 30 Hz) is focussed onto a rotating solid disc of isotopically enriched zinc (⁶⁴Zn, 99.4%, STB Isotope Germany GmbH), producing a plasma. This plasma is then entrained into a pulse of the desired gas mixture (H₂O in helium) yielded via a homebuilt piezoelectric valve. The ensuing pulse is cooled via supersonic jet expansion in the source chamber. The gas pulse traverses through a skimmer (forming the molecular beam), and ions are guided via an electrostatic lens set-up into the centre of the ICR cell. Here, ions can be stored and mass-selected within the 4.7 T magnetic field⁵⁷ under ultra-high vacuum conditions (ca. 5 × 10⁻¹⁰ mbar). The ICR cell is surrounded by a copper jacket, whereby the cell temperature can be controlled and cooled to ca. 80 K via liquid nitrogen,^58,59 minimising the effects of black body infrared radiative dissociation (BIRD).^60–65 It should be noted that we are unable to determine whether the ions are thermalised fully within the cooled ICR cell. However, as shown previously, we expect the large clusters to be thermalized, as IR exchange in the 300–500 cm⁻¹ region is efficient, and there are many IR photons present at 80 K.⁶⁵

On the opposite side of the magnet, a tunable IR OPO laser system (EKSPLA NT277) is coupled into the cell through a CaF₂ window.⁶⁶ Absorption of infrared photons, leading to photodissociation events are measured via mass spectroscopy.⁶⁷ Investigating both precursor and fragment masses provides the mass spectrometric signature of photon absorption. Monitoring the precursor and fragment abundance channels as a function of wavenumber yields the infrared spectrum of the complex of interest. Infrared spectra were recorded in the 2250–4000 cm⁻¹ wavelength region, probing the O–H symmetric and asymmetric stretch bands. Specific details on the laser setup can be found in previous publications.^66,68 Infrared spectra for all clusters were measured at a cell temperature of ca. 80 K, recorded via action spectroscopy, reaction 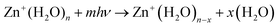1:

The number of photons required to dissociate a water molecule ranges from one to two, details of which are found in the ESI† and previous publications.^69,70 The reported spectra are thus strictly speaking Infrared Multiple Photon Dissociation (IRMPD) spectra. For all cluster sizes, photodissociation leading to loss of water molecules was found to be the only photofragment channel. To account for laser energy and irradiation time, single-photon cross sections, σ, are calculated using a modified Beer–Lambert equation:

where I₀ represents the intensity of the precursor ion, I_i the fragment ion intensity, λ the laser wavelength, E the laser pulse energy, p the number of laser pulses, h the Planck constant, A the area of the laser beam and k, an empirical factor which corrects for any contributions due to BIRD. Further details concerning the calculated infrared cross sections can be found in the ESI,† (Fig. S1). We also tried to analyse the data by calculating an IRMPD yield, but this led to artefacts in the peak shape that were clearly attributable to the laser power curve. The best results were obtained employing eqn (2). To determine the noise level of the IRMPD spectra, we calculate the IR cross section that corresponds to generating a fragment right at the noise level of the mass spectrum.

To complement the experimental findings, the structures, along with their corresponding infrared spectra, were calculated using density functional theory (DFT). Calculations were performed using the B3LYP functional coupled with the aug-cc-pVDZ basis set. Simulated infrared spectra were generated by implementing Gaussian functions to the band positions, each with a full-width-half-maximum (FWHM) of 20 cm⁻¹, using a scaling factor of 0.96. All structures considered represent local minima and are in the doublet spin multiplicity corresponding to the ground state. Other multiplicities, such as quartet or sextet, lie considerably higher (above 600 kJ mol⁻¹) in energy. Calculations were performed using the Gaussian16 software package.⁷¹

Results and discussion

Overall trends: Fig. 1 shows the experimental IRMPD spectra of size-selected Zn⁺(H₂O)_n clusters (n = 2–8, 10, 12, 18 and 35) assuming a one photon process. Measurement of the photodissociation spectrum of n = 1 was attempted but no fragments could be detected, presumably because the water binding energy is too high in addition to there being a lower density of states for this complex. The spectrum for n = 2 shows an intense feature centred at 3590 cm⁻¹, with a shoulder band at 3660 cm⁻¹. Both bands blue-shift to 3600 and 3680 cm⁻¹, respectively, at n = 3. The spectrum for n = 3 also shows another weak, red-shifted feature at 2990 cm⁻¹ and an extremely weak feature just above the noise level at 3200 cm⁻¹. A strong red-shifted band is present at 3130 cm⁻¹ for n = 4, together with an intense band at 3690 cm⁻¹. The emergence of weak features centred at 3370 and 3460 cm⁻¹, respectively, is also observed for n = 4. The experimental IRMPD band positions for each cluster size are presented in Table 1, with most bands red-shifted from the symmetric and asymmetric bands of isolated water.⁷²

Fig. 1 Experimental relative IRMPD photodissociation cross section (arbitrary units) of Zn⁺(H₂O)_n complexes (n = 2–8, 10, 12, 18 and 35) assuming a one-photon process. In each case photodissociation events are due to loss of intact water molecules. The dashed lines in each experimental spectrum correspond to the wavenumbers of the symmetric and asymmetric stretching modes of isolated water at 3657 and 3756 cm⁻¹, respectively.⁷²

Table 1 Experimentally observed IRMPD O–H band position of Zn⁺(H₂O)_n complexes (n = 2–8, 10, 12, 18, & 35) along with the isomer assignment and water binding motif

Cluster	Experimental IRMPD band position/cm^−1	Isomer assignment
Zn^+(H2O)2	3590	IIa
	3660	IIa
Zn^+(H2O)3	2990	IIIc-SA
	3600	IIIa/IIIc
	3680	IIIa/IIIc
Zn^+(H2O)4	3130	IVb-S*A, IVc-SA
	3370	IVa-DA, IVb-DA
	3460	IVb-DA
	3690	IVa–IVd
Zn^+(H2O)5	3180	Va-S*A, Vd-S*A, Vb-SA
	3270	Vc-S*A, Vc-oDA
	3470	Va–Vd-DA
	3540	Va–Vd-DA
	3690	Va–Vd
Zn^+(H2O)6	3210	VIa-SA, VIc-SA, VIb-S*A
	3290	VId-S*A, VIc-S*A, VIb-oDA
	3445	VIb–VId-DA
	3545	VIb–VId-DA
	3680	VIa–VId
	3730	VIa–VId
Zn^+(H2O)7	3210, 3310, 3450, 3490, 3540, 3690, 3730
Zn^+(H2O)8	2990–3650, 3210, 3370, 3460, 3540, 3690, 3730
Zn^+(H2O)10	2990–3650, 3230, 3440, 3540, 3700
Zn^+(H2O)12	2990–3650, 3220, 3450, 3540, 3700
Zn^+(H2O)18	2990–3650, 3220, 3440, 3490, 3540, 3580, 3700
Zn^+(H2O)35	2990–3650, 3220, 3310, 3480, 3550, 3700

---

The most red-shifted band is also present for clusters n > 4, centred at 3220 cm⁻¹ for n = 7, and even in the largest cluster with n = 35, a slightly blue-shifted maximum at 3230 cm⁻¹ can be identified in an overall broad absorption band that is typical for water clusters. The shift to the red, as outlined in many previous publications,^{3,25–42,73–75} is due to the metal-induced polarisation on the water molecules, which removes electron density from bonding orbitals on the O–H bond, causing an observed red-shift. As discussed previously for Zn⁺(H₂O)_n complexes,⁴³ the polarizing effect of Zn⁺, when compared to other singly-charged metal ions,^{3,25–42,73–75} is very strong, despite the apparent large size of the singly occupied 4s orbital. This indicates that the water molecules in turn have a strongly polarizing effect on the 4s valence orbital of Zn⁺, as previously shown for Mg⁺.²⁰

From n = 4 to n = 6, the position of the most red-shifted band gradually shifts to the blue, since the polarising effect is distributed over a larger number of water molecules. For larger clusters, these bands remain in a similar position, as a clear maximum in a broad absorption starting at ca. 2990 cm⁻¹ for n = 8. For all cluster sizes, this most red-shifted band is due to a single hydrogen bond O–H stretch between a single “outer” water and a “core” water molecule, a so-called single-acceptor configuration, denoted “SA”. Note, it is the “core” water hydrogen bonded O–H stretch that is assigned in this case. The “outer” water binding motifs are illustrated in Scheme 1. The second most red-shifted band (first appearing as a shoulder at 3270 cm⁻¹ for n = 5) is retained for all cluster sizes n ≥ 5, gradually blue-shifting from 3270 cm⁻¹ for n = 5 to 3480 cm⁻¹ for n = 35 and is also due to a SA hydrogen bond configuration. Different from the most red-shifted feature, this SA configuration is between a single outer water and a core water molecule, where the core water is also involved in a hydrogen bond with another outer water molecule, or involved also in a double-acceptor configuration. For clarity, hereinafter this second single-acceptor type is denoted “S*A”, while the double acceptor configuration is denoted “DA”. As observed in Scheme 1, the largest red-shift is observed for the SA motif, with the DA motif presenting the smallest red-shift. We are probing the hydrogen bonded O–H bands between core and outer water molecules, whereby outer water molecules are bound to either one (SA) or two (DA) core water molecules. The core O–H in a SA arrangement is bound to one outer water molecule, whereas in a DA arrangement, the hydrogen bonding capacity of the outer water molecule is “shared” between two O–H bonds, leading to strained hydrogen bonds with an imperfect O–H–O angle and an increased length of the hydrogen bond, resulting in a lower degree of red-shift.

Scheme 1 Schematic representation of the Zn⁺(H₂O)₆ cluster showing the three “outer” water configurations; two single-acceptor motifs (SA and S*A, respectively), along with the double-acceptor (DA) motif. “Core” water molecules represent those directly bound to the Zn⁺ centre.

With increasing cluster size, the number of energetically low-lying isomers, and hence the number of different types of core-outer water molecule hydrogen bonding configurations, increases rapidly. This yields many O–H bands with varying degrees of red-shift from the symmetric and asymmetric stretches of isolated water,⁷⁶ resulting in a broad, almost structureless absorption between 2990–3650 cm⁻¹ for n = 8–35. Within this size range, the relative intensity of this broad band increases with respect to the narrow band at ca. 3740 cm⁻¹, observed in the relative IRMPD cross sections in Fig. 1.

All cluster sizes present an intense band between the symmetric and asymmetric stretches of isolated water, starting as a shoulder at 3660 cm⁻¹ for n = 2, blue-shifting to 3690 cm⁻¹ for n = 3–10, and further blue-shifting to 3700 cm⁻¹ for n = 12, 18, 35. This band is assigned to core water molecules for n = 2, 3. For cluster sizes n ≥ 4, this band is due to the asymmetric O–H stretch of either (i) an outer water molecule involved in a DA configuration, or (ii) core water molecules with at least one dangling O–H bond. Cluster sizes n ≥ 6, however, also present a blue-shifted shoulder band, most easily identified in n = 7 centred at 3730 cm⁻¹. This band, which is closest to the asymmetric stretch of isolated water, is due to the asymmetric O–H stretch of an outer water molecule involved in a SA hydrogen bond configuration.

Zn⁺(H₂O)_2–6

To help in further understanding the IRMPD spectra of the smaller cluster sizes n = 2–6, low-lying isomers, along with their simulated infrared spectra, were calculated using DFT and are presented alongside the experimental spectra in Fig. 2. The structural isomers for clusters n = 2–6, along with their respective zero-point corrected energies are shown in Fig. 3.

Fig. 2 Experimental relative IRMPD photodissociation cross section (arbitrary units) along with simulated cross section σ of low-lying isomers for (a) Zn⁺(H₂O)₂, (b) Zn⁺(H₂O)₃, (c) Zn⁺(H₂O)₄, (d) Zn⁺(H₂O)₅, and (e) Zn⁺(H₂O)₆. In each case photodissociation events are due to loss of intact water molecules. The dashed lines in each experimental spectrum correspond to the wavenumbers of the symmetric and asymmetric stretching modes of isolated water at 3657 and 3756 cm⁻¹, respectively.⁷²

Fig. 3 (a) Low-lying isomers of Zn⁺(H₂O)_n clusters (n = 2–6) and (b) Zn⁺(H₂O)₈ & Zn⁺(H₂O)₁₀ calculated at the B3LYP/aug-cc-pVDZ level of theory along with relative energy given in kJ mol⁻¹ inclusive of zero-point energy.

Starting with the smallest cluster, n = 2, the intense feature seen experimentally at 3590 cm⁻¹ and the shoulder band at 3660 cm⁻¹ are in good agreement with the simulated spectrum of structure IIa, presenting bands at 3573 and 3669 cm⁻¹, respectively, assigned as the in-phase and out-of-phase symmetric stretches, and localised asymmetric O–H stretches of the two water molecules (Fig. 2a). As described previously by Duncan and co-workers in their study of Zn⁺(H₂O)_n–Ar complexes (n = 1–4),⁴³ the experimental infrared photodissociation spectrum of Zn⁺(H₂O)₂–Ar was also assigned to the symmetric and asymmetric O–H stretches, only in their study the colder, argon-tagged clusters yielded a highly-resolved spectrum showing four bands, assigned to two isomers with different argon binding sites (the argon atom bound either to the Zn⁺ centre, or the H atom on a water molecule). As mentioned previously, the clusters in our experimental setup are much warmer compared to their argon-tagged counterparts. Given the high energy of 0.9 eV to evaporate a water molecule, our clusters are irradiated for up to two seconds and require at least two photons for dissociation, resulting in an IRMPD process, in contrast to the single-photon absorption in the messenger tagging study of Zn⁺(H₂O)_n–Ar by the Duncan group.⁴³ Another isomer, IIb, was considered, showing a core water molecule bound to the Zn⁺ ion, with the second water hydrogen-bound to the first water molecule. The simulated spectrum of IIb shows an intense band at 2751 cm⁻¹, which is not observed experimentally. Given that this intense feature is not observed, and that IIb is calculated to lie 16.0 kJ mol⁻¹ above the putative global minimum, we conclude that the IRMPD spectrum consists of exclusively isomer IIa. The most intense feature in IIa at 3669 cm⁻¹ comprises of two overlapping bands (with a difference of <1 cm⁻¹) assigned as two localised O–H asymmetric stretches of the two water molecules. The broadening of the observed feature at 3660 cm⁻¹ goes along with an apparent reduced intensity. We attribute this to the IRMPD process, in which the first absorbed photon heats the cluster and excites internal rotations of the water molecules, potentially also the O–Zn–O bending mode. If the asymmetric stretch frequency is sensitive to the relative position of the two H₂O molecules, this explains the loss of intensity as well as the peak broadening. However, this interpretation implies that the symmetric modes are less sensitive to this effect, since the peak remains strong and relatively sharp.

Fig. 2b shows the experimental photodissociation spectrum of Zn⁺(H₂O)₃, along with the simulated spectra of isomers IIIa–IIId. The two intense features at 3600 and 3680 cm⁻¹ are in excellent agreement with the simulated bands at 3583 cm⁻¹ and 3680 cm⁻¹ for isomer IIIa and for the band at 3675 cm⁻¹ in IIIb (black and magenta spectra, respectively), corresponding to the symmetric and asymmetric O–H stretches of the water molecules bound to the Zn⁺ ion. As seen in Fig. 3a, isomer IIIa shows a coordination number of 3, whereas isomer IIIb a coordination number of 2. Isomer IIIa presents a simple simulated spectrum with bands at 3583 and 3680 cm⁻¹, while IIIb also shows a red-shifted band at 3402 cm⁻¹ corresponding to the core water O–H stretches in a DA configuration. A weak, broad absorption is observed experimentally at 2990 cm⁻¹ and an extremely weak feature just above the noise level at 3200 cm⁻¹. The most red-shifted feature is in good agreement with the simulated spectra of isomers IIIc and IIId, (red and green spectra, respectively). In both isomers, this band represents the core water O–H stretch in a SA configuration. Fig. 3a shows that IIIc has one SA configuration, and IIId has two SA configurations, reflected as an increase in intensity for this band in IIId, observed in the green spectrum. However, given that isomer IIId is calculated to lie 22.3 kJ mol⁻¹ above the putative global minimum isomer IIIa, it is unlikely that this isomer is present in the experiment. Thus, the experimentally observed red-shifted band at 2990 cm⁻¹ is assigned as the SA hydrogen bonding core O–H stretch in isomer IIIc. The intense experimental band at 3680 cm⁻¹ presents a tail to the blue, reaching the noise level at ca. 3800 cm⁻¹. This tail can be explained by the O–H stretches of outer water molecules in a SA site, such as that in isomer IIIc. Despite isomer IIIb lying only 0.7 kJ mol⁻¹ above the global minimum structure, the simulated band at 2402 cm⁻¹ (magenta spectrum), i.e. the signature of a DA configuration core water O–H stretch, is not observed. This can be rationalised by considering the experimental conditions, whereby only warmer isomers with fewer hydrogen bonds, i.e.IIIc, survive. Absorption of IR photons (e.g. as a consequence of BIRD, or indeed from the pulsed radiation from the OPO) could also be sufficient to break one of the hydrogen bonds in the DA configuration in isomer IIIb, leading to a SA configuration (such as that in isomer IIIc), thus the signature of the DA would be lost and unobserved in the experimental IRMPD spectrum, since the required second photon cannot be absorbed. The experimental IRMPD spectrum here is different from the messenger tagging spectrum observed in the work of Duncan, which was assigned to exclusively isomers where all three water molecules were directly bound to the Zn⁺ centre, i.e. no observed red-shifted bands below ca. 3500 cm⁻¹.⁴³

The experimental signature of the SA configuration increases in intensity for n = 4, Fig. 2c, shown as an intense band centred at 3130 cm⁻¹. Isomer IVb presents a S*A and IVc presents a SA water molecule, both of which are in good agreement with this red-shifted band (magenta and red spectra, both presenting a band at 3125 cm⁻¹, respectively). This most intense band at 3130 cm⁻¹ shows an increased FWHM of 150 cm⁻¹ (compared to the FWHM of 35 cm⁻¹ for the band at 3600 cm⁻¹, in n = 3) consistent with this band being composed of all three isomers, IVb–IVd, in addition to other low-lying isomers we have not considered. Large-amplitude motion of water molecules in these isomers could also give rise to the increased width of this band, in addition to lifetime broadening if intramolecular vibrational energy redistribution (IVR) rates are increased.

Evidence of DA absorptions are also present in the observed spectrum, centred at 3370 and 3460 cm⁻¹, but are less intense. These bands are in reasonable agreement with simulated spectra of isomers IVa and IVb, presenting bands at 3438 cm⁻¹, and 3359/3507 cm⁻¹ (black and magenta spectra, respectively). All four isomers are within 1.8 kJ mol⁻¹ of energy, so are likely to all contribute to the experimental spectrum. The increased FWHM (102 cm⁻¹) of the band centred at 3690 cm⁻¹ reflects evidence for this, where all four isomers present bands within the asymmetric O–H stretching region between 3585–3735 cm⁻¹. The messenger tagging spectrum of Duncan and co-workers did not present evidence of SA water molecules, and instead, only isomers of DA site water molecules were observed, which were assigned to an intense band at 3426 cm⁻¹.⁴³ This again illustrates the influence of temperature on the IRMPD spectra of these systems.

Upon addition of another water molecule, the number of different hydrogen-bonding configurations increases, reflecting a more complex simulated spectrum, Fig. 2d. The signature of a SA water is also pronounced here, presenting an intense feature centred at 3180 cm⁻¹, along with a shoulder at 3270 cm⁻¹. The band at 3180 cm⁻¹ is in excellent agreement with the S*A water stretches for isomers Va (3172 cm⁻¹) and Vd (3189 cm⁻¹), and the SA water stretch of isomer Vb (3181 cm⁻¹) black, green and magenta spectra, respectively. These SA configurations represent those where the core water is interacting exclusively with one outer water molecule. A different type of configuration, denoted as S*A, is seen in isomers Va, Vc, and Vd, where a core water molecule hydrogen bonds with one outer water but is also involved in a DA configuration with another, outer water molecule. The core water O–H stretch in a S*A configuration presents a slightly less red-shifted band, when compared to the equivalent stretch in a SA configuration for three coordinate structures, such as that seen in isomer Vb. As observed in Fig. 3, isomers Va and Vd present a coordination number of 2. The S*A core O–H stretches in these isomers are comparable in red-shift to SA core stretches in three-coordinate structures, isomer Vb. The shoulder band at 3270 cm⁻¹ can be rationalised when considering the binding motifs for two- and three-coordinate structures. The simulated spectrum of Vc presents a band at 3229 cm⁻¹, assigned as a S*A core O–H stretch, whilst the spectrum of Vd presents a band at 3224 cm⁻¹, assigned as an entirely different binding motif; an outer DA O–H stretch bound to another outer water molecule, denoted as oDA. Given these isomers are calculated to differ by only 0.1 kJ mol⁻¹, it is likely that the observed band at 3270 cm⁻¹ is composed of contributions from both isomers Vc and Vd. Evidence of DA configurations, shown as weaker features at 3470 and 3540 cm⁻¹, are also presented, in good agreement with DA bands present in all four isomers. The band centred at 3690 cm⁻¹ also shows good agreement with the asymmetric bands present for all four isomers.

Similar to n = 5, SA core water bands dominate the experimental spectrum for n = 6, presenting two intense bands at 3210 and 3290 cm⁻¹, Fig. 2e. In a similar fashion, the band at 3210 cm⁻¹ represents a SA configuration whereby the core water interacts with one water exclusively, seen in the spectrum for isomers VIa (3215 cm⁻¹, black) and VIc (3223 cm⁻¹, red), or could come from a S*A configuration from the two-coordinate isomer VIb (3218 cm⁻¹, magenta). The band at 3290 cm⁻¹ is in excellent agreement with the simulated bands for isomers VIb, VIc and VId (3262, 3267, and 3253 cm⁻¹, respectively), representing S*A configurations for VIc and VId. For isomer VIb however, the band represents an outer DA O–H stretch bound to another outer water molecule, the same binding motif, oDA, found for isomer Vd. Evidence for DA configurations are also presented as weaker features at 3445 and 3545 cm⁻¹, and are in reasonable agreement with DA core O–H stretches present in isomers VIb, VIc and VId. A band at 3680 cm⁻¹, with a shoulder at 3730 cm⁻¹, is shown which can be represented as asymmetric O–H stretches of outer water molecules in DA and SA configurations, respectively, with contributions of the asymmetric O–H stretches of core water molecules with free O–H bonds.

Larger clusters

Fig. 4 shows the experimental IRMPD spectra of Zn⁺(H₂O)₈ and Zn⁺(H₂O)₁₀ assuming a one photon process, along with the simulated spectra of low-lying isomers VIIIa–VIIId, and Xa–Xd (see Fig. 3b). The experimental spectrum for n = 8 (Fig. 4a) presents a broad absorption feature between 2990–3650 cm⁻¹, showing a pronounced maximum at 3370 cm⁻¹, along with a shoulder to the red at 3210 cm⁻¹, and two shoulders to the blue at 3460 and 3540 cm⁻¹, respectively. A sharper band due to free O–H stretching modes is also observed at 3690 cm⁻¹. These features are in reasonable agreement with the simulated spectrum of isomer VIIIa, which shows bands at 3171, 3452, and 3688 cm⁻¹, along with an intense feature at 3299 cm⁻¹. Many other bands which overlap, or are very close to the feature at 3299 cm⁻¹, are also observed in the simulated spectrum of isomer VIIIa, however the experimental IRMPD spectrum is in good agreement with a combination of all four low-lying isomers, VIIIa–VIIId. The presence of these overlapping bands contributes to the broad feature in the experimental spectrum. These larger clusters represent a complicated potential-energy landscape, whereby water ligands can interconvert between different isomers across shallow barriers. Thus, at these cluster sizes, we cannot consider isolated isomers exclusively, but instead a fluxional system continually exploring the potential-energy landscape. In this sense, the spectra illustrate structural motifs, rather than individual isomers. Increase in coordination number from three to four leads to higher-lying isomers (e.g.VIIIe, see ESI†), suggesting that at this cluster size, the hydrogen bonding between the water molecules is energetically favoured over the four-coordinate Zn⁺ ion. As observed previously for Mg⁺, Al⁺, and Zn⁺ ions,^29,37,43 the coordination is governed by the valence electron configuration. Both Mg⁺ and Zn⁺ have the same valence configuration, ns¹, causing asymmetric ligand binding arrangements, with both ions presenting a coordination number of three. Incoming ligands experience significant repulsion from the occupied valence s orbital, resulting in lower coordination sites whereby ligands bind to the same side of the metal centre. In the case of Zn⁺, the three water molecules bind to one side of the metal centre in a pyramidal arrangement for cluster sizes n ≥ 6. This coordination of three seems to be retained for larger clusters. For smaller clusters, however, a coordination number of two is energetically preferred for n = 5, whilst the two-coordinate structure (IVb) lies only 0.3 kJ mol⁻¹ higher than the putative global minimum structure for n = 4. At n = 6, the three-coordinate motif (VIa) lies 2.2 kJ mol⁻¹ below the two-coordinate structure (VIb). Whenever a two-coordinate structure is energetically close to the minimum, which is the case at least up to n = 6, it affords at least one additional hydrogen bond, which offsets the energy increase due to the undercoordinated metal centre. With the increased topological flexibility of the larger clusters, this effect is no longer operative, and coordination number of three becomes clearly preferred.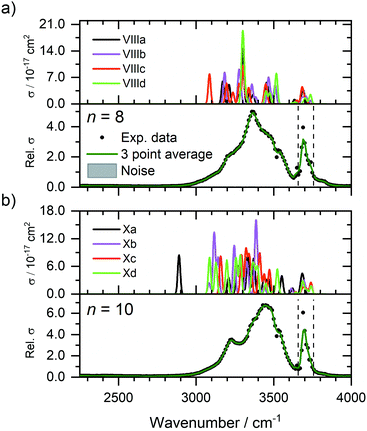

Fig. 4 Experimental relative IRMPD photodissociation cross section (arbitrary units) of (a) Zn⁺(H₂O)₈ and (b) Zn⁺(H₂O)₁₀ along with simulated cross section σ of low-lying isomers. In each case photodissociation events are due to loss of intact water molecules. The dashed lines in each experimental spectrum correspond to the wavenumbers of the symmetric and asymmetric stretching modes of isolated water at 3657 and 3756 cm⁻¹, respectively.⁷²

The experimental spectrum of n = 10 (Fig. 4b) shows a qualitatively similar spectrum, presenting a broad absorption between 2990–3650 cm⁻¹ with a maximum at 3440 cm⁻¹, along with a more-defined red shoulder at 3230 cm⁻¹, and blue shoulder at 3540 cm⁻¹. A sharper band is also observed at 3700 cm⁻¹. The simulated spectra of isomers Xa–Xd present largely similar spectra, showing reasonable agreement with the experimental spectrum. The putative global minimum spectrum (Xa), however, presents a red-shifted band at 2889 cm⁻¹, which is not seen in the experiment. This band is due to the O–H stretch of an outer water molecule, hydrogen bonded to three outer water molecules. This red-shift implies the beginning of the formation of a mobile proton, i.e. significant weakening of the O–H bond.⁷⁷ Isomers Xb–Xd, however, do not show evidence for this red-shifted feature. This would suggest that for larger clusters, there are more water molecules adopting a SA configuration, i.e. warmer, and fewer colder clusters present in the ICR cell, concordant with smaller clusters. This observation is also concordant with previous IR investigations on M⁺(H₂O)_n complexes,^78,79 whereby entropic effects dominate enthalpic effects at elevated temperatures. DA water molecules are secured more rigidly by two hydrogen bonds, thus the isomers with more SA molecules are entropically favoured. Since each mass-selected ion ensemble is exposed to 80 K black-body radiation in the ICR cell, entropically favoured isomers are higher in abundance and hence, more prominent in the observed IRMPD spectra. To fully account for the observed spectra, a temperature-dependent population analysis based on master equation modelling would be needed.

The observed spectra for n = 12, 18 & 35 shown in Fig. 1 look qualitatively similar to those of n = 10, presenting a broad absorption band between 2990–3650 cm⁻¹. The maximum of this absorption at 3220 cm⁻¹ also increases in relative intensity upon increasing cluster size. As no significant changes are observed up to this large cluster size regime, we believe no significant changes in coordination number are apparent. There is also no evidence for significant red-shifted bands, or the advent of a mobile proton within this size regime up to 35 water molecules.

The spectral signature of the mobile proton has been observed previously by Johnson et al.,⁷⁷ a weak, broad and structureless absorption between ca. 2800–3500 cm⁻¹. This spectral signature is not observed in the work presented here, even for the largest cluster Zn⁺(H₂O)₃₅. We thus can rule out the formation of a HZnOH⁺ motif. Evidence of the hydroxide ion is not observed in this cluster size range.

Infrared spectroscopy in the O–H stretching region is not diagnostic in determining the presence of the solvated electron. Johnson and co-workers performed an infrared spectroscopic study of solvated electrons,⁸⁰ the IR spectrum of (H₂O)₂₁⁻ presents a broad feature between 3000–3700 cm⁻¹, with a weak, narrower feature at 3710 cm⁻¹. These features are qualitatively similar to the spectra discussed here for larger clusters, n ≥ 10 (Fig. 1). However, based on these comparisons alone, we cannot confirm, or reject, the presence of the solvated electron. Thus, further experiments in the ultraviolet (UV) wavelength region would be necessary to elucidate the presence, or absence, of the solvated electron, the former observed previously for Mg⁺(H₂O)_n clusters (n = 20–70).²¹

Conclusions

Gas-phase hydrated Zn⁺(H₂O)_n complexes (n = 2–35) were formed via laser ablation and stored in the centre of an ICR cell cooled to ca. 80 K. Infrared photodissociation spectra were recorded in the range of the O–H stretch between 2250–4000 cm⁻¹. In all cases the spectral signature of IR absorption was reflected by dissociation of intact water molecules. The IRMPD spectra present good agreement with the simulated spectra of low-lying isomers. In comparison with previous experiments on argon-tagged complexes with n ≤ 4, pronounced differences arise due to the elevated temperatures in the present study.

The 4s¹ valence electron configuration of the Zn⁺ ion causes asymmetric lower coordination sites causing a retention of coordination number. The IRMPD spectra support a coordination number of three for all cluster sizes with water molecules binding to the same side of the Zn⁺ centre. Additional water molecules, n ≥ 4, form hydrogen bonds with the three, “core” water molecules in SA, S*A, or DA configurations, yielding varying degrees of red-shift from the symmetric and asymmetric stretches of isolated water. In all binding motifs, as the cluster size increases the degree of red-shift decreases due to the decreased metal-induced polarisation on each water molecule. The relative intensities of the 2nd and 3rd coordination sphere O–H bands increase and broaden, whereas 1st coordination sphere bands retain a similar FWHM and band position.

The three-coordinate structure implies that the Zn⁺ ion resides on the cluster surface even for the largest clusters examined here, with the 4s electron exposed. This fits to the observed reactivity with hydrophobic reactants such as O₂ or IC₃H₇, which is relatively high and does not exhibit any obvious size dependence. In line with the D₂O exchange experiment, evidence of a HZnOH⁺ motif is not observed, even at the largest cluster size (n = 35) studied here, which should be evidenced by the IR signature of the mobile proton; a weak unresolved feature at ca. 2800–3500 cm⁻¹.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors gratefully acknowledge support from the Austrian Science Fund FWF, Project No. P29174 and the DK-ALM: W1259-N27. The tunable OPO system is part of the Innsbruck Laser Core Facility, financed by the Austrian Federal Ministry of Science, Research and Economy. The computational results presented have been attained using the HPC infrastructure LEO of the University of Innsbruck.

References

1. M. A. Duncan, Int. Rev. Phys. Chem., 2003, 22, 407.
2. P. Kebarle, Annu. Rev. Phys. Chem., 1977, 28, 445.
3. M. A. Duncan, Annu. Rev. Phys. Chem., 1997, 48, 69.
4. V. E. Bondybey and M. K. Beyer, Int. Rev. Phys. Chem., 2002, 21, 277.
5. A. J. Stace, J. Phys. Chem. A, 2002, 106, 7993.
6. M. K. Beyer, Mass Spectrom. Rev., 2007, 26, 517.
7. N. C. Polfer and J. Oomens, Mass Spectrom. Rev., 2009, 28, 468.
8. V. Artero, M. Chavarot-Kerlidou and M. Fontecave, Angew. Chem., Int. Ed., 2011, 50, 7238.
9. C. Tard and C. J. Pickett, Chem. Rev., 2009, 109, 2245.
10. S. Canaguier, V. Artero and M. Fontecave, Dalton Trans., 2008, 315.
11. B. E. Barton, C. M. Whaley, T. B. Rauchfuss and D. L. Gray, J. Am. Chem. Soc., 2009, 131, 6942.
12. R. Brimblecombe, G. F. Swiegers, G. C. Dismukes and L. Spiccia, Angew. Chem., Int. Ed., 2008, 47, 7335.
13. K. Fuke, K. Hashimoto and S. Iwata, Adv. Chem. Phys., 1999, 110, 431.
14. G. Niedner-Schatteburg and V. E. Bondybey, Chem. Rev., 2000, 100, 4059.
15. W. A. Donald, R. D. Leib, J. T. O'Brien, A. I. S. Holm and E. R. Williams, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18102.
16. D. E. Lessen, R. L. Asher and P. J. Brucat, J. Chem. Phys., 1990, 93, 6102.
17. J. M. Farrar, Int. Rev. Phys. Chem., 2003, 22, 593.
18. K. F. Willey, C. S. Yeh, D. L. Robbins and M. A. Duncan, Chem. Phys. Lett., 1992, 192, 179.
19. C. T. Scurlock, S. H. Pullins, J. E. Reddic and M. A. Duncan, J. Chem. Phys., 1996, 104, 4591.
20. M. Ončák, T. Taxer, E. Barwa, C. van der Linde and M. K. Beyer, J. Chem. Phys., 2018, 149, 44309.
21. T. Taxer, M. Ončák, E. Barwa, C. van der Linde and M. K. Beyer, Faraday Discuss., 2019, 217, 584.
22. J. S. Daluz, A. Kocak and R. B. Metz, J. Phys. Chem. A, 2012, 116, 1344.
23. A. Kocak, G. Austein-Miller, W. L. Pearson, G. Altinay and R. B. Metz, J. Phys. Chem. A, 2013, 117, 1254.
24. Y. Abate and P. D. Kleiber, J. Chem. Phys., 2005, 122, 84305.
25. J. M. Lisy, Int. Rev. Phys. Chem., 1997, 16, 267.
26. J. P. Beck and J. M. Lisy, J. Chem. Phys., 2011, 135, 44302.
27. R. S. Walters and M. A. Duncan, Aust. J. Chem., 2004, 57, 1145.
28. N. R. Walker, R. S. Walters, E. D. Pillai and M. A. Duncan, J. Chem. Phys., 2003, 119, 10471.
29. N. R. Walker, R. S. Walters, M.-K. Tsai, K. D. Jordan and M. A. Duncan, J. Phys. Chem. A, 2005, 109, 7057.
30. R. S. Walters, E. D. Pillai and M. A. Duncan, J. Am. Chem. Soc., 2005, 127, 16599.
31. T. D. Vaden, J. M. Lisy, P. D. Carnegie, E. D. Pillai and M. A. Duncan, Phys. Chem. Chem. Phys., 2006, 8, 3078.
32. P. D. Carnegie, A. B. McCoy and M. A. Duncan, J. Phys. Chem. A, 2009, 113, 4849.
33. P. D. Carnegie, B. Bandyopadhyay and M. A. Duncan, J. Phys. Chem. A, 2008, 112, 6237.
34. P. D. Carnegie, B. Bandyopadhyay and M. A. Duncan, J. Chem. Phys., 2011, 134, 14302.
35. P. D. Carnegie, B. Bandyopadhyay and M. A. Duncan, J. Phys. Chem. A, 2011, 115, 7602.
36. B. Bandyopadhyay and M. A. Duncan, Chem. Phys. Lett., 2012, 530, 10.
37. Y. Inokuchi, K. Ohshimo, F. Misaizu and N. Nishi, Chem. Phys. Lett., 2004, 390, 140.
38. Y. Inokuchi, K. Ohshimo, F. Misaizu and N. Nishi, J. Phys. Chem. A, 2004, 108, 5034.
39. T. Iino, K. Ohashi, K. Inoue, K. Judai, N. Nishi and H. Sekiya, J. Chem. Phys., 2007, 126, 194302.
40. K. Furukawa, K. Ohashi, N. Koga, T. Imamura, K. Judai, N. Nishi and H. Sekiya, Chem. Phys. Lett., 2011, 508, 202.
41. M. F. Bush, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2008, 130, 9122.
42. J. T. O’Brien and E. R. Williams, J. Phys. Chem. A, 2011, 115, 14612.
43. B. Bandyopadhyay, K. N. Reishus and M. A. Duncan, J. Phys. Chem. A, 2013, 117, 7794.
44. B. S. Fox-Beyer, Z. Sun, I. Balteanu, O. P. Balaj and M. K. Beyer, Phys. Chem. Chem. Phys., 2005, 7, 981.
45. C. van der Linde and M. K. Beyer, J. Phys. Chem. A, 2012, 116, 10676.
46. C. van der Linde, R. F. Höckendorf, O. P. Balaj and M. K. Beyer, Chem. – Eur. J., 2013, 19, 3741.
47. I. Herber, W.-K. Tang, H.-Y. Wong, T.-W. Lam, C.-K. Siu and M. K. Beyer, J. Phys. Chem. A, 2015, 119, 5566.
48. I. Gernert and M. K. Beyer, J. Phys. Chem. A, 2017, 121, 9557.
49. A. Akhgarnusch, W. K. Tang, H. Zhang, C.-K. Siu and M. K. Beyer, Phys. Chem. Chem. Phys., 2016, 18, 23528.
50. M. Allemann, H. Kellerhals and K. P. Wanczek, Int. J. Mass Spectrom. Ion Processes, 1983, 46, 139.
51. C. Berg, T. Schindler, G. Niedner-Schatteburg and V. E. Bondybey, J. Chem. Phys., 1995, 102, 4870.
52. T. Schindler, C. Berg, G. Niedner-Schatteburg and V. E. Bondybey, Chem. Phys., 1995, 201, 491.
53. A. Akhgarnusch, R. F. Höckendorf and M. K. Beyer, J. Phys. Chem. A, 2015, 119, 9978.
54. P. Caravatti and M. Allemann, Org. Mass Spectrom., 1991, 26, 514.
55. V. E. Bondybey and J. H. English, J. Chem. Phys., 1981, 74, 6978.
56. T. G. Dietz, M. A. Duncan, D. E. Powers and R. E. Smalley, J. Chem. Phys., 1981, 74, 6511.
57. A. G. Marshall, C. L. Hendrickson and G. S. Jackson, Mass Spectrom. Rev., 1998, 17, 1.
58. R. L. Wong, K. Paech and E. R. Williams, Int. J. Mass Spectrom., 2004, 232, 59.
59. O. P. Balaj, C. B. Berg, S. J. Reitmeier, V. E. Bondybey and M. K. Beyer, Int. J. Mass Spectrom., 2009, 279, 5.
60. D. Thölmann, D. S. Tonner and T. B. McMahon, J. Phys. Chem., 1994, 98, 2002.
61. R. C. Dunbar, Mass Spectrom. Rev., 2004, 23, 127.
62. T. Schindler, C. Berg, G. Niedner-Schatteburg and V. E. Bondybey, Chem. Phys. Lett., 1996, 250, 301.
63. P. D. Schnier, W. D. Price, R. A. Jockusch and E. R. Williams, J. Am. Chem. Soc., 1996, 118, 7178.
64. M. Sena and J. M. Riveros, Rapid Commun. Mass Spectrom., 1994, 8, 1031.
65. B. S. Fox, M. K. Beyer and V. E. Bondybey, J. Phys. Chem. A, 2001, 105, 6386.
66. A. Herburger, C. van der Linde and M. K. Beyer, Phys. Chem. Chem. Phys., 2017, 19, 10786.
67. W. A. Donald, R. D. Leib, M. Demireva and E. R. Williams, J. Am. Chem. Soc., 2011, 133, 18940.
68. A. Herburger, M. Ončák, C.-K. Siu, E. G. Demissie, J. Heller, W. K. Tang and M. K. Beyer, Chem. – Eur. J., 2019, 25, 10165.
69. N. K. Bersenkowitsch, M. Ončák, J. Heller, C. van der Linde and M. K. Beyer, Chem. – Eur. J., 2018, 24, 12433.
70. J. Heller, M. Ončák, N. K. Bersenkowitsch, C. van der Linde and M. K. Beyer, Eur. J. Mass Spectrom., 2019, 25, 122–132.
71. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian Inc., Wallingford CT, 2016.
72. T. Shimanouchi, Tables of molecular vibrational frequencies. Consolidated volume I, National Bureau of Standards, Washington, DC, 1972.
73. Y. Li, G. Wang, C. Wang and M. Zhou, J. Phys. Chem. A, 2012, 116, 10793.
74. T. B. Ward, P. D. Carnegie and M. A. Duncan, Chem. Phys. Lett., 2016, 654, 1.
75. P. D. Carnegie, J. H. Marks, A. D. Brathwaite, T. B. Ward and M. A. Duncan, J. Phys. Chem. A, 2020, 124, 1093.
76. N. Yang, C. H. Duong, P. J. Kelleher and M. A. Johnson, Nat. Chem., 2020, 12, 159.
77. C. J. Johnson, L. C. Dzugan, A. B. Wolk, C. M. Leavitt, J. A. Fournier, A. B. McCoy and M. A. Johnson, J. Phys. Chem. A, 2014, 118, 7590.
78. J. Kim, S. Lee, S. J. Cho, B. J. Mhin and K. S. Kim, J. Chem. Phys., 1995, 102, 839.
79. K. Ohashi, J. Sasaki, G. Yamamoto, K. Judai, N. Nishi and H. Sekiya, J. Chem. Phys., 2014, 141, 214307.
80. N. I. Hammer, J. R. Roscioli, J. C. Bopp, J. M. Headrick and M. A. Johnson, J. Chem. Phys., 2005, 123, 244311.
81. C van der Linde, S Hemmann, R F Höckendorf, O P Balaj and M K Beyer, Reactivity of Hydrated Monovalent First Row Transition Metal Ions M⁺(H₂O)_n, M = V, Cr, Mn, Fe, Co, Ni, Cu, Zn, toward Molecular Oxygen, Nitrous Oxide, and Carbon Dioxide, Journal of Physical Chemistry A, 2013, 117(6), 1011–1020.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp06112c

---