First-principles calculation of ¹¹B solid-state NMR parameters of boron-rich compounds II: the orthorhombic phases MgB₇ and MgB₁₂C₂ and the boron modification γ-B₂₈

Abstract

Based on the work on referencing ¹¹B nuclear magnetic resonance (NMR) spectra for molecular icosahedral boranes and the subsequent transfer to the rhombohedral boron-rich borides of the α-rB₁₂ type, we show that the magic angle spinning (MAS) NMR spectra of boron-rich borides with four or five symmetry-independent boron atoms can also be calculated. The calculations are performed on the level of density functional theory (DFT) using the gauge-including projector-augmented wave (GIPAW) approach. As model compounds o-MgB₁₂C₂ and MgB₇ are used, for which the experimental spectra could be calculated in excellent agreement with a deviation of 1 to 2 ppm. Based on the calculations, the different B atoms can be assigned to the respective signals, taking into account the quadrupolar coupling constants C_q from computation of the electric field gradient (EFG) with its main axis V_zz. It is shown that due to the specific geometric conditions of icosahedra, the magnitudes of V_zz for the boron atoms involved in exohedral B–B bonds to neighbouring icosahedra depend only on the valence electron density of the bond critical point and the distance. This also applies to the bonds to the interstitial B₂ unit in MgB₇, but not to bonds to the heteroatom of the C₂ dumbbell in o-MgB₁₂C₂. Both results are in line with our previous observations for the rhombohedral species (α-rB₁₂; B₁₂X₂ with X = P, As, O). Finally, the spectrum of γ-B₂₈ was calculated, whose structure also contains B₁₂ icosahedra and interstitial B₂ dumbbells. Here, a very similar bonding situation is found for the icosahedron, but the calculations show that the situation for the B₂ unit is clearly different. In general, the only parameter that needs to be varied to fit calculated and measured spectra is the linewidth, as this cannot be calculated. For the cases of o-MgB₁₂C₂ and MgB₇ signal areas are related to corresponding site multiplicities. A prerequisite for the successful application of the chosen method seems to be the presence of a semiconductor with a sufficiently large band gap, which is the case for the compounds investigated.

---

1 Introduction

Due to its distinctive elemental structures, bonding mode and physical properties, B raises questions regarding not only its elemental structures but also the compounds derived from them, such as boron-rich borides. To this date, the exact composition of solid phases and the resulting structure–property relationships are a challenge for both experimentalists and theoreticians.¹

Being an element with noteworthy electron deficit, this element is known to form numerous deltahedral structures such as octahedra or icosahedra. In fact, it is precisely for this reason that B confronts us with certain puzzles, to which the solutions may not only provide an adequate description of interesting properties but often also fertile ground for concept development in chemistry. For example, early work of Longuet-Higgins^2,3 on the electronic structure of molecular B closo-clusters paved the way for the electron counting rules of Wade,⁴ which became a well-known part of common chemistry textbooks. Nevertheless, the investigation of the bonding situation of B polyhedra in molecules⁵ and especially in solid compounds^6–8 is still of essential importance.

The structural determination of the modification γ-B (γ-B₂₈),^9,10 in which icosahedral building units are linked to each other and to B₂ dumbbells, has stimulated a vivid discussion about the bonding situation prevailing there.^11–16 Still, current work is examining the structural influences on problems of the hardness description for this compound.¹⁷ But also for binary borides such as α-SiB_3−x, the distribution of Si in the condensed polyhedra of B is of ongoing interest for an understanding of corresponding physical properties.¹⁸

Nuclear magnetic resonance (NMR) spectroscopy is a microscopic tool to study the electronic structure in numerous boron compounds. Because the nuclear spin I of both naturally occurring isotopes ¹⁰B and ¹¹B is greater than one-half, the B nucleus interacts with the electronic field gradient (EFG). In addition to the Zeeman effect, this generated quadrupole moment leads to a further splitting of the energy levels in the magnetic field. The internuclear couplings, that are the dipolar coupling through space and the J coupling through bonds, generally show several orders of magnitude less contributions in solid-state NMR (SSNMR) spectra of B.¹⁹

The orientation-dependent contributions of many of the mentioned interactions are relevant for the recorded signal shape in SSNMR and can hamper the interpretation of measurements by spectral broadening. These anisotropic components disappear under magic angle spinning (MAS) conditions, that means the sample is physically rotated around an axis which inclines the so called magic angle relative to the external magnetic field. However, even with this approach, a contribution of the quadrupolar coupling remains in second-order and can make unambiguous processing difficult, notably if more than one species is detected in the spectrum.²⁰ Accordingly, the MAS NMR spectra of quadrupolar B nuclei are not only influenced by the chemical shift but also by the quadrupolar coupling, which also affects the observed shifts of the central transition (1/2 ↔ −1/2)^21,22 and influences sideband patterns (±3/2 ↔ ±1/2) as well as the profile via the anisotropy parameter η_q.

Apart from the problem that overlapping signals of several sites may complicate spectra analysis, it is very difficult to guarantee phase purity in case of solid compounds of B. The element is known to incorporate small impurities such as C. This sensitivity leads to an extraordinary difficulty in the synthesis of samples with the requirement for special purity or stoichiometry.^16,23 An example is the study²⁴ on the existence of the tetraboride CaB₄. In particular, the C content of CaB_4−xC_x was found to be rather low (<5%) but its presence turned out to be essential for the synthesis. Of the three different crystallographic positions of boron, only one could be clearly assigned a chemical shift and quadrupole coupling constant from the measured NMR spectra, since the other two showed side band patterns of low intensity. Finally, we would like to point out that deviations from the actual solid phase structure due to impurities can also lead to errors in processed parameters.

A combination of experimental data with calculations on an ab initio level has been proven efficient in this context. Especially in the case of borides the electronic structure could be related to results for quadrupole couplings measured by NMR techniques, since this observable can be derived directly from the electron density distribution. The EFG components for MB₁₂ (M = Y, Zr, Lu) were calculated with cuboctahedral units²⁵ and later the magnitude and orientation of YB₁₂ were confirmed by measurements.²³ In addition, computational studies^26–29 on metal borides mainly consisting of B₆ octahedra show good agreement between theory and experiment. And as recent studies show,³⁰ such calculations of the EFG parameters still help to unveil MAS NMR investigations on the ternary borides YTB₄ (T = Mo, W, Re) with a planar 2D net of B atoms with trigonal-planar surrounding.

Besides octahedra, B₁₂ icosahedra form the main building blocks of many boron-rich borides and are the dominant structural element of all allotropes of B.¹ As ref. 31 and references therein show, chemical shifts of numerous icosahedral closo-(hetero)dodecaboranes have been known for more than five decades. Moreover, theoretical and experimental studies on nuclear quadrupole coupling constants of icosahedral carboranes are also reported.³² On the other hand, to the best of our knowledge there exist to date just small sets of calculated^26,27 or measured^33–35 NMR data for only a few boron-rich borides with icosahedral structure elements, this is particularly true considering nuclear magnetic ¹¹B shifts.¹⁹ Certainly there is not only the already mentioned problem of phase-pure synthesis but also the difficulty of processing measured signals. Several symmetry-independent positions of atoms may lead to complex NMR spectra, which cannot be easily understood despite the knowledge of structure investigated. The main reasons for this are that a simple correlation between the tensor components of the chemical shift or EFG with the electron density a priori is not possible and/or even no comparable values of similar compounds exist. So the common procedure in NMR spectroscopy to compare the chemical shifts of a specific atom to a closely related model system, for example BO₄ tetrahedra or trigonal-planar BO₃ units in borates, is not possible.

Besides, previous work³⁶ have tried to address isotropic chemical ¹¹B shifts in homonuclear bonds of diboron compounds in the theoretical framework of density functional theory (DFT) applying the gauge-including projector-augmented wave (GIPAW) approach.^37,38 However, there the lack of applying an appropriate reference led to computational errors of more than 14 ppm which we think is not suitable for understanding SSNMR spectra where more particular sites may cause signal overlaps. In contrast, a recent report³⁹ presented evidence for calculating isotropic chemical ¹¹B shifts of various closo-(hetero)dodecaboranes with GIPAW demonstrating an accuracy of 1.0 to 2.1 ppm compared to experimental data depending on the applied method of reference. Furthermore, in our previous study⁴⁰ on rhombohedral phases we showed that calculated chemical shifts and quadrupolar coupling constants are in excellent agreement with MAS NMR measurements (in range of ±1 ppm) of the boron modification α-B (α-rB₁₂) and B₁₂P₂ as well as other work on boron-rich borides and also molecular compounds with icosahedral structure element. There, the analysis of the EFG revealed that the highly symmetric arrangement of B atoms to icosahedra and the strength of the outericosahedral bonds lead to a mapping of the predominant bonding situation in values of the quadrupole coupling constant/frequency.

The present study is an extension of our computational DFT investigation on NMR parameters of boron modifications and boron-rich borides which expands the available data sets of this solid state compound class. Our GIPAW calculations are complemented by measured MAS NMR spectra of the orthorhombic phases of MgB₇⁴¹ and o-MgB₁₂C₂⁴² which have been synthesized and characterized by X-ray diffraction (XRD) analysis in our laboratories. Both compounds exhibit high structural similarity in interconnected B₁₂ icosahedra with the inclusion of interstitial B₂ or C₂ dumbbell units, resulting in four (o-MgB₁₂C₂) or five (MgB₇) distinguishable B sites. Adding reasonable values for signal intensities and linewidths under guidance of the eye leads to convincing results for spectra simulation whereas the conventional fitting procedures fail to yield unambiguous parameters sets or even do not converge at all. This makes us confident to also present calculated values of the closely related B modification γ-B₂₈. A comparison of frequently used construction schemes for pseudopotentials (PPs) shows very good agreement.

Additionally, we discuss the electronic structure applying Bader's quatum theory of atoms in molecules (QTAIM)⁴³ in order to gain a deeper understanding in the common and different bonding features. We observe a linear correlation between the large main component V_zz of the EFG for icosahedral atoms in outericosahedral B–B bonds with properties of the bond critical points (BCPs) from Bader's analysis. Consequently, there is a direct mapping between the electronic properties of the bonds external from the B₁₂ unit and measureable quadrupole interaction constants, which in our opinion arises from the particular geometry of the icosahedron.

2 Methods

2.1 Computational details

Table 1 provides an overview of the crystallographic parameters of the investigated compounds. For all calculations DFT is applied using the program package Quantum ESPRESSO (QE)^44,45 and the generalised gradient approximation according to Perdew–Burke–Ernzerhof (PBE)⁴⁶ with a kinetic energy cutoff of 80 Ry for the plane-wave basis set expansion. By aid of the program CIF2CELL⁴⁷ the atomic positions were generated for the corresponding primitive unit cells (see ESI† for details) on which we performed all calculations. We sampled the k-grid by the approach of Monkhorst and Pack⁴⁸ with a precision smaller than , that is for MgB₇ 4 × 6 × 7, for o-MgB₁₂C₂ 6 × 4 × 7, and for γ-B₂₈ 7 × 6 × 5. Structure optimization was carried out under maintenance of the lattice constants with PPs of the Goedecker–Hartwigsen–Hutter contraction⁴⁹ and with assumed convergency for all components of all forces smaller than 2.5 meV Å⁻¹.

Table 1 Details of crystallographic data for the investigated compounds

	MgB7^41	o-MgB12C2^42	γ-B28^10
a Primitive cell.
Composition^a	Mg4B28	Mg2B24C4	B28
Crystal system	Orthorhombic
Space group	Imma (no. 74)		Pnnm (no. 58)
Lattice parameters
a (Å)	10.4782(16)	5.6133(10)	5.0576(4)
b (Å)	5.9769(9)	9.828(2)	5.6245(8)
c (Å)	8.1245(19)	7.9329(15)	6.9884(10)
Volume (Å^3)	508.8	437.6	198.8

---

Using the GIPAW^37,38 algorithm the NMR parameters were determined with PPs from normconserving construction according to Troullier Martins (NC)⁵⁰ as well as with the all-electron projector augmented-wave (PAW) contraction following Kresse and Joubert.⁵¹ With these calculations the principal components of the magnetic shielding tensor are obtained as σ_xx, σ_yy and σ_zz. The isotropic chemical shift δ_iso is computed by the relation δ_iso = m·σ_iso + σ^ref_iso with the isotropic shielding σ_iso = (σ_xx + σ_yy + σ_zz)/3 and σ^ref_iso as the isotropic shielding of a selected reference. For the reference approach we employed the two methods described in literature.²⁰ These are on the one hand the linear regression with m = −0.866 and σ^ref_iso = 80.426 ppm,³⁹ and on the other hand the conservative shielding to shift conversion setting m = −1 and adjusting σ^ref_iso to ensure the calculated shielding σ_iso of (B₁₂H₁₂)²⁻ leads to δ_iso which is measured as −15.3 ppm relative to boron trifluoride diethyl etherate BF₃·OEt₂.³¹ Following the recommendation of ref. 52 we refer to the SIMPSON/Haeberlen convention.‡ ⁵³ with the chemical shift anisotropy δ_csa = m·(σ_zz − σ_iso) as well as the asymmetry η_cs = (σ_yy − σ_xx)/(σ_zz − σ_iso). We report the principal components of the EFG V_ii with |V_zz| ≥ |V_yy| ≥ |V_xx| as the quadrupolar coupling constant C_q = eQV_zz/h and the quadrupolar asymmetry parameter η_q = (V_xx − V_yy)/V_zz using the quadrupole moment Q(¹¹B) = 4.059 × 10⁻³⁰ m².⁵⁴

The analysis according to Bader's QTAIM⁴³ was accomplished with the program CRITIC2.^55,56 For this purpose, the electron density calculated with PAW was mapped onto a real lattice with a three times higher refinement than chosen by QE's default settings. The convergence with respect to the applied k-mesh and the plane-wave cutoff was verified for all reported quantities.

The simulations of the MAS NMR spectra are obtained by applying the DMfit program⁵⁷ in combination with the calculated parameters. In particular, we used the model “Quad 1st” with intensities and linewidths considering our measurements and under guidance of the eye (see ESI† for further information). All illustrations regarding crystal structures were created using VESTA.⁵⁸

2.2 NMR spectroscopy

Reported SSNMR experiments were performed on a Bruker Avance 500 MHz solid-state NMR spectrometer (11.7 T) operating at a Larmor frequency ν_l = 160.48 MHz for ¹¹B using 2.5 mm rotors. Radio frequency pulses were applied at a transverse B₁ field of Grindeq issue 125 kHz corresponding to a π/2 pulse width of 2 μs. All spectra were recorded under MAS conditions at 30 kHz with bearing gas at ambient temperature, leading to sample temperatures of approximately 323 K due to frictional heating. ¹¹B spectra were recorded using a rotor-synchronized Hahn-Echo experiment. The background signal originating from the BN-stator was recorded in a separate experiment and subtracted. According to IUPAC recommendations the spectra were referenced for the unified chemical shift scale using the residual protons in D₂O as secondary standard and the substitution method without reshimming the magnet (Ξ(¹¹B) = 32.083974%).⁵²

3 Results and discussion

3.1 Structural aspects, bonding situation and electronic structure

All investigated compounds crystallize in the orthorhombic crystal system and are closely related to each other regarding their structure. The main structural element are icosahedra of B atoms which are connected to interstitial dumbbell units. In this work we denote the sites of the B₁₂ unit from B(1) to B(4). They form endohedral bonds within the icosahedron and exohedral bonds to the surrounding. The interstitial sites in MgB₇ and γ-B₂₈ are labeled with B(5). With the nomenclature introduced in this work we aim to map the structural units as convenient as possible with regard to the exohedral bonding situation. The common structural arrangement of the compounds can be understood by the example of MgB₇ shown in Fig. 1. In addition, Fig. 1c provides an overview of the used labeling of atoms.

Fig. 1 Crystal structure of MgB₇ and numbering system of the different B sites used in this work; both Mg sites and the interstitial B₂ dumbbell are colored for the sake of appearance: (a) orthorhombic unit cell; (b) projection in [100] direction; (c) numbering of distinguishable B atoms used throughout in this work with exohedral (full) and endohedral (dashed) connections.

Via the B(1) position, the B₁₂ units are linked to rods along the a axis and form a primitive hexagonal packing. Perpendicular to the rods, the icosahedra are connected to each other in layers within the bc-plane over the B(2) atoms. The Mg(2) atoms alternate with dumbbells of B(5) atoms in the trigonally prismatic voids of the hexagonal primitive rod packing, whereas the Mg(1) atoms sit on two of the side faces of the prisms. The interstitial unit is coordinated by six icosahedra via four B(3) and two B(4) positions. In all compounds under investigation, the atoms of the dumbbell, the B(1) and B(4) of the same icosahedron are located in a mirror plane σ_h. And since a C₂ axis runs through the centers of the innericosahedral B(₃)–B(₃) connections, the center of mass of the B₁₂ unit is also a center of inversion. Thus, the polyhedron's point group reduces from I_h to C_2h.

According to Wade,⁴ the formation of an icosahedral B₁₂ skeleton requires 26 electrons for the n + 1 bonding orbitals. However, in order for each atom to give rise to an exohedral 2-electron-2-center (2e2c) bond, 2e are needed in addition to the valency of 12 × 3e = 36e. In case of MgB₇ (Mg₂B₁₂B₂), this is accomplished by the formal transfer of overall 4e by two Mg atoms to the B₁₂ and the B₂ unit. For o-MgB₁₂C₂ the interstitial C atoms contribute 4e each to their four bonds and the Mg(1) site provides its additional 2e to the icosahedron. Therefore, these two compounds are also called electron-precise as there are exclusively exohedral 2e2c bonds and confirmed by color (red MgB₇; colorless o-MgB₁₂C₂), UV/VIS spectra and bandgap calculations.^7,41,42

The atomic distances are listed in Table 2. In MgB₇ and o-MgB₁₂C₂, the intericosahedral B(1)–B(1) and B(2)–B(2) distances are below the respective average values for the innericosahedral B–B distances. Furthermore, these B(1)–B(1) lengths are the shortest in all compounds. Within the B₁₂ units, the atomic distances differ only slightly from the mean values, indicating minor deviations from I_h symmetry. However, notable differences between MgB₇ and o-MgB₁₂C₂ occur for distances related to the interstitial units. The lengths between the icosahedra and the C₂ dumbbell are smaller and the atomic separation of 2.308 Å within the B₂ unit is significantly larger than 1.726 Å for C–C.

Table 2 Selected distances of MgB₇, o-MgB₁₂C₂ and γ-B₂₈ in Å according to optimized atom positions

	MgB7 (X = B(5))	o-MgB12C2 (X = C)	γ-B28 (X = B(5))
a In B(1)–B(1) direction.
Intraicosahedral
B(1)–B(2)	1.815	1.755	1.782
B(1)–B(3)	1.830	1.767	1.787
B(1)–B(4)	1.852	1.759	1.758
B(2)–B(2)	1.861	1.813	1.750
B(2)–B(3)	1.781	1.787	1.849
B(2)–B′(3)^a	1.848	1.785	1.833
B(2)–B(4)	1.791	1.800	1.813
B(3)–B(3)	1.784	1.864	1.868
B(3)–B(4)	1.820	1.789	1.764
Average	1.818	1.787	1.802
Intericosahedral
B(1)–B(1)	1.757	1.632	1.664
B(2)–B(2)	1.806	1.734
B(2)–B(3)			1.834
Others
B(2)–X	2.937	2.922	1.915
B(3)–X	1.747	1.660	2.085
B(4)–X	1.795	1.647	1.674
X–X	2.308	1.726	1.729

---

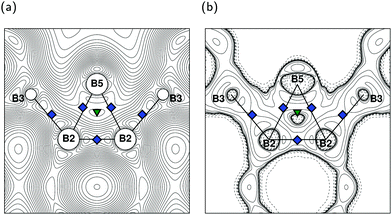
Despite the high structural similarity to MgB₇ and o-MgB₁₂C₂, the exohedral bonding situation between the B₁₂ icosahedron and the interstitial B₂ dumbbell in γ-B₂₈ turns out to be very versatile (see Fig. 2). With its structure determination,^9,10 especially the interactions between the B(2) and B(3) positions with B(5) have been intensively discussed.^10–16 One reason are the atomic distances B(2)–B(3), B(2)–B(5) and B(3)–B(5) outside the polyhedron shown in Table 2, which are in the range of endohedral bonds of all listed compounds. This may cause the introduced labeling of B(2) and B(3) in Fig. 1c to seem less clear. Note that we refer to B(2) as the position where the shortest innericosahedral connection line B(2)–B(2) is perpendicular to σ_h. The other main reason for the debate on the bonding situation in γ-B₂₈ stems by results from QTAIM analysis of the charge distribution, which we discuss in detail below.

Fig. 2 Crystal structure of γ-B₂₈ projected in [1̄00] direction (a) and coordination environment of the B₂ dumbbell in terms of the surrounding B₁₂ icosahedra. (b) Green icosahedra indicate two exohedral 2e2c bonds via the B(4) site, grey icosahedra show two 2e3c bonds (blue triangles) via two B(2) sites and magenta icosahedra are bonded via 1e2c bonds to the grey icosahedra only.

Fig. 3 Properties of calculated electron charge density (PAW) with BCPs (diamond) and RCP (triangle) in B(2)–B(2)–B(5) plane of γ-B₂₈ (see also Fig. 2): (a) contour lines of density from 0.05 to 2.0 e Å⁻³. (b) Positive (solid) and negative (dashed) contour lines of Laplacian for ±(2,4,8) × 10ⁿe Å⁻⁵ (−3 ≤ n ≤ 3).

From a formal point of view, there is no electron donor in γ-B₂₈ (like Mg in MgB₇ and o-MgB₁₂C₂) and consequently there are only 36e − 26e = 10e available to the exohedral interactions and so not all of these can be 2e2c bonds. As our results agree well with those of Mondal et al.¹³ we follow their interpretation. For the exohedral 2e2c bonds between the B₁₂ units via the B(1) atoms, a total of 2e are required. Between the B(4) and B(5) atoms there are also 2e2c bonds for which 2e are needed. The B(2) atoms of an icosahedron form polar-covalent 2-electron-3-center (2e3c) bonds with a B(5) atom of the dumbbell (see Fig. 2b) and contribute overall 4 × 1/2e = 2e per icosahedron. Finally, the exohedral B(2)–B(3) bonds are 1-electron-2-center (1e2c) bonds for which an icosahedron may provide its remaining 4 × 1/2e = 2e. Overall one B₁₂ polyhedron in γ-B₂₈ constitutes eight 1e2c, four 2e2c and two 2e3c exohedral bonds (see also Fig. 2a).

Table 3 gives an overview of the results from QTAIM analysis. In this topological partitioning scheme, the electron density is split into basins fulfilling the zero flux condition along their boundary surface. Each region is assigned to a maximum within interpreted as atom. The respective charges can be derived from the summed charge density within the atomic basins. In general these indicate charge shifts from the electropositive to the electronegative element. The BCPs correspond to the minima on bonding paths between two atoms, while ring critical points (RCPs) are defined by closed paths of bonded atoms. Type and strength of the bonding interaction correlates with values of density and Laplacian at the corresponding points.

Table 3 Parameters from Bader's QTAIM analysis from PAW calculations of the optimized structures with charge q_PAW in e and properties of the BCP^a at r_BCP with charge density ρ in e Å⁻³, the Laplacian ∇²ρ in e Å⁻⁵ and d_BCP as distance between atoms and the BCP in Å

Compound	Site	QTAIM charge		Property of BCP
		Ref. 7	q PAW	ρ(rBCP)	∇^2ρ(rBCP)	d X-BCP, dBCP-Y
a Between exohedral bonds or B(5)–B(5). b LAPW (PW91-LDA) without geometry optimization. c Between B(2)–B(5) (see Fig. 3). d RCP of B(2)–B(2)–B(5): ρ(rRCP) = 0.538 e Å^−3, ∇^2ρ(rRCP) = −0.103 e Å^−5 (see Fig. 3). e Between B(2)–B(3) (see Fig. 3).
MgB7	B(1)	−0.10	−0.07	0.924	−6.713	0.879, 0.879
	B(2)	−0.20	−0.22	0.817	−4.155	0.905, 0.905
	B(3)	−0.13	−0.14	0.905	−6.325	0.917, 0.831
	B(4)	−0.30	−0.35	0.832	−5.286	0.951, 0.849
	B(5)	−0.56	−0.53	0.420	−0.434	1.155, 1.155
	Mg(1)	1.63	1.57
	Mg(2)	1.66	1.68
o-MgB12C2	B(1)	−0.10	−0.07	1.123	−9.646	0.816, 0.816
	B(2)	−0.31	−0.34	0.894	−5.814	0.869, 0.869
	B(3)	0.46	0.48	1.051	−7.888	0.571, 1.090
	B(4)	0.55	0.57	1.062	−4.420	0.557, 1.090
	C	−1.58	−1.63
	Mg	1.68	1.71
γ-B28	B(1)	0.06	0.05	1.091	−9.725	0.832, 0.832
	B(2)	−0.17	−0.19	0.554^c^d	−1.137^c^d	1.077, 0.842^c
	B(3)	0.00	0.01	0.758^e	−4.432^e	0.908, 0.936^e
	B(4)	0.04	0.07	1.089	−9.835	0.829, 0.847
	B(5)	0.24	0.26	0.980	−8.242	0.865, 0.865

---

The properties of the calculated charge distributions in Table 3 are consistent with results of the (linear)-augmented-plane-waves (LAPW) method⁷ and are also in agreement with ref. 9 and 13 for γ-B₂₈. Listed values of the BCPs are associated with the exohedral bond. The negative Laplacians indicate a dominant covalent bonding character. With the exception of B(2)–B(5) in γ-B₂₈, the ellipticities on all shown BCPs (not shown) are close to zero, meaning that all other exohedral interactions can be assumed as straight σ bonds.⁵⁹

In the compounds containing Mg, the metal transfers electrons to the covalent non-metal framework. However, the charges listed above deviate from electron counting rule according to Wade, which assumes equal distributed bonding fractions. As can be seen in case of o-MgB₁₂C₂, the BCPs are shifted towards B due to the more electronegative character of the C₂ dumbbell. This leads to a reduction of the assigned atomic basins and, therefore, to a significant difference in charges of B(3) and B(4) comparing MgB₇ with o-MgB₁₂C₂.

The given BCPs from B(1) to B(4) of MgB₇ and o-MgB₁₂C₂ relate to the strongest bond formation to be exohedral due to highest values of electron density. For γ-B₂₈, this result is only true for the B(1) and B(4) sites, whereas B(2) and B(3) show lower densities than their endohedral bonds. The reason for this is the special bonding situation of these two atomic positions. As shown in Fig. 2, the calculated electron density exhibits exohedral BCPs between B(2) and B(3) and between B(2) and B(5). Contrary to the B(2)–B(3)–B(5) multi-center bond postulated by Rulis et al.,¹⁶ we find an RCP only within the B(2)–B(2)–B(5) formation. The ellipticity of the BCP on B(2)–B(5) (see also Fig. 2) is with 3.6 in typical order of magnitude for endohedral 2e3c icosahedral bonds in molecules⁵ and solid phases⁷ but also for the exohedral equatorial bond in α-rB₁₂.⁶⁰

Our results, in particular the values ρ(r_BCP) and ρ(r_RCP) of the points illustrated in Fig. 2 are in excellent agreement with the analysis of the measured electron density of γ-B₂₈.¹³ Mondal et al.¹³ conclude from the long bond distance (≈1.83 Å) in combination with the small ρ(r_BCP) that B(2)–B(3) is a 1e2c bond. Furthermore, the B(2)–B(2)–B(5) RCP indicates a 2e3c bond, with the BCPs along B(2)–B(5) being noticeable shifted towards B(5), and thus should be considered a polar-covalent bond (compare also Fig. 3 of ref. 13 with Fig. 2). As a recent experimental and theoretical investigation of the mechanical properties suggests, this bond formation to the interstitial B₂ unit are called “ultrasoft bonds”.¹⁷

Despite the same structural element of a B₂ dumbbell in MgB₇ and γ-B₂₈, we observe different electronic situations within the interstitial units. In MgB₇ the BCPs of B(3)–B(5) and B(4)–B(5) are shifted to B(5), which corresponds to the picture of an electropositive bonding partner. And indeed, Bader charge is accumulated by the icosahedron [Mg^3.25+₂B^2.19−₁₂B^1.06−₂] as one would expect according to Wade. In γ-B₂₈, on the other hand, the B₂ unit is positively charged [B^0.52+₂]. Again, the BCPs of the B(2)–B(5) bonds are shifted towards the interstitial unit and the icosahedron accumulates negative charge density. This overall behavior is consistent with the conclusion of Häussermann and Mikhaylushkin¹¹ that the peculiar B₂ dumbbell acts as an electron reservoir for the B₁₂ polyhedron. There is a significant excess of electrons in MgB₇ which is transferred to B₂. This accumulation of charge leads to an increased bond distance of B(5)–B(5) with low electron density at the BCP as well as small ∇²ρ and finally to a weak covalent interaction. In contrast to that, electron density of the interstitial unit is subtracted by the icosahedra in γ-B₂₈. Accordingly, the B₂ dumbbell forms a strong covalent bond with a typical distance of 1.729 Å (comparable to C–C in o-MgB₁₂C₂). Yet referring to Mondal et al.¹³ this represents no explicit charge transfer between icosahedron and interstitial unit. Based on the measured electron density, they find that 1/3e of B(5) is given into the 2e3c bond, so that 1/6e is available for each B(2) atom.

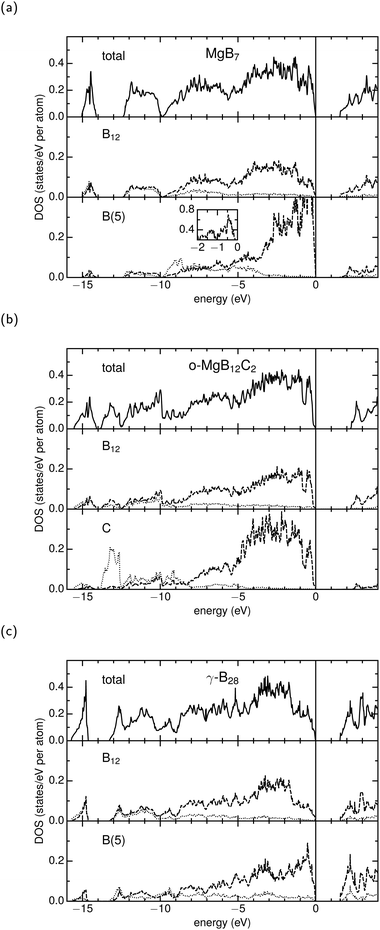
The density of states (DOSs) presented in Fig. 4 are in very good agreement with other work for MgB₇,^7,8,41 o-MgB₁₂C₂^6,7 and γ-B₂₈.^10,14,16 All compounds are characterized by a significant bandgap of at least 1.5 eV. Regarding the icosahedron the atomic relative DOSs show a strong hybridization of the s/p-states and hardly any differences amongst the investigated compounds. In general, the interstitial unit influences the DOS especially in the range of −5 to 0. But in contrast to all B(5) sites, the DOS of o-MgB₁₂C₂ is dominated around −13 eV by the low-lying s-states of the interstitial C atoms. A comparison of the interstitial B(5) atoms in MgB₇ with those in γ-B₂₈ reveals a much higher population of p-states near the Fermi level, while the population of s-states rapidly decreases between −4 eV and −3 eV in MgB₇ in analogy to the one of C in o-MgB₁₂C₂. Overall, in γ-B₂₈ the s-states are more diffuse and show a more distinct interaction to p-states in the aforementioned region. In this respect, B(5) in MgB₇ and C in o-MgB₁₂C₂ show similarities that are evidently extended above the Fermi level at about 2.5 eV: Both interstitial atoms show significantly lower contribution, while B(5) in γ-B₂₈ becomes dominant compared to an icosahedral B atom. This is a manifestation of the earlier described behavior of the B₂ dumbbell being a reservoir or buffer for electrons. While in γ-B₂₈ further accumulation of negative charge is possible, the states of B(5) in MgB₇ are strongly occupied comparable to the sp³ hybridized C in o-MgB₁₂C₂.

Fig. 4 Total (top) and local partial electronic density of states (center: icosahedral B₁₂ unit; bottom: interstitial X₂ unit) of (a) MgB₇, (b) o-MgB₁₂C₂ and (c) γ-B₂₈ for angular components of s (dotted) and p (dashed).

3.2 Calculated NMR parameters and measured MAS NMR spectra

The calculated parameters of the chemical shift and quadrupole coupling are presented in Table 4. To the best of our knowledge, this is the first time that calculated ¹¹B shifts of boron-rich borides are reported to this extent. Since usually only the absolute value of the quadrupole coupling constant can be determined experimentally,¹⁹ we refer to |C_q|. The corresponding components of the EFGs will be discussed below in further detail.

Table 4 Chemical shift parameters δ_iso, δ_csa in ppm and η_cs together with the quadrupolar coupling constants |C_q| and asymmetry parameter η_q calculated with normconserving Troullier–Martins type (NC) and projector augmented-wave (PAW) PPs; expected shift for the center of gravity of the central transition δ_cg (ppm) according to PAW values and the shift from the central transition fit of the recorded spectra δ_ctf (±0.8 ppm)

Compound	Site	NC							PAW						Exp.
		linear regression^a		Conservative					Conservative
		δ iso	δ ^regcsa	δ iso	δ ^refcsa	η cs	|Cq|	η q	δ iso	δ csa	η cs	|Cq|	η q	δ cg	δ ctf
a Referencing according to ref. 39, δ^regcsa/δ^refcsa = 0.866 is assumed (see also methods of ref. 40 for details). b δ cg = δiso + δq with δq = −Cq^2(1 + ηq^2/3)/(40νl).^19,21,22 c For details of the central transition fit see ESI.
MgB7	B(1)	−3.6	10.9	−1.7	12.6	0.17	1389	0.17	−1.5	12.5	0.17	1343	0.16	−2.1	−2.2
	B(2)	6.7	15.9	10.2	18.4	0.99	863	0.54	10.0	18.4	0.96	842	0.53	9.8	11.1
	B(3)	10.3	15.8	14.3	18.3	0.96	1290	0.45	14.0	17.8	0.97	1255	0.45	13.5
	B(4)	29.5	−1.8	36.5	−2.1	0.94	900	0.46	35.8	−1.9	0.87	876	0.46	35.5	34.9
	B(5)	−32.2	12.6	−34.8	14.6	0.28	1505	0.43	−34.2	14.8	0.31	1464	0.44	−34.9	−36.3
o-MgB12C2	B(1)	−13.4	15.7	−13.0	18.2	0.30	1699	0.08	−12.8	17.9	0.29	1643	0.08	−13.6	−3.3
	B(2)	−5.5	−13.5	−3.9	−15.5	0.98	758	0.40	−3.9	−15.2	0.99	744	0.39	−4.1
	B(3)	7.2	−10.3	10.7	−11.9	0.46	852	0.42	10.5	−11.6	0.45	826	0.41	10.3	11.1
	B(4)	30.2	−9.9	37.3	−11.5	0.42	824	0.50	36.5	−11.1	0.44	805	0.49	36.3	35.8
γ-B28	B(1)	−0.5	−12.4	1.8	−14.4	0.92	1786	0.01	1.9	−14.1	0.90	1729	0.02	1.0
	B(2)	−9.4	−22.7	−8.5	−26.2	0.89	457	0.74	−8.2	−25.9	0.89	441	0.69	−8.3
	B(3)	2.8	8.8	5.7	10.2	0.67	364	0.48	5.6	9.9	0.69	364	0.48	5.6
	B(4)	4.6	−9.7	7.7	−11.2	0.22	1818	0.05	7.6	−11.0	0.18	1760	0.06	6.6
	B(5)	4.0	17.6	7.1	20.3	0.78	3398	0.64	7.7	20.7	0.70	3247	0.64	4.0

---

Relative to the values of conservative referencing, the results of PPs with NC and PAW constructions are in good agreement. Only for the shifts of B(5) in γ-B₂₈, a difference of 0.6 ppm leads to the interstitial atoms being more shielded than B(4) according to NC. Likewise, the |C_q| and η_q values show only minor dependence on the applied type of PP. The determined shifts with respect to the linear regression within the NC approach deviate from the conservative method the more the shielding of B increases. The used regression parameters are mainly derived from rather highly shielded ¹¹B species of closo-(hetero)dodecaboranes and are therefore unsuitable for deshielded nuclei,³⁹ whereas the conservative reference to B₁₂H₁₂²⁻ is more stable for a larger shift range of chemical shifts as will become more clear considering the measured MAS NMR spectra.

Similar to the calculation of the shifts of the rhombohedral phases,⁴⁰ the consideration of the correction by the bare macroscopic susceptibility χ_bare plays a crucial role, since it is about −0.7 × 10⁻⁹ m³ kg⁻¹ for the investigated compounds and, thus, contributes to an overall difference of about 14 ppm (see ESI† for details). For comparison, it is in the same range of magnitude as of other diamagnetic boron-rich borides like YB₆ and YB₄ with measured values of −2.6 × 10⁻⁹ m³ kg⁻¹ (ref. 61) and −5.9 × 10⁻⁹ m³ kg⁻¹ (ref. 62) or LaB₄ with −1.0 × 10⁻⁹ m³ kg⁻¹,⁶³ respectively.

As the bare induced field B⁽¹⁾_in(G = 0) is affected by the surface currents of the sample the corresponding magnetic shielding σ(G = 0) is not a bulk property.^37,64,65 Being consistent with the on-site approximation for the reconstruction current it is computed viaχ_bare. For a general shape of nonmagnetic media with small, isotropic susceptibility, it can be shown that the shielding is related to the calculated σ by σ^shape_ij ≃ σ_ij − δ_ij4π[small chi, Greek, macron] (1 − n_j) with [small chi, Greek, macron] = tr(σ_bare)/3 and n_k as depolarization coefficient.⁶⁶ Assuming a spherical sample shape (n_x = n_y = n_z = 1/3) we follow Mauri et al.⁶⁴ that in case of MAS measurements on a solid with isotropic χ_bare, σ is independent of the particular shape of the sample. Thus, the application and quality of this correction depends on a high degree of isotropy for χ_bare. To evaluate this, we may describe the extent of anisotropy following the definition of fractional anisotropy (fa_χ) known from diffusion processes.^67,68 fa_χ is a scalar that quantifies the pointedness of an ellipsoid defined by the eigenvectors and eigenvalues of χ_bare with values between 0 (case of a sphere) and 1 (only one nonzero eigenvalue).§ With values from the PAW calculations we obtain for the here investigated compounds fa_χ(MgB₇) = 5.2%, fa_χ(o-MgB₁₂C₂) = 5.1% and fa_χ(γ-B₂₈) = 3.7% comparable to those of our previous investigation⁴⁰ with fa_χ(B₁₂P₂) = 2.1%, fa_χ(B₁₂As₂) = 2.5% and fa_χ(B₁₂O₂) = 5.4% indicating a minor degree of anisotropy⁶⁹ and confirming the applicability of the used correction.

With respect to the isotropic shifts, we recognize for the two very similar compounds MgB₇ and o-MgB₁₂C₂ an order of the form δ_iso(B(1)) < δ_iso(B(2)) < δ_iso(B(3)) < δ_iso(B(4)). This means that although the charge distribution according to Bader is different, the chemical shifts follow a pattern with respect to the icosahedral building parts in the structures. We find a high similarity in γ-B₂₈ with δ_iso(B(2)) deviating from this pattern, possibly because of the special bonding situation of B(2)–B(5). In addition, for this compound the shift range is much smaller than in MgB₇ or o-MgB₁₂C₂ and a general assignment of δ_iso to a certain B site is not possible. For example, the B(1) sites in MgB₇ and o-MgB₁₂C₂ show a difference in shifts of more than 10 ppm and B(1) in MgB₇ is obtained in a similar shift range as B(2) in o-MgB₁₂C₂. Also, regarding the B(5) atoms in MgB₇ and γ-B₂₈ the calculated isotropic shifts differ strongly by about 40 ppm. The δ_iso of the borides investigated here are therefore neither correlated with the crystallographic position nor with the Bader charge. Probably the amount of overall charge separation has an influence on the broadness of the shift range for MgB₇, o-MgB₁₂C₂ and γ-B₂₈. This correlation is also suggested in the rhombohedral phases, where we obtain from α-rB₁₂, B₁₂As₂ over B₁₂P₂ to B₁₂O₂ an increase in both, the charge separation and the corresponding shift range.⁴⁰

The quadrupole coupling constant of B(1) belongs with values in the range of 1350 to 1750 kHz to the highest values of all polyhedral atoms within a compound, while we find much smaller values for B(2). Especially the |C_q| of B(1) reported here correspond very well with those of rhombohedral phases, which connect B₁₂ icosahedra exohedral in polar position via 2e2c bonds.⁴⁰ They are also comparable with measurements on other B polyhedra like octahedra in YB₆ of 1200 ± 30 kHz,²⁸ in LaB₆ of 1028 kHz²⁹ or B₁₂ cuboctahedra in TB₁₂ (T = Y, Zr, Lu) with about 100 kHz.²⁵ With this background, a comparison to the measured coupling constants of 1300 ± 100 kHz³³ for B₄C and 240 kHz³⁵ for rhombohedral α-SiB_3−x leads to the conclusion that these may be assigned to the B atoms involved in the intericosahedral linkage.

For the sites B(3) and B(4) connected to the interstitial unit, the |C_q| in Table 4 clearly differ between each compound. The value of B(3) in MgB₇ is remarkable, which indicates a coupling about 500 kHz larger than those of B(3) and B(4) in o-MgB₁₂C₂ with 825 kHz. For B₄C literature reports 450 ± 250 kHz,³³ 361, 380, 513 Hzk³⁴ as well as 840 kHz,³⁵ being in the range of those sites bonded to C in o-MgB₁₂C₂. Also the small value of B(3) and the high value of B(4) in γ-B₂₈ are noteworthy, which as we will discuss later is closely related to the electronic situation of the exohedral bond. Similar to the isotropic chemical shifts, the |C_q| of the interstitial B(5) atoms in MgB₇ and γ-B₂₈ differ significantly. Altogether we find small quadrupolar coupling constants up to 1750 kHz for borides with icosahedral structure elements, whereas the high value of B(5) in γ-B₂₈ is outstanding and comparable to the one of hexagonal BN with 3200 kHz.³⁵

The small quadrupolar asymmetry parameters η_q for all B(1) sites and for B(4) in γ-B₂₈ reflect a high degree of symmetry for the EFG around the main axis V_zz. For the remaining positions in MgB₇ and o-MgB₁₂C₂ as well as B(3) we find values in the range of 0.39 and 0.54 similar to those of the equatorial sites in rhombohedral B₁₂P₂ and B₁₂As₂ with 0.47 and 0.30, respectively.⁴⁰ It is interesting that B(2) and B(5) involved in the 2e3c bond in γ-B₂₈ show η_q ≥ 0.64.

In addition, Table 4 contains the expected shifts for the center of gravity δ_cg of the central transition (−1/2 ↔ 1/2) as well as the shifts obtained by conventional central transition fit δ_ctf of the recorded spectra (see ESI† for details). As specified in the footnote of Table 4, δ_q reflects the influence of the quadrupolar coupling and is also dependent on the Larmor frequency ν_l used in the NMR experiment.^19,21,22 The effect that due to quadrupolar coupling the central transition is shifted more high-/upfield than indicated by δ_iso can be significant, especially in case of the C–B–C chain center atom with C_q ≈ 5600 kHz^26,33 in B₄C.⁴⁰ For the compounds investigated here, however, the smaller values of |C_q| and the applied carrier frequency of 500 MHz lead to differences between δ_iso and δ_cg below 1.1 ppm. The only exception is the B(5) site in γ-B₂₈, where we find δ_q = 3.7 ppm due to its larger quadrupolar coupling constant, resulting in δ_cg(B(5)) < δ_cg(B(4)) in contrast to δ_iso(B(5)) > δ_iso(B(4)). Turning to MgB₇ and o-MgB₁₂C₂ we find remarkable agreement between the theoretical expected δ_cg and δ_ctf extracted from the MAS NMR measurements. The values of δ_ctf = 11.1 ± 0.8 ppm in MgB₇ and δ_ctf = −3.3 ± 0.8 ppm in o-MgB₁₂C₂ indicate that the individual signal contributions of B(2) and B(3) as well as those of B(1) and B(2) cannot be resolved by our experiments, respectively.

Fig. 5 and 6 show the measured MAS NMR spectra together with the contributions derived from the parameters of the all-electron PAW construction in Table 4. For the plotted spectra simulation δ_cg is used to set the shift position. Apart from the intensity, the linewidth was adjusted by hand, taking into account the spectral shape of the central transitions only. The resulting area ratios reflect the multiplicities of 1 : 2 : 2 : 1 : 1 in MgB₇ and 1 : 2 : 2 : 1 in o-MgB₁₂C₂ supposed from the symmetry positions (see Table S4 in ESI†). Note that in SSNMR the ratio of intensity/area of contributions does not always correspond to such expectations from site symmetry.^30,40 Indeed, for boron compounds with icosahedra as structure elements it is known that extraction of reliable parameter sets from measured ¹¹B spectra alone is difficult.^34,35 With a comparison of Fig. 5 with Fig. 6 it is evident that the peak at about −35 ppm is caused by the interstitial B(5) site. However, a further assignment of signals is not readily possible and attempts of conventional fit procedure do not provide unambiguous sets of parameters for MgB₇ and o-MgB₁₂C₂.

Fig. 5 Experimental ¹¹B MAS NMR spectrum of MgB₇ measured at 11.7 T with 30 kHz spinning frequency and simulation with parameters from PAW calculation in Table 4 together with site contributions. δ_cg is used in the simulation to set the shift position. Intensities and linewidths adjusted by eye for best fit of central transition shown in (c) (see Table S4 in the ESI† for further details).

Fig. 6 Experimental ¹¹B MAS NMR spectrum of o-MgB₁₂C₂ measured at 11.7 T with 30 kHz spinning frequency and simulation with parameters from PAW calculation in Table 4 together with site contributions. δ_cg is used in the simulation to set the shift position. Intensities and linewidths adjusted by eye for best fit of central transition shown in (c) (see Table S4 in the ESI† for further details).

As mentioned in the introduction the quadrupolar coupling affects the nuclear energy levels in magnetic field and therefore also the satellite transitions (±3/2 ↔ ±1/2) in measured MAS NMR.²⁰ The simulated spectra from the calculated parameters display not only signal shape from −100 to 100 ppm but also the sideband pattern, meaning that the computed |C_q| are also within a reasonable range of value.

MgB₇ shows a shift extension from −40 ppm known for boronhydrides up to 30 ppm common for borates. We are not aware of any other compound containing B with dominant covalency and significant bandgap that spans such a range. The chemical shifts of the B(2) and B(3) sites are close to one another (see Table 4) and hence their contributions in the experimental spectrum in Fig. 5 are not resolved separately. The measurement of o-MgB₁₂C₂, on the other hand, shows a strong difference in shifts between B(2) and B(3) making two different maxima occur. In both experimental spectra the contribution of B(4) is clearly visible near 35 ppm.

As the current review by AngelWong and Bryce¹⁹ reports, complete NMR parameter sets are known for only very few boron-rich borides based on boron polyhedra. Of particular interest here might be compounds T′B_n (T′ = Y, La; n = 4, 6) which are composed of B₆ octahedra incorporating B₂ dumbbells for n = 4 (T′₂[B₆][B₂]). At least structurally there is a similarity to the transition from B₁₂ icosahedra as in α-rB₁₂ to polyhedra additionally linked by an interstitial unit as in MgB₇ and γ-B₂₈. Experimental reports assign for YB₄¹¹B shifts in the range of 5.4 to 34.7 ppm⁶² and for LaB₄ of 18 to 47 ppm.²⁴

In the transition from TB₆ to TB₄, the C_q of the atoms connected to the dumbbell are close to those interconnecting the octahedra. For the 4e and 8j sites in YB₄ (correspond to B(1) and B(3)/B(4)) a value of Grindeq issue 1030 ± 60/80 kHz²⁸ is observed each and in LaB₄ 690 and 800 kHz are reported for 4e and 8j.²⁴ The values of YB₆ and LaB₆ are 1200 ± 30 and 1100 kHz,^28,29 respectively. This observation is also true for B(3) in MgB₇ and B(4) in γ-B₂₈, but should not be generalized, because on one hand it is not valid for B(4) in MgB₇ and B(2) in γ-B₂₈ and on the other hand an unchecked general prediction of the quadrupolar interaction and, thus, also of the EFG among different boron polyhedra and arrangements should be done with care. The case of CaB_4−xC_x (0.21 ≤ x ≤ 0.26) illustrates how problematic the extraction of NMR parameters by fitting procedures of measured spectra solely is. There only the 8j position with 11 ppm and 800 kHz could be assigned. The two remaining sites (4e and 4h) showed satellite transitions with too large linewidth and, therefore, too low intensity in order to determine any isotropic chemical shift or quadrupolar coupling constant.²⁴

The shifts of the B₂ dumbbell in Table 4 remarkably differ not only for MgB₇ and γ-B₂₈, but also in YB₄ with 12.6 ppm⁶² and 42 ppm in LaB₄.²⁴ Overall, caution is required when comparing these structures, because the significant electron density around the Fermi level due to the transition metals has an influence on the magnetic shielding of B. This is especially true for the dumbbell atoms, which, similar to Fig. 4a and c, contribute significantly to the DOS at this area but, in addition, their p-states extend continously above 0 eV and, thus, interacting with the metallic bands.^29,62,70 Besides the influence of the electrons from the valence band (orbital contribution), there is an additional contribution from the interaction of spin-polarized electrons from the conduction band with the magnetic moments of the B nuclei, which is also well known as Knight shift for metallic systems. Thus, we want to emphasize that the significant bandgaps in Fig. 4 are of major importance for the chemical shifts in Table 4 to be reasonable because they are calculated with relying on the orbital contribution of the chemical shielding tensor,^37,38 only. Eventually, considering this contribution is sufficient when systems under investigation are nonmagnetic semiconductors without unpaired electrons or partially filled bands at the Fermi surface. Plane wave approaches to calculate the Knight shift had been developed within the GIPAW⁶⁵ as well as the LAPW⁷¹ method, and had been applied for example to several Heusler phases.^72,73

3.3 Analysis of the EFG

Since the EFG is a tensor evaluated at the location of the nucleus, the orientation of its main axes is limited to the corresponding spatial symmetry. As explained above, in the compounds investigated here a mirror plane σ_h runs through the B(1), B(4) and interstitial atoms. Consequently, there is a C_s point symmetry at those positions. This means for B(1), B(4) and B(5) two axes of the EFG must lie in σ_h with the third being perpendicular to the plane. Note that this consideration does not apply strictly to the positions of B(2) and B(3) with C₁ symmetry.

Table 5 informs about the orientation of the large EFG axis V_zz by the inclined angles relative to the B₁₂ icosahedron defined in Fig. 7. For comparison, (B₁₂H₁₂)²⁻ is added with its closely related structure of ideal I_h symmetry.⁷⁴ The mentioned symmetry condition for B(1), B(4) and B(5) leads to the result that the sum of two of the three angles φ, Θ_Vzz and Φ_Vzz must add up to the remaining angle. As in the rhombohedral boron-rich phases⁴⁰ we also observe here the general tendency of V_zz for B(1) to B(4) to align either along the bond or radially, that is minimizing Θ_Vzz or Φ_Vzz. This can be expected due to the dominance of the 2e2c exohedral bond throughout the investigated compounds as previously described and to the finding that B polyhedra contain almost no charge.⁷ Note that there are also cases of icosahedral B₁₂ arrangements were this does not hold true, as for example in carboranes³² or in B₁₂As₂.⁴⁰

Table 5 Angles in ° related to the orientation of the large V_zz axis of the EFG and to structure geometry with average values θ_av and (see Fig. 7 for definition). Δ[small theta, Greek, macron] denotes the absolute mean deviation from the magic angle θ_mag (≈54.74°) defined as . All values according to PAW PPs and optimized structures

Compound	Site	EFG related		Geometry related
		Θ V zz	Φ V zz	φ	θ av		Δ[small theta, Greek, macron]
a Relative to B(5)–B(5) direction. b Along exohedral B(2)–B(3) direction. c Relative to exohedral BCP of B(2)–B(5) bond (see Fig. 8). d Relative to B(4)–B(5) direction 30.13°.
MgB7	B(1)	0.29	6.79	6.50	57.52	51.79	0.08
	B(2)	10.65	23.47	22.63	57.69	51.99	0.10
	B(3)	6.51	12.41	8.98	58.51	52.87	0.95
	B(4)	12.30	0.99	11.31	59.77	54.23	2.26
	B(5)		6.57^a
o-MgB12C2	B(1)	5.47	0.25	5.71	60.05	54.54	2.56
	B(2)	7.55	21.30	21.84	58.62	53.00	1.07
	B(3)	6.32	4.74	7.84	57.19	51.45	0.42
	B(4)	8.08	16.52	8.44	58.01	52.34	0.44
γ-B28	B(1)	2.18	6.64	4.46	59.11	53.51	1.57
	B(2)^b	12.31	17.76	11.14	58.13	52.45	0.55
		72.09^c		54.62^c
	B(3)^b	37.56	21.72	20.02	57.61	51.89	1.56
		9.60^c		16.33^c
	B(4)	9.95	2.63	7.32	59.10	53.50	0.71
	B(5)		33.54^a^d
(B12H12)^2−		0.02	0.02	0.00	58.28	52.62	0.71

---

Fig. 7 Definition of angles related to (a) the main axis of the EFG V_zz and (b) structure geometry. The dash dotted line points to exohedral bonding partner, dashed line represents radial direction from icosahedral center of mass.

A remarkable feature, that will become central for the relation between the magnitude of V_zz and the exohedral bonding situation, is the special geometrical arrangement of the here investigated polyhedra. The apex angles θ and θ′ of the regular icosahedron are such that the influence of endohedral bonding partners on V_zz can be assumed of minor contribution and to a good approximation its value mainly reflects the exohedral bonding situation. The key condition of this approximation is that 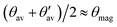is valid with θ_mag as magic angle fulfilling . Therefore, Table 5 additionally shows the absolute deviation from the magic angle as . This spatial property is derived and discussed in detail in ref. 40. There, a particular B site in rhombohedral boron-rich phases for which the exohedral bond being the strongest, V_zz is radially oriented (Φ_Vzz < Θ_Vzz), if Δ[small theta, Greek, macron] > 2°. Here, we find that the V_zz axis aligns in a good approximation with the exohedral bond as Δ[small theta, Greek, macron] ≤ 2° but for higher deviations as in the case of the B(4) site in MgB₇ and the B(1) site in o-MgB₁₂C₂ the V_zz axis is pointing radially. Note that it is not appropriate to reverse this observation, in particular that small Δ[small theta, Greek, macron] do not necessarily lead to an alignment with the exohedral bond as can be seen by the examples of B(3) in o-MgB₁₂C₂ or B(4) in γ-B₂₈. Certainly there are also other influences on the V_zz orientation such as the positive charge of Mg in MgB₇ and o-MgB₁₂C₂. However, assuming these effects is very involved and we do not consider them mandatory for the herein given discussion.

Fig. 8 shows the orientations of the V_zz axes for B(2) and B(3) in the vicinity of the B(5) site and its (exohedral) bonds of γ-B₂₈. We want to note here again that there is no strict condition for the V_zz alignment of these sites according to symmetry considerations. Although for both B(2) and B(3) the BCP of B(2)–B(3) is the closest, V_zz of B(3) is oriented to the BCP of the B(2)–B(5) bonding path. As it is evident from an inspection of Table 3 the magnitude of the electron density at this BCP cannot be the reason for the shown orientation on B(3). In this regard, one has to keep in mind that the relative position of the B₂ unit in γ-B₂₈ changes the exohedral electronic situation for the B(2) and B(3) sites. This is in contrast to all icosahedral sites in MgB₇ and o-MgB₁₂C₂ with distinct 5 + 1 coordination.

Fig. 8 V _zz vectors (arrows) of B(2) and B(3) sites projected on the B(2)–B(2)–B(5) plane of γ-B₂₈ together with BCPs (diamond) and RCP (triangle) from Bader's QTAIM analysis. Underlying contour map corresponds to the calculated electron charge density depicted in Fig. 3a.

A comparison of the possible kink angles φ in Table 5 to the respective BCPs shows how the V_zz axes point to those BCPs which have a smaller deviation from the polyhedral center with vanishing electron density. In particular, φ for B(2) with 11.14° is much smaller towards B(3) than with 54.62° pointing towards B(5). In fact, if V_zz is oriented to the BCP of B(2)–B(5), the influence of the electron density of the endohedral bonds would increase and consequently the gradient of the charge distribution would decrease (see Fig. 8). This means in turn, however, that such an orientation does no longer represent the largest EFG at B(2). A similar situation can be found for B(3), where V_zz points to the BCP of the B(2)–B(5) bond. With an alignment to the exohedral B(2)–B(3) bond a decrease of the gradient can be expected due to the electron density of the endohedral bonds as illustrated in Fig. 8. In γ-B₂₈ the exohedral bonding situation for B(2) is modified by the interaction to the interstitial B₂ dumbbell compared to MgB₇ and o-MgB₁₂C₂ in such way that V_zz of B(3) is not aligned to its exohedral bonding partner B(2).

For the B(5) positions of the interstitial B₂ units in MgB₇ and γ-B₂₈ we observe different orientations of V_zz. While in MgB₇ the V_zz axis points along the bond within the dumbbell, in γ-B₂₈ it is tilted in such a way that it can be associated neither with the direction of B(4)–B(5) nor along B(5)–B(5).

An overview of the full set of EFG components for all B sites can be found in Table 6. The values of the PPs from the NC and PAW approach differ only slightly. Altogether, the icosahedral atoms show negative V_zz values, which in combination with the alignments of the corresponding axes in Table 5 demonstrates that especially the electronic situation of the exohedral bonds is significant. Accordingly, a correlation between the bond strength, that is in terms of Bader's analysis the density value at the exohedral BCP (see Table 3), and V_zz could be suspected. And as the plot (Fig. S1 of ESI†) indicates, the higher the charge ρ(r_BCP) is, the more negative the values of V_zz become for the icosahedral sites. Strictly speaking, this does not apply over all compounds but we obtain an approximately linear relationship within each system.

Table 6 EFG tensor components in 10²⁰ V m⁻² determined by NC and PAW type PPs

Compound	Site	NC			PAW
		V xx	V yy	V zz	V xx	V yy	V zz
a V xx = Vyy due to Ih symmetry.
MgB7	B(1)	5.9	8.2	−14.2	5.7	7.9	−13.7
	B(2)	2.0	6.8	−8.8	2.0	6.6	−8.6
	B(3)	3.6	9.5	−13.1	3.5	9.3	−12.8
	B(4)	2.5	6.7	−9.2	2.4	6.5	−8.9
	B(5)	−4.3	−11.0	15.3	−4.2	−10.8	14.9
o-MgB12C2	B(1)	8.0	9.3	−17.3	7.7	9.0	−16.7
	B(2)	2.3	5.4	−7.7	2.3	5.3	−7.6
	B(3)	2.5	6.2	−8.7	2.5	5.9	−8.4
	B(4)	2.1	6.3	−8.4	2.1	6.1	−8.2
γ-B28	B(1)	9.0	9.2	−18.2	8.7	9.0	−17.6
	B(2)	0.6	4.0	−4.7	0.7	3.8	−4.5
	B(3)	1.0	2.7	−3.7	1.0	2.7	−3.7
	B(4)	8.8	9.7	−18.5	8.5	9.5	−17.9
	B(5)	6.3	28.3	−34.6	5.9	27.2	−33.1
(B12H12)^2−		4.3^a		−8.5	4.1^a		−8.1

---

To further elucidate the values given in Table 6 we point out that holds within the principal axis system of the EFG tensor where P₂ is the second-order Legendre polynomial. As Schwarz et al.²⁶ explain, after decomposing this expression in the lattice V^lat_zz and spherical part 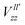the contribution of particular angular momenta can be analyzed. In doing so, the portion of the p orbitals with turns out to be the main component for borides containing B₆ octahedra.^25,28,29 For B atoms in B₁₂ icosahedra in α-rB₁₂ and B₄C this contribution to V_zz in total accounts for even more than 80%.²⁶ Apart from the factor 〈1/r³〉_p which is about 0.69 Å for these compounds, also the magnitude of the so-called anisotropy count Δn_pz = (n_px + n_py)/2 − n_pz with partial charges n_pi in the corresponding p channels is mandatory.

If we assume that the electron excess between the averaged occupation of p_x and p_y is nearly constant compared to p_z for the icosahedral B atoms considered here, it follows that V^pp_zz ∝ 〈1/r³〉_p. Motivated by this and the fact that the V_zz axes are aligned along the exohedral bonds, we plot in Fig. 9 the properties from QTAIM analysis for exohedral bonds in Table 3 with ρ(r_BCP)/d_X-BCP³ against the corresponding V_zz components. In contrast to Fig. S1 of the ESI,† not only the strength of the bond is characterized by ρ(r_BCP) but also the influence of the distance of the accorded BCP to the atom is taken into account. As shown, there is a clear linear relationship and therewith also for measurable C_q/ν_q values of icosahedral B atoms with an exohedral homonuclear bond. This trend is consistent throughout the compounds investigated here and is also valid for polar positions in α-rB₁₂ and B₁₂X₂ (X = P, As, O) with intericosahedral linkage⁴⁰ denoted as others in Fig. 9.

Fig. 9 Values of the EFG main component V_zz from PAW calculations plotted against ρ(r_BCP)/d_X-BCP³ of B sites B(1) to B(4) in the icosahedral B₁₂ units with data from Tables 3 and 6 and of polar atoms B(1) from the first part⁴⁰ of this publication series (denoted as others). The properties of the BCPs are associated with the exohedral bonds and in accordance to the orientation of the V_zz axis.⁷⁵ Filled symbols correspond to properties of sites bonded to the interstitial unit. The trend line is meant to guide the eye.

We want to emphasize that this correlation inherits a very strong simplification, which is not at least valid due to the special polyhedral geometry with satisfying . This results in the crucial importance of the electronic situation along the exohedral bond for values of V_zz. In fact, a comparison of the d_X-BCP in Table 3 and for the rhombohedral phases in ref. 40 reveals that the majority of BCPs of the exohedral bonds are in range of 0.85 Å and, thus, close to the previously mentioned radius of 0.69 Å, in which more than 80% of the EFG components originate from the contribution of the p orbitals. We believe that this observation additionally supports the illustrated relationship in Fig. 9, since the BCPs from QTAIM analysis are close to this distance. The case of γ-B₂₈ is interesting in this context. The remarkably small V_zz value of B(2) seems to correspond to the 1e2c B(2)–B(3) bond with low density. In contrast, we suppose for B(3) that the distance of 1.674 Å to the BCP on the B(2)–B(5) bonding path is essentially responsible for the even smaller value of −3.7 × 10²⁰ V m⁻².

However, the presented approximation is no more valid for changes in Δn_pz caused by a considerable bond polarization. This is indicated as a large shift of the exohedral BCP from QTAIM analysis for icosahedral B atoms. In the case of the equatorial B atoms in B₁₂X₂ (X = P, As, O), that are bonded to interstitial non-boronic atoms, we consequently find large variations in value and sign of V_zz. Furthermore, these fluctuations result in high deviations (not explicitly shown) from the plotted trend line in Fig. 9.

Regarding o-MgB₁₂C₂, B(3) and B(4) are in a polar covalent bonding situation to C and accordingly d_B-BCP significantly decreases compared to all other exohedral bonds. With simply considering Fig. 9 one could therefore superficially expect much more negative V_zz than those of Table 6. However, the more electronegative C decreases the electronic population of the p_z orbital in the vicinity of the B atoms. This reduces the excess Δn_z and also the absolute values of V_zz compared to MgB₇. The underlying assumption here is that in general the exohedral bonds are stronger than the endohedral ones within all icosahedra. Finally, we want to note that values of −8.2 × 10²⁰ and −8.4 × 10²⁰ V cm⁻² computed with PAW agree well with −6.9 × 10²⁰ V cm⁻² calculated for B sites in a similar bonding situation at equatorial positions in B₄C.^26,27

We see a close connection of the present work with the study of Mondal et al.¹⁵ on the bonding situation in α-rB₁₂ and γ-B₂₈ proposing that the orbital order of the 12 external bonding orbitals of the B₁₂ unit persists even if the polyhedra are involved in different exohedral bonds. With the here presented results and those of our previous investigation⁴⁰ we suppose that this orbital order might be related to the orientation and magnitude of the large main axis V_zz of the EFG and, hence, to measurable quadrupole coupling constants C_q or frequencies ν_q of icosahedral B atoms in boron-rich borides.

For the B(5) site in MgB₇ we find the V_zz axis pointing along the interstitial bond with a positive value which means a change in sign of Δn_pz in comparison to the icosahedral sites. This is in line with the values of ρ(r_BCP) in range of 0.832 to 0.905 eV Å⁻³ indicating that the three B(5)–B(12) bonds show higher electron population and are, thus, stronger than the B(5)–B(5) interaction (0.420 eV Å⁻³, see Table 3). Contrary, in γ-B₂₈ the increased valence electron density along B(4)–B(5) is probably responsible for the negative V_zz value. However, the orientation of the axis is less distinct. The electronic situation to the B(2) site but more important to the other B(5) dumbbell atom does have an influence. With the shorter interatomic distance of 1.729 Å and ρ(r_BCP) = 0.980 eV Å⁻³ we consider an increase of bond strength compared to B(5)–B(5) in MgB₇ leading to the observed tilt of the V_zz axis.

4 Conclusion

In conclusion, we have discussed the structure, bonding situation and calculated tensor parameters of the chemical shift and quadrupole coupling for the orthorhombic phases MgB₇, o-MgB₁₂C₂ and γ-B₂₈. Both, the similarities and differences of the exohedral icosahedral bonds as well as those of the interstitial dumbbell units with regard to the DOS were additionally examined.

The values determined by computations using the GIPAW approach were applied to simulate MAS ¹¹B NMR spectra and compared to measurements of MgB₇ and o-MgB₁₂C₂. With this at hand, we successfully explain the measured spectra and clearly assign individual signal contributions to corresponding B sites. In combination with our previous results for rhombohedral phases⁴⁰ we are confident of additional presenting appropriate NMR parameters of the orthorhombic boron phase γ-B₂₈. Overall, the comparison between results from the PP construction schemes of NC and PAW shows only small deviations.

The NMR parameters for atoms of the B₂ dumbbell in MgB₇ and γ-B₂₈ notably differ and show hardly any similarity to those of borides containing B₆ octahedra such as YB₄, LaB₄ or CaB_4−xC_x. This is due to different bonding distances within the B₂ units and also due to the peculiar bonding situation to the boron polyhedra. Regarding YB₄, LaB₄ and CaB_4−xC_x another certain reason is the influence of electrons from the (transition)metal atoms on the shielding of the B atoms. For the here investigated compounds, the Mg atoms play only an indirect role for the ¹¹B shifts due to their almost complete electronic charge transfer, while it is for instance already known for Ca that its deep lying 3d shells may have a significant impact on oxidic shieldings by partially covalent Ca–O bonds in oxides and aluminosilicates.⁷⁶ Furthermore, the semiconducting character indicated by the significant bandgaps ensures a very good agreement of the here reported experimental observations with the ¹¹B shifts computed by orbital contribution to the magnetic shielding only. Yet, for metallic systems with unpaired electrons or partially filled bands at the Fermi surface the electronic spin contribution must be additionally considered as well for reliable results.

The EFG main axis V_zz of atoms in the B₁₂ icosahedra points to a good approximation along the stretched exohedral bond. This observation leads to a linear relation between values of V_zz/C_q/ν_q and properties of BCPs from Bader's analysis; With increasing ratio of the electron density at the BCP to its cubic distance to the respective B atom, the strength of the quadrupole coupling also increases. The underlying reason for this correlation is the great similarity of the exohedral B–B bonds and the close structural relationship, that is the B₁₂ icosahedron as main building block, of the investigated compounds. For such bonds as B–C in o-MgB₁₂C₂ and B–X (X = P, As, O) in rhombohedral phases, however, this statement cannot be confirmed because their bond polarity exceeds the boundaries of this quite simplified model. Concerning the quadrupolar asymmetry η_q there is a correspondence to the electronic bonding situation. While computed values are below 0.20 for B sites involved in 2e2c bonds of the intericosahedral linkage along the hexagonal rods and commonly between 0.40 and 0.55 for those in interstitial linkage, those of sites involved in the exohedral 2e3c bond in γ-B₂₈ are greater than 0.60. Nonetheless, this observation is related to the magnitude of V_zz and consequently to C_q. In cases of large quadrupolar coupling constants where the electron density distribution around the V_zz axis is nearly symmetric, η_q can be expected to approach zero as for the equatorial site in B₁₂O₂.

The reported insights as well as further calculations on NMR parameters of other boron-rich borides with icosahedral structure element may contribute several structure and order variants still under discussion. For example, by means of model calculations one may elucidate at which positions Si atoms are incorporated in B₁₂ icosahedra of α-SiB_3−x providing further knowledge to current studies.¹⁸ Besides the computation of NMR parameters regarding ¹¹B we expect theoretical and experimental investigation of ²⁹Si to play a major role.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr Anke Schaub for the MAS NMR measurements.

Notes and references

1. B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668.
2. H. C. Longuet-Higgins, Q. Rev., 1957, 11, 121.
3. H. Longuet-Higgins and M. d. V. Roberts, Proc. R. Soc. London, Ser. A, 1955, 230, 110–119.
4. K. Wade, J. Chem. Soc. D, 1971, 792–793.
5. S. Mebs, R. Kalinowski, S. Grabowsky, D. Förster, R. Kickbusch, E. Justus, W. Morgenroth, C. Paulmann, P. Luger, D. Gabel and D. Lentz, Inorg. Chem., 2011, 50, 90–103.
6. X. Jiang, J. Zhao, A. Wu, Y. Bai and X. Jiang, J. Phys.: Condens. Matter, 2010, 22, 315503.
7. V. Sagawe, PhD thesis, Albert-Ludwigs-Universität Freiburg im Breisgau, 2013.
8. H. Ozisik, E. Deligoz, K. Colakoglu and E. Ateser, Intermetallics, 2013, 39, 84–88.
9. A. R. Oganov, J. Chen, C. Gatti, Y. Ma, Y. Ma, C. W. Glass, Z. Liu, T. Yu, O. O. Kurakevych and V. L. Solozhenko, Nature, 2009, 457, 863–867.
10. E. Y. Zarechnaya, L. Dubrovinsky, N. Dubrovinskaia, Y. Filinchuk, D. Chernyshov, V. Dmitriev, N. Miyajima, A. El Goresy, H. F. Braun, S. Van Smaalen, I. Kantor, A. Kantor, V. Prakapenka, M. Hanfland, A. S. Mikhaylushkin, I. A. Abrikosov and S. I. Simak, Phys. Rev. Lett., 2009, 102, 8–11.
11. U. Häussermann and A. S. Mikhaylushkin, Inorg. Chem., 2010, 49, 11270–11275.
12. P. Macchi, J. Superhard Mater., 2011, 33, 380–387.
13. S. Mondal, S. Van Smaalen, A. Schönleber, Y. Filinchuk, D. Chernyshov, S. I. Simak, A. S. Mikhaylushkin, I. A. Abrikosov, E. Zarechnaya, L. Dubrovinsky and N. Dubrovinskaia, Phys. Rev. Lett., 2011, 106, 215502.
14. A. R. Oganov, V. L. Solozhenko, C. Gatti, O. O. Kurakevych and Y. Le Godec, J. Superhard Mater., 2011, 33, 363–379.
15. S. Mondal, S. Van Smaalen, G. Parakhonskiy, S. J. Prathapa, L. Noohinejad, E. Bykova, N. Dubrovinskaia, D. Chernyshov and L. Dubrovinsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 1–8.
16. P. Rulis, L. Wang, B. Walker and W. Y. Ching, J. Superhard Mater., 2011, 33, 394–400.
17. S. H. Zhang, X. Zheng, Q. Q. Jin, S. J. Zheng, D. Legut, X. H. Yu, H. Y. Gou, Z. H. Fu, Y. Q. Guo, B. M. Yan, C. Peng, C. Q. Jin, T. C. Germann and R. F. Zhang, Phys. Rev. Mater., 2018, 2, 123602.
18. D. Eklöf, A. Fischer, A. Ektarawong, A. Jaworski, A. J. Pell, J. Grins, S. I. Simak, B. Alling, Y. Wu, M. Widom, W. Scherer and U. Häussermann, ACS Omega, 2019, 4, 18741–18759.
19. Y. T. Angel Wong and D. L. Bryce, Recent Advances in ¹¹B Solid-State Nuclear Magnetic Resonance Spectroscopy of Crystalline Solids, Elsevier Ltd, 1st edn, 2018, vol. 93, pp. 213–279.
20. S. E. Ashbrook and D. McKay, Chem. Commun., 2016, 52, 7186–7204.
21. A. Samoson, Chem. Phys. Lett., 1985, 119, 29–32.
22. K. J. D. MacKenzie and M. E. Smith, Multinuclear Solid-State NMR of Inorganic Materials, Elsevier, 2002, pp. 23–108.
23. Z. Fojud, P. Herzig, O. J. Zogał, A. Pietraszko, A. Dukhnenko, S. Jurga and N. Shitsevalova, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 1–5.
24. R. Schmitt, B. Blaschkowski, K. Eichele and H. J. Meyer, Inorg. Chem., 2006, 45, 3067–3073.
25. B. Jäger, S. Paluch, O. J. Zogał, W. Wolf, P. Herzig, V. B. Filippov, N. Shitsevalova and Y. Paderno, J. Phys.: Condens. Matter, 2006, 18, 2525–2535.
26. K. Schwarz, H. Ripplinger and P. Blaha, Z. Naturforsch., A: Phys. Sci., 1996, 51, 527–533.
27. H. Ripplinger, K. Schwarz and P. Blaha, J. Solid State Chem., 1997, 133, 51–54.
28. B. Jäger, S. Paluch, W. Wolf, P. Herzig, O. J. Zogał, N. Shitsevalova and Y. Paderno, J. Alloys Compd., 2004, 383, 232–238.
29. P. Herzig, Z. Fojud, O. J. Oga, A. Pietraszko, A. Dukhnenko, S. Jurga and N. Shitsevalova, J. Appl. Phys., 2008, 103, 083534.
30. C. Benndorf, M. de Oliveira, C. Doerenkamp, F. Haarmann, T. Fickenscher, J. Kösters, H. Eckert and R. Pöttgen, Dalton Trans., 2019, 48, 1118–1128.
31. S. Heřmánek, Inorg. Chim. Acta, 1999, 289, 20–44.
32. A. Lötz and J. Voitländer, J. Chem. Phys., 1991, 95, 3208–3212.
33. A. H. Silver and P. J. Bray, J. Chem. Phys., 1959, 31, 247–253.
34. D. Lee, P. J. Bray and T. L. Aselage, J. Phys.: Condens. Matter, 1999, 11, 4435–4450.
35. K. Kanehashi and K. Saito, J. Mol. Struct., 2002, 602–603, 105–113.
36. F. A. Perras and D. L. Bryce, J. Chem. Phys., 2013, 138, 174202.
37. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
38. J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401.
39. M. Ludwig, D. Himmel and H. Hillebrecht, J. Phys. Chem. A, 2020, 124, 2173–2185.
40. M. Ludwig and H. Hillebrecht, Phys. Chem. Chem. Phys., 2021, 23, 470–486.
41. A. Pediaditakis, M. Schroeder, V. Sagawe, T. Ludwig and H. Hillebrecht, Inorg. Chem., 2010, 49, 10882–10893.
42. V. Adasch, K. U. Hess, T. Ludwig, N. Vojteer and H. Hillebrecht, Chem. – Eur. J., 2007, 13, 3450–3458.
43. R. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, 1994.
44. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
45. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. Delugas Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
46. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
47. T. Björkman, Comput. Phys. Commun., 2011, 182, 1183–1186.
48. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
49. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662.
50. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006.
51. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
52. R. K. Harris, E. D. Becker, S. M. Cabral De Menezes, P. Granger, R. E. Hoffman and K. W. Zilm, Pure Appl. Chem., 2008, 80, 59–84.
53. M. Bak, J. T. Rasmussen and N. C. Nielsen, J. Magn. Reson., 2000, 147, 296–330.
54. P. Pyykkö, Mol. Phys., 2018, 116, 1328–1338.
55. A. Otero-de-la Roza, M. A. Blanco, A. M. Pendás and V. Luaña, Comput. Phys. Commun., 2009, 180, 157–166.
56. A. Otero-de-la Roza, E. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018.
57. D. Massiot, F. Fayon, M. Capron, I. King, S. Le Calvé, B. Alonso, J.-O. Durand, B. Bujoli, Z. Gan and G. Hoatson, Magn. Reson. Chem., 2002, 40, 70–76.
58. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
59. R. F. Bader, T. S. Slee, D. Cremer and E. Kraka, J. Am. Chem. Soc., 1983, 105, 5061–5068.
60. In context of our previous investigation⁴⁰ we found an ellipticity value ε = 3.84 for the exohedral 2e3c bond in α-rB₁₂.
61. R. Lortz, Y. Wang, U. Tutsch, S. Abe, C. Meingast, P. Popovich, W. Knafo, N. Shitsevalova, Y. B. Paderno and A. Junod, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 024512.
62. O. J. Zogał, P. Florian, D. Massiot, S. Paluch, N. Shitsevalova and D. F. Borshchevsky, Solid State Commun., 2009, 149, 693–696.
63. K. H. J. Buschow and J. H. N. Creyghton, J. Chem. Phys., 1972, 57, 3910–3914.
64. F. Mauri, B. G. Pfrommer and S. G. Louie, Phys. Rev. Lett., 1996, 77, 5300–5303.
65. M. D'Avezac, N. Marzari and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 1–12.
66. T. Thonhauser, D. Ceresoli, A. A. Mostofi, N. Marzari, R. Resta and D. Vanderbilt, J. Chem. Phys., 2009, 131, 101101.
67. P. J. Basser and C. Pierpaoli, J. Magn. Reson., 1996, 111, 209–219.
68. E. Özarslan, B. C. Vemuri and T. H. Mareci, Magn. Reson. Med., 2005, 53, 866–876.
69. For α-rB₁₂ we obtain fa_χ = 48.1% rising from the deviation between the isotropic value [small chi, Greek, macron] and the χ_bare component oriented to the exohedral 2e3c bond.
70. Z. P. Yin and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 035135.
71. R. Laskowski and P. Blaha, J. Phys. Chem. C, 2015, 119, 19390–19396.
72. A. R. Ferreira, K. Reuter and C. Scheurer, J. Phys. Chem. C, 2016, 120, 25530–25540.
73. K. H. Khoo, R. Laskowski and P. Blaha, J. Phys. Chem. C, 2017, 121, 12398–12406.
74. Using the geometry reported in ref. 39.
75. For B(3) in γ-B₂₈ its distance d_X-BCP to the BCP in the B(2)–B(5) direction (see also Fig. 8) with 1.674 Å is chosen.
76. M. Profeta, M. Benoit, F. Mauri and C. J. Pickard, J. Am. Chem. Soc., 2004, 126, 12628–12635.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp06073a

‡ This implies |σ_zz − σ_iso| ≥ |σ_xx − σ_iso| ≥ |σ_yy − σ_iso|.

§ According to ref. 67 and 68 we use with R = χ_bare/tr{χ_bare}.

---