Shape changes and budding of giant vesicles induced by an internal chemical trigger: an interplay between osmosis and pH change†
Received
16th November 2020
, Accepted 1st February 2021
First published on 3rd February 2021
Abstract
Shape transformation and budding of phospholipid/fatty acid giant hybrid vesicles can be induced by an internal chemical stimulus (pH change) when coupled with an osmotic shock. In particular, an autocatalytic enzymatic reaction set (urea–urease system), confined in the lumen of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC)/oleic acid (HOA) vesicles, can force the budding of the hosting vesicle, when properly fed by a trans-membrane substrate infusion. Herein, we elucidate the budding mechanism by simulating the shape changes of a vesicle during the enzymatic reaction. The area-difference-elasticity (ADE) theory is thus implemented to minimize the surface elastic energy and obtain the equilibrium shape at different values of the reduced volume and different values of the reduced preferred area difference (Δa0). Simulations, together with control experiments, unambiguously show that to obtain an effective vesicle shape transformation, the osmotic stress and the pH change in the lumen of the vesicle must act in synergy at the same timescale. Osmotic pressure induces a vesicle deflation (volume loss), while the pH change affects the preferred area difference between the outer and the inner membrane leaflets.
1 Introduction
Design and imitation of life-like functions of artificial (synthetic) cells in abiotic systems have gained much attention in the past few decades due to the studies on the origin of life and the design of new drug carriers in targeted drug delivery applications.1–9 Definition of life contains several important characteristics for an entity having the ability for homeostasis, metabolism, growth, response to external stimuli (e.g. chemotaxis, phototaxis), and self-reproduction.10–14 Among them, self-reproduction is intended as the property of cells to split following the growth of both volume and surface area, the latter favored by the production of membrane-forming molecules. The daughters generally contain a copy of the genetic and biochemical material of the mother cell.12 However, self-replication, as we know, is a complex mechanism resulting from a long story of natural evolution,15 it is thus plausible that such a complex mechanism might be evolved, in prebiotic age, from separate processes such as membrane shape transformation, autonomous self-copying of complex molecules and self-division processes, the latter intended as the splitting of a mother cell without the addition of membrane forming molecules. The trigger of the shape transformation of vesicles, incorporating their self-division, can be categorized into two types of approaches, externally and internally triggered shape transformations. In most studies in synthetic and artificial systems, the deformation and division processes of vesicles were obtained by external triggers (e.g., the addition of the membrane precursors to the solution, changing the temperature, etc.),16–23 even though in biological systems the division is an autonomous process driven by internal mechanism of the cells.24 Therefore, engineering and design of artificial systems having internally trigger mechanisms for the shape transformation are more relevant, elegant and challenging approaches that require complex thinking involving non-trivial design steps.25 In the approach of Sugawara and his coworkers, the division process of giant unilamellar vesicles (GUVs) was mediated by the interplay of the polymerase chain reaction taking place in the lumen of vesicles and the subsequent addition of the membrane precursors to the system.26 The division rate of the vesicles was significantly lower in the absence of the enzymatic reaction. In another interesting study, a protein system was encapsulated into the lumen of GUVs and used to periodically control the shape transformation of GUVs from pear shape to dumbbell shape and to drive budding and merging of the buds with the mother vesicles.27 A novel approach demonstrated that deformation of GUVs shape can also be induced by purely physical stimuli such as inner hydrodynamic forces and mechanical torques generated by active nanoparticles.28,29
Recently,30 we have reported an internally triggered mechanism, in which mixed 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC)/oleic acid (HOA) pH-responsive GUVs (with size ranging between 5 and 50 μm) underwent shape deformations triggered by an autocatalytic enzymatic (urea–urease) reaction31–35 encapsulated inside the vesicles and coupled to a cross-membrane transport of the substrate, urea. The deformations included the following shapes: prolate, pear shape and buds (two vesicles connected by a narrow neck), and we speculated that the deformation dynamics was due to the interplay between an osmotic shock and the pH change taking place in the lumen of the GUVs.
In this work, we thoroughly investigate the role of the pH change and that of the osmotic shock to clarify and model the budding mechanism. Moreover, we interpret the shape changes observed during the urea–urease reaction with the area-difference elasticity (ADE) theory that can be applied to membranes of fixed topology, and therefore it allows to predict the formation of buds but not the membrane rupture and the complete self-division. According to this theory, the morphology of a vesicle with surface area A and volume V is determined by two geometrical parameters, the reduced volume ν and the normalized preferred area difference of the two monolayers Δa0.36 The ADE model has been successfully applied to investigate, among the others, shape changes in binary vesicles of DLPE (1,2-dilauroyl-sn-glycero-3-phosphoethanolamine) and DPPC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine) during heating–cooling cycles21 and shape changes in pure fatty acid vesicles fed externally with NaOH.37 Herein, we propose a model that integrate the pH changes due to the enzymatic reaction with the chemistry of fatty acids and takes into account the osmotic shock to explain the ν and Δa0 changes which cause the vesicles shape transformations.
2 Experimental methods
2.1 Preparation and analysis of giant lipid vesicles
For GUVs preparation and encapsulation of chemical species, the phase transfer method34,38–40 was used, which allowed full encapsulation of chemical species (details are reported in ESI†). Briefly, the method consists in the stratification of a water-in-oil emulsion (enzyme urease, acetic acid and sucrose are dissolved in the water phase) over an aqueous phase (outer solution containing glucose and acetic acid) separated by an interface of amphiphilic molecules mixed in different proportions (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine, POPC and oleic acid, HOA). The formation of the vesicles takes place at the interface of the two phases, where emulsion droplets sink by gravity in the outer phase and get coated by the amphiphilic molecules to form bilayers.
To observe the shape transformation dynamics, vesicles were added with 10 μL of a solution containing [urea] = 180 mM, [glucose] = 200 mM glucose and [CH3COOH] = 1 × 10−3 mM to trigger the division. Samples were investigated by an epifluorescence microscope (ORMATEK TL-INV 100) by taking images every 0.5 s with a CMOS camera (PIXELINK PL-D755CU) both in visible and in fluorescence (λex = 450 nm and λem = 510 nm) mode. Fluorescence intensity was used to characterise the pH change inside the vesicles. Recorded images were analysed by means of ImageJ software.41
2.2 Simulations of the deformation of vesicles
The software Surface Evolver 2.7042 was used to compute the relaxed vesicle shape by minimizing the energy functional W, i.e. the Helfrich energy,43,44 complemented with a term that, according to the ADE theory, accounts for the area difference between the outer and inner leaflets of the lipid membrane,45,46 expressed by| | 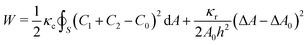 | (1) |
where C1 and C2 are the local principal curvatures, C0 is the local spontaneous curvature and the integral is calculated on the whole surface (S) of the vesicles,47,48κc and κr are the local and the non-local bending moduli, respectively, A is the vesicle area. The spontaneous curvature depends on the shape of the membrane constituents. POPC molecules are approximately cylinder-shaped, which makes their intrinsic curvature close to zero and the bilayer structures are flat.49 Protonated oleic acid molecules have a slightly negative intrinsic curvature,50 while deprotonated oleic acid molecules have a positive curvature. In mixed phospholipid/oleic acid/oleate bilayers, the average spontaneous curvature of a membrane composed of phospholipids and roughly equal amounts of oleic acid and oleate (pH ∼ pKa) is expected to be close to zero (C0 = 0).18 The area difference between the inner and the outer leaflets (ΔA) is generally calculated from the integral of the mean curvature| |  | (2) |
where h is the distance between neutral surfaces of both bilayer leaflets, however, in our case, ΔA is calculated directly from the areas extracted from experimental images.
ΔA0 is the preferred area difference and is given by
| | | ΔA0 = (Nouter − Ninner)ã | (3) |
where
Nouter and
Ninner are the number of molecules in the outer and inner leaflet, respectively,
ã is the cross-sectional area of the amphiphiles. Thus, Δ
A0 depends on the composition of the two membrane monolayers and their interaction with the surroundings, Δ
A depends on the shape.
45 Dividing for the bending energy of a sphere (8π
κc), the reduced energy is obtained
| |  | (4) |
where d
a= d
A/4π
Rs,
c1 =
C1Rs,
c2 =
C2Rs and the reduced area differences are Δ
a = Δ
A/8π
hRs and Δ
a0 = Δ
A0/8π
hRs and
Rs is the radius of the sphere. The ratio
κr/
κc can be infinitely large or can tend to zero. When the ratio is very large the limit is called the “strict bilayer couple” model (BC) and was originally introduced by the requirement of incompressible membrane monolayers leading to the relationship Δ
a = Δ
a0. The limiting case in which the ratio
κr/
κc has the value of zero is called “spontaneous curvature model” (SC). The ADE theory and the limiting cases are discussed in more detail in the following ref.
45 and
51–53. In this work, the
eqn (4) was minimized numerically and the ratio
κr/
κc = 3 was chosen since this value is commonly used to describe phospholipid vesicle morphologies.
21,45
To describe the equilibrium shape of a vesicle at the minimum of the elastic energy, only two parameters can be employed, namely the reduced preferred area difference (Δa0, as previously defined) and the reduced volume (ν). If an equivalent sphere is defined by  , where A is the surface of the vesicle, then the reduced volume can be written as
, where A is the surface of the vesicle, then the reduced volume can be written as
| | 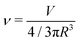 | (5) |
During the energy minimization, the parameters Δa0 and v were constrained to set a given reduced volume v and reduced area Δa, extracted from experimental images.
Radii and geometrical parameters of the vesicles were extracted from experimental frames with the help of ImageJ. The values of the volume V and the surface area A, were calculated by means of the equations reported in the ESI† for each of the shape assumed by the vesicles (sphere, prolate, pear shape and budded limiting shape).
3 Results and discussion
3.1 Conditions for successful divisions
In a typical experiment, a fast enzymatic reaction inducing a pH change inside the GUVs with the consequent division of the vesicles, was obtained in the following conditions: urease (0.5–1.5 U mL−1), pyranine (5.0 × 10−5 M) and acetic acid (1 × 10−6 M) were encapsulated in hybrid giant POPC/HOA vesicles with [POPC] = 2.6 mM and [HOA] = 2.4 mM, urea with a final concentration after mixing of 6.0 × 10−2 M was added to the vesicles suspension to initiate the reaction. Urea penetrated into the vesicles and initiated the urea–urease enzymatic reaction, which caused a pH increase according to the scheme
The low concentration of acetic acid and the high concentration of urea ensured a clock time (i.e. the beginning of the autocatalytic pH increase) within 30 seconds after the addition of the urea substrate with a pH change of the order of 0.5–0.6 units. Fig. 1a reports a typical division process: starting from a spherical shape, the GUV elongates in a prolate form, assumes a pear shape and eventually divides into two daughter vesicles. We found that the self-division process occurred with a probability of ∼25% irrespective of the size of GUVs. The division percentage within samples in the same experimental conditions may unpredictably vary because of the uneven distribution of solutes and amphiphiles (e.g., not all the vesicles in a specimen may contain the pH-sensitive HOA in the membrane), intrinsic to the phase transfer method; for this reason the concentrations of amphiphiles along the text are always intended as those initially mixed in the mineral oil phase.54,55 By means of epifluorescent microscopy, the correlation between the division and a pH change of the aqueous lumen was established, in particular, it was confirmed that the stages of the division process are correlated with the increase of pH inside the vesicles. The recorded pH increase was about a half unit starting from pH = 6.0 and ending at pH = 6.5. After the budding process, the vesicles did not separate from each other and remain connected by a narrow neck, however when the budded vesicles were irradiated by a laser beam, division readily took place. This is in agreement with the studies showing that fission and fusion of the vesicles are activated processes with an energy barrier ranging from 20 to 150kBT, and in cells, these processes are activated by proteins.56 FRAP (fluorescence recovery after photobleaching) experiments revealed that the two lumens of the daughter vesicles were completely isolated, but their membranes were connected by a common neck.30
 |
| | Fig. 1 Self-division of a GUV. (a) Shape transformation of a vesicle governed by the urea–urease enzymatic reaction. (b) Numerically simulated equilibrium shape structures of a vesicle using the Surface Evolver software. In the simulations, both parameters, ν (reduced volume), Δa0 (reduced preferred area difference) were changed. The shape transformation starts from a spherical shape through prolate and pear shapes into two daughter vesicles. | |
To investigate the mechanism of the self-division of the GUVs, we carried out several control experiments. Fig. 2 briefly summarizes our findings. Successful divisions happen in the presence of the enzyme and substrate in the osmotic concentration gradient when the clock (induction) time of the enzymatic reaction was a few ten seconds. Buffered media annihilated the effect of the pH change, and no division was observed. Similarly, in the absence of either enzyme or substrate, no division was also detected. Moreover, in the absence of both, enzyme and substrate, and in the absence of the osmotic concentration gradient (but having enzyme and substrate in the system), no division was observed. Based on these control experiments, we can draw a conclusion that the pH change and initial osmotic concentration gradient are important ingredients of the division process. Moreover, we observed no division when the clock time of the enzymatic reaction was adjusted to ∼2 min by increasing the concentration of the acetic acid in the vesicles even if the initial osmotic concentration gradient was present. From these observations, we can conclude that neither the osmotic concentration gradient nor the pH change alone can induce division. They must act in synergy, approximately at the same time scale.
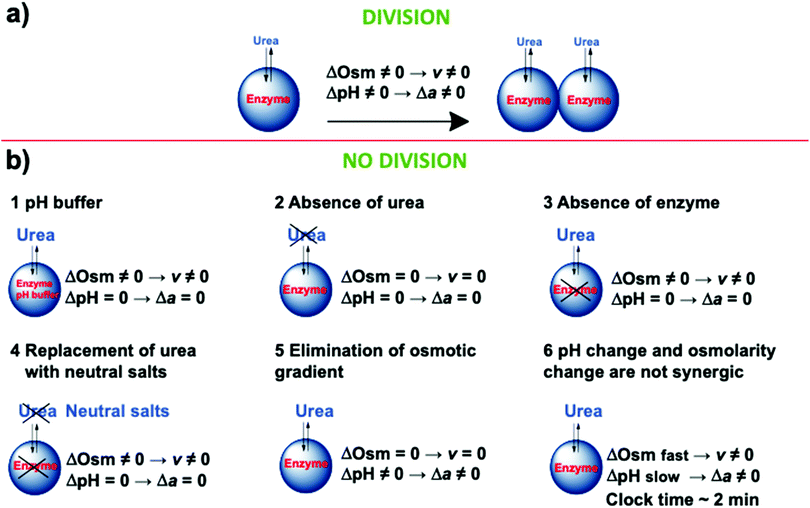 |
| | Fig. 2 Schematic representation of the control experiments with (a) and without (b) division. | |
3.2 Numerical simulations
To rationalize the shape transformation dynamics triggered by the enzymatic reaction in mixed POPC/HOA vesicles, we performed two types of numerical simulations: first, we minimized the energy functional W (eqn (1)) of the structures reported in Fig. 1(a) at given values of ν and Δa0, with the help of the software Surface Evolver; second, we implemented a kinetic model to account for the changes in the reduced preferred area difference (Δa0), following the pH change inside the vesicles.
Fig. 1(b) reports a typical shape deformation trajectory in the Δa0–ν phase space, where the values of the reduced volume and the reduced preferred area difference were adjusted to match the Δa–ν values extracted from the experimental snapshots of Fig. 1(a). Starting from a spherical shape (Δa0 = 1, ν = 1), the volume decreases due to the initial osmotic shock while the area difference remains almost constant until the vesicle reaches a prolate shape at about t = 15 s (Δa0 = 1.037, ν = 0.867); when the enzymatic reaction raises abruptly the pH during the autocatalytic formation of ammonia and carbon dioxide, the solubilisation of oleate molecules in the inner leaflet of the membrane causes Δa0 to significantly increase driving the vesicle to the budded limiting shape (t ∼ 45 s, Δa0 = 1.68, ν = 0.7). During the last phase the reduced volume decreases more slowly since the osmotic pressure is smoothed out by the permeation of the urea from the outside to the vesicle lumen.
To rationalise the shape transformation dynamics of the vesicles we propose a kinetic model based on 7 main chemical species, namely urea (S, substrate), urease (E, enzyme), pyranine (fluorescent dye, pyrOH), oleic acid (HOA), acetic acid (HA), ammonia (NH3) and carbon dioxide (CO2). Some of these chemical species can be located outside of the vesicles having cross membrane properties. The pH inside and outside the vesicles is governed by the following equilibria
| |  | (6) |
| | 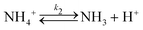 | (7) |
| |  | (8) |
| |  | (9) |
| |  | (10) |
| | 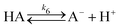 | (11) |
| |  | (12) |
| |  | (13) |
The transfer of the chemical species across the membranes can be considered as a first order process described by the following reactions
| |  | (14) |
| |  | (15) |
| |  | (16) |
| |  | (17) |
where [X]
out is the concentration of the chemical species X outside the vesicles in the water phase. The set of ordinary differential equations (ODEs) derived from the equilibria (6)–(13) and (14)–(17) is reported in the ESI.
†
The ADE energy arises from the deviation in the total area difference ΔA from ΔA0. From a modelling point of view, it is clearer to report the shape transformation dynamics in terms of ΔA0 (or its reduced form Δa0) which depends only on the number of amphiphilic molecules in the membrane and not on the vesicle shape. Therefore, the change of the number of molecules for oleic/oleate in the inner and outer leaflets (POPC molecules were constant) can be related to the pH dynamics described by equilibria (6)–(17).
In particular as pH increases, oleic acid molecules in the inner leaflet are deprotonated and can be solubilised as monomers or larger aggregates into the vesicle's lumen; the loss of oleate is, in turn, compensated by oleic acid molecules diffusing from the outer leaflet. The overall process is sketched in Fig. 3 and described by the following differential equations
| |  | (18) |
| | 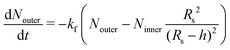 | (19) |
| |  | (20) |
| |  | (21) |
where
NinnerHOA and
NinnerOA− indicate the number of oleic acid molecules (unionized and deionized form) present in the inner leaflet,
NouterHOA and
NouterOA− are the oleic acid molecules in the outer leaflet.
Rs is the radius of the initial spherical vesicle,
h is the distance between the two neutral surfaces. The number of molecules of POPC is considered constant (d
NouterPOPC/d
t = d
NinnerPOPC/d
t = 0). The complete set of ODEs for the molecules of oleic acid can be found in the ESI.
†
 |
| | Fig. 3 Schematic representation of the mechanism of deformation. The enzymatic reaction leads to an increase of pH (from pH 6 to ∼ pH 6.5). Some OA− molecules of the inner leaflet are solubilized into the water pool (the solubility constant is koff) and form vesicles, monomers and nonlamellar aggregates. HOA molecules diffuse from the outer to the inner leaflet with a kinetic constant kf. | |
As stated, the solubility of oleic acid in water solutions is pH-dependent, it increases with the pH undergoing abrupt transitions corresponding to different aggregation states (insoluble → oleate monomers → vesicles → micelles), ESR (electron spin resonance) measurements indicated a change in the aggregation (and solubility) properties of oleic acid at pH 6.3 (pHthres in eqn (21)),57 which is in the range of our experimental conditions. To account for such a behaviour we implemented the pH-dependency through a logistic function in the last term of eqn (21).
In order to compensate the dissolved molecules, oleic acid molecules diffuse from the outer leaflet to the inner leaflet with a rate constant kf (the diffusion of the unionized form is usually higher compared to the ionized form ref. 58 and 59). The transport rate of fatty acids in eqn (19) and (21) takes into account the geometry of the vesicle: in a spherical vesicle, the number of outer molecules (Nouter = 4πRs2/〈ã〉) is always higher than the number of inner molecules (Ninner = 4π(Rs − h)2/〈ã〉) and consequently the relationship Nouter = Ninner4πRs2/4π(Rs − h)2 is respected (〈ã〉 is the average cross section of a molecule). The analytical description of the Nouter/Ninner = Aouter/Ainner is valid only for a spherical vesicle. However, we calculated this ratio for the different vesicle shapes assumed during the budding process (sphere → prolate → pear → double spheres); we extracted surface values from experimental snapshots to find that the ratio Aouter/Ainner slightly varies from 1.005 to 1.009, passing from a sphere to a pear shape. When the solubilization constant is zero Nouter = Ninner4πRs2/4π(Rs − h)2 and dNouter/dt = 0. In contrast, when koff is different from zero, Nouter ≠ Ninner4πRs2/4π(Rs − h)2, the outer oleic acid molecules will diffuse to compensate the dissolved oleate without removing the natural difference of molecules between the outer and the inner leaflet.
The number of molecules is correlated to the reference area of the membrane (A0), the preferred area difference (ΔA0) and the normalized preferred area difference (Δa0)
| |  | (22) |
| | | ΔA0(t) = Nouter(t)〈ã〉 − Ninner(t)〈ã〉 | (23) |
| |  | (24) |
where 〈
ã〉 is the average cross section of the amphiphiles,
h is the distance between the neutral surfaces (
h ∼ 2 nm) and

.
21 The average cross section at the beginning of the experiment (pH ∼ 6) was calculated taking into account the molar fraction composition of the membrane and the single cross sections of POPC (
ãPOPC = 0.69 nm
2)
60 and oleic acid (
ãoleic = 0.34 nm
2, for simplicity oleic and oleate have the same cross sectional area)
61| | 〈ã〉 = ΦãPOPC + (1 − Φ)ãoleic = 0.512![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm2 nm2 | (25) |
Due to electrostatic interactions, the formation of oleate molecules increases the average cross section of the amphiphiles.60 For small pH intervals the increment can be considered linear to the pH, 〈ã〉t = q + mpH with q = 0.11 and m = 0.066, which account for an increase of 7% from pH = 6 to pH = 6.5 as determined by the Wilhelmy film balance experiments.30 The average cross section at pH 6 is comparable with the values of average area per head group simulated at pH 5.5 (0.54 ± 0.01 nm2) and pH 7.5 (0.66 ± 0.01 nm2) for mixed vesicles Lyso-PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) oleic acid = 50%
oleic acid = 50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50%.60 The diffusion constant kf and the solubilisation constant koff were chosen in line with previous works37 and slightly changed to match the timescale of our experiments, i.e. kf = 0.4 s−1 and koff = 0.008 s−1. For simplicity, the diffusion constant kf does not consider the dependence of the flip-flop rate from the vesicle shapes as predicted from molecular dynamics simulations.62 The values of the other relevant parameters (initial conditions, kinetic constants, etc.) are reported in the ESI.†
50%.60 The diffusion constant kf and the solubilisation constant koff were chosen in line with previous works37 and slightly changed to match the timescale of our experiments, i.e. kf = 0.4 s−1 and koff = 0.008 s−1. For simplicity, the diffusion constant kf does not consider the dependence of the flip-flop rate from the vesicle shapes as predicted from molecular dynamics simulations.62 The values of the other relevant parameters (initial conditions, kinetic constants, etc.) are reported in the ESI.†
Fig. 4(a) shows the simulated variation of the pH and the osmolarity (Δosm = osmin − osmout) inside a vesicle, osmolarity was calculated as the sum of the concentrations of the ionic species that cannot cross the membrane due to electro-neutrality constrains, the concentrations of bulky molecules initially encapsulated into the vesicles (enzyme and pyranine) and the concentration of urea. The conversion of urea in NH3 and CO2 leads to a pH increase from ∼ 6 to ∼ 6.4 while the initial osmotic shock (Δosm ∼ 60 mM) is progressively smoothed out by the trans-membrane crossing of the urea from the outside aqueous medium to the lumen of the vesicle. The plots of Fig. 4 have been obtained with the kinetic model here proposed that combines the kinetics of the encapsulated reaction with the most important parameters of the ADE theory. Fig. 4(b) allows us to correlate the time scale of the pH variation with the time scale of the shape deformations. The variation of pH leads to the solubilisation of a certain amount of oleate that, when the buds are formed, can be estimated as the ratio between the dissolved oleic acid and the total molecules of oleic acid in the inner leaflet (∼2%). Therefore, a small solubilization of oleate causes Δa0 to reach the value of 1.8 in about 30 s, corresponding to the limiting shape of two spherical vesicles connected by a narrow neck,63 as shown in Fig. 4(b). For the sake of simplicity, the vesicle's shapes reported in Fig. 4(b) were calculated at the same reduced volume ν = 0.7, which was kept constant during the kinetic simulations.
 |
| | Fig. 4 (a) Simulated pH and Δosm; (b) simulated Δa0 with the corresponding vesicle shape at ν = 0.7. | |
We also performed simulations where we alternatively set koff and kf equal to 0. In the case of koff = 0 we could observe only a small growth of the inner leaflet surface, due to the electrostatic repulsion of the oleate groups. However, Δa0 does not significantly diverge from 1, i.e. the vesicle remains in a spherical form. When kf = 0 none of the molecules from the outer leaflet replaces the solubilised oleate, therefore Δa0 tends to reach unrealistic high values in the timeframe of the experiments. Both the diffusion of oleic acid between the leaflets and the solubilisation of the oleate in the lumen are important to drive the vesicles to a budded shape, but the latter is certainly the leading force of the mechanism. Diffusion of molecules from the outer to the inner leaflet is anyway important for preventing the vesicles to become too unstable.
4 Conclusions
The shape change leading to budding of a hybrid GUVs population was generated through a chemical stimulus inside the lumen (the pH change caused by the enzymatic reaction) and influenced by cross-membrane transport. The dynamics of changes driving the vesicles from a sphere to a budded limiting shape was explained in terms of an osmotic shock coupled to the pH change and rationalised with the support of the ADE theory, i.e. a variation of the number of amphiphilic molecules in the two leaflets of the membrane caused a deviation of Δa0 from Δa. With the help of numerical simulations, the change of the number of amphiphiles has been explained by the dissolution of oleate into the vesicles' lumen and the concomitant diffusion of oleic acid molecules from the outer to the inner leaflet.
Both the pH and the osmotic pressure were previously exploited to control the shape transformation of GUVs. For example, a large variation of the external pH (5–6 units) was found to induce shape changes in pure fatty acid vesicles37 or changes of the preferred curvature of SOPC (1-stearoyl-2-oleoyl-phosphatidylcholine) membranes.64 In recent work, the proper control of the osmotic pressure induced the total division (two vesicles completely separated) in heterogeneous GUVs.65 In our system, the use of an internal chemical trigger and the presence of pH-sensitive molecules in the membrane composition, allows us to attain membrane instabilities even for lower pH jumps (0.5 units), when this is coupled with an osmotic shock. The resemblance to living systems, in which the division is a process governed by the complex biochemical reaction network of the cell, often induced by environmental inputs sensed through crossmembrane transport, makes this system a plausible model for studying the self-division process of protocells under prebiotic conditions.66 Based on this knowledge, novel self-dividing systems can be designed having life-like functions.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
This study was supported by the National Research, Development and Innovation Office of Hungary (NN125752 and K131425) and the NRDI Fund (TKP2020 IES, Grant No. BME-IE-NAT) based on the charter of bolster issued by the NRDI Office under the auspices of the Ministry for Innovation and Technology. Prof. Imre Derényi (Eötvös University) and Prof. Pasquale Stano (University of Salento) are gratefully acknowledged for fruitful discussions.
Notes and references
- V. Noireaux, Y. T. Maeda and A. Libchaber, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 3473–3480 CrossRef CAS.
- E. D'Aguanno, E. Altamura, F. Mavelli, A. Fahr, P. Stano and P. L. Luisi, Life, 2015, 5, 969–996 CrossRef.
- C. Xu, S. Hu and X. Chen, Mater. Today, 2016, 19, 516–532 CrossRef CAS.
- B. C. Buddingh and J. C. M. van Hest, Acc. Chem. Res., 2017, 50, 769–777 CrossRef CAS.
- E. Altamura, R. Fiorentino, F. Milano, M. Trotta, G. Palazzo, P. Stano and F. Mavelli, Biophys. Chem., 2017, 229, 46–56 CrossRef CAS.
-
P. Stano, G. Rampioni, F. DAngelo, E. Altamura, F. Mavelli, R. Marangoni, F. Rossi and L. Damiano, Advances in Bionanomaterials, Springer, Cham, 2018, pp. 141–154 Search PubMed.
-
Y. Miele, Z. Medveczky, I. Lagzi, M. A. Budroni and F. Rossi, in Artificial Life and Evolutionary Computation, ed. S. Cagnoni, M. Mordonini, R. Pecori, A. Roli and M. Villani, Springer International Publishing, Cham, 2019, pp. 138–150 Search PubMed.
- Y. Lyu, R. Peng, H. Liu, H. Kuai, L. Mo, D. Han, J. Li and W. Tan, Chem. Sci., 2020, 11, 631–642 RSC.
- M. A. Budroni, K. Torbensen, S. Ristori, A. Abou-Hassan and F. Rossi, J. Phys. Chem. Lett., 2020, 11, 2014–2020 CrossRef CAS.
- J. Szostak, D. Bartel and P. Luisi, Nature, 2001, 409, 387–390 CrossRef CAS.
-
P. L. Luisi, The Emergence of Life: From Chemical Origins to Synthetic Biology, Cambridge University Press, Cambridge, UK, 2006 Search PubMed.
- K. Ruiz-Mirazo, C. Briones and A. de la Escosura, Chem. Rev., 2014, 114, 285–366 CrossRef CAS.
- F. Mavelli, E. Altamura, L. Cassidei and P. Stano, Entropy, 2014, 16, 2488–2511 CrossRef.
- A. Lopez and M. Fiore, Life, 2019, 9, 49 CrossRef CAS.
- G. Murtas, Mol. BioSyst., 2013, 9, 195–204 RSC.
- T. Baumgart, S. T. Hess and W. W. Webb, Nature, 2003, 425, 821–824 CrossRef CAS.
- T. F. Zhu and J. W. Szostak, J. Am. Chem. Soc., 2009, 131, 5705–5713 CrossRef CAS.
- P. Peterlin, V. Arrigler, K. Kogej, S. Svetina and P. Walde, Chem. Phys. Lipids, 2009, 159, 67–76 CrossRef CAS.
- Y. Sakuma and M. Imai, Phys. Rev. Lett., 2011, 107, 198101 CrossRef.
- Y. Sakuma and M. Imai, Life, 2015, 5, 651–675 CrossRef CAS.
- T. Jimbo, Y. Sakuma, N. Urakami, P. Ziherl and M. Imai, Biophys. J., 2016, 110, 1551–1562 CrossRef CAS.
- J. Dervaux, V. Noireaux and A. J. Libchaber, Eur. Phys. J. Plus, 2017, 132, 284 Search PubMed.
- M. Kurisu, H. Aoki, T. Jimbo, Y. Sakuma, M. Imai, S. Serrano-Luginbühl and P. Walde, Commun. Chem., 2019, 2(117), 1–10 CAS.
- B. Novák and J. J. Tyson, Nat. Rev. Mol. Cell Biol., 2008, 9, 981–991 CrossRef.
- K. Takakura, T. Toyota and T. Sugawara, J. Am. Chem. Soc., 2003, 125, 8134–8140 CrossRef CAS.
- K. Kurihara, M. Tamura, K.-I. Shohda, T. Toyota, K. Suzuki and T. Sugawara, Nat. Chem., 2011, 3, 775–781 CrossRef CAS.
- T. Litschel, B. Ramm, R. Maas, M. Heymann and P. Schwille, Angew. Chem., Int. Ed., 2018, 57, 16286–16290 CrossRef CAS.
- Y. Li and P. R. ten Wolde, Phys. Rev. Lett., 2019, 123, 148003 CrossRef CAS.
- H. R. Vutukuri, M. Hoore, C. Abaurrea-Velasco, L. van Buren, A. Dutto, T. Auth, D. A. Fedosov, G. Gompper and J. Vermant, Nature, 2020, 586, 52–56 CrossRef CAS.
- Y. Miele, Z. Medveczky, G. Hollo, B. Tegze, I. Derenyi, Z. Horvolgyi, E. Altamura, I. Lagzi and F. Rossi, Chem. Sci., 2020, 11, 3228–3235 RSC.
- G. Hu, J. A. Pojman, S. K. Scott, M. M. Wrobel and A. F. Taylor, J. Phys. Chem. B, 2010, 114, 14059–14063 CrossRef CAS.
- F. Muzika, T. Bansagi, I. Schreiber, L. Schreiberová and A. F. Taylor, Chem. Commun., 2014, 50, 11107–11109 RSC.
- B. Krajewska, J. Mol. Catal. B: Enzym., 2016, 124, 70–76 CrossRef CAS.
-
Y. Miele, T. Bánsági, A. Taylor, P. Stano and F. Rossi, in Advances in Artificial Life, Evolutionary Computation and Systems Chemistry, ed. F. Rossi, F. Mavelli, P. Stano and D. Caivano, Springer International Publishing, 2016, pp. 197–208 Search PubMed.
-
Y. Miele, T. Bánsági, A. Taylor and F. Rossi, in Advances in Bionanomaterials I, ed. S. Piotto, F. Rossi, S. Concilio, E. Reverchon and G. Cattaneo, Springer International Publishing, Cham, 2018, pp. 63–74 Search PubMed.
- V. Heinrich, S. Svetina and B. Žekš, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 3112 CrossRef CAS.
- K. Ikari, Y. Sakuma, T. Jimbo, A. Kodama, M. Imai, P.-A. Monnard and S. Rasmussen, Soft Matter, 2015, 11, 6327–6334 RSC.
- S. Pautot, B. J. Frisken and D. A. Weitz, Langmuir, 2003, 19, 2870–2879 CrossRef CAS.
- P. Carrara, P. Stano and P. L. Luisi, ChemBioChem, 2012, 13, 1497–1502 CrossRef CAS.
-
P. Stano, F. Wodlei, P. Carrara, S. Ristori, N. Marchettini and F. Rossi, in Advances in Artificial Life and Evolutionary Computation, ed. C. Pizzuti and G. Spezzano, Springer International Publishing, 2014, pp. 58–74 Search PubMed.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS.
- K. A. Brakke, Exper. Math., 1992, 1, 141–165 CrossRef.
- A. Sakashita, N. Urakami, P. Ziherl and M. Imai, Soft Matter, 2012, 8, 8569–8581 RSC.
- W. Helfrich, Phys. Lett. A, 1974, 50, 115–116 CrossRef.
- S. Svetina and B. Žekš, The
Anatomical Record, 2002, 268, 215–225 CrossRef CAS.
- X. Bian, S. Litvinov and P. Koumoutsakos, Comput. Methods Appl. Mech. Eng., 2020, 359, 112758 CrossRef.
- S. Svetina and B. Žekš, Eur. Biophys. J., 1989, 17, 101–111 CrossRef CAS.
- J. Käs and E. Sackmann, Biophys. J., 1991, 60, 825–844 CrossRef.
-
J. N. Israelachvili, Intermolecular and surface forces, Academic press, 2011 Search PubMed.
- N. Bergstrand and K. Edwards, Langmuir, 2001, 17, 3245–3253 CrossRef CAS.
- L. Miao, U. Seifert, M. Wortis and H.-G. Döbereiner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5389 CrossRef CAS.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- W. Wiese, W. Harbich and W. Helfrich, J. Phys.: Condens. Matter, 1992, 4, 1647 CrossRef.
- P. Stano, D. T. P. Souza, P. Carrara, E. Altamura, E. DAguanno, M. Caputo, P. L. Luisi and F. Mavelli, Mech. Adv. Mater. Struct., 2015, 22, 748–759 CrossRef.
- E. Altamura, P. Stano, P. Walde and F. Mavelli, Int. J. Unconvent. Comput., 2015, 11, 5–21 Search PubMed.
- C. François-Martin, J. E. Rothman and F. Pincet, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1238–1241 CrossRef.
- H. Fukuda, A. Goto, H. Yoshioka, R. Goto, K. Morigaki and P. Walde, Langmuir, 2001, 17, 4223–4231 CrossRef CAS.
- J. A. Hamilton, Prostaglandins, Leukotrienes Essent. Fatty Acids, 1999, 60, 291–297 CrossRef CAS.
- F. Kamp and J. A. Hamilton, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 11367–11370 CrossRef CAS.
- K. Lähdesmäki, O. S. Ollila, A. Koivuniemi, P. T. Kovanen and M. T. Hyvönen, Biochim. Biophys. Acta, Biomembr., 2010, 1798, 938–946 CrossRef.
- P. Walde, T. Namani, K. Morigaki and H. Hauser, Liposome Technol., 2007, 1, 1–19 CAS.
- H. Noguchi and M. Takasu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 041913 CrossRef CAS.
- N. Urakami, T. Jimbo, Y. Sakuma and M. Imai, Soft Matter, 2018, 14, 3018–3027 RSC.
- H.-G. Döbereiner, G. Gompper, C. K. Haluska, D. M. Kroll, P. G. Petrov and K. A. Riske, Phys. Rev. Lett., 2003, 91, 048301 CrossRef.
- Y. Dreher, K. Jahnke, E. Bobkova, J. P. Spatz and K. Göpfrich, Angew. Chem., Int. Ed., 2021 DOI:10.1002/anie.202014174.
- H. W. H. v, B. J. H. M. Roekel, L. H. H. Rosier, P. A. J. Meijer, A. J. Hilbers and W. T. S. Markvoort, Huck and d. T. F. A. Greef, Chem. Soc. Rev., 2015, 44, 7465–7483 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05952h |
| ‡ These authors contributed equally to this work. |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *c and
István
Lagzi
*c and
István
Lagzi
 *d
*d
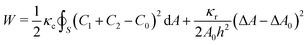


 , where A is the surface of the vesicle, then the reduced volume can be written as
, where A is the surface of the vesicle, then the reduced volume can be written as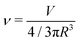

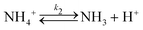



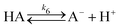







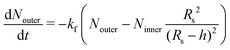




 .21 The average cross section at the beginning of the experiment (pH ∼ 6) was calculated taking into account the molar fraction composition of the membrane and the single cross sections of POPC (ãPOPC = 0.69 nm2)60 and oleic acid (ãoleic = 0.34 nm2, for simplicity oleic and oleate have the same cross sectional area)61
.21 The average cross section at the beginning of the experiment (pH ∼ 6) was calculated taking into account the molar fraction composition of the membrane and the single cross sections of POPC (ãPOPC = 0.69 nm2)60 and oleic acid (ãoleic = 0.34 nm2, for simplicity oleic and oleate have the same cross sectional area)61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm2
nm2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) oleic acid = 50%
oleic acid = 50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50%.60 The diffusion constant kf and the solubilisation constant koff were chosen in line with previous works37 and slightly changed to match the timescale of our experiments, i.e. kf = 0.4 s−1 and koff = 0.008 s−1. For simplicity, the diffusion constant kf does not consider the dependence of the flip-flop rate from the vesicle shapes as predicted from molecular dynamics simulations.62 The values of the other relevant parameters (initial conditions, kinetic constants, etc.) are reported in the ESI.†
50%.60 The diffusion constant kf and the solubilisation constant koff were chosen in line with previous works37 and slightly changed to match the timescale of our experiments, i.e. kf = 0.4 s−1 and koff = 0.008 s−1. For simplicity, the diffusion constant kf does not consider the dependence of the flip-flop rate from the vesicle shapes as predicted from molecular dynamics simulations.62 The values of the other relevant parameters (initial conditions, kinetic constants, etc.) are reported in the ESI.†




