Open Access Article
Open Access ArticleGas-phase reactivity of acyclic α,β-unsaturated carbonyls towards ozone
Jan Niklas
Illmann
 *,
Iulia
Patroescu-Klotz
*,
Iulia
Patroescu-Klotz
 and
Peter
Wiesen
and
Peter
Wiesen
Institute for Atmospheric and Environmental Research, Bergische Universität Wuppertal, 42119 Wuppertal, Germany. E-mail: illmann@uni-wuppertal.de
First published on 21st January 2021
Abstract
We evaluated different approaches to discuss the reactivity of α,β-unsaturated carbonyls comparative to alkene analogues. It was found that the reactivity factors xr, defined as the relative ratio between the rate coefficient of the carbonyl and a core structure, allow a semi-quantitative estimation of substituent effects in α,β-unsaturated acids, aldehydes and esters when the carbonyl containing substituent is replaced by a hydrogen atom. By contrast, it can be shown that the reactivity of the corresponding ketones differs from the other carbonyls. A linear correlation is presented between the xr – values and the number of carbon atoms of the alkyl group of the unsaturated esters, which can be used to predict ozonolysis rate coefficients. For this systematic analysis the following rate coefficients (in 10−18 cm3 molecule−1 s−1) have been determined at 298 ± 2 K and 990 ± 15 mbar and under dry conditions using the relative rate method: k(O3 + methyl methacrylate) = 7.0 ± 0.9, k(O3 + methyl crotonate) = 5.5 ± 1.4, k(O3 + methyl 3-methyl-3-butenoate) = 1.3 ± 0.3, k(O3 + methyl tiglate) = 65 ± 11, k(O3 + 3-penten-2-one) = 31 ± 7, k(O3 + 3-methyl-3-penten-2-one) = 80 ± 19, k(O3 + 4-methyl-3-penten-2-one) = 8.4 ± 0.8.
Introduction
Unsaturated carbonyls are a particular class of OVOCs (Oxygenated Volatile Organic Compounds) emitted into the atmosphere from biogenic and anthropogenic sources. Esters like methyl methacrylate are important intermediates in the polymer industry.1 Unsaturated ketones are mainly used in the food and fragrances industry.2,3 4-Methyl-3-penten-2-one is also utilized for the production of methyl isobutyl ketone (MIBK), a common polar solvent with wide applications in the manufacturing of pharmaceuticals, paints and coatings.4Once released into the atmosphere, the α,β-unsaturated carbonyls are removed by the reaction with atmospheric oxidants like OH and NO3 radicals, O3 or halogen atoms. Considering the time profile of atmospheric concentrations for these species the oxidation by OH radicals will be the dominating process during the daytime5 whereas NO3 radical reactions can only contribute during the night due to their rapid photolysis. The ozonolysis reactions potentially play a role during both day and night. In depth investigation of these processes is relevant for completion of data sets to be used in chemical modelling.
Several studies have shown that unsaturated carbonyls exhibit an unexpected high reactivity towards OH radicals indicating a mechanism other than the simple addition to an olefinic bond.6,7 The kinetics of the ozonolysis reactions of a moderate number of α,β-unsaturated carbonyls have been studied using both the absolute and relative rate method.8–27 However, the systematic analysis of their reactivity towards O3 is at best at the beginning.28
It is quite common to relate a target compound to the reactivity of its core structure in order to explain and/or predict its behaviour towards one of the atmospheric oxidants. In literature, these core structures were obtained by replacing the substituent of interest with –H, –CH3 or the elimination of the carbonyl group as the most common approaches. However, in the case of ozonolysis reactions the resulting conclusion is usually just that carbonyls are less reactive then their core structure due to the deactivating inductive effect of the carbonyl moiety upon olefinic bonds. Neither a comparison of the different approaches nor a systematic analysis of different functional groups has been carried out yet.
In this work a critical comparison of the various selection methods for the core reference structure was performed and tested on the quantification of substituent effects in series of α,β-unsaturated acids, aldehydes, ketones and esters.
In order to enlarge the kinetics data base for reactivity and modelling studies we determined the rate coefficients for the compounds summarised in Table 1 using the relative rate technique and FTIR spectrometry. This work, to the best of our knowledge, represents the first determination of the rate coefficients for methyl 3-methyl-2-butenoate and methyl tiglate with O3. For methyl crotonate and 3-methyl-3-penten-2-one we report here the first rate constant determination using FTIR spectrometry.
Experimental
All experiments were carried out in a 1080 L quartz-glass reaction chamber in (990 ± 15) mbar of synthetic air at (298 ± 2) K. Only a brief description of the chamber will be given here as further details can be found in the previous literature.29 The chamber is closed at both ends by metal flanges bearing several ports for the injection of reactants, addition of bath gases and coupling with analytical devices. The pumping system consists of a turbo-molecular pump backed by a double-stage rotary fore pump. The chamber can be evacuated to 10−4 mbar. Homogeneity of the reaction mixtures is achieved by three magnetically coupled Teflon mixing fans which are evenly placed in the chamber. A White-type mirror system is installed inside the chamber to monitor reaction mixtures via FTIR spectrometry in the spectral range 4000–700 cm−1 and a resolution of 1 cm−1. The system whose base length is (5.91 ± 0.01) m was operated at 82 traverses which yields a total optical path length of (484.7 ± 0.8) m. Spectra were recorded using a Nicolet iS50 instrument equipped with a liquid nitrogen cooled mercury–cadmium–telluride (MCT) detector.During each experiment 50–120 interferograms were co-added per spectrum which results in an averaging period of about 80–190 s. Typically, 15 spectra were recorded per experiment and the first five spectra were collected without oxidant over a period of 20–30 min to check for potential wall losses of the target compound and the reference. After that the reaction was started by single or multiple injection of O3 which was generated by passing a stream of pure oxygen through an electrical discharge in a homemade device. The observed reaction time was usually 20–40 min.
The initial mixing ratios in ppmV (1 ppmV = 2.46 × 1013 molecules cm−3 at 298 K) were: 0.6–0.8 for methyl methacrylate (MMA), 0.6–0.8 for methyl crotonate (MCrot), 0.3 for methyl 3-methyl-2-butenoate (M3M2B), 0.6–0.7 for methyl tiglate (MTig), 1.0–1.2 for 3-penten-2-one (3P2), 1.3–1.8 for 3-methyl-3-penten-2-one (3M3P2), 1.2–1.8 for 4-methyl-3-penten-2-one (4M3P2), 1.3–1.7 for cyclohexene, 1.1 for isoprene, 0.8–0.9 for ethene, 0.9–1.9 for 2-methylpropene, 0.8–1.9 for E2-butene, 0.9–1.9 for 1,3-butadiene and 6000–17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for carbon monoxide.
000 for carbon monoxide.
Materials
The following chemicals were used without further purification (purities as stated by the suppliers): 2-methylpropene (Aldrich, 99%), ethene (Aldrich, 99.5%), E2-butene (Messer, >99%), 1,3-butadiene (Messer, >99%), cyclohexene (Aldrich, 99%), isoprene (Aldrich, 99%), carbon monoxide (Air Liquide, 99.97%), methyl methacrylate (Aldrich, 99%), methyl crotonate (Aldrich, 98%), methyl 3-methyl-2-butenoate (Aldrich, 97%), methyl tiglate (Alfa Aesar, 98%), 3-penten-2-one (Alfa Aesar, tech. 85%), 3-methyl-3-penten-2-one (Aldrich, tech. 90%), 4-methyl-3-penten-2-one (Aldrich, tech. 90%), synthetic air (Messer, 99.9999%), oxygen (Messer, 99.5%). The cis/trans isomer ratio for commercially available 3-penten-2-one is not specified.Results and discussion
The rate coefficients for the gas-phase ozonolysis reactions of selected α,β-unsaturated carbonyls were determined relative to the O3 reactions of at least two references for each target compound. The results are shown in Table 2. Preliminary results of n-butyl acrylate and n-hexyl methacrylate have been included in the discussion of reactivity trends. As these data will be part of a separate publication no experimental details are given here.| Compound | Reference | No. of runs | Consumption/% min–max | k carbonyl/kreference | k carbonyl × 1018/cm3 molecule−1 s−1 |
|---|---|---|---|---|---|
| Methyl methacrylate | 2-Methylpropene | 5 | 0.61 ± 0.03 | 6.9 ± 2.3 | |
| Ethene | 3 | 4.57 ± 0.30 | 7.3 ± 2.4 | ||
| 31–53 | Average | 7.0 ± 0.9 | |||
| Methyl crotonate | 2-Methylpropene | 3 | 0.45 ± 0.01 | 5.1 ± 1.6 | |
| Ethene | 3 | 3.88 ± 0.20 | 6.2 ± 1.9 | ||
| 1,3-Butadiene | 1 | 0.69 ± 0.03 | 4.4 ± 1.3 | ||
| 41–60 | Average | 5.5 ± 1.4 | |||
| Methyl 3-methyl-2-butenoate | 1,3-Butadiene | 3 | 0.19 ± 0.01 | 1.2 ± 0.4 | |
| Ethene | 3 | 0.90 ± 0.03 | 1.4 ± 0.4 | ||
| 15–27 | Average | 1.3 ± 0.3 | |||
| Methyl tiglate | Cyclohexene | 4 | 0.87 ± 0.04 | 68 ± 11 | |
| E2-Butene | 3 | 0.32 ± 0.02 | 60 ± 22 | ||
| 35–65 | Average | 65 ± 11 | |||
| 3-Penten-2-one | Cyclohexene | 3 | 0.38 ± 0.02 | 30 ± 5 | |
| 2-Methylpropene | 1 | 2.76 ± 0.06 | 31 ± 9 | ||
| Isoprene | 1 | 2.64 ± 0.04 | 34 ± 9 | ||
| 26–64 | Average | 31 ± 7 | |||
| 3-Methyl-3-penten-2-one | 2-Methylpropene | 3 | 6.33 ± 0.34 | 72 ± 22 | |
| Cyclohexene | 3 | 0.98 ± 0.04 | 77 ± 11 | ||
| E2-Butene | 3 | 0.48 ± 0.01 | 92 ± 32 | ||
| 32–67 | Average | 80 ± 19 | |||
| 4-Methyl-3-penten-2-one | 2-Methylpropene | 5 | 0.72 ± 0.02 | 8.1 ± 2.5 | |
| 1,3-Butadiene | 3 | 1.39 ± 0.02 | 8.7 ± 2.7 | ||
| 34–62 | Average | 8.4 ± 0.8 | |||
Rate coefficients
The relative rate technique relies on the assumption that both target compound and reference are solely removed by the oxidant as follows| carbonyl + O3 → products; kcarbonyl | (1) |
| reference + O3 → products; kreference | (2) |
| carbonyl + wall → wall; kwall | (3) |
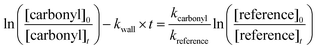 | (4) |
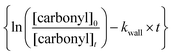 against
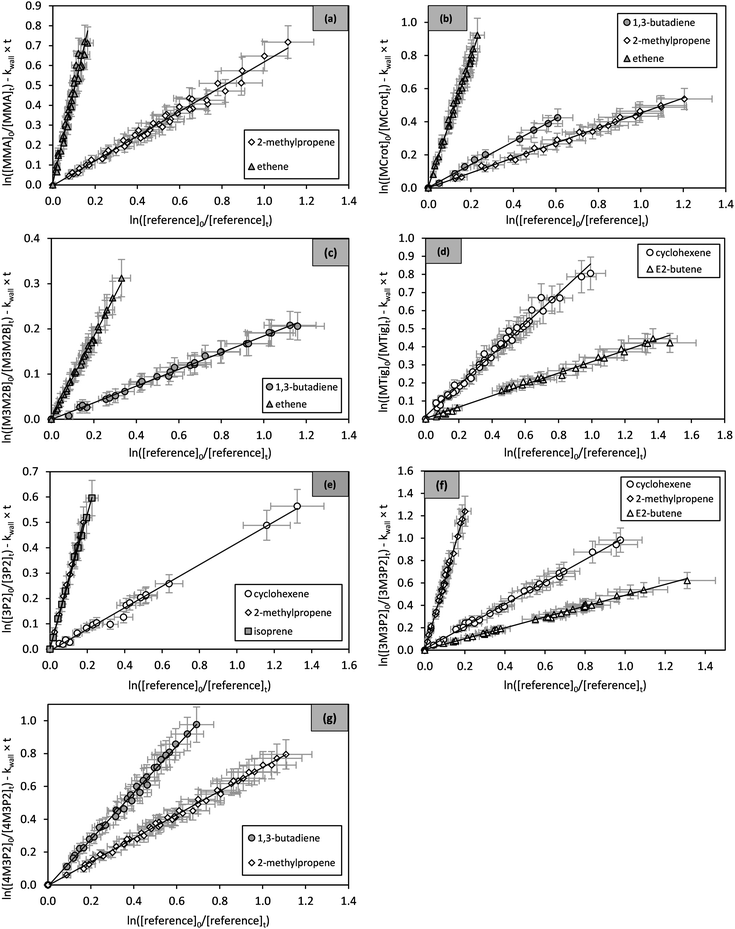
against 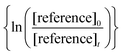 should yield a straight line where the slope represents the relative ratio between kcarbonyl and kreference. The relative rate plots of the investigated species are shown in Fig. 1. The loss rates were typically in the range of (1–4) × 10−5 s−1 for the wall loss and (1–7) × 10−4 s−1 for the loss due to the ozonolysis reaction. Only 3-penten-2-one and methyl crotonate showed a higher variability of the wall loss rate ranging from 0.6 × 10−4 s−1 to 2.4 × 10−4 s−1 and from 0.1 × 10−4 s−1 to 1.6 × 10−4 s−1, respectively. Ozonolysis reactions are known to produce OH radicals with yields up to unity and beyond.30 To scavenge any OH radical formed in the experimental system an excess of CO was added. The linear fit of all kinetic plots are going through the origin within a statistical error of 3σ resulting from the regression analysis. Both scavenger efficiency and insignificant intercepts lead to the conclusion that secondary reactions can be neglected in the present experimental set-up. Hence, the obtained relative ratios
should yield a straight line where the slope represents the relative ratio between kcarbonyl and kreference. The relative rate plots of the investigated species are shown in Fig. 1. The loss rates were typically in the range of (1–4) × 10−5 s−1 for the wall loss and (1–7) × 10−4 s−1 for the loss due to the ozonolysis reaction. Only 3-penten-2-one and methyl crotonate showed a higher variability of the wall loss rate ranging from 0.6 × 10−4 s−1 to 2.4 × 10−4 s−1 and from 0.1 × 10−4 s−1 to 1.6 × 10−4 s−1, respectively. Ozonolysis reactions are known to produce OH radicals with yields up to unity and beyond.30 To scavenge any OH radical formed in the experimental system an excess of CO was added. The linear fit of all kinetic plots are going through the origin within a statistical error of 3σ resulting from the regression analysis. Both scavenger efficiency and insignificant intercepts lead to the conclusion that secondary reactions can be neglected in the present experimental set-up. Hence, the obtained relative ratios 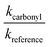 listed in Table 2 solely result from the ozonolysis reaction. The errors represent the 2σ statistical error of the linear regression analysis.
listed in Table 2 solely result from the ozonolysis reaction. The errors represent the 2σ statistical error of the linear regression analysis.
The relative ratios were put on an absolute basis using the following rate coefficients for room temperature recommended by Calvert et al.30 in 10−18 cm3 molecule−1 s−1: k(O3 + ethene) = 1.59 ± 30%, k(O3 + 2-methylpropene) = 11.3 ± 30%, k(O3 + E2-butene) = 190 ± 35%, k(O3 + 1,3-butadiene) = 6.3 ± 30% and k(O3 + isoprene) = 12.8 ± 25%. For cyclohexene the latest recommendation given by Stewart et al.31 has been used: k(O3 + cyclohexene) = (7.8 ± 1.1) × 10−17 cm3 molecule−1 s−1. The rate coefficients for the target species determined with each reference are listed in Table 2. The errors represent the statistical error from the regression analysis and the uncertainty of the reference rate coefficient. For the final results given as the mean of all determinations the arithmetic and the weighted means were compared and found to be insignificantly different. However, the error of the weighted average becomes quite small in some cases. Therefore, to cover all experimental uncertainties we thus prefer to indicate the arithmetic mean together with the corresponding 2σ error.
The following rate coefficients (in 10−18 cm3 molecule−1 s−1) were determined: k(O3 + MMA) = 7.0 ± 0.9, k(O3 + MCrot) = 5.5 ± 1.4, k(O3 + M3M2B) = 1.3 ± 0.3, k(O3 + MTig) = 65 ± 11, k(O3 + 3P2) = 31 ± 7, k(O3 + 3M3P2) = 80 ± 19, k(O3 + 4M3P2) = 8.4 ± 0.8. The rate coefficients for methyl methacrylate and 4-methyl-3-penten-2-one are in excellent agreement with previous determinations.8–10,12 The ozonolysis of 3-penten-2-one has been subject of three previous studies.11–13 While consistent with Greene and Atkinson11 and Sato et al.12 the rate coefficient determined in this work is around 30% higher than the first determination reported in literature.13 However, as already pointed out by Greene and Atkinson,11 the first determination via an absolute rate technique was probably affected by an impurity present in the samples, namely 4-methyl-3-penten-2-one. Thus, this value will not be considered further in the following discussion about reactivity trends.
The kinetics of 3-methyl-3-penten-2-one with ozone has been theoretically14 and experimentally15 investigated, once each. The theoretical investigation by RRKM theory14 yielded a rate coefficient of 2.28 × 10−16 cm3 molecule−1 s−1, which is around three times larger than the value of (80.1 ± 18.7) × 10−18 cm3 molecule−1 s−1 determined in this work. On the other hand, the rate coefficient reported by Wang and co-workers15 is 50% smaller. They determined k(O3 + 3M3P2) with an absolute method by observing the decay of ozone, using a commercial O3-analyzer, at different concentrations of 3-methyl-3-penten-2-one. Ozone monitors based on UV absorption are known to be affected by an interference caused by UV absorbing species.32 Even when negligible under atmospheric conditions this effect becomes more relevant at higher levels of the undesired absorber.33–35 Preliminary tests in our laboratory have shown 3-methyl-3-penten-2-one to photolyze when irradiated at 254 nm. Besides, Wang and co-workers15 do not report any test on possible interferences. Hence, this effect would have been undetected in their experimental set-up and subsequently have led to an underestimation of the decay of ozone. The same reason could apply for methyl crotonate. The rate coefficient determined in this work is, within the experimental uncertainties, still in satisfactorily agreement with the previous study by Grosjean et al.8
The rate coefficients for methyl 3-methyl-2-butenoate and methyl tiglate were experimentally determined within this work for the first time. Gallego-Iniesta and co-workers36 predicted both to be 10.5 × 10−18 cm3 molecule−1 s−1 using a SAR approach with group-reactivity factors given by Pfrang et al.37 While their predictions overestimate the rate coefficients for methyl 3-methyl-2-butenoate by a factor of 8 they underestimate k(O3 + MTig) by a factor of 6. A similar divergence is observed using the recent SAR approach by Jenkin et al.,28 which yields a predicted rate coefficient of 6.5 × 10−18 cm3 molecule−1 s−1 for both species. The reason for these differences will be tentatively explained in the following sections.
Reactivity trends
It is commonly accepted that ozonolysis reactions proceed via a concerted 1,3-dipolar cycloaddition with the electrophilic character of the dipole being dominant. Therefore the rate coefficients should be related to the electron density in the olefinic bond. Different groups were building SAR correlations in an attempt to fill the gaps where experimental determination of rate constants is missing. McGillen et al.38 developed a SAR method for the prediction of ozonolysis rate constants for heteroatomic unsaturated species based on the summation of steric and inductive effects and concluded that, even when not negligible, the steric effects are of minor importance. Besides, the compounds studied here do not contain bulky alkyl substituents and differ only in the number and position of the methyl groups attached to the olefinic bond. Hence, it should be possible to explain the reactivity in terms of inductive effects only.However, a weakness in reactivity discussions is identifying the core structure, to which the kinetics of the target compounds is related. Here, in order to identify the effect of the carbonyl containing substituent a useful approach is the comparison with the structural analogue alkene. As an attempt to quantify the substituent effects a non-dimensional reactivity factor xr is used defined as the ratio between kcarbonyl and kalkene.
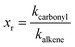 | (5) |
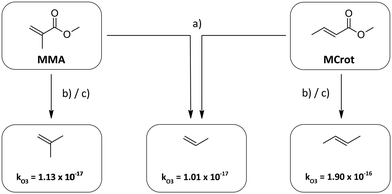 | ||
| Fig. 2 Determination of the analogue structures of methyl methacrylate (MMA) and methyl crotonate (MCrot) according to the different methods. The rate constants for the alkenes are taken from Calvert et al.30 | ||
According to method (b) and (c), on the other hand, the analogue alkenes are 2-methylpropene and E2-butene, respectively. Since k(O3 + propene) ≈ k(O3 + 2-methylpropene) all approaches yield the same xr – value in the case of methyl methacrylate. For methyl crotonate though the results differ significantly due to the much larger rate coefficient of E2-butene compared to propene caused by the inductive effect of the trans-substituted methyl group. Thus method (b) potentially overestimates the deactivating effect of the carbonyl substituent.
Table 3 summarises reactivity factors calculated for a series of unsaturated esters, ketones and aldehydes using the rate coefficients obtained in the present study and literature data, where available. Only species where α- and β-position are substituted with either –H or –CH3 are taken into account. The recommended values given by Calvert et al.30 have been used for the rate coefficients of the analogue alkenes. To compare the different approaches, we considered that the analogue alkenes resulted from replacing the –C(O)R moiety by both (a) a hydrogen atom and (b) a methyl group. For the compounds listed here method (c), i.e. the elimination of the –C(O)– or –C(O)O– moiety, leads to the same structures as method (b) for the ketones and methyl esters and method (a) for the aldehydes, respectively.
| Compound | Reference | T/K | k carbonyl × 1018/cm3 molecule−1 s−1 | Alkene analoguea | x r a | Alkene analogueb | x r b × 102 |
|---|---|---|---|---|---|---|---|
|
Grosjean and Grosjean17 | 291 | 1.05 ± 0.15 | Ethene | 0.6 | Propene | 10.4 |
| Al Mulla et al.18 | 298 ± 3 | 1.19 ± 0.11 | Ethene | 0.75 | Propene | 11.8 | |
| Al Mulla et al.18 | 298 ± 3 | 1.00 ± 0.05 | Ethene | 0.63 | Propene | 9.9 | |
| Bernard et al.9 | 294 | 0.95 ± 0.07 | Ethene | 0.60 | Propene | 9.4 | |
| Average | 1.1 ± 0.2 | 0.66 ± 0.13 | 10.4 ± 2.1 | ||||
|
Grosjean et al.8 | 291 | 7.5 ± 0.9 | Propene | 0.74 | 2-Methylpropene | 66.4 |
| Bernard et al.9 | 294 | 6.7 ± 0.9 | Propene | 0.66 | 2-Methylpropene | 59.3 | |
| Al Mulla et al.18 | 298 ± 3 | 5.75 ± 0.52 | Propene | 0.57 | 2-Methylpropene | 50.9 | |
| Al Mulla et al.18 | 298 ± 3 | 6.66 ± 0.60 | Propene | 0.66 | 2-Methylpropene | 58.9 | |
| Ren et al.10 | 291 | 6.63 ± 0.38 | Propene | 0.66 | 2-Methylpropene | 58.7 | |
| This work | 298 ± 2 | 7.0 ± 0.9 | Propene | 0.70 | 2-Methylpropene | 62.3 | |
| Average | 6.7 ± 1.2 | 0.66 ± 0.11 | 59.4 ± 10.2 | ||||
|
Grosjean et al.8 | 291 | 4.4 ± 0.3 | Propene | 0.44 | E2-Butene | 2.3 |
| This work | 298 ± 2 | 5.5 ± 1.4 | Propene | 0.54 | E2-Butene | 2.9 | |
| Average | 4.9 ± 1.5 | 0.49 ± 0.15 | 2.6 ± 0.8 | ||||
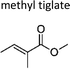
|
This work | 298 ± 2 | 65 ± 11 | Z2-Butene | 0.52 ± 0.08 | 2-Methyl-2-butene | 16.0 ± 2.6 |
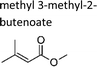
|
This work | 298 ± 2 | 1.3 ± 0.3 | 2-Methyl-propene | 0.12 ± 0.03 | 2-Methyl-2-butene | 0.3 ± 0.1 |
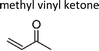
|
Atkinson et al.13 | 296 | 4.77 ± 0.59 | Ethene | 3.00 | Propene | 47.2 |
| Treacy et al.19 | 298 ± 4 | 4.20 ± 0.40 | Ethene | 2.64 | Propene | 41.6 | |
| Grosjean and Grosjean17 | 291 | 5.84 ± 0.39 | Ethene | 3.67 | Propene | 57.8 | |
| Neeb et al.20 | 296 ± 2 | 5.4 ± 0.6 | Ethene | 3.40 | Propene | 53.5 | |
| Al Mulla et al.18 | 298 ± 3 | 4.16 ± 0.33 | Ethene | 2.62 | Propene | 41.2 | |
| Al Mulla et al.18 | 298 ± 3 | 4.48 ± 0.20 | Ethene | 2.82 | Propene | 44.4 | |
| Average | 4.8 ± 1.4 | 3.02 ± 0.86 | 47.6 ± 13.5 | ||||
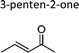
|
Greene and Atkinson11 | 296 | 36.6 ± 1.6 | Propene | 3.62 | E2-Butene | 19.2 |
| Sato et al.12 | 298 | 29.5 ± 4.1 | Propene | 2.92 | E2-Butene | 15.5 | |
| This work | 298 ± 2 | 31 ± 7 | Propene | 3.07 | E2-Butene | 16.3 | |
| Average | 32.4 ± 7.4 | 3.20 ± 0.74 | 17.0 ± 3.9 | ||||
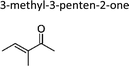
|
This work | 298 ± 2 | 80 ± 19 | Z2-Butene | 0.64 ± 0.15 | 2-Methyl-2-butene | 19.9 ± 4.6 |
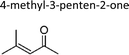
|
Sato et al.12 | 298 | 8.3 ± 1.1 | 2-Methyl-propene | 0.73 | 2-Methyl-2-butene | 2.1 |
| This work | 298 ± 2 | 8.4 ± 0.8 | 2-Methyl-propene | 0.74 | 2-Methyl-2-butene | 2.1 | |
| Average | 8.3 ± 0.1 | 0.74 ± 0.01 | 2.1 ± 0.1 | ||||
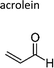
|
Atkinson et al.13 | 296 | 0.28 ± 0.05 | Ethene | 0.18 | Propene | 2.8 |
| Treacy et al.19 | 298 ± 4 | 0.30 ± 0.04 | Ethene | 0.19 | Propene | 3.0 | |
| Grosjean et al.8 | 286 | 0.26 ± 0.05 | Ethene | 0.16 | Propene | 2.6 | |
| Al Mulla et al.18 | 298 ± 3 | 0.363 ± 0.035 | Ethene | 0.23 | Propene | 3.6 | |
| Al Mulla et al.18 | 298 ± 3 | 0.336 ± 0.022 | Ethene | 0.21 | Propene | 3.3 | |
| Average | 0.31 ± 0.08 | 0.19 ± 0.05 | 3.1 ± 0.8 | ||||
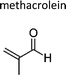
|
Atkinson et al.13 | 296 | 1.12 ± 0.13 | Propene | 0.11 | 2-Methylpropene | 9.9 |
| Treacy et al.19 | 298 ± 4 | 1.1 ± 0.2 | Propene | 0.11 | 2-Methylpropene | 9.7 | |
| Grosjean and Grosjean17 | 290 | 1.08 ± 0.20 | Propene | 0.11 | 2-Methylpropene | 9.6 | |
| Neeb et al.20 | 296 ± 2 | 1.3 ± 0.14 | Propene | 0.13 | 2-Methylpropene | 11.5 | |
| Average | 1.2 ± 0.2 | 0.11 ± 0.02 | 10.2 ± 1.8 | ||||
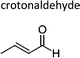
|
Atkinson et al.13 | 296 | 0.90 ± 0.18 | Propene | 0.09 | E2-Butene | 0.5 |
| Grosjean and Grosjean17 | 290 | 1.74 ± 0.20 | Propene | 0.17 | E2-Butene | 0.9 | |
| Sato et al.12 | 298 ± 2 | 1.58 ± 0.23 | Propene | 0.16 | E2-Butene | 0.8 | |
| Average | 1.4 ± 0.9 | 0.14 ± 0.09 | 0.7 ± 0.5 | ||||
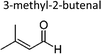
|
Sato et al. 12 | 298 ± 2 | 1.82 ± 0.26 | 2-Methyl-propene | 0.16 ± 0.02 | 2-Methyl-2-butene | 0.5 ± 0.1 |
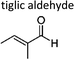
|
Sato et al. 12 | 298 ± 2 | 5.34 ± 0.73 | Z2-Butene | 0.04 ± 0.01 | 2-Methyl-2-butene | 1.3 ± 0.2 |
Based on the electron-withdrawing inductive effect of the carbonyl group and the resonance (mesomeric effect) due to the conjugated olefinic bond one would expect α,β-unsaturated carbonyls to be less reactive than the analogue alkenes and thus xr < 1 for both methods. Method (b) yields reactivity factors between 0.003 and 0.66. This large deviation can be observed even when aldehydes, ketones and methyl esters are treated separately. Besides that, there is no information on a tendency or strength of the deactivating effect of the carbonyl moiety to be gained from this method. Thus, the replacement of the substituent by a methyl group seems not to yield further conclusions.
On the other hand, the replacement by a hydrogen atom, method (a), leads to more consistent results. Except for methyl 3-methyl-2-butenoate whose reactivity towards ozone is less than the analogue alkene by a factor of 10, for all unsaturated methyl esters in Table 3 the average xr – value calculated with method (a) is 0.58 ± 0.19. For the α,β-unsaturated aldehydes a reactivity factor of 0.13 ± 0.11 can be obtained which has been similarly reported by Sato et al.12 Tiglic aldehyde is at the lower limit of the reactivity range, however, up to date only one value was reported.12
It can be concluded that the –C(O)OCH3 moiety reduces the reactivity of the olefinic bond towards ozone by 23–61% whereas the –C(O)H moiety yields a reduction of reactivity by 76–98%. These findings agree well with fundamentals of organic chemistry postulating that the strength of the −I effect varies as following:
| –C(O)H > –C(O)– > –C(O)OR | (6) |
One can argue that experimentally determined rate coefficients might be influenced by the secondary reaction of stabilized CI (= Criegee Intermediate) with carbonyl compounds. Higher than expected rate coefficients of ozonolysis reactions have been reported for acrylic and methacrylic acid when working without sufficient quantities of a CI scavenger.20 By contrast, no such effect was detected for MVK.20 For 3-penten-2-one no such experimental results are available but a similar behaviour toward CIs is expected. Hence it seems plausible to assume that the high rate coefficients obtained here and reported previously11,12 are not the product of secondary consumption by CIs.
Several attempts have been made for the prediction of ozonolysis rate coefficients at room temperature. King et al.41 used perturbation frontier molecular orbital theory (PFMO) and correlated the natural logarithm of the rate coefficients with the energy of the highest occupied molecular orbital (HOMO) over a small range of EHOMO. Pfrang and co-workers updated this concept, originally developed for the prediction of OH, NO3 and O3 reactions of alkenes and conjugated dialkenes only, and extended its applicability to unsaturated ketones, esters, alcohols and ethers.37,42–44 These studies yielded structure–activity relations with group-reactivity factors those predictability has been shown to be less accurate for O3 than for OH and NO3.37 McGillen et al.38 improved the predictability of rate coefficients for ozonolysis reactions of heteroatomic unsaturated species by parameterisation of steric and inductive effects which yielded the definition of a new SAR index (xH). In the case of 3-penten-2-one the rate coefficient calculated based on Pfrang et al.37 and McGillen et al.38 is 3.9 × 10−18 cm3 molecule−1 s−1 and 5.4 × 10−18 cm3 molecule−1 s−1, respectively. This would indicate a lower reactivity towards ozone than propene which is contradicted by the experimentally obtained values. Thus none of these approaches captures the significant increase of reactivity compared to the alkene analogue (resulting from replacement of the carbonyl containing substituent by a hydrogen atom) as observed here for methyl vinyl ketone and 3-penten-2-one. By contrast, the very recent SAR method by Jenkin et al.28 predicts both ketones to be more reactive than their alkene analogues. However, the authors stated that, in contrast to the SAR modifications for alkenes, generic rate coefficients had to be assigned for α,β-unsaturated carbonyls (referred to as “vinylic oxygenated compounds”) simply based on the experimental data of these ketones.28
In the liquid phase, α,β-unsaturated carbonyls are known to exhibit a reactivity other than the reactivity of an olefinic bond or a carbonyl group, respectively, but characteristic conjugate addition reactions (see for example: Rossiter and Swinger45 and references therein). Due to conjugation, the olefinic bond and the carbonyl group are examined as a unit where π-electrons are delocalised thus lowering the electron density in the olefinic bond and reducing the reactivity towards electrophiles. The delocalisation of π-electrons is though limited to planar or nearly planar conformations. Hence, if resonance besides inductive effects significantly impacts the reduced reactivity of the α,β-unsaturated aldehydes and methyl esters, it may be possible that in 3P2 and MVK non-planar conformations are energetically favoured and therefore their reactivity cannot be compared directly with the α,β-unsaturated esters. However, this is just speculation and detailed quantum mechanical calculations are needed to whether support or refuse this hypothesis.
One could intuitively also imagine that the reactivity of 3P2 and MVK indicates an ozonolysis mechanism other than a 1,3-dipolar cycloaddition yielding a 1,2,3-trioxoalane. Criegee already discussed the alternative formation of a σ-complex or a peroxy-epoxide in the liquid phase for systems in which epoxides have been observed.46 However, if this is rate-determining for 3P2 and MVK it should be reflected in the product distribution. At least for MVK methylglyoxal and formaldehyde have been identified as main products, which is in agreement with the initially formed trioxolane.47,48 This reasoning may thus be ruled out.
The outstandingly low rate coefficient for methyl 3-methyl-2-butenoate in comparison to the other α,β-unsaturated methyl esters indicates additional effects reducing its reactivity towards ozone. One could intuitively imagine that the Z-substituted methyl group and the –C(O)OCH3 moiety could repel each other in the initially formed trioxolane. However, this effect cannot be observed in the ketone analogue (4-methyl-3-penten-2-one) whose reactivity is close to the other methyl esters. Besides, as previously mentioned, steric effects are expected to play a minor role. Currently there is no convincing explanation for the low reactivity of methyl 3-methyl-2-butenoate towards ozone.
Dependence of xr on the alkyl chain length
Literature data are even scarcer for ozonolysis reactions of α,β-unsaturated carbonyls with larger linear alkyl substituents attached to the carbonyl moiety. Among α,β-unsaturated ketones only rate coefficients for ethyl vinyl ketone8 and 4-hexen-3-one21 have been reported up to date. In the case of esters kinetic data were published for C2 (4 compounds),9,10,16,22,23 C3 (1 compound)10 and C4 (2 compounds).10,16 These information are shown in Table 4. In addition, preliminary results on the kinetics of n-butyl acrylate and n-hexyl methacrylate performed were included for a more comprehensive analysis. Very recently, Ren et al.10 reported the kinetics of C1–C4 alkyl methacrylates and concluded that longer alkyl substituents may enhance the reactivity of the olefinic bond towards ozonolysis. They further interpreted their results as a proof that the ozonolysis reaction is an electrophilic process.| Alkyl rest | Compound | Reference | T/K | k carbonyl × 1018/cm3 molecule−1 s−1 | x r |
|---|---|---|---|---|---|
| a Ongoing study in our laboratory (measured relative to ethene and 1,3-butadiene). b Ongoing study in our laboratory (measured relative to propene, 1,3-butadiene and isoprene). | |||||
| Acid (n = 0) | Acrylic acid | Neeb et al.20 | 296 ± 2 | 0.65 ± 0.13 | 0.41 ± 0.08 |
| Al Mulla et al.18 | 298 ± 3 | 0.76 ± 0.05 | 0.48 ± 0.03 | ||
| Al Mulla et al.18 | 298 ± 3 | 0.79 ± 0.07 | 0.49 ± 0.04 | ||
| 0.46 ± 0.09 | |||||
| Ethyl (n = 2) | Ethyl acrylate | Bernard et al.9 | 294 | 1.3 ± 0.1 | 0.82 ± 0.06 |
| Ethyl methacrylate | Gai et al.16 | 293 ± 1 | 7.68 ± 0.88 | 0.76 ± 0.09 | |
| Ren et al.10 | 291 | 7.74 ± 0.41 | 0.77 ± 0.04 | ||
| Average | 7.71 ± 0.09 | 0.76 ± 0.01 | |||
| Ethyl 3,3-dimethylacrylate | Gaona-Colman et al.23 | 298 ± 2 | 8.2 ± 1.9 | 0.73 ± 0.17 | |
| Ethyl crotonate | Gaona-Colman et al.22 | 298 ± 2 | 8.0 ± 1.8 | 0.79 ± 0.18 | |
| 0.77 ± 0.08 | |||||
| n-Propyl (n = 3) | n-Propyl methacrylate | Ren et al.10 | 291 | 8.46 ± 0.36 | 0.84 ± 0.04 |
| n-Butyl (n = 4) | n-Butyl acrylate | Gai et al.16 | 293 ± 1 | 2.40 ± 0.29 | 1.51 ± 0.18 |
| Preliminary resultsa | 1.9 ± 0.2 | 1.19 ± 0.11 | |||
| Average | 2.2 ± 0.3 | 1.35 ± 0.45 | |||
| n-Butyl methacrylate | Ren et al.10 | 291 | 9.78 ± 0.58 | 0.97 ± 0.06 | |
| Gaona-Colman et al.22 | 298 ± 2 | 10.0 ± 3.0 | 0.99 ± 0.30 | ||
| Average | 0.98 ± 0.03 | ||||
| 1.16 ± 0.51 | |||||
| n-Hexyl (n =6) | n-Hexyl methacrylate | Preliminary resultsb | 13.6 ± 1.4 | 1.35 ± 0.14 | |
In order to establish a possible relationship between the alkyl chain length and the kinetics of ozonolysis reactions reactivity factors have been calculated for α,β-unsaturated esters according to method (a) using averaged data derived from all available literature references. Following this rationale, the alkyl substituent with zero carbon atoms corresponds to the α,β-unsaturated acids. Up to now, only two studies18,20 reported rate coefficients for acrylic and methacrylic acid. While consistent for acrylic acid the rate coefficients for methacrylic acid differ by a factor of two. Al Mulla and co-workers18 pointed out that, based on the given experimental details, no error in the experimental set-up could be identified and the discrepancies remain unexplained. The latter compound is therefore not considered further. As for the C1 esters, methyl 3-methyl-2-butenoate, as discussed previously, has been excluded.
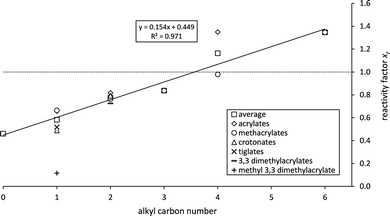
A plot of the averaged xr – values against the carbon number of the alkyl chain yields a straight line with a surprisingly high correlation coefficient (Fig. 3). For a better overview the average values of each substance are also included. The variation of xr for C4 is unsatisfactorily large for one reason mainly. The literature references for n-butyl methacrylate10,22 agree well and yield and average of xr = 0.98 which would be much closer to the regression line. For n-butyl acrylate the unpublished rate coefficient determined in our laboratory is around 30% smaller (xr = 1.19) than previously reported by Gai et al.16 (xr = 1.51). This difference, even when acceptable within experimentally uncertainties, significantly increases the average reactivity factor for C4 and its statistical error.
The consistency of the xr – values observed for the α,β-unsaturated methyl esters is exhibited also in the case of the C2 esters where besides C1 esters most data are available. Their reactivity towards ozone can be explained in the way the carbonyl containing substituent adjacent to the olefinic bond affects it. Even when different approaches exist in literature for the interpretation and quantification of substituent effects the addition principle, first introduced by Taft49 and related to inductive and steric effects, has been generally accepted. Resonance effects have been included later on.50 Furthermore, resonance, if its influence on the reactivity is measurable in comparison to the inductive effects, results from the conjugation between the olefinic bond and the carbonyl group only and thus should be nearly the same for all α,β-unsaturated esters. This fact is supported by the xr – values obtained here for methyl esters (Table 3). Hence, the increasing reactivity factors with the alkyl chain length solely result from the positive inductive effect of the alkyl group. Linear regression analysis yields an intercept of 0.45 ± 0.09 (2σ). Consequently, the pure –C(O)O– moiety, present in the unsaturated acids, reduces the reactivity of the olefinic bond by 46–64%. Irrespective of the experimental uncertainties this deactivation is a factor of 1.3 larger than for the unsaturated methyl esters. This is in agreement with the previously mentioned conclusion by Ren et al.10 and in contradiction to earlier findings by Pfrang and co-workers37 who stated the influence of R being rather small.
The transmission of an inductive effect σ through a molecule has been discussed in two originally alternative mechanisms: by either transmission along bonds or interaction through space (as reviewed for example by Exner51 and references therein). The magnitude of σ according to the latter mechanism, irrespective of its total strength, has been described in literature51 by different functions in dependence of r−n where r is the distance between the atom of interest and the reactive centre of the molecule. This is equivalent to the intuitive notion that the effect of a substituent becomes smaller the more remote it is located. Hence, a logarithmic-like correlation between xr and the number of carbon atoms would be expected where the reactivity factors for the esters with n > 3 become indistinguishable. However, the correlation between xr and the number of carbon atoms shows a remarkable linearity indicating an inductive influence up to C6 for the α,β-unsaturated esters. It would furthermore imply that the influence of every added methylene group is independent from the distance to the olefinic bond and no attenuation of the inductive influence would be visible. It would thus be more general to say for the unsaturated esters that while a carbonyl group has an electron-withdrawing effect, electron-donating alkyl groups are thus lowering the cumulative deactivating effect of the –C(O)OR substituent. The increase of the +I – effect with the length of the alkyl group leads to an overcompensation of the electron-withdrawing effect in case of C4 (= n-butyl) hence exceeding the reactivity of the alkene analogue (Fig. 3). It should be emphasized that these observations contradict our understanding of the inductive influence's transmission. The invariance of the reactivity of terminal alkenes towards ozone is well documented (see for example McGillen et al.52 and references therein). Thus, longer alkyl groups attached to the olefinic bond do not further enhance the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond's reactivity. The presented correlation, on the other hand, unambiguously shows the influence of longer alkyl substituents. Based on that, there seems to be a fundamental difference when the alkyl group is adjacent to the oxygen atom of the –C(O)O– moiety. This effect needs to be further investigated both experimentally and theoretically.
C double bond's reactivity. The presented correlation, on the other hand, unambiguously shows the influence of longer alkyl substituents. Based on that, there seems to be a fundamental difference when the alkyl group is adjacent to the oxygen atom of the –C(O)O– moiety. This effect needs to be further investigated both experimentally and theoretically.
Structure–activity relations
The correlation in Fig. 3 allows to derive a formula for the group-reactivity factor of the carbonyl moiety:| f(–C(O)OCnH2n+1) = (0.154 ± 0.026) × n + (0.449 ± 0.088) | (7) |
| kO3 = kbasic × f(–C(O)OCnH2n+1) | (8) |
| r = (kpred./kobs.)y | (9) |
| Compound (IUPAC nomenclature) | Other name | CAS | Alkene analogue | k obs. | k pred. | r | k pred. | r |
|---|---|---|---|---|---|---|---|---|
| a Based on eqn (7) and (8). b Based on Jenkin et al.28 c An average value of 1.0 × 10−17 cm3 molecule−1 s−1 has been used for the C4–C8 alk-1-enes. d Grosjean et al.8 e Average of the rate coefficients determined by Sato et al.12 and Kalalian et al.24 f trans-Substitution has been assumed for the calculation. g The rate coefficient of Avzianova and Ariya53 has been used for the calculation. h Kalalian et al.24 i Gaona Colmán et al.23 j Average of the rate coefficients determined by Atkinson et al.,25 Grosjean et al.26 and Kalalian et al.24 k Gaona Colmán et al.27 l Neeb et al.20 m McGillen et al.38 | ||||||||
| Prop-2-enal | Acrolein | 107-02-8 | Ethene | 0.31 | 0.21 | 1.49 | ||
| 2-Methylprop-2-enal | Methacrolein | 78-85-3 | Prop-1-ene | 1.2 | 1.3 | 1.14 | 1.2 | 1.04 |
| (E)-But-2-enal | Crotonaldehyde | 123-73-9 | Prop-1-ene | 1.4 | 1.3 | 1.07 | 1.4 | 1.00 |
| 3-Methylbut-2-enal | 3-Methyl-2-butenal | 107-86-8 | 2-Methylprop-1-ene | 1.8 | 1.5 | 1.24 | 1.8 | 1.01 |
| (E)-2-Methylbut-2-enal | Tiglic aldehyde | 497-03-0 | (Z)-But-2-ene | 5.3 | 16 | 3.05 | 5.7 | 1.07 |
| 2-Methylidenebutanal | 2-Ethyl acrolein | 922-63-4 | But-1-enec | 1.1d | 1.3 | 1.22 | 1.4 | 1.33 |
| (E)-Pent-2-enal | E2-Pentenal | 1576-87-0 | But-1-enec | 1.4e | 1.3 | 1.09 | 1.7 | 1.18 |
| 2-Methyl-2-pentenalf | 2-Methyl-2-pentenal | 623-36-9 | (Z)-Pent-2-eneg | 1.6h | 17 | 10.87 | 6.8 | 4.29 |
| (Z)-Pent-2-ene | 7.1i | 17 | 2.42 | 6.8 | 1.05 | |||
| (E)-Hex-2-enal | E2-Hexenal | 6728-26-3 | Pent-1-enec | 1.6j | 1.3 | 1.19 | 1.9 | 1.25 |
| (E)-Hept-2-enal | E2-Heptenal | 18829-55-5 | Hex-1-enec | 2.5k | 1.3 | 1.90 | 2.2 | 1.12 |
| (E)-Oct-2-enal | E2-Octenal | 2548-87-0 | Hept-1-enec | 2.4k | 1.3 | 1.82 | 2.5 | 1.04 |
| (E)-Non-2-enal | E2-Nonenal | 18829-56-6 | Octe-1-nec | 2.1k | 1.3 | 1.58 | 2.7 | 1.33 |
| Prop-2-enoic acid | Acrylic acid | 79-10-7 | Ethene | 0.73 | 0.71 | 1.03 | ||
| 2-Methylprop-2-enoic acid | Methacrylic acid | 79-41-4 | Prop-1-ene | 4.1l | 4.5 | 1.11 | 2.3 | 1.78 |
| (E)-But-2-enoic acid | Crotonic acid | 107-93-7 | Prop-1-ene | 4.5 | 2.3 | |||
| (E)-2-Methylbut-2-enoic acid | Tiglic acid | 80-59-1 | (Z)-But-2-ene | 56 | 2.3 | |||
| (E)-Pent-2-enoic acid | E2-Pentenoic acid | 13991-37-2 | But-1-enec | 3.1m | 4.5 | 1.46 | 2.7 | 1.12 |
| Methyl prop-2-enoate | Methyl acrylate | 96-33-3 | Ethene | 1.0 | 0.96 | 1.09 | 1.5 | 1.43 |
| Methyl 2-methylprop-2-enoate | Methyl methacrylate | 80-62-6 | Prop-1-ene | 6.7 | 6.1 | 1.10 | 6.5 | 1.03 |
| Methyl (E)-but-2-enoate | Methyl crotonate | 623-43-8 | Prop-1-ene | 4.9 | 6.1 | 1.24 | 6.5 | 1.32 |
| Methyl (E)-2-methylbut-2-enoate | Methyl tiglate | 6622-76-0 | (Z)-But-2-ene | 65 | 75 | 1.17 | 6.5 | 9.94 |
| Methyl 3-methylbut-2-enoate | Methyl 3,3-dimethylacrylate | 924-50-5 | 2-Methylprop-1-ene | 1.3 | 6.8 | 5.21 | 6.5 | 4.96 |
| Ethyl prop-2-enoate | Ethyl acrylate | 140-88-5 | Ethene | 1.3 | 1.2 | 1.08 | 1.8 | 1.37 |
| Ethyl 2-methylprop-2-enoate | Ethyl methacrylate | 97-63-2 | Prop-1-ene | 7.7 | 7.7 | 1.01 | 7.7 | 1.00 |
| Ethyl (E)-but-2-enoate | Ethyl crotonate | 623-70-1 | Prop-1-ene | 8.0 | 7.7 | 1.05 | 7.7 | 1.03 |
| Ethyl (E)-2-methylbut-2-enoate | Ethyl tiglate | 5837-78-5 | (Z)-But-2-ene | 95 | 7.7 | |||
| Ethyl 3-methylbut-2-enoate | Ethyl 3,3-dimethylacrylate | 638-10-8 | 2-Methylprop-1-ene | 8.2 | 8.6 | 1.04 | 7.7 | 1.06 |
| Propyl prop-2-enoate | Propyl acrylate | 925-60-0 | Ethene | 1.5 | 2.1 | |||
| Propyl 2-methylprop-2-enoate | Propyl methacrylate | 2210-28-8 | Prop-1-ene | 8.5 | 9.2 | 1.09 | 9.0 | 1.06 |
| Butyl prop-2-enoate | n-Butyl acrylate | 141-32-2 | Ethene | 2.1 | 1.7 | 1.26 | 2.4 | 1.10 |
| Butyl 2-methylprop-2-enoate | n-Butyl methacrylate | 97-88-1 | Prop-1-ene | 9.9 | 11 | 1.09 | 10 | 1.03 |
| Butyl (E)-but-2-enoate | n-Butyl crotonate | 591-63-9 | Prop-1-ene | 11 | 10 | |||
| Pentyl 2-methylprop-2-enoate | n-Amyl methacrylate | 2849-98-1 | Prop-1-ene | 12 | 11 | |||
| Hexyl prop-2-enoate | n-Hexyl acrylate | 2499-95-8 | Ethene | 2.2 | 2.9 | |||
| Hexyl 2-methylprop-2-enoate | n-Hexyl methacrylate | 142-09-6 | Prop-1-ene | 14 | 14 | 1.02 | 13 | 1.07 |
| Hexyl (E)-but-2-enoate | n-Hexyl crotonate | 1617-25-0 | Prop-1-ene | 14 | 13 | |||
For most of the listed species the predicted rate coefficients using the eqn (7) and (8) are similar to those based on the Jenkin28 approach. Huge discrepancies are found for substances where Z2-butene is the analogue structure according to method (a) as for “vinylic esters and acids” Jenkin and co-workers28 only differentiate between two categories of substitution patterns, namely ethene and higher substituted alkenes. More experimental data are thus required. However, for the same reason the recent SAR method underestimates the experimentally determined rate coefficient of methyl tiglate by a factor of 10.
According to a similar rationale α,β-unsaturated aldehydes could be classified as C0, 3-alken-2-ones as C1, 4-alken-3-ones as C2, and so on. However, an attempt to apply this treatment for aldehydes and ketones proved difficult first due to lack of reference data. For longer alkyl chains (n > 2) kinetic information are missing for target carbonyls. Even so the reactivity factors xr for ethyl vinyl ketone and 4-hexen-3-one should be much lower than the values one obtains using method (a) directly, i.e. 3.77 and 6.34, respectively. The cause of the significant enhancement of the reactivity towards ozone observed for ketones comparative to other α,β-unsaturated carbonyls cannot be satisfactorily explained yet.
Nevertheless, the xr – value determined for the aldehydes can also be applied to predict longer chain or higher substituted α,β-unsaturated aldehydes according to eqn (8) when using f(–CHO) = 0.130 instead of f(–C(O)OCnH2n+1). In doing so the r-values are <1.25 for methacrolein, crotonaldehyde, 3-methyl-2-butenal, 2-ethyl acrolein, E2-pentenal and E2-hexenal (Table 5). Exceptions are, as previously mentioned, tiglic aldehyde (r = 3.05) and 2-methyl-2-pentenal. For the latter compound two determinations of the rate coefficient (in 10−18 cm3 molecule−1 s−1) are found in the literature: 7.1 ± 1.623 (r = 3.83) and 1.58 ± 0.2024 (r = 17.21). Kalalian et al.24 argued that the difference of a factor of 5 can be attributed to an OH interference in the other study. On the contrary, Gaona Colmán et al.23 argued that any influence of OH cannot be very significant based on similar results when determining the rate coefficient relative to the ozonolysis reaction of either 2-methylpropene or 1,3-butadiene. Thus, before rating the predictability of this species a re-determination of the rate coefficient is needed. On the other hand the predictive capacity of eqn (8) applied for aldehydes seems to be less accurate for longer E2-alkenals. But given that rate coefficients for C7–C9E2-alkenals have only been determined once in the absence of an OH scavenger27 it could also be worth re-investigating these compounds.
Conclusions
Room-temperature rate coefficients for the gas-phase ozonolysis of a series of acyclic α,β-unsaturated carbonyls have been determined using the relative rate technique. The discussion of reactivity in terms of a relative ratio between the target compound and a core structure has already been quite common. However, we have shown here that only the replacement of the carbonyl containing substituent by a hydrogen atom provides a useful tool for the quantification of the deactivating effect of the carbonyl moiety upon the olefinic bond in the case of ozonolysis reactions. This concept is validated by the consistency of the xr – values of the α,β-unsaturated acids, esters with different n-alkyl chain length and aldehydes. The linearity between xr and the number of carbon atoms up to C6 further indicates a cumulative nature of the positive inductive effect of the alkyl group in the case of the esters. This is in contradiction to the intuitive notion that the influence of a substituent on a reactive centre is smaller the more remote it is located. This effect needs to be further investigated for a larger pool of substances to prove if the presented correlation is able to well predict rate coefficients for ozonolysis reactions. On the other hand, this concept points out that the reactivity of most of the ketones differs from other α,β-unsaturated carbonyls as shown by the large xr – values. This effect solely becomes visible using method (a). In order to explain the complex reactivity of the ketones detailed quantum mechanical calculations are needed.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge funding from the EU Horizon 2020 research and innovation programme through the EUROCHAMP-2020 Infrastructure Activity (grant agreement no. 730997) and the Deutsche Forschungsgemeinschaft (DFG) through the grant agreement WI 958/18-1.References
- W. Bauer, Jr., Ullmann's Encyclopedia of Industrial Chemistry, 2011 DOI:10.1002/14356007.a16_441.pub2.
- C. Chapuis and D. Jacoby, Appl. Catal., A, 2001, 221, 93 CrossRef CAS.
- D. R. Bickers, P. Calow, H. A. Greim, J. M. Hanifin, A. E. Rogers, J.-H. Saurat, I. G. Sipes, R. L. Smith and H. Tagami, Regul. Toxicol. Pharmacol., 2003, 37, 218 CrossRef CAS.
- S. Sifniades, A. B. Levy and H. Bahl, Ullmann's Encyclopedia of Industrial Chemistry, 2011 DOI:10.1002/14356007.a01_079.pub3.
- J. G. Calvert, A. Mellouki, J. J. Orlando, M. J. Pilling and T. J. Wallington, The Mechanisms of Atmospheric Oxidation of the Oxygenates, Oxford University Press, New York, 2011 Search PubMed.
- M. B. Blanco, I. Barnes and P. Wiesen, J. Phys. Chem. A, 2012, 116, 6033 CrossRef CAS PubMed.
- J. P. Colomer, M. B. Blanco, A. B. Peñéñory, I. Barnes, P. Wiesen and M. A. Teruel, Atmos. Environ., 2013, 79, 546 CrossRef CAS.
- D. Grosjean, E. Grosjean and E. L. Williams, II, Int. J. Chem. Kinet., 1993, 25, 783 CrossRef CAS.
- F. Bernard, G. Eyglunent, V. Daële and A. Mellouki, J. Phys. Chem. A, 2010, 114, 8376 CrossRef CAS PubMed.
- Y. Ren, M. Cai, V. Daële and A. Mellouki, Atmos. Environ., 2019, 200, 243 CrossRef CAS.
- C. R. Greene and R. Atkinson, Int. J. Chem. Kinet., 1994, 26, 37 CrossRef CAS.
- K. Sato, B. Klotz, T. Taketsuga and T. Takayanagi, Phys. Chem. Chem. Phys., 2004, 6, 3969 RSC.
- R. Atkinson, S. M. Aschmann, A. M. Winer and J. N. Pitts, Jr., Int. J. Chem. Kinet., 1981, 13, 1133 CrossRef CAS.
- X. Wang, J. Sun, L. Bao, Q. Mei, B. Wie, Z. An, J. Xie and M. He, J. Phys. Chem. A, 2019, 123, 2745 CrossRef CAS.
- J. Wang, L. Zhou, W. Wang and M. Ge, Phys. Chem. Chem. Phys., 2015, 17, 12000 RSC.
- Y. Gai, M. Ge and W. Wang, Chem. Phys. Lett., 2009, 473, 57 CrossRef CAS.
- E. Grosjean and D. Grosjean, Int. J. Chem. Kinet., 1998, 30, 21 CrossRef CAS.
- I. Al Mulla, L. Viera, R. Morris, H. Sidebottom, J. Treacy and A. Mellouki, ChemPhysChem, 2010, 11, 4069 CrossRef CAS PubMed.
- J. Treacy, M. E. Hag, D. O'Farrell and H. Sidebottom, Ber. Bunsenges. Phys. Chem., 1992, 96, 422 CrossRef CAS.
- P. Neeb, A. Kolloff, S. Koch and G. K. Moortgat, Int. J. Chem. Kinet., 1998, 30, 769 CrossRef CAS.
- E. Grosjean and D. Grosjean, J. Atmos. Chem., 1999, 32, 205 CrossRef CAS.
- E. Gaona Colmán, M. B. Blanco, I. Barnes and M. A. Teruel, Chem. Phys. Lett., 2013, 579, 11 CrossRef.
- E. Gaona Colmán, M. B. Blanco, I. Barnes and M. A. Teruel, Atmos. Environ., 2015, 109, 272 CrossRef.
- C. Kalalian, E. Roth and A. Chakir, Int. J. Chem. Kinet., 2018, 50, 47 CrossRef CAS.
- R. Atkinson, J. Arey, S. M. Aschmann, S. B. Corchnoy and Y. Shu, Int. J. Chem. Kinet., 1995, 27, 941 CrossRef CAS.
- E. Grosjean, D. Grosjean and J. S. Seinfeld, Int. J. Chem. Kinet., 1996, 28, 373 CrossRef CAS.
- E. Gaona Colmán, M. B. Blanco, I. Barnes and M. A. Teruel, RSC Adv., 2015, 5, 30500 RSC.
- M. E. Jenkin, R. Valorso, B. Aumont, M. J. Newland and A. R. Rickard, Atmos. Chem. Phys., 2020, 20, 12921 CrossRef CAS.
- I. Barnes, K. H. Becker and N. Mihalopoulos, J. Atmos. Chem., 1994, 18, 267 CrossRef CAS.
- J. G. Calvert, R. Atkinson, J. A. Kerr, S. Maldronich, G. K. Moortgat, T. J. Wallington and G. Yarwood, The Mechanisms of Atmospheric Oxidation of the Alkenes, Oxford University Press, New York, 2000 Search PubMed.
- D. J. Stewart, S. H. Almabrok, J. P. Lockhart, O. M. Mohamed, D. R. Nutt, C. Pfrang and G. Marston, Atmos. Environ., 2013, 70, 227 CrossRef CAS.
- A. W. Turnipseed, P. C. Andersen, C. J. Williford, C. A. Ennis and J. W. Birks, Atmos. Meas. Tech., 2017, 10, 2253 CrossRef CAS.
- E. J. Dunlea, S. C. Herndon, D. D. Nelson, R. M. Volkamer, B. K. Lamb, E. J. Allwine, M. Grutter, C. R. Ramos Villegas, C. Marquez, S. Blanco, B. Cardenas, C. E. Kolb, L. T. Molina and M. J. Molina, Atmos. Chem. Phys., 2006, 6, 3163 CrossRef CAS.
- E. J. Williams, F. C. Fehsenfeld, B. T. Jobson, W. C. Kuster, P. D. Goldan, J. Stutz and W. A. McClenny, Environ. Sci. Technol., 2006, 40, 5755 CrossRef CAS PubMed.
- M. Fiedrich, R. Kurtenbach, P. Wiesen and J. Kleffmann, Atmos. Environ., 2017, 165, 57 CrossRef CAS.
- M. P. Gallego-Iniesta, B. Cabañas, S. Salgado, E. Martínez and P. Martín, Atmos. Environ., 2014, 90, 133 CrossRef.
- C. Pfrang, M. D. King, C. E. Canosa-Mas, M. Flugge and R. P. Wayne, Atmos. Environ., 2007, 41, 1792 CrossRef CAS.
- M. R. McGillen, A. T. Archibald, T. Carey, K. E. Leather, D. E. Shallcross, J. C. Wenger and C. J. Percival, Phys. Chem. Chem. Phys., 2011, 13, 2842 RSC.
- I. W. M. Smith and A. R. Ravishankara, J. Phys. Chem. A, 2002, 106, 4798 CrossRef CAS.
- A. Mellouki, G. Le Bras and H. Sidebottom, Chem. Rev., 2003, 103, 5077 CrossRef CAS PubMed.
- M. D. King, C. E. Canosa-Mas and R. P. Wayne, Phys. Chem. Chem. Phys., 1999, 1, 2231 RSC.
- C. Pfrang, M. D. King, C. E. Canosa-Mas and R. P. Wayne, Atmos. Environ., 2006, 40, 1170 CrossRef CAS.
- C. Pfrang, M. D. King, C. E. Canosa-Mas and R. P. Wayne, Atmos. Environ., 2006, 40, 1180 CrossRef CAS.
- C. Pfrang, M. D. King, M. Braeckevelt, C. E. Canosa-Mas and R. P. Wayne, Atmos. Environ., 2008, 42, 3018 CrossRef CAS.
- B. E. Rossiter and N. M. Swingle, Chem. Rev., 1992, 92, 771 CrossRef CAS.
- R. Criegee, Angew. Chem., 1975, 87, 765 CrossRef CAS.
- D. Grosjean, E. L. Williams, II and E. Grosjean, Environ. Sci. Technol., 1993, 27, 830 CrossRef CAS.
- Y. Ren, B. Grosselin, V. Daële and A. Mellouki, Faraday Discuss., 2017, 200, 289 RSC.
- R. W. Taft, J. Am. Chem. Soc., 1952, 74, 3120 CrossRef CAS.
- S. Ehrenson, R. T. C. Brownlee and R. W. Taft, Prog. Phys. Org. Chem., 1973, 10, 1 CAS.
- O. Exner, J. Phys. Org. Chem., 1999, 12, 265 CrossRef CAS.
- M. R. McGillen, M. Ghalaieny and C. J. Percival, Phys. Chem. Chem. Phys., 2011, 13, 10965 RSC.
- E. V. Avzianova and P. A. Ariya, Int. J. Chem. Kinet., 2002, 34, 678 CrossRef CAS.
| This journal is © the Owner Societies 2021 |