On the molecular basis of H₂O/DMSO eutectic mixtures by using phenol compounds as molecular sensors: a combined NMR and DFT study

Abstract

NMR and DFT studies of phenol compounds as molecular sensors were carried out to investigate H₂O/DMSO eutectic mixtures at a molecular level. The experimental ¹H NMR chemical shifts of the OH groups, δ_exp(OH), of phenol, paracoumaric acid, and vanillic acid show maximum deshielding and, thus, hydrogen bond interactions in the range of mole fractions 0.20 < χ(DMSO) < 0.33. In the mole fractions χ(DMSO) < 0.2, a progressive decrease in δ_exp(OH) was observed which demonstrates a decrease in hydrogen bond interactions at infinite dilution in H₂O, despite the increase in the number of available hydrogen bond acceptor and donor sites. DFT calculated δ_calc(OH) of minimum energy solvation clusters were shown to be in reasonable agreement with the pattern in experimental δ_exp(OH) data. The chemical shift deshielding and, thus, increased hydrogen bond interactions in the natural product + DMSO + nH₂O (n = 2, 3) solvation clusters, relative to complexes in DMSO or H₂O solutions, cannot be attributed to a single structural parameter of the cooperative interactions between H₂O and DMSO molecules with the phenol OH groups of the natural products. The minimum energy conformers of phenol compounds + 2H₂O + DMSO complexes are in excellent agreement with a recent low temperature neutron diffraction experiment of 3D₂O + DMSO and demonstrate a general structural motif of solvation complexes. The combined use of ¹H NMR and DFT studies with emphasis on δ(OH) of phenol compounds, as molecular sensors, can provide an effective method for the study of solute–solvent interactions at the atomic level.

---

Introduction

Several mixtures of water with organic solvents show properties deviating from linearity, such as freezing point, density, viscosity, and adiabatic and isothermal compressibility.¹ Typical examples are dimethyl sulfoxide (DMSO), glycerol, and several other hydrophilic non-electrolytes, which protect several types of cells from damage during freezing and thawing, allowing them to be stored for very long periods at low temperatures.² This was attributed to the prevention of damaging crystal formation, and reduction of the concentration of electrolytes during freezing.^3,4 Recently a new generation of deep-eutectic solvents has emerged as promising green media for multiple applications, including catalysis, synthesis, extraction and separation processes.^5–11 Hydrogen bonding was identified as the main driving force of this phenomenon. In general, the strength of the hydrogen bonds can be correlated with the phase-transition temperature stability and solvent properties of the respective mixtures.⁹

For a system consisting of water and DMSO, extreme deviation from additivity was observed. At a mole fraction χ(DMSO) ≃ 0.33, a very low freezing point was measured (−140 °C). A stable DMSO/H₂O (1 : 2) cluster was suggested to be responsible for this unusually low melting point.¹² Each such subunit is rather loosely hydrogen bounded to the next subunit, thus, resulting in an overall structure that prevents crystallization. Further research revealed the formation of a rather complex phase diagram, and the dominance of stable DMSO/H₂O (1 : 3) clusters.¹³

Numerous experimental and theoretical studies have been reported on DMSO/water aqueous mixtures including neutron scattering,^14,15 investigation of the structure and dynamics of hydrogen bonding,¹⁶ solvation dynamics and vibrational relaxation.¹⁷ MD simulations at ambient temperature have been carried out to evaluate three models of pure liquid DMSO and in DMSO/H₂O mixtures.¹⁸ Statistical analysis of the hydrogen bond network revealed the presence of DMSO + 2H₂O and not DMSO + 3H₂O complexes. MD simulation estimated two regions of co-solvent DMSO–water clusters: χ(DMSO) = 0.12–0.17 and χ(DMSO) = 0.27–0.35. In the second region, there is an anomalous solvation trend observed due to high viscosity while in the first region the solvation increases due to the formation of strong hydrogen bonded DMSO/H₂O (1 : 2) complexes.¹⁹ DFT and polarizable force field have been utilized to investigate energetic and structural properties of DMSO–water clusters.²⁰ Quantum chemical studies were also utilized to investigate inter-cluster interaction modes of the freezing behavior, particularly of DMSO/H₂O (1 : 3) clusters.²¹ Water dynamics in H₂O/DMSO binary mixtures were studied with the use of polarization selective pump–probe experiments, 2D IR vibrational echo spectroscopy and IR absorption spectroscopy.²² IR spectroscopy of the S=O stretching mode combined with MD and quantum chemistry models were used to quantify hydrogen-bond populations in DMSO/H₂O mixtures.²³ MD studies of a DMSO/H₂O (1 : 3) cluster using the AMBER force field suggested a value of ∼2.89 ± 0.11 water molecules around each DMSO molecule.²⁴ Nevertheless, the driving forces behind non-covalent interactions in hydration of DMSO which is a dipolar aprotic solvent with both hydrophilic and hydrophobic properties, are not sufficiently understood.²⁵

The phenols are major constituents of many biological and naturally occurring compounds and are ubiquitous in the plant and animal kingdom. Interestingly, around 7% of the current drugs contain phenol groups. Furthermore, it is well known that experimental ¹H NMR chemical shifts, δ_exp(OH), of phenol –OH groups are very sensitive to OH⋯O hydrogen bond interactions.^26–32 Linear correlation between X-ray diffraction r(O⋯O) distances and δ_exp(OH) ¹H NMR chemical shifts was suggested for a variety of β-diketone enol compounds with intramolecular O–H⋯O hydrogen bonds.³³ A linear relationship has also been presented between δ_exp(OH) and H⋯O distances, determined from neutron diffraction.³⁴ Very good linear correlations between experimental and computed δ(OH) ¹H NMR chemical shifts and between hydrogen bond distances O⋯H(O) and δ(OH) have been suggested by employing a variety of quantum chemical methods.^35–42

The objective of the present study was to address three important issues. First to investigate the importance of hydrogen bonds in DMSO/H₂O eutectic mixtures by using, as molecular sensors, phenol (Ph, 1), paracoumaric acid (PCA, 2), and vanilic acid (VA, 3) (Fig. 1). As discussed above, δ(OH) of phenol compounds are very sensitive to hydrogen bonding interactions and, furthermore, they are significantly deshielded relative to the chemical shifts of H₂O. Overlapping, therefore, with the strong H₂O peak can be avoided which results in accurate δ_exp(OH) values, contrary to the case of e.g., alcohol type OH groups. Second, to utilize the agreement between experimental and DFT computed ¹H NMR chemical shifts of phenol OH groups as a tool for investigating solute–solvent interactions and accurate structural models at the atomic level. Third to investigate whether there is a general structural pattern of phenol compound + (2, 3) H₂O + DMSO solvation complexes. The molecules selected are secondary metabolites derived from plants and contain a single phenol OH group. Compounds with multiple phenol OH groups were not used in order to avoid strong overlapping of the resonances and, thus, uncertainties in the determination of the chemical shifts. Phenol (1), occurs in the essential oil from tobacco leaves (Nicotiannatabacum, Solanaceace) and pine needles (Pinus Sylvestris, Pinaceae)⁴³ and has the ability to encounter the gut microbes.⁴⁴ Paracoumaric acid (2) was found in many plants, such as plumbaginaceae's root, leaf and flower,⁴⁵ and has been used to treat diabetes, hypertension and cardiovascular diseases.⁴⁶ Vanillic acid has been isolated from origanum vulgare and acts as anti-melanogenesis agent.⁴⁷

Fig. 1 Chemical structures of the compounds used in the present work: phenol, Ph(1), paracoumaric acid, PCA(2), and vanillic acid, VA(3).

Results and discussion

NMR spectroscopy

The feasibility of obtaining high resolution ¹H NMR resonances of phenol OH groups was demonstrated by the use of dry non-protic solvents, addition of acids, such as trifluoracetic acid (TFA), and or by decreasing the temperature.^29,48,49 Solvents with significantly different dielectric constants, solvation, and hydrogen bonding ability were shown to induce large ¹H NMR chemical shift differences, and that the solvation state of the phenol OH group is a key factor in determining the value of δ_exp(OH). Solvent effects, therefore, on δ_exp(OH) have been used as a direct measurement of solvation changes and inter- and intramolecular hydrogen bond interactions.^31,36,49

The use of ¹H NMR of hydroxyl protons in H₂O or H₂O/organic solvent mixtures, however, presents experimental challenges due to chemical exchange among hydroxyl protons, and protic solvents. Fig. 2(Aa) illustrates the OH ¹H NMR spectral region of (1) for various mole fractions, χ(DMSO), of DMSO/H₂O mixtures at 300 K. For mole fractions χ(DMSO) = 1–0.35 relatively sharp resonances were observed which allowed the accurate determination of chemical shifts. A linear correlation of δ_exp(OH) vs. χ(DMSO) was observed for χ(DMSO) ≥ 0.35 which shows an increase in deshielding and, thus, in hydrogen bond interactions upon increasing the concentration of H₂O. This is to be expected since an increasing number of water molecules will increase the number of available sites of hydrogen bond acceptors, and donors. In the range of mole fractions 0.2 ≤ χ(DMSO) ≤ 0.33, a broad maximum of δ_exp(OH) and, thus, in hydrogen bond strength was observed. This range of mole fractions corresponds to mole ratios of H₂O/DMSO of 2/1–4/1 (Table S1, ESI†). For mole fraction χ(DMSO) < 0.2, a progressive decrease in δ(OH) was observed which demonstrates a decrease in hydrogen bond interactions at infinite dilution in H₂O. The OH resonance at mole fractions χ(DMSO) < 0.1 cannot be distinguished from the baseline.

Fig. 2 Selected ¹H NMR spectra of the OH resonance (a), and δ(OH) (b) of Ph(1), as a function of the mole fraction, χ(DMSO), of DMSO/H₂O mixtures at 300 K (A), 280 K (B) and 270 K (C). The chemical shift intercepts, δ_interc, of the linear correlations for χ(DMSO) ≥ 0.35, and the chemical shift differences Δδ = δ_interc − δ(χ(DMSO) = 1), are the following: T = 300 K, δ_interc = 9.89 ppm, Δδ = 0.52 ppm; T = 280 K, δ_interc = 10.08 ppm, Δδ = 0.63 ppm; T = 270 K, δ_interc = 10.18 ppm, Δδ = 0.65 ppm. For χ(DMSO) > 0.88 in B(b) and χ(DMSO) > 0.83 in C(b), the solutions were frozen, therefore, OH chemical shifts were obtained through extrapolation of the linear dependence of δ(¹H) vs. T in the temperature range of 292–318 K.

Similar experiments were performed at 280 K and 270 K (Fig. 2(Ba) and (Ca)) in order to reduce the proton exchange rate and, thus, linewidths which would allow a better definition of the OH chemical shifts for mole fractions χ(DMSO) < 0.3. For mole fractions χ > 0.88 and 0.83 the solutions were frozen at 280 K and 270 K, respectively, therefore the OH chemical shifts were obtained through extrapolation of the linear dependence of δ_exp(OH) vs. T³¹ in the temperature range of 292–318 K. By decreasing the temperature, the proton exchange is reduced, however, even at 270 K the resonances are still very broad which prohibit accurate estimation of the chemical shifts for χ(DMSO) ≤ 0.1.

From the above it is evident that, in the three temperatures investigated, δ_exp(OH) values strongly deviate from linearity for χ(DMSO) < 0.35 and the extrapolated value of δ_exp(OH) at infinite dilution in H₂O is smaller than that in the range of mole fractions 0.2 ≤ χ(DMSO) ≤ 0.33. This demonstrates weaker hydrogen bond interactions at infinite dilution in H₂O, despite the increase in the available hydrogen bond acceptor and donor sites, provided that δ_exp(OH) is not affected by proton exchange. Assuming that the spin ½ nucleus, without J coupling, jumps instantaneously from one site to the other, then, the rate constant τ_OH⁻¹ is the probability of the phenol OH nucleus jumping per unit time and τ_H2O⁻¹ is that of the H₂O site. If the exchange is slow, that is when τ_OH⁻¹, τ_H2O⁻¹ ≪ |ν_OH − ν_H2O|, then, the line shapes reduce to two Lorentzian lines with maxima at ν_OH, the resonance frequency of the phenol OH site, and ν_H2O, the resonance frequency of the H₂O, with intensities P_OH and P_H2O and widths τ_OH⁻¹ and τ_H2O⁻¹. In this limit the only effect of the exchange is to produce a life-time broadening.^50,51 As the exchange gets more rapid and τ_OH⁻¹, τ_H2O⁻¹ become comparable with ν_OH − ν_H2O, then, the peaks at ν_OH and ν_H2O move towards each other. Since the natural line width, especially at low temperatures, is dominated by field inhomogeneity broadening, it appears plausible to extract it from the internal reference signal of DSS and subtract it from the exchange-broadened lines, at a given temperature, using the equation τ_OH⁻¹ = Δν_1/2(OH) − Δν_1/2(DSS) where Δν_1/2(OH) and Δν_1/2(DSS) are the linewidths of the OH group and DSS, respectively.⁵⁰ Tables S2 and S3 (ESI†) show that in all cases Δν/τ_OH⁻¹ > 10 which demonstrates that the slow exchange regime τ_OH⁻¹ ≪ |ν_OH − ν_H2O| is fulfilled and no effect of chemical exchange on δ_exp(OH) is expected. The minor effect of increasing the water content on τ_OH⁻¹, for 0.2 < χ(DMSO) < 0.4 (Table S3 in ESI†) can be attributed to increased hydrogen bonding interactions of Ph(1) + nH₂O + DMSO (n = 2–4) subunits, which are loosely bound to each other, thus, resulting in reduced proton exchange (see also discussion on DFT calculations).

Fig. 3 illustrates the OH ¹H NMR spectral region and correlation of δ_exp(OH) vs. χ(DMSO) of PCA(2) at 300 K, 280 K and 270 K. The resulting linewidths were found to be broader, than those obtained with Ph(1). This can be attributed to the presence of the carboxyl group which increases proton exchange rate constant and, thus, linewidths. For mole fractions χ(DMSO) = 1–0.35, a linear correlation of δ(OH) vs. χ(DMSO) is evident. In the range of mole fractions 0.20 ≤ χ(DMSO) ≤ 0.33, a broad maximum of δ(OH) was observed. Since the slow exchange regime τ_OH⁻¹ ≪ |ν_OH − ν_H2O| is fulfilled (Table S4, ESI†), it can be concluded that the broad maximum of δ(OH) corresponds to a maximum in hydrogen bonding interactions, as in the case of Ph(1). Again, the extrapolated value of δ_exp(OH) at infinite dilution in H₂O is smaller than that in the region of the mole fractions 0.20 ≤ χ(DMSO) ≤ 0.33. Similar behavior has been observed for VA(3) (Fig. S1 and Table S5, ESI†). The resulting linewidths were found to be broader than in the case of Ph(1) due to the presence of the carboxyl group which enhances proton exchange rate constants. Nevertheless, again a broad maximum at χ(DMSO) = 0.35–0.2 was observed. The OH resonance at mole ratios χ(DMSO) < 0.12 cannot be distinguished from the baseline, therefore, the extrapolated value of δ_exp(OH) at infinite dilution in H₂O could not be obtained accurately.

Fig. 3 Selected ¹H NMR spectra of the OH resonances (a), and δ(OH) (b) of paracoumaric acid (2), as a function of the mole fraction, χ(DMSO), of DMSO/H₂O mixtures at 300 K (A), 280 K (B) and 270 K (C). The chemical shift intercepts, δ_interc, of the linear correlations for χ(DMSO) ≥ 0.35, and the chemical shift differences Δδ = δ_interc − δ(χ(DMSO) = 1), are the following: T = 300 K, δ_interc = 10.62 ppm, Δδ = 0.60 ppm; T = 280 K, δ_interc = 10.72 ppm, Δδ = 0.64 ppm; T = 270 K, δ_interc = 10.92 ppm, Δδ = 0.73 ppm. For χ(DMSO) > 0.90 in B(b) and χ(DMSO) > 0.80 in B(c), the solutions were frozen, therefore, OH chemical shifts were obtained through extrapolation of the linear dependence of δ(¹H) vs. T in the temperature range of 292–318 K.

DFT calculations

It has been demonstrated that the calculated phenolic OH ¹H NMR chemical shifts, δ_calc(OH), using the conductor-like polarizable continuum model (CPCM), deviate significantly from the experimental values, especially in the case of solvents having high dielectric constants and hydrogen bond strengths.³⁵ This is due to the fact that this model is the quantum chemical formulation of the Onsager reaction field model for bulk solvent effects which does not include specific solute–solvent interactions.^52,53 In contrast, the use of discrete phenol + solvent complexes results in an excellent agreement between the calculated OH chemical shifts and the experimental values.^35,37,42

The present computational study was performed by using the Gaussian 09 with the DFT method⁵⁴ with the structures optimized in the gas phase by using the standard functional B3LYP as well as the APFD with corrections for dispersion interactions, with the 6-31+G(d) basis set. The ¹H NMR chemical shifts were calculated with the GIAO (Gauge-Independent Atomic Orbital) and CSGT (Continuous Set of Gauge Transformations)⁵⁵ methods by using the B3LYP/6-311+G(2d,p) level in the gas phase.

The optimized structures of the phenol molecules with various discrete water and DMSO molecules, were obtained successively starting with the phenol type molecules by adding various numbers of water molecules followed by DMSO molecules in various possible positions, in such a way that they act either as donors or acceptors. The resulting molecular geometries were verified as energy minima on the potential energy surface (PES) by performing frequency calculations at the same level (zero imaginary frequencies). Four solvation clusters were examined for each of the three natural products of Fig. 1: (i) with a single solvation molecule of DMSO, (ii) with DMSO + 2H₂O, (iii) with DMSO + 3H₂O, and (iv) with 3H₂O. In the case of VA(3), due to the proximity of hydroxy and methoxy groups at the ortho position, the importance of intramolecular hydrogen bonding was investigated also in VA + nH₂O (n:1, 2) solvation clusters.

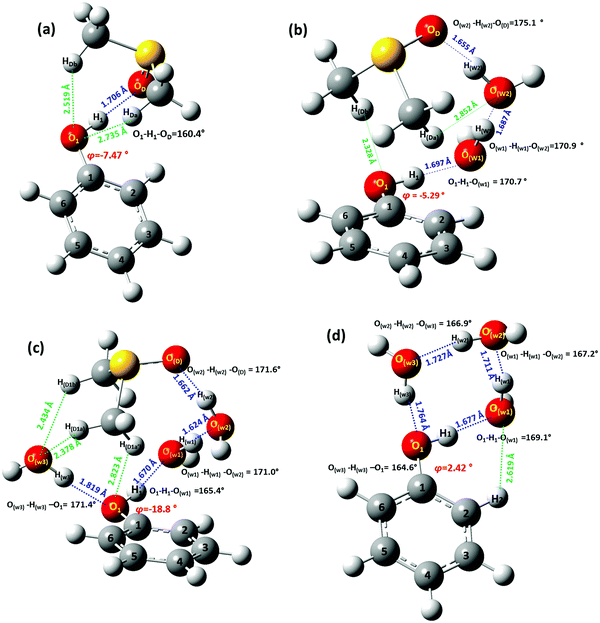
Due to the existence of different configurations at each mole ratio, it is necessary to identify the key hydrogen bond interactions, particularly in the minimum energy configurations. Selected structural and conformational properties of Ph(1) + solvent complexes, energy minimized using the APFD/6-31+G(d) and B3LYP/6-31+G(d) methods in the gas phase, are shown in Fig. 4 and Fig. S2, (ESI†) respectively. The minimum energy configuration of Ph(1) with a single molecule of DMSO (Fig. 4) is characterized by a rather strong intermolecular hydrogen bond of O₁–H₁⋯O_D = 1.706 Å and an angle O₁–H₁⋯O_D = 160.4°. These values are comparable to those found for the phenol OH⋯DMSO intermolecular hydrogen bond interaction in the natural product emodin.³⁸ The torsion angles O₁–H₁⋯O_D–S, and C₁–O₁–H₁⋯O_D were found to be 10.26° and 68.37°, respectively, which demonstrate a non-planar arrangement. It can be noted the long-range interactions of the CH₃ groups of DMSO with O₁ (O₁⋯H_Da = 2.735 Å and O₁⋯H_Db = 2.519 Å).

Fig. 4 Minimum energy structures of Ph (1) + DMSO (a), (1) + 2H₂O + DMSO (b), (1) + 3H₂O + DMSO (c), (1) + 3H₂O (d) solvation complexes, with energy minimization using the APFD/6-31+G(d) method in the gas phase.

In the minimum energy solvation complex Ph + 2H₂O + DMSO, a water molecule (W₁) is hydrogen bonded with the OH group of Ph (H₁⋯O_w1 = 1.697 Å and O₁–H₁⋯O_w1 = 170.7°) (Fig. 4b). W₁ is hydrogen bonded with the second molecule of water (W₂) (O_w2⋯H_w1 = 1.687 Å and O_w2⋯H_w1–O_w1 = 170.9°). W₂ is hydrogen bonded with the DMSO molecule (H_w2⋯O_D = 1.655 Å and O_w2–H_w2 ⋯O_D = 175.1°). This preferential coordination of the DMSO molecule is stabilized also because of secondary interactions of the methyl groups with the OH group of Ph (H_Db⋯O₁ = 2.328 Å) and the water molecule W₂ (H_Da⋯O_w2 = 2.852 Å).

In the minimum energy configuration of Ph + 3H₂O + DMSO solvation cluster (Fig. 4c), two molecules of water, W₁ and W₃, are hydrogen bonded with the OH group of Ph (W₁: O_w1⋯H₁ = 1.670 Å and O_w1⋯H₁– O₁ = 165.4°; W₃: H_w3⋯O₁ = 1.819 Å and O_w3–H_w3⋯O₁ = 171.4°). W₁ is also hydrogen bonded with W₂ (H_w1⋯O_w2 = 1.624 Å and O_w1– H_w1⋯O_w2 = 171.0°). W₂ is also hydrogen bonded with DMSO (H_w2⋯O_D = 1.662 Å and O_w2– H_w2 ⋯O_D = 171.6°). It can be noted that the observed coordination of DMSO is stabilized also because of secondary interactions with the water molecule W₃ (H_D1b⋯O_w3 = 2.434 Å and H_D1a⋯O_w1 = 2.378 Å) and the OH group of Ph (H_D1a′⋯O₁ = 2.823 Å).

The minimum energy configuration of the Ph + 3H₂O solvation cluster is shown in Fig. 4d. The three water molecules and the OH group of Ph are hydrogen bonded in a cyclic order with hydrogen bond lengths in the range of 1.677–1.764 Å and hydrogen bond angles 164.6°–169.1°.

Selected structural and conformational properties of Ph(1) + solvent complexes with energy minimization using the B3LYP functional with the 6-31+G(d) basis set are shown in Fig. S2 (the ESI†). The hydrogen bond properties of the Ph + DMSO complex are very similar to those obtained by using the APFD functional. There are minor differences in bond angles and torsion angles; the hydrogen bond lengths are invariably shorter using the APFD functional due to the empirical dispersion correction term for noncovalent intermolecular interactions (Fig. 4 and Fig. S2, ESI†).

Table 1 shows calculated, δ_calc(OH) ¹H NMR chemical shifts of Ph + DMSO, Ph + 2H₂O + DMSO, Ph + 3H₂O + DMSO, and Ph + 3H₂O solvation complexes, with energy minimization at the B3LYP/6-31+G(d) and APFD/6-31+G(d) levels. In practice, the various configurations of each solvation complex that exist within a 0.0 to 3.0 kcal mol⁻¹ Gibbs energy window, can contribute to the overall computational chemical shift. For a given solvation species of Table 1 a Boltzmann analysis was performed in order to determine the relative contribution of each configuration to the overall computational chemical shift, δ_calc,_Wg, using the equation^56,57

where i and j are configurations of a given solvation complex, G is the Gibbs energy of a particular configuration, R is the universal gas constant, and T is 298 K.

Table 1 Computed ¹H NMR chemical shifts, ppm, of various configurations of different molecular cluster compositions of Ph(1), in the gas phase, δ_calc,g, relative Gibbs ΔG values, kcal mol⁻¹, and experimental chemical shifts, δ_exp, with energy minimization at the B3LYP/6-31+G(d), and APFD/6-31+G(d) levels with NMR calculations at the GIAO (A) and CSGT (B) level. δ_calc,Wg are the ¹H NMR chemical shifts in the gas phase of various solvation configurations, weighted by the respective Boltzmann factors

Composition of solvation clusters	B3LYP/6-31+G(d)					APFD/6-31+G(d)
	ΔG	δ calc,g (ppm)	δ calc,Wg (ppm)	δ calc,g (ppm)	δ calc,Wg (ppm)	ΔG	δ calc,g (ppm)	δ calc,Wg (ppm)	δ calc,g (ppm)	δ calc,Wg (ppm)	δ exp
	(A) GIAO			(B) CSGT		(A) GIAO			(B) CSGT
a Denotes that H2O molecules are hydrogen bonded with the OH group of Ph(1). b Denotes that the DMSO molecule is hydrogen bonded with the OH group of Ph(1).
Ph + DMSO	0.33	8.61	8.81	7.65	7.90	0.00	9.69	9.35	8.93	8.66	9.53
Ph + DMSO	0.00	9.02		8.15		1.11	9.07		8.43
Ph + 2H2O + DMSO^a	0.00	10.50	10.41	9.93	9.76	0.00	10.84	10.84	10.29	10.27	9.99
Ph + 2H2O + DMSO^a	1.46	9.15		8.47		1.76	9.52		8.93
Ph + 2H2O + DMSO^a	1.32	10.71		10.05		2.11	11.45		10.85
Ph + DMSO + 2H2O^b	2.66	9.11		8.59		2.95	10.09		9.51
Ph + DMSO + 2H2O^b	0.57	10.19		9.57		1.28	11.31		10.64
Ph + DMSO + 3H2O^b	5.50	10.23	10.19	9.84	9.84	2.65	11.67	11.19	11.21	10.78	10.00
Ph + 3H2O + DMSO^a	0.00	11.19		9.84		0.00	11.18		10.78
Ph + 3H2O	0.00	10.43	9.95	9.79	9.87	0.12	11.14	11.11	10.46	10.44	9.91
Ph + 3H2O	0.73	8.32		10.14		0.00	11.08		10.42

---

The δ_calc(OH) ¹H NMR chemical shifts by the GIAO method, weighted by the respective Boltzmann factors (Table 1), δ_calc,Wg, were aligned in accord to the tendencies of the experimental chemical shifts. Thus, a maximum in the chemical shift was obtained with the Ph + 3H₂O + DMSO solvation cluster, and a small reduction in the chemical shift of the Ph + 3H₂O solvation cluster. By using the CSGT method, the Ph + 3H₂O + DMSO solvation cluster has a slightly smaller chemical shift (9.84 ppm) than the Ph + 3H₂O cluster (9.87 ppm), contrary to the experimental data. With minimization of the structures at the APFD/6-31+G(d) level, the calculated OH ¹H NMR chemical shifts, for both the GIAO and CSGT methods, weighted by the respective Boltzmann factors (Table 1), δ_calc,Wg, were aligned in accord to the tendencies of the experimental chemical shifts, δ_exp. Comparison of the Ph + 3H₂O and Ph + 3H₂O + DMSO solvation complexes using both B3LYP and APFD functionals shows that: (i) the incorporation of the DMSO molecule increases the size of the cycling structure and (ii) the increase in the chemical shift in the Ph + 3H₂O + DMSO complex cannot be attributed to a single structural parameter of the cooperative interactions between H₂O and DMSO molecules with the phenol OH group.

Conformational analysis of PCA(2) has been performed with a variety of DFT methodologies by several groups.^58,59 Four minimum energy conformers A, B, C and D were obtained with PES calculations of the torsion angles C5–C4–C3–C2 and C3–C2–C1–O1a (Fig. 5). The global minimum energy conformer is A; conformer B, with energy very similar to that of A, has been observed in the X-ray crystal structure of the PCA.⁶⁰ The stronger intramolecular interaction between the electron lone pair of the carboxylic oxygen, =O1a, and the olefinic hydrogen, =C3–H, is responsible for the stabilization of conformers A and B vs. C and D. A similar stabilization is also observed for most of the configurations of the solvation complexes PCA + DMSO, PCA + 2H₂O + DMSO, PCA + 3H₂O + DMSO and PCA + 3H₂O.

Fig. 5 The four minimum energy conformers of PCA(2) in the gas phase with minimization at the APFD/6-31+G(d) level.

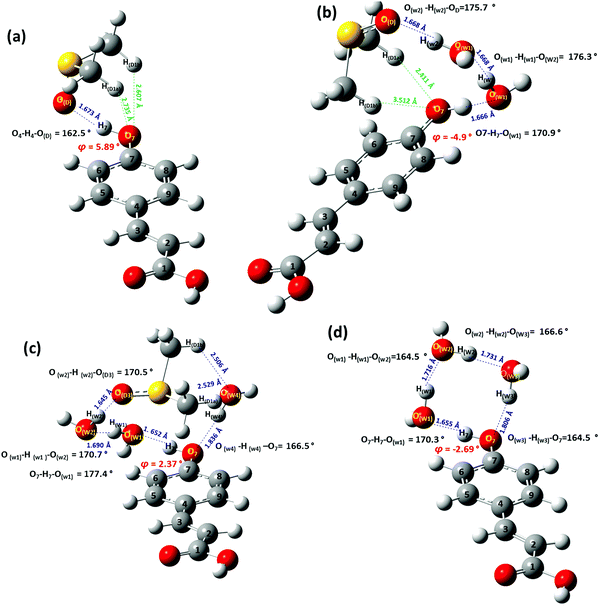
Selected structural and conformational properties of PCA + solvent complexes, using the APFD/6-31+G(d) and B3LYP/6-31+G(d) energy minimization methods, in the gas phase, are shown in Fig. 6 and Fig. S3 (the ESI†), respectively. The PCA + DMSO hydrogen bond interaction (SO_(D)⋯H₇ = 1.673 Å, O_(D)⋯H₇–O₇ = 162.5°) is very similar to that of the Ph + DMSO complex. Secondary interactions of the two methyl groups of DMSO with the phenol OH oxygen of PCA (H_D1a⋯O₇ = 2.735 Å and H_D1b⋯O₇ = 2.607 Å) are within the limits of the van der Waals radii definition.

Fig. 6 Minimum energy structures of PCA (2) + DMSO (a), (2) + 2H₂O + DMSO (b), (2) + 3H₂O + DMSO (c), (2) + 3H₂O (d) solvation complexes with energy minimization using the APFD/6-31+G(d) method in the gas phase.

In the PCA + 2H₂O + DMSO solvation complex, a water molecule (W₁) forms a hydrogen bond interaction with the OH group of PCA ((O₇)H₇⋯O_w1 = 1.666 Å and O₇–H₇⋯O_w1 = 170.9°). W₁ is, also, hydrogen bonded with the second molecule of water (W₂) (O_w2⋯H_w1 = 1.668 Å and O_w1–H_w1⋯O_w2 = 176.3°). W₂ is hydrogen bonded to the (S)O of the DMSO molecule (H_w2⋯O_D = 1.688 Å, O_w2–H_w2⋯O_D = 175.7°). It can be noted that this preferential coordination of the DMSO molecule is stabilized, also, because of secondary interactions H_D1a⋯O₇ = 2.411 Å, and H_D1b⋯O₇ = 3.512 Å (Fig. 6b).

In the PCA + 3H₂O + DMSO solvation cluster, two molecules of water, W₁ and W₃, are hydrogen bonded with the OH group of PCA (W₁: H₇⋯O_w1 = 1.652 Å and O₇–H₇⋯O_w1 = 177.4°; W₃: O₇⋯H_w3 = 1.836 Å and O₇⋯H_w3–O_w3 = 166.5°). W₁ is also hydrogen bonded to W₂ (H_w1⋯O_w2 = 1.690 Å and O_w1–H_w1⋯O_w2 = 170.7°). W₂ is also hydrogen bonded to DMSO (H_w2⋯O_D = 1.645 Å and O_w2–H_w2⋯O_D = 170.5 Å). It can be noted that this coordination of the DMSO is, furthermore, stabilized because of secondary interactions with the water molecule W₃ (H_D1b⋯O_w3 = 2.506 Å, H_D1a⋯O_w3 = 2.529 Å).

The minimum energy configuration of the PCA + 3H₂O solvation cluster is shown in Fig. 6d. The three water molecules and the OH group of the PCA molecule are hydrogen bonded in a cyclic order with hydrogen bond lengths in the range of 1.655 Å to 1.806 Å and hydrogen bond angles 164.5° to 170.3°.

Selected structural and conformational properties of PCA + solvent complexes, using the B3LYP/6-31+G(d) energy minimization method, in the gas phase, are shown in Fig. S3 (the ESI†). The hydrogen bond lengths are longer with the B3LYP functional, as in the case of phenol (1) + solvent complexes.

The calculated ¹H-NMR chemical shifts, δ_calc,g, of the four conformational states A, B, C and D (Fig. 5) and various solvation configurations of PCA, in the gas phase, are shown in Table 2. The ¹H NMR chemical shifts with the GIAO and CSGT methods, of the PCA + DMSO + 3H₂O and PCA + 3H₂O complexes, weighted by the respective Boltzmann factors, were aligned in accord to the tendencies of δ_exp, with energy minimization at the APFD/6-31+G(d) level. Similar tendencies were obtained at the B3LYP36-31+G(d)/CSGT level (Table 2). Comparison of the PCA + 3H₂O and PCA + 3H₂O + DMSO solvation complexes using both B3LYP and APFD functionals shows that: (i) the incorporation of the DMSO molecule increases the size of the cycling structure and (ii) the increase in the chemical shift in the PCA + 3H₂O + DMSO complex cannot be attributed to a single structural parameter of the cooperative interactions between H₂O and DMSO molecules with the PCA OH group.

Table 2 Computed ¹H NMR chemical shifts, ppm, of various configurations of different molecular cluster compositions of four conformational states (A, B, C and D, Fig. 5) of PCA (2) in the gas phase, δ_calc,g, relative Gibbs ΔG values, kcal mol⁻¹, and experimental chemical shifts, δ_exp, with energy minimization at the B3LYP/6-31+G(d), and APFD/6-31+G(d) levels with NMR calculations at the GIAO (A) and CSGT (B) level. δ_calc,Wg are the ¹H NMR chemical shifts in the gas phase of various conformational and solvation configurations weighted by the respective Boltzmann factors

B3LYP/6-31+G(d)						APFD/6-31+G(d)
Composition of solvation conformers^a	ΔG	δ calc,g (ppm)	δ calc,Wg (ppm)	δ calc,g (ppm)	δ calc,Wg (ppm)	ΔG	δ calc,g (ppm)	δ calc,Wg (ppm)	δ calc,g (ppm)	δ calc,Wg (ppm)	δ exp
	(A) GIAO			(B) CSGT		(A) GIAO			(B) CSGT
a For the definition of conformers A, B, C, and D see Fig. 5. b Denotes that H2O molecules are hydrogen bonded with the OH group of PCA. c Denotes that the DMSO molecule is hydrogen bonded with the OH group of PCA.
PCA+ DMSO conformer A	0.03	9.97	9.97	9.04	9.05	0.00	10.58	10.57	9.88	9.86	10.19
PCA+ DMSO conformer B	0.00	9.96		9.05		0.12	10.56		9.85
PCA + DMSO conformer C	0.78	9.98		9.06		0.84	10.58		9.87
PCA + DMSO conformer D	0.77	9.96		9.04		0.77	10.57		9.86
PCA + 2H2O + DMSO^b conformer A	0.00	11.37	11.35	10.76	10.73	0.12	11.68	11.65	11.13	11.09	10.64
PCA + 2H2O + DMSO^b conformer B	0.60	11.39		10.76		0.00	11.68		11.12
PCA + 2H2O + DMSO^b conformer C	0.59	11.37		10.75		0.73	11.69		11.13
PCA + 2H2O + DMSO^b conformer D	1.13	11.40		10.77		0.89	11.69		11.14
PCA + 2H2O + DMSO^b conformer A	2.34	9.97		9.28		2.42	10.29		9.65
PCA + 2H2O + DMSO^b conformer B	2.51	9.92		9.25		2.15	10.17		9.53
PCA + 2H2O + DMSO^b conformer C	3.02	9.99		9.25		2.42	10.19		9.51
PCA + 2H2O + DMSO^b conformer D	2.77	9.95		9.27		2.99	10.24		9.56
PCA + H2O + DMSO + H2O^b conformer A	2.04	11.62		11.00		2.69	12.24		11.74
PCA + H2O + DMSO + H2O^b conformer B	2.09	11.61		11.00		2.12	12.24		11.73
PCA + H2O + DMSO + H2O^b conformer C	2.54	11		11.00		3.33	12.21		11.72
PCA + H2O + DMSO + H2O^b conformer D	2.64	11.62		11.01		3.37	12.26		11.75
PCA + DMSO + 2H2O^c conformer A	4.93	10.58		9.81		3.83	11.61		11.00
PCA + DMSO + 2H2O^c conformer B	5.84	10.60		9.81		3.71	11.61		10.97
PCA + DMSO + 2H2O^c conformer C	6.93	10.65		10.06		4.60	11.59		10.98
PCA + DMSO + 2H2O^c conformer D	5.60	10.56		9.82		4.67	11.64		10.92
PCA +3H2O + DMSO^b conformer A	0.00	11.07	11.09	10.55	10.55	0.00	12.02	12.00	11.45	11.40	10.64
PCA +3H2O + DMSO^b conformer B	0.20	11.13		10.56		0.18	11.99		11.42
PCA +3H2O + DMSO^b conformer C	0.61	11.09		10.55		0.98	12.02		11.44
PCA +3H2O + DMSO^b conformer D	0.68	11.09		10.54		0.96	11.99		11.43
PCA + DMSO + 3H2O^c conformer A	3.45	10.84		10.26		4.59	10.61		9.98
PCA + DMSO + 3H2O^c conformer B	3.30	10.85		10.26		4.09	10.60		9.92
PCA + DMSO + 3H2O^c conformer C	3.83	10.84		10.27		5.34	10.59		9.94
PCA + DMSO + 3H2O^c conformer D	3.87	10.84		10.27		5.25	10.65		9.97
PCA + 3H2O conformer A	0.00	11.08	11.10	10.51	10.51	0.00	11.65	11.67	11.14	11.13	10.50
PCA + 3H2O conformer B	0.18	11.14		10.50		0.16	11.71		11.13
PCA + 3H2O conformer C	0.56	11.07		10.49		0.88	11.68		11.10
PCA + 3H2O conformer D	0.69	11.10		10.52		0.93	11.64		11.07

---

The proximity of hydroxyl and methoxy groups at the ortho position in VA(3) may result in the formation of intramolecular hydrogen bonds.^61,62 Thus, the X-ray structure determination of vanillic acid and theobromide co-crystal hydrate (VA·THBR·2 H₂O)^63,64 shows that the hydroxyl and methoxy groups of VA adopt an in-out conformation which results in the formation of an intramolecular hydrogen bond. A water molecule acts as a bifurcated acceptor to the OH group of VA (O–H⋯O(W₁) = 2.719(2) Å, H⋯O(W₁) = 1.859(3) Å and O–H⋯O(W₁) = 165(2)°) and to a second water molecule ((W₂) O–H⋯O(W₁) = 2.868(2) Å, H⋯O(W₁) = 2.064 Å and (W₂) O–H⋯O(W₁) = 157(3)°). The oxygen atom of the second water molecule forms also a hydrogen bond with the second hydrogen atom of the first H₂O in a ring motif. The X-ray structure determination of VA(3) and isonicotinamide hydrate (2VA·2INM·2H₂O)^63,64 shows that the hydroxyl and methoxy groups of VA adopt the out–out conformation with a water molecule playing a bridging role ((W) O–H⋯O(H)VA = 2.945(2) Å, H⋯O(H)VA = 2.296(2) Å and (W) O–H⋯O(H)VA = 133(2)°; (W) O–H⋯O(CH₃)VA = 3.051(2) Å, H⋯O(CH₃)VA = 2.243(3) Å and (W) O–H⋯O(CH₃)VA = 158(2)°). This water molecule also links two VA molecules.

Several solvation species of VA, including intra- and intermolecular hydrogen bonds were investigated (Fig. 7). Selected structural and conformational properties of VA(3) + solvent complexes with energy minimization using the APFD and B3LYP functionals with the 6-31+G(d) basis set are shown in Fig. S4 and S5 (the ESI†), respectively. In the minimum energy complex of vanillic acid + DMSO, the phenol OH hydrogen forms a bifurcated hydrogen bond with DMSO (H₄⋯O_D = 1.716 Å and O₄–H₄⋯O_D = 153.9°) and O₃ of the methoxy group (H₄⋯O₃ = 2.241 Å). Secondary interactions of the methyl groups of DMSO with the phenol OH group (H_D1a⋯O₄ = 2.695 Å and H_D1b⋯O₄ = 2.502 Å) contribute to the stability of this particular configuration. It can be noted that the torsion angle φ(C₃C₄O₄H₄) = −39.3°, strongly deviates from planarity.

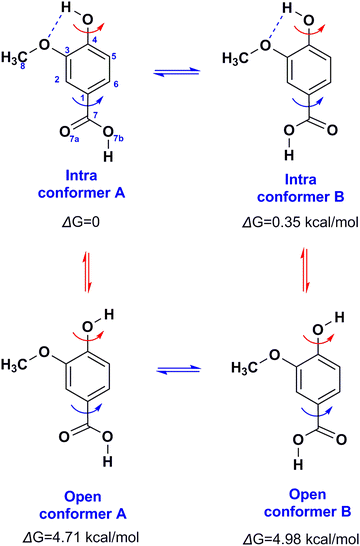Fig. 7 The four minimum energy conformers of VA in the gas phase with energy minimization at the B3LYP/6-31+G(d) level.

In the VA + 2H₂O + DMSO solvation complex (Fig. S4b, ESI†), the hydroxyl and methoxy groups adopt an anti-conformation. A water molecule (W₁) forms a hydrogen bond interaction with the OH group of VA (H₄⋯O_w1 = 1.689 Å and O₄–H₄⋯O_w1 = 165.0°). W₁ is hydrogen bonded with the second molecule of water (W₂) (O_w2⋯H_w1 = 1.685 Å and O_w1–H_w1⋯O_w2 = 176.1°). W₂ is hydrogen bonded with the S(O) of the DMSO molecule (H_w2⋯O_D = 1.659 Å and O_w2–H_w2⋯O_D = 173.4°). It can be noted that this preferential coordination of the DMSO molecule is stabilized also because of secondary interactions H_Da⋯O₄ = 2.628 Å and H_D2⋯O₃ = 2.413 Å (Fig. S4b, ESI†).

In the minimum energy configuration of the VA + 3H₂O + DMSO solvation cluster (Fig. S4c, ESI†), the hydroxyl and methoxy groups adopt an anti-conformation. Two molecules of water, W₁ and W₃, are hydrogen bonded with the OH group of VA (W₁: O_w1⋯H₄ = 1.680 Å and O_w1–H₄⋯O₄ = 168.8°; W₃: H_w3⋯O₄ = 1.936 Å and O_w3–H_w3⋯O₄ = 137.0°). W₁ is also hydrogen bonded with water molecule W₂ (H_w1⋯O_w2 = 1.659 Å and O_w1–H_w1⋯O_w2 = 176.1°). W₂ is also hydrogen bonded with DMSO (H_w2⋯O_D = 1.644 Å and O_w2–H_w2⋯O_D = 174.7°). The methyl groups of DMSO form secondary interactions with the water molecule W₃ (O_w3⋯H_D3b = 2.202 Å) and the methoxy group (O₃⋯H_D3a = 2.615 Å). The torsion angle φ(C₅C₄O₄H₄) = −8.43° is significantly reduced relative to that in the VA + DMSO complex.

In the minimum energy configuration of the VA + 3H₂O solvation cluster, the hydroxyl and methoxy groups adopt an anti-conformation (Fig. S4d, ESI†). The three water molecules and the OH group of VA are hydrogen bonded in a cyclic order with hydrogen bond lengths in the range of 1.589–1.763 Å and hydrogen bond angles 152.9°–164.2°. The water molecule W₃ forms a very short hydrogen bond with O₄ of VA (1.589 Å), however, the hydrogen bond angle O_w3–H_w3⋯O₄ strongly deviates from linearity (152.9°). The torsion angle φ(C₅C₆C₄O₄) = −14.5° is larger than that of the VA + 3H₂O + DMSO solvation cluster.

Selected structural and conformational properties of VA + solvent complexes with energy minimization using the B3LYP functional with the 6-31+G(d) basis set in the gas phase, are shown in Fig. S5 (the ESI†). The structures and hydrogen bond properties are very similar to those obtained by the use of APFD functional. The hydrogen bond lengths are longer and the φ torsion angles smaller by using the B3LYP functional.

Fig. S6 (ESI†) illustrates minimum energy structures of VA + 2H₂O and VA + H₂O complexes. In the VA + 2H₂O solvation cluster the hydroxyl and methoxy groups adopt anti-conformation as in the case of VA + 3H₂O. The two molecules of water and the OH group of VA are hydrogen bonded in a cyclic order with hydrogen bond lengths of 1.745–1.957 Å, which are significantly longer than those in the VA + 3H₂O complex. This results also in hydrogen bond angles which strongly deviate from linearity (138.2°–152.5°). In the VA + H₂O complex the hydroxyl and methoxy groups adopt an in-out conformation which results in a rather weak intramolecular hydrogen bond (O₃⋯H₄ = 2.376 Å). The water molecule W₁ plays a bridging role, forming a hydrogen bond interaction with the OH group (O_w1⋯H₄ = 1.759 Å and O_w1⋯H₄–O₄ = 167.7°) and the methoxy group of VA (H_w1⋯O₃ = 1.909 Å and O_w1–H_w1⋯O₃ = 136.6°).

From the above it can be concluded that in the case of VA + DMSO complexes the most stable configurations are those with an intramolecular hydrogen bond interaction (Table S6, ESI†). In the case of VA + 2H₂O + DMSO solvation complexes most of the open configurations are significantly more stable than those with intramolecular hydrogen bond interactions. Similarly, in VA + 3H₂O + DMSO solvation complexes the open configurations are the most stable with negligible population of the molecular clusters with intramolecular hydrogen bond interactions (Table S6, ESI†). The proximity of hydroxyl and methoxy groups in vanillic acid may result also in reduced solvent accessibility. Contrary to the case of VA + 3H₂O and VA + 2H₂O, low energy configurations of the VA + H₂O complex with intramolecular hydrogen bond interactions were obtained.

The computational ¹H NMR chemical shifts of the solvation complex VA + 3H₂O + DMSO, with energy minimization using the B3LYP/6-31+G(d) and the APFD/6-31+G(d) methods, weighted by the respective Boltzmann factors, δ_calc,wg, values were found to be smaller than those of the VA + 3H₂O complex for both the GIAO and CSGT methods in the gas phase. This is not in agreement with the tendencies of the experimental chemical shifts (Table S6, ESI†). Since the computational ¹H NMR chemical shifts of the VA + 2H₂O and VA + H₂O complexes are significantly smaller than those of the VA + 3H₂O + DMSO complex, very probably, in solution state, there is an equilibrium of various VA + nH₂O (n = 3–1) solvation species.

From the comparison of experimental and computational NMR chemical shifts of the phenol OH groups of the natural products of Fig. 1, it appears to be conclusive that hydrogen bond interactions in the solvation clusters of natural product + 3H₂O + DMSO are stronger than in DMSO or H₂O. The enhanced hydrogen bond interactions can be attributed to the significant cooperative nature of the interaction between the H₂O and DMSO molecules and the OH groups of the natural products.

Effects of higher Ph + nH₂O (n > 4) solvation clusters

Preliminary calculations of Ph(1), as a molecular sensor, in the presence of nineteen (19) discrete water molecules were performed using the semi empirical AM1 method. The H₂O molecules were distributed uniformly around the phenyl ring and the hydroxyl group (Fig. S8 in ESI†) which can act both as a hydrogen donor and acceptor. In order to increase the accuracy of the calculation the force constants and frequencies at every optimization step (by using the Opt = CalcAll keyword) were computed, since it is known that the calculation of frequencies defines the curvature of the Potential Energy Surface (PES). From the final optimized structure, the nine nearest to the hydroxyl group water molecules were chosen and reoptimized again using the AM1 methodology (Fig. S8(c) in ESI†). The next steps involved optimization of the Ph(1) molecule with the nearest 1, 3, 4 and 5 discrete water molecules, including also the complex with nine H₂O molecules, by using the DFT method and employing the B3LYP functional and the 6-31+G(d) basis set. Representative optimized structures are shown in Fig. S9 in ESI.† Fig. S10 in ESI† shows GIAO calculations (at the B3LYP/6-311+G(2d,p) level) of the OH chemical shifts of various Ph(1) + nH₂O (1–9) solvation clusters. The computational chemical shift of the Ph(1) + 3H₂O complex shows the best agreement with the experimental value and, thus, this molecular cluster is a good approximation of the structure of Ph(1) in aqueous solution.

Comparison with neutron diffraction data

Recently, neutron powder diffraction data have been reported⁶⁵ from a number a flash-frozen aqueous solutions of DMSO with mole fractions χ(DMSO) = 0.25–0.67. Three stoichiometric hydrates were obtained which were crystalized on warming between 175 K and 195 K. A DMSO + 3D₂O complex and two different polymorphs of DMSO + 2D₂O complexes have been identified. Of particular interest is the structure of DMSO + 3D₂O complex in an asymmetric unit, which has no structural analogue in the CSD database (Fig. 8). Two of the symmetry-non-equivalent water molecules O_W1 and O_W2 are involved in hydrogen bonding only with other water molecules. The third water molecule forms two hydrogen bonds with the DMSO oxygen and accepts one hydrogen bond via O_W2. Of particular interest are the H⋯O contacts between methyl hydrogens and both water and DMSO oxygen atoms which represent a significant fraction of the Hirshfeld surface area.⁶⁵ The water molecule W3 of the neutron powder diffraction structure is replaced by the phenol compounds in the (1,2,3) + 2H₂O + DMSO solvation complexes (Fig. 8). The hydrogen bond distances and hydrogen bond angles are very similar in all cases, which demonstrate a common structural motif of the solvation species. A main difference was found in the two H⋯O_W3 contacts of the methyl hydrogens of DMSO with W3 in the neutron diffraction study (2.561 Å and 3.245 Å, Fig. 8a) while those in the computational study are very similar and close to 2.5 Å (Fig. 8b–d). This can be attributed to the ability of W3 to from further hydrogen bond interactions with additional D₂O molecules which are not possible in the case of the aromatic OH group.

Fig. 8 Structural similarities of the DMSO + 3D₂O complex motif of the neutron powder diffraction data (a),⁶⁵ with the minimum energy structures of Ph(1) + 2H₂O + DMSO (b), PCA(2) + 2H₂O + DMSO (conformer D) (c) and VA(3) + 2H₂O + DMSO (d) with energy minimization using the B3LYP/6-31+G(d) method in the gas phase.

Experimental procedure

NMR experiments were performed on Bruker AVANCE III HD 400 and 500 spectrometers. Samples of the natural products were dissolved in 0.6 ml of mixtures of H₂O with DMSO-d₆ with solute concentration of ∼25 mM. 5 mm NMR tubes were used. In variable temperature NMR studies with solutions of various molar concentrations, the selection of the appropriate referencing process is of critical importance. For mobile isotropic media there are two main methods of referencing: (a) internal referencing, where the reference compound is added directly to the system under study and is almost invariably used for ¹H and ¹³C NMR. (b) External referencing, involving sample and reference contained separately in coaxial cylindrical tube. These methods have various advantages and disadvantages. For (a) the shielding of the reference nucleus depends on the solvent and on the concentration of both solute and reference owing to the effects of intermolecular interactions. The chemical shifts of 3-(trimethylsilyl) propane-1-sulfonate (DSS) in dilute aqueous and DMSO-d₆ solutions were found to be 0.0173 ppm and −0.0246 ppm, respectively, on the scale with TMS as zero.⁶⁶ In our study, these differences are very small, falling well below the anticipated range of solvents effects (Δδ ∼ 0.52 to 0.73 ppm of Fig. 2, 3 and Fig. S1 in ESI†). Furthermore, due to low molar concentrations of solutes (c = 25 mM) and DSS (c = 0.8 mM), intermolecular interactions would be expected to have negligible effects on chemical shifts. External reference procedures (b) generally require corrections arising from differences in bulk magnetic susceptibility between sample and reference. For the usual coaxial cylindrical arrangement, the correction for superconducting magnets is given by:

δ_true − δ_obs = ⅓(κ_sample − κ_reference)

where κ refers to the relevant volume susceptibility of the sample and reference. In our case the magnetic susceptibility corrections at room temperature of H₂O is −9.035 ppm and of DMSO-d₆ is −7.73 ppm, therefore, a correction of δ_true − δ_obs = 0.43 ppm is required which is comparable to the range of solvent effects (Δδ ∼ 0.52 to 0.73 ppm of Fig. 2, 3 and Fig. S1 in ESI†). Furthermore, it has been shown that in the case several binary mixtures of organic liquids the value of magnetic susceptibility is not an additive property because of the influence of various factors, such as intermolecular forces. This is especially the case for H₂O/DMSO mixtures which deviate from linearity and estimates for magnetic susceptibility at variable temperatures would require corrections for variations for solvent density which are not negligible.^67,68 It can, therefore, be concluded that the external reference procedure (b) has several disadvantages relative to internal procedure (a). The procedure (a), therefore, was utilized in the present study with standard DSS, δ(¹H) = 0.00 ppm. All spectra were acquired with an acquisition time of 2.1 s, relaxation delay of 5 s, 32 K data points and 90° pulse length.

Chemicals

Phenol (1), p-coumaric acid (2), and vanillic acid (3), were purchased from Sigma-Aldrich.

Computational methods

The computational study was performed by using the Gaussian 09 with the DFT method.⁵⁴ The structures were optimized by using two functionals, B3LYP and APFD, and the 6-31+G(d) basis set. The optimized structures of the phenol compounds with various discrete water and DMSO molecules were obtained successively starting with phenol (the sensor) and adding first various numbers of water molecules followed by DMSO in various possible positions in such a way that they act either as donors or acceptors. From the resulting structures, those having the lowest energies, were selected. The ¹H NMR chemical shifts were calculated with the GIAO and CSGT methods⁵⁵ by using the B3LYP/6-311+G(2d,p) level in the gas phase. Comparative studies using the CPCM^52,53 were not performed since in the case of mixed solvation complexes there is no appropriate continuum model. The computed geometries were optimized by performing frequency calculations at the same level (zero imaginary frequencies). DSS was optimized at the same levels of the theory and was the reference for computed ¹H NMR chemical shifts. The computational chemical shifts of DSS and TMS were found to be identical, in excellent agreement with a minor experimental chemical shift difference of 0.02 ppm.⁶⁸

Conclusions

This paper presents an extensive NMR and DFT analysis of hydrogen bonding interactions in H₂O/DMSO eutectic mixtures by using phenol OH groups of natural products as molecular sensors. The ¹H NMR chemical shifts of the OH groups are strongly dependent on specific solute–solvent interactions, demonstrating maximum hydrogen bonding interactions in the range of mole fractions χ(DMSO) = 0.33 to 0.20 for Ph(1) PCA(2), and VA(3). DFT calculated ¹H NMR chemical shifts of various solvation species were found to be in reasonable agreement with experimental chemical shifts even with computationally less demanding level of theory. The increased hydrogen bond interactions in the natural product + nH₂O (n = 2, 3) + DMSO solvation clusters, relative to complexes with DMSO or H₂O, cannot be attributed to a single structural parameter of the cooperative interactions between the phenol OH groups of the natural products with H₂O and DMSO molecules. The excellent agreement of the recent neutron powder diffraction data of a DMSO + 3D₂O complex⁶⁵ with our minimum energy conformers of [Ph(1), PCA(2), VA(3)] + 2H₂O + DMSO complexes demonstrates a common structural motif of the above solvation species. We would, therefore, expect that the combined use of ¹H NMR studies and DFT calculations of phenol OH groups will provide a very effective method for the structural and electronic description of solute–solvent interactions at an atomic level,⁶⁹ and more specific in the field of eutectic mixtures and ionic liquids.^70,71

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. D. Martin and H. G. Hauthal, Dimethylsulfoxid, Akademie-Verlag, Berlin DDR, vol. 190, 1971.
2. A. U. Smith, Biological Effects of Freezing and Supercooling, London, Edward, Arnold, 1961.
3. J. Farrant, Nature, 1965, 205, 1284–1287.
4. J. L. Chaytor, J. M. Tokarew, L. K. Wu, M. Leclere, R. Y. Tam, C. J. Capicciotti, L. Guolla, E. V. Moos, C. S. Findlay, D. S. Allan and R. N. Ben, Glycobiology, 2012, 22, 123–133.
5. A. P. Abbott, G. Capper, D. L. Davies, R. K. Rasheed and V. Tambyrajah, Chem. Commun., 2003, 70–71.
6. I. Mamajanov, A. E. Engelhart, H. D. Bean and N. V. Hud, Angew. Chem., Int. Ed., 2010, 49, 6310–6314.
7. H. Zhao, G. A. Baker and S. Holmes, Org. Biomol. Chem., 2011, 9, 1908–19016.
8. Y. Dai, G. J. Witkamp, R. Verpoorte and Y. H. Choi, Anal. Chem., 2013, 85, 6272–6278.
9. M. Francisco, A. van den Bruinhorst and M. C. Kroon, Angew. Chem., Int. Ed., 2013, 52, 3074–3085.
10. E. L. Smith, A. P. Abbott and K. S. Ryder, Chem. Rev., 2014, 114, 11060–11082.
11. B. Olivares, F. Martínez, L. Rivas, C. Calderón, J. M. Munita and P. R. Campodonico, Sci. Rep., 2018, 8, 14900.
12. R. N. Havemeyer, J. Pharm. Sci., 1966, 55, 851–853.
13. D. H. Rasmussen and A. P. MacKenzie, Nature, 1968, 220, 1315–1317.
14. A. K. Soper and A. Luzar, J. Chem. Phys., 1992, 97, 1320–1331.
15. A. K. Soper and A. Luzar, J. Phys. Chem., 1996, 100, 1357–1367.
16. A. Luzar and D. Chandler, J. Chem. Phys., 1993, 98, 8160–8173.
17. R. M. Stratt and M. Maroncelli, J. Phys. Chem., 1996, 100, 12981–12996.
18. A. Vishynyakov, A. P. Lyubartsev and A. Laaksonen, J. Phys. Chem. A, 2001, 105, 1702–1710.
19. D. Banik, N. Kundu, J. Kuchlyan, A. Roy, C. Banerjee, S. Ghosh and N. Sarkar, J. Phys. Chem., 2015, 142, 504–505.
20. Q. Zhang, X. Zhang and D. X. Zhao, J. Mol. Liq., 2009, 145, 67–81.
21. B. Kirchner and M. Reiher, J. Am. Chem. Soc., 2002, 124, 6206–6215.
22. D. B. Wong, K. P. Sokolowsky, M. I. El-Barghouthi, E. E. Fenn, C. H. Giammanco, A. L. Sturlaugson and M. D. Fayer, J. Phys. Chem. B, 2012, 116, 5479–5490.
23. K.-I. Oh, K. Rajesh, J. F. Stanton and C. R. Baiz, Angew. Chem., Int. Ed., 2017, 129, 11533–11537.
24. S. S. Stachura, C. J. Malajzuk and R. L. Mancera, J. Mol. Model., 2018, 24, 174.
25. B. Bagchi, Water in Biological and Chemical Processes: From Structure and Dynamics to Function, Cambridge University Press, 2013.
26. C. L. Perrin and J. B. Nielson, Ann. Rev. Phys. Chem., 1997, 48, 511–544.
27. R. J. Abraham and M. Mobli, Magn. Reson. Chem., 2007, 45, 865–877.
28. P. M. Tolstoy, B. Koeppe, G. S. Denisov and H.-H. Limbach, Angew. Chem., Int. Ed., 2009, 48, 5745–5747.
29. P. Charisiadis, V. Exarchou, A. N. Troganis and I. P. Gerothanassis, Chem. Commun., 2010, 46, 3589–3591.
30. P. Charisiadis, A. Primikyri, V. Exarchou, A. Tzakos and I. P. Gerothanassis, J. Nat. Prod., 2011, 74, 2462–2466.
31. V. G. Kontogianni, P. Charisiadis, A. Primikyri, C. G. Pappas, V. Exarchou, A. G. Tzakos and I. P. Gerothanassis, Org. Biomol. Chem., 2013, 11, 1013–1025.
32. M. H. Abraham, R. J. Abraham, Jr, W. E. Acree, A. E. Aliev, A. J. Leo and W. L. Whaley, J. Org. Chem., 2014, 79, 11075–11083.
33. V. Bertolasi, P. Gilli, V. Ferretti and G. Gilli, J. Chem. Soc., Perkin Trans. 2, 1997, 945–952.
34. G. A. Jeffrey and Y. O. Yeon, Acta Crystallogr., Sect. B: Struct. Sci., 1986, 42, 410–413.
35. M. G. Siskos, V. G. Kontogianni, C. G. Tsiafoulis, A. G. Tzakos and I. P. Gerothanassis, Org. Biomol. Chem., 2013, 11, 7400–7411.
36. P. Charisiadis, V. G. Kontogianni, C. G. Tsiafoulis, A. G. Tzakos, M. Siskos and I. P. Gerothanassis, Molecules, 2014, 19, 13643–13682.
37. M. G. Siskos, A. G. Tzakos and I. P. Gerothanassis, Org. Biomol. Chem., 2015, 13, 8852–8868.
38. M. G. Siskos, M. I. Choudhary, A. G. Tzakos and I. P. Gerothanassis, Tetrahedron, 2016, 72, 8287–8293.
39. M. G. Siskos, M. I. Choudhary and I. P. Gerothanassis, Org. Biomol. Chem., 2017, 15, 4655–4666.
40. M. G. Siskos, M. I. Choudhary and I. P. Gerothanassis, Molecules, 2017, 22, 415.
41. M. G. Siskos, M. I. Choudhary and I. P. Gerothanassis, Tetrahedron, 2018, 74, 4728–4737.
42. S. H. Mari, P. C. Varras, A. tul-Wahab, M. I. Choudhary, M. G. Siskos and I. P. Gerothanassis, Molecules, 2019, 24, 2290.
43. J. H. P. Tyman, Synth. Nat. Phenols, 1996, 52, 1.
44. J. C. Espín, A. González-Sarrías and F. A. Tomás-Barberán, Biochem. Pharmacol., 2017, 139, 82–93.
45. J. B. Harborne, Phytochemistry, 1967, 6, 1415–1428.
46. L. Botes, F. Van der Westhuizen and D. Loots, Molecules, 2008, 13, 2169–2180.
47. T. H. Chou, H. Y. Ding, W. J. Hung and C. H. Liang, Exp. Dermatol., 2010, 19, 742–750.
48. E. V. Borisov, W. Zhang, S. Bolvig and P. E. Hansen, Magn. Reson. Chem., 1998, 36, S104–S110.
49. P. Charisiadis, V. G. Kontogianni, C. G. Tsiafoulis, A. G. Tzakos and I. P. Gerothanassis, Phytochem. Anal., 2017, 28, 159–170.
50. R. M. Lynden-Bell, Prog. NMR Spectrosc., 1967, 2, 163–204.
51. C. S. Johnson, Jr, Adv. Magn. Reson., 1965, 1, 33–102.
52. B. Mennucci, J. M. Martínez and J. Tomasi, J. Phys. Chem. A, 2001, 105, 7287–7296.
53. R. A. Klein, B. Mennucci and J. Tomasi, J. Phys. Chem. A, 2004, 108, 5851–5863.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Gaussian, Inc., Wallingford CT, 2010.
55. C. Trindle and D. Shillady, Electronic Structure Modeling: Connections Between Theory and Software, CRC Press, 2008.
56. K. W. Wiitala, T. R. Hoye and C. J. Cramer, J. Chem. Theory Comput., 2006, 2, 1085–1092.
57. M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Chem. Rev., 2012, 112, 1839–1862.
58. M. Sathisha, G. Meenakshic, S. Xavier and S. Sebastian, Acta Phys. Pol., A, 2017, 131, 1512–1518.
59. E. C. Semidalas and C. E. Semidalas, Vib. Spectrosc., 2019, 101, 100–108.
60. N. Kumar, V. Pruthi and N. Goel, J. Mol. Struct., 2015, 1085, 242–248.
61. C. Lourence, M. Berthelot and J. Gratone, in PATAI's Chemistry of Functional Groups, ed. Z. Rappaport, John Wiley & Sons, Ltd, Chichester, UK, 2009, pp. 1–75.
62. S. M. Vilas-Boas, V. Vieira, P. Brandão, R. S. Alves, J. A. P. Coutinho, S. P. Pinho and O. Ferreiraoa, J. Mol. Liq., 2019, 289, 111089.
63. A. Jacobs and F. M. Amombo Noa, CrystEngComm, 2015, 17, 98–106.
64. F. M. Amombo Noa and G. Mehlana, CrystEngComm, 2018, 20, 896–905.
65. A. D. Fortes, J. Ponsonby, O. Kirichek and V. Garcia-Sakai, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 733–748.
66. R. K. Harris, E. D. Becker, S. M. Cabral de Menezes and R. Goodfellow, Pure Appl. Chem., 2001, 73, 1795–1818.
67. R. E. Hoffman, J. Magn. Reson., 2006, 178, 237–247.
68. R. E. Hoffman, Magn. Reson. Chem., 2006, 44, 606–616.
69. A. Fayaz, M. G. Siskos, P. C. Varras, M. I. Choudhary, A. tul-Wahab and I. P. Gerothanassis, Phys. Chem. Chem. Phys., 2020, 22, 17401–17411.
70. M. Strauch, A.-M. Bonsa, B. Golub, V. Overbeck, D. Michalik, D. Paschek and R. Ludwig, Phys. Chem. Chem. Phys., 2016, 18, 17788–17794.
71. S. Chen and E. I. Izgorodina, Phys. Chem. Chem. Phys., 2017, 19, 17411–17425.

---

Footnote

† Electronic supplementary information (ESI) available: ¹H NMR spectral region, minimum energy structures of solvation species of phenol, paracoumaric acid and vanillic acid, tables of proton exchange rates. See DOI: 10.1039/d0cp05861k

---