Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum and classical effects in DNA point mutations: Watson–Crick tautomerism in AT and GC base pairs†
L.
Slocombe
 *a,
J. S.
Al-Khalili
b and
M.
Sacchi
*a,
J. S.
Al-Khalili
b and
M.
Sacchi
 c
c
aLeverhulme Quantum Biology Doctoral Training Centre, UK. E-mail: l.slocombe@surrey.ac.uk
bDepartment of Physics, University of Surrey, Guildford, GU2 7XH, UK
cDepartment of Chemistry, University of Surrey, Guildford, GU2 7XH, UK. E-mail: m.sacchi@surrey.ac.uk
First published on 29th January 2021
Abstract
Proton transfer along the hydrogen bonds of DNA can lead to the creation of short-lived, but biologically relevant point mutations that can further lead to gene mutation and, potentially, cancer. In this work, the energy landscape of the canonical A–T and G–C base pairs (standard, amino–keto) to tautomeric A*–T* and G*–C* (non-standard, imino–enol) Watson–Crick DNA base pairs is modelled with density functional theory and machine-learning nudge-elastic band methods. We calculate the energy barriers and tunnelling rates of hydrogen transfer between and within each base monomer (A, T, G and C). We show that the role of tunnelling in A–T tautomerisation is statistically unlikely due to the presence of a small reverse reaction barrier. On the contrary, the thermal populations of the G*–C* point mutation could be non-trivial and propagate through the replisome. For the direct intramolecular transfer, the reaction is hindered by a substantial energy barrier. However, our calculations indicate that tautomeric bases in their monomeric form have remarkably long lifetimes.
1 Introduction
Within the blueprint of life, spontaneous ‘spelling mistakes’ can occur, leading to potentially catastrophic errors. One possible candidate for these spontaneous mutations is the quantum mechanical tunnelling of hydrogen atoms within the bonds binding the DNA duplex together, or within the base.1,2 Hydrogen transfer in DNA bases leads to the creation of short-lived biologically relevant mutagens; referred to as tautomers. Keto–enol and amino–imino tautomerism are thought to be candidates for spontaneous mutation of DNA during replication and repair.In this work, the energy landscape of the canonical (standard, amino–keto) and tautomeric (non-standard, imino–enol) forms of the adenine–thymine (A–T) and guanine–cytosine (G–C) monomers and base pairs are modelled with the ab inito quantum mechanical approach of density functional theory (DFT). The reaction pathway of transfer can be modelled with transition state theory, providing an energy landscape of the process.
A careful choice of the computational and theoretical methodology is required to obtain an accurate representation of the potential energy surface and the proton transfer process along the hydrogen bonds. The resulting double minima configuration, representing the two potential wells of the canonical and tautomeric state, allows the proton to be transferred either via tunnelling or classical over-the-barrier hopping. There have been numerous studies attempting to ascertain whether tautomerism could lead to non-trivial populations of mutagenic nucleotides; however, the contribution to replication and translation errors have not yet been definitively established.
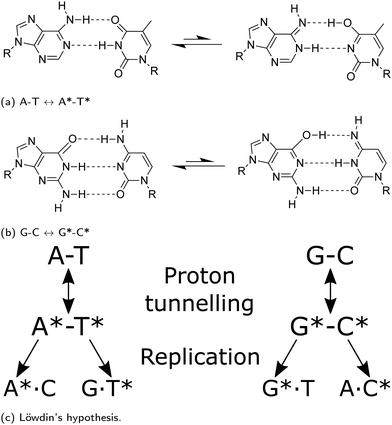
Watson and Crick proposed3 that if nucleotide bases maintain an energetically unfavourable tautomeric form, they can pair in a Watson–Crick (WC) conformation: tautomeric forms of purines matching with the wrong pyrimidines, or vice versa. The pairing rules of the mismatch would follow the scheme shown in Fig. 1. The proton transfer pathway would contribute to the occurrence of transition errors. Molecular biology asserts that the replicative and translational machinery has a high fidelity. However, a considerable number of different sources of endogenous DNA damage have been identified; these include oxidative damage, depurination and depyrimidination, strand breaks, deamination.4 Likewise, exogenous pathways, such as damaging agents or UV radiation, also play a significant role.5 Each leading to a plethora of potentially mutagenic pathways, provided they are not caught by DNA repair pathways, which are typically able to keep-up with the damages to ensure genetic stability.5 Experimental approaches have widely been used to measure the rate of spontaneous mutation6 and estimate that genomic information can be copied with approximately only one error occurring per 108–1011 bases replicated.7 Furthermore, depending on the type, polymerases possess exonuclease activity allowing proofreading to bring down the mutation rate. However, recent crystallographic observations of the active site of polymerase lambda suggest that proton transfer could lead to the misincorporation of wobble mismatches by adopting WC-like geometries that mimic the canonical base pairs.8–10 Furthermore, NMR relaxation dispersion experiments successfully measured the misincorporation in both DNA, and RNA duplexes.9,10 The work presented in this paper attempts to investigate a pathway for spontaneous mutations via proton transfer. A tautomer is thought not to distort the DNA double helix; consequently it might evade fidelity checkpoints of the replisome.
As highlighted in a recent review,11 several previous studies have reported the minimum energy path of the proton transfer reaction from the canonical to the base pairs’ tautomeric state. The conclusions drawn in these works vary because of the substantial differences in the computational methods applied to calculate the system energy along the reaction path. While some authors report that there is no stable minimum associated to rare A*–T* tautomer,12–14 others describe the presence of shallow minima.15 A few authors even report that A*–T* structures are stable enough to cause mutation down the DNA replication line.16
Brovarets et al.17–20 have been among the first to address the wide variance in the existent computational studies on A–T and G–C tautomerisation reactions. In particular, they applied second-order Møller–Plesset perturbation theory (MP-2) with a relatively large basis set and observed that tautomerisation mechanism processing via double proton transfer might not be responsible for the generation of the WC mutagenic tautomers. They concluded that, as the tautomeric forms are dynamically unstable,20 the lifetimes of these states are too short for real vibrational modes to develop. Additionally, Brovarets et al. explored other pathways which could lead to spontaneous point mutations, namely the Hoogsteen base pairings (achieved by rotating the base around the glycosidic bond).20 However, the Hoogsteen tautomeric pairings appear to have a small reverse barrier and hence deemed too unstable to be biologically relevant. On the contrary, they suggest that the rare mispairs A*·C, G·T*, and H*·T (H-hypoxanthine a DNA base arising from the deamination of A) are biologically relevant as these tautomers have long enough lifetimes to allow incorporation of point defects during the replication process and cause replication errors.20
As a first approximation, the majority of the theoretical studies on DNA point mutations assume the nucleotides are isolated with no surrounding biological structure.12–20 In contrast, other studies have attempted to capture surrounding biological structure, such as the stacking interactions when DNA is coiled up in storage.21,22 However, this is still an open problem; there are no studies that include the proteins of the replisome. Villani suggested that the stacking interaction enhances the hydrogen bond-accepting capacity, but reduces the donating strength of DNA bases – depending on the hydrogen bond “bridge”. Introduction of the stacking interaction leads to significant modification of both static and dynamic properties of G–C.21 However, critically, this model lacks effects such as solvent interactions (implicit or explicit treatment of water solvation), the back-bone, and counter ions.
A more recent paper22 attempted to tackle more fully the biological environment of the nucleobases, employing a quantum mechanical/molecular mechanical (QM/MM) approach. A base pair and a microsolvent shell were included in the QM region, whereas, the rest of the helix, water, and counter ions, were modelled with MM. According to their results, the G–C tautomer is meta-stable in the gas phase. However, it becomes unstable in the biological (water solvated) DNA environment. The inclusion of solvation effects and DNA backbone structure leads to an increased asymmetry in the G–C PES, causing a significant reduction of the reverse barrier and stability of the tautomeric state. A limitation of this study is the adoption of a lower-tier functional, BLYP exchange–correlation functional with D3-BJ correction; we will now highlight the issues of the choice of functional.
There is increasing evidence that general-gradient-approximation (GGA) functionals might fail to describe hydrogen bonding in DNA accurately and that the structure and energies of the base pairs are highly dependant on the details of the theoretical model used.20,23–25 Brovarets et al.20 and other authors23–25 suggest that B3LYP with a high basis set can reach an accuracy comparable to perturbation theory calculations for the A–T and G–C dimers.
On the other hand, single-stranded DNA is transiently observable during the replication process; therefore an alternative pathway for tautomerisation might involve intra-base proton transfer, whereby a single proton shifts from one hydrogen bonding site to another within the same monomer.26–28 Intra-base tunnelling studies show that the reaction has a high forward barrier; however, when water is included near the donor site, the barrier is reduced.26–28
Godbeer et al.29–31 combined density functional theory studies with an open quantum systems approach using dissipative terms in the Lindblad equation and applied it to the A–T base pair, to include thermal nuclear quantum effects (NQEs). The derivation of the model used was based on the work by Meyer and Ernst,32,33 who studied Benzoic acid. Godbeer et al. demonstrated that the dissipative Lindblad term couples the eigenstates localised in the canonical well to the excited states in the tautomeric well, leading to thermally assisted tunnelling. Furthermore, increasing the temperature of the bath leads to stronger coupling to the environment and hence an enhanced rate of thermally assisted tunnelling. Quantum thermalisation can be correlated with a similar enhancement predicted by a simpler model in which it is produced by successive von-Neumann measurements,30 whereby the frequency of observation/measurement is increased, and an anti-Zeno effect is observed. A transition state search using CASTEP at B3LYP level provided a description of the potential surface for the proton transfer. Godbeer et al. varied the potential shape (barrier and asymmetry) and determined the effect on the tunnelling probability. A maximum tunnelling probability was reported to be on the order of 10−9 for the A–T base pair suggests that tunnelling plays a small role in the A–T system due to the large asymmetry.
Other authors have also explored NQEs.34–36 Pohl et al.34 used path integral molecular dynamics, corroborated with experimental deuterium-induced NMR chemical shifts, to investigate hydrogen-bonded isocytosine pairs (an analogue of the G–C pairing). They concluded that inter-base proton transfer reactions across the hydrogen bonds do not take place in the isocytosine system. However, it is unclear whether this result will directly translate to the G–C pair. Furthermore, Fang et al. directly investigated the NQEs in DNA base pairs, also using path integral molecular dynamics,35 and concluded that, at room temperature, NQEs strengthen the duplex hydrogen bonding interaction by ∼0.5 kcal mol−1, as a consequence of the tightening of the hydrogen bonds.
Pérez and workers36 also explored NQEs in DNA analogues of A–T and G–C by explicitly including them in Car–Parrinello path integral molecular dynamics (CPPIMD) calculations. The CPPIMD approach accounts not only for the thermal fluctuations of a typical molecular dynamics simulation but includes nuclear tunnelling and zero-point energy effects. By comparing classical molecular dynamics and path integral methods, Pérez and workers determined that NQEs altered the potential energy surface of the proton transfer reaction. In particular, CPPIMD simulations suggest that for both complexes, G–C and A–T, NQEs reduce the reaction barrier by 2–3 kcal mol−1, therefore playing a crucial role in the formation of tautomers.
In this work, we seek to obtain an accurate energy landscape for the proton transfer mechanisms in nucleobases using state of the art DFT methods described in Section 2. We address the double proton transfer in A–T and G–C bases pairs (Section 4.1) and the intra-base transfer pathway (Section 4.2). From the PES calculated with DFT, we obtain a quantum corrected rate equation, accounting for quantum tunnelling of the protons. Section 3 outlines the methods used to acquire the forward and reverse reaction rates presented in Section 4.3.
2 Minimum energy path computational details
We performed calculations with CASTEP 19.1,37–43 a plane-wave pseudopotential DFT method with periodic lattice conditions. Calculations are conducted at the Γ-point under isolated molecule boundary conditions. We found that padding of 10 Å is sufficient to prevent the spurious interaction of the periodically repeated supercells. Norm conserving pseudopotentials are employed in all the calculations reported in this work.44 The plane wave energy cut-off was optimised by varying the cut-off and comparing the single point energy. A cut-off value of 1100 eV was used throughout, determined via a plane-wave cut-off energy convergence test.The atomic simulation environment (ASE)45,46 was used throughout this work to connect CASTEP to Python3. All the structures were optimised using a force tolerance of 0.01 eV Å−1. The biological environment of DNA has been approximated by embedding the nucleobases in an implicit solvent field. For the implicit solvent field, we use a value of solvent surface tension (4.7624 × 10−5Eha0−2) and an apolar factor (0.281075) corresponding to water.47
We obtained the potential energy landscapes describing the proton transfer reactions using a machine learning approach to the nudged elastic band algorithm (ML-NEB).48,49 The ML-NEB approach seeks to minimise the number of DFT single point energy calculations required to gain an accurate depiction of the minimum energy path (MEP). In our treatment, we collect the movement of the protons transferring (and other atoms moving to facilitate the transfer) into a single axis. The reaction pathway contains a general description of the transfer process; the energetic landscape of this pathway is then explored using ML-NEB. The ML-NEB algorithm incorporates a Gaussian regression model to produce a surrogate description of the true MEP. Thus the uncertainty in the energy points on surrogate MEP becomes the convergence criteria.
We conducted a benchmark of the ML-NEB algorithm against the standard full image NEB calculation to determine its validity. Results using the G–C base pair using the PBE functional indicate that the ML-NEB algorithm accurately reproduced the full path, but at a fraction of the computational cost. The statistical uncertainty in the surrogate model associated with the ML-NEB calculations is computed and displayed.
Note that the error bars on the PES correspond only to the error estimated by the machine-learned surrogate description. The error bars do not account for the inaccuracies of the DFT methods employed.
3 Obtaining a tunnelling correction
A pseudo-one-dimensional PES can represent the proton transfer in nucleobases with a transition state separating the canonical and tautomeric configurations. Using the ML-NEB calculated reaction path and the associated uncertainties, an asymmetric Eckart potential can be fitted to the PES. The fitted Eckart potential takes the form,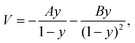 | (1) |
| y = −exp(2πx/L). | (2) |
| A = ΔV1 − ΔV2, | (3) |
| B = [(ΔV2)1/2 + (ΔV1)1/2]2, | (4) |
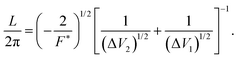 | (5) |
The temperature-dependent tunnelling factor of a potential barrier can be defined by,
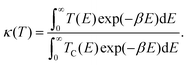 | (6) |
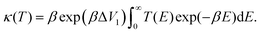 | (7) |
Consequently, rate constants, kf and kr are obtained from,
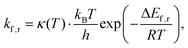 | (8) |
Here the integrand within the Laplace transform in eqn (7) is approximated by using both the semi-classical Wentzel–Kramers–Brillouin (WKB) approximation50 and by numerically solving the Schrödinger equation by scattering Gaussian wave packets with a range of momentum values from of the fitted potential. The WKB approach is modelled using the following transmission coefficient.
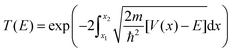 | (9) |
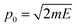 , which is then weighted by a Boltzmann distribution (the other term in the integrand in eqn (7)). The Gaussian is then integrated over time until it encounters the barrier, from which it scatters. The transmission probability is calculated as the probability of finding the wave packet on the other side of the barrier.
, which is then weighted by a Boltzmann distribution (the other term in the integrand in eqn (7)). The Gaussian is then integrated over time until it encounters the barrier, from which it scatters. The transmission probability is calculated as the probability of finding the wave packet on the other side of the barrier.
In order to calculate the spatial partial derivative in the Schrödinger equation we use the pseudo-spectral method.51 To propagate the wave packet in time, we use a fourth-order method based on the expansion of Chebyshev polynomials (ROCK4)52 implemented in DifferentialEquations.jl.53
For this model we also assume, as previously observed,31,36 by that the two protons undergo an asynchronous transfer, that is the rate-determining step is the passage of a single proton across the barrier, with the other proton transferring to preserve electroneutrality. We employ a grid of 211 spacial elements describing the reaction coordinate and set the effective mass of the tunnelling wave packet to that of a proton (1836 a.u., Hartree atomic units). The initial Gaussian takes the form,
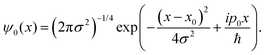 | (10) |
4 Results and discussions
4.1 Canonical base pairs
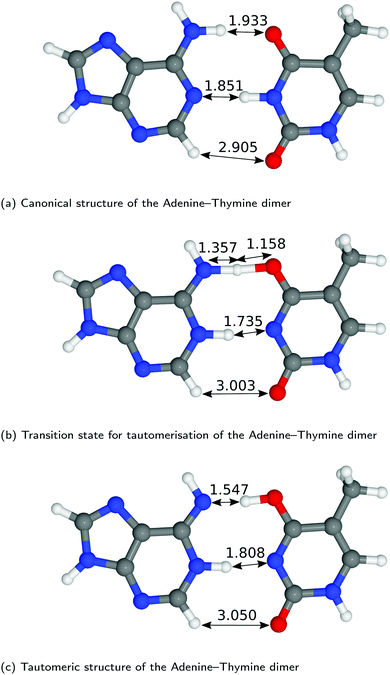
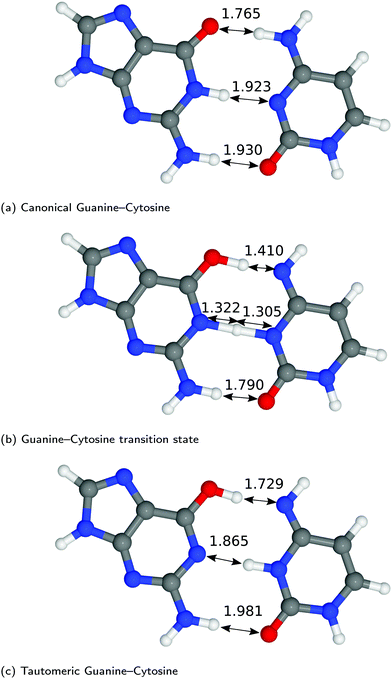
The structures of A–T and G–C are displayed in Fig. 2 and 3. We choose to terminate the glycosidic bond (which would bond with the DNA backbone) with hydrogens, truncating the bases so that they are now an isolated system. Although the global minimum of the isolated G–C tautomer in the gas phase is slightly different from the one in Fig. 3, Marian,54 the G*–C* configuration that we and other authors have considered is the only one that is biologically relevant.19The hydrogen-bond lengths shown in both Fig. 2 and 3 are close to the results of the MP-2 calculations reported by Brovarets et al.20 For the A–T pairing, the hydrogen bonds of both the canonical and tautomeric state are within 10% of the MP-2 results. For G–C, the initial and final images on the reaction path correspond to the two bases moving closer to facilitate the proton transfer. Other workers also report a moderate shift (of the order of about 0.1 Å) during the proton transfer process.20 For the case of double-stranded DNA Das et al.55 demonstrate that the degree of shifting is slightly limited in the case of double-stranded DNA and shows a dependence on the size of the QM region and the choice of the exchange–correlation functional.55 As a first approximation, the tautomerisation will follow a similar pathway in the double-stranded DNA. At the transition state, the top and middle protons move in a concerted manner. Whereas for A–T, the initial images correspond to a rotation of the A monomer towards the top oxygen. The middle proton is then transferred, followed by the top proton asynchronously.
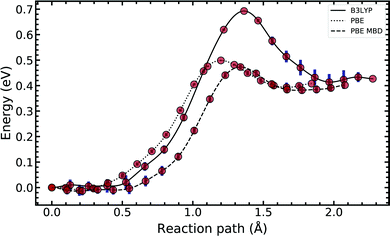
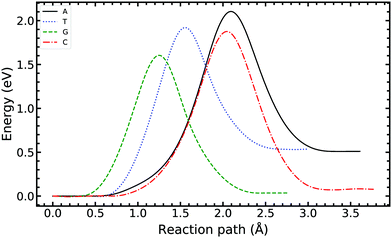
In Fig. 4, we compared the impact of the choice of exchange–correlation functionals and the inclusion of dispersion corrections on the G–C double proton transfer energy landscape. The choice of functional significantly affects the length of the hydrogen bonds in the G–C transition state. In comparison, while employing the PBE functional, the results differ by an average of 3.7% compared to B3LYP. Furthermore, the location of the transition state along the reaction coordinate is shifted towards the reactant (or “late barrier”, according to Polanyi's rule56). However, more significantly, the height of the barrier is significantly lower.
Introducing many-body dispersion corrections reduces the average difference between the hydrogen bond lengths to 2.6%. Nevertheless, it fails to remedy the lower barrier. Calculations utilising GGA functionals provide significantly worse predictions of barrier and asymmetry compared to higher levels of theory.20,23–25 In summary, we suggest caution and a careful comparison between the use of functional and dispersion corrections is required when modelling this system.
Fig. 5 compares the MEP for the tautomeric transfer reaction of the G–C and A–T base pairs.
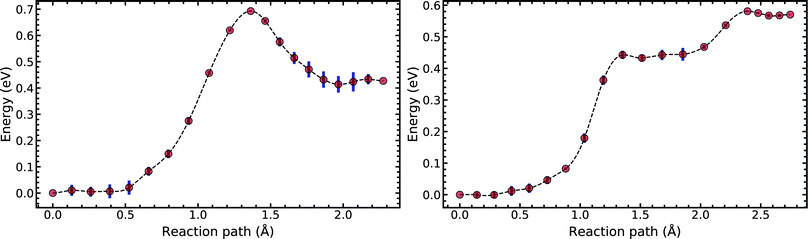 | ||
| Fig. 5 Minimum energy path of the transfer reaction of the canonical to the tautomeric state of guanine–cytosine (left) and adenine–thymine base pairs (right). | ||
Applying the ML-NEB algorithm to the A–T double proton transfer reaction shows that the forward and reverse reaction barrier are 0.581 eV and 0.011 eV respectively. The small reverse reaction barrier indicates that the tautomeric state could be unstable. With a small reverse barrier, the likelihood of the tautomeric state being populated is trivial. Our suggestion is in line with the conclusions of other authors, who go further to suggest that the A–T tautomeric state vanishes when looking at the free energy landscape.13 The forward and reverse barrier reported by Godbeer et al.29,31 is significantly higher than reported here. We believe that the authors overestimated the barrier by using overly loose convergence criteria in the transition state search algorithm. The early termination of the convergence cycle leads to an under-converged transition state structure. On the other hand, Godbeer et al.'s value for the asymmetry compares well with the results presented here, to within 0.02%. We also agree to within 7% of Brovarets et al.17,20 for both the barrier and asymmetry.
In Fig. 5 we report the PES for A–T tautomerisation calculated with B3LYP. The PES of A–T features a rather “drawn-out” dissociation path with an energy plateau between 1.4 and 2.1 Å, followed by a small barrier at the TS (2.4 Å). The small reverse reaction barrier calls in to question the stability of the A–T tautomer; it is unclear if there is a bound state in the second well. These features in the PES of A–T were previously observed by Brovarets et al.17,20 and can be explained by the highly asynchronous nature of the double proton transfer mechanism in A–T. The proton transfer begins with one of the N–H bond of T elongating, followed by the displacement of the amino proton of A (see Fig. 2). We therefore confirm that A–T WC-tautomerisation follows a concerted and asynchronous process. The pathway does not contain an intermediate minimum, and the protons move with a small time delay. The flat midsections of the MEP correspond to the transfer of amide proton from T to A.
G–C tautomerisation has a 0.693 eV barrier, 0.112 eV higher than A–T tautomerisation. In contrast to A–T, the G–C double proton transfer reaction has a significant reverse barrier, 0.266 eV, but the hydrogen bonds dissociate in a concerted asynchronous manner, similar to the A–T process.
By comparison, Pérez and workers36 suggest that A–T has a lower forward reaction barrier of ∼0.43 eV (compared to 0.581 eV) and a larger reverse barrier of ∼0.04 eV (compared to 0.011 eV). While the reverse barrier differs by value by almost four-fold, they offer a similar narrative; A–T has a forward barrier several times larger than the thermal energy but a very shallow second tautomeric well. At the same time, for the G–C reaction, Pérez et al. offer a lower forward barrier of ∼0.43 eV compared to 0.581 eV with the same reverse barrier as A–T. At this point, our narratives differ, they suggest that the incorporation of NQE into the PES destabilises the GC tautomer. However, they use the BLYP function in their CPPIMD calculations which underestimates the reaction barrier for this system. Furthermore, the structures simulated in CPPIMD lack the structure of the rest of the base (as they simulate DNA base pair analogues) and solvent interactions.
4.2 Intra-base transfer
We now turn our attention to single-stranded DNA, as this is the form it assumes when it passes through the replisome. As a first-order approximation, we consider the case where the bases are embedded in an implicit solvent field. We apply the ML-NEB algorithm to the intra-base transfer process for all four monomers: A, T, G, and C. The corresponding reaction paths are presented in Fig. 6, while a full depiction is given in the ESI.†Table 1 summarises for ease of comparison the energy differences in the intramolecular paths for tautomerisation.| Reaction | E f | E r | ΔE |
|---|---|---|---|
| A–T ↔ A*–T* | 0.581 | 0.011 | 0.570 |
| G–C ↔ G*–C* | 0.693 | 0.266 | 0.427 |
| A ↔ A* | 2.104 | 1.595 | 0.510 |
| T ↔ T* | 1.920 | 1.385 | 0.535 |
| G ↔ G* | 1.604 | 1.567 | 0.036 |
| C ↔ C* | 1.876 | 1.799 | 0.077 |
For the A and T monomers, the forward barrier (2.104 eV and 1.920 eV respectively) is more than double the value for the A–T canonical pair mutation. Furthermore, the asymmetry between the canonical and tautomeric state is of the same order as the forward barrier of the canonical system. On the other hand, for G and C, the forward barrier is significant with values of 1.604 eV and 1.876 eV respectively. However, the reverse reaction barrier is similar in value to the forward barrier resulting in a small asymmetry.
For the intra-base transfers, the reaction paths are 0.2–1.5 Å longer than the corresponding bonded configurations. On average, the forward reaction barrier height for intramolecular tautomerisation is 1.239 eV higher than that calculated for the WC base pairs. Furthermore, the images along the reaction path of A and C describe significant buckling and shifting of the ring structure to facilitate the transfer.
4.3 Tunnelling rates
We now turn our attention to obtaining a rate equation describing the proton transfer reactions, eqn (8). We apply a quantum tunnelling correction using the WKB approximation and a Gaussian wave packet scattering approach. From the corrected rate, we can approximate the lifetime of the canonical and tautomeric states.The WKB approximation is a straightforward evaluation of eqn (9) and the results are given in Table 2.
| Reaction | Tunnelling correction | τ f | τ r |
|---|---|---|---|
| A·T ↔ A*·T* | 1.090 | 9.768 × 10−4 | 1.752 × 10−13 |
| G·C ↔ G*·C* | 7.071 | 1.165 × 10−2 | 5.486 × 10−10 |
| A ↔ A* | 6.371 × 105 | 9.370 × 1016 | 1.192 × 108 |
| T ↔ T* | 1.411 × 106 | 3.297 × 1013 | 2.180 × 104 |
| G ↔ G* | 1.997 × 106 | 1.053 × 108 | 2.001 × 107 |
| C ↔ C* | 1.436 × 106 | 5.754 × 1012 | 2.089 × 1011 |
| A·T ↔ A*·T* | 1.612 × 101 | 6.607 × 10−5 | 1.185 × 10−14 |
| G·C ↔ G*·C* | 1.222 × 102 | 6.739 × 10−4 | 3.175 × 10−11 |
| A ↔ A* | 1.690 × 108 | 3.532 × 1014 | 4.492 × 105 |
| T ↔ T* | 1.684 × 108 | 2.762 × 1011 | 1.826 × 102 |
| G ↔ G* | 4.124 × 107 | 5.101 × 106 | 9.691 × 105 |
| C ↔ C* | 6.487 × 107 | 1.274 × 1011 | 4.625 × 109 |
On the other hand, obtaining a tunnelling correction by numerically solving the Schrödinger equation requires a loop over a range of incident energies, this allows sufficient sampling of eqn (7). The result for the G–C double proton transfer reaction is shown in Fig. 7.
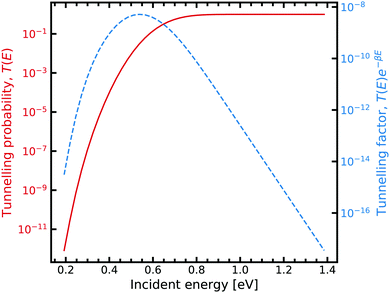 | ||
| Fig. 7 Tunnelling through the G–C potential using the scattering approach. Incident energies are picked with a Boltzmann weighting and are looped over forming the integrand in eqn (7). For further information on the calculation details, see text. | ||
Fig. 7 shows the strong decay of the tunnelling probability of the wave packet at low incident energies. As the incident energy approaches the potential barrier energy value, the transmission to the other side of the barrier quickly approaches unity. Fig. 7 also shows how the Boltzmann weighting begins to dominate with increasing incident energy. Consequently, a linear relationship is exhibited when plotted in log-space. In the low energy regime, the integrand also quickly drops off due to the large energy difference between the entrance and exit channel. We note that tight numerical tolerances due to the sampling of very small numbers. Consequently, the errors in the time integrator dominate. This problem is overcome by performing a 4-th order interpolation and extrapolation to smaller incident energy values.
Table 2 shows the result of applying the WKB and scattering tunnelling correction for the proton transfer reactions. The reaction rate is evaluated at room temperature 298.15 K.
Across all cases, the WKB semi-classical tunnelling correction predicts a lower tunnelling factor than the Gaussian wave packet scattering approach, by about one order of magnitude. However, the WKB approach is a semi-classical (high energy) approximation, and as such is unlikely to describe tunnelling accurately for low values of incident energy.
To obtain a tunnelling correction, we evaluate eqn (7) for the Gaussian wave packet scattering approach. The A–T double proton transfer reaction has a tunnelling correction of 16.12 (refer to the values in the bottom panel of Table 2). The high tunnelling correction indicates that tunnelling can play a role in the formation of the A–T tautomer. Nevertheless, the lifetime of the tautomeric A–T state estimated with a tunnelling-corrected rate equation is on the order of 10−14 seconds. Consequently, hardly any of the A*–T* spontaneously created through the WC path will survive long enough to pass through the replication machinery.
On the other hand, for G–C, the tunnelling correction is an order of magnitude larger, with a value of 122.2, suggesting that quantum effects can play a decisive role in determining the tautomeric populations. The lifetime of the tautomeric state is also short, on the order of 10−11 seconds, but 1000 fold larger than the A*–T* lifetime. While the population of the tautomeric state may be transient, this pathway could lead to spontaneous point mutations, provided it can pass through the replication machinery.
The large energy requirements for intramolecular tautomerisation in A, T, G and C translate to a statistically small concentration of tautomers created through these mechanisms. However, the lifetime of the tautomeric forms produced by intramolecular proton transfer would be, on average, 109 longer than the corresponding tautomeric pairs (A*–T* and G*–C*). Tunnelling interactions dominate the rate equation, as indicated by the high tunnelling factors, on the order of 108. However, due to the high reaction barrier, the classical “over the barrier” thermal contribution is trivial and overall the reaction rate is low.
Fig. 8a shows the Arrhenius plot for the forward double proton transfer reaction (see eqn (8)) from the canonical to the tautomeric configuration for G–C. The quantum corrected forward rate shows a strong temperature dependence. At high temperature, both the classical and quantum corrected rates follow the expected linear Arrhenius behaviour. However, with increasing temperature, the corrected rate diverges from the classical and begins to flatten out. The divergence signals a substantial contribution of tunnelling accounted for by the κ term (eqn (7)). The tunnelling contribution observed in the figure (κ) vanishes at high temperature as expected since at high temperature the quantum contribution should tend to zero. For the reverse reaction rate, shown in Fig. 8b, the quantum corrected rate is largely temperature-independent, showing a flat inverse parabolic shape which varies by an order of magnitude. Both the forward and reverse rate have a non-trivial contribution due to tunnelling.
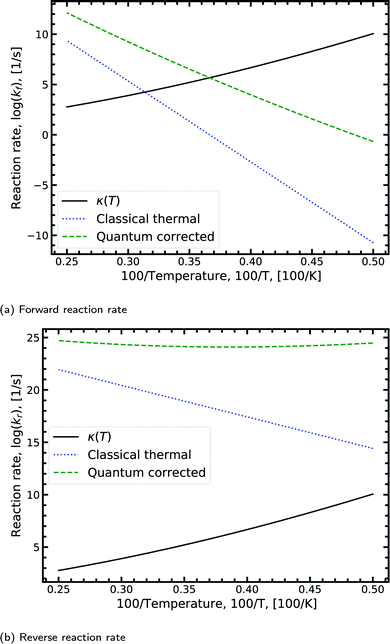 | ||
| Fig. 8 Displaying the Arrhenius plot with quantum tunnelling corrections to the forward and reverse reaction rates (see eqn (8)) for the double proton transfer of the guanine–cytosine system. The quantum correction is determined using eqn (7), where the transmission coefficient is evaluated using the Scattering approach. | ||
We note that the quantum correction, κ, is multiplicative to the classical thermal rate and thus additive on the log scale shown in Fig. 8, refer to eqn (8). Reading off the quantum corrected curve at 298.15 K recovers the G–C forward rate value presented in Table 2. Other figures for the other reactions presented in Table 2 can be found in the ESI.†
The combined studies of the hydrogen-bonded and isolated nucleobases indicate that the tautomeric states are more likely to be formed via double proton tunnelling in the hydrogen-bonded conformation than in the single-stranded configuration. However, in the single-stranded monomeric configuration, the tautomeric state is significantly more stable. If the tautomeric state were to survive the dissociation process, the monomeric tautomeric base would be stable enough to lead to a point mutation.
5 Conclusions
We report a detailed computational study of the tautomeric double proton transfer reactions in the canonical DNA base pairs. We also compare these results with the rare intra-base proton transfer as an alternative pathway to tautomerisation.By calculating the transition state structure of the tautomerisation reaction using two popular exchange–correlation-functionals, PBE and B3LYP, we have been able to resolve some of the discrepancies between DFT results observed in the literature. We conclude that GGA functionals such as PBE do not allow the same level of accuracy of higher levels of theory such as MP-2. Instead, our B3LYP calculations produce results close to those of the MP-2 calculations.20 Adding many-body dispersion corrections to PBE does not significantly increase the accuracy of this functional for modelling the proton transfer reaction.
The ML-NEB transition state calculations show that the tautomeric configuration of G–C could play a role in spontaneous point mutations provided it can survive long enough to pass through the replication machinery. On the other hand, for A–T, we report a small reverse reaction barrier; indicating that the A–T tautomer is unstable. Consequently, the likelihood of the tautomeric state being populated via double proton transfer from the canonical state is trivial and is unlikely to be a biologically relevant pathway for spontaneous point mutations.
The ML-NEB transition state calculations determine that the G–C reverse reaction has a significant reverse barrier. On the other hand, for A–T, we report a small reverse reaction barrier; indicating that the A–T tautomer is unstable. Quantum mechanical corrections to the rate equation demonstrate that the rate of formation of tautomers is sensitive to tunnelling. Furthermore, the rate of formation of tautomers demonstrates a strong temperature dependence. However, the lifetime of the WC-tautomeric states is small. G–C could play a role in spontaneous point mutations provided it can survive long enough to pass through the replication machinery. On the other hand, for A–T, the likelihood of the tautomeric state being populated via double proton transfer from the canonical state is trivial and is unlikely to be a biologically relevant pathway for spontaneous point mutations.
The combined studies of the hydrogen-bonded and dissociated forms of the DNA bases indicate that the tautomeric state is more likely to be formed via proton tunnelling in the hydrogen-bonded conformation over the single-stranded configuration. However, any quantum tunnelling is expected to compete with other environmental mechanisms; such as the deamination pathway,57 or the polarisation interactions of aqueous solution.58
The inclusion of more direct environmental interactions, such as the phosphate groups of the DNA backbone and π–π stacking interactions with the adjacent nucleotides, could alter the energy landscape. However, recent works employing multiscale QM/MM approaches59 suggest that the including stacking interaction with dispersion corrections and modelling water molecules with force fields provide a correction which is within the error bar of the high-level quantum chemical theory used to describe the system. Nonetheless, the inclusion of quantum calculations on interactions of the local rearrangement and polarisation of water molecules could significantly alter the energy landscape. In addition, a full quantum treatment of the dissipative and decoherent nature of the surrounding environment is required, modelling the tunnelling proton as an open quantum system. These will be reported on in a subsequent paper.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for financial support from the Leverhulme Trust. We acknowledge helpful discussions with the members of the Leverhulme Quantum Biology Doctoral Training Centre. Particular thanks go to Antonio Pantelias-Garcés and Max Winokan, whom both offered many productive conversations. The authors thank the University of Surrey for access to Eureka, its High-Performance Computing facility. We acknowledge support from the HPC IT team, particularly Pritesh Tailor for his assistance.Notes and references
- P.-O. Löwdin, Rev. Mod. Phys., 1963, 35, 724–732 CrossRef.
- P.-O. Löwdin, Quantum Genetics and the Aperiodic Solid, Academic Press, 1966, vol. 2, pp. 213–360 Search PubMed.
- J. D. Watson and F. H. C. Crick, Cold Spring Harbor Symp. Quant. Biol., 1953, 18, 123–131 CrossRef CAS.
- R. De Bont and N. van Larebeke, Mutagenesis, 2004, 19, 169–185 CrossRef CAS.
- C. Bernstein, A. R. Prasad, V. Nfonsam and H. Bernstein, DNA Damage, DNA Repair and Cancer, IntechOpen, Rijeka, 2013 Search PubMed.
- J. W. Drake, B. Charlesworth, D. Charlesworth and J. F. Crow, Genetics, 1998, 148, 1667–1686 CAS.
- W.-J. Wu, W. Yang and M.-D. Tsai, Nat. Rev. Chem., 2017, 1, 1–16 CrossRef CAS.
- A. Rozov, N. Demeshkina and E. Westhof, et al. , Trends Biochem. Sci., 2016, 41, 798–814 CrossRef CAS.
- I. J. Kimsey, E. S. Szymanski and W. J. Zahurancik, et al. , Nature, 2018, 554, 195–201 CrossRef CAS.
- I. J. Kimsey, PhD thesis, Duke University, 2016.
- Y. Kim, F. Bertagna and E. M. DSouza, et al. , Quantum Rep., 2021, 3, 80–126 CrossRef.
- J. Florián and J. Leszczyński, J. Am. Chem. Soc., 1996, 118, 3010–3017 CrossRef.
- L. Gorb, Y. Podolyan and P. Dziekonski, et al. , J. Am. Chem. Soc., 2004, 126, 10119–10129 CrossRef CAS.
- J. P. Cerón-Carrasco, A. Requena and J. Zúñiga, et al. , J. Phys. Chem. A, 2009, 113, 10549–10556 CrossRef.
- G. Villani, Phys. Chem. Chem. Phys., 2010, 12, 2664–2669 RSC.
- G. Villani, J. Chem. Phys., 2005, 316, 1–8 CAS.
- O. O. Brovarets and D. M. Hovorun, J. Biomol. Struct. Dyn., 2015, 33, 2716–2720 CrossRef CAS.
- O. O. Brovarets and D. M. Hovorun, J. Biomol. Struct. Dyn., 2014, 32, 127–154 CrossRef CAS.
- O. O. Brovarets and D. M. Hovorun, J. Biomol. Struct. Dyn., 2014, 32, 1474–1499 CrossRef CAS.
- O. O. Brovarets and D. M. Hovorun, J. Biomol. Struct. Dyn., 2019, 37, 1880–1907 CrossRef CAS.
- G. Villani, Phys. Chem. Chem. Phys., 2013, 15, 19242–19252 RSC.
- D. Soler-Polo, J. I. Mendieta-Moreno and D. G. Trabada, et al. , J. Chem. Theory Comput., 2019, 15, 6984–6991 CrossRef CAS.
- P. Jurečka, J. Šponer, J. Černý and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985–1993 RSC.
- T. van der Wijst, C. F. Guerra, M. Swart and F. M. Bickelhaupt, Chem. Phys. Lett., 2006, 426, 415–421 CrossRef CAS.
- A. Bende, Theor. Chem. Acc., 2010, 125, 253–268 Search PubMed.
- L. Gorb and J. Leszczynski, J. Am. Chem. Soc., 1998, 120, 5024–5032 CrossRef CAS.
- L. Gorb, Y. Podolyan and J. Leszczynski, THEOCHEM, 1999, 487, 47–55 CrossRef CAS.
- Y. Podolyan, L. Gorb and J. Leszczynski, Int. J. Mol. Sci., 2003, 4, 410–421 CrossRef CAS.
- A. Godbeer, PhD thesis, University of Surrey (UK), Guildford, 2014.
- A. D. Godbeer, J. S. Al-Khalili and P. D. Stevenson, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 012102 CrossRef.
- A. D. Godbeer, J. S. Al-Khalili and P. D. Stevenson, Phys. Chem. Chem. Phys., 2015, 17, 13034–13044 RSC.
- R. Meyer and R. R. Ernst, J. Chem. Phys., 1987, 86, 784–801 CrossRef CAS.
- R. Meyer and R. R. Ernst, J. Chem. Phys., 1990, 93, 5518–5532 CrossRef CAS.
- R. Pohl, O. Socha and P. Slavíček, et al. , Faraday Discuss., 2018, 212, 331–344 RSC.
- W. Fang, J. Chen and M. Rossi, et al. , J. Phys. Chem. Lett., 2016, 7, 2125–2131 CrossRef CAS.
- A. Pérez, M. E. Tuckerman, H. P. Hjalmarson and O. A. von Lilienfeld, J. Am. Chem. Soc., 2010, 132, 11510–11515 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- M. C. Payne, M. P. Teter and D. C. Allan, et al. , Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS.
- S. J. Clark, M. D. Segall and C. J. Pickard, et al. , Z. Krist., 2005, 220, 567–570 CAS.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef.
- E. McNellis, J. Meyer and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205414 CrossRef.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef.
- A. H. Larsen, J. J. Mortensen and J. Blomqvist, et al. , J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef.
- S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66 CrossRef CAS.
- J. Dziedzic, H. H. Helal and C.-K. Skylaris, et al. , EPL, 2011, 95, 43001 CrossRef.
- M. H. Hansen, J. A. G. Torres, P. C. Jennings, et al., arXiv preprint arXiv:1904.00904, 2019.
- J. A. G. Torres, P. C. Jennings and M. H. Hansen, et al. , Phys. Rev. Lett., 2019, 122, 156001 CrossRef.
- M. Razavy, Quantum Theory Of Tunneling, World Scientific Publishing Company, 2nd edn, 2013 Search PubMed.
- R. Kosloff, Annu. Rev. Phys. Chem., 1994, 45, 145–178 CrossRef CAS.
- A. Abdulle, SIAM J. Sci. Comput., 2002, 23, 2041–2054 CrossRef.
- C. Rackauckas and Q. Nie, J. Open Res. Softw., 2017, 5, 15 CrossRef.
- C. M. Marian, J. Phys. Chem. A, 2007, 111, 1545–1553 CrossRef CAS.
- S. Das, K. Nam and D. T. Major, J. Chem. Theory Comput., 2018, 14, 1695–1705 CrossRef CAS.
- J. C. Polanyi, Acc. Chem. Res., 1972, 5, 161–168 CrossRef CAS.
- S. Tolosa, J. Sansón and A. Hidalgo, J. Mol. Liq., 2020, 308, 113036 CrossRef CAS.
- Z. Lv, S. Cui, F. Guo and G. Zhang, AIP Adv., 2019, 9, 015015 CrossRef.
- A. Gheorghiu, P. V. Coveney and A. A. Arabi, Interface Focus, 2020, 10, 20190120 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05781a |
| This journal is © the Owner Societies 2021 |