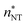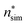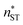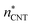Open Access Article
Open Access ArticleHomogeneous nucleation of carbon dioxide in supersonic nozzles II: molecular dynamics simulations and properties of nucleating clusters†
Roope
Halonen‡
 *a,
Valtteri
Tikkanen‡
*a,
Valtteri
Tikkanen‡
 a,
Bernhard
Reischl
a,
Bernhard
Reischl
 a,
Kayane K.
Dingilian
a,
Kayane K.
Dingilian
 b,
Barbara E.
Wyslouzil
b,
Barbara E.
Wyslouzil
 bc and
Hanna
Vehkamäki
bc and
Hanna
Vehkamäki
 a
a
aInstitute for Atmospheric and Earth System Research/Physics, University of Helsinki, P.O. Box 64, FI-00014, Helsinki, Finland. E-mail: roope.halonen@helsinki.fi
bWilliam G. Lowrie Department of Chemical and Biomolecular Engineering, The Ohio State University, Columbus, Ohio 43210, USA
cDepartment of Chemistry and Biochemistry, The Ohio State University, Columbus, Ohio 43210, USA
First published on 5th February 2021
Abstract
Large scale molecular dynamics simulations of the homogeneous nucleation of carbon dioxide in an argon atmosphere were carried out at temperatures between 75 and 105 K. Extensive analyses of the nucleating clusters' structural and energetic properties were performed to quantify these details for the supersonic nozzle experiments described in the first part of this series [Dingilian et al., Phys. Chem. Chem. Phys., 2020, 22, 19282–19298]. We studied ten different combinations of temperature and vapour pressure, leading to nucleation rates of 1023–1025 cm−3 s−1. Nucleating clusters possess significant excess energy from monomer capture, and the observed cluster temperatures during nucleation – on both sides of the critical cluster size – are higher than that of the carrier gas. Despite strong undercooling with respect to the triple point, most clusters are clearly liquid-like during the nucleation stage. Only at the lowest simulation temperatures and vapour densities, clusters containing over 100 molecules are able to undergo a second phase transition to a crystalline solid. The formation free energies retrieved from the molecular dynamics simulations were used to improve the classical nucleation theory by introducing a Tolman-like term into the classical liquid-drop model expression for the formation free energy. This simulation-based theory predicts the simulated nucleation rates perfectly, and improves the prediction of the experimental rates compared to self-consistent classical nucleation theory.
1 Introduction
The nucleation of clusters from a supersaturated vapour has a great significance in atmospheric and engineering processes. Nucleation of CO2 is of particular importance, for example, in the context of carbon capture and storage (CCS) technologies,1 as well as in cloud formation in the Martian mesosphere.2 Modelling nucleation, or analysing experimental results, usually assumes that clusters are in a well defined phase, either solid or liquid, and that the respective bulk properties can be used to calculate nucleation rates, critical cluster sizes, etc. However, if nucleation takes place under extreme physical conditions in terms of temperature and pressure, the properties of the nucleating clusters may deviate substantially from those of the equilibrium phase. In the first part of this series,3 we studied the homogeneous nucleation of carbon dioxide in an argon atmosphere in supersonic nozzles at temperatures between 75 and 92 K with corresponding CO2 partial pressures of 39 to 793 Pa, using multiple experimental techniques. Position-resolved pressure trace measurements, small angle X-ray scattering (SAXS) measurements, and Fourier transform infrared (FTIR) spectroscopy were used to determine the onset of nucleation, particle size distributions and aerosol number densities, and the phase of the largest clusters, respectively. While the FTIR spectra suggested that nanometer sized particles had well-defined crystal structures, as expected at these temperatures and pressures, molecular dynamics (MD) simulations revealed that the small clusters critical to the initial stages of nucleation were liquid-like, despite temperatures over 100 K below the triple point of CO2, Tt = 216.55 K. This second paper in the series is devoted to a detailed analysis of the properties of the nucleating clusters, and the implications regarding theoretical modelling of the nucleation process.The theoretical treatment of nucleation has traditionally been a unification of kinetic and equilibrium thermodynamic factors; however cluster energetics should also be considered to account for possible non-equilibrium effects. Recently, the standard kinetic scheme behind the majority of nucleation theories has been validated by atomistic simulations.4,5 In classical nucleation theory (CNT), the thermodynamics related to nucleation, i.e. the clusters' formation free energies, are treated in a simple fashion using the bulk properties of the nucleating substance. While the CNT formalism often fails drastically to predict measured nucleation rates quantitatively, the theory is able to provide qualitative trends matching the observed data. Several extensions and modifications have therefore been introduced to the classical theory. Many of them are phenomenological, while some require a model of molecular interactions.6–13
A very general expression for both the cluster formation free energy ΔWn and potential energy Un of a cluster containing n monomers is
| ΔWn or Un = An + Bn2/3 + Cn1/3+ …, | (1) |
Since many nucleation experiments (and simulations) are carried out at temperatures below the triple point, the clusters formed as a result of a rapid, non-equilibrium process may not exhibit the thermodynamically most stable phase. The lack of empirical data for the relevant bulk properties at these low temperatures also means that important properties such as surface tension need to be extrapolated from measurements at higher temperatures, or obtained directly from simulation. Finally, the formation of a cluster releases a considerable amount of latent heat, and due to the limited number of thermalising collisions with the carrier gas, the temperature of the nucleating clusters may deviate from the bath temperature. The classical treatment of this non-isothermal effect, developed by Feder et al.,15 captures the deviation from thermodynamic equilibrium in a simple correction factor applied to the nucleation rate.
The main difficulty in theoretically estimating nucleation rates is modelling the formation free energy of clusters with sufficient accuracy.16 For the proper treatment of small clusters, atomistic modelling is often unavoidable. For very small clusters, minimum energy structures at 0 K can be calculated using quantum chemical methods, and free energies can be obtained using principles of statistical mechanics.17 For larger clusters, atomistic interactions can be described using classical force fields, and free energies can be obtained from Monte Carlo methods.16,18 These free energetics can then be combined with the standard kinetic scheme of nucleation to calculate actual nucleation rates. In both approaches, it is assumed that the clusters are in perfect thermal equilibrium. However, in this study we are modelling the time evolution of the nucleation process directly using molecular dynamics simulations to account for possible non-equilibrium properties of emerging clusters, which are not captured in the indirect modelling limited to equilibrium conditions. The drawback of direct nucleation simulations is the restriction to conditions where nucleation occurs on a time scale accessible in the simulation. This typically corresponds to nucleation rates that are many orders of magnitude higher than in the experimental processes being modelled.
While many studies on the homogeneous nucleation of the Lennard-Jones fluid and H2O have been carried out using MD simulations,5,19–23 direct nucleation simulations of carbon dioxide remain rare. To our knowledge, only Horsch et al.24,25 have used MD simulations to study homogeneous CO2 nucleation from the vapour phase. Even though these simulations were carried out in a similar manner to this work, several major differences exist. In particular, the authors used a different force field, and the simulations were performed at higher temperatures corresponding to atmospheric rather than the experimental nozzle conditions. Furthermore, temperature control was achieved by a global velocity scaling scheme, which may result in an unphysical removal of latent heat from the nucleating clusters.4,21
The outline of the paper is as follows. Section 2 explains the theoretical framework of nucleation and the details of the molecular dynamics simulations. Section 3 presents detailed results of nucleation simulations and the analyses of the nucleating clusters. Section 4 describes the simulation-based improvement of classical nucleation theory. Section 5 summarizes and concludes the work.
2 Theories and methods
2.1 Theoretical framework of nucleation
The classical nucleation theory (CNT), or one of its variants, is often applied to predict nucleation rates and to interpret results obtained from experiments and simulations. In CNT, the formation of a new phase from a supersaturated vapour is assumed to proceed through a critical cluster, and clusters can only grow by monomer addition and decay by monomer loss. By combining equilibrium thermodynamics with kinetic gas theory, the classical expression for the nucleation rate in a supersaturated vapour is given as26,27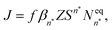 | (2) |
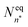 is the equilibrium critical cluster density, f is the non-isothermal correction factor, Z is the Zeldovich factor, and S is the saturation ratio defined as the ratio between the vapour pressure of the monomers and equilibrium pressure over the bulk liquid. The collision rate between monomers and an n-cluster with radii r1, and rn, respectively, can be obtained from kinetic gas theory at temperature T as
is the equilibrium critical cluster density, f is the non-isothermal correction factor, Z is the Zeldovich factor, and S is the saturation ratio defined as the ratio between the vapour pressure of the monomers and equilibrium pressure over the bulk liquid. The collision rate between monomers and an n-cluster with radii r1, and rn, respectively, can be obtained from kinetic gas theory at temperature T as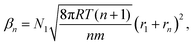 | (3) |
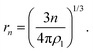 | (4) |
In equilibrium with bulk liquid (i.e. S = 1), the cluster distribution Neqn is related to the total number density of monomers and clusters Neqtot in the system and the equilibrium formation free energy ΔWeqn of an n-cluster as
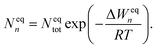 | (5) |
![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) n = SnNeqn, n = SnNeqn, | (6) |
![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 1, eqn (2) can be written as
1, eqn (2) can be written as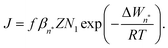 | (7) |
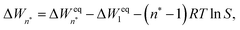 | (8) |
| ΔWeqn = Anσn = A1σnn2/3, | (9) |
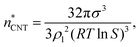 | (10) |
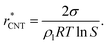 | (11) |
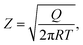 | (12) |
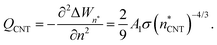 | (13) |
Various corrections or extensions to the CNT liquid-drop model have been suggested, many of them concentrate on the radius-related term in eqn (1). A common modification to CNT is to include the size-dependency of the droplet's surface tension in the formation free energy expression by using the Tolman equation,14
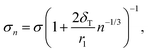 | (14) |
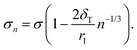 | (15) |
Classical nucleation theory also assumes perfect thermal equilibrium throughout the system. However, cluster formation involves the release of substantial amounts of latent heat, which requires subsequent collisions with the carrier gas to be dissipated. To account for any non-isothermal effects, we use the classical non-isothermal correction factor of Feder et al.,15
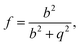 | (16) |
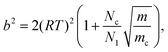 | (17) |
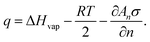 | (18) |
| qn = Un−1 − Un, | (19) |
In this work, the nucleation rates calculated using eqn (7)–(13), (16), (17), and (19) are denoted by JCNT.
2.2 Molecular dynamics simulation of carbon dioxide
Classical molecular dynamics simulations (MD) are employed to study the homogeneous nucleation of CO2 clusters in an atmosphere of CO2 and Ar. CO2 molecules are described by the TraPPE potential,38 using a rigid geometry with a C–O bond length of 1.16 Å and O–C–O angle of 180°. This potential has been fitted to reproduce the experimental liquid–vapour coexistence line and the Clausius–Clapeyron curve of the saturated vapour pressure, and it also reproduces the low-temperature vapour–liquid equilibria and solid–vapour equilibria reasonably well.39 Argon is modelled as a nonpolar atom with only pairwise interactions with C, O and other Ar atoms. The pairwise interactions between atoms i and j with partial charges qi and qj, separated by a distance rij, are described by the sum of Lennard-Jones and Coulomb interactions as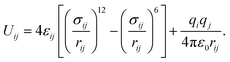 | (20) |
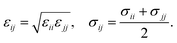 | (21) |
All simulations have been carried out with the LAMMPS MD code,41 using a velocity-Verlet integrator and a time step of 5 fs. Lennard-Jones and Coulomb interactions were cut off at 10 Å and 100 Å, respectively. For large systems with low density, evaluating the Coulomb interaction in real space only, but with a large cut-off, was found to be an efficient yet accurate alternative to the usual Ewald-type approach. The standard approach of using a global thermostatting algorithm is not suitable for directly simulating a nucleating vapour, as it leads to an unphysical removal of latent heat from the nucleating clusters. It has been shown that the best way to avoid this artefact is to introduce explicit carrier gas molecules in the simulation, and apply a thermostat only to the latter, even though this increases the computational cost significantly.4,5,19–21 Here, we have applied a Nosé–Hoover thermostat with time constant 0.1 ps to the Ar atoms. This approach prevents heating of the carrier gas due to latent heat release. However, at the studied conditions, this is a minor effect and we chose to neglect it in the simulation setup.
Clusters are distinguished from the vapour by using a Stillinger criterion42 with a carbon–carbon distance cut-off of 6 Å, roughly corresponding to the position of the second peak in the radial distribution function of liquid CO2.
To study the structural and energetic properties of the emerging clusters, we saved the atomic positions and velocities of clusters larger than four monomers from the nucleation simulations for further analysis. The structural and energetic properties of the isolated clusters were then evaluated in separate microcanonical MD simulation runs. These NVE simulations were carried out for 1 ns or until the cluster evaporated: the integrity of the cluster was checked every 50 ps and, in case one or more molecules had evaporated, the last 50 ps of the simulation data were discarded.
Moreover, a subset of these isolated clusters were also equilibrated by coupling them directly to a Nosé–Hoover thermostat with a time constant of 5 ps. In these simulations, the Nosé–Hoover thermostat mimics heat exchange with carrier gas of a well-defined temperature. By choosing a relatively weak coupling, we ensure that the clusters are able to explore phase space efficiently and have a chance to undergo a liquid-to-solid phase transition. The duration of these NVT simulations varied by cluster size. The simulations were run until a clear transition from the initial state was observed as a drop in potential energy.
3 Results and discussion
3.1 Direct nucleation simulations
We have studied 10 individual systems of supersaturated CO2 vapour at different densities and temperatures. The selected bath temperatures, T = 75, 90 and 105 K, correspond to extremely undercooled vapour and overlap with the experimental temperature range in part I of this study.3 The simulated CO2 number densities are slightly higher than the experimental ones. To observe nucleation on a computationally accessible time-scale, nucleation rates in the simulations have to be on the order of 1024 cm−3 s−1, whereas the supersonic nozzle experiments3 were constrained to rates of about 1017 cm−3 s−1. All the simulated systems consisted of 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CO2 molecules and an equal number of thermalizing Ar gas atoms. This corresponds to the upper end of CO2
000 CO2 molecules and an equal number of thermalizing Ar gas atoms. This corresponds to the upper end of CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar ratios in the experiments where CO2 concentrations reached 39 mol%.
Ar ratios in the experiments where CO2 concentrations reached 39 mol%.
The nucleation rates can be calculated from the time evolution of the cluster density using the Yasuoka–Matsumoto threshold method:19
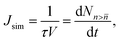 | (22) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) is the number density of clusters larger than some threshold size
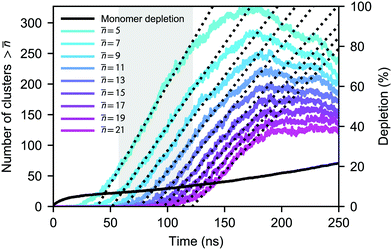
is the number density of clusters larger than some threshold size ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) . Here, τ is proportional to the slope of the linear part of the curve, shown in Fig. 1 (equivalent graphs are shown for the other simulation runs in ESI,† Fig. S1), during the nucleation stage. This nucleation stage is arbitrarily estimated as the time period when the number of clusters n >
. Here, τ is proportional to the slope of the linear part of the curve, shown in Fig. 1 (equivalent graphs are shown for the other simulation runs in ESI,† Fig. S1), during the nucleation stage. This nucleation stage is arbitrarily estimated as the time period when the number of clusters n > ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) lies between 20% and 80% of the observed maximum. However, the main results of this study are rather insensitive to this definition. Ideally, τ should be constant if
lies between 20% and 80% of the observed maximum. However, the main results of this study are rather insensitive to this definition. Ideally, τ should be constant if ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) is sufficiently larger than the critical size. In our case, however, the monomer density is decreasing too quickly as discussed below and nucleation, consequently, slows down. We have estimated the nucleation rates using multiple threshold sizes, and verified that the magnitude of the rate for an individual run remains largely unaffected by that choice.
is sufficiently larger than the critical size. In our case, however, the monomer density is decreasing too quickly as discussed below and nucleation, consequently, slows down. We have estimated the nucleation rates using multiple threshold sizes, and verified that the magnitude of the rate for an individual run remains largely unaffected by that choice.
The average nucleation rates Jsim are presented in Table 2 and Fig. 2. The results clearly show that the nucleation rate increases with saturation ratio S. Additional information about the nucleation rate calculations and equilibrium pressure can be found in the ESI.†
| T (K) | N (Å−3) | N 1 (Å−3) | D (%) | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S S |
J sim (cm−3 s−1) | J ΔW (cm−3 s−1) | J ST (cm−3 s−1) | J CNT (cm−3 s−1) |
|---|---|---|---|---|---|---|---|---|
| 75 | 2.0 × 10−6 | 1.83 × 10−6 | 8.5 | 12.01 | 7.5 × 1022 | 1.9 × 1023 | 6.7 × 1022 | 1.2 × 10−2 |
| 75 | 4.0 × 10−6 | 3.42 × 10−6 | 14.6 | 12.63 | 8.4 × 1023 | 1.9 × 1024 | 6.4 × 1023 | 2.0 × 10−1 |
| 75 | 6.0 × 10−6 | 4.88 × 10−6 | 18.7 | 12.99 | 2.9 × 1024 | 6.5 × 1024 | 2.1 × 1024 | 7.7 × 10−1 |
| 75 | 1.0 × 10−5 | 7.55 × 10−6 | 24.5 | 13.42 | 1.2 × 1025 | 2.8 × 1025 | 8.2 × 1024 | 3.2 × 100 |
| 90 | 6.0 × 10−6 | 5.48 × 10−6 | 8.6 | 8.79 | 3.6 × 1023 | 7.4 × 1023 | 2.9 × 1023 | 4.5 × 102 |
| 90 | 8.0 × 10−6 | 7.08 × 10−6 | 11.5 | 9.04 | 1.0 × 1024 | 2.1 × 1024 | 1.0 × 1024 | 3.0 × 103 |
| 90 | 1.0 × 10−5 | 8.57 × 10−6 | 14.3 | 9.23 | 2.9 × 1024 | 5.6 × 1024 | 2.7 × 1024 | 1.6 × 104 |
| 90 | 1.3 × 10−5 | 1.07 × 10−5 | 17.9 | 9.45 | 7.4 × 1024 | 1.5 × 1025 | 7.5 × 1024 | 7.6 × 104 |
| 105 | 2.0 × 10−5 | 1.71 × 10−5 | 14.4 | 6.86 | 2.8 × 1024 | 6.0 × 1024 | 3.3 × 1024 | 5.9 × 106 |
| 105 | 3.0 × 10−5 | 2.38 × 10−5 | 20.7 | 7.19 | 2.2 × 1025 | 4.5 × 1025 | 2.9 × 1025 | 3.0 × 108 |
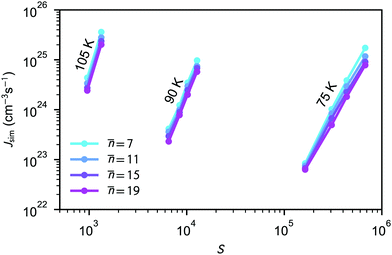 | ||
Fig. 2 Simulated nucleation rates for four different threshold values ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) shown as a function of saturation ratio S. According to the nucleation theorem, eqn (23), for constant temperature, the slope of a presented line on this graph equals approximately the critical cluster size n*. shown as a function of saturation ratio S. According to the nucleation theorem, eqn (23), for constant temperature, the slope of a presented line on this graph equals approximately the critical cluster size n*. | ||
As the number of molecules is kept constant during the simulations, the monomer pool is continuously depleted due to cluster formation. The simulated nucleation process is relatively aggressive, clusters are formed quickly and in large numbers, and most of the simulation runs do not reach a steady monomer concentration as shown in Fig. 1 for one case. To estimate the monomer density (and saturation ratio) at which the nucleation actually takes place, we have calculated the average monomer density at the nucleation stage corresponding to n > 5. In the case of the densest system at 75 K, almost one quarter of the monomers are lost to clusters already after 5 ns. At higher temperatures, the number of clusters formed and consequently the extent of depletion are smaller, yet the nucleation rates are on the same order of magnitude as in the simulations carried out at 75 K.
During the nucleation stage, the possibility for cluster–cluster collisions is very minor; the ratio of dimers to free monomers is at most ∼0.05. However, after the nucleation stage, the reduction in the number of small clusters in Fig. 1 and Fig. S1 (ESI†) is due to the abundance of very large clusters, which eventually start to scavenge other clusters via coagulation, in addition to the increase in monomer depletion.
Even though we find a systematic decrease of τ with threshold size, as shown in Fig. 1 and Fig. S1 (ESI†), the slopes suggest that the critical sizes are below 7, 9, and 11 monomers at T = 75, 90, and 105 K, respectively (see ESI†). If the cluster growth follows classical theory, the critical cluster size can be estimated from the first nucleation theorem:43
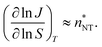 | (23) |
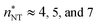 at T = 75, 90, and 105 K, respectively. These values are compared with results derived from theoretical models in Section 4 and Table 3. The selected threshold size has only a slight impact on the results obtained through the nucleation theorem.
at T = 75, 90, and 105 K, respectively. These values are compared with results derived from theoretical models in Section 4 and Table 3. The selected threshold size has only a slight impact on the results obtained through the nucleation theorem.
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (the critical size should be smaller than this), nucleation theorem
(the critical size should be smaller than this), nucleation theorem 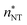 , free energy profile calculated from the simulated cluster distributions
, free energy profile calculated from the simulated cluster distributions 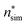 , simulation-based theory
, simulation-based theory 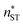 , and classical theory
, and classical theory 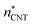 . The planar surface tensions extrapolated from Fig. 3 are used to calculate
. The planar surface tensions extrapolated from Fig. 3 are used to calculate 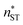 and
and 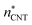
| T (K) | N (Å−3) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
|
||||
|---|---|---|---|---|---|---|
| 75 | 2.0 × 10−6 | <7 | 3.6 | 8.1 | 6.5 | 16.5 |
| 75 | 4.0 × 10−6 | <7 | 3.6 | 7.6 | 5.9 | 15.6 |
| 75 | 6.0 × 10−6 | <7 | 3.6 | 7.3 | 5.6 | 15.1 |
| 75 | 1.0 × 10−5 | <7 | 3.6 | 7.0 | 5.3 | 14.7 |
| 90 | 6.0 × 10−6 | <9 | 4.7 | 8.9 | 8.0 | 18.9 |
| 90 | 8.0 × 10−6 | <9 | 4.7 | 9.1 | 7.5 | 18.1 |
| 90 | 1.0 × 10−5 | <9 | 4.7 | 9.0 | 7.1 | 17.5 |
| 90 | 1.3 × 10−5 | <9 | 4.7 | 7.9 | 6.7 | 16.9 |
| 105 | 2.0 × 10−5 | <11 | 6.5 | 10.3 | 9.1 | 20.7 |
| 105 | 3.0 × 10−5 | <11 | 6.5 | 8.6 | 7.9 | 18.9 |
βn−1![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) n−1 − αn n−1 − αn![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) n = 0, n = 0, | (24) |
| βn−1Nn−1 − αnNn = J, | (25) |
![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) n =
n = ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔWn/RT), we can derive the following relationship for the free energy change upon monomer addition using eqn (24) and (25):
exp(−ΔWn/RT), we can derive the following relationship for the free energy change upon monomer addition using eqn (24) and (25):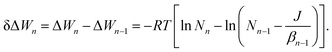 | (26) |
![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 1, the monomer formation free energy is by definition zero. The n-cluster formation free energy is now easily computed as
1, the monomer formation free energy is by definition zero. The n-cluster formation free energy is now easily computed as 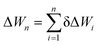 . Note, that possible size-independent liquid-drop model terms of ΔWn are now neglected, but this is equivalent to the “self-consistent” free energy treatment in eqn (8).
. Note, that possible size-independent liquid-drop model terms of ΔWn are now neglected, but this is equivalent to the “self-consistent” free energy treatment in eqn (8).
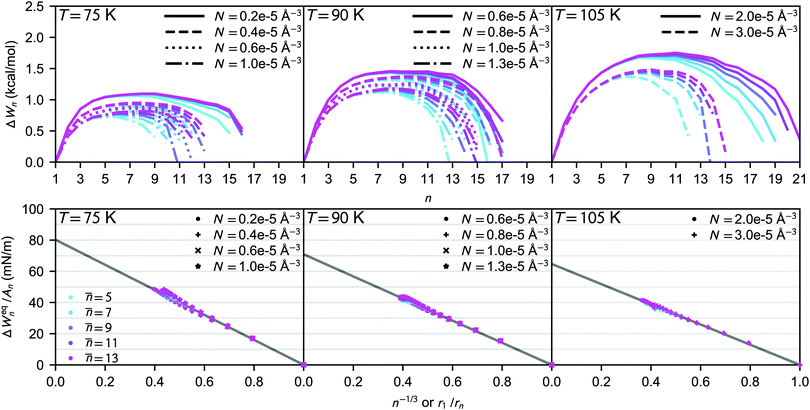
In order to retrieve the formation free energies from the simulations, we have analysed the cluster distributions during the nucleation stage (as defined earlier, using the “20–80%” rule) to calculate J using different threshold values ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) . The free energy curves obtained using eqn (26) are shown in the upper panel of Fig. 3. At each temperature studied, a clear barrier can be seen, whose height decreases as the vapour density increases. The shape of the tail of the curve at the largest cluster sizes is affected by the threshold size
. The free energy curves obtained using eqn (26) are shown in the upper panel of Fig. 3. At each temperature studied, a clear barrier can be seen, whose height decreases as the vapour density increases. The shape of the tail of the curve at the largest cluster sizes is affected by the threshold size ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) used; this might be a consequence of the shift of the nucleation stage in time (eventually nucleation is hindered by depletion, and coagulation becomes significant). The value used for the collision rate βn also affects the shape somewhat: the barrier becomes sharper if the collision rate is reduced. However, both the barrier height and the subcritical free energies are rather robust against changes in threshold size and collision rate.
used; this might be a consequence of the shift of the nucleation stage in time (eventually nucleation is hindered by depletion, and coagulation becomes significant). The value used for the collision rate βn also affects the shape somewhat: the barrier becomes sharper if the collision rate is reduced. However, both the barrier height and the subcritical free energies are rather robust against changes in threshold size and collision rate.
To reduce the calculated formation free energies at supersaturation (S > 1) to equilibrium values (S = 1), the volume-dependent term shown in eqn (9) must be subtracted. According to the extended liquid-drop model, the equilibrium formation energy of an n-cluster is
ΔWeqn = ΔWn + (n − 1)RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = A1σn2/3 + Cn1/3. S = A1σn2/3 + Cn1/3. | (27) |
The values extrapolated from the data give quite reasonable values for the surface tension (σ = limn→∞ΔWeqn/An), of about 80.2, 70.9 and 64.7 mN m−1 at T = 75, 90 and 105 K, respectively. These simulation-based “planar surface tensions” are higher than those obtained from the thermophysical relations of Quinn44 (55.2, 50.8, 46.4 mN m−1) and Lielmezs–Herrick3,45 (67.9, 60.2 and 53.4 mN m−1), and there is a slight dependence on vapour density. Notably, the simulated cluster distributions used in eqn (26) correspond to non-isothermal conditions, hence the effect of insufficient thermalisation is embodied in the ΔWn (the barrier is higher as nucleation is suppressed). The nonisothermality is inherently a thermodynamic effect and thus related to the free energies, yet in the theory of Feder et al.,15 the effect of excess energy is reduced to a prefactor in the nucleation rate expression.
To test the reliability of the kinetic scheme of the classical theory (eqn (7)), we have used the barrier heights shown in the upper panel of Fig. 3 to back-calculate the simulated nucleation rates. As the planar surface tension can be evaluated from the results shown in Fig. 3, we have used eqn (12) and (13) to estimate the value of the Zeldovich factor. The results are shown in Table 2 as JΔW. The kinetic scheme seems to work rather well as the back-calculated nucleation rates are within a factor of two of the directly calculated ones, corresponding to an uncertainty of RT in the barrier height.
3.2 Cluster analysis
We performed a detailed analysis of the structural and energetic properties of CO2 clusters during the nucleation stage and compared them to their equilibrated counterparts.From the direct nucleation simulations, a large set of clusters in the size range n = 5…315, was extracted and examined in isolation. For each combination of temperature and vapour pressure, the collected sample consisted of at least tens of thousands of statistically different configurations for clusters containing 10 monomers or less, and, for example, at least hundreds of configurations for 50-clusters. For sizes exceeding 100 molecules, the sample did not contain configurations for each individual cluster size.
To study the size-specific properties of nucleation-stage clusters, all of the isolated clusters were simulated in NVE for a maximum of 1 ns, and the potential energy, U, and kinetic energy, K, were stored. As evaporation events are rather frequent in the studied size range, the runs were divided into 50 ps sub-runs. In case of evaporation, the simulation was terminated and the last 50 ps of data discarded, to avoid spurious contributions to the average from fragmented clusters. As the resulting energy distributions were near-Gaussian, they are well-described by the mean values of the energy.
The properties of equilibrated clusters of different sizes were investigated by simulating a subset of the clusters isolated from the nucleation simulations in NVT for a few to hundreds of nanoseconds, depending on the cluster size and temperature. For small clusters, at least tens of different cases were studied for each size, with sample standard deviations of U being very small (a few percent at most). For clusters exceeding the size n = 50, even a single cluster could yield useful information, as all large clusters exhibited well-defined crystalline configurations.
As shown in Fig. 4, the deviation between the equimolar radius rMDn obtained from the analysis of the clusters' radial density profiles and the liquid-drop radius rn increases for the smaller clusters. This difference can be fitted quite accurately as
| rMDn = (1 − an−1/3)rn, | (28) |
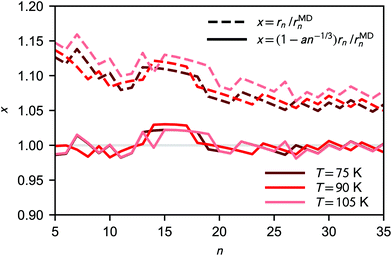 | ||
| Fig. 4 Ratio of liquid-drop radius and simulated equimolar radius (dashed lines) as a function of cluster size. The solid lines shows the fitted correction to the liquid-drop model (a ≈ 0.25). | ||
The consequences of a deviation in cluster size compared to classical theory are mostly thermodynamical, i.e., related to the surface area in eqn (9); the effect on the collision rate is very minor. In line with kinetic theory, possible effects due to long-range interactions on collision rates28,30,31 are neglected. The implications of the radius correction is further discussed in Section 4.
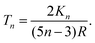 | (29) |
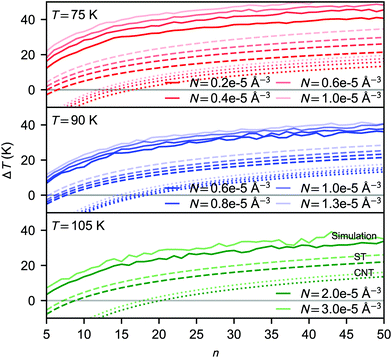 | ||
| Fig. 5 Average cluster temperature difference relative to the bath temperature as a function of cluster size: for simulations carried out at 75 K (upper panel), 90 K (middle panel) and 105 K (lower panel). The solid lines correspond to average kinetic energies calculated from the NVE simulations. The predicted values using eqn (30) are shown for CNT and the simulation-based theory as dotted and dashed lines, respectively. | ||
The temperature difference expression related to the non-isothermal theory is given as15,21
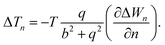 | (30) |
In rather similar nucleation simulations of Lennard-Jones vapour, Wedekind et al.21 found that the cluster temperature distributions were skewed, diverging from Gaussian, and they focused on the peak value instead of the mean of the cluster temperature distribution. In our case, as shown in Fig. S3 (ESI†), the temperature distributions of CO2 clusters are clearly Gaussian, and there is little difference between mean and peak values.
It has been a subject of a long debate whether the subcritical clusters are colder than the bath temperature or hotter just like the rest of the clusters in a non-isothermal system. Following the seminal study by Feder et al.,15 the “cool cluster” hypothesis has both been supported21,47 and rejected.48–51 The observed discrepancy between the simulated and theoretical cluster temperature shift may at first appear as a failure of eqn (16), however, as already briefly discussed by Feder et al.,15 the observed ΔTn might always be positive. The reason is that even if the majority of the subcritical clusters are above the bath temperature, nucleation is mainly promoted by the rare “cold” and stable clusters. A more elaborate discussion about the cluster temperatures is presented by barrett.50
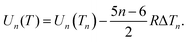 | (31) |
| Un = An + Bn2/3. | (32) |
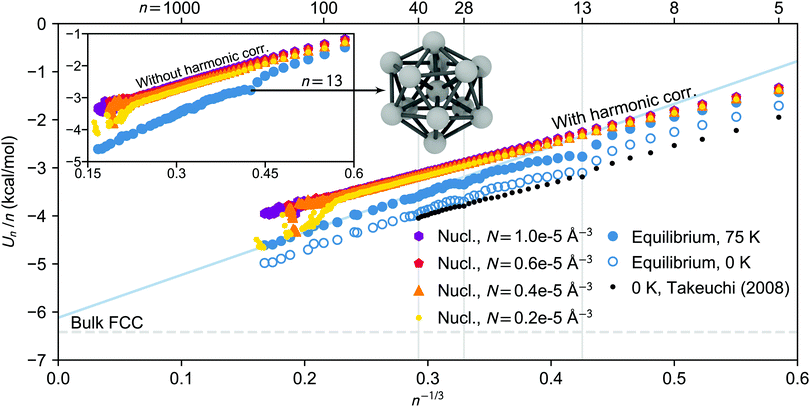 | ||
| Fig. 6 Potential energy per molecule as a function of n−1/3 for clusters isolated from nucleation simulation carried out at 75 K. The energies of the nucleating clusters at different vapour densities (from NVE simulations) are shown as colourful dots, triangles, pentagons and hexagons, and the equilibrated cluster energies (from NVT simulations) are indicated as filled blue circles. In the inset the energies of the nucleating clusters are given without harmonic correction, while the energies in the main figure are harmonically scaled to 75 K (the blue solid line shows the extrapolated n−1/3 dependence for the large equilibrated clusters). The bulk FCC cohesive energy value at 75 K is shown by the horizontal dashed line. The open circles illustrate the equilibrated potential energies harmonically scaled to 0 K, and the black dots are the geometry optimized global minimum energies obtained by Takeuchi.52 In addition, the equilibrium structure of the icosahedral 13-cluster is illustrated (the oxygen atoms are omitted) and the exceptionally stable cluster sizes (13, 28 and 40) are marked by vertical gray lines. | ||
The surface energies, or surface enthalpies, retrieved from NVE results using the liquid-drop model given in eqn (32) are not directly comparable to the surface tension, i.e., surface free energy, which also includes surface entropy. In fact, molleman and Hiemstra53 recently found Tolman lengths of different magnitudes and even different signs for surface free energy and surface enthalpy of water. Using the liquid-drop radius model, the surface energy can be estimated from eqn (32) as
| ΔHsurf = B/A1. | (33) |
While the potential energies of the nucleating clusters show an almost perfectly linear dependence on n−1/3, the equilibrated cluster potential energies manifest an irregular size dependency in Fig. 6. At the studied temperatures, the face centred cubic (FCC) phase is the stable crystallographic structure of bulk CO2. Yet, the energetically most favorable structure of small clusters can be very different due to the large fraction of under-coordinated molecules at the surface. In case of small clusters of simple liquids such as CO2, it has been widely reported that an icosahedral packing is preferred over a cubo-octahedral shape.52,54,55 Despite these structural ambiguities, we have compared the potential energy extrapolated linearly to n → ∞ from the largest clusters in the simulation, with cohesive energies of bulk FCC systems at equal temperatures. The extrapolated values are relatively close to the bulk value even though the largest clusters analysed contain only about 200 molecules, and clusters this small may still have mixed structures deviating from perfect FCC. The surface enthalpies are 109 and 104 mN m−1 at 75 and 90 K, respectively, which surprisingly correspond exactly to the values obtained from the parameterisation by Lielmezs and Herrick.3,45 Interestingly, for both NVE and NVT simulated clusters, the ratio of the regression coefficients follows rather well the empirical relation56B/A ≈ −2/3.
In the first part of this series, we only analysed the structural differences between nucleating and equilibrated clusters of size n > 10 by calculating the carbon–carbon radial distribution functions and visualising the cluster geometries, as shown in Fig. 11 in ref. 3.
The potential energies presented in Fig. 6, as well as Fig. S5 and S6 (ESI†), confirm the clear difference between nucleating and equilibrated clusters for n ≳ 10 at temperatures of 75 and 90 K. However, nucleating clusters are energetically comparable with the equilibrated ones for n < 10, due to the large fraction of under-coordinated and therefore loosely bound molecules. At the highest studied temperature of 105 K, the discrepancy in energy between nucleating and equilibrated clusters only appears at sizes n ≳ 60.
We observe that the largest clusters considered in this analysis, n ≳ 100, may undergo a phase transition in the nucleation simulation when both temperature and vapour density are low enough (T = 75 K and N = 0.2 × 10−5 Å−3). Even though the relative amount of carrier gas is about equal in all simulations, at low density the clusters accumulate less latent heat and have more time for relaxation between growth events, enabling the transition. Indeed, in the first part of this series,3 Fourier transform infrared spectroscopy identified that the large, nano-scale CO2 particles had a cubic crystal structure. Furthermore, Ramos et al.57 showed that the Raman spectra of growing CO2 clusters in a free-jet expansion indicate a cross-over size n ≈ 150…400 between liquid and solid phases at very similar conditions as discussed here.
We have compared our equilibrium cluster energies with values by takeuchi,52 who calculated the global minimum (0 K) energies for CO2 clusters n = 4…40 using the MOM potential. This model uses five partial charge sites, but the LJ parameters of MOM are less than 5% smaller than the corresponding TraPPE values.58 To our knowledge, this is the only other study systematically probing the structures and energies of CO2 clusters n > 13. After scaling the potential energies obtained in the NVT simulations to 0 K using the harmonic approximation, the scaled potential energies are in relatively good agreement with the global minimum values even though the force fields differ slightly. However, the scaled potential energies are still systematically higher than the reported global minimum values, which is partly due to the ensemble averaging over multiple minima. The difference in energy may also arise from thermal fluctuations in the configuration and the vibrational anharmonicities which are usually more pronounced for loosely bound systems. Indeed, the difference is larger at higher temperatures (see Fig. S5 and S6, ESI†). Based on the Lindemann index analysis, the thermal motion of the smallest equilibrated clusters at 75 K is comparable to the thermal motion of the nucleating clusters of the same size (see ESI† and Fig. S7 for details). This supports the assumption that the equilibrium phase of small pre-icosahedral (i.e. n < 13) clusters can be characterized as liquid-like.
The equilibrium simulations at 75 and 90 K identify enhanced stability of 13, 28 and 40-clusters, a result that is also found by Takeuchi52 (see Fig. S8, ESI† for more detail), and consequently for these sizes the difference between average equilibrium potential energies and global minimum values is very small (less than 3% at 75 K). In many studies of solid clusters, “magic numbers” such as 13, 55, 147,… are of particular interest as they correspond to very tightly bound and highly symmetric icosahedral shapes.55 As mentioned before, at 105 K the icosahedral shape and configurational energy minimum of the 13-, or 55-clusters is not observed during the NVT simulation, where all clusters below size ∼60 are found to be liquid-like. This is in line with results by Maillet et al.,54,59 who observed that using the MOM potential, both 13- and 55-clusters undergo a phase transition between 90 and 100 K.
In summary, the nucleating clusters are energetically and structurally very different from the equilibrium, or global minima configurations. Despite the strong undercooling, the nucleating clusters are more liquid-like, and should be treated accordingly when predicting nucleation rates at these conditions.
4 Simulation-based improvement on CNT
In Section 3.1.1, we found reasonable agreement between theory and atomistic simulations by importing the nucleation barrier height obtained from the MD simulation into the theoretical kinetic equation of nucleation. The validity of the kinetic scheme of nucleation has been also recently reported by Halonen et al.4 and Ayuba et al.5 In addition, in Sections 3.1.1 and 3.2.3, we have demonstrated that the nucleating CO2 clusters are liquid-like and a radius-related term should be taken into account while applying CNT-like theory to predict homogeneous nucleation. Here we present an improvement to the classical theory, in similar fashion as Tanaka et al.,22 by expressing the critical radius and the Q parameter in the Zeldovich factor in terms of their classical counterparts.If the requirement for self-consistency is followed (i.e. ΔWeq1: = 0), the linear behaviour of ΔWeqn/An seen from the lower panel of Fig. 3 would imply that the liquid-drop model coefficient C = −A1σ, which translates into a Tolman-like constant δT = r1/2. Applying this result, we can introduce a simulation-based theory (ST) which states that the critical cluster size can be written as
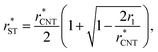 | (34) |
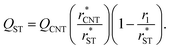 | (35) |
It would be imprudent to claim that the Tolman length for pure CO2 clusters is positive and its value to be r1/2 (actually, it is recently estimated to be negative35). The origin of the n1/3 term is not necessarily only due to the effect of curvature on surface tension, but other physical effects with the same functional form might also be present. As discussed in Section 3.2.1, the simulated cluster radii are related to the liquid-drop radii by eqn (28). This deviation from the liquid-drop radii gives a rather clear indication of a non-Tolman-like effect. As both the surface area (An = 4πrn2) and the “Tolman” term (2δT/rn) depend on the cluster radius, the correction to the cluster radius introduces an additional term in the formation free energies:
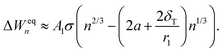 | (36) |
We have also used the effective planar surface tensions extrapolated from Fig. 3 to calculate the theoretical estimates for nucleation rates in the simulated systems using eqn (27), (34) and (35), instead of eqn (9), (11) and (13), respectively. As these surface tensions are obtained from non-equilibrium simulations, the non-isothermal correction should not be applied here.
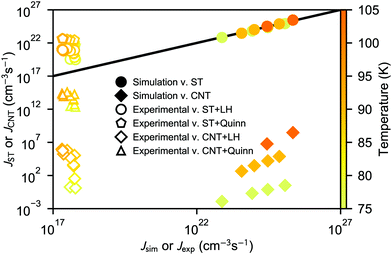
The nucleation rates from simulation and both classical (CNT) and simulation-based (ST) theories are reported in Table 2 and illustrated in Fig. 7. The agreement between simulation and ST is perfect, whereas the values from CNT are several orders of magnitude off. The critical cluster sizes are reported in Table 3. Again, the theoretical values from ST are close, but still smaller, than the estimated threshold values used to calculate the nucleation rates from direct MD simulation data. The agreement between critical cluster size 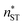 and the locations of the top of the nucleation barriers shown Fig. 3 is also quite good, whereas CNT overpredicts the critical size by about a factor of two. The critical cluster size obtained from the first nucleation theorem is systematically smaller than observed in the simulation, this is in line with findings of wedekind and Reguera,60 and Napari et al.,61 who used alternative simulation methods to study the nucleation in supersaturated Lennard-Jones vapour.
and the locations of the top of the nucleation barriers shown Fig. 3 is also quite good, whereas CNT overpredicts the critical size by about a factor of two. The critical cluster size obtained from the first nucleation theorem is systematically smaller than observed in the simulation, this is in line with findings of wedekind and Reguera,60 and Napari et al.,61 who used alternative simulation methods to study the nucleation in supersaturated Lennard-Jones vapour.
It may seem at first glance that the reason for the excellent agreement between simulation and ST predictions is that the nucleation rate estimated directly from the nucleation simulations is inserted in eqn (26) to compute the formation free energies. However, the theoretical prediction does not strongly depend on the value of J. For example, the position of the top of the free energy barrier, the linear behaviour shown in the bottom panels of Fig. 3, and the extrapolated surface tension, remain the same when J is chosen to be several orders of magnitude higher. However, such a radical change of J alters the shape of the free energy barrier for over-critical clusters. The perfect agreement between ST predictions and simulations is due to the fact that both the size dependence of the formation free energy (i.e., the thermodynamics), as well as the kinetic scheme are well described.
The theoretical nucleation rates corresponding to the experimental conditions of Dingilian et al.3 are also presented in Fig. 7. The thermophysical properties of liquid CO2 as well as surface tension parameterisations by Quinn, and Lielmezs and Herrick, needed to calculate the nucleation rates are given in Table S1 (ESI†). Here the non-isothermal correction is included, and the value of q is estimated from the cluster potential energies (see ESI†). The nucleation rate values from ST are a couple orders of magnitude higher than the experimental rates, and using the Lielmezs–Herrick relation for surface tension yields a slightly better agreement than using the Quinn relation. The CNT predictions using the Quinn relation are slightly lower than the experimental rates, but still quite close, whereas using CNT with the Lielmezs–Herrick relation underpredicts the experimental rates by over ten orders of magnitude.
While the uncertainty in surface tension of small, severely undercooled liquid clusters is the main concern in the context of this work, other sources of error exist as well. Some additional terms might still be missing in the liquid-drop model, other than the ones related to radius. Accounting for the effect of vapour–cluster interactions in highly supersaturated systems can increase the nucleation barrier,4,62 and this can have a substantial effect on the results. Also the effect of long-range interactions and possible non-accomodation of collision rates are neglected in the classical view of nucletion.28–31
5 Conclusions
We have carried out large scale molecular dynamics simulations of the homogeneous nucleation of CO2 in Ar carrier gas in a similar range of temperatures (75 to 105 K) as in the supersonic nozzle experiments in the first part of this series.3 We calculated nucleation rates using the threshold method for ten different combinations of temperature and vapour pressure and derived the respective cluster formation free energies from the obtained cluster distributions. Analysis of the size dependence of the free energies using a liquid-drop model clearly indicated the need to incorporate an additional Tolman-like term ∝ n1/3 into the free energy expression, as proposed by Tanaka et al.22 for Lennard-Jones fluid. Using this finding, we were able to formulate a simulation-based improvement on classical nucleation theory, leading to a highly accurate prediction of the simulated nucleation rates. Here, values of the planar surface tension obtained from an extrapolation of the size dependence of the equilibrium formation free energies were used. At these deeply undercooled temperatures, the surface tension values were significantly higher compared to extrapolated values using parameterizations for liquid CO2. The simulation-based theory did not predict the experimental nucleation rates as accurately as the simulated nucleation rates. However, the difference was only 1–5 orders of magnitude, while the predictions of self-consistent classical nucleation theory were off by 3–18 orders of magnitude, indicating that the simulation-based theory offers a significant improvement.As demonstrated through the thermophysical properties retrieved from the MD simulations, the standard Szilard–Farkas kinetic scheme of nucleation describes the simulated homogeneous nucleation of CO2 rather well. As already discussed in the first part of this series, the major problem in theoretically estimating the nucleation rate of extremely undercooled CO2 is the inaccuracy of the available surface tension parameterisation. The experiments are carried out over 100 K below the triple point, conditions in which liquid is a highly unstable phase. The analysis of the TraPPE–CO2 clusters shows considerably higher planar surface tension than for liquid CO2. On the other hand, the obtained surface enthalpies of liquid clusters are in good agreement with the surface tension relation of Quinn.44
From the nucleation simulations we isolated clusters and studied their structural and energetic properties. Due to insufficient thermalization of the nucleating clusters through collisions with the carrier gas, the clusters accumulate a significant amount of latent heat from individual monomer captures. Based on the analysis of the kinetic energy, we observed cluster temperatures systematically above the temperature of the carrier gas. The energetic analysis revealed that during the nucleation stage, clusters containing fewer than 100 molecules were liquid-like at all studied temperatures and pressures. While the majority of these clusters undergoes a phase transition to the solid state upon equilibration, some of the smallest clusters remain liquid-like despite the strong undercooling. Over a century ago, Ostwald63 observed in the context of crystal growth from solution that the phase transition occurred through intermediate metastable phases until the most stable phase was reached. Here we have demonstrated that this empirical step rule is equally valid for clusters in the gas phase in extremely undercooled conditions, where the stable cluster structure is crystalline.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was completed with the financial support of the ERC grant no. 692891-DAMOCLES, the University of Helsinki, Faculty of Science ATMATH project, and the National Science Foundation under grant number CBET-1511498. Supercomputing resources were provided by the CSC-IT Center for Science, Ltd, Finland, and the Finnish Grid and Cloud Infrastructure (urn:nbn:fi:research-infras-2016072533) at the University of Helsinki. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357.References
- J. Gibbins and H. Chalmers, Energy Policy, 2008, 36, 4317–4322 CrossRef
.
- A. Määttänen, F. Montmessin, B. Gondet, F. Scholten, H. Hoffmann, F. González-Galindo, A. Spiga, F. Forget, E. Hauber and G. Neukum,
et al.
, Icarus, 2010, 209, 452–469 CrossRef
.
- K. K. Dingilian, R. Halonen, V. Tikkanen, B. Reischl, H. Vehkamäki and B. E. Wyslouzil, Phys. Chem. Chem. Phys., 2020, 22, 19282–19298 RSC
.
- R. Halonen, E. Zapadinsky and H. Vehkamäki, J. Chem. Phys., 2018, 148, 164508 CrossRef
.
- S. Ayuba, D. Suh, K. Nomura, T. Ebisuzaki and K. Yasuoka, J. Chem. Phys., 2018, 149, 044504 CrossRef
.
- W. G. Courtney, J. Chem. Phys., 1961, 35, 2249–2250 CrossRef CAS
.
- S. L. Girshick and C.-P. Chiu, J. Chem. Phys., 1990, 93, 1273–1277 CrossRef CAS
.
- H. Reiss, W. K. Kegel and J. I. Katz, Phys. Rev. Lett., 1997, 78, 4506–4509 CrossRef CAS
.
- A. Dillmann and G. Meier, J. Chem. Phys., 1991, 94, 3872–3884 CrossRef CAS
.
- D. Reguera and J. Rubí, J. Chem. Phys., 2001, 115, 7100–7106 CrossRef CAS
.
- R. McGraw and A. Laaksonen, Phys. Rev. Lett., 1996, 76, 2754 CrossRef CAS
.
- D. Reguera and H. Reiss, Phys. Rev. Lett., 2004, 93, 165701 CrossRef CAS
.
- G. K. Schenter, S. M. Kathmann and B. C. Garrett, Phys. Rev. Lett., 1999, 82, 3484–3487 CrossRef CAS
.
- R. C. Tolman, J. Chem. Phys., 1949, 17, 333–337 CrossRef CAS
.
- J. Feder, K. Russell, J. Lothe and G. Pound, Adv. Phys., 1966, 15, 111–178 CrossRef CAS
.
- J. Merikanto, E. Zapadinsky, A. Lauri and H. Vehkamäki, Phys. Rev. Lett., 2007, 98, 145702 CrossRef
.
- J. Elm, J. Kubečka, V. Besel, M. J. Jääskeläinen, R. Halonen, T. Kurtén and H. Vehkamäki, J. Aerosol Sci., 2020, 149, 105621 CrossRef
.
- B. Chen, J. I. Siepmann, K. J. Oh and M. L. Klein, J. Chem. Phys., 2001, 115, 10903–10913 CrossRef CAS
.
- K. Yasuoka and M. Matsumoto, J. Chem. Phys., 1998, 109, 8451–8462 CrossRef CAS
.
- K. Yasuoka and M. Matsumoto, J. Chem. Phys., 1998, 109, 8463–8470 CrossRef CAS
.
- J. Wedekind, D. Reguera and R. Strey, J. Chem. Phys., 2007, 127, 064501 CrossRef
.
- K. K. Tanaka, J. Diemand, R. Angélil and H. Tanaka, J. Chem. Phys., 2014, 140, 194310 CrossRef
.
- R. Angélil, J. Diemand, K. K. Tanaka and H. Tanaka, J. Chem. Phys., 2015, 143, 064507 CrossRef
.
- M. Horsch, J. Vrabec, M. Bernreuther, S. Grottel, G. Reina, A. Wix, K. Schaber and H. Hasse, J. Chem. Phys., 2008, 128, 164510 CrossRef
.
- M. Horsch, Z. Lin, T. Windmann, H. Hasse and J. Vrabec, Atmos. Res., 2011, 101, 519–526 CrossRef CAS
.
-
F. F. Abraham, Homogeneous Nucleation: The Pretransition Theory of Vapor Condensation, Academic Press, New York, 1974 Search PubMed
.
-
H. Vehkamäki, Classical nucleation theory in multicomponent systems, Springer Science & Business Media, 2006 Search PubMed
.
- R. Halonen, E. Zapadinsky, T. Kurtén, H. Vehkamäki and B. Reischl, Atmos. Chem. Phys., 2019, 19, 13355–13366 CrossRef CAS
.
- E. Goudeli, J. Lee and C. J. Hogan Jr, J. Aerosol Sci., 2020, 105558 CrossRef CAS
.
- O. H. Vasilev and H. Reiss, J. Chem. Phys., 1996, 105, 2946–2947 CrossRef CAS
.
- O. H. Vasilev and H. Reiss, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 3950–3954 CrossRef CAS
.
- D. Saltz, J. Chem. Phys., 1994, 101, 6038–6051 CrossRef CAS
.
- Y. A. Lei, T. Bykov, S. Yoo and X. C. Zeng, J. Am. Chem. Soc., 2005, 127, 15346–15347 CrossRef CAS
.
- N. Bruot and F. Caupin, Phys. Rev. Lett., 2016, 116, 056102 CrossRef
.
- P. Rehner, A. Aasen and Ø. Wilhelmsen, J. Chem. Phys., 2019, 151, 244710 CrossRef CAS
.
- F. M. Kuni, A. P. Grinin and A. K. Shchekin, Physica A, 1998, 252, 67–84 CrossRef CAS
.
- J. Barrett, J. Phys. A: Math. Gen., 1994, 27, 5053–5068 CrossRef CAS
.
- J. J. Potoff and J. I. Siepmann, AIChE J., 2001, 47, 1676–1682 CrossRef CAS
.
- B. Chen, J. J. Potoff and J. I. Siepmann, J. Phys. Chem. B, 2001, 105, 3093–3104 CrossRef CAS
.
-
J. O. Hirschfelder, C. F. Curtiss and R. B. Bird, Molecular theory of gases and liquids, Wiley, New York, 1954 Search PubMed
.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
.
- F. H. Stillinger Jr, J. Chem. Phys., 1963, 38, 1486–1494 CrossRef
.
- D. Kashchiev, J. Chem. Phys., 1982, 76, 5098–5102 CrossRef CAS
.
- E. L. Quinn, J. Am. Chem. Soc., 1927, 49, 2704–2711 CrossRef CAS
.
- J. Lielmezs and T. Herrick, Chem. Eng. J., 1986, 32, 165–169 CrossRef CAS
.
- R. Span and W. Wagner, J. Phys. Chem. Ref. Data, 1996, 25, 1509–1596 CrossRef CAS
.
- J. Ter Horst, D. Bedeaux and S. Kjelstrup, J. Chem. Phys., 2011, 134, 054703 CrossRef CAS
.
- B. E. Wyslouzil and J. H. Seinfeld, J. Chem. Phys., 1992, 97, 2661–2670 CrossRef CAS
.
- J. Barrett, C. Clement and I. Ford, J. Phys. A: Math. Gen., 1993, 26, 529–548 CrossRef CAS
.
- J. C. Barrett, J. Chem. Phys., 2011, 135, 096101 CrossRef
.
- J. W. Schmelzer, G. S. Boltachev and A. S. Abyzov, J. Chem. Phys., 2013, 139, 034702 CrossRef
.
- H. Takeuchi, J. Phys. Chem. A, 2008, 112, 7492–7497 CrossRef CAS
.
- B. Molleman and T. Hiemstra, Phys. Chem. Chem. Phys., 2018, 20, 20575–20587 RSC
.
- J.-B. Maillet, A. Boutin, S. Buttefey, F. Calvo and A. H. Fuchs, J. Chem. Phys., 1998, 109, 329–337 CrossRef CAS
.
- F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371 CrossRef CAS
.
-
K. Hansen, Statistical physics of nanoparticles in the gas phase, Springer International Publishing, 2nd edn, 2018 Search PubMed
.
- A. Ramos, J. Fernández, G. Tejeda and S. Montero, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 053204 CrossRef
.
- C. Murthy, S. O'Shea and I. McDonald, Mol. Phys., 1983, 50, 531–541 CrossRef CAS
.
- J.-B. Maillet, A. Boutin and A. H. Fuchs, J. Chem. Phys., 1999, 111, 2095–2102 CrossRef CAS
.
- J. Wedekind and D. Reguera, J. Chem. Phys., 2007, 127, 154516 CrossRef
.
- I. Napari, J. Julin and H. Vehkamäki, J. Chem. Phys., 2009, 131, 244511 CrossRef
.
- K. J. Oh and X. C. Zeng, J. Chem. Phys., 2000, 112, 294–300 CrossRef CAS
.
- W. Ostwald, Z. Phys. Chem., 1897, 22, 289–330 CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05653g |
| ‡ Both authors contributed equally to this work. |
| This journal is © the Owner Societies 2021 |