Nature of the different emissive states and strong exciton–phonon couplings in quasi-two-dimensional perovskites derived from phase-modulated two-photon micro-photoluminescence spectroscopy

Abstract

Quasi two-dimensional perovskites have attracted great attention for applications in light-emitting devices and photovoltaics due to their robustness and tunable highly efficient photoluminescence (PL). However, the mechanism of intrinsic PL in these materials is still not fully understood. In this work, we have analysed the nature of the different emissive states and the impact of temperature on the emissions in quasi two-dimensional methyl ammonium lead bromide perovskite (q-MPB) and cesium lead bromide perovskite (q-CPB). We have used spatially resolved phase-modulated two-photon photoluminescence (2PPL) and temperature-dependent 2PPL to characterize the emissions. Our results show that at room temperature, the PL from q-MPB is due to the recombination of excitons and free carriers while the PL from q-CPB is due to the recombination of excitons only. Temperature-dependent measurements show that in both materials the linewidth broadening is due to the interactions between the excitons and optical phonons at high temperatures. Comparing the characteristics of the emissions in the two systems, we conclude that q-CPB is better suited for light emitting devices. With a further optimization to reduce the impact on the environment, q-CPB-based LEDs could perform as well as OLEDs.

---

Introduction

The last few years have witnessed a dramatic development of metal halide perovskite (MHP) materials for optoelectronic applications.^1–5 MHP is a promising candidate for the realization of next-generation light-emitting diodes (LEDs) owing to its sharp emission peak,^6,7 high luminescence quantum yield (QY),^4,8 composition-dependent tunability, and easy and low-cost solution-processable synthesis.^5,9–11 In order to enhance the device performance, intense efforts have been made in recent years to develop new perovskite materials and device architectures, and significant research has been carried out to understand the processes that contribute to or also limit the PL.^12,13 By suppressing nonradiative recombination and balancing carrier injection, the luminescence efficiency of perovskite-based devices has been significantly improved.^14–17

Despite a significant increase in efficiency, the development of 3D-perovskite-based LEDs is plagued by their poor stability.^18,19 Firstly, because of their soft structure, they can easily decompose at high-temperature or high-humidity. Secondly, organic cations and halides can move under electric field, giving rise to the transformation of the perovskite structure.²⁰ These factors remain the critical bottleneck for commercial applications. Two-dimensional (2D) structures have emerged as a possible solution to this issue.²¹ Although the application of 2D perovskites in LEDs is stimulated by improved device-operational stability compared to the 3D analogues, the emission from pure 2D materials is limited because of strong exciton–phonon coupling due to fast and efficient exciton trapping processes.²² Nowadays, the most popular strategy to solve the problem is to use quasi-2D perovskites.^23–25 The quasi-2D perovskites contain a distribution of grains with dimensionality ranging from 2D to 3D.^24,25 By tuning the ratio of 2D to 3D composition, the energy landscape can be tailored such that the charge carriers can be funnelled and concentrated in the lowest band gap radiative domains.²⁶ Quasi-2D perovskites take advantage of the cascading of the excitons from the low-dimensionality grains down to the higher-dimensional grains for efficient radiative recombination.²⁷ Compared to 3D perovskites, quasi-2D perovskites show significant tolerance to larger and more complex organic ligands, making their structure more versatile and tunable.^3,24 Very recently, the emission efficiency of quasi-2D perovskites has reached up to ∼20%.¹ This encouraging progress shows that quasi-2D hybrid perovskites are promising candidates for the fabrication of efficient light-emitting devices. Due to the complex structure and composition compared to 3D and 2D halide perovskites, many fundamental, yet intriguing processes remain to be explored in quasi-2D perovskite. These investigations are necessary for a long-term improvement in LED device performance.

Although there are some reports on underlying physical processes that govern PL in q-2D material,^3,28–30 a systematic and unified description of the recombination mechanisms is lacking. In this regard, phase modulation in nonlinear spectroscopic techniques can provide valuable information about the different types of PL recombination mechanisms and particularly the PL contributions from different electronic states in semiconductor material and other photo-active systems.^31–33 These techniques have enabled measurements of extremely small nonlinear signals that are completely covered by background noise. One of the advantages of these techniques is that the effects of ultrafast nonlinear interactions are imprinted on ‘action signals’ such as fluorescence and photocurrent, which can be phase-synchronously detected. The phase-modulation technique can also be used to separate the relevant linear and nonlinear signal from other possible interaction pathways. Reybon and co-workers have used phase modulation to separate the nonlinear optical signal induced in a collinear pump–probe geometry.³⁴ Subsequently, Tian et al.³⁵ have shown that a pair of absorption-induced phase-modulated beams gives rise to the loss modulation at twice the modulation frequency 2(ϕ₂ − ϕ₁). More recently, Karki et al. have introduced detailed theoretical calculations for all of the modulation frequencies, at which different coherent and incoherent nonlinear signals can be observed.³⁶ This approach has also been used to investigate the different recombination processes in organo-halide semiconductors (mainly crystals of MPB) based on the order of the recombination.³⁷

In this contribution, we have carried out spatially resolved phase-modulated two-photon photoluminescence spectroscopy (2PPL), and temperature-dependent 2PPL to understand the underlying mechanisms that contribute to the emission and other relevant photophysical processes in q-MPB and q-CPB. The results are compared with the previous measurements of phase modulated 2PPL of bulk crystals to elucidate the similarities and differences. The spatially resolved spectra of q-MPB at room temperature show a variation in the peak position indicating multiple origins of the emission. Previous results on micro-crystals of MPB have shown contributions from the recombination of free carriers as well as excitons, which also contributes to the variation of the spectra in q-MPB films.^9,38–40 On the contrary, the emission from q-CPB is uniform with contributions only from the recombination of the excitonic species. Such exclusively excitonic emission has not been reported previously from high sensitivity measurements on perovskites at room temperature.

Our temperature-dependent measurements show that at high temperatures, the PL linewidth broadening in both q-MPB and q-CPB is due to the interaction between the excitons and the optical phonons. At low temperatures the linewidth narrows down as the optical phonons are not populated. We have determined the coupling strengths of the exciton–optical-phonon. Our results are important for the better understanding of the photo-physics of quasi-2D systems. More importantly, the results indicate that the elementary properties of q-CPB are most advantageous for the development of high-efficiency LEDs.

Experimental

Absorption

For absorption measurements, the particles dispersed in hexane were drop-casted on a cover slip followed by drying at room temperature. Absorption spectra were taken using a PerkinElmer Lambda 950 spectrometer.

Phase-modulated two-photon PL (2PPL)

The details of 2PPL have been described elsewhere.^39,41,42 In brief, a mode-locked Ti-Sapphire oscillator (Synergy from Femtolasers) was used to generate laser pulses with a duration of approx. 15 fs and a central wavelength of 790 nm at a repetition rate of 80 MHz. The output of the laser beam was split into two beams, each beam was passed through a Mach–Zehnder interferometer to produce the identical replica of the beams. Each arm of the interferometer was equipped with an acousto-optic modulator (AOM), which modulated the phases of the pulses with carrier frequency ω. The two AOMs were synchronously driven at frequencies ϕ₁ = 54.95 MHz and ϕ₂ = 55 MHz, which shifted the carrier frequencies to ω + ϕ₁ and ω + ϕ₂, respectively. The difference in the frequency shift was therefore ϕ_a = ϕ₂ − ϕ₁ = 50 kHz. A pair of chirped mirrors was used to compensate the group-velocity dispersion induced by the beam splitters and the AOMs. The temporal overlap between the pulses was optimized by using a delay line. Then, one of the outputs from the interferometer was directed to an inverted microscope (Nikon Ti-S). The output PL signal was separated from the excitation beam by a dichroic mirror (FF670-sdi01-25 × 36, Semrock). The scattered light from the excitation beam was further reduced by using a short pass filter (OD4, Edmund optics, #84-698) with a cut-off at 625 nm before the light entered the spectrometer. A reflective objective (36×/0.5 NA, Edmund optics, Part No. 83684410) focused the excitation beam onto the sample. The PL was detected with an avalanche photodiode (APD) (LCSA3000-01, Laser Components) and the resulting signal intensity was digitized at a rate of 10 mega samples per second by a 14-bit digitizer (ATS9440, AlazarTech). The digitized signal was further analysed by fast Fourier transforms or a generalized lock-in amplifier^43–45 to obtain the amplitudes of the modulated signals at 50, 100, 150, and 200 kHz. The second output of the interferometer was used as a reference to compensate the long-term power fluctuations.

For the temperature-dependent PL measurements, the sample was placed in a temperature-controlled stage (Linkam Scientific Instruments, LTS420E-P). A platinum resistor sensor placed near the surface was used to measure the temperature. The control of the temperature between 79 and 283 K was facilitated employing a temperature-control system with a linear cooling rate of 3 K min⁻¹.

Analysis of 2PPL data

The number of electrons (n_e) or holes (n_h), excited by two phase-modulated beams with frequency difference ϕ_a shows modulations at ϕ_a and 2ϕ_a, and the relative amplitudes are given by the expression, n_e = n_h ∝ 3 + 4 cos(ϕ_at) + cos(2ϕ_at).³⁷ The derivation of the expression is given in the ESI.† As the excitonic recombination is directly proportional to the population of bound e–h pairs, which itself scales linearly with n_e, the PL from excitons is given by the same expression. In contrary, the PL from free charges follows a second-order recombination, which is proportional to n_en_h = n_e² ∝ 56 cos(ϕ_at) + 28 cos(2ϕ_at) + 8 cos(3ϕ_at) + cos(4ϕ_at).³⁷

Results and discussions

Absorption and PL spectroscopy are employed to confirm the formation of q-2D perovskite. Panel A of Fig. 1 shows the absorption spectra of synthesized q-MPB and q-CPB, as red and black curve, respectively. For q-MPB, the lowest energy absorption peak centred at ∼526 nm corresponds to the pure 3D phase and the other absorption peaks at higher energies (centred at ∼434, 454, and 484 nm) are from the layered perovskites with n = 2, 3, 4, or higher order.²⁵ Similarly, for q-CPB, the absorption peak centred at ∼520 nm corresponds to the pure 3D phase and the peaks at lower wavelengths ∼431, 450 and 483 nm correspond to layered perovskite with n = 2, 3, 4 or higher order.²⁶ The spectra demonstrate that both samples are ensembles of mixed rather than single phase layers, which is in good agreement with the previously reported absorption spectrum of q-2D perovskite.^25,26,46,47 An accurate determination of the layers in q-2D perovskites is challenging since a mixture between different phases is thermodynamically favoured. We have employed lead bromide (PbBr₂) : methylammonium bromide (MABr) or cesium bromide (CsBr) to hexylammonium bromide (HexBr) molar ratio of 3 : 2 : 2x, where x = 0.5. In this case, one expects that the as-prepared particles are in q-2D perovskite with a number of layers (n) between n = 2 and 3.^11,47 As opposed to the absorption spectra, the PL spectra show single peaks centred at ∼536 and 529 nm for q-MPB and q-CPB, respectively (Fig. 1B). As discussed later, the peak position in q-MPB varies with the sample position. The value given here is the average of the spectra over a sample area. Nevertheless, both peaks are Stokes shifted from the corresponding lowest energy absorption peaks. Clearly, irrespective of the significant absorption by multi-layered domains of q-2D perovskites, only the domains with highest numbers of layers that have lowest bandgap emit. This indicates a downhill energy transfer from lower to higher order multilayer structures. The blue shift observed in both absorption and emission peak in q-CPB compared to that in q-MPB suggests a higher confinement effect in q-CPB.^18,48

Fig. 1 (A) Absorption (“LEP”, signifies low energy peak) and (B) average PL spectra of q-MPB (red) and q-CPB (black) thin films, respectively. Thin film XRD pattern of (C) q-MPB and (D) q-CPB particles (inset shows the low angle peaks). SEM images of (E) q-MPB and (F) q-CPB particles. (G) Raster scanned spatial 2PPL mapping of 60 μm × 60 μm area of q-MPB film, and (H) PL at two different regions of the film. (I) Raster-scanned spatial PL mapping of 60 μm × 60 μm area of the film of q-CPB and (J) PL spectra at two regions of the film.

There are also differences in the linewidths of the PL spectra shown in Fig. 1B. The FWHM in q-MPB is about 102 meV, which is bigger than the FWHM in q-CPB (91 meV). A number of factors including morphological differences, presence of different emissive states, and coupling to the phonons lead to the observed differences in the spectral features. Thus, we have systematically carried out different measurements to better understand the photo-physics of both samples.

To elucidate the composition and structure of q-MPB and q-CPB, we have used X-ray diffraction (XRD) and scanning electron microscopy (SEM). Panels C and D of Fig. 1 show the XRD pattern of q-MPB and q-CPB, respectively. The XRD patterns of both samples show prominent peaks that match with the standard diffraction patterns, and the low-angle peaks with 2θ < 10° can be clearly observed, suggesting the formation of a low-dimensional quasi-2D perovskite structure.⁴⁷ SEM images of q-MPB and q-CPB (Panels E and F of Fig. 1, respectively) show nanosheets of similar sizes (∼200–250 nm). These results indicate that the structural features alone do not explain the differences in the spectra of the samples.

Previous measurements of PL microscopy in bulk crystals of MPB have shown significant variation in the emission intensity and spectra.^37,38,49 It is interesting to investigate if such inhomogeneity is also present in the quasi-2D crystals. We have used spatially resolved 2PPL spectroscopy to study the spatial variations in the emission.

Firstly, we have investigated the PL spectra at room temperature for both samples (Panels G and I of Fig. 1). We have observed a variation of the PL spectra for different regions only in the q-MPB film. The peak positions vary from 2.29 eV (541 nm) to 2.31 eV (536 nm). On the other hand, q-CPB shows uniform emission spectra with the peak at 2.34 eV (529 nm). Panels H and J of Fig. 1 show the normalized PL of q-MPB and q-CPB films at two different regions. Variations in the position of the peaks that have been observed previously in 2D and 3D perovskites have been attributed to the presence of different types of recombination processes, mainly the recombination of the free carriers, excitons and self-trapped excitons.^37,38,40 Typically, the emission from free carriers is blue-shifted compared to that from the excitons. The variation is explained based on the assumption that the distribution of free carriers and excitons is not uniform over the crystal volume. Our results show that this applies only to q-MPB and not to q-CPB.

Since the temperature dependence of the PL yields important information about characteristics of the emitting states, we have measured the emission spectra of q-MPB and q-CPB films at various temperatures. The resulting PL spectra shown in Panels A and B of Fig. 2 are averaged over the sample images shown in Panels G and I, respectively. As shown in Fig. 2A and B, the emission spectra in both samples become narrower at lower temperatures, which can be attributed to the reduction in population of longitudinal optical (LO) phonons that broaden the spectrum. A more detailed analysis of the coupling between the LO phonons and free carriers and excitons is presented below (see discussion of Fig. 4). The broad and asymmetric PL line shape at high temperature can be explained by the co-existence of multiple phases. At a temperature below 150 K, the asymmetric PL band shape converts to a symmetric shape, which indicates the transition from multiple phases to a single phase. While the change of the line shape could be clearly seen, we did not observe a shift of the PL peak energy, as the emissions of the two phases are close to each other.^7,22 It is important to note that the emission observed from q-MPB is red shifted at low temperatures, while no such shift is observed in q-CPB. These features are analogous to those, which have been reported before for MPB and CPB perovskites.^50,51 The detailed evolution of the PL peak energy as a function of temperature is presented in Fig. 2C and D. In the organic–inorganic hybrid perovskite, the dielectric constant increases with increasing temperature, and consequently the exciton binding energy decreases as the collective rotational motion of the organic cation increases.^50,52 This rotational motion of the organic cation and its consequence for the exciton binding energy also depends on the different phases of the material.^50,53 In case of the inorganic perovskite, the variation of the exciton binding energy with increasing temperature is very small. In this case, the dielectric screening mechanism is controlled by the motion of atoms within the lead halide cage.⁵¹ This suggests that the properties of the emitting states in q-MPB may vary with temperature and phase while they should be almost constant in q-CPB. However, it is difficult to quantify the nature of the emitting states using the temperature-dependent spectra alone. Thus, to accurately quantify the nature of the different emitting states, we have used the recently developed method of 2PPL spectroscopy using two phase-modulated beams from a mode-locked femtosecond oscillator (for details see Experimental part).^36,37

Fig. 2 Temperature dependent 2PPL of (A) q-MPB and (B) q-CPB. PL peak energy as a function of temperature for (C) q-MPB and (D) q-CPB.

Phase modulated 2PPL is a simplification of more extended measurements that use two intensity-modulated laser beams.⁵⁴ Such measurements have been used to identify second-order recombination processes in thin film organic semiconductors. In 2PPL, when two phase-modulated beams at frequencies ϕ₁ and ϕ₂ are combined in an interferometer, the intensity modulates at the frequency ϕ_a = ϕ₂ − ϕ₁. Such beams can be used to induce two-photon absorption in a fluorescent sample. The subsequent emission modulates at multiple frequencies nϕ_a, where n is an integer. The modulation contributions can be determined from a Fourier-transform calculation of the time-resolved signal. Two-photon absorption of a beam modulated at ϕ_a modulates the excited population at ϕ_a and 2ϕ_a (two frequencies). If the emission is from the excitons, and thus being linearly proportional to its population, the emission also modulates at ϕ_a and 2ϕ_a. The recombination of free-carriers, on the other hand, is a second-order process that is proportional to the product of free-electrons and holes. This adds further nonlinearity to the process, resulting in a signal, which now shows additional modulations at higher frequencies 3ϕ_a and 4ϕ_a. These modulations are observed even at low intensities and are therefore a clear indication of the involvement of the second-order process. A detailed theoretical discussion of the recombination processes that contribute to different orders of modulations is given in ref. 37.

Pure excitonic recombination in molecular systems has been investigated previously by 2PPL. In these measurements, one observes a ratio of 4 : 1 for the signal amplitudes at ϕ_a and 2ϕ_a.^37,55 Similarly, in the emission spectrum from the recombination of the free carriers, an amplitude ratio of 56 : 28 : 8 : 1 for the contributions at ϕ_a, 2ϕ_a, 3ϕ_a, and 4ϕ_a is expected. When the processes in a system results in both emissions, the ratio of the higher harmonics obtained from the Fourier analysis of the signal differs from the ratios expected for either type of recombination. In a typical measurement, the signals at 2ϕ_a and 3ϕ_a are used to calculate the individual contributions from the excitons and free charges as given by the following equations:

A_fc(2ϕ_a) = 3.5A(3ϕ_a), (1)

A_ex(2ϕ_a) = A(2ϕ_a) − A_fc(2ϕ_a), (2)

where A(2ϕ_a) and A(3ϕ_a) are the amplitudes of the signals at 2ϕ_a and 3ϕ_a, respectively. A_fc(2ϕ_a) and A_ex(2ϕ_a) are the contributions to the emission at 2ϕ_a from the free charges and excitons, respectively. Although the signal at 4ϕ_a can also be used instead of the signal at 3ϕ_a, it is often ignored because of poorer signal to noise ratio.

The Fourier transform of the PL spectrum from q-MPB films is shown in Fig. 3A. Distinct modulations at ϕ_a, 2ϕ_a, 3ϕ_a, and 4ϕ_a (50, 100, 150, and 200 kHz, respectively) can be observed. Clearly, in these films, excitons as well as free carriers contribute to the PL. In contrast, the Fourier transform of the PL spectrum from q-CPB (Fig. 3B) yields modulations only at ϕ_a and 2ϕ_a, which indicates that this emission is from the excitons alone. These results are in perfect agreement with the temperature dependence of the PL spectra shown in Fig. 2.

Fig. 3 Fourier transforms of the PL intensities of (A) q-MPB and (B) q-CPB. Spatially resolved PL maps of (C) excitonic and (D) free-carrier emissions of q-MPB. (E) Shows the spatial dependence of the ratio of the two emission intensities (excitonic/free charges).

As the emission in q-MPB has contributions from free carriers as well as excitons, we have further analysed the 2PPL signals to determine the spatial distribution of both excited species. Panels C and D of Fig. 3 show the contributions to the signal at 2ϕ_a from excitonic and free-carrier emissions, respectively. Both contributions vary considerably over the sample, which can be attributed to the commonly observed morphological inhomogeneity in the films of perovskites. Nevertheless, the two images are not identical. This suggests that the excitons and free carriers are not localized in the same regions of the sample. Others have observed such segregation at microscopic level in bulk crystals of MPB using transient absorption microscopy.⁵⁶ These measurements have only been able to identify the difference in the contributions from the free carriers and excitons. More importantly, the results show that in the bulk crystals the emission in most regions is dominated by free carriers with very few localized micro-spots where excitonic emission prevails. More quantitative results that have been obtained using phase modulated 2PPL agree with the previous results.³⁷

Our results from phase-modulated 2PPL on q-MPB, on the other hand, show that the major contribution to the emission is from the excitons. To demonstrate this, we have quantified the spatially resolved contributions to the emission in q-MPB by calculating the ratio of the amplitudes of the signal from the excitons and free carriers at 2ϕ_a (Panels C and D of Fig. 3, respectively). Fig. 3E shows the ratio of the two emissions (excitons/free charges). Here too, a strong spatial variation of the contributions of excitons and free charges to the PL can be observed. The ratio ranges from 4 : 1 to 16 : 1 with an average of 9 : 1 over the range of the image shown in Panel E. Clearly, the dimensionality of the MPB particles determines the prevalence of the emissive species with free carriers dominating the emission in the bulk and excitons in the systems with reduced dimensions (2D and nanoparticles).

Our results also indicate that two distinct mechanisms control the contribution of free carriers and excitons in q-2D perovskites. Firstly, there is the difference in the physical properties induced by the cation group. It is well known that q-CPB has a low dielectric constant,^19,57 which provides a very weak electric-field screening. As a result, the Coulomb interaction between the electrons and holes increases,⁵⁸ and consequently the binding energy between them is stronger. This naturally gives rise to a dominant contribution of the excitons at room temperature irrespective of the dimensionality of the systems. q-MPB, on the other hand, contains an organic cation that yields a higher dielectric constant. This significantly enhances the screening of the electric field and reduces the Coulomb interactions between electrons and holes.^57,58 In this case, the binding energy of the electrons and holes is much weaker and we therefore expect free carriers at room temperature. This explains why emission in q-MPB has contributions from excitons as well as free carries and the emission in q-CPB is only from the excitons. Secondly, a factor that governs the distribution of free carriers and excitons is the presence of different phases at high temperature. As the band gap energy and exciton binding energy vary for different phases, the contribution of free carriers and excitons also varies accordingly.^50,59

The characteristics of the emission spectra of perovskites, mainly the linewidths, are also relevant for specialized applications. Broad linewidths are important in the development of short pulsed lasers.²² It can also be a benefit for a polariton laser with low threshold as it accelerates the polariton relaxation.^60,61 The linewidths of the PL from the perovskites are strongly influenced by the coupling between the electronic excitation (free carriers and excitons) and phonons. Moreover, strong charge-phonon coupling has a considerable impact on LED and photovoltaic applications as it affects the charge-carrier mobility, trapping, and cooling.²² To better understand these interactions, we have analysed the temperature dependence of the PL spectra. The results are presented in Fig. 4. Panels A and B of Fig. 4 show the spectra taken in the temperature range from 80 to 298 K for the q-MPB and q-CPB films, respectively. The emission line-width broadening with rising temperature can be used to quantify the coupling constants. In general, the interaction between electronic excitations and phonons can be described by two scattering processes, the scattering from acoustic phonons and longitudinal optical (LO) phonons (Fröhlich scattering).¹⁷ The linewidth broadening of the symmetric PL line shapes of q-MPB and q-CPB (Panels C and D of Fig. 4, respectively) can be assigned to the interaction of phonons with excitons since they dominate the emission.

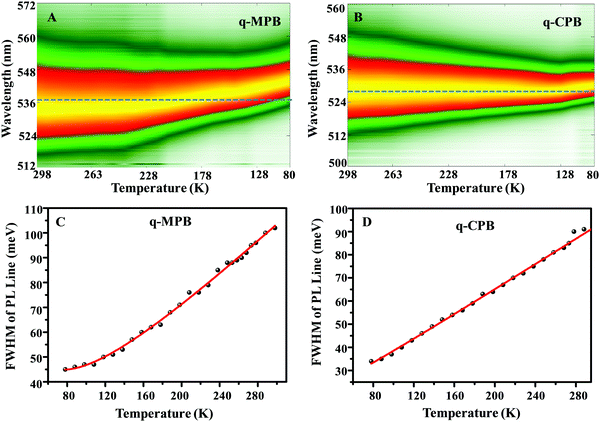Fig. 4 Temperature-dependent PL maps obtained from (A) q-MPB and (B) q-CPB while cooling from room temperature to 80 K. Temperature-dependent FWHM spectral widths of the PLs observed from (C) q-MPB, and (D) q-CPB (the red curve results from a fit using eqn (3); for details see main text).

It is well known that excitons can couple to both optical and acoustic phonons.^22,62 As the optical phonon has higher energy than the acoustic phonon, at high temperatures, the interactions between excitons and optical phonons dominate. At low temperature (<100 K), the population of the optical phonons is reduced and, therefore, the acoustic phonons start to dominate.

The relationship between PL linewidth and phonon scattering is described by the following equation,

Γ(T) = Γ₀ + Γ_ac + Γ_LO + Γ_imp = Γ₀ + γ_acT + γ_LON_LO(T) + γ_impe^−E_b/k_BT (3)

where Γ₀ describes the temperature-independent inhomogeneous broadening. Γ_ac is the contribution from acoustic-phonon scattering and γ_ac is the corresponding phonon-coupling strength. Γ_LO corresponds to the homogeneous broadening that results from LO-phonon scattering with a coupling strength γ_LO. Exciton–phonon coupling, in general, is proportional to the occupation numbers N of the respective phonons, as given by the Bose–Einstein distribution functions, taken as N_LO(T) = 1/[e^E_LO/k_BT − 1] for LO phonons, where E_LO is the energy of the respective phonons. For acoustic phonons, the phonon energy is much less than k_BT at room temperature and linearly depends on the coupling strength. The final term Γ_imp describes the inhomogeneous broadening due to ionic impurity. γ_imp is the contribution to the line width broadening when impurities are fully ionized and E_b is the average binding energy of the impurities.^63,64 Recently, it was reported that scattering due to impurities does not play a major role here.^22,62 Therefore, we consider Γ_imp ≈ 0 for the rest of our analysis.

Specifically, the LO phonon term in eqn (3) accounts for the interaction between LO phonons and excitons. As the energy of the optical phonons in perovskite semiconductors is typically on the order of 10 meV,⁶² at low temperature (T < 100 K) the population of the optical phonons is very small. Thus, the homogeneous broadening in this regime predominantly results from acoustic phonons. Therefore, we can fit the low temperature regime (T < 100 K) with the inhomogeneous broadening term at 0 K (Γ₀) combined with acoustic phonon scattering (Γ_ac). The acoustic phonon coupling strengths from the fits are given in Table 1. The obtained acoustic phonon coupling strength (γ_ac) of q-CPB (0.25 ± 0.1 meV K⁻¹) is higher than in q-MPB (0.15 ± 0.1 meV K⁻¹).⁶² It is important to note that the calculated γ_ac may contain some systematic errors, as we have not done measurements at temperatures below 78 K. The obtained γ_ac is based on the acoustic phonon scattering within the temperature range from 100 K to 78 K. At higher temperatures, optical phonons are emitted significantly by high energy excitons, and in addition, the thermal occupation of the optical phonons increases the probability of the scattering of excitons from optical phonons. Consequently, optical-phonon coupling is more important than acoustic-phonon coupling at room temperature. To quantify the exciton–phonon interaction mechanism in a temperature regime above 200 K, we have fitted our experimental data using eqn (3), including the mechanisms based on the temperature-dependent inhomogeneous broadening (Γ₀) and the Fröhlich coupling to the LO phonon modes (Γ_LO). The resulting coupling strength and the broadenings are given in Table 1.

Table 1 Line-width parameters obtained from fitting the experimental result using eqn (3)

Sample	Γ 0 (meV)	γ LO (meV)	γ ac (meV K^−1)
q-MPB	32 ± 1	56 ± 1	0.15 ± 0.1
q-CPB	26 ± 1	45 ± 2	0.25 ± 0.1

---

We have also fitted the data including the scattering by the impurities, but, they do not improve the quality of the fits, which indicates that their contribution to the spectral broadening is negligible, which agrees well with the results mentioned above.^22,62 Our results show that the LO phonon coupling strength is higher in q-MPB (56 ± 1 meV) than in q-CPB (45 ± 2 meV).

Conclusions

Using temperature-dependent photoluminescence (PL) micro-spectroscopy and phase-modulated two-photon photoluminescence spectroscopy (2PPL), we have shown that a q-MPB film has two contributions in the PL spectrum, which can be assigned to the recombination of the free charges and excitons. In contrast to the bulk crystals where the dominant contribution to the emission is from free carriers, in q-MPB we have observed larger a contribution from the excitons. Nevertheless, the relative contributions from the two emitting states show large variation within a sample. On the other hand, the PL of q-CPB is from the excitons only. We have conducted an in-depth analysis of the coupling between the charge carriers and phonons within a temperature range of 80 K to room temperature in q-MPB and q-CPB films. In both q-MPB and q-CPB samples, the interaction between excitons and optical phonons dominates at higher temperatures whereas the interaction with acoustic phonons becomes the most important contribution at low temperatures (<100 K). Altogether, the results presented contribute to a fundamental understanding of the different mechanisms of emission from different states, linewidth broadening, and exciton–phonon dynamics in q-MPB and q-CPB. The results are important with respect to a use of quasi-2D perovskites for various optical and opto-electronic devices. Our results also show that q-CPB is more suitable for applications in LEDs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. G. is thankful to the Alexander von Humboldt Foundation, Germany for the award of a postdoctoral fellowship and financial support. J. H. acknowledges financial support from the Research Foundation-Flanders (FWO, Grant No. G983.19N, G0A5817N, and G0H6316N) and the Flemish government through long-term structural funding Methusalem (CASAS2, Meth/15/04). B. P acknowledges a postdoctoral fellowship from the Research Foundation-Flanders (FWO Grant No. 1275521N).

References

1. N. K. Kumawat, X.-K. Liu, D. Kabra and F. Gao, Nanoscale, 2019, 11, 2109–2120.
2. J. S. Manser, J. A. Christians and P. V. Kamat, Chem. Rev., 2016, 116, 12956–13008.
3. C. Qin, T. Matsushima, W. J. Potscavage, A. S. Sandanayaka, M. R. Leyden, F. Bencheikh, K. Goushi, F. Mathevet, B. Heinrich, G. Yumoto, Y. Kanemitsu and C. Adachi, Nat. Photonics, 2019, 14, 1–6.
4. J. M. Richter, M. Abdi-Jalebi, A. Sadhanala, M. Tabachnyk, J. P. Rivett, L. M. Pazos-Outón, K. C. Gödel, M. Price, F. Deschler and R. H. Friend, Nat. Commun., 2016, 7, 13941.
5. T. M. Brenner, D. A. Egger, L. Kronik, G. Hodes and D. Cahen, Nat. Rev. Mater., 2016, 1, 15007.
6. C. M. Sutter-Fella, Y. Li, M. Amani, J. W. Ager III, F. M. Toma, E. Yablonovitch, I. D. Sharp and A. Javey, Nano Lett., 2015, 16, 800–806.
7. S. Ghosh, Q. Shi, B. Pradhan, P. Kumar, Z. Wang, S. Acharya, S. K. Pal, T. Pullerits and K. J. Karki, J. Phys. Chem. Lett., 2018, 9, 4245–4250.
8. L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Bertolotti, N. Masciocchi, A. Guagliardi and M. V. Kovalenko, J. Am. Chem. Soc., 2016, 138, 14202–14205.
9. M. A. Becker, R. Vaxenburg, G. Nedelcu, P. C. Sercel, A. Shabaev, M. J. Mehl, J. G. Michopoulos, S. G. Lambrakos, N. Bernstein and J. L. Lyons, Nature, 2018, 553, 189.
10. B. Pradhan, G. S. Kumar, S. Sain, A. Dalui, U. K. Ghorai, S. K. Pradhan and S. Acharya, Chem. Mater., 2018, 30, 2135–2142.
11. H. Bhatia, J. A. Steele, C. Martin, M. Keshavarz, G. Solis-Fernandez, H. Yuan, G. Fleury, H. Huang, I. Dovgaliuk and D. Chernyshov, Chem. Mater., 2019, 31, 6824–6832.
12. M. Zhang, H. Yu, M. Lyu, Q. Wang, J.-H. Yun and L. Wang, Chem. Commun., 2014, 50, 11727–11730.
13. V. D’Innocenzo, A. R. Srimath Kandada, M. De Bastiani, M. Gandini and A. Petrozza, J. Am. Chem. Soc., 2014, 136, 17730–17733.
14. K. Lin, J. Xing, L. N. Quan, F. P. G. de Arquer, X. Gong, J. Lu, L. Xie, W. Zhao, D. Zhang and C. Yan, Nature, 2018, 562, 245.
15. L. Zuo, H. Guo, D. W. deQuilettes, S. Jariwala, N. D. Marco, S. Dong, R. DeBlock, D. S. Ginger, B. Dunn and M. Wang, Sci. Adv., 2017, 3, e1700106.
16. S. Ghosh, Q. Shi, B. Pradhan, A. Mushtaq, S. Acharya, K. J. Karki, T. Pullerits and S. K. Pal, J. Phys. Chem. Lett., 2020, 4, 1239–1246.
17. J. A. Steele, P. Puech, B. Monserrat, B. Wu, R. X. Yang, T. Kirchartz, H. Yuan, G. Fleury, D. Giovanni, E. Fron, M. Keshavarz, E. Debroye, G. Zhou, T. C. Sum, A. Walsh, J. Hofkens and M. B. J. Roeffaers, ACS Energy Lett., 2019, 4, 2205–2212.
18. H. Kim, K. A. Huynh, S. Y. Kim, Q. V. Le and H. W. Jang, Phys. Status Solidi RRL, 2019, 1900435.
19. J. Li, L. Luo, H. Huang, C. Ma, Z. Ye, J. Zeng and H. He, J. Phys. Chem. Lett., 2017, 8, 1161–1168.
20. Z. Chen, Y. Guo, E. Wertz and J. Shi, Adv. Mater., 2019, 31, 1803514.
21. K. Zheng and T. Pullerits, J. Phys. Chem. Lett., 2019, 10, 5881–5885.
22. L. Ni, U. Huynh, A. Cheminal, T. H. Thomas, R. Shivanna, T. F. Hinrichsen, S. Ahmad, A. Sadhanala and A. Rao, ACS Nano, 2017, 11, 10834–10843.
23. J. Yan, W. Qiu, G. Wu, P. Heremans and H. Chen, J. Mater. Chem. A, 2018, 6, 11063–11077.
24. J. Byun, H. Cho, C. Wolf, M. Jang, A. Sadhanala, R. H. Friend, H. Yang and T. W. Lee, Adv. Mater., 2016, 28, 7515–7520.
25. Z. Yuan, Y. Shu, Y. Xin and B. Ma, Chem. Commun., 2016, 52, 3887–3890.
26. Y. F. Ng, S. A. Kulkarni, S. Parida, N. F. Jamaludin, N. Yantara, A. Bruno, C. Soci, S. Mhaisalkar and N. Mathews, Chem. Commun., 2017, 53, 12004–12007.
27. G. Grancini and M. K. Nazeeruddin, Nat. Rev. Mater., 2019, 4, 4–22.
28. M. Cui, C. Qin, Y. Jiang, M. Yuan, L. Xu, D. Song, Y. Jiang and Y. Liu, J. Phys. Chem. Lett., 2020, 11, 5734–5740.
29. F. Meng, X. Liu, Y. Chen, X. Cai, M. Li, T. Shi, Z. Chen, D. Chen, H. L. Yip and C. Ramanan, Adv. Funct. Mater., 2020, 30, 1910167.
30. M. Wang, H. Zou, J. Zhang, T. Wu, H. Xu, S. Haacke and B. Hu, J. Phys. Chem. Lett., 2020, 11, 3647–3652.
31. J.-H. Zhong, J. Vogelsang, J.-M. Yi, D. Wang, L. Wittenbecher, S. Mikaelsson, A. Korte, A. Chimeh, C. L. Arnold and P. Schaaf, Nat. Commun., 2020, 11, 1–10.
32. Q. Bian, F. Ma, S. Chen, Q. Wei, X. Su, I. A. Buyanova, W. M. Chen, C. S. Ponseca, M. Linares, K. J. Karki, A. Yartsev and O. Inganäs, Nat. Commun., 2020, 11, 1–9.
33. K. J. Karki, J. R. Widom, J. Seibt, I. Moody, M. C. Lonergan, T. Pullerits and A. H. Marcus, Nat. Commun., 2014, 5, 1–7.
34. K. L. Hall, G. Lenz, E. P. Ippen and G. Raybon, Opt. Lett., 1992, 17, 874–876.
35. P. Tian and W. S. Warren, Opt. Lett., 2002, 27, 1634–1636.
36. K. J. Karki, L. Kringle, A. H. Marcus and T. Pullerits, J. Opt., 2015, 18, 015504.
37. P. Kumar, Q. Shi and K. J. Karki, J. Phys. Chem. C, 2019, 123, 13444–13450.
38. S. Ghosh, S. K. Pal, K. J. Karki and T. Pullerits, ACS Energy Lett., 2017, 2, 2133–2139.
39. K. J. Karki, M. Abdellah, W. Zhang and T. Pullerits, APL Photonics, 2016, 1, 046103.
40. J.-C. Blancon, H. Tsai, W. Nie, C. Stoumpos, L. Pedesseau, C. Katan, M. Kepenekian, C. Soe, K. Appavoo, M. Sfeir, S. Tretiak, P. M. Ajayan, M. G. Kanatzidis, J. Even, J. J. Crochet and A. D. Mohite, Science, 2017, eaal4211.
41. Q. Shi, S. Ghosh, A. S. Sarkar, P. Kumar, Z. Wang, S. K. Pal, T. Pullerits and K. J. Karki, J. Phys. Chem. C, 2018, 122, 3818–3823.
42. Q. Shi, S. Ghosh, P. Kumar, L. C. Folkers, S. K. Pal, T. Pullerits and K. J. Karki, J. Phys. Chem. C, 2018, 122, 21817–21823.
43. S. Fu, A. Sakurai, L. Liu, F. Edman, T. Pullerits, V. Öwall and K. J. Karki, Rev. Sci. Instrum., 2013, 84, 115101.
44. K. Karki, M. Torbjörnsson, J. R. Widom, A. H. Marcus and T. Pullerits, J. Instrum., 2013, 8, T05005.
45. K. J. Karki, Phys. Rev. A, 2017, 96, 043802.
46. M. Yuan, L. N. Quan, R. Comin, G. Walters, R. Sabatini, O. Voznyy, S. Hoogland, Y. Zhao, E. M. Beauregard, P. Kanjanaboos, Z. Lu, D. H. Kim and E. H. Sargent, Nat. Nanotechnol., 2016, 11, 872–877.
47. M. Wei, F. P. G. de Arquer, G. Walters, Z. Yang, L. N. Quan, Y. Kim, R. Sabatini, R. Quintero-Bermudez, L. Gao, J. Z. Fan, A. Gold-Parker, M. F. Toney and E. H. Sargent, Nat. Energy, 2019, 4, 197–205.
48. M. C. Brennan, J. E. Herr, T. S. Nguyen-Beck, J. Zinna, S. Draguta, S. Rouvimov, J. Parkhill and M. Kuno, J. Am. Chem. Soc., 2017, 139, 12201–12208.
49. S. G. Motti, M. Gandini, A. J. Barker, J. M. Ball, A. R. S. Kandada and A. Petrozza, ACS Energy Lett., 2016, 1, 726–730.
50. K. Galkowski, A. Mitioglu, A. Miyata, P. Plochocka, O. Portugall, G. E. Eperon, J. T.-W. Wang, T. Stergiopoulos, S. D. Stranks, H. J. Snaith and R. J. Nicholas, Energy Environ. Sci., 2016, 9, 962–970.
51. Z. Yang, A. Surrente, K. Galkowski, A. Miyata, O. Portugall, R. J. Sutton, A. A. Haghighirad, H. J. Snaith, D. K. Maude, P. Plochocka and R. J. Nicholas, ACS Energy Lett., 2017, 2, 1621–1627.
52. Y. Yamada, T. Nakamura, M. Endo, A. Wakamiya and Y. Kanemitsu, IEEE J. Photovolt., 2014, 5, 401–405.
53. J. Even, L. Pedesseau and C. Katan, J. Phys. Chem. C, 2014, 118, 11566–11572.
54. J. Bergqvist, W. Tress, D. Forchheimer, A. Melianas, Z. Tang, D. Haviland and O. Inganäs, Prog. Photovoltaics, 2016, 24, 1096–1108.
55. P. Kumar and K. Karki, J. Phys. Commun., 2019, 3, 035008.
56. S. Nah, B. Spokoyny, C. Stoumpos, C. Soe, M. Kanatzidis and E. Harel, Nat. Photonics, 2017, 11, 285.
57. S. Govinda, B. P. Kore, M. Bokdam, P. Mahale, A. Kumar, S. Pal, B. Bhattacharyya, J. Lahnsteiner, G. Kresse, C. Franchini, A. Pandey and D. D. Sarma, J. Phys. Chem. Lett., 2017, 8, 4113–4121.
58. L. Etgar, Energy Environ. Sci., 2018, 11, 234–242.
59. K. Galkowski, A. Mitioglu, A. Surrente, Z. Yang, D. Maude, P. Kossacki, G. Eperon, J.-W. Wang, H. Snaith, P. Plochocka and R. J. Nicholas, Nanoscale, 2017, 9, 3222–3230.
60. L. Orosz, F. Réveret, F. Médard, P. Disseix, J. Leymarie, M. Mihailovic, D. Solnyshkov, G. Malpuech, J. Zuniga-Pérez, F. Semond, M. Leroux, S. Bouchoule, X. Lafosse, M. Mexis, C. Brimont and T. Guillet, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 121201.
61. M. Maragkou, A. Grundy, T. Ostatnický and P. Lagoudakis, Appl. Phys. Lett., 2010, 97, 111110.
62. A. D. Wright, C. Verdi, R. L. Milot, G. E. Eperon, M. A. Pérez-Osorio, H. J. Snaith, F. Giustino, M. B. Johnston and L. M. Herz, Nat. Commun., 2016, 7, 11755.
63. J. Lee, E. S. Koteles and M. Vassell, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 5512.
64. S. Rudin and T. Reinecke, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 3017.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthesis, characterization, and details of phase modulated 2PPL of q-MPB and q-CPB perovskite. See DOI: 10.1039/d0cp05538g

‡ S. G. and B. P. contributed equally.

---