Open Access Article
Open Access ArticleModelling interactions of cationic dimers in He droplets: microsolvation trends in HenK2+ clusters†
Nissrin
Alharzali
ab,
Raúl
Rodríguez-Segundo
ac and
Rita
Prosmiti
 *a
*a
aInstitute of Fundamental Physics (IFF-CSIC), CSIC, Serrano 123, 28006 Madrid, Spain. E-mail: rita@iff.csic.es; Tel: +34 915616800
bLaboratory of Interfaces and Advanced Materials, Faculty of Science, University of Monastir, 5019 Monastir, Tunisia
cAtelgraphics S. L., Mota de Cuervo 42, 28043, Madrid, Spain
First published on 11th November 2020
Abstract
We report the results of a detailed theoretical investigation of small K2+-doped He clusters. The structural characteristics and stabilities of such cations are determined from ab initio electronic structure calculations at the MRCI+Q level of theory. The underlying interactions show a multireference character and such effects are analyzed. The interaction potentials are constructed employing an interpolation technique within the inverse problem theory method, while the nuclear quantum effects are computed for the trimers, their spatial arrangements are discussed, and information was extracted on the orientational anisotropy of the forces. We found that energetically the most stable conformer corresponds to linear arrangements that are taking place under large amplitude vibrations, with high zero-point energy. We have further looked into the behavior of higher-order species with various He atoms surrounding the cationic dopant. By using a sum of potentials approach and an evolutionary programming method, we analyzed the structural stability of clusters with up to six He atoms in comparison with interactions energies obtained from MRCI+Q quantum chemistry computations. Structures containing Hen motifs that characterize pure rare gas clusters, appear for the larger K2+-doped He clusters, showing selective growth during the microsolvation process of the alkali-dimer cation surrounded by He atoms. Such results indicate the existence of local solvation microstructures in these aggregates, where the cationic impurity could get trapped for a short time, contributing to the slow ionic mobility observed experimentally in ultra-cold He-droplets.
Research in the field of cluster science continues to grow aiming to establish the connection with nanoscale science, as clusters could serve as building blocks for new materials with designed/tailored properties.1 In some cases the system evolves from finite-size toward bulk properties smoothly allowing extrapolation from few-body to many-body behavior, while sometimes significant changes in the nanoscopic properties occur, enabling different applications.2
Among such clusters, the investigation of nano-sized He droplets has received a great deal of attention during the last few years, being a challenge for both theoreticians and experimentalists.3–22 Nowadays, He nanodroplets are used as ultracold homogeneous matrices for spectroscopic studies, providing a unique environment for the isolation of otherwise hardly accessible molecules, allowing detailed study of a wide variety of molecular dopants, neutral or charged.3,4,8,15,23–26
From experimental and theoretical evidence it turns out that alkali metal atoms and dimer dopants have a series of interesting properties due to the unusual bonding behavior of such systems.14,27–34 They both are weakly bound, attached to the surface of the He droplet usually forming a dimple-like deformation on it, and atoms typically desorb upon excitation, or when more alkali atoms are attached, then they surf on the surface eventually forming cold molecules, e.g. high-spin alkali dimers, through collisions.35–39 When moving to the charged alkali dopants, the interaction between the cationic impurity and the surrounding He atoms is much stronger, leading to the formation of solvation shells, the so-called snowball structure.28–30,40,41 Such highly compressed He regions owing to electrostriction, indicate the existence of compact localized microstructures (solid-like shells) surrounded by less localized He atomic regimes (liquid-like shells), and have been widely used to interpret the low mobility of ions experimentally observed.42,43
Concerning investigations involving charged dopants, information on the underlying intermolecular, markedly orientational ionic forces, and on the microscopic structures and energetics of alkali-cation-He complexes is essential. In this vein, several theoretical studies have been reported on alkali cations in He clusters,27,31,40,41,44,45 while there is also a number of them exploring the lighter alkali dimer cationic complexes,10,46–48 indicating critical dependence on the minor details of the interaction potential, and computational difficulties for carrying out modern quantum chemistry computations in weakly interacting heavy-atom-containing molecular systems. Moreover, recently high-resolution mass spectra of the lighter Na2+ and K2+ alkali dimers in Hen clusters have been obtained by electron ionization of doped He droplets.30 It has been found30 that the size dependence of the experimental ion yield of the clusters with up to 20 He atoms exhibits distinct anomalies that have not been observed previously, indicating that the number of atoms predicted in the first solvation subshell is overestimated by theory.30 Such anomalies have been found to be more pronounced in the Na2+Hen with n = 2 and 6, while in the K2+Hen clusters minor anomalies are observed at n = 2, 5, 9 and 12.30
Given the importance of the underlying interactions in the microsolvation processes of such charged impurities in He-clusters, their accurate description requires detailed knowledge of the electronic properties. The advances in the computational capabilities, both software and hardware, have made very precise calculations of such finite-size complexes containing an increasing number of He atoms affordable. However, the intriguing interplay between weak intermolecular interactions and the role of quantum effects on their binding present a real challenge for the theorists. Thus, the present work is directed at studying the structures and energies of different finite-size Hen–K2+ clusters. We intend to study the forces between the potassium-dimer cation and He atom by high level ab initio multi-reference calculations for constructing reliable potential energy surfaces able to describe high-order complexes. We build up a global analytical ab initio-based model potential for the trimer, based on the reproducing kernel Hilbert-space (RKHS) and the inverse problem theory,49 which was employed to calculate the vibrational quantum states and zero-point effects. Furthermore, we adopt a simplified sum of potential approach, up to three-body terms, to represent K2+-doped clusters containing an increasing number of He atoms, and their structuring was investigated by optimal potential configurations through an evolutionary programming (EP) algorithm.50,51
This article is organized as follows: the next section describes the computational details and methods implemented, as well as the results obtained. It contains four subsections including: the electronic structure calculations of the trimer interaction energies, the construction of its potential energy surface by a general interpolation scheme, the trimer's bound quantum states, the sum of potential representation, structures and energetics of higher order K2+-doped He clusters, respectively. Finally, the last section summarizes some concluding remarks.
1 Computational methods and results
1.1 Ab initio electronic structure calculations: multireference character effects
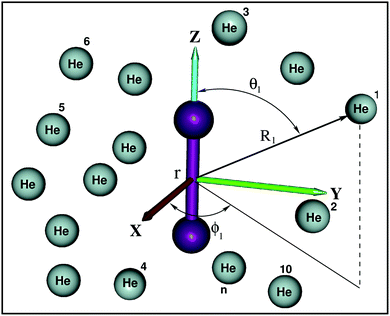
All ab initio calculations have been performed with the Molpro program.52 The potential energy of a He atom interacting with the K2+(2Σ+g) ion are computed using the Jacobi coordinates (r, R, θ), where r and R are the vectors joining the two atoms in the K2+ dimer, and the center of mass of the K2+ with the He atom, respectively, with θ being the angle between them. The interaction energies using the supermolecular approach are given by: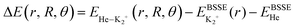 , where EHe–K2+ is the total energy of the complex, and EBSSE is the basis set superposition error (BSSE) corrected total energies of the corresponding He and K2+ monomers. The BSSE correction was included for all molecular configurations using the counterpoise method.53
, where EHe–K2+ is the total energy of the complex, and EBSSE is the basis set superposition error (BSSE) corrected total energies of the corresponding He and K2+ monomers. The BSSE correction was included for all molecular configurations using the counterpoise method.53
In our calculations, the r bond length of the K2+ dimer ion was kept fixed at its experimental equilibrium value of re = 4.4 Å,54 while the intermolecular R distances ranged from R = 4.5 to 20 Å, and the angle θ varied between 0 and 90° by steps of 10°. Scalar relativistic effects were accounted for by using relativistic and quasi-relativistic effective small-core potentials (ECPs), such as ECP10MDF(11s,11p,5d,3f)55 and ECP10MWB(7s,6p),56 respectively, for the K atoms. Core–core and core–valence correlation effects were entirely neglected in the small-core calculations. Also, for the K atoms we also used all electrons basis sets, such as the 6-31G(3df)57 and def2-QZVP,58 while for the He atom we used the large augmented correlation consistent basis sets aug-cc-pV5Z (AV5Z) and aug-cc-pV6Z (AV6Z).59,60 Interaction energies were computed at three different levels of theory: second-order Møller–Plesset perturbation theory (MP2), couple-cluster single and double excitations with perturbative triples (CCSD(T)), and internally contracted multireference configuration interaction (MRCI+Q). In the MRCI calculations, the orbitals were optimized in the state-averaged complete active space self-consisted-field (CASSCF) calculations, and the CASSCF wave functions were used as reference functions. The Davidson correction (+Q) was applied to the MRCI energies to account approximately for higher excitations, and to reduce size consistency error. All grid configurations and their corresponding energies were organized and analyzed using DENEB software utilities.61
In Table 1 we list the calculated interaction energies using the indicated basis sets for He and K atoms at the linear and T-shaped geometries of the HeK2+ complex. We also report energies at the complete basis set (CBS) limit, using for each basis set for the K atoms, the AV5Z and AV6Z basis sets for He atoms to extrapolate the energies to the (approximate) CBS value. We performed extrapolation of the correlation energies utilizing the two-point single inverse power function first introduced by Schwartz62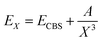 , with X = 5 and 6. As it can be seen, by using the relativistic ECPs for the K atoms, the computed energies are found to be in accord with those from all electron calculations for both geometries of the system at each level of calculation. In turn, we could notice that the MP2, CCSD(T) and MRCI+Q interaction energies for the T-shaped geometry show some relatively small differences between them, while for the linear geometry the MRCI+Q energy values are considerably much lower than those of MP2 and CCSD(T) for all basis sets used.
, with X = 5 and 6. As it can be seen, by using the relativistic ECPs for the K atoms, the computed energies are found to be in accord with those from all electron calculations for both geometries of the system at each level of calculation. In turn, we could notice that the MP2, CCSD(T) and MRCI+Q interaction energies for the T-shaped geometry show some relatively small differences between them, while for the linear geometry the MRCI+Q energy values are considerably much lower than those of MP2 and CCSD(T) for all basis sets used.
| K/He atom | MP2 | CCSD(T) | MRCI+Q |
|---|---|---|---|
| ECP(Basis set) | θ = 0/90° | ||
| ECP10MWB(7s,6p)/AV5Z | −24.84/−3.67 | −26.86/−4.40 | −33.40/−4.27 |
| ECP10MWB(7s,6p)/AV6Z | −25.38/−3.71 | −27.42/−4.46 | −34.30/−4.33 |
| ECP10MWB(7s,6p)/CBS56 | −26.12/−3.76 | −28.18/−4.54 | −35.25/−5.21 |
| ECP10MDF(11s,11p,5d,3f)/AV5Z | −25.37/−4.54 | −27.64/−5.82 | −35.56/−5.60 |
| ECP10MDF(11s,11p,5d,3f)/AV6Z | −25.49/−4.58 | −27.36/−5.95 | −36.33/−5.81 |
| ECP10MDF(11s,11p,5d,3f)/CBS56 | −25.65/−4.63 | −28.02/−6.12 | −37.38/−6.09 |
| All e−(6-31G(3df))/AV5Z | −25.05/−4.15 | −26.84/−5.21 | −34.07/−5.03 |
| All e−(6-31G(3df))/AV6Z | −25.23/−4.20 | −27.00/−5.30 | −34.57/−5.11 |
| All e−(6-31G(3df))/CBS56 | −25.47/−4.26 | −27.26/−5.42 | −35.25/−5.21 |
| All e−(def2-QZVP)/AV5Z | −25.45/−4.34 | −27.14/−5.53 | −35.56/−5.33 |
| All e−(def2-QZVP)/AV6Z | −25.63/−4.39 | −27.33/−5.61 | −35.99/−5.40 |
| All e−(def2-QZVP)/CBS56 | −25.87/−4.45 | −27.59/−5.71 | −36.58/−5.49 |
Thus, we performed further single-reference MP2 and CCSD(T) and multi-reference MRCI+Q calculations at various angular orientations of He–K2+(2Σ+g) by minimizing the energy at each R distance using the all-electron 6-31G(3df) and def2-QZVP basis sets, as well as the ECP10MDF(11s,11p,5d,3f) ones for K atoms and the AV6Z for the He atom. Fig. 1 shows the minimum energy path as a function of θ angle between the linear and T-shaped potential wells for such calculations. One can see that the energy values from each ab initio method slightly depend on the type of basis set used here for the K atoms, with the ECP10MDF(11s,11p,5d,3f) data being lower by less than 0.4 cm−1 from the energies obtained with the def2-QZVP basis set. Also, we found small differences, of less than 0.2 cm−1, between the CCSD(T) and MRCI+Q energies (see inset plot in Fig. 1) for angular orientations with θ ≥ 50°, while in contrast, for linear and bent orientations with θ < 50° the interaction energies highly depend on the level of theory employed. In particular, at these configurations the single-reference methods estimate energies of near 10 cm−1 higher than those of the MRCI+Q one. In a first step, we monitored the T1, D1 and T1/D1-diagnostics,63,64 as proposed for open shell complexes, from the single reference UCCSD(T) coupled cluster calculations. These diagnostics have been widely used to test the validity of single-reference methods. Such criteria have been useful for qualitative analysis, while quantitative relationships suggested for the possible significant multireference character have been difficult to interpret. In general, the criteria T1 < 0.02, D1 < 0.05 and the T1/D1 < 0.4 have been proposed for CCSD calculations. We also checked the expectation value of 〈S2−Sz2−Sz〉 of spin contamination in the UCSSD wavefunction, as well as the weight C02 of the leading configuration in the CASSCF wavefunction65 as given by the MRCI computations, with C02 values smaller than 0.90, indicating the significant multireference character of the system.
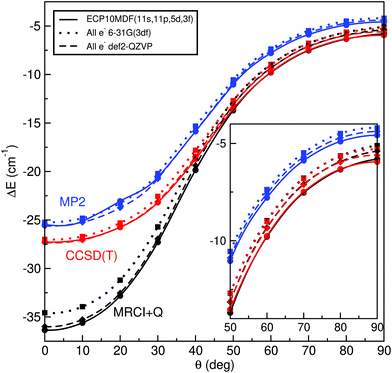 | ||
| Fig. 1 Interaction energies obtained from the indicated MP2, CCSD(T) and MRCI+Q ab initio methods and basis sets along the minimum energy path as a function of angle θ for the HeK2+ (see text). | ||
Such analysis provides similar trends and in Fig. S1 (see ESI†) we present the values of each of the above most widely used CC diagnostics as a function of the R distance, for the selected values of angle θ (see left panel), and as a function of θ with R = Re(θ) (see right panel). We found that T1 spans from 0.3 to 0.001, D1 from 0.5 to 0.002, while T1/D1 from 0.9 to 0.6 as θ goes from 0 to 90° and R distances are between 4.5 to 6.5 Å. One can see that both T1 and D1 criteria, indicate single-reference character of the system around the corresponding equilibrium configurations, while their ratio, used to examine the homogeneity of the electronic structure, suggests the need for a multireference electron correlation procedure, especially for θ < 60° (see right panels in Fig. S1, ESI†), as well as all diagnostics shown in the left panels of Fig. S1 (ESI†) for selected R and θ configurations. On the basis of these comparisons, and taking into account the MRCI+Q results obtained for the K2+ spectroscopic constants (Table S1 in ESI†),77–82 we decided to perform the final calculations at the MRCI level of theory using the small-core ECP10MDF pseudo-potentials with the large (11s,11p,5d,3f) basis set for the potassium atom and the aug-cc-pV6Z for the He atom.
1.2 Representation of the potential energy surface: orientational anisotropy effects
For representing the potential energy surface of Hen–K2+ we employed a general interpolation scheme based on the RKHS method proposed by Ho and Rabitz.49 Following the RKHS scheme49 the interaction energy is written as,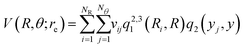 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, NR and Nθ are the number of ab initio calculated points in the R and θ coordinates, respectively. The expressions of the one-dimensional reproducing kernel functions, qn,m1 and q2 for the distance-like, R, and angle-like, θ, variables, respectively49 are given by,
θ, NR and Nθ are the number of ab initio calculated points in the R and θ coordinates, respectively. The expressions of the one-dimensional reproducing kernel functions, qn,m1 and q2 for the distance-like, R, and angle-like, θ, variables, respectively49 are given by,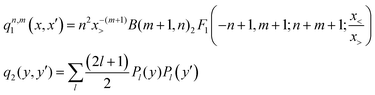 | (2) |
The vij coefficients were obtained by solving eqn (1), with V(Ri,θj,re) being the calculated ab initio MRCI+Q interaction energies at the corresponding (Ri,θj,re) grid point. Fig. S2 (see the left panel, ESI†) shows the RKHS potential curves together with the ab initio MRCI+Q interaction energies along the R coordinate for each θ angle from 0 to 90°. One can see the angular anisotropy of the PES, with the potential curve for θ = 0 (linear configurations) to present the deepest minimum, while the interaction for other angular orientations becomes less attractive with those of the T-shaped to count for −5.846 cm−1. Further, in Fig. S2 (see the right panel, ESI†) the long range part of the interaction, as obtained from the MRCI+Q data for linear and T-shaped configurations compared very well with the expected 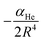 asymptotic behavior, with αHe being the polarizability of the He atom given in ref. 66, indicating the quality of the electronic quantum calculations at these potential regions.
asymptotic behavior, with αHe being the polarizability of the He atom given in ref. 66, indicating the quality of the electronic quantum calculations at these potential regions.
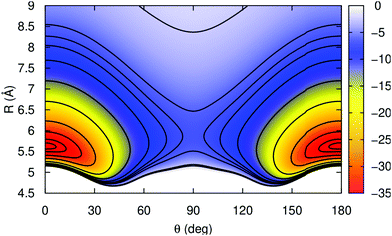
In Fig. 2 a 2D contour plot of the RKHS potential surface is displayed. The K2+ bond length is kept fixed at its equilibrium re = 4.4 Å, while the He atom is moving in the (θ, R)-plane. The potential has two symmetric minima at linear geometries with Re = 5.62 Å, and a well-depth value of 36.355 cm−1, while the barrier between them is 30.509 cm−1 higher in energy, and corresponds to a T-shaped configuration with the He atom at R = 5.82 Å from the K2+ molecular ion.
Table 2 list the interaction energies of the He–K2+(2Σ+g) complex along the minimum energy path for different angular orientations of the He atom computed by the present MRCI+Q, RKHS PES and previously reported studies.46,47 One can see that RKHS PES describes the He–K2+ interaction in excellent agreement with the MRCI+Q data, with an overall average difference of 0.04 cm−1. Also comparison with the previously reported values46,47 shows some significant differences along all angular orientations.
| (θ, R) | ΔEMRCI+Q |
V(R,θ,re)/δ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) |
Literature |
|---|---|---|---|
| a From ref. 46. b From ref. 47. | |||
| (0, 5.62) | −36.344 | −36.355/0.011 | — |
| (0, 5.5) | −35.465 | −35.490/0.025 | −38a |
| (0, 5.4) | −32.353 | −32.420/0.068 | −70b |
| (10, 5.62) | −35.490 | −35.484/−0.006 | — |
| (10, —) | — | — | −35.92a |
| (20, 5.41) | −32.728 | −32.731/0.003 | — |
| (20, —) | — | — | −31.48a |
| (30, 5.31) | −27.295 | −27.314/0.019 | — |
| (30, —) | — | — | −22.96a |
| (40, 5.41) | −19.823 | −19.808/−0.015 | — |
| (40, —) | — | — | —14.81a |
| (50, 5.51) | −13.685 | −13.701/0.016 | − |
| (50, −) | — | — | −8.88a |
| (60, 5.62) | −9.800 | −9.779/−0.021 | — |
| (60, —) | — | — | −5.92a |
| (70, 5.72) | −7.529 | −7.558/0.029 | — |
| (70, —) | — | — | −4.4a |
| (80, 5.82) | −6.344 | −6.308/−0.036 | — |
| (80, —) | — | — | −4.07a |
| (90, 5.82) | −5.808 | −5.846/0.038 | — |
| (90, 6.1) | −5.633 | −5.679/0.046 | −4a |
| (90, 5.53) | −5.215 | −5.273/0.058 | −6b |
1.3 Bound state calculations: quantum effects
We performed variational quantum nuclear calculations employing the present RKHS PES for the He–K2+(2Σ+g) complex, and the full spectrum of its bound eigenstates was obtained. As the spin-rotation constant of the open shell K2+(2Σ+g) diatom is two orders of magnitude smaller than its rotational constant B, we neglected this coupling, and its effect on the rotational levels of a 2Σ molecule.67,68 Thus, the corresponding Hamiltonian for the complex is the same as that for a closed-shell 1Σ diatom, and in Jacobi coordinates it is written as,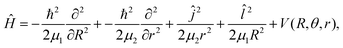 | (3) |
![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) are the angular momentum operators associated with the vectors r and R, respectively, leading to a total angular momentum Ĵ =
are the angular momentum operators associated with the vectors r and R, respectively, leading to a total angular momentum Ĵ = ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) + ĵ, and V(R, θ, r) is the RKHS potential given in eqn (1).
+ ĵ, and V(R, θ, r) is the RKHS potential given in eqn (1).
We are interested in the vibrational bound eigenstates of the whole system, so we carried out variational discrete variable representation (DVR) calculations, following the procedure described in our previous studies.69–71 The Hamiltonian is represented as a product of radial, fn(R), and angular, Θ(JMp)jΩ, basis functions. For the R coordinate we used a DVR basis set based on the particle in a box eigenfunctions,69 while the angular basis functions are eigenfunctions of the parity (p), with M being the projection of J on the space-fixed z-axis, and Ω its projection on the body-fixed z-axis, which is chosen here along the R vector. Specifically, for the present J = 0 calculations we used 100 DVR radial grid points over the range from 4.5 to 20 Å, and orthonormalized Legendre polynomials {Pj(cosθ)} in θ coordinate with up to j = 40, and 41 values for even (p = +1) and odd (p = −1) parity symmetry, respectively, achieving a convergence of 0.005 cm−1 in the calculations. The rotational constant is taken equal to 0.0445 cm−1 for the K2+, and the standard atomic masses of He and K are 4.0026 and 39.0983 μ, respectively. By diagonalizing the corresponding Hamiltonian matrix we obtained the eigenenergies and eigenfunctions.
In Table 3 we list the energies of all 14 vibrational bound states (even(e) and odd(o)) of the HeK2+ using the present MRCI+Q/RKHS surface, and compare them with the previously reported theoretical data46 available. As can be seen, the ground and the first excited vibrational states are double degenerated with even and odd parity states having the same energy, while the states with energy values higher than the T-shaped potential barrier show splitting between the even and odd symmetries that increases as the energy increases. By comparing with the previous data available for an MP2/6-31G(3df) surface,46 one can see that the present PES supports in total 14 bound states, three more states than the MP2 surface, with their energy spacings being quite different. The MRCI+Q/RKHS surface predicts a shallower potential well with a more stable HeK2+ conformer than the MP2 one. The computed binding energies are −18.67 and −17.47 cm−1 for the MRCI+Q/RKHS and MP2 PESs, respectively, with the corresponding zero-point energies being 17.67 and 20.53 cm−1, accounting for 48.6 and 54% of their potential well-depths.
| No. state (n) | This work | From ref. 46 |
|---|---|---|
| 0 | −18.67/−18.67 | −17.47/−17.47 |
| 1 | −11.00/−11.00 | −8.57/−8.57 |
| 2 | −4.98/−4.96 | −3.57/−3.57 |
| 3 | −4.39/−4.34 | −2.48/−2.33 |
| 4 | −2.07/−1–13 | −0.73/−0.26 |
| 5 | −0.94/−0.47 | −0.27/— |
| 6 | −0.19/−0.16 | — |
In Fig. 3 and 4 we display the radial and angular probability distributions, respectively, for all even parity vibrational states of the He–K2+ cluster. One can clearly see that ground and first excited vibrational states are localized in the linear potential well, while higher lying states (above the T-shaped barrier) are delocalized, with He atoms undergoing large amplitude radial and bending motions. The corresponding probability distributions for the n = 2–6 states are moving to larger R values showing an increasing number of nodes in both R and θ coordinates, presenting a more complicated nodal pattern gradually. Both radial and angular probability distributions of these states, especially of the n = 4–6 ones, show clear differences between those of even and odd parity symmetry (see Fig. S3 in ESI†), with the even state wavefunctions up to n = 4 describing the bent He–K2+ complexes. We should also note that the even and odd n = 5 and 6 states are localized in the angular coordinate, while their radial distributions are broad especially for the even n = 6 state.
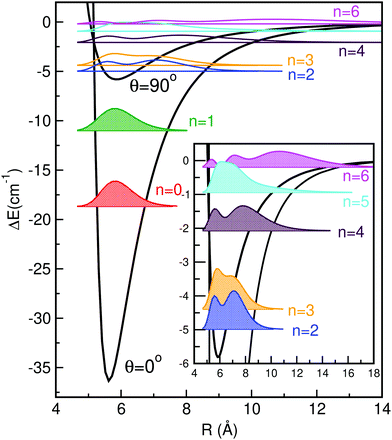 | ||
| Fig. 3 Radial distributions of all even parity bound states of HeK2+ using the present MRCI+Q/RKHS surface. | ||
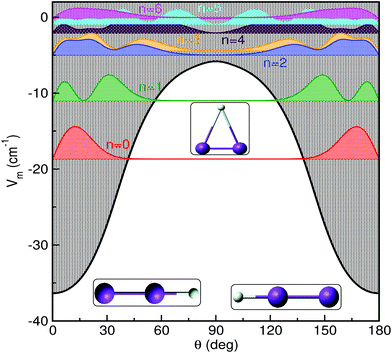 | ||
| Fig. 4 Angular distributions of all even parity bound states of HeK2+ using the MRCI+Q/RKHS surface. | ||
1.4 Energetics and structures of higher-order clusters: Microsolvation effects
Following our previous work on larger He-doped clusters18,72–75 we represent the analytical PES of higher order HenK2+ using the sum-of-potentials approach based on the sum of the MRCI+Q/RKHS three-body parameterized HeK2+ interactions plus the He–He one,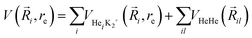 | (4) |
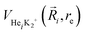 terms are the present MRCI+Q/RKHS potential of the HeK2+ complex. and
terms are the present MRCI+Q/RKHS potential of the HeK2+ complex. and 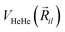 is the potential function for He2 given in ref. 76.
is the potential function for He2 given in ref. 76. 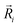 are the vectors connecting the center of mass of K2+ with each He atom, while θi are the angles between each
are the vectors connecting the center of mass of K2+ with each He atom, while θi are the angles between each 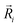 vector and the K2+ axis (see Fig. 5). In turn, we follow the (#T1/T2,#L1/#L2,#B1/B2) notation to label the number of He atoms in T-shaped (T1 for θ = 90° and T2 for θ = 270°), linear (L1 for θ = 0° and L2 for θ = 180°), and for bent configurations, B1 for 90 < θ < 270 and B2 for 270 < θ < 90 for any ϕ value, respectively. In this way one could classify the different structures of higher-order HenK2+ clusters.
vector and the K2+ axis (see Fig. 5). In turn, we follow the (#T1/T2,#L1/#L2,#B1/B2) notation to label the number of He atoms in T-shaped (T1 for θ = 90° and T2 for θ = 270°), linear (L1 for θ = 0° and L2 for θ = 180°), and for bent configurations, B1 for 90 < θ < 270 and B2 for 270 < θ < 90 for any ϕ value, respectively. In this way one could classify the different structures of higher-order HenK2+ clusters.
In order to validate the sum-of-potential approach (see eqn (4)) adapted here, we carried out MRCI+Q/ECP10MDF/AV6Z calculations for the tetratomic He2K2+ cluster. In Fig. 6 we display the potential energy values obtained from the analytical expression of eqn (4) together with the MRCI+Q computed interaction energies for the He2K2+ cluster along its R1 and R2 distances at selected orientantional configurations, such as those with He atoms in linear and/or T-shaped geometries. In particular, we chose to check interaction energies along three different cluster orientations, the (0/0, 1/1, 0/0), (1/1, 0/0, 0/0) and (1/0, 1/0, 0/0), corresponding to the global and low-energy local minima on He2K2+ PES. In this way, one could validate the proposed analytical potential approach, as the energies obtained from the sum-of-products expression of eqn (4) are in excellent agreement with the corresponding ab initio MRCI+Q values, using the same basis sets for K and He atoms as in the trimer case for all configurations considered here for the tetratomic He2K2+ cluster.
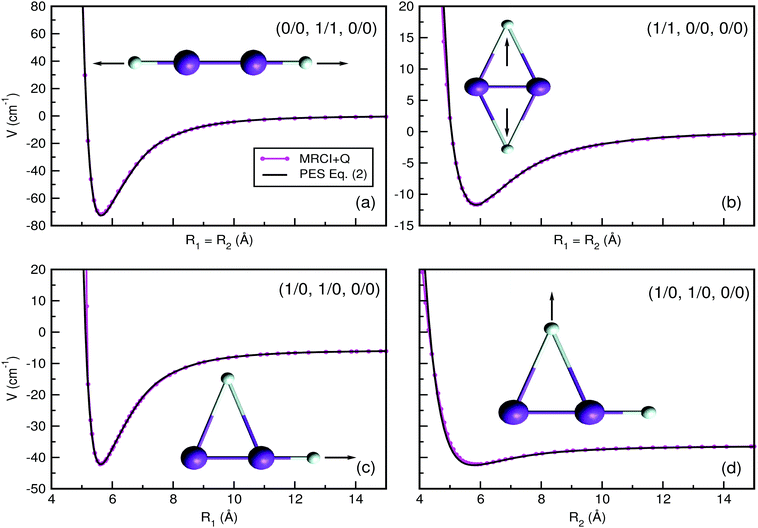 | ||
| Fig. 6 Potential curves obtained for the He2K2+ cluster using the sum-of-potentials approach of eqn (4), (solid lines), together with the calculated MRCI+Q/AV6Z interaction energies (solid-circle lines) as a function of (a) R1 for the (0/0, 1/1, 0/0) structure, (b) R1 =R2 for the (1/1, 0/0, 0/0) configuration, and (c and d) R1 and R2 for the (1/0, 1/0, 0/0) configuration, respectively. The arrows in each configuration indicate which He atoms are moving along the R1/R2 coordinates. | ||
In turn, we carried out a systematic search to identify optimal energy structures, such as global and local minima, on the HenK2+ PESs of higher-order clusters. An evolutionary programming algorithm50 is employed to find the lowest energy structures and study the structural optimization of HenK2+ clusters, with n up to 6 He atoms. Such algorithms have been proven to be an attractive and efficient way to solve numerical optimization problems in multi-dimensional space, as gradients of the potential are not needed, while the search space-narrowing is automatically realized by the self-adaptation of mutation.18,50,51 Briefly, we start by generating an initial population of ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) = 10 individuals (for each HenK2+ cluster in our case). Each individual is characterized by a pair of real vectors (χi,ηi)i=1−
= 10 individuals (for each HenK2+ cluster in our case). Each individual is characterized by a pair of real vectors (χi,ηi)i=1−![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ), containing the Cartesian coordinates, χi, of all cluster atoms and their standard deviation, ηi, for Gaussian mutation (strategy parameter) that controls the evolution of the dispersion of the population in time. The initial coordinates χi with ηi = 1 are chosen randomly in the interval (0, Δ), with Δ being a displacement factor that increases the resolution power. Each parent set (χi,ηi) evolves to generate a new population by mutation,50 while for each individual of the joint parent-child group (2
), containing the Cartesian coordinates, χi, of all cluster atoms and their standard deviation, ηi, for Gaussian mutation (strategy parameter) that controls the evolution of the dispersion of the population in time. The initial coordinates χi with ηi = 1 are chosen randomly in the interval (0, Δ), with Δ being a displacement factor that increases the resolution power. Each parent set (χi,ηi) evolves to generate a new population by mutation,50 while for each individual of the joint parent-child group (2![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) individuals) q (tournament size equals 10) opponents are randomly chosen from the 2
individuals) q (tournament size equals 10) opponents are randomly chosen from the 2![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) − 1 individuals, to compare each other, and the individual in each encounter with the lower potential energy wins. The best
− 1 individuals, to compare each other, and the individual in each encounter with the lower potential energy wins. The best ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) individuals then become parents for the next generation and so on. Convergence is achieved when the potential energy difference between two consecutive generations is below a threshold value of 10−3 cm−1.
individuals then become parents for the next generation and so on. Convergence is achieved when the potential energy difference between two consecutive generations is below a threshold value of 10−3 cm−1.
Thus, for each HenK2+ cluster we localized the optimized structures on its PES (see eqn (4)), and by carrying out additional frequency analysis of the Hessian eigenvalues we could characterize the nature of the stationary PES points. We were able to identify several minima on each cluster's PES, with those lying close in energy to the global minimum being important as they could be accessible by including quantum zero-point effects.
In turn, in Table S2 (see the ESI†) we list the computed energies of various low-energy structures for the HenK2+ clusters with n up to 6 He atoms, obtained from the EP method50 using the sum-of-potential approach (see eqn (4)), together with their comparison with previously reported values available in the literature.10,46 One can see that the difference in the energy values varies, depending on the size cluster and the optimal configuration, with most energies of the global minima showing differences of a few cm−1, while for the remaining optimal structures we also found differences in their ordering, especially for the cluster with n = 4 and 5 He atoms.
In Fig. 7 we display the configurations of the selected optimal structures for each cluster. For the He2K2+ we show six optimal structures with the (0/0, 0/0, 2/0) structure being the global minimum on the PES at an energy of −76.5 cm−1, while the linear (0/0, 1/1, 0/0) and (0/0, 1/0, 1/0) ones are found to be very close in energy, within 3.8 and 5.4 cm−1, respectively. Also, all T-shaped configurations are found to be relatively less stable than the others, with the (1/1, 0/0, 0/0) located at an energy of just −11.64 cm−1 (see Fig. 7). For the He3K2+ cluster five optimal structures are shown with the global minimum (0/0, 0/0, 3/0) structure found at an energy of −123.9 cm−1, while the next structures are higher at relatively close energies of −112.8, −106.1, −85.4 and −78.6 cm−1 corresponding to bent, linear and T-shaped configurations. In turn, the He4K2+ optimal structures are found well separated in energy with the global minimum at −166.1 cm−1 for the (0/0, 0/0, 4/0) configuration, while the two lower in energy (0/0, 0/0, 5/0)/(0/0, 0/0, 6/0) and (0/0, 0/0, 3/2)/(0/0, 0/0, 3/3) configurations for the He5K2+/He6K2+ clusters are close in energy within just ∼3.9 cm−1. By analysing the cluster structures as the number of He increases, one can figure out that the He atoms prefer to locate themselves at one end of the K2+ forming Hen-motifs, such as triangles, rhombs, trapezoids and rings, or symmetrically at its ends forming equilateral He3 in the case of He5,6K2+ systems. The stronger He-K2+ interaction at linear configurations forces the sequential He atoms to get attached at the two ends of the dimeric cation. Such selective growth of the small HenK2+ clusters around the two sides of the cation is due to the competition between the weak He–K2+ and He–He interactions, giving rise to localized He-networks. The formation of such individual compact motifs during the microsolvation process could cause the trapping of the dopant for a short time, and such features could be related to the slow mobility of ions in He-droplets. However, we should point out that all structures discussed here correspond to classical optimal structures on the PES of each cluster, and quantum zero-point energy effects are expected to cause significant changes in their stability, especially for those that are close in energy.
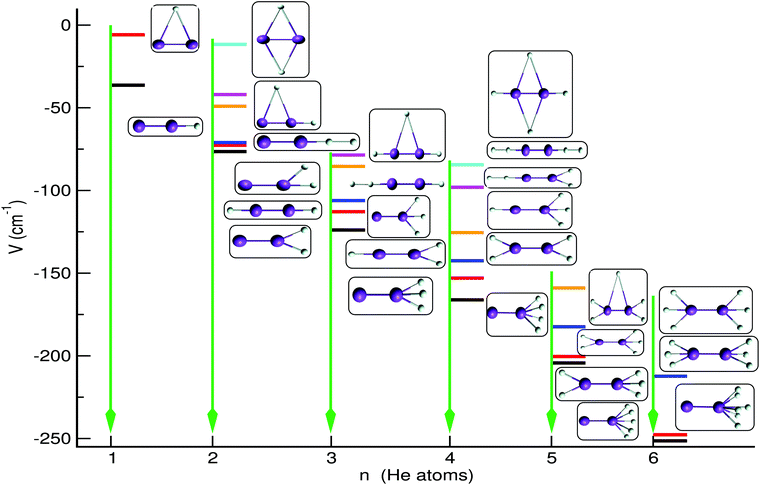 | ||
| Fig. 7 Schematic representation of optimal low-lying structures and their energetics obtained using the sum-of-potential Hen=1−6K2+ PESs. | ||
Finally, in Fig. 8 we report the classical binding, De, and evaporation energies, Dn, given as the difference between the total energies En−1 and En of adjacent size clusters (with n > 1) in their most stable (global minima, see inset plots) configurations, Dn = −En + En−1, for each HenK2+ cluster, as a function of the He atoms number n (cluster size), and compare them with experimental values of HenK2+ ion yields, as determined recently by high-resolution mass spectroscopy.30 One can see that the De values drop down rapidly, with a rate of increase in the binding of 2.1De1, 3.4De1, 4.5De1, 5.6De1 and 6.9De1 with De1 = 36.36 cm−1 for the n = 1 cluster. Above n = 4 the rate of energy acquisition is higher, with cluster structures marked by the formation of the He3 motifs at the ends of the K2+ cation. Distinct minor anomalies in the ion yield with the increase in the size n of the HenK2+ clusters have been observed,30 and are most likely caused by anomalies in evaporation energies. As we can see the patterns of experimental ion yield values and theoretical evaporation energies are similar for such small size clusters, especially for the n = 3 and 4 cases, where the energy separation between the global potential minimum and low-lying local minima is large (more than 10 cm−1). This suggests that such classical minima structures can be classified as bound quantum states once zero-point corrections are included.
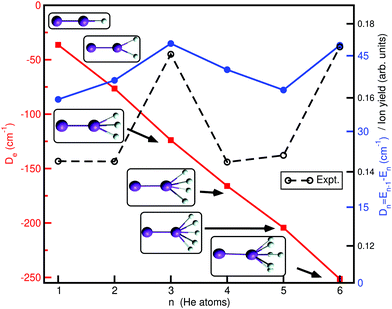 | ||
| Fig. 8 Binding, De1 and evaporation, Dn, energies for the global potential minima (see inset plots) as a function of the cluster size n. Experimental ion yield values30 are also shown for comparison reasons. | ||
2 Summary and conclusions
The present work is focused on the study of intermolecular interactions between the K2+ dimeric cations and one or few He atoms. Such small size species are theoretically tractable by high-level ab initio computations, and reliable interaction forces could be obtained. Thus, as a first step the He–K2+ PES has been constructed from MRCI+Q/ECP10MDD/AV6Z data using the RKHS interpolation scheme. The strength of intermolecular interaction depends of the charge and size of the impurity, and in contrast to lighter alkali-cation dimers, we found that the He–K2+ interaction shows a high multireference character, especially at configurations with θ < 60°. The ZPE and all excited vibrational states of the trimer were computed from nuclear quantum calculations. We found a high ZPE value that counts up to 48.6% of its potential well-depth, although quantum effects do not alter the stability of the classical potential minima. The most stable conformer is linear, while higher vibrational bound states exhibit large amplitude motions, and the states lying at energies above the T-shaped barrier give rise to double structures.The sum-of-potentials approach, based on the ab initio three-body MRCI+Q HeK2 and two-body He–He terms, has been checked and found to provide an accurate and realistic representation of higher-order HenK2+ clusters. Small size HenK2+ clusters can be used as model microsolutions, and accurate knowledge of their potential can provide a very useful initial information on structures and solvation shells. The most stable potential structures for each cluster were obtained via an evolutionary programming algorithm energy optimizations. New insights into their energetics highlight the competition between weak He–K2+ and He–He intermolecular interactions, which control the stabilization of low-lying energy conformers. We clearly see that during the initial cluster growth with n > 2 formation of He n motifs, such as triangles, rhombs or ring-like structures are more favored, indicating a selective growth of these clusters during the microsolvation process. The existence of such localized compact structures should also be expected to influence short-time solute–solvent dynamics, and related with slow mobility of ions observed in He-droplets. Furthermore, by comparing binding and evaporation energies with experimental ion yield values as a function of size n, we identify some minor anomalies for small HenK2+ clusters. Such classical description of the energetics and spatial arrangements of the clustering process should be extended to explicitly include thermal and nuclear quantum effects. Although thermal effects at typically low-T in He droplets, are not expected to alter the classical solvation behavior of K2+ in He clusters, quantum effects may affect the microscopic behavior of such doped clusters, especially in cases where the global and local potential minima are close in energy. The anisotropy of the underlying PES is reflected in the solvation structure, and such information could be used for describing the transition from a molecular aggregate to a dissolved molecule.
The computational cost for nuclear full quantum treatments is becoming really high on moving to larger dimensional systems. However, benchmark studies for small species could serve for testing other approaches to deal with higher dimensional systems with an increasing number of particles. Currently, path-integral molecular dynamics (PIMD) simulations are in progress for such He n-nanodroplet model systems for studying microsolvation quantum and thermal effects for modeling short-time solute–solvent dynamics.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Prof. Pablo Villarreal and Prof. Hamid Berriche for useful discussions. The authors thank the “Centro de Calculo del IFF/SGAI-CSIC” and the CESGA-Supercomputing centre for allocation of computer time. This work has been supported by the MINECO grant No. FIS2017-83157-P and Communidad de Madrid grant Ref: IND2017/AMB-7696, and COST Action CA18212(MD-GAS). N. A. acknowledges financial support from the Ministry of Higher Education and Scientific Research of Tunisia.References
- P. Jena and Q. Sun, Chem. Rev., 2018, 118, 5755–5870 CrossRef.
- G. W. F. Drake, Springer Handbook of Atomic, Molecular, and Optical Physics, Springer-Verlag, New York, New York, 2006 Search PubMed.
- J. P. Toennies, A. F. Vilesov and K. B. Whaley, Phys. Today, 2001, 54, 31–37 CrossRef.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef.
- J. Tang and A. R. W. McKellar, J. Chem. Phys., 2003, 119, 5467–5477 CrossRef.
- Y. Xu, W. Jäger, J. Tang and A. R. W. McKellar, Phys. Rev. Lett., 2003, 91, 163401 CrossRef.
- C. Di Paola, F. A. Gianturco, D. López-Durán, M. P. de Lara-Castells, G. Delgado-Barrio, P. Villarreal and J. Jellinek, ChemPhysChem, 2005, 6, 1348–1356 CrossRef CAS.
- M. Y. Choi, G. E. Douberly, T. M. Falconer, W. K. Lewis, C. M. Lindsay, J. M. Merritt, P. L. Stiles and R. E. Miller, Int. Rev. Phys. Chem., 2006, 25, 15–75 Search PubMed.
- M. P. de Lara-Castells, R. Prosmiti, G. Delgado-Barrio, D. López-Durán, P. Villarreal, F. A. Gianturco and J. Jellinek, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 053201 CrossRef.
- F. Marinetti, L. Uranga-Piña, E. Coccia, D. López-Durán, E. Bodo and F. A. Gianturco, J. Phys. Chem. A, 2007, 111, 12289–12294 CrossRef CAS.
- R. E. Zillich and K. B. Whaley, J. Phys. Chem. A, 2007, 111, 7489–7498 CrossRef CAS.
- D. Bonhommeau, M. Lewerenz and N. Halberstadt, J. Chem. Phys., 2008, 128, 054302 CrossRef CAS.
- J. A. Ramilowski, D. Mikosz, A. A. Farrelly, J. L. C. Fajín and B. Fernández, J. Phys. Chem. A, 2007, 111, 12275–12288 CrossRef CAS.
- R. Prosmiti, G. Delgado-Barrio, P. Villarreal, E. Yurtsever, E. Coccia and F. A. Gianturco, J. Phys. Chem. A, 2009, 113, 14718–14729 CrossRef CAS.
- C. Callegari and W. E. Ernst, Handbook of High-Resolution Spectroscopy, Hoboken, NJ, 2011, pp. 1551–1594 Search PubMed.
- G. Guillon, A. Zanchet, M. Leino, A. Viel and R. E. Zillich, J. Phys. Chem. A, 2011, 115, 6918–6926 CrossRef CAS.
- Y. Ajili, K. Hammami, N. E. Jaidane, M. Lanza, Y. N. Kalugina, F. Lique and M. Hochlaf, Phys. Chem. Chem. Phys., 2013, 15, 10062–10070 RSC.
- R. Pérez de Tudela, P. Barragán, A. Valdés and R. Prosmiti, J. Phys. Chem. A, 2014, 118, 6492–6500 CrossRef.
- P. Villarreal, R. Rodríguez-Cantano, T. González-Lezana, R. Prosmiti, G. Delgado-Barrio and F. A. Gianturco, J. Phys. Chem. A, 2015, 119, 11574–11582 CrossRef.
- R. Rodríguez-Cantano, T. González-Lezana and P. Villarreal, Int. Rev. Phys. Chem., 2016, 35, 37–68 Search PubMed.
- F. Coppens, J. von Vangerow, M. Barranco, N. Halberstadt, F. Stienkemeier, M. Pi and M. Mudrich, Phys. Chem. Chem. Phys., 2018, 20, 9309–9320 RSC.
- D. Verma, R. M. P. Tanyag, S. M. O. O'Connell and A. F. Vilesov, Adv. Phys.: X, 2019, 4, 1553569 Search PubMed.
- K. Nauta and R. E. Miller, Science, 2000, 287, 293–295 CrossRef.
- S. Moroni and S. Baroni, Comput. Phys. Commun., 2005, 169, 404–407 CrossRef.
- F. Stienkemeier and K. K. Lehmann, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, R127–R166 CrossRef CAS.
- M. Gatchell, P. Martini, F. Laimer, M. Goulart, F. Calvo and P. Scheier, Faraday Discuss., 2019, 217, 276–289 RSC.
- C. Di Paola, F. Sebastianelli, E. Bodo, F. A. Gianturco and M. Yurtsever, J. Chem. Theory Comput., 2005, 1, 1045–1054 CrossRef CAS.
- S. Müller, M. Mudrich and F. Stienkemeier, J. Chem. Phys., 2009, 131, 044319 CrossRef.
- M. Theisen, F. Lackner and W. E. Ernst, Phys. Chem. Chem. Phys., 2010, 12, 14861–14863 RSC.
- L. An der Lan, P. Bartl, C. Leidlmair, R. Jochum, S. Denifl, O. Echt and P. Scheier, Chem. – Eur. J., 2012, 18, 4411–4418 CrossRef CAS.
- M. Rastogi, C. Leidlmair, L. An der Lan, J. Ortiz de Zárate, R. Pérez de Tudela, M. Bartolomei, M. I. Hernández, J. Campos-Martínez, T. González-Lezana, J. Hernández-Rojas, J. Bretón, P. Scheier and M. Gatchell, Phys. Chem. Chem. Phys., 2018, 20, 25569–25576 RSC.
- A. Castillo-García, T. González-Lezana, G. Delgado-Barrio and P. Villarreal, Eur. Phys. J. D, 2018, 72, 102 CrossRef.
- M. Blancafort-Jorquera, A. Vilá and M. González, Phys. Chem. Chem. Phys., 2018, 29737–29753 RSC.
- P. Stipanović and L. V. Markić, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 155101 CrossRef.
- G. Auböck, J. Nagl, C. Callegari and W. E. Ernst, J. Phys. Chem. A, 2007, 111, 7404–7410 CrossRef.
- E. Bodo, F. A. Gianturco, E. Yurtsever and M. Yurtsever, Mol. Phys., 2005, 103, 3223–3231 CrossRef CAS.
- G. Auböck, M. Aymar, O. Dulieu and W. E. Ernst, J. Chem. Phys., 2010, 132, 054304 CrossRef.
- W. C. S. Roman Krems and B. Friedrich, Cold Molecules: Theory, Experiment, Applications, CRC Press, Boca Raton, 2009 Search PubMed.
- R. Rodríguez-Cantano, T. González-Lezana, R. Prosmiti, G. Delgado-Barrio, P. Villarreal and J. Jellinek, J. Chem. Phys., 2015, 142, 164304 CrossRef.
- E. Coccia, E. Bodo, F. Marinetti, F. A. Gianturco, E. Yildrim, M. Yurtsever and E. Yurtsever, J. Chem. Phys., 2007, 126, 124319 CrossRef CAS.
- S. Paolini, F. Ancilotto and F. Toigo, J. Chem. Phys., 2007, 126, 124317 CrossRef.
- W. I. Glaberson and W. W. Johnson, J. Low Temp. Phys., 1975, 20, 313–338 CrossRef CAS.
- P. Moroshkin, V. Lebedev and A. Weis, Phys. Rev. Lett., 2009, 102, 115301 CrossRef CAS.
- M. Rossi, M. Verona, D. E. Galli and L. Reatto, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 212510 CrossRef.
- D. E. Galli, D. M. Ceperley and L. Reatto, J. Phys. Chem. A, 2011, 115, 7300–7309 CrossRef CAS.
- E. Bodo, E. Yurtsever, M. Yurtsever and F. A. Gianturco, J. Chem. Phys., 2006, 124(7), 74320 CrossRef CAS.
- C. Ghanmi, H. J. Al Qarni, O. Al-Hagan and H. Berriche, AIP Conf. Proc., 2018, 1976, 020026 CrossRef.
- N. Alharzali, H. Berriche, P. Villarreal and R. Prosmiti, J. Phys. Chem. A, 2019, 123, 7814–7821 CrossRef.
- T. Ho and H. Rabitz, J. Chem. Phys., 1996, 104, 2584–2597 CrossRef.
- M. Iwamatsu, Comput. Phys. Commun., 2001, 142, 214–218 CrossRef.
- D. Fogel, Evolutionary Computation: Toward a New Philosophy of Machine Intelligence, IEEE Press-Wiley, Hoboken, New Jersey, 2006.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. M. Schütz, et al., MOLPRO, Version 2012.1, A Package of Ab Initio Programs, see http://www.molpro.net.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef.
- A. Henriet, J. Phys. B: At. Mol. Phys., 1985, 18, 3085–3103 CrossRef.
- I. S. Lim, P. Schwerdtfeger, B. Metz and H. Stoll, J. Chem. Phys., 2005, 122, 104103 CrossRef.
- T. Leininger, A. Nicklass, W. K”uchle, H. Stoll, M. Dolg and A. Bergner, Chem. Phys. Lett., 1996, 255, 274–280 CrossRef CAS.
- K. Schuchardt, B. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975–2988 CrossRef CAS.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- DENEB 1.30 beta: the Nanotechnology Software by Atelgraphics, 2020, https://www.atelgraphics.com.
- C. Schwartz, Phys. Rev., 1962, 126, 1015–1019 CrossRef.
- T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199–207 CrossRef.
- T. J. Lee, Chem. Phys. Lett., 2003, 372, 362–367 CrossRef.
- W. Jiang, N. J. DeYonker and A. K. Wilson, J. Chem. Theory Comput., 2012, 8, 460–468 CrossRef.
- R. Prosmiti, C. Cunha, P. Villarreal and G. Delgado-Barrio, J. Chem. Phys., 2003, 119, 4216–4222 CrossRef.
- L. Veseth, J. Phys. B: At. Mol. Phys., 1971, 4, 20–27 CrossRef.
- M. Dubernet, D. Flower and J. M. Hutson, J. Chem. Phys., 1991, 94, 7602–7618 CrossRef CAS.
- R. Prosmiti, C. Cunha, P. Villarreal and G. Delgado-Barrio, J. Chem. Phys., 2002, 117, 7017–7023 CrossRef CAS.
- L. Garcia-Gutierrez, L. Delgado-Tellez, A. Valdés, R. Prosmiti, P. Villarreal and G. Delgado-Barrio, J. Phys. Chem. A, 2009, 113, 5754–5762 CrossRef CAS.
- L. Delgado-Tellez, A. Valdés, R. Prosmiti, P. Villarreal and G. Delgado-Barrio, J. Chem. Phys., 2011, 134, 214304 CrossRef.
- A. Valdés, R. Prosmiti, P. Villarreal and G. Delgado-Barrio, J. Chem. Phys., 2005, 122, 044305 CrossRef.
- A. Valdés, R. Prosmiti, P. Villarreal and G. Delgado-Barrio, J. Chem. Phys., 2006, 125, 014313 CrossRef.
- Á. Valdés, P. Barragán, R. Pérez de Tudela, J. S. Medina, L. Delgado-Tellez and R. Prosmiti, Chem. Phys., 2012, 399, 39–45 CrossRef.
- A. Valdés and R. Prosmiti, J. Phys. Chem. A, 2013, 117, 7217–7223 CrossRef.
- R. A. Aziz and M. J. Slaman, J. Chem. Phys., 1991, 94, 8047–8053 CrossRef CAS.
- P. Fuentealba, H. Preuss, H. Stoll and L. Von Szentpály, Chem. Phys. Lett., 1982, 89, 418–422 CrossRef CAS.
- S. Magnier and M. Aubert-Frécon, J. Quant. Spectrosc. Radiat. Transfer, 2003, 78, 217–225 CrossRef CAS.
- A. Jraij, A. R. Allouche, S. Magnier and M. Aubert-Frecon, Can. J. Phys., 2008, 86, 1409–1415 CrossRef CAS.
- S. Leutwyler, M. Hofmann, H.-P. Harri and E. Schumacher, Chem. Phys. Lett., 1981, 77, 257–260 CrossRef CAS.
- M. Broyer, J. Chevaleyre, G. Delacretaz, S. Martin and L. Wöste, Chem. Phys. Lett., 1983, 99, 206–212 CrossRef.
- W. C. Stwalley and H. Wang, J. Mol. Spectrosc., 1999, 195, 194–228 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05406b |
| This journal is © the Owner Societies 2021 |