QM/MM study of the stability of dimethyl ether in zeolites H-ZSM-5 and H-Y

Abstract

The methanol-to-hydrocarbons (MTH) process transforms C₁ carbon sources to higher hydrocarbons, but details of the mechanism that leads to the formation of the first carbon–carbon bond remain unclear. Here, we present a computational investigation of how a crucial intermediate, dimethyl ether (DME), interacts with different zeolite catalysts (H-ZSM-5, H-Y) to gain insight into the initial stages in the MTH process. We use QM/MM computational simulations to model the conversion of methanol to DME in H-ZSM-5, which is a well characterised and important reaction intermediate. We analyse and compare the stability of DME on several acid sites in H-ZSM-5 and H-Y, and show that the more acidic and open “intersection sites” in the H-ZSM-5 framework are able to bond strongest with DME, with complete deprotonation of the acid site occurring. The conversion of methanol to DME in H-ZSM-5 is calculated as requiring a higher activation energy than framework methoxylation, which indicates that a stepwise (indirect) mechanism, through a methoxy intermediate, is the most likely route to DME formation during the initiation of the MTH process.

---

1. Introduction

The methanol-to-hydrocarbons (MTH) process has attracted widespread attention as an alternative to processes such as fluidised-bed catalytic cracking and steam cracking to form olefins, aromatics and fuel.^1,2 Interest in the MTH process is due, in particular, to the potential for production of methanol from biomass-derived syngas, which would bypass crude oil and transform this existing industrial process into a sustainable technology.^1,3,4

The MTH process has an induction period that is characterized by the low reactivity of methanol in the initial stages until the first C–C species are formed.^5–7 After the induction period, the process reaches a steady-state in which methanol conversion is characterised by two distinct reaction cycles leading to the formation of olefins and aromatics.^8,9 The first steps in the MTH process are either the indirect formation of dimethyl ether (DME) via methoxy or direct formation (Scheme 1). Theoretical studies show that both direct and indirect reaction routes are competitive for DME formation, depending on the working temperature of the reaction. Specifically, increasing the temperature leads to the direct conversion of methanol to DME becoming the dominant reaction pathway.¹⁰ The reactant loading may also play a key role, as shown by investigations conducted at room temperature and high methanol loading (more than three molecules per acid site) where methanol is reported to convert to methoxy spontaneously;^11,12 however, in these instances no further formation of DME is observed. Experimental studies suggest that the direct formation of DME from methanol is preferred over the indirect route (via methoxy), specifically when “isolated” acid sites^10,13 exist in the H-ZSM-5 catalyst; in contrast, the methoxylation pathway is more prevalent when having a “paired” acid site.¹³ Furthermore, an increase in reaction rates for both direct and indirect reaction is observed with an increase in acid site strength and density.^9,13

Scheme 1 Illustration of dual cycle mechanism of the MTH process, with initial stage highlighted in dashed box describing the two main methanol conversion routes (top): direct formation (I) and indirect formation, via methoxy (II), of DME, alkene cycle (middle), aromatic cycle (bottom).

The next important reaction step after initiation is suggested to be the conversion of DME and methoxymethyl groups to form dimethoxyethane.¹⁴ Previous temporal analysis of product studies¹⁴ showed that the formation of dimethoxyethane was correlated with the end of the induction period and start of the steady-state reaction regime, in addition to being the first C–C species formed. Transient kinetic analysis¹⁵ also showed that the rate limiting step in the formation pathway of propylene is the conversion of the initial C–C species, i.e. dimethoxyethane. Further oligomerisation of propylene would then lead to species such as 1–5 hexadiene, which would skeletally rearrange to form cyclic carbocationic species and initiate the aromatic cycle.¹⁶

IR^17,18 and NMR¹⁹ studies show that, even at low coverages, DME can be either physisorbed or chemisorbed to the zeolite, highlighting that there are acid sites in the zeolite catalyst (H-ZSM-5, H-Y) with different bonding capabilities. Theoretical simulations of DME adsorption in zeolite catalysts have been restricted to small cluster models or small unit cell periodic systems (H-ZSM-22),^10,20,21 for which DME adsorption is reported as being feasible in either a physisorbed or a chemisorbed state. Temperature programmed desorption experiments suggest the existence of high, medium and low temperature desorbing sites, though their location and structure remains unclear.²² Quasi-elastic Neutron Scattering experiments of DME adsorbed in H-ZSM-5 indicated that the DME is more likely to be mobile at the channel intersections rather than in the channels.²³ Previous computational studies, involving the adsorption of other methylated oxygenates, such as methanol or ethanol, showed that the stronger acid bonding site is situated at the intersection of channels in H-ZSM-5.²⁴ Clearly, DME is present in both the initiation and propagation of the MTH process, through the sustained formation of dimethoxyethane. A clear understanding of the structural features of the catalyst that lead to the formation of DME, and control the reactivity of DME, could be used to further enhance the reaction rate and control the selectivity between the aromatic and olefinic cycles.

In this study, we use a computational approach to determine the stability and reactivity of methanol and DME at the zeolite active site. The results obtained are used to understand what catalytic features are necessary to direct the methanol conversion towards a desired product. In order to develop an accurate description of the catalytic process, hybrid quantum and molecular mechanical (QM/MM) simulations were performed to elucidate DME formation and adsorption on several Brønsted acid sites. Specifically, the acid sites of zeolites H-ZSM-5 and H-Y were analysed owing to their different capabilities in adsorbing and activating both methanol and DME, to gain insight into the structural features that can influence catalytic reactivity in zeolites.^{11,12,17–19} Our methodology is presented in Section 2, with results presented in the subsequent section.

2. Methodology

2.1 QM/MM simulations

Computations were performed using a hybrid quantum- and molecular-mechanical (QM/MM) approach coupled with an embedded-cluster model of the bulk zeolite of interest. The embedded-cluster models are beneficial as they remove the periodic boundary conditions that can hinder charge non-neutral models and/or high-level calculations of large unit cell systems, such as zeolites, whilst maintaining the correct long-range electrostatics for the active site of interest. The spherical embedded-cluster models were initially created using the experimental unit cell and structure of siliceous MFI²⁵ and FAU.²⁶ The embedded-clusters were centred on a Si tetrahedral (T-)site of interest; MFI has 12 symmetry inequivalent T-sites, and we considered the Al substituent in the straight channel [T1 (M7)], the sinusoidal channel [T4 (Z6)] and the more open channel intersections [T12 (I2)]; FAU has only one symmetry inequivalent T-site, which was considered substituted to form zeolite H-Y. Al positions have proven difficult to characterise in experiment and it is acknowledged that the selection of active sites for simulations introduces an aspect of selective bias; however, some Al positions are commonly assumed more favourable than others, with the T12 and T1 sites often reported to be substituted.²⁷ Where Al has been substituted for Si at the T-site of interest, a charge-compensating proton has been added on adjacent oxygens to ensure charge neutrality of the system. The Brønsted proton is positioned towards the centre of the supercage in each model; this configurations is recognized as having the highest deprotonation energy,²⁸ which indicates that these are the most stable structures for the system and thus most likely to be present in real catalytic reactions. Specifically, the Brønsted protons are positioned on the oxygens O27 (connected to T1), O11 (connected to T4) and O8 (connected to T12) as per IZA structure database nomenclature.²⁹

The embedded-cluster models are partitioned in to regions that are evaluated using different energetic calculations: a central QM region is defined, which encompasses the chemically active part of our model; and then a surrounding MM region encapsulates the QM region, ensuring long-range structural and electrostatic effects to ensure the correct bulk representation for the high-accuracy QM calculations. In our previous work, we showed that an appropriate QM region includes atoms up to the fifth nearest neighbour (the third oxygen atom) from the central T-site.^30,31 For the QM calculations, the terminal oxygens at the edge of the QM region are saturated with “link” hydrogen atoms to ensure correct electronic structure for the terminal oxygens. The terminal “link” atoms do not inadvertently affect the electronic solution of the overall QM calculations as an additional bond-dipole correction is added at the bond bridging the QM and MM boundary, which ensures an accurate local electrostatic potential.³² Encapsulating the QM region are two concentric MM regions: the inner MM region contains atoms that can move during a geometry optimisation; and the outer region is frozen to ensure a bulk-like structure at the far limit from any chemical reactions. In our calculations, the inner and outer MM regions extend from the central T-site to a radius of 10.58 Å (20a₀) and 21.17 Å (40a₀), respectively. In summary, these settings lead to models with 1653 atoms for H-Y, with 62 QM atoms and 130 inner MM atoms; 2165 atoms for H-ZSM-5 [T12 (I2)], with 74 QM atoms and 197 inner MM atoms; 2180 atoms for H-ZSM-5 [T1 (M7)], with 67 QM atoms and 207 inner MM atoms; and 2155 atoms for H-ZSM-5 [T4 (Z6)], with 72 QM atoms and 184 inner MM atoms.

For the geometrically optimised models of dimethyl ether adsorbed on the zeolite acid site (Section 3.1), the QM energy has been calculated using hybrid-density functional theory with the B97-D functional^33,34 as implemented in the NWChem software package.³⁵ In the case of the models used to calculate the conversion of bi-methanol to dimethyl ether (Section 3.3), the geometric optimisation and subsequent calculation of the associated transition state were conducted using with the Becke97-3 exchange–correlation (XC) functional,³³ with dispersion effects being corrected by single point calculations on the geometrically optimised models with B97-D, as provided in the GAMESS-UK code.³⁶ These conditions have shown to save computational time while maintaining a high level of accuracy, as explained in a previous study.³⁰ In addition, the energetic contribution, from the dispersion correction, to the transition barrier was expected to not be as significant as for the adsorption energies. The atomic orbitals are represented using the Ahlrichs and Taylor TZVP Gaussian basis sets.³⁷ Our models contain no unpaired electrons and therefore we employed Restricted Hartree–Fock (RHF) conditions throughout our simulations, corresponding to overall singlet spin multiplicity. The self-consistent field (SCF) convergence criteria was set to an energy change of less than 2.72 × 10⁻⁶ eV (1 × 10⁻⁷ Hartrees) between SCF iterations.^38,39 The MM energy was calculated using DL_POLY,⁴⁰ employing the forcefield of Hill and Sauer.^41,42 The coordination dependent charges in the original forcefield are replaced in this work with fixed 1.2 and −0.6e point charges for silicon and oxygen, respectively, as parameterised in the work of Sherwood et al.³²

Management of the QM/MM calculations was performed using the ChemShell software package,⁴³ with geometry optimisation performed in a Cartesian coordinate space using the Limited-Memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) algorithm.^44–48 Structural convergence was deemed complete when the maximum gradient of atoms in the active QM and MM regions was below 0.015 eV Å⁻¹. Vibrational frequencies were calculated with a task-farmed finite-difference approach,³⁶ allowing us to confirm that geometries correspond to local minima.^48,49 For the vibrational calculations, only the active site, first neighbour framework atoms, and the adsorbate atoms were displaced; comparison of this approximation against displacement of all atoms in the QM region shows no difference in vibrational frequencies.³⁰ No scaling factor has been used to scale our vibrational frequencies; we note that previous work has used a scaling factor to align vibrational frequencies with experiment, with values between 0.9–0.9614,^50–53 but no such scaling was possible due to the absence of necessary benchmarking and derivation in the literature.

The transition state energies were determined by employing the nudged elastic band (NEB) method⁵⁴ in a task-farmed mode, with the reaction path represented by 15 images. To ensure computational efficiency for the NEB calculations, the outer QM atoms were fixed in place whilst inner framework atoms (active site to second nearest neighbour) and the adsorbate were unrestricted during the optimisations; benchmarking of these geometric restrictions against a fully flexible NEB calculation shows a difference in the transition state energies of <10 kJ mol⁻¹, but with the latter requiring a prohibitively large computational cost, as further discussed in Section S1 of ESI.† The transition state was confirmed through vibrational frequency analysis finding only one imaginary frequency.

Where considered, the energy of the deprotonated zeolite includes the addition of the Jost correction^55,56 to account for the truncation of the MM polarisation at the end of the first (flexible) MM region. Deprotonation leaves a charge in the QM region of the simulation (−1e) and the electrostatic effects of this charge would be relatively long-ranging; however, atoms are only free to move in the inner regions of our calculations. In reality, atoms within the fixed MM region would be perturbed towards slightly lower energy positions, in response to the localised electron on the QM O⁻, and the Jost correction accounts for this approximation by calculating the energy gained in the fixed region:^55,56

where Q is the charge of the defective system, R is the radius of the inner relaxed region (in a₀) and ε is the dielectric constant of the material. The dielectric constant of FAU and MFI are taken as 2.65 and 3.38, respectively, as calculated using classical shell model methods.⁵⁷

2.2. Energy analysis

The adsorption energy (E_ads) of a sorbate to the zeolite framework is calculated as:

E_ads = E[ZeOH + Sorbate] − E[ZeOH] − E[Sorbate] (2)

where, E[ZeOH], E[Sorbate] and E[ZeOH + Sorbate] are the total energy of the zeolite sorbent, the gas-phase sorbate and the combined guest–host system, respectively, each in their optimised geometry. Due to our use of an atom-centred basis set, it is necessary to include a basis-set-superposition-error (BSSE)⁵⁸ for the combined system; the BSSE was calculated as the percentage of the adsorption energy as determined from a previous study³⁰ of methanol adsorption, on the same active sites as those analysed here, under the same conditions, and is less than 10 kJ mol⁻¹. The BSSE correction is included in all results.

In addition to the adsorption energy (E_ads), the bonding strength of protonated sorbate to the zeolite conjugate base (E_ion-pair), was calculated as:

E_ion-pair = E[ZeOH + Sorbate] − E[SorbateH⁺] − E[ZeO⁻] (3)

with E[ZeOH + Sorbate], E[SorbateH⁺], E[ZeO⁻] representing the absolute energies of the combined guest–host system, the protonated gas-phase sorbate and the deprotonated zeolite sorbent, respectively. Also, the deprotonation energy (E_dep) of the zeolite acid site was calculated as:

E_dep = E[ZeO⁻] − E[ZeOH] (4)

where E[ZeO⁻] and E[ZeOH] are the absolute energies of the deprotonated and protonated states of the zeolite.

3. Results

3.1. Adsorption of DME

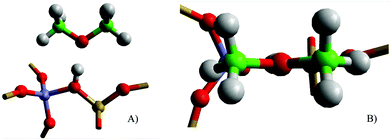
Initially, the stability of DME is considered when adsorbed at the Brønsted acid sites of H-Y and H-ZSM-5. The computational models were constructed with the DME bonding through the oxygen linker to the Brønsted proton similar to single methanol adsorption, with the plane of DME perpendicular to the plane of the zeolite pore around the active site, ensuring a suitable guest–host interaction (Fig. 1).

Fig. 1 Illustration of the initial orientation of DME on the active site before geometric optimisation, with side (A) and top views (B). Atomic species are highlighted for Al (purple), Si (yellow), C (green), O (red), H (light grey).

After geometry optimisation, the DME adsorption energy (E_ads) is calculated to be exothermic at all acidic sites, as shown by the results in Table 1. The highest stability is for the T12 site of ZSM-5, with E_ads = −143 kJ mol⁻¹, followed by adsorption on H-Y > ZSM-5, T1 [M7] > T4 [Z6]. The adsorption energies calculated are stronger than in previous small cluster theoretical studies of DME, where E_ads is reported as −62 kJ mol⁻¹;⁵⁹ or −89 and −97 kJ mol⁻¹.^20,21 Experimental calorimetric studies report an adsorption enthalpy, in H-ZSM-5, of −90 kJ mol⁻¹ at 323 K.⁶⁰ In addition, TPD investigations for DME in H-ZSM-5 report an adsorption enthalpy of −100 kJ mol⁻¹, at low temperature desorption sites; and −110 kJ mol⁻¹ at medium temperature desorption sites (i.e. weakly bonded sites), both at low reactant loadings (∼1 adsorbate per acid site); and −125 kJ mol⁻¹ for high temperature desorption sites (i.e. strongly bonded sites),²² having a capacity of adsorbing ∼2.5 adsorbates per acid site, similar to the adsorption energies obtained in our simulations (Table 1). Further differences between experimental and theoretical results may arise from the experimental processing method used⁶¹ or from measurements performed at different reactant coverage, and with varying acid site strength or acid site density.^62,63

Table 1 Calculated adsorption energy (E_ads) for the optimised models in this study using the B97-D exchange correlation functional, alongside previous small cluster^20,21,59 and periodic^10,64 work. The calculated adsorption enthalpy (H_ads, B97-D) and Gibbs free energy (G_ads, B97-D), both at 300 K, are also presented and compared to experimental adsorption enthalpies (H_ads, exp).^22,60 All values are presented in kJ mol⁻¹

Zeolite model	Energy quantity
	E ads		H ads		G ads
	B97-D	Previous work (theory)	B97-D	Previous work (exp)	B97-D
H-Y	−132		−105	—	−140
H-ZSM-5 (T12 [I2])	−143		−132	−90^60 −125^22	−153
H-ZSM-5 (T4 [Z6])	−122		−103		−131
H-ZSM-5 (T1 [M7])	−129		−107		−137
Molecular cluster		−62;^59 −97^20,21
H-ZSM-22		−52^10
SSZ-13		−85^64

---

As shown in Fig. 2, deprotonation of the active site is observed in all systems after geometry optimisation; in the case of the T12 [I2] model, which has the strongest adsorption energy, the proton is completely transferred on to the DME. Previous theoretical simulations of DME adsorption have predicted the proton remaining on the zeolite: small clusters models of the active site (4T-sites in cluster, simulated with PBE;²¹ 5T-sites/B3LYP⁵⁹), and simulations that used periodic representations of H-ZSM-22 (simulated with rPBE)¹⁰ or small unit cell (CHA) periodic systems (simulated with PW91)⁶⁴ observe that the proton remains bonded to the active site. The differences in the structure of deprotonated H-Y and H-ZSM-5 indicate that the presence of the zeolite lattice around the active site is important to the simulation of charge distribution, and also that the type of lattice can influence the protonated state of the active site. Experimental work using IR^17,18 and NMR¹⁹ spectroscopy report that there is a mixture of physisorbed and chemisorbed state DME in the zeolite pores even at low loadings (equivalent to one adsorbate per acid site) and low temperatures (373 K); however, the approximately equidistant positioning of the Brønsted proton between the zeolite and DME seen in the H-Y and T1 [M7] models may explain the difficulty in unequivocally determining the state of DME by experimental means.

Fig. 2 Optimised structures for DME adsorbed on H-ZSM-5 and H-Y sites, as labelled. Bonding interactions between the active site and the DME adsorbate are highlighted with dashed lines; distances are presented in Ångstrom.

Analysis of the geometry for the DME-adsorbed systems (Table 2) shows interesting variations between the different adsorption sites. In most cases, the proton stabilises between the zeolite Brønsted acid site and the DME adsorbate, marginally closer to the DME adsorbate at a distance of 1.13–1.18 Å with the proton not completely transferred to DME; but for H-ZSM-5 (T12 [I2]), where the proton fully transfers to DME, the distance between the proton and the oxygen of DME is 1.06 Å. These results show that there is a shallow potential energy surface for proton transfer, which, as noted, may explain the interplay between physisorbed and chemisorbed states reported in experiment.^17–19 The variation in adsorbed structures corroborates with the difficulties reported in determining interactions involving the Brønsted proton during experimental spectroscopic work. It is noted that the DME methyl groups are significantly closer to the active site for the H-ZSM-5 (T12 [I2]), where the distance is 2.27 Å, which may indicate that there is a stronger electron induced effect on O_DME when the DME methyl groups are closer to the framework oxygen. Comparison with side on adsorbed methanol on the same sites shows no similar connection between methyl interaction with the zeolite and deprotonation or adsorption energy.³⁰ Further analysis of the atomic charges, provided in Table S1 of the ESI,† shows that the relative charge on the Brønsted proton is slightly larger when closer to the DME adsorbate, and also that the largest charge difference between the two main reaction points on DME, the oxygen and carbon atoms, is encountered when the Brønsted proton is closest to DME. These observations imply a more activated form (or closer to the activated state) of DME, specifically when adsorbed on H-ZSM-5 instead of H-Y.

Table 2 Geometric observables from DME adsorbed on to the zeolite active sites. Specifically, the distance is reported between the Brønsted proton and the zeolite active site d(O_Zeo–H_B), the Brønsted proton and the oxygen of DME d(H_B–O_DME), between the deprotonated oxygen site and oxygen of DME d(O_Zeo–O_DME), and between the closest hydrogen of the DME methyl group to the zeolite framework d(O_Zeo*–H_CH3). All values are in Ångstroms

	d(OZeo–HB)	d(HB–ODME)	d(OZeo–ODME)	d(OZeo*–HCH3)
H-Y	1.23	1.18	2.41	2.97
H-ZSM-5 (T12 [I2])	1.48	1.06	2.54	2.27
H-ZSM-5 (T4 [Z6])	1.30	1.13	2.42	2.86
H-ZSM-5 (T1 [M7])	1.24	1.17	2.41	2.81

---

A linear trend is observed between the distances of the proton to DME and to the framework active site (Fig. S2 of ESI†). One can consider this indicative of a correlation between the interactions occurring around the Brønsted proton; we might expect from this trend that the distance between DME and the framework oxygen site is relatively constant, and in general this is the case, but an exception occurs for the H-ZSM-5 (T12 [I2]) system where the proton has fully transferred to the DME. The distance between the Brønsted proton and the zeolite oxygen also correlates somewhat with the adsorption energy of DME (Fig. S3 of ESI†), though the quality of the fit is lower than that for the geometric observables in Fig. S2 (ESI†), as demonstrated by the lower R² (0.51). Trends can also be extracted for the distance between the zeolite and DME oxygen atoms, d(O_Zeo–O_DME), and potentially the distance can be used as a descriptor for the strength of DME adsorption, which we consider can be characterised as strong or weak depending on the hydrogen bonds formed between DME and the active site.

Correlation between the adsorption energy of DME and the geometric observables associated with the Brønsted proton indicate that the bonding of the oxygen (DME) to the active site dominates the overall adsorption process, with the interaction between the methyl groups of DME and the zeolite walls having limited effect. Therefore, in order to understand further the nature of the proton transfer to DME, the framework deprotonation energy (E_dep) was calculated for the initial zeolite models in the absence of DME, and the proton affinity (E_PA) was calculated for DME in gas-phase (Table 3).

Table 3 Deprotonation energy (E_dep) of the zeolite models, and the proton affinity (E_PA) of DME. Also presented is the ion-pair interaction between protonated DME and zeolite site (E_ion-pair), calculated as mentioned in Section 2.2. All values are presented in kJ mol⁻¹

	E dep	Previous work (theoretical)^28	E ion-pair
H-Y	1144	1081; 1166	−431
H-ZSM-5 (T12 [I2])	1131		−427
H-ZSM-5 (T4 [Z6])	1186		−457
H-ZSM-5 (T1 [M7])	1145		−430

---

	E PA	Previous work (experimental)^65
DME	847	802

---

E _dep is calculated as being in the range of 1144–1186 kJ mol⁻¹ when using the B97-D XC functional, which is in agreement with previous QM/MM work using the similar B97-2 XC functional for simulations of H-Y and H-ZSM-5 (E_dep = 1081–1166 kJ mol⁻¹).²⁸ The E_PA of DME is 847 kJ mol⁻¹, which is also in good correspondence with the experimental proton affinity of 802 kJ mol⁻¹ (determined at 300 K).⁶⁵ Most importantly, the E_PA is ∼300 kJ mol⁻¹ less than the E_dep, so complete proton transfer and desorption of protonated DME would be significantly endothermic. This observation indicates why the DME proton is preferentially stabilised between both the zeolite active site and the DME oxygen.

To clarify further the stability of DME at the zeolite active site, analysis was performed on the bonding energy between the protonated DME and conjugated base active site (E_ion-pair). Here, the H-ZSM-5 (T4 [Z6]) model has the highest bonding strength. The deprotonation energy (E_dep) can be considered as a measure of basicity of the conjugated base active site, and with this perspective a direct correlation is noted relative to the energy of the ion pair, E_ion-pair as shown in Fig. 3, which can be used to determine the characteristics of the active site most likely to lead to strongly bonded DME.

Fig. 3 Plot of deprotonation energy (E_dep) against bonding strength of protonated DME to the zeolite conjugate base (E_ion-pair), presented in kJ mol⁻¹. The line of best fit is given with an R² of 0.9751 to quantify the error in the fit.

3.2. Vibrational frequency analysis

Vibrational frequencies were calculated for the adsorbed DME molecule in order to correlate results with IR experimental data. The vibrational frequencies for the O_DME–H_B stretch were calculated in the interval between 1500–1600 cm⁻¹ (Table 4), with the exception of the H-ZSM-5 (T12 [I2]) model where the stretch is observed at a much higher frequency of 2174 cm⁻¹. The difference observed for H-ZSM-5 (T12 [I2]) is a consequence of the shorter O_DME–H_B bond. The calculated O_DME–H_B vibrational frequencies are within the range reported for the experimental ABC triplet vibrational signature corresponding to the O–H⋯O interactions, which are in the regions of 1500–1700 cm⁻¹, 2100–2500 cm⁻¹ and 2800–3000 cm⁻¹ when inserting DME in H-ZSM-5 and H-Y.⁶⁶

Table 4 Calculated IR vibrational frequencies for DME adsorbed in zeolites H-Y and H-ZSM-5. Specifically given are the stretch frequencies relating to the hydrogen bonds of the Brønsted proton to the zeolite active site, ν(O_Zeo–H_B), and from the proton to the DME oxygen, ν(H_B–O_DME), alongside symmetric, mixed and asymmetric motion of both CH₃ groups of the DME molecule, with M₂ representing the methyl group closest to the zeolite framework. All values are given in cm⁻¹

	ν(OZeo–HB)	ν(HB–ODME)
H-Y	1511	1570
H-ZSM-5 (T12 [I2])	1593	2174
H-ZSM-5 (T4 [Z6])	1557	1592
H-ZSM-5 (T1 [M7])	1513	1579

---

	ν(CH3)
	Symmetric		Mixed		Asymmetric
	M 1	M 2	M 1	M 2	M 1	M 2
H-Y	2960	2987	3069	3089	3114	3120
H-ZSM-5 (T12 [I2])	2989	2991	3097	3100	3140	3149
H-ZSM-5 (T4 [Z6])	2977	2984	3089	3093	3111	3119
H-ZSM-5 (T1 [M7])	2961	2965	3065	3079	3089	3107
DME(g)	2865	2877	2920	2924	3039	3043
[DME]H^+(g)	2994	3079	3132	3151	3176	3199

---

Fig. 4 shows the correlation between d(O_DME–H_B) and ν(O_DME–H_B), which gives further insight into the nature of the interactions that occur with the adsorbate in the zeolite pores, clearly showing once more that the extent of the proton transfer is strongly correlated with the strength of the interaction. The effect of the proton transfer on vibrational properties is also reflected in the CH₃ frequencies in Table 4: when DME is protonated, the frequencies increase, as observed in experimental IR reports.⁶⁶ IR studies, referred to above, further validate our findings that DME can deprotonate the active site in H-ZSM-5 and, in a separate associated study, a higher proportion of non-protonated DME is observed in H-Y when increasing adsorbate loadings.⁶⁶

Fig. 4 Graph of the distance between the oxygen of the DME and the Brønstead proton, d(O_DME–H_B), versus the stretch vibrational frequency of the oxygen of the DME and the Brønsted proton, ν(O_DME–H_B). Values are presented in Ångstroms and cm⁻¹, respectively. A line of best fit is given with an R² of 0.8634 to quantify error in the fit.

3.3. Formation of DME

To understand the potential of methanol directly converting to DME at the active site in zeolitic systems, the direct conversion of two methanol molecules to DME and water was modelled at the T12 [I2] position of H-ZSM-5, with the indirect DME formation mechanism (via methoxy) being subject for a later study. The open I2 site is chosen because of its greatest stability for DME adsorption (E_ads = −142 kJ mol⁻¹). The adsorption energy of an individual methanol molecule on the T12 [I2] site has been previously reported as −120 kJ mol⁻¹,³⁰ and the adsorption energy is −86 kJ mol⁻¹ for the co-adsorption of a second methanol. Using a bidentate configuration of the two methanol molecules (Stages 1–4), we have performed simulations to identify the barrier for direct DME formation using the nudged-elastic band (NEB) method. The results were tested further by inclusion of dispersion corrections in the exchange–correlation functional, which had a significant effect on the reaction barrier; the resulting dispersion corrected energy barrier being ∼30 kJ mol⁻¹ lower compared to the B97-3 case (Table 5), revealing an overall activation barrier of 238 kJ mol⁻¹ (Fig. 5). The main interactions contributing to the added stabilisation of the transition state arise from the hydrogen bonds of water and methanol with the active site, and interaction of the CH₃⁺ moiety with methanol. In the initial stages of the reaction pathway, a methyloxonium (protonated methanol) rotates its methyl group towards the oxygen of the second methanol (Stage 2); then, the C–O bond of the methyloxonium breaks, forming methyl and water (Stage 3), which is the source of the overall activation energy of 238 kJ mol⁻¹. The subsequent formation of DME and water (Stage 4) is an exothermic stabilisation from the transition state, with an energy decrease of −191 kJ mol⁻¹. The energy that would then be required to desorb the DME and water is 152 kJ mol⁻¹.

Table 5 Comparison of geometric and energetic (ΔE) observables of each step, from the reaction path of methanol condensation to DME and water, with labels as described for Fig. 5, and ‘Stage 5’ indicating desorption of the products. The scheme clarifying the geometric observables is provided in Fig. 5. Energies are given in kJ mol⁻¹, and distances are given in Ångstroms

	ΔE
	Stage 1	Stage 2	Stage 3	Stage 4	Stage 5
B97-3	−142	90	181	−126	92
B97-D	−205	87	151	−191	152
PBC, rev-PBE^10	−99	39	85	−121	77
Cluster, PBE^21	−130	62	89	−119	83

---

	Geometric observables
	d(C1–O2)	d(O2–C3)	d(C3–O4)
B97-3	1.43	2.13	2.35
PBC, rev-PBE^10	1.47	1.97	2.04
Cluster, PBE^21	1.45	1.99	1.95

---

Fig. 5 The reaction barrier for conversion of two methanol molecules into DME and water, modelled with B97-3 and B97-D XC functionals, at the H-ZSM-5 (T12 [I2]) active site, with comparison against previous small cluster²¹ and periodic boundary condition¹⁰ approaches. The main reaction stages are illustrated, specifically ‘Stage 1’ representing the adsorption of the two methanol reactants, ‘Stage 2’ the rotation of reactants stage, ‘Stage 3’ the breaking of methanol C–O bond stage, and ‘Stage 4’ the formation of the dimethyl ether and water.

Previous simulation work used small cluster representations of the H-ZSM-5 active site, or periodic boundary conditions,^10,21 coupled with lower levels of theory than hybrid-DFT, and both reported lower reaction barriers of 151 and 124 kJ mol⁻¹, respectively. The small cluster theoretical studies used density functional theory with a non-local density approximation and a DZVP basis set,^20,21 whilst the PBC simulations were conducted in H-ZSM-22 using a planewave basis and the rev-PBE exchange–correlation functional.¹⁰ Considering that the initial and final stages have a similar configuration of the adsorbates, the lower reaction barriers reported previously can be related to either the choice of settings or their model for the reaction pathway. For example, a reaction path is previously considered where the Brønsted proton transfers from the methyloxonium back to the zeolite active site during the methanol rotation (Stage 2), and remains there prior to the C–O bond breaking and formation of water (Stage 3). In the transition state observed in this previous work, the methyl is closer to the methanol (∼2 Å) than in our simulations (2.13 Å). The transfer of the Brønsted proton back to the active site in previous simulations may facilitate a smoother transition through the methanol rotation stage (Stage 2); however, it is also noted that experimental studies see a higher conversion rate of methanol to DME with higher catalyst acidity¹⁰ and/or higher acid site density,¹³ which illustrates how proton transfer to the methanol is potentially an influential effect in real catalytic systems.

The higher values calculated for the activation energy calculated in this study would suggest that this mechanism would only occur to a very limited extent. It is, of course likely that the energy barrier will be modified by interaction with other DME molecules or other molecular species. These effects along with a study of the indirect mechanism will be reported in a future study.

4. Summary and conclusions

QM/MM simulations have been used to model the adsorption of DME on acid sites in zeolites H-Y and H-ZSM-5. DME tends to deprotonate the active site, highlighting a very broad and shallow potential energy surface for the proton to transfer from the acid site to DME. The most significant proton transfer is achieved at the T12 [I2] site in H-ZSM-5, which we suggest relates to the deprotonation energy of the acid site and the open configuration of DME at the active site. The strength of the zeolite conjugate base active site was shown to influence the stability of the protonated DME at the active site, by a direct correlation between the deprotonation of the active site and the ion-pair bonding energies. These observations indicate that the stronger Brønsted acidic character of the T12 site of H-ZSM-5 can be responsible for the superior catalytic performances compared to zeolite H-Y.^11,12 Analysis of the vibrational frequencies shows that the geometry and types of interactions calculated match with IR spectroscopic experimental data, indicating that the O–H⋯O vibrational frequencies can be used to evaluate the protonated state of DME within the zeolite pores.

Subsequently, the direct conversion of methanol to DME was investigated using the nudged-elastic band method, with the reaction pathway determined different to previous reports. Our work shows that the active site remains unprotonated during the reaction pathway, whereas previous work had the proton stabilising on the zeolite during the transition from methanol to DME, which could be an artefact of the poorer ability for GGA exchange–correlation functionals to localise electrons. Our new observations show the importance of the acidity and conjugate base formed, and of the alignment of the methanol reactant prior to the main transition state (Stage 2). Further investigations are necessary to determine the influence of the configuration of DME on the deprotonation of the active site, the effect of further solvents on the DME conversion, and the role of the DME orientation on the subsequent transformation to olefins.

Author contributions

The investigation plan was derived by all authors, and the calculations performed by SAFN. The manuscript was written through contributions of all authors, and all authors have given approval to the final version of the manuscript.

Notes

The raw data from which all energetic results were derived is available to access at DOI: http://10.17035/d.2020.0122278013.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Computing facilities for this work were provided by ARCCA at Cardiff University, Supercomputing Wales, and through our membership of the UK's HPC Materials Chemistry Consortium (MCC), which is funded by the EPSRC (EP/R029431). SAFN wishes to thank the School of Chemistry, Cardiff University for a studentship. AJL acknowledges funding by the UKRI Future Leaders Fellowship program (MR/T018372/1).

References

1. P. Tian, Y. Wei, M. Ye and Z. Liu, ACS Catal., 2015, 5, 1922–1938.
2. U. Olsbye, S. Svelle, M. Bjrgen, P. Beato, T. V. W. Janssens, F. Joensen, S. Bordiga and K. P. Lillerud, Angew. Chem., Int. Ed., 2012, 51, 5810–5831.
3. C. D. Chang and A. J. Silvestri, J. Catal., 1977, 47, 249–259.
4. M. Guisnet and J.-P. Gilson, Zeolites for Cleaner Technologies, Imperial College Press, London, 2002, p. 391.
5. J. F. Haw and D. M. Marcus, Top. Catal., 2005, 34, 41–48.
6. J. Wang, Y. Wei, J. Li, S. Xu, W. Zhang, Y. He, J. Chen, M. Zhang, A. Zheng, F. Deng, X. Guo and Z. Liu, Catal. Sci. Technol., 2015, 6, 89–97.
7. J. F. Haw, J. B. Nicholas, W. Song, F. Deng, Z. Wang, T. Xu and C. S. Heneghan, J. Am. Chem. Soc., 2000, 122, 4763–4775.
8. I. Yarulina, A. D. Chowdhury, F. Meirer, B. M. Weckhuysen and J. Gascon, Nat. Catal., 2018, 1, 398–411.
9. U. Olsbye, S. Svelle, M. Bjørgen, P. Beato, T. V. W. Janssens, F. Joensen, S. Bordiga and K. P. Lillerud, Angew. Chem., Int. Ed., 2012, 51, 5810–5831.
10. P. G. Moses and J. K. Nørskov, ACS Catal., 2013, 3, 735–745.
11. S. K. Matam, R. F. Howe, A. Thetford and R. C. A. Catlow, Chem. Commun., 2018, 54, 12875–12878.
12. A. J. O’Malley, S. F. Parker, A. Chutia, M. R. Farrow, I. P. Silverwood, V. García-Sakai and C. R. A. Catlow, Chem. Commun., 2016, 52, 2897–2900.
13. J. R. Di Iorio, C. T. Nimlos and R. Gounder, ACS Catal., 2017, 7, 6663–6674.
14. T. Omojola, D. B. Lukyanov, N. Cherkasov, V. L. Zholobenko and A. C. van Veen, Ind. Eng. Chem. Res., 2019, 58, 16479–16488.
15. T. Omojola, D. B. Lukyanov and A. C. Veen, Int. J. Chem. Kinet., 2019, 51, 528–537.
16. M. Vandichel, D. Lesthaeghe, J. V. der Mynsbrugge, M. Waroquier and V. Van Speybroeck, J. Catal., 2010, 271, 67–78.
17. T. Fujino, M. Kashitani, J. N. Kondo, K. Domen, C. Hirose, M. Ishida, F. Goto and F. Wakabayashi, J. Phys. Chem., 1996, 100, 11649–11653.
18. T. R. Forester and R. F. Howe, J. Am. Chem. Soc., 1987, 109, 5076–5082.
19. Z. Luz and A. J. Vega, J. Phys. Chem., 1986, 90, 4903–4905.
20. S. R. Blaszkowski and R. A. van Santen, J. Am. Chem. Soc., 1996, 118, 5152–5153.
21. S. R. Blaszkowski and R. A. van Santen, J. Phys. Chem. B, 1997, 101, 2292–2305.
22. T. Omojola, N. Cherkasov, A. McNab, D. Lukyanov, J. Anderson, E. Rebrov and A. van Veen, Catal. Lett., 2018, 148, 474–488.
23. A. Zachariou, A. Hawkins, D. Lennon, S. F. Parker, Suwardiyanto, S. K. Matam, C. R. A. Catlow, P. Collier, A. Hameed, J. McGregor and R. F. Howe, Appl. Catal., A, 2019, 569, 1–7.
24. C. M. Nguyen, M.-F. Reyniers and G. B. Marin, Phys. Chem. Chem. Phys., 2010, 12, 9481–9493.
25. G. Artioli, C. Lamberti and G. L. Marra, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 2–10.
26. A. K. C. J. A. Hriljac, M. M. Eddy, J. A. Donohue and G. J. Ray, J. Solid State Chem., 1993, 106, 66–72.
27. B. C. Knott, C. T. Nimlos, D. J. Robichaud, M. R. Nimlos, S. Kim and R. Gounder, ACS Catal., 2018, 8, 770–784.
28. A. J. O’Malley, A. J. Logsdail, A. A. Sokol and C. R. A. Catlow, Faraday Discuss., 2016, 188, 235–255.
29. Database of Zeolite Structures, http://www.iza-structure.org/databases.
30. S. A. F. Nastase, A. J. O’Malley, C. R. A. Catlow and A. J. Logsdail, Phys. Chem. Chem. Phys., 2019, 21, 2639–2650.
31. J. To, A. A. Sokol, S. A. French and C. R. A. Catlow, J. Phys. Chem. C, 2008, 112, 7173–7185.
32. P. Sherwood, A. H. De Vries, S. J. Collins, S. P. Greatbanks, N. A. Burton, M. A. Vincent and I. H. Hillier, Faraday Discuss., 1997, 106, 79–92.
33. T. W. Keal and D. J. Tozer, J. Chem. Phys., 2005, 123, 121103.
34. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
35. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. De Jong, Comput. Phys. Commun., 2010, 181, 1477–1489.
36. M. F. Guest, I. J. Bush, H. J. Van Dam, P. Sherwood, J. M. H. Thomas, J. H. Van Lenthe, R. W. Havenith and J. Kendrick, Mol. Phys., 2005, 103, 719–747.
37. R. Ahlrichs and P. R. Taylor, J. Chim. Phys., 1981, 78, 315–324.
38. D. R. Hartree, Math. Proc. Cambridge Philos. Soc., 1928, 24, 426.
39. V. Fock, Z. Phys., 1930, 61, 126–148.
40. W. Smith, C. W. Yong and P. M. Rodger, Mol. Simul., 2002, 28, 37–41.
41. J. R. Hill and J. Sauer, J. Phys. Chem., 1994, 98, 1238–1244.
42. J.-R. Hill and J. Sauer, J. Phys. Chem., 1995, 99, 9536–9550.
43. S. Metz, J. Kästner, A. A. Sokol, T. W. Keal and P. Sherwood, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 101–110.
44. C. G. Broyden, Math. Comput. Biomed. Appl., 1970, 24, 365.
45. R. Fletcher, Comput. J., 1970, 13, 317–322.
46. D. Goldfarb, Math. Comput. Biomed. Appl., 1970, 24, 23.
47. D. F. Shanno, Math. Comput. Biomed. Appl., 1970, 24, 647.
48. J. Kästner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, J. Phys. Chem. A, 2009, 113, 11856–11865.
49. W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637–649.
50. F. Haase and J. Sauer, J. Am. Chem. Soc., 1995, 117, 3780–3789.
51. J. Kotrla, D. Nachtigallova, L. Kubelková, L. Heeribout, C. Doremieux-Morin and J. Fraissard, J. Phys. Chem. B, 1998, 102, 2454–2463.
52. A. Goodrow and A. T. Bell, J. Phys. Chem. C, 2008, 112, 13204–13214.
53. K. Hemelsoet, A. Ghysels, D. Mores, K. De Wispelaere, V. Van Speybroeck, B. M. Weckhuysen and M. Waroquier, Catal. Today, 2011, 177, 12–24.
54. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
55. A. A. Sokol, S. T. Bromley, S. A. French, C. R. A. Catlow and P. Sherwood, Int. J. Quantum Chem., 2004, 99, 695–712.
56. W. Jost, J. Chem. Phys., 1933, 1, 466–475.
57. R. Poloni and J. Kim, J. Mater. Chem. C, 2014, 2, 2298–2300.
58. F. B. van Duijneveldt, J. G. C. M. van Duijneveldt-van de Rijdt and J. H. van Lenthe, Chem. Rev., 1994, 94, 1873–1885.
59. D. Lesthaeghe, V. Van Speybroeck, G. B. Marin and M. Waroquier, Angew. Chem., Int. Ed., 2006, 45, 1714–1719.
60. G. Pope, J. Chem. Soc., Faraday Trans., 1993, 89, 1139–1141.
61. T. Omojola, N. Cherkasov, A. I. McNab, D. B. Lukyanov, J. A. Anderson, E. V. Rebrov and A. C. van Veen, Catal. Lett., 2018, 148, 474–488.
62. S. Etemadi and U. Olsbye, Catalytic investigations of zeolite based methanol to hydrocarbons catalysts, Master’s thesis, University of Oslo, 2015, pp. 75–122.
63. U. Olsbye, S. Svelle, M. Bjrgen, P. Beato, T. V. W. Janssens, F. Joensen, S. Bordiga and K. P. Lillerud, Angew. Chem., Int. Ed., 2012, 51, 5810–5831.
64. R. Shah, J. D. Gale and M. C. Payne, J. Phys. Chem. B, 1997, 101, 4787–4797.
65. B. J. Smith and L. Radom, J. Am. Chem. Soc., 1993, 115, 4885–4888.
66. A. Zecchina, S. Bordiga, G. Spoto, D. Scarano, G. Spanò and F. Geobaldo, J. Chem. Soc., Faraday Trans., 1996, 92, 4863–4875.

---

Footnote

† Electronic supplementary information (ESI) available: Additional information is provided in a separate section containing a more detailed discussion further explaining the approximations made for the transition state calculations, alongside charge and geometric analysis of adsorbed DME in zeolites H-Y and H-ZSM-5. See DOI: 10.1039/d0cp05392a

---