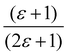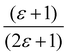Open Access Article
Open Access ArticleProperties of the tert-butyl halide solvolysis transition states†
Michael H.
Abraham
 *a,
Filomena
Martins
*a,
Filomena
Martins
 *b,
Ruben
Elvas-Leitão
*b,
Ruben
Elvas-Leitão
 bc and
Luís
Moreira
bd
bc and
Luís
Moreira
bd
aDepartment of Chemistry, University College London, 20 Gordon St, London WC1H 0AJ, UK. E-mail: m.h.abraham@ucl.ac.uk
bCentro de Química Estrutural (CQE), Faculdade de Ciências, Universidade de Lisboa, Campo Grande, Edifício C8, 1749-016, Lisboa, Portugal. E-mail: filomena.martins@ciencias.ulisboa.pt
cÁrea Departamental de Engenharia Química, Instituto Superior de Engenharia de Lisboa, IPL, R. Conselheiro Emídio Navarro, 1959-007 Lisboa, Portugal
dInstituto Superior de Educação e Ciências (ISEC Lisboa), Alameda das Linhas de Torres, 174, 1750-142 Lisboa, Portugal
First published on 25th January 2021
Abstract
We have obtained properties (or descriptors) of the transition states in the solvolysis of tert-butyl chloride, bromide and iodide. We show that all three transition states, in both protic and in aprotic solvents, are highly dipolar and are strong hydrogen bond acids and strong hydrogen bond bases, except for the tert-butyl iodide transition state in aprotic solvents, which has a rather low hydrogen bond acidity. Thus, the transition states are stabilized by solvents that are hydrogen bond bases (nucleophiles) and are hydrogen bond acids (electrophiles). We show also that the partition of the transition states between water and solvents is aided by both nucleophilic and electrophilic solvents and conclude that the rate of solvolysis of the three halides is increased by both nucleophilic and electrophilic solvents.
1 Introduction
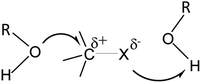
Although the mechanism of solvolysis of tert-butyl chloride has been studied for the past 85 years,1 questions about the mechanism still remain unsettled, especially whether or not there is nucleophilic assistance by solvents. Gajewski2 has referred to this solvolysis as “…the most misunderstood reaction in organic chemistry” and has put forward arguments based on his multiple parameter equation3 that there is no positive nucleophilic solvent participation in the solvolysis. Dvorko et al.4–7 used the multi-parameter Koppel-Palm equation to reach a similar conclusion for the solvolysis of tert-butyl chloride, as did Ponomarev et al.8 for the solvolysis of tert-butyl bromide and tert-butyl iodide.9 Indeed, these workers4–8 suggest that there is a small negative effect of nucleophilic solvation in the solvolysis of the three halides in protic solvents. However, it should be mentioned that Serebryakov10 regards the various correlation analyses4–8 to be unsound. Application of the multi-parameter Kamlet–Taft equation to rate constants for the tert-butyl chloride solvolysis also indicated11–13 that there was no, or little, positive nucleophilic assistance, as also suggested by Farcasiu et al.14 This is contrary to a long-established position15–18 that the rate of solvolysis of the tert-butyl halides is increased by nucleophilic solvent participation, or by “nucleophilic assistance/cation solvation”.The tert-butyl halide transition states are generally regarded to be somewhere in between the relatively non-polar tert-butyl halides and the polar tert-butyl halide ion pairs, with the leaving halide atom in the transition state C⋯X bond carrying a partial negative charge. Then electrophilic solvents (hydrogen bond acids) can solvate the leaving halide, leading to a reduction in the energy of the transition state and to an increase in the rate constant. There will also be a corresponding partial positive charge on the carbon atom of the C⋯X bond – as shown in Scheme 1 for hydroxylic solvents. Then nucleophilic solvents (hydrogen bond bases) would be expected to solvate this area of the transition state, leading again to an increase in the rate constant. But according to various workers,2–9,11–14 there is no rate enhancement due to nucleophilic solvents, and hence there must be no nucleophilic solvation of the transition state. Dvorko et al.6 rationalized the lack of nucleophilic assistance as being due to an intermediate ion pair that they described as R−[O]X− but this does not seem to make the cause of the lack of nucleophilic assistance any clearer.
We have set out a multi-parameter equation,19–22 that we have used to obtain information on the properties of a large number of neutral compounds from the effects of solvents on compound solubilities or on compound water–solvent partitions. More recently, we have extended the equations to ionic compounds such as permanent ions and ion-pairs.23,24 Very relevant to the present study is the application to betaine25 and to aminoacids.26 In these cases, we found that the ionic form of the equation had to be used, in accordance with complete charge separation in these compounds. So application of our equations to the tert-butyl halide transition states may lead to information as to the extent of charge separation in the transition states, to the hydrogen-bond acidity (electrophilicity) and hydrogen-bond basicity (nucleophilicity) of the transition states, and hence to the role of solvent as a nucleophile (hydrogen bond base) and an electrophile (hydrogen bond acid).
2 Materials and Methods
2.1 Materials
For experiments carried out in this work, tert-butyl chloride and tert-butyl bromide were purchased from BDH (purity > 99%) and tert-butyl iodide was purchased from Aldrich (purity > 95%). tert-Butyl iodide was regularly purified by column chromatography (Silica gel 60). Solvents were obtained commercially and used without further purification from Aldrich, Merck and Koch-Light (>99% + purity) and their water content was always <2% v/v. Solvent mixtures were prepared by volume using pure solvents and freshly collected double deionized water, obtained with a Milli-Q system from Millipore (Bedford, MA, USA) with a resistivity of 18.2 MΩ.2.2 Procedures
Kinetic curves were followed by conductimetry using an automated Wayne Kerr B905 conductance bridge. Temperature control was always better than ±0.01 K. Substrate concentration was 0.01 mol dm−3 and, whenever deemed necessary, 0.02 mol dm−3 of 2,6-lutidine (a weak base) was added to the solvent to capture the produced acid and prevent its further reactivity. In some cases, calibration curves were performed. Reactions were followed up to 90% of the apparent plateau. Mean k values result from at least 3 different runs and showed a standard deviation better than 5%. All k values were determined using a Microsoft Excel spreadsheet specifically designed by us for this purpose.27,282.3 Theory
Our method is based on eqn (1) and (2), set up for correlation of processes involving a given neutral solute in a variety of solvents.19–22 The dependent variable is log Ps, where Ps is a water–solvent partition coefficientLog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps = c + eE + sS + aA + bB + vV Ps = c + eE + sS + aA + bB + vV | (1) |
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps = c + eE + sS + aA + bB + lL Ps = c + eE + sS + aA + bB + lL | (2) |
The independent variables, or descriptors, are properties of the neutral solutes as follows.19–22E is the solute excess molar refraction in cm3 mol−1/10, S is the solute dipolarity/polarizability, A is the overall solute hydrogen bond acidity, B is the overall solute hydrogen bond basicity, V is the McGowan's characteristic molecular volume in cm3 mol−1/100 and L is the logarithm of the gas to hexadecane partition coefficient at 298 K.
In the extension of eqn (1)23,24 to include permanent ions such as K+ and Cl−, ion pairs such as Me4N+Cl−, deprotonated carboxylic acids, RCO2−, and protonated amines, the independent variables E, S, A, B and V were the same in eqn (1) and (3) so that only two extra variables were needed to incorporate the ionic solutes, J+ for cationic solutes and J− for anionic solutes. Then eqn (1) becomes eqn (3), where J+ = 0 for anions, J− = 0 for cations and J+ = J− = 0 for neutral molecules.
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps = c + eE + sS + aA + bB + vV + j+J+ + j−J− Ps = c + eE + sS + aA + bB + vV + j+J+ + j−J− | (3) |
The coefficients in eqn (1) and (3) for various solvents are given in Table 1.19–24
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps
Ps
| Solvent | c | e | s | a | b | v | j + | j − |
|---|---|---|---|---|---|---|---|---|
| a Volume % alcohol. | ||||||||
| Perfluorooctane | 0.492 | −0.051 | −2.588 | −3.424 | −3.974 | 3.377 | ||
| Pentane | 0.369 | 0.386 | −1.568 | −3.535 | −5.215 | 4.514 | ||
| Heptane | 0.297 | 0.634 | −1.755 | −3.571 | −4.946 | 4.488 | ||
| Cyclohexane | 0.159 | 0.784 | −1.678 | −3.740 | −4.929 | 4.577 | ||
| Benzene | 0.142 | 0.464 | −0.588 | −3.099 | −4.625 | 4.491 | ||
| Dichloromethane | 0.319 | 0.102 | −0.187 | −3.058 | −4.090 | 4.324 | −3.984 | 0.086 |
| Trichloromethane | 0.191 | 0.105 | −0.403 | −3.112 | −3.514 | 4.395 | −3.155 | −3.705 |
| 1,2-Dichloroethane | 0.183 | 0.294 | −0.134 | −2.801 | −4.291 | 4.180 | 4.180 | −3.429 |
| tert-Butyl chloride (n-BuCl) | 0.222 | 0.273 | −0.569 | −2.918 | −4.883 | 4.456 | ||
| Diethyl ether | 0.350 | 0.358 | −0.820 | −0.588 | −4.956 | 4.350 | 0.434 | −10.124 |
| Dioxane | 0.123 | 0.347 | −0.033 | −0.582 | −4.810 | 4.110 | −5.883 | 4.649 |
| Tetrahydrofuran | 0.223 | 0.363 | −0.384 | −0.238 | −4.932 | 4.450 | −2.278 | −2.132 |
| Ethyl acetate | 0.328 | 0.369 | −0.446 | −0.700 | −4.904 | 4.150 | 4.243 | −2.232 |
| Propanone | 0.313 | 0.312 | −0.121 | −0.608 | −4.753 | 3.942 | −2.288 | 0.078 |
| Cyclohexanone | 0.077 | 0.249 | 0.028 | −0.891 | −4.917 | 4.283 | ||
| Acetonitrile | 0.413 | 0.077 | 0.326 | −1.566 | −4.391 | 3.364 | −2.234 | 0.101 |
| Nitromethane | 0.023 | −0.091 | 0.793 | −1.463 | −4.364 | 3.460 | −3.781 | −0.149 |
| N-Methylpyrrolidone | 0.147 | 0.532 | 0.225 | 0.840 | −4.794 | 3.674 | −1.797 | 0.105 |
| Dimethylsulfoxide | −0.194 | 0.327 | 0.791 | 1.260 | −4.540 | 3.361 | −3.387 | 0.132 |
| Dimethylfomamide | −0.305 | −0.058 | 0.343 | 0.358 | −4.865 | 4.486 | −3.605 | 0.415 |
| Dimethylacetamide | −0.271 | 0.084 | 0.209 | 0.915 | −5.003 | 4.557 | −2.125 | 0.286 |
| Propylene carbonate | 0.004 | 0.168 | 0.504 | −1.283 | −4.407 | 3.421 | −1.989 | 0.341 |
| Sulfolane | 0.000 | 0.147 | 0.601 | −0.318 | −4.541 | 3.290 | −1.200 | −0.792 |
| Chlorobenzene | 0.065 | 0.381 | −0.521 | −3.183 | −4.700 | 4.614 | −4.536 | −1.486 |
| Nitrobenzene | −0.152 | 0.525 | 0.081 | −2.332 | −4.494 | 4.187 | −3.373 | 0.777 |
| Benzonitrile | 0.097 | 0.285 | 0.059 | −1.605 | −4.562 | 4.028 | −2.729 | 0.136 |
| Acetophenone | 0.177 | 0.365 | 0.000 | −1.537 | −4.658 | 3.958 | ||
| Aniline | −0.156 | 0.325 | −0.006 | 1.289 | −3.512 | 3.841 | ||
| N-Methylpropanamide | ||||||||
| N-Methylformamide | 0.114 | 0.407 | −0.287 | 0.542 | −4.085 | 3.471 | −3.733 | 3.869 |
| Formamide | −0.171 | 0.070 | 0.308 | 0.589 | −3.152 | 2.432 | −3.152 | 2.432 |
| Water | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Methanol | 0.276 | 0.334 | −0.714 | 0.243 | −3.320 | 3.549 | −2.609 | 3.027 |
| Ethanol | 0.222 | 0.471 | −1.035 | 0.326 | −3.596 | 3.857 | −3.172 | 3.146 |
| Propan-1-ol | 0.139 | 0.405 | −1.029 | 0.247 | −3.767 | 3.986 | −3.077 | 2.834 |
| Butan-1-ol | 0.165 | 0.401 | −1.011 | 0.056 | −3.958 | 4.044 | −3.605 | 2.685 |
| Pentan-1-ol | 0.150 | 0.536 | −1.229 | 0.141 | −3.864 | 4.077 | −3.387 | 2.816 |
| Hexan-1-ol | 0.115 | 0.492 | −1.164 | 0.054 | −3.978 | 4.131 | −3.100 | 2.940 |
| Heptan-1-ol | 0.035 | 0.398 | −1.063 | 0.002 | −4.342 | 4.317 | −3.318 | 2.751 |
| Octan-1-ol | −0.034 | 0.489 | −1.044 | −0.024 | −4.235 | 4.218 | −3.334 | 2.706 |
| Ethylene glycol | −0.270 | 0.578 | −0.511 | 0.715 | −2.619 | 2.729 | −1.300 | 2.363 |
| 1,2-Propylene glycol | −0.149 | 0.754 | −0.966 | 0.684 | −3.134 | 3.247 | −1.381 | 3.057 |
| Propan-2-ol | 0.099 | 0.344 | −1.049 | 0.406 | −3.827 | 4.033 | −3.896 | 2.889 |
| sec-Butanol | 0.127 | 0.253 | −0.976 | 0.158 | −3.882 | 4.114 | −3.700 | 2.700 |
| Isobutanol | 0.188 | 0.354 | −1.127 | 0.016 | −3.568 | 3.986 | −3.700 | 2.830 |
| tert-Butanol | 0.211 | 0.171 | −0.947 | 0.331 | −4.085 | 4.109 | −4.455 | 2.953 |
| 2-Methylbutan-1-ol | 0.104 | 0.400 | −1.185 | 0.187 | −3.921 | 4.151 | ||
| tert-Pentanol | 0.177 | 0.316 | −1.125 | 0.306 | −4.112 | 4.178 | ||
| 2-Methoxyethanol | 0.175 | 0.326 | −0.140 | 0.000 | −4.086 | 3.630 | −1.295 | 1.508 |
| Trifluoroethanol | 0.395 | −0.094 | −0.594 | −1.280 | −1.274 | 3.088 | −1.113 | 0.957 |
| HFIP | 0.533 | −0.901 | −0.535 | −0.539 | −0.832 | 3.080 | ||
| Acetic acid | 0.175 | 0.174 | −0.454 | −1.073 | −2.789 | 3.725 | ||
| 100% Ethanola | 0.222 | 0.471 | −1.035 | 0.326 | −3.596 | 3.857 | −3.172 | 3.146 |
| 96 | 0.238 | 0.353 | −0.833 | 0.297 | −3.533 | 3.724 | ||
| 95 | 0.239 | 0.328 | −0.795 | 0.294 | −3.514 | 3.697 | −2.985 | 2.943 |
| 90 | 0.243 | 0.213 | −0.575 | 0.262 | −3.450 | 3.545 | −2.794 | 2.837 |
| 80 | 0.172 | 0.175 | −0.465 | 0.260 | −3.212 | 3.323 | −2.466 | 2.722 |
| 70 | 0.063 | 0.085 | −0.368 | 0.311 | −2.936 | 3.102 | −2.203 | 2.550 |
| 60 | −0.040 | 0.138 | −0.335 | 0.293 | −2.675 | 2.812 | −1.858 | 2.394 |
| 50 | −0.142 | 0.124 | −0.252 | 0.251 | −2.275 | 2.415 | −1.569 | 2.051 |
| 40 | −0.221 | 0.131 | −0.159 | 0.171 | −1.809 | 1.918 | −1.271 | 1.676 |
| 30 | −0.269 | 0.107 | −0.098 | 0.133 | −1.316 | 1.414 | −0.841 | 1.290 |
| 20 | −0.252 | 0.042 | −0.040 | 0.096 | −0.823 | 0.916 | −0.677 | 0.851 |
| 10 | −0.173 | −0.023 | −0.001 | 0.065 | −0.372 | 0.454 | −0.412 | 0.401 |
| 0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 100% Methanola | 0.276 | 0.334 | −0.714 | 0.000 | −3.320 | 3.549 | −2.609 | 3.027 |
| 95 | 0.270 | 0.278 | −0.520 | 0.230 | −3.368 | 3.365 | −2.661 | 2.909 |
| 90 | 0.258 | 0.250 | −0.452 | 0.229 | −3.206 | 3.175 | −2.629 | 2.707 |
| 80 | 0.172 | 0.197 | −0.319 | 0.241 | −2.912 | 2.842 | −2.540 | 2.421 |
| 70 | 0.098 | 0.192 | −0.260 | 0.266 | −2.558 | 2.474 | −2.267 | 2.164 |
| 60 | 0.053 | 0.207 | −0.238 | 0.272 | −2.157 | 2.073 | −1.978 | 1.872 |
| 50 | 0.023 | 0.223 | −0.222 | 0.264 | −1.747 | 1.662 | −1.588 | 1.569 |
| 40 | 0.020 | 0.222 | −0.205 | 0.218 | −1.329 | 1.259 | −1.329 | 1.259 |
| 30 | 0.016 | 0.187 | −0.172 | 0.165 | −0.953 | 0.898 | −0.823 | 0.930 |
| 20 | 0.022 | 0.142 | −0.138 | 0.088 | −0.574 | 0.559 | −0.465 | 0.599 |
| 10% Methanol | 0.012 | 0.072 | −0.081 | 0.026 | −0.249 | 0.266 | −0.185 | 0.287 |
3 Results and discussion
Partition coefficients of the tert-butyl halide transition states, Tr, from water to solvents, as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps, were obtained from eqn (4), as described before29,30
Ps, were obtained from eqn (4), as described before29,30Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps (Tr) = log Ps (Tr) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps (tert-BuX) + log Ps (tert-BuX) + log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k(S) − log k(S) − log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k(W) k(W) | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps (tert-BuX) is the water to solvent partition coefficient of the corresponding halide, and k(S) and k(W) are the tert-butyl halide rate constants in the solvent S and in water.
Ps (tert-BuX) is the water to solvent partition coefficient of the corresponding halide, and k(S) and k(W) are the tert-butyl halide rate constants in the solvent S and in water.
Thermodynamic data on the initial states were available,29–31 and these in turn were used to derive the descriptors for the tert-butyl halides in eqn (1) and in eqn (2), as set out in detail elsewhere.21,22,30 The obtained values are in Table 2. In Table 3, Kw is the gas to water partition coefficient. There is nothing exceptional about the descriptors for the tert-butyl halides. In particular, they have zero electrophilicity (hydrogen-bond acidity, A) and very little nucleophilicity (hydrogen-bond basicity, B).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k/s−1, for solvolysis of the tert-butyl halides at 298 K
k/s−1, for solvolysis of the tert-butyl halides at 298 K
| Solvent | tert-Butyl chloride | tert-Butyl bromide | tert-Butyl iodide | |||
|---|---|---|---|---|---|---|
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k k |
Ref. | Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k k |
Ref. | Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k k |
Ref. | |
a This work.
b Values obtained by interpolation and by regression against log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values for tert-butyl chloride.
c Values obtained by temperature extrapolation.
d Volume % alcohol. k values for tert-butyl chloride.
c Values obtained by temperature extrapolation.
d Volume % alcohol.
|
||||||
| Perfluorooctane | −16.16 | 36 | ||||
| Pentane | −16.00 | 29 | −13.30 | 11 | −11.20 | 11 |
| Heptane | −16.00 | 36 | ||||
| Cyclohexane | −14.50 | 36 | ||||
| Benzene | −12.16 | 12 | −6.56 | 6 | ||
| Toluene | −7.04 | 6 | ||||
| Dichloromethane | −10.45 | 12 | −7.21 | 8 | −6.12 | 6 |
| Trichloromethane | −9.72 | 4 | −7.47 | 6 | ||
| 1,2-Dichloroethane | −9.54 | 12 | −6.15 | 6 | ||
| tert-Butyl chloride (n-BuCl) | −13.6 | 4 | ||||
| Diethyl ether | −12.74 | 12 | −10.00 | 11 | −8.20 | 11 |
| Dioxane | −10.80 | 5 | −8.52 | 6 | −6.78 | 11 |
| Tetrahydrofuran | −11.00 | 12 | −8.30 | 11 | −6.57 | 11 |
| Ethyl acetate | −11.50 | 12 | −8.70 | 11 | −7.02 | 11 |
| Propanone | −9.90 | 12 | −7.13 | 6 | −5.21 | 11 |
| Cyclohexanone | −9.61 | 4 | ||||
| Acetonitrile | −8.73 | 29 | −5.90 | 6 | −4.25 | |
| Nitromethane | −8.13 | 4 | −5.51 | −3.89 | ||
| N-Methylpyrrolidone | −8.97 | 5 | −6.00 | 6 | −4.55 | 11 |
| Dimethylsulfoxide | −7.34 | 36 | −4.45 | −2.68 | ||
| Dimethylformamide | −8.55 | 12 | −5.56 | −3.70 | ||
| Dimethylacetamide | −9.30 | 5 | −5.92 | −5.00 | 11 | |
| Propylene carbonate | −8.81 | 30 | −5.47 | −4.02 | 11 | |
| Sulfolane | −7.91 | 4 | −5.18 | 6 | ||
| Fluorobenzene | −6.58 | 6 | ||||
| Chlorobenzene | −11.34 | 12 | −9.44 | 6 | −6.58 | 6 |
| Bromobenzene | −6.59 | 6 | ||||
| Iodobenzene | −6.51 | 6 | ||||
| Nitrobenzene | −9.72 | 29 | −6.95 | 6 | −5.52 | 6 |
| Benzonitrile | −9.83 | 30 | −7.11 | 6 | −5.43 | 6 |
| Acetophenone | −10.13 | 4 | ||||
| Aniline | −6.10 | −3.84 | −2.80 | |||
| N-Methylpropanamide | −5.54 | 8 | ||||
| N-Methylformamide | −7.33 | 5 | ||||
| Formamide | −4.40 | 12 | −2.85 | 6 | −1.98 | |
| Water | −1.54 | 12 | −0.12 | 6 | 0.188 | 6 |
| Methanol | −6.10 | 12 | −4.46 | 34 | −3.910 | 34 |
| Ethanol | −7.07 | 12 | −5.24 | 37 | −4.650 | 34 |
| Propan-1-ol | −7.33 | 12 | −5.44 | 6 | −4.86 | 34 |
| Butan-1-ol | −7.52 | 12 | −5.61 | 6 | −4.95 | 34 |
| Pentan-1-ol | −7.45 | 32 | −5.64 | 32 | −5.29 | 32 |
| Hexan-1-ol | −7.45 | 4 | ||||
| Octan-1-ol | −7.52 | 4 | ||||
| Ethylene glycol | −4.60 | 5 | −3.03 | 34 | −2.55 | 34 |
| 1,2-Propylene glycol | −5.51 | 32 | −4.03 | 32 | −3.56 | 32 |
| Propan-2-ol | −7.74 | 29 | −5.67 | 34 | −5.05 | 6 |
| sec-Butanol | −8.10 | 31 | −5.78 | 6 | −5.40 | 34 |
| Isobutanol | −7.40 | −5.68 | 6 | −5.19 | 34 | |
| tert-Butanol | −8.27 | 12 | −6.32 | 6 | −5.84 | 11 |
| 2-Methylbutan-1-ol | −7.60c | −5.71 | −5.40 | |||
| tert-Pentanol | −8.77 | 5 | ||||
| 2-Methoxyethanol | −6.63c | −4.75 | −3.90 | |||
| Trifluoroethanol | −3.89 | −2.62 | 6 | |||
| HFIP | −2.70 | 12 | −1.45 | 6 and 12 | ||
| Acetic acid | −6.70 | 4 | −5.52 | 6 | ||
| 100% Ethanold | −7.07 | 12 | −5.24 | 37 | −4.65 | 34 |
| 96 | −6.72 | 35 | −4.99 | −4.25 | ||
| 95 | −6.32 | 35 | −4.62 | −4.18 | ||
| 90 | −5.78 | 35 | −4.15 | 37 | −3.69 | |
| 80 | −5.03 | 35 | −3.44 | 37 | −3.03 | |
| 70 | −4.44 | 35 | −2.87 | −2.56 | ||
| 60 | −3.91 | 35 | −2.42 | 37 | −2.12 | |
| 50 | −3.38 | 35 | −1.88 | −1.67 | ||
| 40 | −2.84 | 35 | −1.38 | −1.15 | ||
| 30 | −2.31 | 35 | −0.88 | −0.732 | ||
| 20 | −1.98 | 35 | −0.57 | −0.398 | ||
| 10 | −1.72 | 35 | −0.33 | −0.079 | ||
| 0 | −1.54 | 35 | −0.12 | 33 | 0.188 | 33 |
| 100% Methanold | −6.10 | 12 | −4.46 | 34 | −3.903 | 34 |
| 95 | −5.530 | 33 | −4.05 | 33 | −3.553 | 33 |
| 90 | −4.859 | 33 | −3.67 | 33 | −3.221 | 33 |
| 80 | −4.032 | 33 | −3.00 | 33 | −2.627 | 33 |
| 70 | −3.412 | 33 | −2.48 | −2.107 | 33 | |
| 60 | −2.964 | 33 | −2.00 | −1.653 | 33 | |
| 50 | −2.598 | 33 | −1.56 | 33 | −1.254 | 33 |
| 40 | −2.304 | 33 | −1.20 | 33 | −0.900 | 33 |
| 30 | −2.060 | 33 | −0.88 | 33 | −0.582 | 33 |
| 20 | −1.859 | 33 | −0.60 | 33 | −0.299 | 33 |
| 10% Methanol | −1.685 | 33 | −0.34 | 33 | −0.044 | 33 |
| Compound | E | S | A | B | V | L | Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kw Kw |
|---|---|---|---|---|---|---|---|
| tert-Butyl chloride | 0.142 | 0.300 | 0.000 | 0.030 | 0.7946 | 2.286 | −0.80 |
| tert-Butyl bromide | 0.305 | 0.320 | 0.000 | 0.065 | 0.8427 | 2.563 | −0.40 |
| tert-Butyl iodide | 0.589 | 0.320 | 0.000 | 0.070 | 0.9304 | 3.350 | −0.39 |
3.1 tert-Butyl chloride
Several years ago we studied the structure of the tert-butyl chloride transition state using reaction field theory36 Our results indicated that the transition state had decidedly different structures in protic and in aprotic solvents, and so it seems appropriate to apply our equations separately to data in protic and aprotic solvents. Rate constants at 298 K were obtained from various sources4,5,12,29–37 and also in this work, and are given in Table 2 as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k in s−1. The corresponding values of the water to solvent partition coefficients as log
k in s−1. The corresponding values of the water to solvent partition coefficients as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps(Tr) were simply obtained through eqn (4).
Ps(Tr) were simply obtained through eqn (4).
Unfortunately, we only have 20 values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps(Tr) in aprotic solvents to use in eqn (3), rather too small a number to analyse using six independent variables in an LFER (the term in eE was not significant). However, we give details of eqn (1) and (3) applied to exactly the same data set, as eqn (5) and (6) in Table 4. In eqn (5) and (6) and subsequent equations, N is the number of data points (solvents), SD is the regression standard deviation, R2 is the determination coefficient and F is the Fisher F-statistic. The leave-one-out statistics are PRESS, Q2 and the predictive standard deviation, PSD. The errors on the coefficients are in parentheses.
Ps(Tr) in aprotic solvents to use in eqn (3), rather too small a number to analyse using six independent variables in an LFER (the term in eE was not significant). However, we give details of eqn (1) and (3) applied to exactly the same data set, as eqn (5) and (6) in Table 4. In eqn (5) and (6) and subsequent equations, N is the number of data points (solvents), SD is the regression standard deviation, R2 is the determination coefficient and F is the Fisher F-statistic. The leave-one-out statistics are PRESS, Q2 and the predictive standard deviation, PSD. The errors on the coefficients are in parentheses.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps(Tr), in aprotic solvents
Ps(Tr), in aprotic solvents
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps(Tr) Ps(Tr) |
c | e | s | a | b | v | j + | j − | N | SD | R 2 | F | PRESS | Q 2 | PSD | Eqn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Aprotic | 4.008 (1.920) | — | 1.621 (0.374) | 0.404 (0.115) | 2.182 (0.435) | 0.402 (0.387) | 0.0643 (0.0566) | 0.0918 (0.0513) | 20 | 0.494 | 0.882 | 16 | 14.204 | 0.472 | 1.045 | (5) |
| Aprotic | 4.191 (1.981) | — | 1.732 (0.361) | 0.423 (0.118) | 2.175 (0.438) | 0.302 (0.386) | — | — | 20 | 0.515 | 0.852 | 22 | 11.924 | 0.557 | 0.892 | (6) |
The small values of Q2 and the large values of PSD show that these equations are not well founded, but they indicate that the addition of the ionic descriptors in eqn (5) does not lead to any improvement over eqn (6).
More data are available for reactions in protic solvents and, in Table 5, we give equations that use exactly the same data set for eqn (1) and (3). Eqn (7) is marginally better statistically than eqn (8) but suffers from a set of chemically unreasonable coefficients. In particular, the a-coefficient is negative, which is technically impossible, and the v-coefficient is far too small to describe the solvent effect on a medium-sized species.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps(Tr), in protic solvents
Ps(Tr), in protic solvents
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps(Tr) Ps(Tr) |
c | e | s | a | b | v | j + | j − | N | SD | R 2 | F | PRESS | Q 2 | PSD | Eqn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Protic | 0.271 (0.169) | 1.161 (1.051) | 2.703 (0.599) | −1.354 (0.531) | 1.110 (0.461) | 0.116 (0.523) | 0.182 (0.212) | 1.333 (0.303) | 41 | 0.384 | 0.928 | 61 | 10.768 | 0.841 | 0.571 | (7) |
| Protic | 0.383 (0.198) | 1.589 (0.817) | 3.197 (0.478) | 0.453 (0.432) | 1.912 (0.393) | 1.675 (0.423) | — | — | 41 | 0.475 | 0.883 | 53 | 17.750 | 0.738 | 0.712 | (8) |
We conclude that the ionic eqn (3), when applied to the effect of protic solvents on the tert-butyl chloride transition state yields an inferior equation to the equation for ‘neutral’ compounds, eqn (1). Thus, in contrast to compounds such as betaine and the α-aminoacids, these results indicate that the tert-butyl chloride transition state does not possess a complete charge separation, in agreement with the reaction field calculations, and other studies,36 which suggest a charge separation of about 0.80 units in protic solvents.
Dvorko et al.4 have suggested that the solvolysis of tert-butyl chloride in aprotic and in protic solvents is determined by the ionization of the covalent C–Cl bond. This involves consecutive formation of three ion pairs, a contact ion pair, a loose ion pair and a solvent separated ion pair, as shown in eqn (9). Now if the transition state does not carry a unit charge separation, it cannot lie between any of the suggested ion pairs but must lie between the RX substrate and the first ion pair. Then as regards the nature of the transition state, the various subsequent ion pairs are irrelevant.
| RX = R+X− = R+⋯X− = R+/Solv/X− → Products | (9) |
Another consequence is that we are no longer restricted to the set of equations of the form of eqn (3), but we can apply a much larger set of equations of the form of eqn (1) to solvent effects on the transition state. These equations are given in Table 6 as eqn (10) and (11) and include all the solvents for which we have the coefficients in eqn (1) and the corresponding rate constants.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps(Tr), in aprotic and protic solvents
Ps(Tr), in aprotic and protic solvents
| Log Ps(Tr) | c | e | s | a | b | v | N | SD | R 2 | F | PRESS | Q 2 | PSD | Eqn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Aprotic | 2.513 (1.885) | 1.194 (0.741) | 2.338 (0.225) | 0.591 (0.127) | 2.472 (0.465) | 1.037 (0.373) | 28 | 0.673 | 0.940 | 69 | 19.684 | 0.882 | 0.945 | (10) |
| Protic | 0.372 (0.199) | 1.344 (0.606) | 3.295 (0.441) | 0.655 (0.366) | 2.178 (0.341) | 1.961 (0.367) | 44 | 0.477 | 0.901 | 69 | 17.134 | 0.803 | 0.671 | (11) |
As regards the effect of solvent hydrogen bond acidity, a, (solvent electrophilicity) and solvent hydrogen bond basicity, b, (nucleophilicity) on the partition of the transition state, eqn (10) and (11) are unambiguous. Solvent hydrogen bond basicity (nucleophilicity) greatly increases log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PsTr. In both aprotic and protic solvents, the b-coefficient is very large. Solvent hydrogen bond acidity, a, (electrophilicity) also stabilizes the transition state, although now the effect is not so large (a = 0.591 and 0.655). Both sets of solvents stabilize the transition state through transition state-solvent dipole–dipole and dipole-induced dipole interactions (s = 2.338 and 3.295).
PsTr. In both aprotic and protic solvents, the b-coefficient is very large. Solvent hydrogen bond acidity, a, (electrophilicity) also stabilizes the transition state, although now the effect is not so large (a = 0.591 and 0.655). Both sets of solvents stabilize the transition state through transition state-solvent dipole–dipole and dipole-induced dipole interactions (s = 2.338 and 3.295).
Eqn (10) and (11) can be interpreted in terms of properties or descriptors of the transition state, but we can employ our usual method19–21,38 to obtain these directly. We construct a set of simultaneous equations with known values of c, e, s, a, b and v, see Table 1, and with values of logPsTr as the dependent variable. Then the set can be solved by trial-and-error to obtain the unknowns E, S, A, B and V. It is useful to estimate E as 0.20 (slightly larger than that for tert-butyl chloride) and V as 0.8000 (again, slightly larger than V for tert-butyl chloride at 0.7946), so that only S, A and B need to be determined. For aprotic solvents we have 26 simultaneous equations (we excluded N-methylformamide as a considerable outlier) that we solved with SD = 0.50 log units to give the descriptors in Table 7. For protic solvents we solved 41 simultaneous equations with SD = 0.61 log units to yield the descriptors in Table 7. In general, the descriptors for the tert-butyl chloride transition state are quite compatible with our descriptors for various ions and ion-pairs, as shown in Table 7.
| Species | E | S | A | B | V |
|---|---|---|---|---|---|
| t-BuCl(Tr) protic solvents | 0.20 | 2.27 | 0.66 | 1.03 | 0.8000 |
| t-BuCl(Tr) aprotic solvents | 0.20 | 2.63 | 0.45 | 1.75 | 0.8000 |
| Me4N+Cl− ion pair | 0.00 | 2.93 | 1.04 | 1.75 | 0.9913 |
| Me4N+ | −0.10 | 1.31 | 0.68 | 0.00 | 0.7635 |
| Cl− | 0.10 | 3.52 | 0.00 | 2.32 | 0.2278 |
| Acetate− | 0.42 | 2.19 | 0.00 | 2.93 | 0.4433 |
| t-BuBr(Tr) Protic solvents | 0.35 | 2.19 | 0.40 | 0.96 | 0.8500 |
| t-BuBr(Tr) Aprotic solvents | 0.35 | 3.06 | 0.40 | 1.49 | 0.8500 |
| Me4N+Br− ion pair | 0.07 | 2.11 | 0.89 | 2.18 | 1.0701 |
| Br− | 0.17 | 2.74 | 0.00 | 1.82 | 0.3066 |
| t-BuI(Tr) protic solvents | 0.65 | 2.47 | 0.35 | 0.85 | 0.9400 |
| t-BuI(Tr) aprotic solvents | 0.65 | 3.02 | 0.17 | 1.24 | 0.9400 |
| Me4N+I− ion pair | 0.28 | 2.51 | 0.75 | 1.48 | 1.1696 |
| I− | 0.38 | 3.55 | 0.00 | 1.34 | 0.4081 |
It is of some interest that the Me4N+ ion is stabilized by solvents that are nucleophilic (hydrogen bond bases|), with A = 0.68, see Table 7. This suggests that nucleophilic solvents can approach the central N+ atom in spite of the adjacent four methyl groups. Thus, it is no surprise that the central carbon atom in the tert-butyl chloride transition state can also be approached and solvated by nucleophilic solvents, with A = 0.66 and 0.45, Table 7. We can conclude that the tert-butyl chloride transition state in both protic and in aprotic solvents is very dipolar (S = 2.27 and 2.63), has a significant hydrogen bond acidity (A = 0.66 and 0.45) and a large hydrogen bond basicity (B = 1.03 and 1.75), so that it will be stabilized by solvents that are hydrogen bond bases (nucleophiles) and that are hydrogen bond acids (electrophiles). These properties are quite consistent with the coefficients shown in eqn (10) and (11). The ground state is almost unaffected by nucleophilic and electrophilic solvents, see Table 3, where A = 0.00 and B = 0.03, and so the effect of nucleophilic solvents on stabilizing the transition state will inevitably lead to an increase in the rate constant.
Our conclusion is so contrary to the conclusions reached from the application of other multi-parameter equations to tert-butyl chloride rate constants, that we are obliged to discuss possible reasons. Gajewski2,3 has used his linear free energy relationship to show that there is no positive nucleophilic solvent participation in the solvolysis and Dvorko et al.4–7 used the multi-parameter Koppel–Palm linear free energy relationship with similar results. Use of the Kamlet–Taft equation also indicated11–13 that there was little nucleophilic solvent participation. However, the Kamlet–Taft equation is not a linear free energy equation. The independent variables are calculated from solvatochromic measurements,39 and are therefore spectroscopic energies and not free energies. Quite recently, Catalan and Reichardt40 have applied an equation due to Catalan41 to the solvolysis of tert-butyl chloride. The equation contains four independent variables, all of which are derived from solvatochromic measurements and hence, again, are related to spectroscopic energies. The equation is therefore not appropriate for the analysis of a dependent variable that is a free energy. We therefore concentrate only on the equations given by Gajewski and by Dvorko.
Gajewski applied his equation to Winstein–Fainberg Y-values for seven solvents and obtained eqn (12), Table 8. We recalculated his equation and obtained a slightly different equation, eqn (13), using a corrected (ε − 1)/(2ε + 1) value from Marcus, for HFIP, as also shown in Table 8.42 In these equations, ε is the solvent dielectric constant, a′ is a descriptor based on the partition of the potassium ion, b′ is a descriptor based on the partition of the chloride ion, and CED is the cohesive energy density.
Unfortunately, both eqn (12) and (13) are statistically invalid because they only have seven data points for four independent variables, as can be seen from the low value of Q2 and the large value of PSD in eqn (13). Therefore, no valid information can be drawn in these circumstances.
In an interesting application, Gajewski2 obtained values for the transfer of the tert-butyl chloride transition state itself and regressed these against the independent variables in eqn (12) to obtain eqn (14) for 23 protic and aprotic solvents. Again, we used the same Y-values and independent variables as listed by Gajewski with the corrected ε value for HFIP and obtained eqn (15), as depicted in Table 9.
Results in Table 9, although statistically not very good, are in line with our own results presented in Table 6, with both solvent nucleophilicity (b′) and solvent electrophilicity (a′) stabilizing the transition state.
Koppel and Palm9 applied their well-known equation to the solvolysis of tert-butyl chloride, with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k/s−1 as the dependent variable, using 23 protic and aprotic solvents – Table 10 – where Ye is the dielectric constant function used by Gajewski, P is the refractive index function and E is the solvent electrophilicity. In eqn (16) the solvent nucleophilicity, B, was not significant, and so this equation suggests the absence of any nucleophilic solvent participation. Dvorko et al.5 also applied the Koppel–Palm equation to the solvolysis of tert-butyl chloride in a larger number of aprotic and protic solvents and obtained a similar equation, except that the coefficient of the electrophilicity descriptor is very small (0.083) so that neither solvent electrophilicity nor solvent nucleophilicity have any real effect on the reaction rate. These results are also presented in Table 10 together with the treatment for aprotic and protic solvents taken separately (δ2 stands for the cohesive energy density).
k/s−1 as the dependent variable, using 23 protic and aprotic solvents – Table 10 – where Ye is the dielectric constant function used by Gajewski, P is the refractive index function and E is the solvent electrophilicity. In eqn (16) the solvent nucleophilicity, B, was not significant, and so this equation suggests the absence of any nucleophilic solvent participation. Dvorko et al.5 also applied the Koppel–Palm equation to the solvolysis of tert-butyl chloride in a larger number of aprotic and protic solvents and obtained a similar equation, except that the coefficient of the electrophilicity descriptor is very small (0.083) so that neither solvent electrophilicity nor solvent nucleophilicity have any real effect on the reaction rate. These results are also presented in Table 10 together with the treatment for aprotic and protic solvents taken separately (δ2 stands for the cohesive energy density).
| Ref. | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k k |
const | Y e | P | E | B | δ 2 | N | SD | R 2 | Eqn |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Koppel–Palm9 | Protic + aprotic | −19.89 | 13.39 | 13.46 | 0.378 | — | — | 23 | 4.8% | 0.964 | (16) |
| Dvorko et al.5 | Protic + aprotic | −19.9 | 17.9 | 5.53 | 0.083 | — | — | 42 | 0.670 | 0.943 | (17) |
| Dvorko et al.5 | Aprotic | −20.6 | 14.5 | 13.0 | 0.136 | — | — | 21 | 0.610 | 0.904 | (18) |
| Dvorko et al.5 | Protic | −13.6 | 16.6 | — | 0.037 | −1.24 | 0.0014 | 20 | 0.630 | 0.929 | (19) |
Based on these results, Dvorko et al.5 concluded that in all solvents, the electrophilicity descriptor leads to an increase in the reaction rate, and that the nucleophilicity descriptor has no influence on reaction rate except in protic solvents where it actually leads to a small reduction in reaction rate.
Thus, of the linear free energy relationships applied to tert-butyl chloride rate constants or to transfers of the tert-butyl chloride transition state, our equations and Gajewski's (recalculated) equation indicate that both protic and aprotic solvents stabilize the transition state and lead to an increase in rate, but the Koppel–Palm equation suggests that there is no nucleophilic involvement of the solvent. Since both the Me4N+ ion and the Me4N+Cl− ion pair are stabilized by nucleophilic solvents, as seen in Table 7, the results of the Koppel–Palm equation appear to be incompatible with these solvent effects. It is possible that the differences between the outcomes of the various equations are due to our equation and Gajewski's equation using properties of the transition state as the dependent variable, whereas in the Koppel–Palm equation, rate constants, as log k, are used. We can check this by regressions of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k – Table 11.
k – Table 11.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k (tert-butyl chloride) using coefficients from Table 1
k (tert-butyl chloride) using coefficients from Table 1
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k k |
c | e | s | a | b | v | N | SD | R 2 | F | PRESS | Q 2 | PSD | Eqn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All solvents | −0.511 (0.278) | 1.653 (0.529) | 1.792 (0.202) | 1.081 (0.081) | 2.850 (0.204) | 1.202 (0.227) | 74 | 0.787 | 0.956 | 298 | 49.56 | 0.949 | 0.854 | (20) |
| Aprotic | 2.162 (1.415) | 1.407 (0.615) | 2.351 (0.193) | 0.560 (0.141) | 2.855 (0.328) | 0.555 (0.314) | 29 | 0.579 | 0.961 | 113 | 13.495 | 0.931 | 0.766 | (21) |
| Protic | −1.061 (0.204) | 1.026 (0.590) | 2.765 (0.428) | 1.341 (0.327) | 2.152 (0.350) | 1.023 (0.374) | 45 | 0.490 | 0.958 | 179 | 15.144 | 0.932 | 0.623 | (22) |
It is clear that our above conclusions about nucleophilic participation are not due to the use of transition state quantities as the dependent variable instead of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k. Eqn (20)–(22) show that solvent nucleophilic participation increases the rate, and eqns (10), (11) and (15) show that nucleophilic solvents stabilize the transition state. Our descriptors for the transition state itself show that the transition state exhibits considerable hydrogen bond acidity (electrophilicity) and considerable hydrogen bond basicity (nucleophilicity) in line with known properties of species such as Me4N+, Cl− and the Me4N+Cl− ion pair.
k. Eqn (20)–(22) show that solvent nucleophilic participation increases the rate, and eqns (10), (11) and (15) show that nucleophilic solvents stabilize the transition state. Our descriptors for the transition state itself show that the transition state exhibits considerable hydrogen bond acidity (electrophilicity) and considerable hydrogen bond basicity (nucleophilicity) in line with known properties of species such as Me4N+, Cl− and the Me4N+Cl− ion pair.
3.2 tert-Butyl bromide
We follow the same procedure as for tert-butyl chloride. Rate constants, as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k, that we used6,8,11,33,37 and those from this work are in Table 2. We calculated the transition state partition coefficients through eqn (4). For the partition of the tert-butyl bromide transition state we obtain eqn (23) and (24) in Table 12, using aprotic and protic solvents, separately. In eqn (23) the point for dioxane was left out and in eqn (24) that for acetic acid was left out. Eqn (23) is only just statistically viable, with 19 data points for five independent variables, but suggests that there is stabilization of the transition state by electrophilic and nucleophilic aprotic solvents. Eqn (24), however, is statistically very good. We can thus conclude that hydrogen bond acids (electrophilic solvents) stabilize the transition state, and that hydrogen bond bases (nucleophilic solvents) greatly stabilize the transition state.
k, that we used6,8,11,33,37 and those from this work are in Table 2. We calculated the transition state partition coefficients through eqn (4). For the partition of the tert-butyl bromide transition state we obtain eqn (23) and (24) in Table 12, using aprotic and protic solvents, separately. In eqn (23) the point for dioxane was left out and in eqn (24) that for acetic acid was left out. Eqn (23) is only just statistically viable, with 19 data points for five independent variables, but suggests that there is stabilization of the transition state by electrophilic and nucleophilic aprotic solvents. Eqn (24), however, is statistically very good. We can thus conclude that hydrogen bond acids (electrophilic solvents) stabilize the transition state, and that hydrogen bond bases (nucleophilic solvents) greatly stabilize the transition state.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps(Tr), in aprotic and protic solvents
Ps(Tr), in aprotic and protic solvents
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps(Tr) Ps(Tr) |
c | e | s | a | b | v | N | SD | R 2 | F | PRESS | Q 2 | PSD | Eqn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Aprotic | 3.583 (2.085) | 0.489 (0.747) | 2.510 (0.390) | 0.498 (0.116) | 2.242 (0.314) | 0.869 (0.357) | 19 | 0.469 | 0.961 | 95 | 8.039 | 0.890 | 0.786 | (23) |
| Protic | 0.199 (0.120) | 0.703 (0.377) | 2.600 (0.284) | 0.648 (0.253) | 1.718 (0.218) | 1.578 (0.233) | 41 | 0.287 | 0.935 | 101 | 5.910 | 0.867 | 0.410 | (24) |
We can obtain descriptors for the tert-butyl bromide transition state by using our simultaneous equation method, as before. We took E = 0.35 and V = 0.850, by comparison to values for tert-butyl bromide and for the other species in Table 7 and obtained a set of 17 simultaneous equations for aprotic solvents. These were solved by trial-and-error to give the transition state descriptors in Table 7 with an SD of only 0.285![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units. We left out dioxane solvent which was a considerable outlier. For protic solvents we had 39 simultaneous equations (leaving out tert-butanol and acetic acid) which we solved with SD = 0.350
log units. We left out dioxane solvent which was a considerable outlier. For protic solvents we had 39 simultaneous equations (leaving out tert-butanol and acetic acid) which we solved with SD = 0.350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units. The descriptors are in Table 7. In general, the transition state properties are in accord with the partition coefficient equations. The transition state is highly dipolar, is a very strong hydrogen bond base and a moderately strong hydrogen bond acid. It will therefore be stabilized by electrophilic and nucleophilic solvents.
log units. The descriptors are in Table 7. In general, the transition state properties are in accord with the partition coefficient equations. The transition state is highly dipolar, is a very strong hydrogen bond base and a moderately strong hydrogen bond acid. It will therefore be stabilized by electrophilic and nucleophilic solvents.
3.3 tert-Butyl iodide
We could access a reasonable number of rate constants for tert-butyl iodide,6,11,32–34 and from this work, as set out in Table 2. Equations for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PsTr(Aprotic) and log
PsTr(Aprotic) and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PsTr(Protic) are given as eqn (25) and (26) in Table 13.
PsTr(Protic) are given as eqn (25) and (26) in Table 13.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps(Tr), in aprotic and protic solvents
Ps(Tr), in aprotic and protic solvents
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ps(Tr) Ps(Tr) |
c | e | s | a | b | v | N | SD | R 2 | F | PRESS | Q 2 | PSD | Eqn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Aprotic | 3.468 (2.011) | 1.247 (0.667) | 2.414 (0.354) | 0.315 (0.095) | 2.043 (0.376) | 1.012 (0.334) | 23 | 0.488 | 0.940 | 53 | 7.321 | 0.872 | 0.654 | (25) |
| Protic | 0.070 (0.099) | 1.835 (0.441) | 3.154 (0.324) | 0.099 (0.277) | 1.972 (0.338) | 2.071 (0.375) | 39 | 0.237 | 0.906 | 74 | 3.812 | 0.832 | 0.340 | (26) |
We were also able to use our simultaneous equation method to obtain descriptors for the tert-butyl iodide transition state. By comparison to the various species in Table 7, we took E = 0.65 and V = 0.9400. Then for protic solvents we had a set of 36 equations (leaving out the equations for solvents tert-butyl alcohol and 2-methoxyethanol) which we solved to yield the descriptors in Table 7, with SD = 0.230![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units. For aprotic solvents we had 21 solvents that we solved with SD = 0.378 log units; the descriptors are also in Table 7. The transition state is thus stabilized by electrophilic solvents, although not to the same extent as are the tert-butyl chloride and tert-butyl bromide transition states. The transition state A-values are quite small (0.17, 0.35) which indicates that the transition state is weakly stabilized by solvents that are hydrogen bond bases (nucleophiles).
log units. For aprotic solvents we had 21 solvents that we solved with SD = 0.378 log units; the descriptors are also in Table 7. The transition state is thus stabilized by electrophilic solvents, although not to the same extent as are the tert-butyl chloride and tert-butyl bromide transition states. The transition state A-values are quite small (0.17, 0.35) which indicates that the transition state is weakly stabilized by solvents that are hydrogen bond bases (nucleophiles).
4 Conclusions
The descriptors for the three transition states are quite in line with descriptors for various other species given in Table 7. The three transition states are all moderately strong hydrogen bond acids, but not quite as strong as the corresponding ion pairs Me4N+X−. Thus, the transition states are stabilized by nucleophilic solvents, just as are the ion pairs, with the stabilization decreasing along the series Cl > Br > I. Since the ground states are unaffected by solvent nucleophilicity, Table 3, it follows that the reaction rates will be increased by nucleophilic solvents. If solvent nucleophilicity is unimportant,4–9 then it follows that the transition states, with a substantial charge separation, must be unaffected by solvent nucleophilicity,4–9 whereas the ion pairs are greatly stabilized by nucleophilic solvents – a conclusion that makes little sense. Our own conclusion is unambiguous. The three transition states are stabilized by nucleophilic solvents that consequently increase the rates of reaction.The effect of electrophilic solvents is not in contention. They will greatly increase the rate of reaction through considerable stabilization of the transition states. The B-values of the transition states are all very large, just as are the B-values of the ion pairs. All these species are stabilized through interaction of the electrophilic solvents with the leaving halide in the transition states and the formed halide ion in the ion pairs.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
F. Martins, R. Elvas-Leitão and L. Moreira acknowledge support from Fundação para a Ciência e a Tecnologia, Portugal (UIDB/00100/2020).References
- E. D. Hughes, Mechanism of substitution at a saturated carbon atom. Part V. Hydrolysis of tert-butyl chloride, J. Chem. Soc., 1935, 255–257 RSC.
- J. J. Gajewski, Is the tert-butyl chloride solvolysis the most misunderstood reaction in organic chemistry? Evidence against nucleophilic solvent participation in the tert-butyl chloride transition state and for increased hydrogen bond donation to the 1-adamantyl chloride solvolysis transition state, J. Am. Chem. Soc., 2001, 123, 10877–10883 CrossRef CAS.
- J. J. Gajewski, A semi-theoretical multiparameter approach to correlate solvent effects on reactions and equilibria, J. Org. Chem., 1992, 57, 5500–5506 CrossRef CAS.
- G. F. Dvorko, V. V. Zaliznyi and N. E. Ponomarev, Kinetics and mechanism of monomolecular heterolysis of commercial organohalogen compounds, XXIX. Solvent effects on the activation parameters of heterolysis of tert-butyl chloride, Russ. J. Gen. Chem., 2002, 72, 1414–1438 CrossRef CAS.
- G. V. Dvorko, V. V. Zaliznyi and N. E. Ponomarev, Kinetics and mechanism of monomolecular heterolysis of commercial organohalogen compounds. XXXI. Correlation analysis of solvation effects in heterolysis of tert-butyl chloride, Russ. J. Gen. Chem., 2002, 72, 1549–1555 CrossRef CAS.
- G. V. Dvorko, E. A. Ponomareva, N. E. Ponomarev, V. V. Zaliznyi and L. V. Koshchii, Nature of solvation effects and mechanism of heterolysis of tert-alkyl halides, Russ. J. Gen. Chem., 2007, 77, 1535–1558 CrossRef CAS.
- G. V. Dvorko and E. A. Ponomareva, Effect of nucleophilic solvent on the kinetic parameters of the reactions of unimolecular heterolysis. Mechanism of the covalent bond heterolysis, Russ. J. Gen. Chem., 2010, 80, 1615–1625 CrossRef CAS.
- N. E. Ponomarev, V. V. Zaliznyi and G. F. Dvorko, Kinetics and mechanism of monomolecular heterolysis of commercial organohalogen compounds, XXXVIII. Correlation analysis of solvent effects on the activation parameters of heterolysis of t-BuBr and t-BuI., Russ. J. Gen. Chem., 2004, 74, 1368–1375 CrossRef CAS.
- I. A. Koppel and V. A. Palm, The influence of solvent on organic reactivity, in Advances in Linear Free Energy Relationships, ed. N. B. Chapman and J. Shorter, Plenum Press, 1972 Search PubMed.
- I. M. Serebryakov, On the “Negative effect of nucleophilic solvation” in homomolecular heterolysis., Russ. J. Gen. Chem., 2013, 83, 32–37 CrossRef CAS.
- M. H. Abraham, R. W. Taft and M. J. Kamlet, Linear solvation energy relationships. 15. Heterolytic decomposition of the tert-butyl halides, J. Org. Chem., 1981, 46, 3053–3056 CrossRef CAS.
- M. H. Abraham, R. M. Doherty, M. J. Kamlet, J. M. Harris and R. W. Taft, Linear solvation energy relationships. Part 37. An analysis of contributions of dipolarity-polarizability, nucleophilic assistance, electrophilic assistance, and cavity terms to solvent effects on t-butyl halide solvolysis rates, J. Chem. Soc., Perkin Trans. 2, 1987, 913–920 RSC.
- M. H. Abraham, R. M. Doherty, M. J. Kamlet, J. M. Harris and R. W. Taft, Linear solvation energy relationships. Part 38. An analysis of the use of solvent parameters in the correlation of rate constants with special reference to the solvolysis of t-butyl chloride, J. Chem. Soc., Perkin Trans 2, 1987, 1097–1101 RSC.
- D. Farcasiu, J. Jahme and C. Ruchardt, Relative reactivity of bridgehead adamantly and homoadamantyl substrates from solvolyses with heptafluorobutyrate as a highly reactive carboxylate leaving group. Absence of SN2 character of solvolysis of tert-butyl derivatives, J. Am. Chem. Soc., 1985, 107, 5717–5722 CrossRef CAS.
- A. J. Parker, U. Mayer, R. Schmid and V. Gutmann, Correlation of solvent effects on rates of solvolysis and SN2 reactions, J. Org. Chem., 1978, 43, 1843–1854 CrossRef CAS.
- T. W. Bentley and G. E. Carter, The SN2-SN1 spectrum. 4. The SN2 intermediate mechanism for solvolysis of tert-butyl chloride: a revised Y scale of solvent ionizing power based on solvolysis of 1-adamantyl chloride, J. Am. Chem. Soc., 1982, 104, 5741–5747 CrossRef CAS.
- C. G. Swain, M. S. Swain, A. L. Powell and S. Alunni, Solvent effect on chemical reactivity. Evaluation of anion and cation solvation components, J. Am. Chem. Soc., 1983, 105, 502–513 CrossRef CAS.
- K. Takeuchi, M. Takasuka, E. Shiba, T. Kinoshita, T. Okazaki, J.-L. M. Abboud, R. Notario and O. Castano, Experimental and theoretical evaluation of energetics for nucleophilic solvent participation in the solvolysis of tertiary alkyl chlorides on the basis of gas phase bridgehead carbocation stabilities, J. Am. Chem. Soc., 2000, 122, 7351–7357 CrossRef CAS.
- M. H. Abraham, Scales of hydrogen bonding: their construction and application to physicochemical and biochemical processes, Chem. Soc. Rev., 1993, 22, 73–83 RSC.
- M. H. Abraham, A. Ibrahim and A. M. Zissimos, The determination of sets of solute descriptors from chromatographic measurements, J. Chromatogr. A, 2004, 1037, 29–47 CrossRef CAS.
- M. H. Abraham, R. E. Smith, R. Luchtefeld, A. J. Boorem, R. Luo and W. E. Acree Jr., Prediction of solubility of drugs and other compounds in organic solvents, J. Pharm. Sci., 2010, 99, 1500–1515 CrossRef CAS.
- M. H. Abraham, W. E. Acree Jr., D. Hoekman, A. J. Leo and M. L. A. Medlin, New method for the determination of Henry's Law constants air-water-partition coefficients, Fluid Phase Equilib., 2019, 502, 112300 CrossRef CAS.
- M. H. Abraham and W. E. Acree Jr., Equations for the transfer of neutral molecules and ionic species from water to organic phases, J. Org. Chem., 2010, 75, 1006–1015 CrossRef CAS.
- M. H. Abraham and W. E. Acree Jr., Descriptors for ions and ion-pairs for use in linear free energy relationships, J. Chromatogr. A, 2016, 1430, 2–14 CrossRef CAS.
- M. H. Abraham and W. E. Acree Jr., Analysis of the solubility of betaine; calculation of descriptors and physicochemical properties, Fluid Phase Equilib., 2015, 387, 1–4 CrossRef CAS.
- M. H. Abraham and W. E. Acree Jr., Solvation descriptors for zwitterionic α-aminoacids, estimation of their water–solvent partition coefficients, solubilities and hydrogen-bond acidity and hydrogen-bond basicity, ACS Omega, 2019, 4, 2883–2892 CrossRef CAS.
- L. Moreira, F. Martins and R. E. Leitão, A step by step build-up of an excel spreadsheet: estimation of rate constants through Solver, determination of associated errors and choice of curve's extent, J. Chem. Educ., 2006, 83, 1879–1883 CrossRef CAS.
- L. Moreira, M. Reis, R. Elvas-Leitao, M. H. Abraham and F. Martins, Quantifying solvent effects through QSPR: a new look over different model equations, J. Mol. Liq., 2019, 291, 111244 CrossRef CAS.
- M. H. Abraham, Substitution at saturated carbon. Part XIV. Solvent effects on the free energies of ions, ion-pairs, non-electrolytes and transition states in some SN and SE reactions., J. Chem. Soc., Perkin Trans. 2, 1972, 1343–1357 RSC.
- M. H. Abraham, P. L. Grellier, A. Nasahzadeh and R. A. C. Walker, Substitution at saturated carbon. Part 26. A complete analysis of solvent effects on initial states and transition states for the solvolysis of the t-butyl halides in terms of G, H, and S using the unified method, J. Chem. Soc., Perkin Trans. 2, 1988, 1717–1724 RSC.
- R. M. C. Gonçalves, A. M. N. Simões, L. M. P. C. Albuquerque and E. A. Macedo, Study of initial- and transition-state solvation in the solvolysis of tert-butyl halides in alcohols from infinite dilution activity coefficients, J. Phys. Org. Chem., 1993, 6, 133–138 CrossRef.
- R. M. C. Gonçalves, A. M. N. Simões and L. M. P. C. Albuquerque, Quantitative formulation of reactivity in terms of solvent and substrate properties. Solvolysis of tert-butyl halides in hydroxylic solvents, J. Chem. Soc., Perkin Trans. 2, 1991, 825–828 RSC.
- E. A. Moelwyn-Hughes, The kinetics of the solvolysis of t-butyl chloride, bromide and iodide in methanol–water solutions, J. Chem. Soc., 1962, 4301–4307 RSC.
- L. M. P. C. Albuquerque, M. L. C. Moita and R. M. C. Gonçalves, Kinetics and mechanism of solvolysis of 3-chloro-3-ethylpentane in alcohols as solvents. Application of multiparameter equations and factor analysis to the solvolytic reactions of tert-alkyl halides, J. Phys. Org. Chem., 2001, 14, 139–145 CrossRef CAS.
- A. H. Fainberg and S. Winstein, Correlation of solvolysis rates. III. t-Butyl chloride in a wide range of solvent mixtures, J. Am. Chem. Soc., 1956, 78, 2770–2777 CrossRef CAS.
- M. H. Abraham and R. J. Abraham, Application of reaction field theory to the calculation of solvent effects on the t-butyl chloride solvolysis and the Me4N+ Cl− ion pair, J. Chem. Soc., Perkin Trans. 2, 1974, 47–52 RSC.
- E. Grunwald and S. Winstein, The correlation of solvolysis rates, J. Am. Chem. Soc., 1948, 70, 846–854 CrossRef CAS.
- E. D. Clarke and L. Mallon, The Determination of Abraham descriptors and their Application to Crop Protection Research”, in Modern Methods in Crop Protection Research, ed. P. Jeschke, W. Krämer, U. Schirmer and M. Witschel, Wiley-VCH Verlag GmbH & Co., 2012 Search PubMed.
- R. W. Taft, J.-L. M. Abboud, M. J. Kamlet and M. H. Abraham, Linear solvation energy relations, J. Solu. Chem., 1985, 14, 153–186 CrossRef CAS.
- J. Catalan and C. Reichardt, Comments on “Quantifying solvent effects through QSPR: a new look over different model equations”, J. Mol. Liq., 2020, 298, 111922 CrossRef CAS.
- J. Catalan, Towards a generalized treatment of the solvent effect based on four empirical scales: dipolarity SdP, a new scale, polarizability SP, acidity SA and basicity SB of the medium, J. Phys. Chem. B, 2009, 113, 5951–5960 CrossRef CAS.
- Y. Marcus, The Properties of Solvents, John Wiley & Sons, Chichester, 1998 Search PubMed.
Footnote |
| † In memoriam of Professor Michael H. Abraham, who passed away on January 19th, 2021, during the revision of this manuscript. |
| This journal is © the Owner Societies 2021 |