Magnetic deflection of neutral sodium-doped ammonia clusters

Abstract

We describe the setup and the performance of a new pulsed Stern–Gerlach deflector and present results for small sodium-doped ammonia clusters Na(NH₃)_n (n = 1–4) in a molecular beam. NaNH₃ shows the expected deflection of a spin ½ system, while all lager clusters show much smaller deflections. Experimental deflection ratios are compared with the values calculated from molecular dynamics simulations. The comparison reveals that intracluster spin relaxation in NaNH₃ takes place on a time scale significantly longer than 200 μs. Assuming that intracluster relaxation is the cause of the reduced deflection, relaxation times seem to be on the order of 200 μs for all larger clusters Na(NH₃)_n (n = 2–4). Our work is a first attempt to understand the magnetic properties of isolated, weakly-bound clusters with relevance to the variety of diamagnetic and paramagnetic species expected in solvated electron systems.

---

1. Introduction

The discovery of concentration-dependent colours of alkali metal–ammonia solutions in the early 19th century by Sir Humphry Davy and later reported by W. Weyl¹ sparked a large series of experimental and theoretical works on excess electrons in alkali metal ammonia solutions² (and references therein). In dilute blue coloured solutions, a variety of diamagnetic and paramagnetic species may exist (solvated electrons, electron–cation pairs, solvated metal atoms and bipolarons).^2–5 In bulk solutions the paramagnetic species have been investigated via electron spin resonance (ESR)⁶ and nuclear magnetic resonance (NMR) spectroscopy⁷ (and references therein). Neutral sodium doped ammonia clusters Na(NH₃)_n have previously served as model systems to study the electronic properties of the ‘ammoniated’ electron via photoion spectroscopy, photoelectron spectroscopy and ab initio methods^8–20 (and references therein). Photoion spectroscopy has revealed that the ion appearance energy of Na(NH₃)_n decreases systematically with increasing number of solvent molecules¹⁵ (and references therein). Various effects such as increasing delocalization of the 3s electron with increasing cluster size, surface and bulk localization of the electron, closing of solvation shells and cluster symmetry can contribute to the decrease in the ion appearance energy and the ionization (binding) energy. From n = 1 to 4, for example, a substantial decrease of ∼1.4 eV was observed. A similar trend for the ionization (binding) energy was later found in photoelectron studies and in high-level ab initio calculations.^17–19 Experiments and calculations for the smaller clusters are consistent with surface electrons (compared to internally solvated electrons), which essentially can be described as an unpaired electron of Na that is perturbed by the solvent molecules.^17–19 These studies also reveal many structural isomers for a given cluster size. An intriguing result of the high-level ab initio study by Gunina and Krylov¹⁹ concerns the electronic properties. The study found that the hydrogen-bond network of the NH₃ solvent molecules contributes significantly to the overall electronic properties, such as the dipole moment. Angle-resolved photoelectron spectroscopy provides experimental access to the photoelectron anisotropy (photoelectron anisotropy parameter β) and thus to the orbital character of the unpaired electron. Experimental and calculation results^17,18 show that the lowest electronic states of small clusters have high s-character and thus large β values. The β values decrease with increasing cluster size, except for highly symmetric clusters (e.g. n = 4; magic number for the photoelectron anisotropy). Generally, the decrease in β is accompanied by an increase in the electric dipole moment. Effective polarizabilities of Na(NH₃)_n were determined from electric deflection studies.²¹ Yet, detailed knowledge of the magnetic properties of the solvated electron in free clusters is still not established. To the best of our knowledge, we present the first study on the magnetic properties of small (n = 1–4) sodium doped ammonia clusters Na(NH₃)_n investigated via Stern–Gerlach deflection.

The original Stern–Gerlach experiment was designed to determine the magnetic moment of isolated silver atoms;²² later various other isolated atoms,²³ several molecules with a nonzero spin S^24–34 and metallic and bi-metallic clusters^35–47 were investigated with Stern–Gerlach setups (except for ref. 46). For molecular systems and metal clusters, additional degrees of freedom like vibrations and rotations are accessible compared with atomic systems. It has been shown that the overall molecular rotations can induce Zeeman-like sublevels.^27,28 Several groups^48–50 gave theoretical explanations of why transitions between Zeeman-like sublevels can occur and how Stern–Gerlach deflection experiments could be influenced by so-called intramolecular spin relaxation (ISR) and its intracluster analog. Amirav and Navon provided experimental evidence of ISR effects in isolated molecules.^25,26 In their deflection studies on the molecular beams of paramagnetic molecules and stable organic radicals, they observed smaller-than predicted deflection magnitudes and incomplete spin refocusing involving two Stern–Gerlach magnets. These two experimental results were interpreted as ISR processes occurring on faster time scales than the interaction time with the magnetic field. In one case, however, this interpretation was disputed.²⁸ Later, various groups investigated the magnetic properties of free Fe_m, Co_m, and Ni_m clusters (m = 10–1000) via Stern–Gerlach deflection.^36,38,41,44 Hereby, one-sided deflection toward high field instead of symmetric magnetic deflection was observed. This asymmetric deflection behaviour was interpreted as being due to rapid ISR⁴⁹ occurring among the perturbed, spin-rotation induced Zeeman sublevels. Studies on one-dimensional metal–organic sandwich clusters^51–54 show similar one-sided deflection in the high-field direction, indicating that intracluster spin relaxation occurs within the complexes as they traverse the magnetic field. In recent studies, Schäfer and co-workers investigated spin relaxation processes via spin refocusing of paramagnetic superatoms with two Stern–Gerlach magnets.^55,56

Here, we present a new setup for a pulsed Stern–Gerlach experiment, characterize its performance and study the magnetic properties of neutral sodium doped ammonia clusters, which can be seen as solvated electron precursors. An overview of previous Stern–Gerlach setups is provided in ref. 57 along with a description of a new strong permanent magnet gradient deflector and its comparison with commonly employed electromagnets. Similar to the experiments of various groups highlighted above, we investigate the deflection magnitude in relation to a predicted (from a molecular dynamics (MD) approach) deflection magnitude. With this we aim to probe the cluster size dependent magnetic properties of neutral Na(NH₃)_n (n = 1–4) clusters. Studying the size dependent magnetic properties of sodium doped ammonia clusters will lead to a better understanding of the involved paramagnetic species in bulk sodium ammonia solutions. In the present study, we focus on the interpretation of cluster size dependent intracluster relaxation times.

2. Methods

2.1. Experimental setup

Fig. 1 shows the experimental setup for the current study of the size-dependent magnetic properties of neutral sodium doped ammonia clusters Na(NH₃)_n (n = 1–4). It consists of four chambers (A–D) which are separated by skimmers, in order to produce a well-defined molecular beam along with differential pumping (Fig. 1a). For the detection of ion kinetic energies, we use velocity map imaging (VMI).⁵⁸ Mass spectra were produced by collecting time-of-flight (TOF) signals using the same ion optics as that in the case of VMI.

Fig. 1 (a) Sketch of the experimental setup consisting of the source chamber (A), the Na-oven chamber (B), the deflection chamber (C) and the ionization/detection chamber (D). See text for details. (b) Side view with dimensions along the molecular beam propagation axis. (c) Side view of the deflector consisting of three electromagnets with relevant dimensions and the axis system (right). Shaded areas correspond to epoxy parts. (d) Cross section of the deflector flight channel and calculated z-component of the magnetic field gradient. A detailed description of the mechanical and electronic design is given in Sections S1 and S2 of the ESI.†

2.1.1 Cluster formation and sodium doping process. Ammonia clusters are formed in vacuum in the source chamber (A) by continuous neat supersonic expansion (stagnation pressure: ∼6 bar) through a temperature controlled (T_nozzle = 115 °C) nozzle (nominal orifice diameter: 35 μm). During operation, the chamber pressure is typically maintained below ∼5 × 10⁻⁴ mbar. After passing through the source chamber, the cluster beam enters the Na-oven chamber (B) through a 2 mm diameter skimmer. Sodium doped ammonia clusters are formed via collisions with Na atoms inside the oven.^59–61 The Na vapour pressure is controlled by the oven temperature (T_oven = 195 °C). A typical working pressure of ∼4 × 10⁻⁶ mbar is maintained in the oven chamber.

2.1.2 Pulsed Stern–Gerlach deflection. After the doping process, the cluster beam enters the deflection chamber (C) through a 1.5 mm diameter skimmer. The dimensions, parallel to the molecular beam propagation (y-axis), of the deflection chamber are shown in Fig. 1b and c. Furthermore, the cross section of the flight channel and the magnetic field gradient in the z-direction are displayed in Fig. 1d. The magnetic force in the z-direction causes deflection of paramagnetic clusters. The diverging paramagnetic cluster beam is separated from the non-diverging diamagnetic cluster beam by a 2 mm diameter detection skimmer, placed 21.5 cm after the exit of the deflector. The deflector is operated at repetition rates between 1 and 5 Hz and typical chamber pressures of ∼1 × 10⁻⁷ mbar. The mechanical and electronic design of the deflector are discussed in detail in Sections S1 and S2 of the ESI.† The performance of the deflector was tested for an effusive Na atom beam (Section S3, ESI†).

2.1.3 Ionization by UV laser light and VMI detection. Once the clusters traverse the detection skimmer and reach the centre of the extraction zone, the clusters are ionized and then detected. Single photon ionization of sodium doped ammonia clusters was achieved using light from a pulsed (20 Hz) nanosecond (∼7 ns) 266 nm (4.66 eV) Nd:YAG laser (Quantel Ultra). For single photon ionization of bare sodium atoms, pulsed (20 Hz) nanosecond (∼7 ns) 212 nm (5.85 eV) laser light generated by tripling the output of a dye laser was used.⁶² The propagation direction and the polarization vector lie in a plane parallel to the ion detector. Two-dimensional (2D) VMI experiments on the photoelectrons/ions formed upon VUV ionization of sodium doped ammonia clusters were carried out with perpendicular extraction (see Fig. 1a). In this configuration, the molecular beam axis and the TOF axis are perpendicular. This arrangement allows the determination of velocity distributions along the molecular beam propagation axis, which is discussed in detail in Section 2.2.

Upon ionization, the ions are accelerated by a Wiley-McLaren type extractor optimized for either TOF conditions or VMI conditions (0 to ±15 kV). The ionization region is located between the repeller and the extractor plate. The extraction region and a 20 cm field-free drift region are shielded by two concentric mu-metal cylinders. The position sensitive detector is composed of a pair of 40 mm diameter microchannel plates (MCPs) in a chevron stack which are coupled to a phosphor screen (Photonis USA, Inc.; APD), followed by a charge coupled device (CCD) camera. The front of the MCP assembly is kept at ground potential when the voltage on the back plate is used to ‘gate’ the detector. A high voltage switch (Behlke) is used to vary the MCP bias voltage by 500 V so that the gain is only high when the ions of interest are impinging on the detector. The luminescence of the screen is recorded by the CCD camera. Individual frames (12 bit grayscale image, 1/3 inch sensor, 1024 × 768 pixel) are taken for each laser shot, summed up in real time using NuAcq software⁶³ and saved to a computer connected to the CCD camera.

2.1.4 Timing sequence of a deflection measurement. A deflection measurement consists of a series of TOF measurements. For each TOF mass spectrum the time delay between the deflector timing t_d and the timing of the ionizing laser t_L is varied. Throughout the presented work t_d was varied relative to t_L. This is shown in the upper sketch of Fig. 2.

Fig. 2 Sketch of the timing sequence of a deflection measurement. The relative timing between deflection (t_d) and ionization (t_L) is varied for various TOF measurements (upper sketch). The deflector consists of three individual coils, which can be operated with different offset timings (t₁, t₂, t₃) relative to t_d. The lower sketch shows the experimentally measured magnetic field pulses (I_d = 300 A) for each coil timing, t₁, t₂, and t₃.

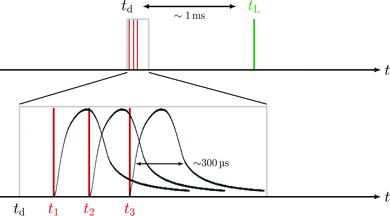
The lower sketch of Fig. 2 shows that each individual coil can be operated with timings t₁, t₂, and t₃. Throughout one deflection measurement, these coil timings are constant relative to the absolute deflector timing t_d. The relative integrated TOF mass signal θ_rel is defined as the ratio of the integrated TOF mass signal with the deflector switched on and the integrated TOF mass signal with the deflector switched off.

θ_rel for various t_d allows us to analyse the deflection ratio γ_d for different cluster sizes.The optimal timings t₁, t₂, and t₃ (relative to t_d) were determined empirically, supported by global optimization of a simplified model. This model returns an estimate for γ_d as a function of t₁, t₂, and t₃. The computational cost needed to achieve sufficient statistics using a 3D MD simulation (as used for verification, vide infra) would have been too high to be executing fast global optimization on an office computer. Therefore, we employed a 1D model where only the position along the central axis of the molecular beam (y coordinates) is considered. In space, this model uses the y coordinates corresponding to the dimensions of the electromagnets and ionization region. In time, the duration of a square wave pulse (starting at each trigger time) and the timing of the ionization laser pulse act as fixed parameters. The final parameter is a threshold value, which is used to decide if a particle was deflected or not. A particle is considered to be deflected if its time spent in the magnetic field is above this threshold. This value was tuned to reproduce the deflection ratios observed in the actual experiment. To fully sample the parameter space at a low computational cost, a method inspired by ray tracing was implemented. For this, the model was represented in a 2D space-time, which is on a flat surface defined by (y, t) coordinates. On this surface, the magnetic pulse appears as a box (magnet length × on-time) and the ionization volume can be represented by a 1D pixel array located at the ionization time. Cluster trajectories travel as straight lines over this plane, with a slope depending on their velocity. Each ray will intersect the boxes as a function of its slope and ionization pixel, and these intersections reflect the time spent in the magnetic field. If the sum of the temporal cutting ranges through the boxes is above the threshold parameter, it is deflected. Finally, the results are scaled with a simulated or measured velocity distribution. This converts the uniform set of trajectories into realistic intensities and facilitates the computation of γ_d using eqn (2). The actual implementation of this model was done using MATLAB. Processing all trajectories in collective, fixed-size arrays, using a model that exclusively relies on elementary single-cycle operations, the calculation of γ_d(t₁, t₂, t₃) is sufficiently fast to be utilized within a global optimization algorithm. Relying on the built-in algorithms of MATLAB, a scatter-search mechanism was used together with a sequential quadratic programming method for the refinement stage. Two classes of solutions were found. For low fields (requiring high threshold values), the magnets are triggered sequentially, to deflect the dominant part of the velocity distribution in a joint effort. For high fields (low threshold values), the central magnet is triggered first to also deflect slow clusters, even before those fast clusters that reach the ionization volume at the same time entered the first magnet.

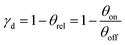2.2. Measured velocity distributions of Na(NH₃)_n

Since the deflector is operated in a pulsed manner, the coil timings t_i (i = 1, 2, 3) have to be synchronized with t_L. The time delay between deflection and ionization (Fig. 2) depends on the cluster size specific velocity distributions. The knowledge of individual cluster beam velocity distributions is thus crucial to optimize the deflector timings for high deflection ratios. To determine cluster velocity distributions, photoions were extracted perpendicular to the molecular beam propagation axis (Fig. 1a). The extraction field was set to optimized VMI conditions. Time of flight based mass-gating was used to record the size-selected photoion images of Na(NH₃)_n (n = 1–4) shown in Fig. 3a. The velocities of the neutral clusters in the molecular beam correspond to a displacement of the photoions in the detector plane. The cluster-resolved velocities can be determined by the displacement of the image centre (white cross in Fig. 3a). The velocity v is calculated using the equation:

v = (2·C·V_R·r²/m)^1/2 (3)

where V_R is the voltage on the repeller, r is the radial position in the image, m is the cluster mass and C is a setup dependent calibration constant. The velocity distributions are plotted as coloured lines in Fig. 3b. The velocity distributions were retrieved by averaging over four different extraction settings (V_R = 10 kV, 7 kV, 5 kV and 3 kV). This is feasible because the cluster velocity distributions in the molecular beam do not depend on the extraction settings (V_R and MCP gating times). Furthermore, a calculated 1D Maxwell–Boltzmann velocity distribution for an effusive Na-beam at 265 °C convoluted with an exponential transmission function (see Section S3, ESI†) is shown as a black dashed line in Fig. 3b. The effusive Na-atoms have a centre velocity of 1000 ms⁻¹ and a full-width at half-maximum (FWHM) of 870 ms⁻¹. In comparison, Na(NH₃)₄ has a centre velocity of 1070 ms⁻¹ and a FWHM of 350 ms⁻¹. The significant difference in beam velocities (magnitude and width) arises from the differences in the generation of effusive and molecular beams.

Fig. 3 (a) Na(NH₃)_n (n = 1–4) ion images measured in perpendicular extraction at V_R = 7 kV. (b) Experimental Na(NH₃)_n velocity distributions retrieved from ion images. The calculated velocity distribution for an effusive Na-beam at 265 °C is shown as a dashed line (see the ESI,† Section S3). Its distribution function is given by the convolution of a 1D Maxwell–Boltzmann distribution with an exponential transmission function.

Comparing the velocity distributions of doped ammonia clusters, two effects can be seen with increasing cluster size. Firstly, the centre velocity v_c shifts to slightly higher velocities, and secondly the FWHM decreases (Table 1). These differences can be attributed to collisions occurring between the bare clusters and sodium atoms inside the oven during the doping process. Due to momentum conservation, lighter particles deviate further from their initial molecular beam velocity than heavier particles. This explains why the velocity profiles are essentially cluster size independent on the high velocity side of the distributions (Fig. 3b). This part of the velocity distributions reflects collisions between Na and clusters with little momentum transfer, thus largely retaining the initial neat NH₃ supersonic velocity distribution.

Table 1 Centre velocities v_c and FWHM of the measured velocity distributions of Na(NH₃)_n

Cluster	v c/ms^−1	FWHM/ms^−1
NaNH3	970	540
Na(NH3)2	1000	445
Na(NH3)3	1020	420
Na(NH3)4	1070	350

---

2.3. Modelling of the deflection

To verify our experimental results, we chose a MD approach to simulate the cluster trajectories from the entry of the deflection chamber until ionization. For this approach, firstly, a detailed model of the cluster beam is essential. Secondly, a detailed description of the inhomogeneous magnetic field is needed. In our model we describe the cluster beam by the initial velocity and mass of each particle. The initial velocities in the y-direction are randomly sampled from the cluster size specific molecular beam velocity distribution, which is discussed in detail in Section 2.2. The initial velocities in the x- and z-directions are calculated using their beam divergence angle and the velocity in the y-direction. The initial particle coordinates are defined by the position and diameter of the entrance skimmer (see Fig. 1b). Hereby the skimmer position defines the y-coordinate and the diameter defines the possible x, z-coordinates of the Gaussian beam profile. By sampling enough particles (>10⁵) a nearly continuous distribution of initial properties is achieved. The experimental dimensions described in Section 2.1 are accounted for by our MD approach.

The force caused by the inhomogeneous potential in the flight channel is defined as the negative gradient of the Zeeman potential (neglecting the contribution of the electron orbital angular momentum L = 0).

where μ_B is the Bohr magneton, g_s the gyromagnetic ratio of the total spin angular momentum S⃑, B⃑ the magnetic field and F⃑ is the force. The force field for the MD simulations is defined by the magnetic field gradients, obtained from a COMSOL simulation assuming a 2D model of the deflector cross section (see Fig. 1d) and a DC current of 1000 A. As in the experiment the force field is only applied during the on-time of the magnetic field pulses. For an accurate description of the magnetic pulse profiles, we used a Hall probe for the time-resolved measurement of the pulses inside the deflector flight channel. These magnetic pulse profiles (see Fig. 2) were measured for various peak currents and used as input for our MD simulations. Current specific scaling factors are determined in relation to the integrated magnetic field pulse profile at 1000 A. An additional magnetic field measurement showed that the induction at the end of each metal bridge is approximately 20% of the peak pulse inside the deflector flight channel. We therefore define the magnetic field magnitude in the epoxy layers to be 20% of the current specific scaling factor of the electromagnetic coils. The forces applied during the pulse are calculated using eqn (5). As in the experiment, the three electromagnets can be pulsed with individual timings t₁, t₂, and t₃. Due to the experimental dimensions, not all particle trajectories will reach the ionization region, and consequently we introduce the following conditions to simulate the particle trajectories. Particles that collide with the deflector walls are considered ‘lost’. Only particles that are transmitted through the detection skimmer can be detected. Only particles that are in the ionization region at time t_L can be detected.

As an output, the MD simulation creates x,z-coordinates for each trajectory in the detection skimmer plane. These coordinates resemble the molecular beam cross section. In Fig. 4, the visualization of such an output (10⁶ trajectories) is shown for three spin states −1/2, 0 and +1/2 for particles with the same mass as NaNH₃. The magnetic field gradient in the z-direction deflects paramagnetic particles in either the positive or the negative z-direction depending on m_S. In the centre of the flight channel (x = 0), the field gradient along the z-axis is close to constant. The gradient in the x-direction causes one spin component to diverge (see Fig. 4a), while it focuses the other spin component (see Fig. 4c). The relative signal passing through the detection skimmer, shown as a white circle in Fig. 4, and reaching the ionization region at the same time, is calculated using the following equation:

where θ_mS=+1/2, θ_mS=−1/2 and θ_S=0, respectively represent the number of trajectories of each individual spin state passing through the detection skimmer, reaching the ionization region at t_L and subsequently being ionized. Simulating trajectories without a magnetic field is equivalent to simulating trajectories for S = 0. Therefore, θ_S=0 represents the ion signal when the deflector is switched off. By varying t_d with respect to t_L, relative signals can be evaluated for each time delay. This procedure generates a relative signal dip, which is compared to the experimental data.

Fig. 4 MD simulations of a particle with the same mass as NaNH₃ for spin states (a) m_S = –1/2, (b) S = 0 and (c) m_S = +1/2. 10⁶ trajectories were calculated for all simulations. The white lines indicate the cross section of the flight channel, while the white dotted lines represent the borders of the epoxy layers. The white circle represents the detection skimmer.

In a further step, we simulated the trajectories reaching the ionization region. Trajectories that pass through the detection skimmer and overlap with the Gaussian laser beam profile of 4.8 mm FWHM are treated as ionized. For those ionized particles, an output file is created. It contains the spin state, ionization coordinates and velocity vectors. In addition, the output files are translated into input files for SIMION. SIMION® 8.0⁶⁴ is used to simulate the trajectories of the generated photoions in the electrostatic extraction field and at which positions they impinge on the 2D plane of the ion detector. With this combination of simulations, we are able to simulate the full trajectories from neutral clusters entering the deflector to photoions colliding with the position-sensitive detector (see Section 3.1).

3. Results

3.1. Coil contributions to the deflection of NaNH₃

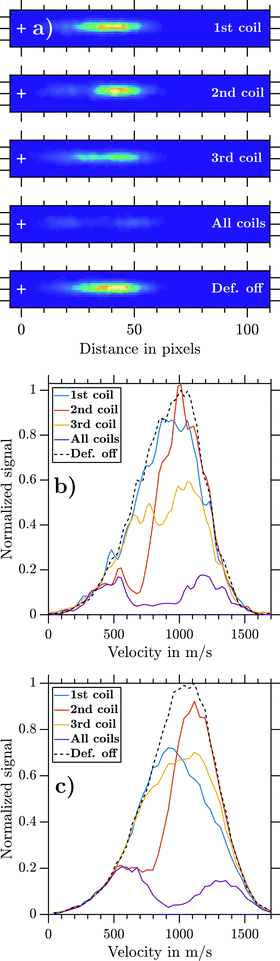
Fig. 5 visualizes the influence of the individual coils on the deflection for the example of NaNH₃. For that purpose, mass-gated NaNH₃ photoions were extracted perpendicular to the molecular beam propagation axis and detected via VMI while operating the deflector at I_d = 300 A (Fig. 5a). For the experiment where all coils (‘all coils’) were used, the electromagnets were fired in an optimized t₂ < t₁ < t₃ sequence. Hereby, t_d was set to a timing where the highest possible deflection ratio is achievable. By operating each electromagnet separately (1st, 2nd, and 3rd coils), we aim to understand the individual deflection contribution. A further ion image was recorded when the magnetic field was turned off. These recorded ion images are shown in Fig. 5a on the same colour code intensity scale. Operating the deflector clearly reduces the ions impinging the 2D detector plane. Each coil acts on a subset of the cluster distribution and all coils acting together cause a decreased ion signal of θ_rel = 0.19.

Fig. 5 (a) NaNH₃ ion images measured with V_R = 5 kV for different coil settings. The coils of the deflector were pulsed individually (1st, 2nd, or 3rd coil), together (all coils) with a t₂ < t₁ < t₃ coil sequence and I_d = 300 A, or not at all (Def. off). (b) Experimental NaNH₃ velocity distributions retrieved from the photoion VMIs in panel a. (c) Corresponding simulated NaNH₃ velocity distributions obtained by combining MD and SIMION simulations. The displacement coordinates on the detector were calculated and then transformed into velocity coordinates.

The retrieved experimental NaNH₃ velocity distributions for each ion image are shown in Fig. 5b. The 2nd coil (orange line), being switched on first, mainly acts on particles with slow velocities of about 500 ms⁻¹. The 1st coil (blue line) acts on particles traveling with about 1000 ms⁻¹ and the 3rd coil (yellow line) acts on almost the full width of the distribution. The violet line shows all coils being fired, with residual signal remaining from particles at the fast and slow ends of the velocity distribution. These results visualize the functioning of the pulsed deflector and clearly show how critical it is to properly set the coil timings for a given cluster velocity distribution. To achieve reasonable deflection ratios, the magnetic field pulses have to act on the full velocity distribution. If the coil timings are not set well, a certain part of the velocity distribution will not be deflected. Finding such optimal coil timings in the experiment can be challenging. Due to the repetition rate (1–5 Hz) of the deflector, tracking of experimental deflection signals would be prohibitively time consuming. Therefore, we decided to rely on our simplified model for global optimization of the coil timings (Section 2.1.4).

Fig. 5c displays the corresponding simulated NaNH₃ velocity distributions obtained from a combination of MD simulations with SIMION simulations (Section 2.3). The experimental and simulated data show good general agreement if all coils are operated simultaneously. Yet the experimental results for the 1st and 3rd coils are only partially verified. While the simulation overestimates the deflection ratio of the 1st coil, deflection by the 3rd coil is underestimated. The experimental and simulated deflection ratios γ_d (eqn (2)) of the individual coils are summarized in Table 2.

Table 2 Experimental and simulated deflection ratios γ_d for each individual electromagnetic coil and all coils together

	1st coil	2nd coil	3rd coil	All coils
γ d (experiment)	0.09	0.25	0.33	0.81
γ d (simulation)	0.23	0.25	0.19	0.77

---

3.2. Deflection ratios for Na(NH₃)_n: experiment vs. MD simulations

3.2.1 NaNH₃. Fig. 6a shows, as an example, the integrated relative TOF signals θ_rel as a function of t_d (circles) at I_d = 300 A with a 2σ error. The average signal intensity of the five or four (for 600 A and 700 A) late timings defines θ_rel = 1 and their standard deviation defines the error bars (2σ) of a measurement. The minimum error of θ_rel for each cluster size measurement series was taken to be half of the average error determined from all of the studied deflector currents. For comparison, the results of the MD simulations are shown as diamonds. The experimental θ_rel decreases to a minimum of 0.31(7), which corresponds to the minimum of the MD simulation of θ_rel = 0.32. The comparison of experimental and simulation data shows very good agreement across the sampled deflector timings t_d. This indicates that the deflection process of NaNH₃ at 300 A is correctly described by the interaction of the magnetic moment and the inhomogeneous magnetic field . The same holds for larger currents (not shown). NaNH₃ TOF signals of four representative t_d (0, 4.6, 4.8 and 10.0 ms) are marked as open black circles in Fig. 6a and shown as representative TOF traces in Fig. 6b. The TOF traces are baseline subtracted, background corrected and smoothed before the signal peaks are integrated. The dashed lines indicate the integration window applied to retrieve integrated NaNH₃ TOF signals for each t_d.

Fig. 6 (a) Relative integrated NaNH₃ TOF signal θ_rel (2000 shots per data point) as a function of t_d (circles with 2σ error), compared with MD simulations (diamonds). (b) NaNH₃ TOF signals for four representative t_d corresponding to the open black circles at 0, 4.6, 4.8 and 10.0 ms in panel a. The deflector was operated at I_d = 300 A.

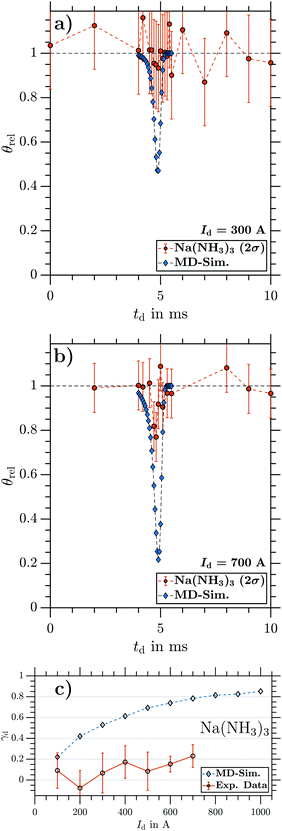
By changing the integration window to larger cluster sizes, we are able to obtain equivalent data as in Fig. 6 for all cluster sizes Na(NH₃)_n (n = 1–4) from the same TOF traces (see Sections 3.2.2 and 3.2.3 for results on larger clusters). Repeating measurements and MD simulations for several magnetic field strengths by varying I_d provides the maximum γ_d (corresponding to the minima as in Fig. 6a) as a function of I_d. Fig. 7 shows the maximal γ_d as a function of I_d for NaNH₃, obtained from the experimental data (circles) and from the simulations (diamonds). With increasing magnetic field strength, the experimental γ_d increases reaching a maximum of 0.78(7) at I_d = 700 A. For all different I_d, the experimental and simulated γ_d agree very well within error bars (2σ). Due to the fact that the applied MD approach does not take any intracluster spin relaxation (ISR) times^30,48,49 into account, the good agreement between experiment and simulation reveals that for NaNH₃ the intracluster spin relaxation time has to be significantly longer than the interaction time with the magnetic field gradient^25,26 (see discussion in Section 4).

Fig. 7 Maximal γ_d as a function of I_d for NaNH₃. Circles: experiment. The error indicates 2σ. Diamonds: MD simulation. The deflector was operated in a t₁ < t₂ < t₃ coil timing sequence.

3.2.2 Na(NH₃)₂. Fig. 8 shows equivalent data as in Fig. 7, but for Na(NH₃)₂ instead of NaNH₃. Within error bars, γ_d is larger than 0 for all experimental data points and reaches a maximal value of γ_d = 0.39(8) at I_d = 700 A. In other words, deflection is observed for Na(NH₃)₂ for all applied magnetic field gradients. Yet an agreement with the MD simulations is not found for any applied deflector current. By increasing the cluster size, several effects have to be taken into account that influence the degree of deflection. On one hand, a higher magnetic force has to be applied to deflect a heavier particle to the same extent as a lighter particle. On the other hand, the FWHM of the velocity distribution decreases for heavier particles, which results in a higher γ_d (Section 2.2 and Section S3, ESI†). Both of these effects are taken into account in the MD simulations. Nonetheless, the experimental results and MD simulations show crucial deviations which cannot be explained within 2σ error of each measurement. As discussed in Section 4, a possible explanation for the discrepancies is ISR processes,^30,48,49 which for Na(NH₃)₂ would occur at the same time scale comparable to or slightly faster than the interaction time with the magnetic field gradient.^25,26

Fig. 8 Maximal γ_d as a function of I_d for Na(NH₃)₂. Circles: experiment. The error indicates 2σ. Diamonds: MD simulation. The deflector was operated in a t₁ < t₂ < t₃ coil timing sequence.

3.2.3 Na(NH₃)₃ and Na(NH₃)₄. Fig. 9 and 10 (circles) show that the effects observed for Na(NH₃)₂ become even more significant when increasing the cluster size further to Na(NH₃)₃ and Na(NH₃)₄, respectively. At a current of 300 A (panel a), θ_rel = 1 within 2σ error for all sampled deflector timings t_d, meaning that both Na(NH₃)₃ and Na(NH₃)₄ show no clear deflection. At currents of 700 A (Fig. 9b) and 600 A (Fig. 10b), both Na(NH₃)₃ and Na(NH₃)₄ are slightly deflected, with maximal signal depletions of θ_rel = 0.77(11) and θ_rel = 0.79(7), respectively. Again, substantial deviations are found when compared with the MD simulations (diamonds). These deviations are best summarized by the maximal γ_d as a function of the current I_d (panels c in Fig. 9 and 10). Clear deflection within error bars is only achieved for the highest currents of I_d ∼ 600–700 A, even though it is worth mentioning that the average values of γ_d also lie slightly above zero for almost all other currents. For the higher currents, the MD simulations predict γ_d ∼ 0.7, which is in disagreement with the experimental values of γ_d ∼ 0.2.

Fig. 9 θ _rel as a function of t_d of Na(NH₃)₃ recorded at (a) I_d = 300 A and (b) I_d = 700 A. (c) Maximal γ_d as a function of I_d for Na(NH₃)₃. Circles: experiment. The error indicates 2σ. Diamonds: MD simulation.

Fig. 10 θ _rel as a function of t_d of Na(NH₃)₄ recorded at (a) I_d = 300 A and (b) I_d = 600 A. (c) Maximal γ_d as a function of I_d for Na(NH₃)₄. Circles: experiment. The error indicates 2σ. Diamonds: MD simulation.

In summary, we observe the same deflection as expected from MD simulations for the smallest cluster NaNH₃ at all currents (Fig. 7), while the larger clusters Na(NH₃)_n (n = 2–4; Fig. 8–10) show strongly reduced deflection compared with the simulations. Na(NH₃)₂ experiences small but clear deflection at all currents. For Na(NH₃)₃ and Na(NH₃)₄, in contrast, clear deflection within error bars could be seen only at higher currents. For comparison, at a current of I_d ∼ 700 A, the simulations predict γ_d values around 0.8 for all cluster sizes, while the experimentally observed deflection ratios systematically decrease from γ_d ∼ 0.8 for NaNH₃ to γ_d ∼ 0.4 for Na(NH₃)₂ to γ_d ∼ 0.2 for Na(NH₃)₃ and Na(NH₃)₄. As discussed in the following section this hints that spin relaxation times decrease with increasing cluster size.

4. Discussion

Since the effect of increasing cluster mass is already accounted for by our MD-simulations, the reduced deflection we observe for larger clusters might at first sight be interpreted phenomenologically as an indication of a reduction in the effective magnetic moment with increasing cluster size. Such dependence of the magnetic moment on cluster size and structure was found to explain the magnetic deflection experiments of isolated bi-metal clusters. Thus, the different magnetic moments of a single magnetic impurity (Co) in non-magnetic metallic hosts of discrete size (Nb_n) have been explained within the framework of the Anderson impurity model, in terms of the increase of the local moment with increasing host band gap (HOMO–LUMO gap).⁴⁷ Such arguments, however, are not applicable to our system of single spin 1/2 doped weakly interacting molecular clusters. The host molecules (NH₃) are closed shell with a very large HOMO–LUMO gap (liquid ammonia band gap: 7 eV).⁶⁵ The intermolecular interaction (a few tenths of an eV) is too weak to perturb the electronic structure of the host significantly. The effect of clustering on the electronic structure of the dopant is more pronounced. According to ab initio calculations the HOMO–LUMO (s–p) gap of about 2 eV in bare Na is reduced to 1.5 eV, 0.9 eV and 0.8 eV in Na(NH₃), Na(NH₃)₂ and Na(NH₃)₃, respectively.¹⁹ But the unpaired electron still largely retains its s-character. Within an earlier study of the photoelectron spectrum of the solvated electron in Na-doped ammonia clusters, we performed extensive DFT calculations on Na(NH₃)_n≤30.^17,18 The s-character of the unpaired electron of 96% in Na(NH₃) decreases only slightly to about 93% in Na(NH₃)₄. In all these cases the unpaired electron mainly resides on the surface of the cluster (see Fig. 11). There is some delocalization of the spin density over the NH₃ host molecules, which tends to increase with cluster size, but with 16% in Na(NH₃)₄ it still remains rather modest for the cluster sizes considered in the present work. It appears unlikely that any of these effects could change the magnetic moment significantly in these pure spin 1/2 systems. This leaves intracluster spin relaxation as a more plausible reason for the reduced deflection observed in our experiments.

Fig. 11 Isosurfaces of the HOMOs of Na(NH₃)_n clusters: (a) NaNH₃, (b) Na(NH₃)₂, (c) Na(NH₃)₃, (d) Na(NH₃)₄ isomer IA with all eclipsed arrangement of NH₃ and (e) asymmetric isomer IC. (d) and (e) are adapted with permission from ref. 17 Copyright © 2015 American Chemical Society.

In order to discuss our results in terms of possible intracluster spin relaxation processes, a characteristic spin relaxation time τ is compared with the cluster specific interaction time t_m with the magnetic field for two different cases. If τ > t_m, the electronic spin state does not ‘flip’ when the cluster traverses the deflector setup (i.e. when the cluster interacts with the magnetic field) and free spin (atom-like) deflection behaviour would be observed. This matches the assumptions of our MD simulation, which, therefore, should reproduce the experimentally observed deflection ratios. This was successfully verified using a beam of Na atoms, which exhibit no spin relaxation (Fig. S1, ESI†) during t_m. Very good agreement between the MD simulation and experimental data was observed for NaNH₃ (Fig. 7), suggesting negligible intracluster spin relaxation during t_m. In our experiment, t_m is ∼200 μs considering the centre velocity of NaNH₃ (∼1000 ms⁻¹) and the deflector length. Therefore, the intracluster spin relaxation time for NaNH₃ must be longer than 200 μs.

If τ ≤ t_m, the electron spin state stochastically ‘flips’ while travelling through the magnetic field. These statistical fluctuations of the spin reduce deflection and cause a broadening of the molecular beam cross section.^25,26 In our setup, this would result in partial deflection. Since these effects are not included in our MD model, the simulations for cases with τ ≤ t_m no longer reproduce the measured deflection ratios. If τ ≪ t_m, γ_d values of zero are expected, while τ values on the order of t_m would result in reduced, but non-zero deflection ratios. The latter would explain our observations for Na(NH₃)₂ at all currents and for Na(NH₃)₃ and Na(NH₃)₄ at higher currents. With this explanation, typical intracluster relaxation times would be on the order of 200 μs.

If the decrease of intracluster relaxation times in larger clusters is the reason for the observed reduced deflection, how does this size dependence come about? The electronic structure might play a role here, as both the spatial extension of the unpaired electron and its average separation from the Na core increase with cluster size.¹⁹ Given that these effects are not dramatic we expect other contributions to be more important. A detailed theoretical description on spin relaxation processes in isolated molecules and clusters was previously given by Knickelbein.⁴⁹ In his interpretation of Stern–Gerlach experiments, intracluster/intramolecular spin relaxation (ISR) becomes more likely the higher the density of the rovibrational states. Overall rotations of molecular clusters induce Zeeman-like eigenstates in the presence of an external magnetic field. Transitions between such Zeeman sublevels may occur within the conservation laws of internal energy and total angular momentum. The free molecule or cluster can undergo intramolecular or intracluster spin relaxation processes. In such processes, the molecule or cluster serves as a ‘thermal bath’ for its own spin, especially when the system is large and the temperature is high enough to populate many intramolecular states.

In our study of sodium doped ammonia clusters, we expect analogous Zeeman-like sublevels with possible transitions occurring between the sublevels. Yet, the weak non-covalent bonds between the sodium atom and ammonia molecules and between ammonia molecules cause distinct differences to previously investigated free molecules^{25–29,31–34} and cluster systems.^{30,35–45,47,51–56} They are rather floppy systems undergoing large amplitude motions with low characteristic frequencies. Many of these represent hindered internal rotations whose vibrational angular momenta provide an effective coupling mechanism to the spin of the unpaired electron. While the rovibrational dynamics of these systems are evidently highly anharmonic, a harmonic analysis of the DFT calculations for the structures shown in Fig. 11 already provides a qualitative picture. The Na–N stretching and bending harmonic wavenumbers of NaNH₃ are calculated to be 231 cm⁻¹ and 323 cm⁻¹, respectively. Considering the level of theory and experimental uncertainties, this is consistent with experimental results with values for the fundamental wavenumbers ranging from 195 cm⁻¹ to 215 cm⁻¹ for the stretching and 278 cm⁻¹ for the bending fundamental.^66,67 At estimated cluster temperatures in the range of 110–145 K,²¹ excited states of these low-frequency vibrations (vibrational temperature ∼300 K) are barely populated. This situation changes drastically for the larger clusters Na(NH₃)_n≥2.⁶⁸ Here new types of low frequency modes arise, i.e. internal rotation of NH₃ around the Na–N axis and N–Na–N bending, with calculated harmonic wavenumbers of 20 cm⁻¹ and 31 cm⁻¹ for the NH₃ rotation and 41 cm⁻¹ for the N–Na–N bending. This is consistent with a value of 25 cm⁻¹ derived for the latter via ZEKE-PFI spectroscopy.⁶⁷ The corresponding vibrational temperature falls in the range between 30 K and 60 K. Compared with NaNH₃, this leads to an abrupt increase in thermally accessible states. With each NH₃ molecule added, the number of internal modes with vibrational temperatures well below the estimated cluster temperature increases further with a corresponding exponential increase in the thermally accessible density of states.

The excited states of the NH₃ internal rotation and N–Na–N bending (hindered orbiting of NH₃ around Na) are associated with large vibrational angular momenta, which couple to the cluster's rotational states and subsequently induce a highly perturbed Zeeman-like splitting pattern. Thus the increase of the rovibrational density of states to which the spin of the unpaired electron can couple would explain the decrease of the magnetic deflection upon the addition of NH₃ molecules to the Na-doped clusters. This density of coupling states is low for NaNH₃ translating into slow ISR. Adding a second NH₃ molecule produces a sudden increase in the density of coupling states as new types of low frequency internal motions arise. ISR accelerates accordingly and abruptly reduces the observed magnetic deflection. Adding more NH₃ molecules further enhances the effect, but does so more gradually.

While we believe that this is the dominant cause for the cluster size dependence of the magnetic deflection we observe, other effects can also contribute. For example, hyperfine coupling might have to be taken into account. Furthermore, the molecular beam can contain multiple structural isomers for a given cluster size at the estimated cluster temperature. Each structural isomer would exhibit a particular Zeeman splitting pattern with possible transitions occurring between the Zeeman-like sublevels. Thereby spin relaxation would depend on the current geometry of the clusters, which might vary on the timescale of the experiment. The above phenomena would imply a marked temperature dependence of the spin relaxation process, which would be interesting to investigate in future work.

5. Conclusions

We have implemented a pulsed Stern–Gerlach deflection experiment to study the magnetic properties of sodium-doped ammonia clusters. The testing of the experimental setup for an effusive Na atom beam and the comparison with molecular dynamics simulations confirm the expected performance of the design.

The present experimental study for Na(NH₃)_n (n = 1–4) is a first attempt to understand the magnetic properties of sodium doped ammonia clusters, which can be seen as a model system for solvated electron precursors. The combination of deflection experiments with molecular dynamics simulations provides, for the first time, insights into time-scales of intracluster spin relaxation in these small weakly-bound clusters. For NaNH₃, we expect intracluster spin relaxation to take place on a timescale substantially longer than 200 μs. The partial deflection that is observed for the larger clusters of Na(NH₃)_n (n = 2–4) compared with molecular dynamics simulations, that do not take intracluster relaxation effects into account, suggests the relaxation times for these clusters to be in the order of 200 μs. We propose an acceleration of intra-cluster spin relaxation in n > 1 clusters as a result of Zeeman-like spin-rotation coupling. The emergence of very low frequency internal rotation modes for n > 1 leads to a drastic increase in the thermally accessible density of rovibrational states to which the spin can couple, which could explain the abrupt decrease of the deflection for clusters with n > 1. However, to obtain a more definite explanation of the observed cluster size dependence, further magnetic deflection experiments (e.g. spin refocusing with two Stern–Gerlach magnets) and modelling of intracluster relaxation processes should be carried out. Detailed studies of the magnetic and electronic properties of solvated electrons in clusters will lead to a better understanding of the paramagnetic and diamagnetic species in bulk alkali metal ammonia solutions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are very grateful to Prof. Gunnar Jeschke for carrying out initial calculations to estimate approximate spin relaxation times for small sodium doped clusters and to Dr David Luckhaus for helping us to modify his molecular dynamics program. We would like to thank David Stapfer and Markus Steger from the mechanical and electronic LPC workshops of ETH Zurich and Haim Sade from the Weizmann CNC unit for their technical contributions to the experimental setup and their continuing support during the improvement of the setup. We also thank Nina Bersenkowitsch for her contribution as an exchange student at the early stage of this project. This project was financially supported by the Swiss National Science Foundation (project nr. 200020_172472), ETH Zurich and the Israel Science Foundation.

References

1. W. Weyl, Ann. Phys., 1864, 199, 350–367.
2. E. Zurek, P. P. Edwards and R. Hoffmann, Angew. Chem., Int. Ed., 2009, 48, 8198–8232.
3. J. M. Herbert and L. D. Jacobson, J. Chem. Phys. A, 2011, 115, 14470–14483.
4. P. Voehringer, Annu. Rev. Phys. Chem., 2015, 66, 97–118.
5. D. Holton and P. Edwards, Chem. Br., 1985, 21, 1007.
6. A. Meyer and M. van Gastel, J. Chem. Phys. A, 2011, 115, 1939–1945.
7. P. P. Edwards, J. Phys. Chem., 1984, 88, 3772–3780.
8. I. Hertel, C. Hüglin, C. Nitsch and C. Schulz, Phys. Rev. Lett., 1991, 67, 1767.
9. C. Nitsch, C. Schulz, A. Gerber, W. Zimmermann-Edling and I. Hertel, ZPhys-e.D: At., Mol. Clusters, 1992, 22, 651–658.
10. C. Steinbach and U. Buck, J. Chem. Phys., 2005, 122, 134301.
11. I. Dauster, M. A. Suhm, U. Buck and T. Zeuch, Phys. Chem. Chem. Phys., 2008, 10, 83–95.
12. K. Hashimoto and K. Daigoku, Chem. Phys. Lett., 2009, 469, 62–67.
13. T. Almeida and B. C. Cabral, J. Chem. Phys., 2010, 132, 094307.
14. B. L. Yoder, J. H. Litman, P. W. Forysinski, J. L. Corbett and R. Signorell, J. Phys. Chem. Lett., 2011, 2, 2623–2628.
15. T. Zeuch and U. Buck, Chem. Phys. Lett., 2013, 579, 1–10.
16. R. Signorell, B. L. Yoder, A. H. C. West, J. J. Ferreiro and C. M. Saak, Chem. Sci., 2014, 5, 1283–1295.
17. A. H. West, B. L. Yoder, D. Luckhaus and R. Signorell, J. Chem. Phys. A, 2015, 119, 12376–12382.
18. A. H. C. West, B. L. Yoder, D. Luckhaus, C. M. Saak, M. Doppelbauer and R. Signorell, J. Phys. Chem. Lett., 2015, 6, 1487–1492.
19. A. O. Gunina and A. I. Krylov, J. Chem. Phys. A, 2016, 120, 9841–9856.
20. J. V. Barnes, B. L. Yoder and R. Signorell, J. Phys. Chem. A, 2019, 123, 2379–2386.
21. A. l. Carrera and E. Marceca, J. Chem. Phys. A, 2015, 119, 4207–4213.
22. W. Gerlach and O. Stern, Z. Phys., 1922, 9, 349–352.
23. N. Ramsey, Molecular Beams, OUP, Oxford, 1985.
24. D. J. Meschi and A. W. Searcy, J. Chem. Phys., 1969, 51, 5134–5138.
25. A. Amirav and G. Navon, Phys. Rev. Lett., 1981, 47, 906.
26. A. Amirav and G. Navon, Chem. Phys., 1983, 82, 253–267.
27. N. Kuebler, M. Robin, J. Yang, A. Gedanken and D. Herrick, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 737.
28. A. Gedanken, N. Kuebler, M. Robin and D. Herrick, J. Chem. Phys., 1989, 90, 3981–3993.
29. A. Gedanken, N. A. Kuebler, M. B. Robin and D. R. Herrick, J. Am. Chem. Soc., 1989, 111, 5568–5572.
30. D. Herrick, M. Robin and A. Gedanken, J. Mol. Spectrosc., 1989, 133, 61–81.
31. A. Gedanken, V. Kelner and E. Sominksa, Chem. Phys. Lett., 1994, 221, 274–278.
32. A. Malakhovskii and A. Gedanken, J. Chem. Soc., Faraday Trans., 1996, 92, 329–332.
33. A. Malakhovskii, E. Sominska and A. Gedanken, J. Chem. Soc., Faraday Trans., 1996, 92, 1319–1322.
34. M. Alagia, V. Aquilanti, D. Ascenzi, N. Balucani, D. Cappelletti, L. Cartechini, P. Casavecchia, F. Pirani, G. Sanchini and G. G. Volpi, Isr. J. Chem., 1997, 37, 329–342.
35. D. Cox, D. Trevor, R. Whetten, E. Rohlfing and A. Kaldor, J. Chem. Phys., 1986, 84, 4651–4656.
36. W. A. De Heer, P. Milani and A. Chtelain, Phys. Rev. Lett., 1990, 65, 488.
37. P. Ballone, P. Milani and W. de Heer, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 10350.
38. J. Bucher, D. Douglass and L. Bloomfield, Phys. Rev. Lett., 1991, 66, 3052.
39. W. De Heer, P. Milani and A. Châtelain, ZPhys-e.D: At., Mol. Clusters, 1991, 19, 241–245.
40. I. M. Billas, A. Chatelain and W. A. de Heer, Science, 1994, 265, 1682–1684.
41. T. Hihara, S. Pokrant and J. Becker, Chem. Phys. Lett., 1998, 294, 357–362.
42. A. Châtelain, Philos. Mag. B, 1999, 79, 1367–1378.
43. N. Hamamoto, N. Onishi and G. Bertsch, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 1336.
44. M. B. Knickelbein, J. Chem. Phys., 2002, 116, 9703–9711.
45. X. Xu, S. Yin, R. Moro and W. A. de Heer, Phys. Rev. Lett., 2005, 95, 237209.
46. D. Dieleman, M. Tombers, L. Peters, J. Meyer, S. Peredkov, J. Jalink, M. Neeb, W. Eberhardt, T. Rasing and G. Niedner-Schatteburg, Phys. Chem. Chem. Phys., 2015, 17, 28372–28378.
47. A. Diaz-Bachs, L. Peters, R. Logemann, V. Chernyy, J. Bakker, M. Katsnelson and A. Kirilyuk, Phys. Rev. B, 2018, 97, 134427.
48. D. Herrick, M. Robin and A. Gedanken, Chem. Phys., 1989, 130, 201–209.
49. M. B. Knickelbein, J. Chem. Phys., 2004, 121, 5281–5283.
50. H. Wennerstrom and P. O. Westlund, Phys. Chem. Chem. Phys., 2012, 14, 1677–1684.
51. K. Miyajima, A. Nakajima, S. Yabushita, M. B. Knickelbein and K. Kaya, J. Am. Chem. Soc., 2004, 126, 13202–13203.
52. K. Miyajima, M. B. Knickelbein and A. Nakajima, Polyhedron, 2005, 24, 2341–2345.
53. K. Miyajima, M. B. Knickelbein and A. Nakajima, Eur. Phys. J. D, 2005, 34, 177–182.
54. K. Miyajima, S. Yabushita, M. B. Knickelbein and A. Nakajima, J. Am. Chem. Soc., 2007, 129, 8473–8480.
55. U. Rohrmann and R. Schäfer, J. Chem. Phys. C, 2015, 119, 10958–10961.
56. T. M. Fuchs and R. Schafer, Phys. Rev. A, 2018, 98, 063411.
57. J. Liang, T. M. Fuchs, R. Schäfer and V. V. Kresin, Rev. Sci. Instrum., 2020, 91, 053202.
58. A. T. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484.
59. B. L. Yoder, J. H. Litman, P. W. Forysinski, J. L. Corbett and R. Signorell, J. Phys. Chem. Lett., 2011, 2, 2623–2628.
60. S. Schütte and U. Buck, Int, J. Mass Spectrom., 2002, 220, 183–192.
61. C. Bobbert, S. Schütte, C. Steinbach and U. Buck, Eur. Phys. J. D, 2002, 19, 183–192.
62. R. Signorell, M. Goldmann, B. L. Yoder, A. Bodi, E. Chasovskikh, L. Lang and D. Luckhaus, Chem. Phys. Lett., 2016, 658, 1–6.
63. W. Li, S. D. Chambreau, S. A. Lahankar and A. G. Suits, Rev. Sci. Instrum., 2005, 76, 063106.
64. D. A. Dahl, Int, J. Mass Spectrom., 2000, 200, 3–25.
65. T. Vogler and P. Vöhringer, Phys. Chem. Chem. Phys., 2018, 20, 25657–25665.
66. D. A. Rodham and G. A. Blake, Chem. Phys. Lett., 1997, 264, 522–530.
67. X. Peng and W. Kong, J. Chem. Phys., 2002, 117, 9306–9315.
68. C. P. Schulz, A. Scholz and I. V. Hertel, Isr. J. Chem., 2004, 44, 19–25.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04647g

---