An effective potential for Frenkel excitons†
Received
2nd September 2020
, Accepted 9th December 2020
First published on 7th January 2021
Abstract
Excitation energy transfer (EET) is a ubiquitous process in life and materials sciences. Here, a new and computationally efficient method of evaluating the electronic EET couplings between interacting chromophores is introduced that is valid in a wide range of intermolecular distances. The proposed approach is based on the effective elimination of electron repulsion integrals from the excitonic Hamiltonian matrix elements via the density-fitting approach and distributed multipole approximation. The excitonic Hamiltonian represented in a basis including charge transfer (CT) states is re-cast in terms of the effective one-electron potential functions (EOPs) and adapted into the effective fragment parameter (EFP) framework. Calculations for model systems indicate that the speedup of at least three orders of magnitude, as compared to the state-of-the-art methods, can be achieved while maintaining the accuracy of the EET couplings even at short intermolecular distances.
1 Introduction
Excitation energy transfer (EET) is a nonadiabatic phenomenon governing the nonradiative transfer of excitation energy between two chromophores characterized by overlapping spectral features which enable their resonance coupling. It is of fundamental importance for understanding the early stages of photosynthesis or functioning of light-harvesting complexes in general. Thus EET is of central importance to many branches of materials and life sciences. Its strong dependence on the distance and orientation of the coupled chromophores led to the development of several time-resolved spectroscopic techniques, in particular the single-molecule Förster resonance energy transfer, allowing the determination of the mechanisms of biomolecular processes.1,2
Since the EET phenomenon and the theoretical framework for its description were recently reviewed thoroughly,3–8 here we provide only a brief outline of the recent developments. At large intermolecular distances EET coupling can be adequately described by the Förster model9 which assumes the purely Coulombic interaction between the transition densities of chromophores, and computationally efficient schemes have been developed over recent years that take into account the spatial extent and shape of transition densities.10–12 However, an accurate description of EET coupling constants become more difficult at short intermolecular distances due to wavefunction overlap and exchange interactions.13–15 A robust description of EET coupling in such cases is provided by the Frenkel exciton model16 in which the excitons are localized on individual chromophores. Such an approach is quite reliable in the weak-coupling limit17 and can be extended to account for intermolecular charge transfer states.18–21
To accurately account for short-range effects, fragment density approaches (FDAs) were developed,13,22,23 in which the analysis of the Hamiltonian is performed in the eigenstate basis for the initial and final EET states of interest. In particular, the fragment excitation difference (FED) approach,13 which is a generalization of the energy splitting in dimer (ESD) method24 for nonsymmetric systems, provides reasonably accurate values of EET at all physically meaningful intermolecular distances. A different strategy was adopted within the so-called transfer-integral (TI) approach.24,25 This technique stems from a standard two-state diabatic Landau–Zener model in which the off-diagonal Hamiltonian matrix element, called the transfer integral,24 couples the initial and final states in a nonadiabatic process of electron or excitation energy transfer. This approach can be generalized to interactions among many-level systems, which introduces the so-called indirect coupling matrix elements via intermediate (bridge) states in addition to the direct interaction between initial and final states.25,26 In the context of electronic EET this approach was proposed by Scholes and Harcourt as the superexchange coupling (SEC) method26,27 and was recently reintroduced by Fujimoto as the transition-density-fragment interaction transfer-integral (TDFI-TI) model.28–31
The main advantage of the TI approach is that the EET coupling can be directly expressed via the donor and acceptor transition densities by means of perturbation theory which allows time-consuming calculations in the eigenstate space of an entire system to be avoided. Unfortunately, from the perspective of ab initio electronic structure calculations all the above techniques require the evaluation of the four-center electron repulsion integrals (ERIs) and excited state properties for a given instantaneous orientation of interacting chromophores. Even though nonadiabatic dynamics simulations of interacting chromophores are nowadays possible due to growing computational power and introduction of efficient computational protocols,18–20 the time-consuming contractions involving 4-index tensors are still a serious bottleneck which generally prohibits systematic studies of large aggregates.
In this paper we introduce a new efficient method to calculate the electronic EET couplings within the TI approach that is valid in both the long- and short-range regimes and is based on the recently introduced effective one-electron potential (EOP) operators technique to eliminate ERIs from fragment-based models.32 Although we focus here on the singlet–singlet (SS) EET, extension to the triplet–triplet (TT) EET can be readily achieved from the corresponding TI model.
To test the proposed technique we assume the configuration interaction singles33 (CIS) wavefunction of interacting molecules. For clarity of demonstration, we consider a simple model case in which only the non-degenerate frontier orbitals of the coupled chromophores are kept active to construct the excitonic Hamiltonian.26,27 An example of the thus formulated variant of the transfer-integral CIS (TI/CIS) method, proposed by Fujimoto,31 is a starting point for the introduction of the effective one-electron potential transfer-integral (EOP-TI) approach, which is the main purpose of this paper. Although in a general case more orbitals might be required to describe the bridging composite states in the SEC model, we believe that the application of the EOP method would then be straightforward. In the following sections we outline the relevant theoretical framework and discuss the results obtained for model systems, focusing on the accuracy and efficiency of the introduced approximations. Finally, we show that the proposed EOP-TI method de facto introduces a way to construct an effective fragment potential for EET couplings.
2 Theoretical methodology
2.1 Transfer-integral model of EET coupling
In the simplest version of the TI/CIS approach, the Hamiltonian of an aggregate of molecules A and B is constructed assuming the weak-coupling exciton model approximation involving the following four configurations:| | | |Φ1〉 = |Ψ(e)A ⊗ Ψ(g)B〉, | (1a) |
| | | |Φ2〉 = |Ψ(g)A ⊗ Ψ(e)B〉, | (1b) |
| | | |Φ3〉 = |Ψ(+)A ⊗ Ψ(−)B〉, | (1c) |
| | | |Φ4〉 = |Ψ(−)A ⊗ Ψ(+)B〉, | (1d) |
where superscripts g and e denote the ground and excited states of a molecule, and ‘+’ and ‘−’ label the cationic and anionic states, respectively, whereas| | |ΨX ⊗ ΨY〉 ≡ ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) {|ΨX〉 ⊗ |ΨY〉} {|ΨX〉 ⊗ |ΨY〉} | (2) |
denotes the antisymmetrized Hartree product of the monomer wavefunctions with ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) being the standard antisymmetrization operator and ‘⊗’ denoting the outer product. Instead of diagonalizing the excitonic Hamiltonian in such a basis, one may adopt the perturbation theory to obtain the approximate expression for the EET coupling constant:26,31
being the standard antisymmetrization operator and ‘⊗’ denoting the outer product. Instead of diagonalizing the excitonic Hamiltonian in such a basis, one may adopt the perturbation theory to obtain the approximate expression for the EET coupling constant:26,31| | 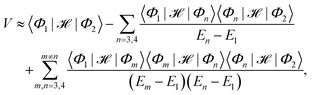 | (3) |
where En ≡ 〈Φn|![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − E0|Φn〉 and E0 is the ground state energy of the aggregate. The first two site energies are given by31
− E0|Φn〉 and E0 is the ground state energy of the aggregate. The first two site energies are given by31| | E1 ≡ 〈Φ1|![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − E0|Φ1〉 = EAe→g + ΔEAe→g(B), − E0|Φ1〉 = EAe→g + ΔEAe→g(B), | (4a) |
| | E2 ≡ 〈Φ2|![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − E0|Φ2〉 = EBe→g + ΔEBe→g(A), − E0|Φ2〉 = EBe→g + ΔEBe→g(A), | (4b) |
where EXe→g is the excitation energy of isolated molecule X and ΔEXe→g(Y) accounts for the mean-field environmental effect due to the other molecule, which is given by| | 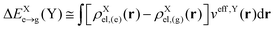 | (5) |
with the effective one-electron potential given by| | 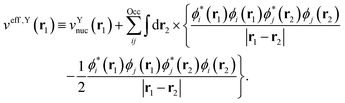 | (6) |
If basis functions 3 and 4 are approximated as the HOMO and LUMO of monomers (i.e., the frontier orbital approximation), the remaining two site energies are given by| | E3 ≡ 〈Φ3|![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − E0|Φ3〉 ≈ −εAH + εBL − (ϕAHϕAH|ϕBLϕBL), − E0|Φ3〉 ≈ −εAH + εBL − (ϕAHϕAH|ϕBLϕBL), | (7a) |
| | E4 ≡ 〈Φ4|![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − E0|Φ4〉 ≈ εAL − εBH − (ϕALϕAL|ϕBHϕBH), − E0|Φ4〉 ≈ εAL − εBH − (ϕALϕAL|ϕBHϕBH), | (7b) |
where εXj is the energy of the jth Hartree–Fock orbital ϕXj associated with molecule X, and the two-electron integral (ERI) is defined by| | 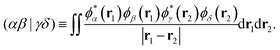 | (8) |
The first term in eqn (3) is the, so-called, direct coupling, which is composed of two contributions as follows:
| | 〈Φ1|![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) |Φ2〉 = V0Coul + V0Exch |Φ2〉 = V0Coul + V0Exch | (9) |
where the Förster (or Coulomb) coupling is given by
| | 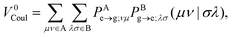 | (10) |
whereas the Dexter (or pure exchange) coupling is
| | 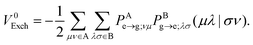 | (11) |
In the above equations,
PXg→e is the transition one-particle density matrix of molecule X in AO representation.
V0Coul, which is usually a leading term for SS EET (but vanishes for TT EET), can be efficiently evaluated by various multipole expansion or electrostatic potential fitting models published to date.
10–12V0Exch was reported to be rather negligible for SS EET even for close intermolecular contacts,
12,31 but is known to be non-negligible for TT EET.
13,34,35 However, unlike the direct Coulombic coupling, the second- and third-order terms in
eqn (3), which are collectively referred to by Fujimoto as the indirect coupling,
31 as well as direct exchange coupling for TT EET, become increasingly important at short intermolecular distances. Unfortunately, the evaluation of such couplings is computationally quite demanding, even if the frontier orbital approximation of
eqn (7) is assumed, since it requires evaluation of the ERIs.
Since the TI/CIS model was found to provide quite reliable estimates of EET coupling constants for many organic molecules,15,31,36 we consider this model as a starting point to develop a computationally more efficient scheme that does not require time-consuming calculations of ERIs at all. First, in Section 2.2 we derive the EOP model based on the TI/CIS approach proposed earlier by Scholes and Ghiggino26 and Fujimoto31 (hereonin referred to as the EOP-TI/CIS or, in short, EOP-TI model). Next, we validate it against the various formulations of the TI/CIS method with increasing accuracy for a few selected model complexes in Section 3. Finally, we conclude our findings in Section 4. The auxiliary derivations are outlined in the appendices.
2.2 EOP-based model
In this section, we derive the approximation of the TI/CIS model that is completely free from ERIs. This is possible due to effective elimination of ERIs according to the general prescription:32| | 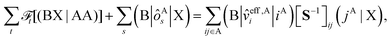 | (12) |
where the capital italic letters denote subsets of orbitals associated with a particular fragment and X = A or B, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) t is an arbitrary linear functional of ERIs, and ôAs and
t is an arbitrary linear functional of ERIs, and ôAs and ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) eff,Ai represent an arbitrary one-electron operator and an EOP operator associated with a molecule or fragment A, respectively. First of all, the coulombic EET coupling can be approximated by the distributed multipole expansion of the transition densities of interacting monomers in a dimer using the distributed transition-density cumulative atomic multipole moments (TrCAMM) approach, developed by some of us previously:12
eff,Ai represent an arbitrary one-electron operator and an EOP operator associated with a molecule or fragment A, respectively. First of all, the coulombic EET coupling can be approximated by the distributed multipole expansion of the transition densities of interacting monomers in a dimer using the distributed transition-density cumulative atomic multipole moments (TrCAMM) approach, developed by some of us previously:12| | | V0Coul ≈ ρAe→g ⊙ ρBg→e, | (13) |
where the symbol ‘⊙’ denotes the tensor contractions involved in the multipole expansion of the interaction energy between the generalized one-electron densities and the superscript ‘0’ indicates that the matrix elements are not affected by the overlap between molecular wavefunctions (this issue shall be addressed later in Section 2.2.4).
The diagonal elements for the first two basis states that are necessary for the overlapping corrections and also for the evaluation of the indirect EET couplings can be approximated (see the ESI†) by neglecting the environmental correction ΔEXe→g, i.e.,
Although this correction was found to be negligible in all the systems studied in this work (Tables S1 and S2, ESI
†), this assumption should be tested for other chromophores and electronic transitions. All the other components of the model involve ERIs between the HOMO and LUMO of monomers A and B. These can be grouped into the following three categories:
32
1. Integrals of type (ϕXiϕXj|ϕYkϕYl), or Coulomb-like integrals. These involve HOMO–LUMO interactions in the expressions for E3 and E4 from eqn (7). These shall be treated in this work by the distributed multipole expansion of the form:
| | | (ϕXiϕXj|ϕYkϕYl) ≈ ρXij ⊙ ρYkl, | (15) |
where
| | 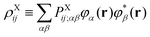 | (16) |
and
PXij is the associated effective one-particle density matrix in the AO basis given by
| | | PXij;αβ = CXαi(CXβj)*. | (17) |
In this work, the CAMM method is used to generate the distributed multipole moments from such density matrices, as discussed in
ref. 32.
2. Integrals of type (ϕXiϕXj|ϕXkϕYl), or overlap-like integrals. Matrix elements needed to evaluate EET coupling due to electron and hole transfer processes involve overlap-like ERIs. These shall be treated by the extended density fitting (EDF) technique,32i.e.,
| | (ϕXiϕXj|ϕXkϕYl) ≡ −(ϕXk|![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) Xij|ϕYl) Xij|ϕYl) | (18) |
where
| | 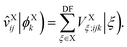 | (19) |
In the above, the ‘DF’ label indicates the auxiliary AO basis set used for density fitting, and the effective potential operator is defined by
32| | 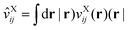 | (20) |
with its spatial form given as
| | 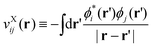 | (21) |
(here, note that
ϕj(
r) ≡ (
r|
ϕj)).
3. Integrals of type (ϕXiϕYj|ϕXkϕYl), or exchange-like integrals. These cannot be treated by means of the effective one-electron operators, but nonetheless constitute the V0Exch matrix element and also conribute to the indirect coupling. Such integrals can be treated by a number of approximations, which allow one to express ERIs in terms of the one-electron overlap and other ERIs.37 In this work, the Mulliken approximation is assumed where only two-electron Coulomb-like integrals are necessary, i.e.,
| | 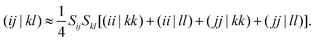 | (22) |
Thus, one can find that the remaining diagonal matrix elements are
| | | E3 ≈ −εAH + εBL − ρAHH ⊙ ρBLL, | (23a) |
| | | E4 ≈ εAL − εBH − ρALL ⊙ ρBHH. | (23b) |
In the following subsections, the off-diagonal Hamiltonian matrix elements shall be discussed in detail in order to effectively remove all ERIs from the formulation.
2.2.1 Indirect coupling via electron and hole transfer.
The indirect coupling terms can be intuitively decomposed into electron, hole and charge transfer terms.26,31 The electron transfer (ET) matrix elements are| | 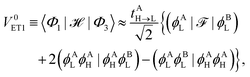 | (24) |
along with the twin term, V0ET2 ≡ 〈Φ2|![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) |Φ4〉, which were introduced earlier by Fujimoto.31 In the above,
|Φ4〉, which were introduced earlier by Fujimoto.31 In the above, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) is the Fock operator of the entire molecular aggregate. Note that here tAH→L are the CIS amplitudes of isolated monomer A, whereas
is the Fock operator of the entire molecular aggregate. Note that here tAH→L are the CIS amplitudes of isolated monomer A, whereas 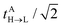 reflects the approximate amplitude in a dimer with monomer B being in its ground state. Here, we also approximate the Fock operator by neglecting the interchromophore relaxation:
reflects the approximate amplitude in a dimer with monomer B being in its ground state. Here, we also approximate the Fock operator by neglecting the interchromophore relaxation:| | 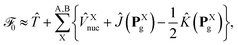 | (25) |
where ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ≡ −½∇2 is the one-electron kinetic energy operator,
≡ −½∇2 is the one-electron kinetic energy operator, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) Xnuc is the operator associated with the electrostatic potential energy between nuclei and electrons in molecule X, and the Coulomb and exchange operators are defined by
Xnuc is the operator associated with the electrostatic potential energy between nuclei and electrons in molecule X, and the Coulomb and exchange operators are defined by| | 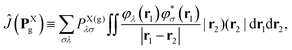 | (26a) |
| | 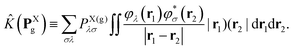 | (26b) |
Note that the decomposition of the kinetic energy operator into particular molecular contributions is arbitrary. However, consider the following partitioning of the total Fock operator:in which the auxiliary operator is defined as| | 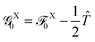 | (28) |
and 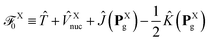 is the Fock operator of isolated molecule X. Here, the contribution from the one-electron kinetic energy operator was symmetrically partitioned in between the two interacting molecules. Thus one can rewrite eqn (24) as
is the Fock operator of isolated molecule X. Here, the contribution from the one-electron kinetic energy operator was symmetrically partitioned in between the two interacting molecules. Thus one can rewrite eqn (24) as| | 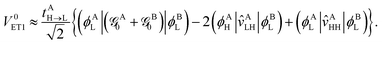 | (29) |
Now, by using the EOP technique32 for overlap-like effective-potential operator matrix elements of type (AA|AB) one can collect operators associated to a particular molecule and group them into one effective one-electron operator as| | 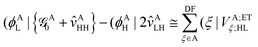 | (30) |
and| | 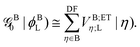 | (31) |
In the above transformations that involve the EDF in an auxiliary basis set space, VA;ETξ;HL and VB;ETη;L are the EOP matrix elements associated with the above effective potentials, separately defined for molecules A and B. This allows one to further recast V0ET1 into| | 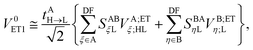 | (32) |
which has a particularly simple form as compared to the original expression in eqn (24) that involves four-center electron repulsion integrals. Note that, if the EOP matrices are considered as effective fragment parameters (EFPs), only overlap integrals between auxiliary basis functions and the LUMOs of molecules A and B are necessary, i.e.,| | 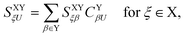 | (33) |
where| | 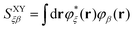 | (34) |
and CXβU is the SCF LCAO-MO matrix element for isolated molecule X associated with the Uth MO. It is straightforward to show that the twin term ET2 is| | 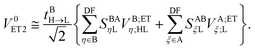 | (35) |
Note that EOP matrices for ET1 and ET2 terms share a similar structure. Therefore a joint superscript ‘ET’ is used here to label the EOP matrices and additional subscripts L and HL denote the dependence on only the LUMO or on both the HOMO and LUMO, respectively.
Similar considerations apply to the hole transfer (HT) matrix elements. The corresponding expression
| | 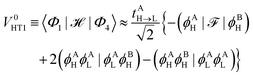 | (36) |
can be recast as
| | 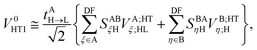 | (37) |
with the effective potential matrices given by
| | 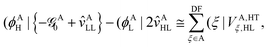 | (38a) |
| | 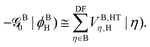 | (38b) |
The twin term HT2 is accordingly
| | 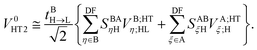 | (39) |
As it was shown, to compute the Hamiltonian matrix elements associated with the electron and hole transfer, in total eight different EOP matrices need to be precomputed and stored in a file. Note that each of these matrices is actually just a vector of length equal to the size of the auxiliary basis set chosen. Therefore, it can be predicted that the computational cost of the evaluation of the EOP-based Hamiltonian matrix elements is negligible as compared to the original formulation of the TI/CIS method. In Appendix A, the explicit and convenient to implement working formulae for the EOP matrix elements are given in terms of the AOs.
2.2.2 Indirect coupling via charge transfer.
The Hamiltonian matrix element that is associated with the charge transfer process is| | | V0CT = 2(ϕAHϕBL|ϕALϕBH) − (ϕAHϕBH|ϕALϕBL). | (40) |
Since it involves ERIs of type (AB|AB), EOPs cannot be readily defined here. However, the application of the Mulliken approximation from eqn (22) to eqn (40) yields| | 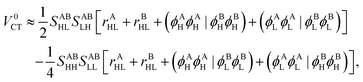 | (41) |
where| | | rXHL ≡ (ϕXHϕXH|ϕXLϕXL). | (42) |
First of all, note that rAHL and rBHL are just constant numbers associated with the isolated monomers and independent of the molecular aggregate. Also, the remaining four ERIs can be considered as Coulombic interactions between the HOMO and LUMO of unperturbed molecular wavefunctions:| | | (ϕAHϕAH|ϕBHϕBH) ≈ ρAHH ⊙ ρBHH, | (43a) |
| | | (ϕALϕAL|ϕBLϕBL) ≈ ρALL ⊙ ρBLL, | (43b) |
| | | (ϕAHϕAH|ϕBLϕBL) ≈ ρAHH ⊙ ρBLL, | (43c) |
| | | (ϕALϕAL|ϕBHϕBH) ≈ ρALL ⊙ ρBHH. | (43d) |
In the limiting case when multipole expansion is truncated on the monopole terms, one finds that| | 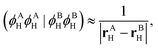 | (44) |
where the charge centroids of the HOMOs are given by| | rXH = (ϕXH|![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) |ϕXH). |ϕXH). | (45) |
Note that, once occupied molecular orbitals are localized, the above approximation should yield the correct description. However, the LUMOs are usually quite delocalized. Here, we use the distributed cumulative atomic charges to represent these:38| | 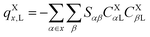 | (46) |
and one can find that assuming this one obtains| | 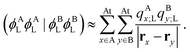 | (47) |
The two remaining ERIs can then be approximated as follows:| | 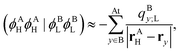 | (48) |
and similarly for the twin ERIs. To summarize the derivation, the CT matrix element is approximately given by| | 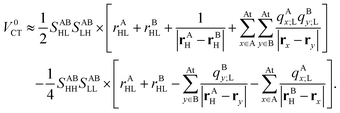 | (49) |
Thus, the computational cost of the above expression is negligible as compared to the original formula in eqn (40).
2.2.3 Approximate pure exchange coupling.
The Mulliken approximation can also be used to treat the pure exchange coupling (eqn (11)) which leads to| | 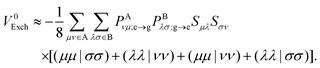 | (50) |
Here, such ERIs that involve AOs in two different molecules are approximated by| | 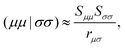 | (51) |
where rμσ is the distance between the centers of the μth and σth AOs. That leads to the following approximate expression:| | 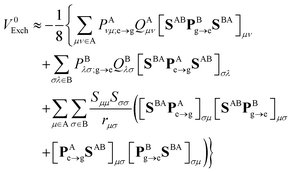 | (52) |
with Qμν ≡ (μμ|νν). Note that QAμν and QBλσ are just matrix elements of constant matrices. Although these are not second-rank tensors (i.e., they do not transform under Euclidean rotations as other AO matrices), they can be easily computed from a small set of proper fourth-rank tensors, which is shown in Appendix B. Therefore, the EFP methodology can still be used to calculate pure exchange Dexter contribution to the EET coupling and the computational cost of the overall procedure is negligible as compared to the evaluation of eqn (11) involving ERIs in the AO space directly.
2.2.4 Complete model of EET coupling.
To summarize, the overall form of the EOP-TI/CIS model is still given as in the original TI/CIS model26,31 by| | | V ≈ VDirect + VIndirect, | (53) |
where the direct and indirect coupling constants are, respectively,| | | VDirect ≡ VCoul + VExch + VOvlp, | (54a) |
| | | VIndirect ≡ VTI(2) + VTI(3), | (54b) |
with| | 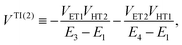 | (55a) |
| | 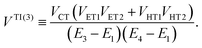 | (55b) |
In the above, the direct EET coupling contributions are| | 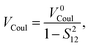 | (56a) |
| | 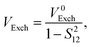 | (56b) |
| | 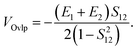 | (56c) |
whereas the indirect EET coupling is evaluated from the overlap-corrected ET, HT and CT matrix elements that read| | 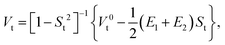 | (57) |
where ‘t’ denotes one of the matrix element types (ET1, ET2, HT1, HT2, CT) and St is the appropriate overlap integral between basis states.
Despite the same general form, the differences between the original TI/CIS model and the newly derived EOP-based approach are quite significant. The Hamiltonian matrix elements are evaluated from the effective fragment parameters, for which only the one-electron integrals are needed. Therefore, the computational cost is significantly reduced as compared to the parent TI/CIS model. In particular, the V0Coul term is evaluated by using the TrCAMM method developed previously,12 whereas V0Exch and V0CT are computed using the approximate Mulliken formulae in eqn (52) and (49), respectively. In turn, the electron and hole transfer terms V0ET1, V0ET2, V0HT1 and V0HT2 are treated by the EDF with EOP effective matrices as effective parameters spanned in the auxiliary AO basis set (eqn (32), (35), (37), (39) and (58)–(63)). Note that the evaluation of eqn (56) and (57) is computationally inexpensive because it involves computing only approximate overlap integrals between basis states.31
On the other hand, the relaxation effects due to the intermolecular interactions are not included in the current EOP-based model. Note that in the TDFI-TI/CIS model the basis states and all the one-particle density matrices are built from the self-consistently adjusted fragment ground-state densities according to the DFI method.28 However, as demonstrated in the following section, we do not expect major differences due to the relaxation effects.
2.3 Adaptation of the EOP-TI/CIS method as effective fragment potentials
In the previous sections, all interfragment ERIs were effectively eliminated from the original TI/CIS equations by using the EOP technique. Here, note that the following quantities, which are sufficient to evaluate the resulting EOP-TI/CIS EET coupling constant without calculating the interfragment ERIs, are functions of the isolated electronic chromophores:
• TrCAMMs of monomers A and B,
• excitation energies EAg→e and EBg→e, as well as the corresponding transition density matrices PAe→g and PBg→e,
• (pp|qq)A and (pp|qq)B tensor elements from Appendix B,
• VA;ETξ;HL, VB;ETη;L, VA;HTξ;L and VB;HTη;HL vector elements, each of length equal to the size of the auxiliary EOP basis set,
• CIS HOMO–LUMO amplitudes tAH→L and tBH→L,
• CAMMs of HOMO and LUMO densities from eqn (43), as well as the canonical orbital energies,
• distributed atomic charges qAx,L and qBy,L from eqn (46),
• localized HOMO centroids rAH and rBH from eqn (45), as well as intrafragment (and invariant with respect to the Euclidean rotations of chromophores) Coulomb-type ERIs rAHL and rBHL from eqn (42), and finally.
• primary and auxiliary basis sets.
Therefore, only one preparative calculation per chromophore is required to obtain all of the above quantities that constitute the EFPs, much like obtaining the EFPs for calculating the interaction energy by means of the second generation of the effective fragment potential (EFP2) method.39 The rate-determining step in computing the EFPs is the calculation of the CIS amplitudes which can be nowadays performed efficiently even for large molecules.
Such EOP-TI/CIS EFPs can be subsequently used in routine calculations of EET coupling constants in conjunction with the molecular dynamics and rigid molecule algorithm as developed previously in the context of calculations of the solvatochromic vibrational frequency shifts of infrared probes in condensed phases (SolEFP).40–45 Note that, once EFPs are computed, the evaluation of the EOP-TI/CIS equations requires only one-electron overlap integrals which are relatively inexpensive to calculate.
3 Results and discussion
All the models and approximations that were discussed so far were implemented in our inhouse plugin EOPDev46 to the Psi4 quantum chemistry package,47 along with the direct CIS method utilizing the Davidson–Liu simultaneous expansion approach.48–50 In this work, the tested levels of the TI/CIS theory are characterized by the treatment of the Fock operator in the expressions for the off-diagonal ET and HT Hamiltonian matrix elements. For example, in the case of V(0)ET1, the approximations denoted here as VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) and VTI(
) and VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) collectively refer to using eqn (24) and (29), respectively. VTI(
0) collectively refer to using eqn (24) and (29), respectively. VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) DFI0) indicates that the approximate Fock matrix was used as in eqn (29) but including the interfragment interactions in a self-consistent manner through the DFI process.28 The EOP-based model is denoted as VTI(
DFI0) indicates that the approximate Fock matrix was used as in eqn (29) but including the interfragment interactions in a self-consistent manner through the DFI process.28 The EOP-based model is denoted as VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) EOP0) and additionally utilizes the TrCAMM approximation for V(0)Coul, as well as the Mulliken approximation for V(0)Exch (eqn (52)) and V(0)CT (two variants are tested: the CAMM-based vatiant from eqn (41) with eqn (43) or the distributed charge-based variant from eqn (49)). Environmental correction terms from eqn (5) were included in all models except the VTI(
EOP0) and additionally utilizes the TrCAMM approximation for V(0)Coul, as well as the Mulliken approximation for V(0)Exch (eqn (52)) and V(0)CT (two variants are tested: the CAMM-based vatiant from eqn (41) with eqn (43) or the distributed charge-based variant from eqn (49)). Environmental correction terms from eqn (5) were included in all models except the VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) EOP0) model. In order to test the EOP-TI/CIS model we chose the EET coupling between the lowest-lying bright 1ππ* states of ethylene (1 1B1u) and 7-aminocoumarin (1 1A′) in stacked molecular dimers, having D2h and Cs symmetry, respectively. To test the performance and applicability of the proposed methodology we also performed preliminary calculations on the “special pair” in the reaction center of photosystem I (PS-I).10,14,51 To improve the convergence of the distributed multipole expansion of the Coulombic EET coupling constants, the transition densities used to compute the TrCAMMs were symmetrized as suggested by Belov et al.52 Occupied core orbitals were included in the CIS calculations except from the PS-I model for which the frozen-core approximation was utilized.
EOP0) model. In order to test the EOP-TI/CIS model we chose the EET coupling between the lowest-lying bright 1ππ* states of ethylene (1 1B1u) and 7-aminocoumarin (1 1A′) in stacked molecular dimers, having D2h and Cs symmetry, respectively. To test the performance and applicability of the proposed methodology we also performed preliminary calculations on the “special pair” in the reaction center of photosystem I (PS-I).10,14,51 To improve the convergence of the distributed multipole expansion of the Coulombic EET coupling constants, the transition densities used to compute the TrCAMMs were symmetrized as suggested by Belov et al.52 Occupied core orbitals were included in the CIS calculations except from the PS-I model for which the frozen-core approximation was utilized.
All the reported results were obtained assuming the 6-31G(d) basis set53 and, when required, the cc-pVDZ-JKFIT density-fitting basis set.54 To obtain EOP matrices for ET and HT Hamiltonian matrix elements, the EDF scheme32 was utilized with aug-cc-pVDZ-JKFIT54 as the auxiliary EOP basis set. Further details of calculations and the selected geometries of the studied complexes are provided in the ESI.†
3.1 Accuracy of transfer integral approximations
The total magnitudes of EET couplings between stacked ethylene molecules in the 1 1B1u states and 7-aminocoumarin in the 1 1A′ states, obtained for the selected geometries, are compiled in Table 1. The equilibrium geometry of the ethylene dimer was optimized using the MP2/6-31G(d) method assuming D2h symmetry of the complex and EET couplings were then computed for the selected intermolecular distances (RAB) by translation of the molecules along the intermolecular axis. The RAB distance between the neighboring carbon atoms of 4.169 Å corresponds to the minimum energy structure. At a distance of 6.0 Å the V0Exch term drops below 0.002 cm−1 and the total coupling is virtually identical to Coulomb contribution, whereas the structure for RAB = 3.0 Å represents the region of large overlap of molecular wavefunctions where V0Exch exceeds 1700 cm−1. The 7-aminocoumarin (7AC) dimer was prepared as reported in our previous study.12 The structures of two flat 7AC molecules optimized at the MP2/6-31g(d) level were superimposed and shifted with respect to the intermolecular axis. Such a rigid potential energy (PE) scan shows a minimum at RAB = 3.6 Å, while the regions of large and negligible overlap, identified analogously as in the ethylene dimer (i.e. based on the magnitudes of V0Exch), occur at intermolecular distances of roughly 2.6 and 4.6 Å, respectively.
Table 1 EET couplings (in cm−1) computed between the lowest-lying bright 1ππ* states in the studied ethylene and 7-aminocoumarin stacked dimers at various levels of approximation (indicated in parentheses by the corresponding Fock matrix estimate) to the CIS reference values. All the results were computed for the selected intermolecular distances RAB (given in Å) assuming the 6-31G(d) basis set
|
R
AB
|
(Ethylene)2 |
(7AC)2 |
| 3.0 |
4.169 |
6.0 |
2.6 |
3.6 |
4.6 |
|
V
ESD
|
9893 |
1973 |
495 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 291 291 |
2433 |
868 |
V
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) ) |
7990 |
1744 |
495 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 576 576 |
1782 |
840 |
V
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) DFI0) DFI0) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156 156 |
1762 |
495 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241 241 |
1942 |
835 |
V
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) 0) |
9953 |
1766 |
495 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135 135 |
1949 |
842 |
V
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) EOP0) EOP0) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 481 481 |
1772 |
494 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 617 617 |
2175 |
837 |
The reference values of the total EET coupling VESD were calculated using the energy splitting in dimer (ESD) method,24,55 in which the coupling is calculated as half of the splitting between the corresponding adiabatic excited state energies in a dimer. In the case of the studied symmetric complexes this method provides the accurate electronic coupling. The transfer-integral VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) values, computed assuming the exact Fock matrix of the dimer, are very close to the ESD reference at large and intermediate intermolecular separations and become more approximate at shorter distances. The VTI(
) values, computed assuming the exact Fock matrix of the dimer, are very close to the ESD reference at large and intermediate intermolecular separations and become more approximate at shorter distances. The VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) results represent the limiting accuracy of the TI/CIS frontier-orbitals model which is semi-quantitative at equilibrium geometries and becomes only qualitatively correct at shorter distances. Their calculations for the ethylene dimer took 9.2 s of CPU time on one core of the 1.2 GHz AMD EPYC 7301 16-core processor. The VTI(
) results represent the limiting accuracy of the TI/CIS frontier-orbitals model which is semi-quantitative at equilibrium geometries and becomes only qualitatively correct at shorter distances. Their calculations for the ethylene dimer took 9.2 s of CPU time on one core of the 1.2 GHz AMD EPYC 7301 16-core processor. The VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) DFI0) values correspond to the original transition-density-fragment interaction method (TDFI-TI) of Fujimoto,31 because the density-fragment interaction (DFI) method28,29 is used to take into account molecular surroundings in the Fock matrix of the chromophores in a self-consistent fashion. These are overestimated at short distances and underestimated at the equilibrium geometry by roughly 10–20% (depending on the system). As expected, all the tested models predict virtually identical results at large intermolecular separations.
DFI0) values correspond to the original transition-density-fragment interaction method (TDFI-TI) of Fujimoto,31 because the density-fragment interaction (DFI) method28,29 is used to take into account molecular surroundings in the Fock matrix of the chromophores in a self-consistent fashion. These are overestimated at short distances and underestimated at the equilibrium geometry by roughly 10–20% (depending on the system). As expected, all the tested models predict virtually identical results at large intermolecular separations.
The effect of mutual polarization taken into account in the TDFI-TI method via the block-localized self-consistent density-fragment interaction procedure28 seems to be rather small. This may be inferred from Table 1 by a comparison of VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) DFI0) and VTI(
DFI0) and VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) magnitudes, the relative differences of which are below 2% even at short intermolecular distances. In the latter approach the dimer Fock matrix was constructed from the Fock matrices of monomers assuming the symmetric partitioning introduced in eqn (27) and (28), and thus the interacting monomer ground-state densities were not relaxed in this case. Both calculations took about 3.2 s in the same CPU (cf. Table S3 in the ESI†) which shows about 20% speedup with respect to the calculations of VTI(
0) magnitudes, the relative differences of which are below 2% even at short intermolecular distances. In the latter approach the dimer Fock matrix was constructed from the Fock matrices of monomers assuming the symmetric partitioning introduced in eqn (27) and (28), and thus the interacting monomer ground-state densities were not relaxed in this case. Both calculations took about 3.2 s in the same CPU (cf. Table S3 in the ESI†) which shows about 20% speedup with respect to the calculations of VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) using the exact Fock matrix of the ethylene dimer. Note, however, that the reported timings do not include the time to solve the SCF and CIS problems for the monomers – VTI(
) using the exact Fock matrix of the ethylene dimer. Note, however, that the reported timings do not include the time to solve the SCF and CIS problems for the monomers – VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) DFI0) calculations are obviously longer than VTI(
DFI0) calculations are obviously longer than VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) ones in terms of the elapsed time since the Hartree–Fock problem for the monomers is solved in a block-localized self-consistent fashion for the whole complex.
0) ones in terms of the elapsed time since the Hartree–Fock problem for the monomers is solved in a block-localized self-consistent fashion for the whole complex.
It is interesting to note that the corresponding EOP-TI calculations took only a few milliseconds of CPU time, which is nearly three orders of magnitude faster (cf. Table S3, ESI†), while showing virtually no signs of loss in the accuracy, as the VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) EOP0) values obtained for the ethylene dimer reproduce consistently the VTI(
EOP0) values obtained for the ethylene dimer reproduce consistently the VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) estimates with a 1–2% accuracy even at short distances. In the case of the 7AC complex the speedup is more spectacular, since VTI(
0) estimates with a 1–2% accuracy even at short distances. In the case of the 7AC complex the speedup is more spectacular, since VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) calculations took about 25 minutes while VTI(
0) calculations took about 25 minutes while VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) EOP0) only 79 milliseconds (nearly 20
EOP0) only 79 milliseconds (nearly 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times faster). The speedup is even larger for PS-I, for which the respective timings are about 137 hours vs. 6 seconds. The relative differences of total couplings are larger in this system (within about ±7%) but one could argue that at short distances the EOP-TI values are, in fact, consistently closer to the reference values. This, however, is entirely due to the cancellation of errors. The fact is that essentially all the discussed TI models show quite similar accuracy, but the EOP-TI approach is simply much more efficient.
000 times faster). The speedup is even larger for PS-I, for which the respective timings are about 137 hours vs. 6 seconds. The relative differences of total couplings are larger in this system (within about ±7%) but one could argue that at short distances the EOP-TI values are, in fact, consistently closer to the reference values. This, however, is entirely due to the cancellation of errors. The fact is that essentially all the discussed TI models show quite similar accuracy, but the EOP-TI approach is simply much more efficient.
The same conclusions arise from the analysis of the PE cuts shown in Fig. 1, where in panels (a) and (c) the total TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) )/CIS couplings and their components are plotted along with the reference ESD values for the model systems in the vicinity of their equilibrium geometries. The total TI(
)/CIS couplings and their components are plotted along with the reference ESD values for the model systems in the vicinity of their equilibrium geometries. The total TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) coupling (marked with gray lines and asterisks) underestimates slightly the ESD values (shown as black lines with circles) at equilibrium and shorter distances. The agreement is at least semi-quantitative unless the region of very large overlap is considered, which would however be hardly accessible in any real physical situation (note the corresponding interaction energies plotted as gray dashed lines vs. the right axis). For instance, in the 7AC dimer this occurs for ΔRAB below −0.9 Å (cf.Fig. 1c), where the TI(
) coupling (marked with gray lines and asterisks) underestimates slightly the ESD values (shown as black lines with circles) at equilibrium and shorter distances. The agreement is at least semi-quantitative unless the region of very large overlap is considered, which would however be hardly accessible in any real physical situation (note the corresponding interaction energies plotted as gray dashed lines vs. the right axis). For instance, in the 7AC dimer this occurs for ΔRAB below −0.9 Å (cf.Fig. 1c), where the TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) estimates start to diverge from the ESD coupling, but the intermolecular repulsion in this region exceeds 190 kJ mol−1.
) estimates start to diverge from the ESD coupling, but the intermolecular repulsion in this region exceeds 190 kJ mol−1.
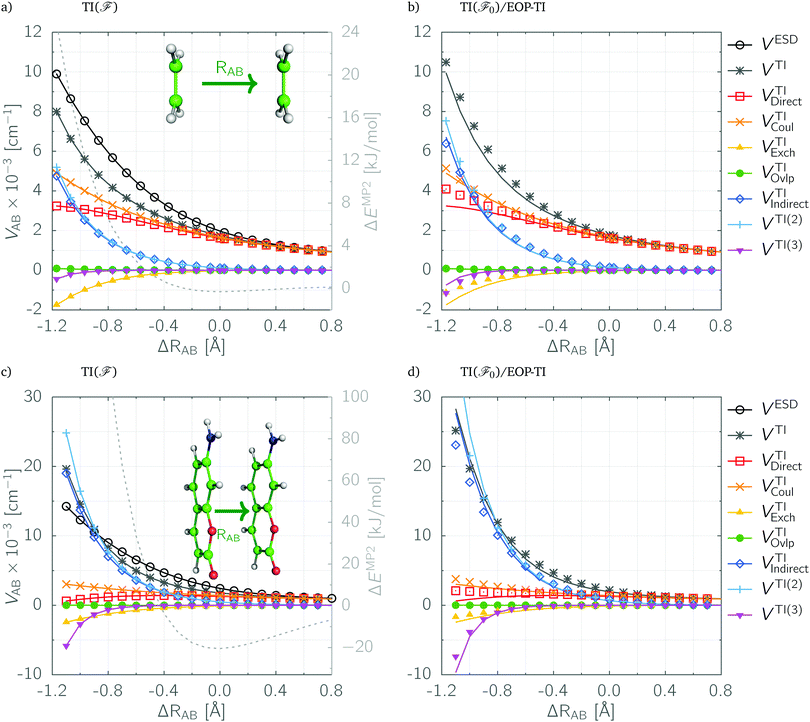 |
| | Fig. 1 EET couplings and their partitioning in symmetric ethylene (a and b) and 7AC dimers (c and d) as a function of intermolecular separation. ΔRAB is the translation with respect to the equilibrium distance. In the left panels (a and c) the reference ESD values are plotted along with the best TI/CIS estimates obtained for the exact dimeric Fock matrix. In the right panels (b and d) the TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) results plotted as solid lines are compared with their EOP-TI( 0) results plotted as solid lines are compared with their EOP-TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) estimates shown as points. 0) estimates shown as points. | |
3.2 Partitioning of EET couplings
In Tables 2 and 3 the detailed partitioning of EET couplings in ethylene and 7AC dimers, respectively, is shown for the selected intermolecular separations. At large distances the total coupling VTI is determined solely by the direct electrostatic contribution which can be accurately approximated from TrCAMM expansion. At the equilibrium geometry the exchange, overlap and third-order VTI(3) terms are still negligible. However, the total indirect coupling is already significant and almost exclusively due to the second-order terms VTI(2). The same applies also to the special pair of photosystem I (cf. Table S4 of the ESI†), which was chosen to test the performance of the EOP-TI scheme. The vanishingly small values of VOvlp terms indicate that the relevant adiabatic states of monomers in the studied model systems are virtually orthogonal. Only in the case of the ethylene dimer in the large-overlap region do they rise slightly. Even though the studied ethylene dimer is very weakly bound, having an interaction energy of less than 1 kJ mol−1 in the MP2/6-31G(d) minimum energy structure, the corresponding interaction energy in the 7AC dimer amounts to about 20 kJ mol−1. Thus, it appears that the above conclusions could be general for interacting systems in the vicinity of equilibrium geometry. In the region of large overlap the exchange and third-order terms become significant. In fact, the indirect coupling becomes the leading component with a dominant contribution from the second-order terms. In general the VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) partitioning, being a starting point for the introduction of EOP approximation, agrees quantitatively with the corresponding TDFI estimates. The differences between these two methods are essentially due to the lack of relaxation effects in the former. The largest differences are in the magnitudes of second-order terms, which still fall within a few percent margin, unless the Mulliken approximation is utilized. It is interesting to note that in the case of the special pair of PS-I (Table S4, ESI†) at the experimental geometry the agreement is virtually quantitative, for both the total coupling (171 vs. 178 cm−1) and its components. The latter being mostly due to the direct electrostatic coupling VCoul (157 vs. 161 cm−1) and the second-order indirect contribution VTI(2) (15.8 vs. 17.6 cm−1).
0) partitioning, being a starting point for the introduction of EOP approximation, agrees quantitatively with the corresponding TDFI estimates. The differences between these two methods are essentially due to the lack of relaxation effects in the former. The largest differences are in the magnitudes of second-order terms, which still fall within a few percent margin, unless the Mulliken approximation is utilized. It is interesting to note that in the case of the special pair of PS-I (Table S4, ESI†) at the experimental geometry the agreement is virtually quantitative, for both the total coupling (171 vs. 178 cm−1) and its components. The latter being mostly due to the direct electrostatic coupling VCoul (157 vs. 161 cm−1) and the second-order indirect contribution VTI(2) (15.8 vs. 17.6 cm−1).
Table 2 Partitioning of EET couplings computed between the lowest-lying bright 1ππ* states of ethylene molecules in stacked alignment at various levels of approximation to the TI/CIS method. Indentation indicates constituents of a given term or its approximation. All the results, given in cm−1, were computed for the selected intermolecular distances RAB (given in Å) assuming the 6-31G(d) basis set. The superscript ‘M’ indicates the values estimated using the Mulliken approximation: eqn (52) for the EOP-TI model and eqn (50) for the remaining models. The VTI(3) values in the EOP-TI results were computed assuming either the distributed multipolar expansion truncated on |R|−5 terms or on atomic monopoles (values in parentheses) in VCT calculations
| TI/CIS model |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) ) |
TDFI |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) 0) |
EOP |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) ) |
TDFI |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) 0) |
EOP |
|
|
R
AB = 3.0 |
4.169 |
|
V
TI
|
7990 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156 156 |
9953 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 481 (10 481 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500) 500) |
1744 |
1762 |
1766 |
1772 (1772) |
|
|
| VDirect |
3239 |
3221 |
3239 |
4093 |
1626 |
1622 |
1626 |
1622 |
|
|
| VCoul |
4896 |
4885 |
4896 |
— |
1654 |
1649 |
1654 |
— |
| VTrCAMMCoul |
5133 |
5120 |
5133 |
5133 |
1638 |
1634 |
1638 |
1638 |
| VExch |
−1743 |
−1751 |
−1743 |
— |
−30 |
−29 |
−30 |
— |
| VMExch |
−1174 |
−1179 |
−1174 |
−1125 |
−19 |
−18 |
−19 |
−18 |
| VOvlp |
86 |
86 |
86 |
86 |
2 |
2 |
2 |
2 |
|
|
| VIndirect |
4751 |
6936 |
6714 |
6388 (6407) |
118 |
140 |
141 |
150 (150) |
|
|
| VTI(2) |
5189 |
7708 |
7462 |
7533 |
118 |
140 |
141 |
150 |
| VTI(3) |
−438 |
−773 |
−748 |
— |
0 |
0 |
0 |
— |
| VTI(3),M |
−695 |
−1225 |
−1185 |
−1145 (−1126) |
0 |
0 |
0 |
0 (0) |
Table 3 Partitioning of EET couplings computed between the lowest-lying bright 1ππ* states of two 7AC molecules in stacked alignment at various levels of approximation to the TI/CIS method. Indentation indicates constituents of a given term or its approximation. All the results, given in cm−1, were computed for the selected intermolecular distances RAB (given in Å) assuming the 6-31G(d) basis set. The superscript ‘M’ indicates the values estimated using the Mulliken approximation: eqn (52) for the EOP-TI model and eqn (50) for the remaining models. The VTI(3) values in the EOP-TI results were computed assuming either the distributed multipolar expansion truncated on |R|−5 terms or on atomic monopoles (values in parentheses) in VCT calculations
| TI/CIS model |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) ) |
TDFI |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) 0) |
EOP |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) ) |
TDFI |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) 0) |
EOP |
|
|
R
AB = 2.6 |
3.6 |
|
V
TI
|
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 576 576 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241 241 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135 135 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 703 (19 703 (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 617) 617) |
1782 |
1942 |
1949 |
2175 (2175) |
|
|
| VDirect |
859 |
700 |
859 |
1987 |
1294 |
1286 |
1294 |
1352 |
|
|
| VCoul |
2803 |
2903 |
2803 |
— |
1397 |
1389 |
1397 |
— |
| VTrCAMMCoul |
3344 |
3543 |
3344 |
3344 |
1422 |
1414 |
1422 |
1422 |
| VExch |
−1960 |
−2220 |
−1960 |
— |
−104 |
−104 |
−104 |
— |
| VMExch |
−1412 |
−1605 |
−1412 |
−1373 |
−73 |
−73 |
−73 |
−71 |
| VOvlp |
16 |
18 |
16 |
15 |
1 |
1 |
1 |
1 |
|
|
| VIndirect |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 717 717 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 541 541 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 276 276 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 716 (17 716 (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630) 630) |
487 |
656 |
655 |
823 (823) |
|
|
| VTI(2) |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 427 427 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271 271 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776 776 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 545 545 |
490 |
659 |
658 |
827 |
| VTI(3) |
−2710 |
−5730 |
−4500 |
— |
−2 |
−3 |
−3 |
— |
| VTI(3),M |
−2993 |
−6292 |
−4971 |
−3829 (−3914) |
−2 |
−3 |
−3 |
−4 (−4) |
The excellent agreement of EOP-TI estimates with TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) results is demonstrated for a broader range of intermolecular distances in Fig. 1. In panels (b) and (d) the latter are plotted as solid lines while the former as points. In the vicinity of equilibrium geometry the agreement is nearly quantitative and starts deteriorating in the hardly accessible region of very large overlap. However, since the EOP-TI couplings start to underestimate the TI(
0) results is demonstrated for a broader range of intermolecular distances in Fig. 1. In panels (b) and (d) the latter are plotted as solid lines while the former as points. In the vicinity of equilibrium geometry the agreement is nearly quantitative and starts deteriorating in the hardly accessible region of very large overlap. However, since the EOP-TI couplings start to underestimate the TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) values, which in turn overestimate the reference ESD values, the EOP-TI results are consistently closer to the reference. In fact, this is true also at larger intermolecular separations, since the major difference in EOP-TI components is found for the second-order terms being overestimated at large distances and underestimated at short distances.
0) values, which in turn overestimate the reference ESD values, the EOP-TI results are consistently closer to the reference. In fact, this is true also at larger intermolecular separations, since the major difference in EOP-TI components is found for the second-order terms being overestimated at large distances and underestimated at short distances.
The basis set extension effects are discussed thoroughly in the ESI† (see Fig. S1). Generally, the choice of aug-cc-pVDZ-JKFIT as the auxiliary EOP basis set is sufficient even for more flexible orbital basis sets, at least for the first-row atom molecules studied here. The choice of the orbital basis set is more critical, particularly for the calculations of indirect couplings. However, the latter constitute only about 20–30% of the total TI/CIS coupling at minimum energy geometries of the studied model systems. The direct contribution, on the other hand, is sufficiently saturated already in the split-valence polarized double-zeta basis set. Interestingly, the TI/CIS values converge quickly to the exact ESD coupling with basis set extension.
3.3 Accuracy of Mulliken and multipolar expansion approximations
The accuracy of the Mulliken approximation for the estimation of pure exchange coupling VExch appears to be semi-quantitative at the equilibrium geometry and becomes qualitative at shorter intermolecular distances, as the VMExch term underestimates significantly the magnitude of exchange coupling (cf.Tables 2 and 3). It is interesting to note here that the simplified model of VExch in the EOP-TI model from eqn (52) works qualitatively well for both studied systems, as the coupling strength is systematically underestimated. In the case of indirect coupling terms, the Mulliken approximation can be utilized to estimate the magnitude of VCT matrix elements and, hence, the third-order VTI(3) terms. In fact, this approximation is necessary in the EOP-TI model. However, it works very well and provides the quantitative accuracy of VMCT terms at equilibrium geometry but becomes more approximate in the region of large overlap of molecular wavefunctions (cf.Table 4). It is also interesting to note that the magnitudes of VMCT terms, calculated in the EOP-TI method assuming the distributed multipolar expansion truncated either on |R|−5 terms or on atomic monopoles (values in parentheses), are virtually identical at equilibrium geometry and remain very close even at shorter distances.
Table 4 Electron, hole and charge transfer (ET, HT and CT, respectively) Hamiltonian matrix elements calculated at various levels of approximation for EET couplings between the lowest-lying bright 1ππ* states in ethylene and 7AC dimers in stacked alignment. All the results, given in cm−1, were computed for the selected intermolecular distances RAB (given in Å) assuming the 6-31G(d) basis set. The superscript ‘M’ indicates the values estimated using the Mulliken approximation: eqn (52) for the EOP-TI model and eqn (50) for the remaining models. The VCT values in the EOP-TI results were computed assuming the distributed multipolar expansion truncated either on |R|−5 terms or on atomic monopoles (values in parentheses)
| TI/CIS model |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) ) |
TDFI |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) 0) |
EOP |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) ) |
TDFI |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) 0) |
EOP |
| (Ethylene)2 |
R
AB = 3.0 |
4.169 |
|
V
ET1
|
−4306 |
−4485 |
−4393 |
−4516 |
−1170 |
−1172 |
−1172 |
−1248 |
|
V
HT1
|
6626 |
9422 |
9337 |
9591 |
1161 |
1379 |
1383 |
1383 |
|
V
CT
|
−849 |
−853 |
−849 |
— |
−15 |
−15 |
−15 |
— |
| VMCT |
−1346 |
−1352 |
−1346 |
−1347 (−1325) |
−23 |
−22 |
−23 |
−23 (−22) |
| TI/CIS model |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) ) |
TDFI |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) 0) |
EOP |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) ) |
TDFI |
TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) 0) |
EOP |
| (7AC)2 |
R
AB = 2.6 |
3.6 |
|
V
ET1
|
−7025 |
−7348 |
−7403 |
−7317 |
−1782 |
−1849 |
−1838 |
−2107 |
|
V
HT1
|
8368 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 195 195 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 978 978 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976 976 |
1928 |
2510 |
2511 |
2767 |
|
V
CT
|
−1163 |
−1316 |
−1163 |
— |
−65 |
−65 |
−65 |
— |
| VMCT |
−1284 |
−1445 |
−1284 |
−1286 (−1315) |
−67 |
−67 |
−67 |
−67 (−68) |
In Table 4 the relevant Hamiltonian matrix elements necessary for calculating indirect coupling terms are reported for the studied model systems at selected geometries and levels of TI approximation. The magnitudes of VET1 and VET2 terms are identical due to the symmetry of the studied complexes and the same applies to the corresponding HT terms. It should be noted that the signs of these terms depend on the arbitrary phases of frontier orbitals (this is true for all the TI components). However, this does not affect the total magnitude of EET coupling. In this work we adhere to certain convention for which the total coupling is positive. Unfortunately, we have found certain discrepancies between our results and those reported by Fujimoto.31 A careful analysis of the formula for the CT term given in eqn (40) shows that it should always be negative. A similar inspection of the formulas for ET and HT terms (eqn (24) and (36)) shows that, even though their signs may vary, the resultant VTI(2) and VTI(3) terms, defined in eqn (55), should have opposite signs. Fujimoto, however, reported both terms as having the same positive sign. We were also unable to reproduce the total magnitudes of VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) DFI0), which, as shown in Fig. 3 of Fujimoto's paper,31 seem to be virtually identical to VESD. This is quite surprising considering the crudeness of approximation (frontier orbitals and block-localized Fock matrix). For instance our TDFI-TI results, reported in Table 1, show a relative error of about 3% at a distance of 3 Å.
DFI0), which, as shown in Fig. 3 of Fujimoto's paper,31 seem to be virtually identical to VESD. This is quite surprising considering the crudeness of approximation (frontier orbitals and block-localized Fock matrix). For instance our TDFI-TI results, reported in Table 1, show a relative error of about 3% at a distance of 3 Å.
4 Summary and a few concluding remarks
In this work, the effective one-electron potential operators technique of electron-repulsion integral elimination was used to introduce a new efficient variant of the transfer integral approach to calculate excitation energy transfer couplings. The EOP technique was adopted to estimate the EET couplings between singlet bright states in ethylene and 7-aminocoumarine dimers assuming the TI/CIS super-exchange model of Scholes and Harcourt within the frontier orbital approximation introduced earlier by Fujimoto.
It was shown that the EOP-TI/CIS method provides semi-quantitative results even at short distances and the computational cost is reduced by at least 3 orders of magnitude, as compared to the TDFI-TI/CIS calculations. This speedup is expected to increase with the system size as in the 7-aminocoumarine dimer the EOP-TI/CIS calculations were nearly 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times faster than the most efficient variant of the TDFI-TI/CIS approach.
000 times faster than the most efficient variant of the TDFI-TI/CIS approach.
In fact, the EOP-TI/CIS method was found to be so efficient that it is readily applicable in molecular dynamics simulations. This is due to its EOP-based formulation which defines the EET coupling in terms of effective fragment potential parameters which could be determined prior to the simulation in a fully automated fashion for a given excited state of each of the interacting molecules. We note here that the computational costs can be further reduced by applying much smaller tailored density fitting auxiliary EOP basis sets.32
It is anticipated here that the EOP-TI/CIS method can be extended to a general multi-state model with multiple electron–hole pairs and bridging CT states,19,20 because the mathematical form of ERIs within the TIs remains the same as that in the current EOP-TI/CIS model. In other words the extended density fitting EOP method is in principle applicable to any ET- and HT-like matrix elements, whereas the Mulliken approximation and distributed multipole expansion are applicable to any CT-like matrix element.
Conflicts of interest
There are no conflicts to declare.
Appendices
A Explicit formulae for ET and HT EOP matrix elements
As developed in ref. 32, the matrix elements of the EOP operators are computed from the EDF scheme, according to which (in general the TI/CIS case)| | 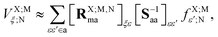 | (58) |
where| | 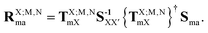 | (59) |
In the above equations, the auxiliary matrices are defined by| | | TX;M,NmX = Smm−1SmaTX;M,NaXSXX−1, | (60a) |
| | | SXX−1 = ({TX;M,NaX}†SamSmm−1SmaTX;M,NaX)½, | (60b) |
| | TX;M,NaX = Saa−1![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) UX;M,NaX, UX;M,NaX, | (60c) |
where the overlap matrix block corresponding to two AO basis sets ‘x’ and ‘y’ is| | 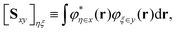 | (61) |
and the symbol ‘m’ denotes the (generally incomplete) auxiliary EOP AO basis set, whereas the symbol ‘a’ denotes the intermediate AO basis set that approximately fulfills the resolution of identity. The similarity transformation matrix TX;M,NaX is obtained from the eigenvectors of the co-variance matrix, WX;M,Naa:| | 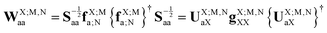 | (62) |
The operator ![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) in eqn (60c) selects only eigenvectors (columns of) UX;M,NaX associated with the non-vanishing eigenvalues stored in the diagonal matrix gX;M,NXX. The elements of vector fX;MN for M = ET1, ET2, HT1 and HT2 and N = H, L and HL are given by
in eqn (60c) selects only eigenvectors (columns of) UX;M,NaX associated with the non-vanishing eigenvalues stored in the diagonal matrix gX;M,NXX. The elements of vector fX;MN for M = ET1, ET2, HT1 and HT2 and N = H, L and HL are given by| | 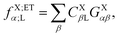 | (63a) |
| | 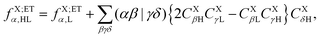 | (63b) |
| | 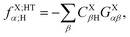 | (63c) |
| | 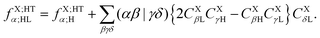 | (63d) |
Here, the auxiliary one-electron operator ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) X0 represented in space spanned by the intermediate and primary AO basis sets needs to be computed. This can be done by inverting the following matrix equation to obtain GXαβ:
X0 represented in space spanned by the intermediate and primary AO basis sets needs to be computed. This can be done by inverting the following matrix equation to obtain GXαβ:| | 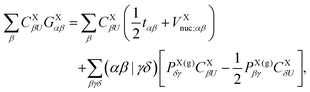 | (64) |
where| | 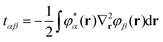 | (65a) |
and| | 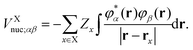 | (65b) |
In the above, Zx is the atomic number of the xth atom and 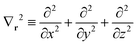 . In this work, the auxiliary EOP basis set was assumed to be identical to the intermediate basis set, i.e., conventional density fitting was used with [RX;M,Nma]ξε = δξε. However, by utilizing the general EDF scheme from eqn (58), additional reduction of computational cost is possible through optimization of the auxiliary EOP basis set.
. In this work, the auxiliary EOP basis set was assumed to be identical to the intermediate basis set, i.e., conventional density fitting was used with [RX;M,Nma]ξε = δξε. However, by utilizing the general EDF scheme from eqn (58), additional reduction of computational cost is possible through optimization of the auxiliary EOP basis set.
B Effective parameters for Dexter coupling
The Euclidean rotation of a shell of np atomic orbitals with angular momentum p is given byin which the shell |p) ≡ {…,φμ(r),…} and R(p) is the np × np rotation matrix. Consider now the integrals of type (pp|qq). It immediately follows that| | | (p′p′|q′q′) = R(p) ⊗ R(p) ⊗ R(q) ⊗ R(q)::(pp|qq) | (67) |
and the Q matrix from eqn (52) can be readily constructed by using| | | Q ≡ (diag[pp]|diag[qq]), | (68) |
where ‘diag’ denotes taking the diagonal of a matrix. The symbol ‘::’ denotes the fourfold tensor contraction 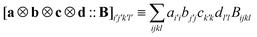 for arbitrary matrices a, b, c, d and a fourth-rank tensor B. Note that the number of (pp|qq) integrals scales quadratically with the size of the basis set which means that memory requirements to store them on a disk or in a file are relatively small and comparable to sizes of typical AO matrices. Therefore, all the (pp|qq) integrals can be treated as effective fragment parameters and the computational cost of superimposition onto a target geometry, which is described by eqn (68) and (67), is relatively small.
for arbitrary matrices a, b, c, d and a fourth-rank tensor B. Note that the number of (pp|qq) integrals scales quadratically with the size of the basis set which means that memory requirements to store them on a disk or in a file are relatively small and comparable to sizes of typical AO matrices. Therefore, all the (pp|qq) integrals can be treated as effective fragment parameters and the computational cost of superimposition onto a target geometry, which is described by eqn (68) and (67), is relatively small.
Acknowledgements
This project was funded by the National Science Centre, Poland (grant no. 2016/23/P/ST4/01720) within the POLONEZ 3 fellowship. The POLONEZ programme has received funding from the Horizon 2020 research and innovation programme of the European Union under the Marie Skłodowska-Curie grant agreement no. 665778.
Notes and references
-
E. Haas, Protein Folding Handbook, Wiley-VCH Verlag GmbH, Weinheim, Germany, 2005, pp. 573–633 Search PubMed
 .
.
- E. Lerner, T. Cordes, A. Ingargiola, Y. Alhadid, S. Chung, X. Michalet and S. Weiss, Science, 2018, 359, 6373 CrossRef
 .
.
- T. Renger, Photosynth. Res., 2009, 102, 471–485 CrossRef CAS
 .
.
- Z.-Q. You and C.-P. Hsu, Int. J. Quantum Chem., 2014, 114, 102–115 CrossRef CAS
 .
.
- A. Olaya-Castro and G. D. Scholes, Int. Rev. Phys. Chem., 2011, 30, 49–77 Search PubMed
 .
.
- A. Chenu and G. D. Scholes, Annu. Rev. Phys. Chem., 2015, 66, 69–96 CrossRef CAS
 .
.
- C. Curutchet and B. Mennucci, Chem. Rev., 2017, 117, 294–343 CrossRef CAS
 .
.
- L. Cupellini, M. Corbella, B. Mennucci and C. Curutchet, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1392 Search PubMed
 .
.
- T. Förster, Ann. Phys., 1948, 437, 55–75 CrossRef
 .
.
- M. E. Madjet, A. Abdurahman and T. Renger, J. Phys. Chem. B, 2006, 110, 17268–17281 CrossRef CAS
 .
.
- K. J. Fujimoto, J. Chem. Phys., 2014, 141, 214105 CrossRef
 .
.
- B. Błasiak, M. Maj, M. Cho and R. W. Góra, J. Chem. Theory Comput., 2015, 11, 3259–3266 CrossRef
 .
.
- C.-P. Hsu, Z.-Q. You and H.-C. Chen, J. Phys. Chem. C, 2008, 112, 1204–1212 CrossRef CAS
 .
.
- M. E.-A. Madjet, F. Müh and T. Renger, J. Phys. Chem. B, 2009, 113, 12603–12614 CrossRef
 .
.
- B. Shi, F. Gao and W. Liang, Chem. Phys., 2012, 394, 56–63 CrossRef CAS
 .
.
- J. Frenkel, Phys. Rev., 1931, 37, 1276–1294 CrossRef
 .
.
- A. Sisto, D. R. Glowacki and T. J. Martinez, Acc. Chem. Res., 2014, 47, 2857–2866 CrossRef CAS
 .
.
- T. Fujita, S. Atahan-Evrenk, N. P. D. Sawaya and A. Aspuru-Guzik, J. Phys. Chem. Lett., 2016, 7, 1374–1380 CrossRef CAS
 .
.
- X. Li, R. M. Parrish, F. Liu, S. I. L. Kokkila Schumacher and T. J. Martínez, J. Chem. Theory Comput., 2017, 13, 3493–3504 CrossRef CAS
 .
.
- T. Fujita and Y. Mochizuki, J. Phys. Chem. A, 2018, 122, 3886–3898 CrossRef CAS
 .
.
- I. O. Glebov, M. I. Kozlov and V. V. Poddubnyy, Comput. Theor. Chem., 2019, 1153, 12–18 CrossRef CAS
 .
.
- R. J. Cave and M. D. Newton, Chem. Phys. Lett., 1996, 249, 15–19 CrossRef CAS
 .
.
- A. A. Voityuk and N. Rösch, J. Chem. Phys., 2002, 117, 5607–5616 CrossRef CAS
 .
.
- M. D. Newton, Chem. Rev., 1991, 91, 767–792 CrossRef CAS
 .
.
- M. A. Ratner, J. Phys. Chem., 1990, 94, 4877–4883 CrossRef CAS
 .
.
- G. D. Scholes and K. P. Ghiggino, J. Chem. Phys., 1994, 101, 1251–1261 CrossRef CAS
 .
.
- G. D. Scholes and R. D. Harcourt, J. Chem. Phys., 1996, 104, 5054–5061 CrossRef CAS
 .
.
- K. Fujimoto and W. Yang, J. Chem. Phys., 2008, 129, 054102 CrossRef
 .
.
- K. J. Fujimoto and S. Hayashi, J. Am. Chem. Soc., 2009, 131, 14152–14153 CrossRef CAS
 .
.
- K. J. Fujimoto, J. Chem. Phys., 2010, 133, 124101 CrossRef
 .
.
- K. J. Fujimoto, J. Chem. Phys., 2012, 137, 034101 CrossRef
 .
.
- B. Błasiak, J. D. Bednarska, M. Chołuj, R. W. Góra and W. Bartkowiak, J. Comput. Chem., 2020 DOI:10.1002/jcc.26462
 .
.
- J. B. Foresman, M. Head-Gordon, J. A. Pople and M. J. Frisch, J. Phys. Chem., 1992, 96, 135–149 CrossRef CAS
 .
.
- Z.-Q. You, C.-P. Hsu and G. R. Fleming, J. Chem. Phys., 2006, 124, 044506 CrossRef
 .
.
- S. Yeganeh and T. V. Voorhis, J. Phys. Chem. C, 2010, 114, 20756–20763 CrossRef CAS
 .
.
- S. S. Skourtis, C. Liu, P. Antoniou, A. M. Virshup and D. N. Beratan, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8115–8120 CrossRef CAS
 .
.
- O. Ayed, E. Bernard and B. Silvi, THEOCHEM, 1986, 135, 159–168 CrossRef
 .
.
- W. Sokalski and R. Poirier, Chem. Phys. Lett., 1983, 98, 86–92 CrossRef CAS
 .
.
- M. S. Gordon, Q. A. Smith, P. Xu and L. V. Slipchenko, Annu. Rev. Phys. Chem., 2013, 64, 553–578 CrossRef CAS
 .
.
- B. Błasiak, H. Lee and M. Cho, J. Chem. Phys., 2013, 139, 044111 CrossRef
 .
.
- B. Błasiak and M. Cho, J. Chem. Phys., 2014, 140, 164107 CrossRef
 .
.
- B. Błasiak and M. Cho, J. Chem. Phys., 2015, 143, 164111 CrossRef
 .
.
- B. Błasiak, A. W. Ritchie, L. J. Webb and M. Cho, Phys. Chem. Chem. Phys., 2016, 18, 18094–18111 RSC
 .
.
- B. Błasiak, C. H. Londergan, L. J. Webb and M. Cho, Acc. Chem. Res., 2017, 50, 968–976 CrossRef
 .
.
- R. J. Xu, B. Blasiak, M. Cho, J. P. Layfield and C. H. Londergan, J. Phys. Chem. Lett., 2018, 9, 2560–2567 CrossRef CAS
 .
.
-
B. Błasiak, M. Chołuj, J. D. Bednarska, R. W. Góra and W. Bartkowiak, globulion/eopdev: EOPDev 1.0.0, 2020-11-19, 2020, DOI: http://10.5281/zenodo.4281062.
- J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. A. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke, M. L. Abrams, N. J. Russ, M. L. Leininger, C. L. Janssen, E. T. Seidl, W. D. Allen, H. F. Schaefer, R. A. King, E. F. Valeev, C. D. Sherrill and T. D. Crawford, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 556–565 CAS
 .
.
- E. R. Davidson, J. Comput. Phys., 1975, 17, 87–94 CrossRef
 .
.
-
B. Liu, Numerical Algorithms in Chemistry: Algebraic Methods, Lawrence Berkeley Laboratory, University of California, Berkeley, CA, USA, 1978, pp. 49–53 Search PubMed
 .
.
- R. M. Parrish, E. G. Hohenstein and T. J. Martínez, J. Chem. Theory Comput., 2016, 12, 3003–3007 CrossRef CAS
 .
.
- P. Jordan, P. Fromme, H. T. Witt, O. Klukas, W. Saenger and N. Krauß, Nature, 2001, 411, 909 CrossRef CAS
 .
.
- A. S. Belov, D. V. Khokhlov and V. V. Poddubnyi, Dokl. Phys. Chem., 2016, 468, 63–66 CrossRef CAS
 .
.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS
 .
.
- F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291 RSC
 .
.
- E. F. Valeev, V. Coropceanu, D. A. da Silva Filho, S. Salman and J.-L. Brédas, J. Am. Chem. Soc., 2006, 128, 9882–9886 CrossRef CAS
 .
.
Footnote |
| † Electronic supplementary information (ESI) available: Diagonal Hamiltonian matrix elements, timings of various variants of TI/CIS EET coupling calculations, discussion of basis set extension effects, and Cartesian coordinates of the studied model systems. See DOI: 10.1039/d0cp04636a |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
Wojciech
Bartkowiak
*,
Wojciech
Bartkowiak
 and
Robert W.
Góra
and
Robert W.
Góra
 *
*
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) {|ΨX〉 ⊗ |ΨY〉}
{|ΨX〉 ⊗ |ΨY〉}![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) being the standard antisymmetrization operator and ‘⊗’ denoting the outer product. Instead of diagonalizing the excitonic Hamiltonian in such a basis, one may adopt the perturbation theory to obtain the approximate expression for the EET coupling constant:26,31
being the standard antisymmetrization operator and ‘⊗’ denoting the outer product. Instead of diagonalizing the excitonic Hamiltonian in such a basis, one may adopt the perturbation theory to obtain the approximate expression for the EET coupling constant:26,31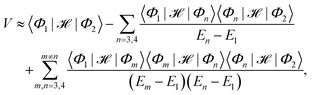
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − E0|Φn〉 and E0 is the ground state energy of the aggregate. The first two site energies are given by31
− E0|Φn〉 and E0 is the ground state energy of the aggregate. The first two site energies are given by31![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − E0|Φ1〉 = EAe→g + ΔEAe→g(B),
− E0|Φ1〉 = EAe→g + ΔEAe→g(B),![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − E0|Φ2〉 = EBe→g + ΔEBe→g(A),
− E0|Φ2〉 = EBe→g + ΔEBe→g(A),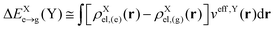
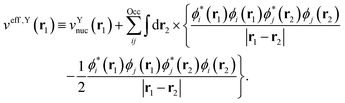
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − E0|Φ3〉 ≈ −εAH + εBL − (ϕAHϕAH|ϕBLϕBL),
− E0|Φ3〉 ≈ −εAH + εBL − (ϕAHϕAH|ϕBLϕBL),![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − E0|Φ4〉 ≈ εAL − εBH − (ϕALϕAL|ϕBHϕBH),
− E0|Φ4〉 ≈ εAL − εBH − (ϕALϕAL|ϕBHϕBH),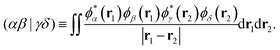
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) |Φ2〉 = V0Coul + V0Exch
|Φ2〉 = V0Coul + V0Exch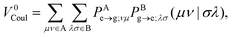
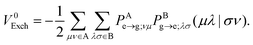
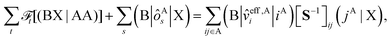
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) t is an arbitrary linear functional of ERIs, and ôAs and
t is an arbitrary linear functional of ERIs, and ôAs and ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) eff,Ai represent an arbitrary one-electron operator and an EOP operator associated with a molecule or fragment A, respectively. First of all, the coulombic EET coupling can be approximated by the distributed multipole expansion of the transition densities of interacting monomers in a dimer using the distributed transition-density cumulative atomic multipole moments (TrCAMM) approach, developed by some of us previously:12
eff,Ai represent an arbitrary one-electron operator and an EOP operator associated with a molecule or fragment A, respectively. First of all, the coulombic EET coupling can be approximated by the distributed multipole expansion of the transition densities of interacting monomers in a dimer using the distributed transition-density cumulative atomic multipole moments (TrCAMM) approach, developed by some of us previously:12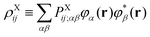
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) Xij|ϕYl)
Xij|ϕYl)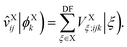
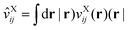
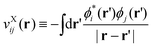
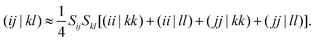
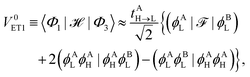
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) |Φ4〉, which were introduced earlier by Fujimoto.31 In the above,
|Φ4〉, which were introduced earlier by Fujimoto.31 In the above, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) is the Fock operator of the entire molecular aggregate. Note that here tAH→L are the CIS amplitudes of isolated monomer A, whereas
is the Fock operator of the entire molecular aggregate. Note that here tAH→L are the CIS amplitudes of isolated monomer A, whereas 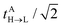 reflects the approximate amplitude in a dimer with monomer B being in its ground state. Here, we also approximate the Fock operator by neglecting the interchromophore relaxation:
reflects the approximate amplitude in a dimer with monomer B being in its ground state. Here, we also approximate the Fock operator by neglecting the interchromophore relaxation: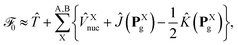
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ≡ −½∇2 is the one-electron kinetic energy operator,
≡ −½∇2 is the one-electron kinetic energy operator, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) Xnuc is the operator associated with the electrostatic potential energy between nuclei and electrons in molecule X, and the Coulomb and exchange operators are defined by
Xnuc is the operator associated with the electrostatic potential energy between nuclei and electrons in molecule X, and the Coulomb and exchange operators are defined by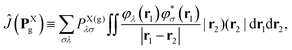
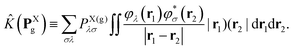
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0 ≈
0 ≈ ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) A0 +
A0 + ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) B0,
B0,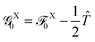
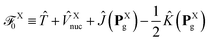 is the Fock operator of isolated molecule X. Here, the contribution from the one-electron kinetic energy operator was symmetrically partitioned in between the two interacting molecules. Thus one can rewrite eqn (24) as
is the Fock operator of isolated molecule X. Here, the contribution from the one-electron kinetic energy operator was symmetrically partitioned in between the two interacting molecules. Thus one can rewrite eqn (24) as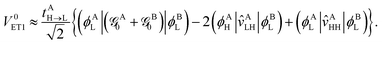
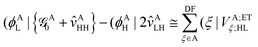
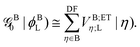
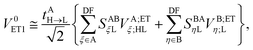
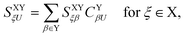
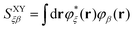
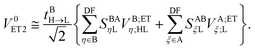
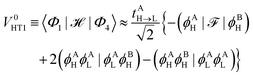
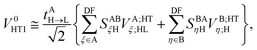
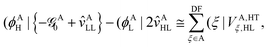
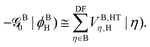
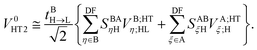
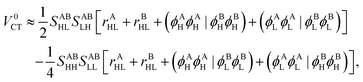
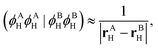
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) |ϕXH).
|ϕXH).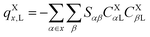
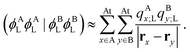
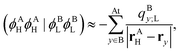

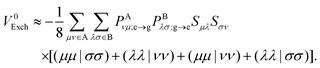
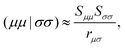
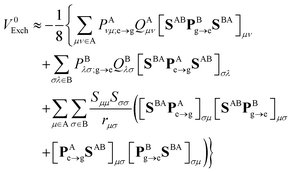
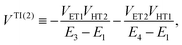
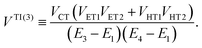
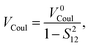
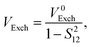
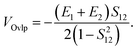
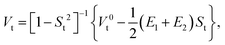
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) and VTI(
) and VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) collectively refer to using eqn (24) and (29), respectively. VTI(
0) collectively refer to using eqn (24) and (29), respectively. VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) DFI0) indicates that the approximate Fock matrix was used as in eqn (29) but including the interfragment interactions in a self-consistent manner through the DFI process.28 The EOP-based model is denoted as VTI(
DFI0) indicates that the approximate Fock matrix was used as in eqn (29) but including the interfragment interactions in a self-consistent manner through the DFI process.28 The EOP-based model is denoted as VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) EOP0) and additionally utilizes the TrCAMM approximation for V(0)Coul, as well as the Mulliken approximation for V(0)Exch (eqn (52)) and V(0)CT (two variants are tested: the CAMM-based vatiant from eqn (41) with eqn (43) or the distributed charge-based variant from eqn (49)). Environmental correction terms from eqn (5) were included in all models except the VTI(
EOP0) and additionally utilizes the TrCAMM approximation for V(0)Coul, as well as the Mulliken approximation for V(0)Exch (eqn (52)) and V(0)CT (two variants are tested: the CAMM-based vatiant from eqn (41) with eqn (43) or the distributed charge-based variant from eqn (49)). Environmental correction terms from eqn (5) were included in all models except the VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) EOP0) model. In order to test the EOP-TI/CIS model we chose the EET coupling between the lowest-lying bright 1ππ* states of ethylene (1 1B1u) and 7-aminocoumarin (1 1A′) in stacked molecular dimers, having D2h and Cs symmetry, respectively. To test the performance and applicability of the proposed methodology we also performed preliminary calculations on the “special pair” in the reaction center of photosystem I (PS-I).10,14,51 To improve the convergence of the distributed multipole expansion of the Coulombic EET coupling constants, the transition densities used to compute the TrCAMMs were symmetrized as suggested by Belov et al.52 Occupied core orbitals were included in the CIS calculations except from the PS-I model for which the frozen-core approximation was utilized.
EOP0) model. In order to test the EOP-TI/CIS model we chose the EET coupling between the lowest-lying bright 1ππ* states of ethylene (1 1B1u) and 7-aminocoumarin (1 1A′) in stacked molecular dimers, having D2h and Cs symmetry, respectively. To test the performance and applicability of the proposed methodology we also performed preliminary calculations on the “special pair” in the reaction center of photosystem I (PS-I).10,14,51 To improve the convergence of the distributed multipole expansion of the Coulombic EET coupling constants, the transition densities used to compute the TrCAMMs were symmetrized as suggested by Belov et al.52 Occupied core orbitals were included in the CIS calculations except from the PS-I model for which the frozen-core approximation was utilized.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 291
291![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) )
)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 576
576![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) DFI0)
DFI0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156
156![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241
241![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0)
0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135
135![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) EOP0)
EOP0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 481
481![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 617
617![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) values, computed assuming the exact Fock matrix of the dimer, are very close to the ESD reference at large and intermediate intermolecular separations and become more approximate at shorter distances. The VTI(
) values, computed assuming the exact Fock matrix of the dimer, are very close to the ESD reference at large and intermediate intermolecular separations and become more approximate at shorter distances. The VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) results represent the limiting accuracy of the TI/CIS frontier-orbitals model which is semi-quantitative at equilibrium geometries and becomes only qualitatively correct at shorter distances. Their calculations for the ethylene dimer took 9.2 s of CPU time on one core of the 1.2 GHz AMD EPYC 7301 16-core processor. The VTI(
) results represent the limiting accuracy of the TI/CIS frontier-orbitals model which is semi-quantitative at equilibrium geometries and becomes only qualitatively correct at shorter distances. Their calculations for the ethylene dimer took 9.2 s of CPU time on one core of the 1.2 GHz AMD EPYC 7301 16-core processor. The VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) DFI0) values correspond to the original transition-density-fragment interaction method (TDFI-TI) of Fujimoto,31 because the density-fragment interaction (DFI) method28,29 is used to take into account molecular surroundings in the Fock matrix of the chromophores in a self-consistent fashion. These are overestimated at short distances and underestimated at the equilibrium geometry by roughly 10–20% (depending on the system). As expected, all the tested models predict virtually identical results at large intermolecular separations.
DFI0) values correspond to the original transition-density-fragment interaction method (TDFI-TI) of Fujimoto,31 because the density-fragment interaction (DFI) method28,29 is used to take into account molecular surroundings in the Fock matrix of the chromophores in a self-consistent fashion. These are overestimated at short distances and underestimated at the equilibrium geometry by roughly 10–20% (depending on the system). As expected, all the tested models predict virtually identical results at large intermolecular separations.![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) DFI0) and VTI(
DFI0) and VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) magnitudes, the relative differences of which are below 2% even at short intermolecular distances. In the latter approach the dimer Fock matrix was constructed from the Fock matrices of monomers assuming the symmetric partitioning introduced in eqn (27) and (28), and thus the interacting monomer ground-state densities were not relaxed in this case. Both calculations took about 3.2 s in the same CPU (cf. Table S3 in the ESI†) which shows about 20% speedup with respect to the calculations of VTI(
0) magnitudes, the relative differences of which are below 2% even at short intermolecular distances. In the latter approach the dimer Fock matrix was constructed from the Fock matrices of monomers assuming the symmetric partitioning introduced in eqn (27) and (28), and thus the interacting monomer ground-state densities were not relaxed in this case. Both calculations took about 3.2 s in the same CPU (cf. Table S3 in the ESI†) which shows about 20% speedup with respect to the calculations of VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) using the exact Fock matrix of the ethylene dimer. Note, however, that the reported timings do not include the time to solve the SCF and CIS problems for the monomers – VTI(
) using the exact Fock matrix of the ethylene dimer. Note, however, that the reported timings do not include the time to solve the SCF and CIS problems for the monomers – VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) DFI0) calculations are obviously longer than VTI(
DFI0) calculations are obviously longer than VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) ones in terms of the elapsed time since the Hartree–Fock problem for the monomers is solved in a block-localized self-consistent fashion for the whole complex.
0) ones in terms of the elapsed time since the Hartree–Fock problem for the monomers is solved in a block-localized self-consistent fashion for the whole complex.![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) EOP0) values obtained for the ethylene dimer reproduce consistently the VTI(
EOP0) values obtained for the ethylene dimer reproduce consistently the VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) estimates with a 1–2% accuracy even at short distances. In the case of the 7AC complex the speedup is more spectacular, since VTI(
0) estimates with a 1–2% accuracy even at short distances. In the case of the 7AC complex the speedup is more spectacular, since VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) calculations took about 25 minutes while VTI(
0) calculations took about 25 minutes while VTI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) EOP0) only 79 milliseconds (nearly 20
EOP0) only 79 milliseconds (nearly 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times faster). The speedup is even larger for PS-I, for which the respective timings are about 137 hours vs. 6 seconds. The relative differences of total couplings are larger in this system (within about ±7%) but one could argue that at short distances the EOP-TI values are, in fact, consistently closer to the reference values. This, however, is entirely due to the cancellation of errors. The fact is that essentially all the discussed TI models show quite similar accuracy, but the EOP-TI approach is simply much more efficient.
000 times faster). The speedup is even larger for PS-I, for which the respective timings are about 137 hours vs. 6 seconds. The relative differences of total couplings are larger in this system (within about ±7%) but one could argue that at short distances the EOP-TI values are, in fact, consistently closer to the reference values. This, however, is entirely due to the cancellation of errors. The fact is that essentially all the discussed TI models show quite similar accuracy, but the EOP-TI approach is simply much more efficient.![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) )/CIS couplings and their components are plotted along with the reference ESD values for the model systems in the vicinity of their equilibrium geometries. The total TI(
)/CIS couplings and their components are plotted along with the reference ESD values for the model systems in the vicinity of their equilibrium geometries. The total TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) coupling (marked with gray lines and asterisks) underestimates slightly the ESD values (shown as black lines with circles) at equilibrium and shorter distances. The agreement is at least semi-quantitative unless the region of very large overlap is considered, which would however be hardly accessible in any real physical situation (note the corresponding interaction energies plotted as gray dashed lines vs. the right axis). For instance, in the 7AC dimer this occurs for ΔRAB below −0.9 Å (cf.Fig. 1c), where the TI(
) coupling (marked with gray lines and asterisks) underestimates slightly the ESD values (shown as black lines with circles) at equilibrium and shorter distances. The agreement is at least semi-quantitative unless the region of very large overlap is considered, which would however be hardly accessible in any real physical situation (note the corresponding interaction energies plotted as gray dashed lines vs. the right axis). For instance, in the 7AC dimer this occurs for ΔRAB below −0.9 Å (cf.Fig. 1c), where the TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ) estimates start to diverge from the ESD coupling, but the intermolecular repulsion in this region exceeds 190 kJ mol−1.
) estimates start to diverge from the ESD coupling, but the intermolecular repulsion in this region exceeds 190 kJ mol−1.![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) partitioning, being a starting point for the introduction of EOP approximation, agrees quantitatively with the corresponding TDFI estimates. The differences between these two methods are essentially due to the lack of relaxation effects in the former. The largest differences are in the magnitudes of second-order terms, which still fall within a few percent margin, unless the Mulliken approximation is utilized. It is interesting to note that in the case of the special pair of PS-I (Table S4, ESI†) at the experimental geometry the agreement is virtually quantitative, for both the total coupling (171 vs. 178 cm−1) and its components. The latter being mostly due to the direct electrostatic coupling VCoul (157 vs. 161 cm−1) and the second-order indirect contribution VTI(2) (15.8 vs. 17.6 cm−1).
0) partitioning, being a starting point for the introduction of EOP approximation, agrees quantitatively with the corresponding TDFI estimates. The differences between these two methods are essentially due to the lack of relaxation effects in the former. The largest differences are in the magnitudes of second-order terms, which still fall within a few percent margin, unless the Mulliken approximation is utilized. It is interesting to note that in the case of the special pair of PS-I (Table S4, ESI†) at the experimental geometry the agreement is virtually quantitative, for both the total coupling (171 vs. 178 cm−1) and its components. The latter being mostly due to the direct electrostatic coupling VCoul (157 vs. 161 cm−1) and the second-order indirect contribution VTI(2) (15.8 vs. 17.6 cm−1).
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) )
)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0)
0)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) )
)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0)
0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156
156![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 481 (10
481 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500)
500)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) )
)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0)
0)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) )
)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0)
0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 576
576![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241
241![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135
135![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 703 (19
703 (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 617)
617)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 717
717![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 541
541![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 276
276![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 716 (17
716 (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630)
630)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 427
427![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271
271![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776
776![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 545
545![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) results is demonstrated for a broader range of intermolecular distances in Fig. 1. In panels (b) and (d) the latter are plotted as solid lines while the former as points. In the vicinity of equilibrium geometry the agreement is nearly quantitative and starts deteriorating in the hardly accessible region of very large overlap. However, since the EOP-TI couplings start to underestimate the TI(
0) results is demonstrated for a broader range of intermolecular distances in Fig. 1. In panels (b) and (d) the latter are plotted as solid lines while the former as points. In the vicinity of equilibrium geometry the agreement is nearly quantitative and starts deteriorating in the hardly accessible region of very large overlap. However, since the EOP-TI couplings start to underestimate the TI(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0) values, which in turn overestimate the reference ESD values, the EOP-TI results are consistently closer to the reference. In fact, this is true also at larger intermolecular separations, since the major difference in EOP-TI components is found for the second-order terms being overestimated at large distances and underestimated at short distances.
0) values, which in turn overestimate the reference ESD values, the EOP-TI results are consistently closer to the reference. In fact, this is true also at larger intermolecular separations, since the major difference in EOP-TI components is found for the second-order terms being overestimated at large distances and underestimated at short distances.![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) )
)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0)
0)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) )
)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0)
0)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) )
)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0)
0)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) )
)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0)
0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 195
195![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 978
978![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976
976![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) DFI0), which, as shown in Fig. 3 of Fujimoto's paper,31 seem to be virtually identical to VESD. This is quite surprising considering the crudeness of approximation (frontier orbitals and block-localized Fock matrix). For instance our TDFI-TI results, reported in Table 1, show a relative error of about 3% at a distance of 3 Å.
DFI0), which, as shown in Fig. 3 of Fujimoto's paper,31 seem to be virtually identical to VESD. This is quite surprising considering the crudeness of approximation (frontier orbitals and block-localized Fock matrix). For instance our TDFI-TI results, reported in Table 1, show a relative error of about 3% at a distance of 3 Å.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times faster than the most efficient variant of the TDFI-TI/CIS approach.
000 times faster than the most efficient variant of the TDFI-TI/CIS approach.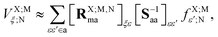
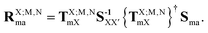
![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) UX;M,NaX,
UX;M,NaX,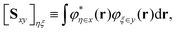
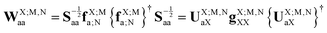
![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) in eqn (60c) selects only eigenvectors (columns of) UX;M,NaX associated with the non-vanishing eigenvalues stored in the diagonal matrix gX;M,NXX. The elements of vector fX;MN for M = ET1, ET2, HT1 and HT2 and N = H, L and HL are given by
in eqn (60c) selects only eigenvectors (columns of) UX;M,NaX associated with the non-vanishing eigenvalues stored in the diagonal matrix gX;M,NXX. The elements of vector fX;MN for M = ET1, ET2, HT1 and HT2 and N = H, L and HL are given by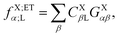
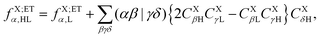
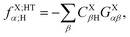
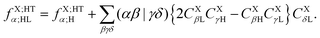
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) X0 represented in space spanned by the intermediate and primary AO basis sets needs to be computed. This can be done by inverting the following matrix equation to obtain GXαβ:
X0 represented in space spanned by the intermediate and primary AO basis sets needs to be computed. This can be done by inverting the following matrix equation to obtain GXαβ: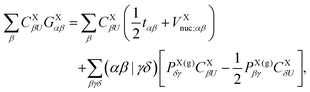
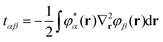
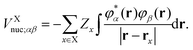
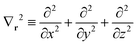 . In this work, the auxiliary EOP basis set was assumed to be identical to the intermediate basis set, i.e., conventional density fitting was used with [RX;M,Nma]ξε = δξε. However, by utilizing the general EDF scheme from eqn (58), additional reduction of computational cost is possible through optimization of the auxiliary EOP basis set.
. In this work, the auxiliary EOP basis set was assumed to be identical to the intermediate basis set, i.e., conventional density fitting was used with [RX;M,Nma]ξε = δξε. However, by utilizing the general EDF scheme from eqn (58), additional reduction of computational cost is possible through optimization of the auxiliary EOP basis set.
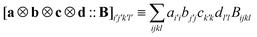 for arbitrary matrices a, b, c, d and a fourth-rank tensor B. Note that the number of (pp|qq) integrals scales quadratically with the size of the basis set which means that memory requirements to store them on a disk or in a file are relatively small and comparable to sizes of typical AO matrices. Therefore, all the (pp|qq) integrals can be treated as effective fragment parameters and the computational cost of superimposition onto a target geometry, which is described by eqn (68) and (67), is relatively small.
for arbitrary matrices a, b, c, d and a fourth-rank tensor B. Note that the number of (pp|qq) integrals scales quadratically with the size of the basis set which means that memory requirements to store them on a disk or in a file are relatively small and comparable to sizes of typical AO matrices. Therefore, all the (pp|qq) integrals can be treated as effective fragment parameters and the computational cost of superimposition onto a target geometry, which is described by eqn (68) and (67), is relatively small.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

