Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Multi-phonon proton transfer pathway in a molecular organic ferroelectric crystal†
Matthew T. O.
Okenyi
 a,
Laura E.
Ratcliff
a,
Laura E.
Ratcliff
 *a and
Aron
Walsh
*a and
Aron
Walsh
 *ab
*ab
aDepartment of Materials, Imperial College London, London SW7 2AZ, UK. E-mail: laura.ratcliff08@imperial.ac.uk; a.walsh@imperial.ac.uk
bDepartment of Materials Science and Engineering, Yonsei University, Seoul 03722, Korea
First published on 11th January 2021
Abstract
While the majority of ferroelectrics research has been focused on inorganic ceramics, molecular ferroelectrics can also combine large spontaneous polarization with high Curie temperatures. However, the microscopic mechanism of their ferroelectric switching is not fully understood. We explore proton tautomerism in the prototypical case of croconic acid, C5O5H2. In order to determine how efficiently ferroelectricity in croconic acid is described in terms of its Γ-point phonon modes, the minimum energy path between its structural ground states is approximated by projection onto reduced basis sets formed from subsets of these modes. The potential energy curve along the minimum energy path was found to be sensitive to the order of proton transfer, which requires a large subset (≳8) of the modes to be approximated accurately. Our findings suggest rules for the construction of effective Hamiltonians to describe proton transfer ferroelectrics.
1 Introduction
A ferroelectric is a material that exhibits a spontaneous, switchable electric polarization. Since polarization switching is the crucial function, the microscopic mechanism by which this switching occurs holds important scientific interest. This topic has been researched both experimentally1–4 and theoretically5–7 over the course of many decades for many systems.Different theoretical approaches have been used to provide insights into ferroelectrics. Before the development of ab initio methods like density functional theory (DFT),8,9 polarization reversal processes were modelled using continuum methods such as the Landau–Ginzburg theory,10 from which models for domain nucleation and growth could be derived.5,11 More recently, DFT has been used to model the atomic structure of defect-free ferroelectric crystals;12 and the atomic structure and properties of domain walls,13 which is outside the realm of applicability of continuum models. It has also been used to calculate the parameter values of effective Hamiltonian models14 constructed in order to simulate large systems beyond the reach of first-principles methods.15,16
The microscopic switching mechanism of organic ferroelectrics such as potassium dihydrogen phosphate and triglycine sulphate is characterised by proton transfer between molecular units. Croconic acid (CRCA) is another member of this category.17,18 The motion of protons parallel and perpendicular to the polar axis, and consequent electronic rearrangement are understood to induce the observed polarization in CRCA.18 Like many proton transfer ferroelectrics, however, it is less thermally stable than inorganic ferroelectrics such as lead zirconate titanate and polymer ferroelectrics such as polyvinylidene fluoride. The relative ease of practical experimentation and potential application to future devices might explain why, upon surveying the literature, more progress has been made toward explaining switching mechanisms in the latter types of ferroelectrics19,20 than in proton transfer ferroelectrics.
In previous work, the degrees of freedom for an effective Hamiltonian for barium titanate were constructed by projecting the unstable phonon modes of the crystal onto individual unit cells.21 This effective Hamiltonian successfully described the phase transition sequence of the material. On the other hand, a similar effective Hamiltonian for the proton transfer ferroelectric potassium dihydrogen phosphate (KDP) used its unstable gamma point mode to derive the degrees of freedom22 but significantly overestimated KDP's phase transition temperature and predicted a second order phase transition, rather than the weakly first order transition that is experimentally observed.22
In this study, the possibility of describing the ferroelectricity of the proton transfer ferroelectric croconic acid (CRCA) by selecting the correct subset of its phonon modes was considered. The minimum energy path (MEP) for polarization switching in CRCA has been calculated with the nudged elastic band method23 in previous work,24 and found to involve pairwise transfer of protons. Any reduced basis of atomic displacements that can be used to describe ferroelectricity in CRCA must at least be able to express the MEP. Therefore, the ability of the phonon modes of CRCA to efficiently describe ferroelectricity in CRCA was assessed by using these modes as a basis in which to approximate the MEP.
The following analysis bears similarities with previous work20 which decomposed polar distortions of two other proton transfer ferroelectrics 1-cyclobutene-1,2-dicarboxylic acid and 2-phenylmalondialdehyde. Both analyses seek to conceptualise the collective atomic distortions that give rise to ferroelectricity in proton transfer ferroelectrics. On the other hand, the authors of ref. 20 decompose the polar distortions of these materials into three different types of atomic distortion instead of the spectra of the materials' Γ-point phonon modes.
2 Methods
The ground-state crystal structure of CRCA has the Pca21 space group, which is polar. The initial crystal structure of CRCA was taken from entry 147324 of the Cambridge Crystallographic Data Centre and was obtained from X-ray diffraction.25 As a starting point, we linearly interpolate a path between the two orientation states, where the direction of polarization is reversed. The mid-point is a non-polar structure that has the space group Pbcm. Equivalently, it is the minimal supergroup from which the Pca21 structure is obtained through the smallest atomic displacements, i.e. Pbcm-CRCA would be its prototype phase, as defined by Aizu.26 We take the Pbcm structure to approximate the hypothetical paraelectric phase, which CRCA would reach if it did not thermally decompose at T ≈ 450 K.17Firstly, we optimise the crystal structures separately under the constraints of the Pca21 and Pbcm symmetry elements. The total energy and forces were calculated from plane-wave DFT as implemented in the Quantum Espresso27,28 and Abinit29 software packages. To determine whether dispersion corrections to the exchange–correlation energy functional would give a more accurate description of the potential energy surface, geometry optimizations were performed with two different dispersion-corrected functionals: DFT-D330 (Abinit's implementation) and vdW-DF231 (Quantum Espresso's implementation). The normal modes were calculated at the Γ point by finite differences with the Phonopy package.32 Further computational details are given in the Appendix.
3 Results
3.1 Crystal structure
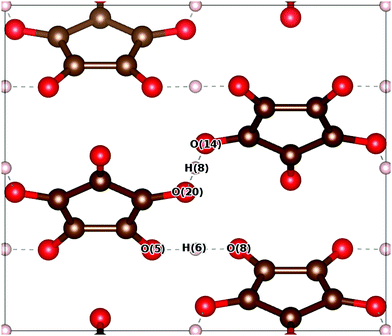
The optimised structure of the Pca21 phase can be compared to the results of neutron scattering experiments.33 The unit cell dimensions, OH/O⋯H bond lengths and angles are presented in Table 1. We distinguish between ‘hinge’ protons and ‘terrace’ protons whose associated OH⋯O triplets are oriented parallel to the [001] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] directions, respectively. The hinge and terrace triplets are indicated in Fig. 1 as O(5)–H(6)–O(8) and O(20)–H(8)–O(14), respectively.
10] directions, respectively. The hinge and terrace triplets are indicated in Fig. 1 as O(5)–H(6)–O(8) and O(20)–H(8)–O(14), respectively.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] as ‘terrace’ protons is used. θhinge and θterrace refer to angles of the corresponding triples
10] as ‘terrace’ protons is used. θhinge and θterrace refer to angles of the corresponding triples
| Pca21 | Pbcm | |||||||
|---|---|---|---|---|---|---|---|---|
| GGA-PBE + DFT-D3 | GGA-PBE | vdW-DF2 | Expt.a | vdW-DF2 | ||||
| Result | Error | Result | Error | Result | Error | |||
| a S. Mukhopadhyay et al., Chemical Physics, 2013, 427, 95–100. | ||||||||
| a (bohr, %) | 16.44 | 0.94 | 17.20 | 5.60 | 16.63 | 2.13 | 16.29 | 16.62 |
| b (bohr, %) | 10.00 | 3.82 | 10.87 | 12.88 | 9.81 | 1.89 | 9.63 | 9.70 |
| c (bohr, %) | 20.44 | 0.89 | 20.62 | 0.03 | 20.98 | 1.71 | 20.63 | 20.32 |
| l(OH)hinge (bohr, %) | 1.96 | 2.91 | 1.95 | 2.16 | 1.92 | 0.98 | 1.90 | 2.33 |
| l(O⋯H)hinge (bohr, %) | 2.87 | 5.39 | 2.95 | 2.72 | 3.12 | 2.82 | 3.03 | 2.33 |
| l(OH)terrace (bohr, %) | 1.95 | 2.83 | 1.94 | 1.93 | 1.92 | 1.02 | 1.90 | 2.31 |
| l(O⋯H)terrace (bohr, %) | 2.87 | 5.74 | 2.97 | 2.46 | 3.09 | 1.34 | 3.04 | 2.31 |
| θ hinge (deg., deg.) | 167.2 | 0.9 | 167.2 | 0.9 | 167.4 | 0.7 | 168.1 | 169.4 |
| θ terrace (deg., deg.) | 174.1 | 1.9 | 172.9 | 0.7 | 172.0 | 0.2 | 172.2 | 180.0 |
The vdW-DF2 functional gave lattice parameters of a similar overall accuracy to DFT-D3, while uncorrected PBE gave much larger errors for the a and b parameters but a smaller error for the c parameter. This is consistent with earlier results;33 dispersion interactions between pleated layers of CRCA binds these layers together.
vdW-DF2 also gave the most accurate bond lengths and angles; however these parameters were also well reproduced by the uncorrected functional. This may be explained by the fact that strong hydrogen bonds (i.e. those possessing donor-hydrogen-acceptor angles (∠DHA) ∼ 180°) exist between the C5O5H2 molecules in CRCA. Such bonds are understood to contain a smaller dispersive element than that of weak hydrogen bonds, which generally have ∠DHA substantially smaller than 180°.34
As vdW-DF2 gave the most accurately optimized structure overall, it was used for the subsequent calculations of the dynamical matrix at Γ and the minimum energy path. For the calculation of the Born effective charge (BEC) tensor, a structure found by Pbcm symmetry-constrained relaxation of CRCA with the uncorrected PBE functional was used. The accurate bond lengths and angles predicted by this functional implied that the electronic rearrangement induced by atomic displacement that contributes to the BEC tensor would also be accurately predicted. Further details are given in the Appendix.
3.2 Vibrational structure
A complete listing of the normal modes of Pbcm-CRCA, including irreducible representations, is given in the ESI.† As there are N = 48 atoms in the unit cell, there are 144 (3N) phonon branches. Referring to these modes by their associated Pbcm symmetry labels would be ambiguous; therefore, in the following we refer to each mode by its index when the modes are arranged in order of ascending frequency. Modes 0–6 are imaginary, while modes 7–9 are acoustic (zero frequency) translations. The remaining modes are stable with positive frequencies.3.3 The minimum energy path
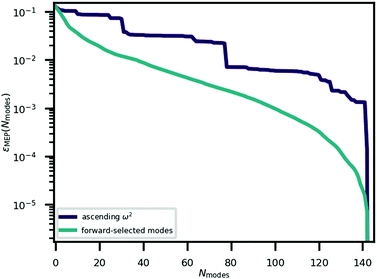
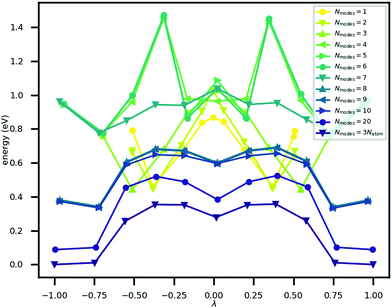
The minimum energy path for ferroelectric switching in CRCA has been calculated according to the nudged elastic band algorithm in previous work24 which used the same vdW-DF231 exchange–correlation functional employed here. This calculation was reproduced in the present work in order to determine how efficiently the Γ-point phonon modes approximate this path. The result of this calculation is illustrated in Fig. 3. The energy barrier associated with this path is 0.045 eV per proton. The 12% difference relative to the corresponding value calculated in the prior work24 (0.051 eV per proton) could be due to the different unit cell dimensions used in the present work. Nevertheless, the MEPs calculated in both works involve the transfer of the 8 protons in the unit cell of CRCA in 4 successive pairs.Approximations to the minimum energy switching path were made by repeatedly projecting it onto a reduced basis comprised of a varying number (Nmodes) of Γ-point phonon modes. The order in which modes were added to the basis was found by forward-selection so that the most important modes were added first. Specifically, the algorithm involved the following steps. For Nmodes = 1,…,3Natom:
1. Calculate the error in approximating the MEP according to
 | (1) |
2. Add the mode which gives the smallest εMEP value, and remove it from the set of remaining modes.
3. If Nmodes < 3Natom, increment Nmodes by 1 and return to step 1, else terminate.
The energy along approximations to the MEP found by adding modes to the basis in the order described above was evaluated. The results of these calculations are illustrated in Fig. 3 which plots the potential energy against a coordinate, λ, normalised between −1 and +1, that quantifies the location of an atomic configuration on a line in 3Natom-dimensional configuration space between the two orientation states. Precisely, λ is defined as
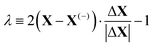 | (2) |
3.4 Proton transfer extent and the minimum energy path
An explanation of how the PECs of approximations to the MEP improved for Nmodes ≤ 8 was sought. As described in previous work24 and reproduced here, the MEP of ferroelectric switching in CRCA involves successive pairwise transfer of protons. Crucially, the protons of CRCA transfer in a well-defined order which is only accurately reproduced with 8 modes in the basis. This is illustrated in Fig. 4 which plots the mean absolute error in proton transfer extent defined as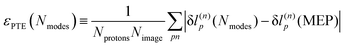 | (3) |
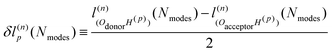 | (4) |
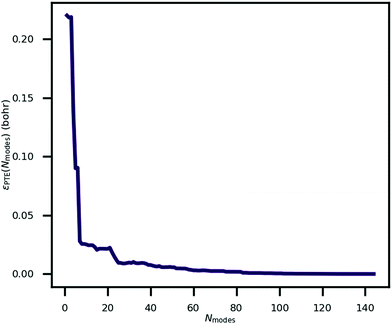 | ||
| Fig. 4 The mean absolute error in proton transfer extent, as defined in eqn (3), incurred by approximating the minimum energy path for ferroelectric switching in croconic acid by a finite number of phonon modes, Nmodes. | ||
It can be seen in the figure that between Nmodes = 1 and 8, εPTE drops significantly by 88% to a small plateau, at which point the qualitative shape of the MEP PEC is recaptured. The configuration of hydroxyl bond lengths appears to be a critical determinant of the potential energy of the crystal.
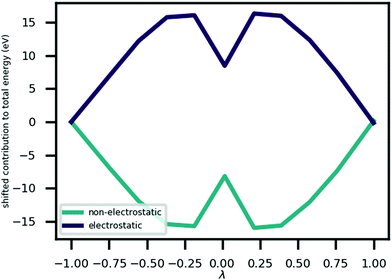
Fig. 3 shows that the MEP PEC features a local minimum at its centre; the structure at λ = 0 is metastable. An analysis of the contributions to the potential energy for each image in the MEP suggests that this state is stabilised by electrostatic interactions in the system. This analysis is illustrated in Fig. 5 which plots the electrostatic (Hartree plus ionic) and non-electrostatic contributions to total energy for each MEP image. The figure shows a drop in electrostatic energy at the centre of the MEP which is evidently greater than the increase in non-electrostatic contribution to the total energy for that image.
The Born effective charge (BEC) tensors of each H ion in CRCA has a large anomalous component i.e. the proportion of its value beyond the formal charge of the ion. This is shown in Table 2, that reports the norms of the BEC tensor associated with H ion displacements along the three coordinate axes i.e.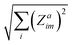 for ion a, displacement direction m. The configuration of hydroxyl bond lengths in CRCA, therefore, has a significant effect on the electrostatic energy, stabilising the λ = 0 structure, as well as affecting the coordination of valence electrons in the ions surrounding the hydroxyl bonds.
for ion a, displacement direction m. The configuration of hydroxyl bond lengths in CRCA, therefore, has a significant effect on the electrostatic energy, stabilising the λ = 0 structure, as well as affecting the coordination of valence electrons in the ions surrounding the hydroxyl bonds.
| Ion | Norm of Born effective charge tensor in direction (e) | ||
|---|---|---|---|
| x | y | z | |
| H (terrace) | 3.10 | 2.15 | 1.58 |
| H (hinge) | 0.28 | 0.40 | 4.02 |
4 Conclusion
The analysis of the phonon modes of a crystal structure can often be used to describe mechanisms of the structural phase transitions for a given material. While this is well established to the specific cases of inorganic perovskite ferroelectrics, this study has demonstrated that the mechanism of field-induced polarization switching in croconic acid – and, likely, in other proton transfer ferroelectrics – is not efficiently expressed in terms of its phonon modes.As described in Section 1, the successful effective Hamiltonian for barium titanate15 constructed its degrees of freedom by projecting the three unstable modes of the crystal onto individual unit cells, and also including strain. We have shown, however, that the shape of the potential energy curve along the minimum energy switching path of CRCA is sensitive to the precise order of proton transfer, and that the proton transfer mechanism requires at least 8 modes to be approximated accurately enough for the resulting potential energy curve to be qualitatively similar in shape to that of the ideal path. If the construction of an effective Hamiltonian similar to ref. 15 were attempted, at least this many modes would need to be projected onto individual unit cells to construct the degrees of freedom, leading to an impractical number of polynomial terms to fit. A basis for atomic displacements that allows individual atoms to move independently, instead of collectively within a unit cell, would be more suitable for the description of ferroelectricity in a proton transfer ferroelectric.
Computational details
For the ground state DFT calculations, an SCF convergence tolerance of 10−10 Ry per ion on the total energy was used. A cutoff of 200 Ry and Monkhorst–Pack mesh of (3, 3, 2) was sufficient to converge the ground state energy within a tolerance of 8.0 × 10−4 Ry per ion, and atomic forces to within a tolerance of 4.0 × 10−5 Ry per bohr. Ultrasoft pseudopotentials35,36 were used to approximate the core electrons. Dispersion-corrected functionals31,37 were used as described in Section 3.In order to compute the non-analytical term correction38 to the dynamical matrix at Γ the Born effective charge tensor was calculated according to density functional perturbation theory38 as implemented in Abinit. Following the structure optimisation, the Kohn–Sham wavefunctions from the Pbcm structure were recalculated with an SCF convergence condition of the absolute difference between the squared residual of the Kohn–Sham potential at successive SCF iterations falling below a threshold of 10−18 Ha2. The first order wavefunctions with respect to perturbations of atomic positions were calculated with an SCF convergence tolerance on the squared (effective) potential residual of 10−8 Ha2. The potential energy surface calculations were supported by custom scripts to generate distorted atomic configurations and post-process the resulting Quantum Espresso output files.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported through a studentship in the Centre for Doctoral Training on Theory and Simulation of Materials at Imperial College London funded by the EPSRC (EP/L015579/1). LER acknowledges support from an EPSRC Early Career Research Fellowship (EP/P033253/1) and the Thomas Young Centre under grant number TYC-101. Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk). We are grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1). We would finally like to thank Karin Rabe for insightful discussions and advice.Notes and references
- E. A. Little, Phys. Rev., 1955, 98, 978–984 CrossRef CAS.
- A. Gruverman, B. J. Rodriguez, C. Dehoff, J. D. Waldrep, A. I. Kingon, R. J. Nemanich and J. S. Cross, Appl. Phys. Lett., 2005, 87, 082902 CrossRef.
- G. Vizdrik, S. Ducharme, V. M. Fridkin and S. G. Yudin, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 094113 CrossRef.
- C. T. Nelson, P. Gao, J. R. Jokisaari, C. Heikes, C. Adamo, A. Melville, S.-H. Baek, C. M. Folkman, B. Winchester, Y. Gu, Y. Liu, K. Zhang, E. Wang, J. Li, L.-Q. Chen, C.-B. Eom, D. G. Schlom and X. Pan, Science, 2011, 334, 968–971 CrossRef CAS.
- W. J. Merz, Phys. Rev., 1954, 95, 690–698 CrossRef CAS.
- V. Y. Shur and E. L. Rumyantsev, Ferroelectrics, 1994, 151, 171–180 CrossRef CAS.
- X. Xia, Y. Wang, Z. Zhong and G. J. Weng, Proc. R. Soc. A, 2016, 472, 20160468 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- Structural Phase Transitions I. Landau theory: Advances in Physics: vol. 29, no. 1, https://www.tandfonline.com/doi/abs/10.1080/00018738000101346.
- R. C. Miller and G. Weinreich, Phys. Rev., 1960, 117, 1460–1466 CrossRef CAS.
- R. D. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5828–5844 CrossRef CAS.
- B. Meyer and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104111 CrossRef.
- Y.-H. Shin, V. R. Cooper, I. Grinberg and A. M. Rappe, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 054104 CrossRef.
- W. Zhong, D. Vanderbilt and K. M. Rabe, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 6301–6312 CrossRef CAS.
- Y.-H. Shin, I. Grinberg, I.-W. Chen and A. M. Rappe, Nature, 2007, 449, 881–884 CrossRef CAS.
- S. Horiuchi, Y. Tokunaga, G. Giovannetti, S. Picozzi, H. Itoh, R. Shimano, R. Kumai and Y. Tokura, Nature, 2010, 463, 789–792 CrossRef CAS.
- S. Horiuchi, K. Kobayashi, R. Kumai and S. Ishibashi, Nat. Commun., 2017, 8, 14426 CrossRef CAS.
- N. Setter, D. Damjanovic, L. Eng, G. Fox, S. Gevorgian, S. Hong, A. Kingon, H. Kohlstedt, N. Y. Park, G. B. Stephenson, I. Stolitchnov, A. K. Taganstev, D. V. Taylor, T. Yamada and S. Streiffer, J. Appl. Phys., 2006, 100, 051606 CrossRef.
- A. Stroppa, D. Di Sante, S. Horiuchi, Y. Tokura, D. Vanderbilt and S. Picozzi, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 014101 CrossRef.
- W. Zhong, D. Vanderbilt and K. M. Rabe, Phys. Rev. Lett., 1994, 73, 1861–1864 CrossRef CAS.
- G. Colizzi, PhD thesis, Queen’s University Belfast, 2005.
- H. Jónnson, G. Mills and K. W. Jacobsen, Classical and Quantum Dynamics in Condensed Phase Simulations, World Scientific, 1998, ch.16, pp. 385–404 Search PubMed.
- S. Mukhopadhyay, M. J. Gutmann, M. Jiménez-Ruiz, D. B. Jochym, K. T. Wikfeldt, K. Refson and F. Fernandez-Alonso, Phys. Chem. Chem. Phys., 2017, 19, 32216–32225 RSC.
- D. Braga, L. Maini and F. Grepioni, CrystEngComm, 2001, 3, 27–29 RSC.
- K. Aizu, Phys. Rev. B: Solid State, 1970, 2, 754–772 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. D. Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS.
- X. Gonze, F. Jollet, F. Abreu Araujo, D. Adams, B. Amadon, T. Applencourt, C. Audouze, J. M. Beuken, J. Bieder, A. Bokhanchuk, E. Bousquet, F. Bruneval, D. Caliste, M. Côté, F. Dahm, F. Da Pieve, M. Delaveau, M. Di Gennaro, B. Dorado, C. Espejo, G. Geneste, L. Genovese, A. Gerossier, M. Giantomassi, Y. Gillet, D. R. Hamann, L. He, G. Jomard, J. Laflamme Janssen, S. Le Roux, A. Levitt, A. Lherbier, F. Liu, I. Lukačević, A. Martin, C. Martins, M. J. T. Oliveira, S. Poncé, Y. Pouillon, T. Rangel, G. M. Rignanese, A. H. Romero, B. Rousseau, O. Rubel, A. A. Shukri, M. Stankovski, M. Torrent, M. J. Van Setten, B. Van Troeye, M. J. Verstraete, D. Waroquiers, J. Wiktor, B. Xu, A. Zhou and J. W. Zwanziger, Comput. Phys. Commun., 2016, 205, 106–131 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- K. Lee, É. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- S. Mukhopadhyay, M. J. Gutmann, M. Jura, D. B. Jochym, M. Jimenez-Ruiz, S. Sturniolo, K. Refson and F. Fernandez-Alonso, Chem. Phys., 2013, 427, 95–100 CrossRef CAS.
- J. Ireta, J. Neugebauer and M. Scheffler, J. Phys. Chem. A, 2004, 108, 5692–5698 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef.
- A. Dal Corso, Comput. Mater. Sci., 2014, 95, 337–350 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355–10368 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04236f |
| This journal is © the Owner Societies 2021 |