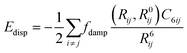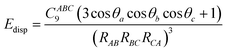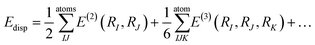Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Density functional theory predictions of the mechanical properties of crystalline materials
Evan
Kiely
a,
Reabetswe
Zwane
bc,
Robert
Fox
bc,
Anthony M.
Reilly
 bc and
Sarah
Guerin
bc and
Sarah
Guerin
 *ac
*ac
aDepartment of Physics, Bernal Institute, University of Limerick, V94 T9PX, Ireland. E-mail: sarah.guerin@ul.ie
bSchool of Chemical Sciences, Dublin City University (DCU), Glasnevin, D09 C7F8 Dublin, Ireland
cSSPC, Science Foundation Ireland Research Centre for Pharmaceuticals, University of Limerick, V94 T9PX, Ireland
First published on 2nd July 2021
Abstract
The mechanical properties of crystalline materials are crucial knowledge for their screening, design, and exploitation. Density functional theory (DFT), remains one of the most effective computational tools for quantitatively predicting and rationalising the mechanical response of these materials. DFT predictions have been shown to quantitatively correlate to a number of experimental techniques, such as nanoindentation, high-pressure X-ray crystallography, impedance spectroscopy, and spectroscopic ellipsometry. Not only can bulk mechanical properties be derived from DFT calculations, this computational methodology allows for a full understanding of the elastic anisotropy in complex crystalline systems. Here we introduce the concepts behind DFT, and highlight a number of case studies and methodologies for predicting the elastic constants of materials that span ice, biomolecular crystals, polymer crystals, and metal–organic frameworks (MOFs). Key parameters that should be considered for theorists are discussed, including exchange–correlation functionals and dispersion corrections. The broad range of software packages and post-analysis tools are also brought to the attention of current and future DFT users. It is envisioned that the accuracy of DFT predictions of elastic constants will continue to improve with advances in high-performance computing power, as well as the incorporation of many-body interactions with quasi-harmonic approximations to overcome the negative effects of calculations carried out at absolute zero.
Introduction
Knowing the mechanical properties of a material is a necessary requirement for the vast majority of materials scientists and engineers, from composites in the aeronautical and automotive industries,1–3 to pharmaceutical crystals4–6 and biomaterials.7–9 The mechanical properties of a material tell us a lot about its longevity, its ability to withstand damage, and its potential applications.10 We are now in a period where shape-memory alloys,11 flexible electronics,12,13 ferroelastics,14–16 and other mechanically-complex and exciting materials are becoming commonplace. As well this, modelling tools such as finite element analysis (FEA) often require prior knowledge of properties such as the Young's modulus to accurately predict the behaviour and performance of materials.17,18 More recently, expansions of Pugh mechanical analysis have been used in the derivation of hardness descriptors,19 in the search for new materials for hard coating applications. This has also guided researchers in the search for an inorganic compound with a hardness greater than diamond.20 Elastic tensors can also be used to screen for materials with specific thermal properties, as it allows for the estimation of trends in heat capacities and thermal conductivities.21–23 By knowing the full anisotropic elastic tensor the elastic response of composite materials can be predicted when combined with mathematical homogenization theories. This has allowed for the design of such materials with engineered stiffness.24,25 Additionally, elastic properties are widely used in the field of geophysics, where acoustic velocities can be used to interpret seismic data.26,27Of all the molecular modelling tools, density functional theory28–30 remains one of the most efficient methods of calculating the mechanical properties of a material.31–33 While DFT can be used to study almost any material of suitable size, its strength lies in predicting the properties of crystals.34–36 Herein we discuss the various DFT methodologies that can be used to calculate the mechanical properties of crystals, as well as exploring other computational chemistry methods that are used today in this endeavour. The limitations of and challenges facing DFT-based predictions mechanical properties are discussed, as well as the exciting future that lies ahead if these challenges are overcome.
Why are mechanical properties important?
The elastic and mechanical properties of materials can be characterized by calculating second-order elastic constants. These are the measure of proportionality between stress (or energy) and strain within the region of Hooke's law. Elastic constants are broadly determined by applying a strain to a crystal, and measuring the resulting stress.37 Elastic constants of molecular crystals can be determined experimentally using ultrasonic methods that rely on elastodynamics.38 In recent years, theoretical studies have been used to estimate elastic constants with the help of first-principles methods in order to guide experiments and alleviate pressure on trial-and-error investigations. An increase in computational power has provided an avenue for DFT-led studies that can screen for materials with optimum properties prior to being fabricated or grown in the lab.Research into the mechanical behaviour of a new class of solid-state materials is central to both the design and optimal performance of potential technological applications. Take for example metal–organic frameworks (MOFs) where theorists and experimentalists can examine the elasticity of these hybrid frameworks by examining their Young's modulus, Poisson's ratio, bulk modulus and shear modulus.39 Also crucial are discussions on their hardness, plasticity, yield strength and fracture behaviour. For these materials predicted elastic properties such as compressibility and bulk moduli can be compared to high-pressure X-ray crystallography.40 Spectroscopic ellipsometry has also been used to estimate the elastic moduli of MOF nanoparticles and deposited films.41 Nanoindentation has emerged as a key technique for quantifying the mechanical properties of crystalline materials (Fig. 1),42–44 and recently nanoindentation data has been used to train machine learning algorithms.45
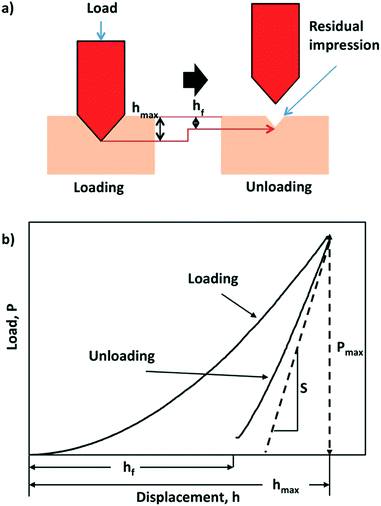 | ||
| Fig. 1 Schematic of the nanoindentation process and measurement (a) diagram showing the working principles of indenting the sample via loading and unloading, (b) a corresponding load–displacement curve showing the effect of the loading and unloading process. S is the contact stiffness of unloading. Reproduced with permission from Wiley.46 | ||
In the pharmaceutical industry, it is of utmost importance to understand the elastic and mechanical properties of active pharmaceutical ingredients (APIs). For the API, mechanical properties govern physicochemical properties such as solubility, tabletability, stability and the bioavailability of a drug substance. It is especially important as roughly one in two APIs can exist in multiple solid forms, with each form markedly showing different physicochemical and mechanical properties.47,48 Unwanted phase transformations during the development stages (the handling, manufacturing, processing and even the storage) of the API and drug can occur.49–51 In the case of polymorphism, the solid–solid transformations can also cause formulation problems. Since polymorphs of the same molecular crystal have differences in interaction energies, other polymorphs tend to transform into the polymorph with the least free energy, and therefore the most stable polymorph. The resulting polymorphs can have undesirable properties, such as in the case of ritonavir and rotigotine.52,53 Unwanted phase transformations can affect the drug stability during its lifespan and in the handling of the drug, particularly if a shearing stress is applied. The piroxicam–succinic acid co-crystal for example is formed via the application of mechanical stress to the two components, but undergoes decomposition when shearing occurs. These process-induced transformations are difficult to predict and control due to lack of understanding of the mechanochemical process at an atomistic level. DFT calculations can be a crucial tool to understand and quantify polymorph stability, and can be used to study the interactions between APIs, co-formers, and excipients in both amorphous and crystalline environments.
What is density functional theory?
For single electron systems (2D potential well, hydrogen atom) it is possible to obtain an exact solution to the Schrödinger equation.54 However, for any system more complicated than this it is impossible to precisely solve the Schrödinger equation and obtain a mathematical description of the system i.e. the wavefunction.55 The simplest goal of density functional theory (DFT) calculations is to get an approximate solution to the many-body Schrödinger equation, which gives the ground state properties of the system.The term DFT comes the fact that the functional used in DFT calculations is the electron density,56 which is itself a function of space and time (mathematically, a functional takes a function and gives a resulting scalar value). The Hohenberg–Kohn theorem57 tells us that the total ground state energy of a many-electron system is a functional of the density. The total energy of the system is written in terms of a number of individual energy contributions,58 each of which are functionals of the charge density:
• ion–electron potential energy
• ion–ion potential energy
• electron–electron energy
• kinetic energy
• exchange–correlation energy.
The most computationally challenging energy contributions are the kinetic energy and the exchange–correlation energy. The kinetic energy is calculated using the Kohn–Sham orbitals.59 Generally, these do not correspond to actual electron orbitals – they are orthonormal orbitals. The Kohn–Sham orbitals map the system of interacting electrons on to a system of non-interacting electrons moving in an effective potential. The exchange–correlation energy accounts for the exchange interaction due to repulsion between electrons with parallel spins, and the correlation interaction, which is the correlated motion between electrons of anti-parallel spins due to their mutual coulombic repulsion. In its simplest implementation, exchange–correlation effects are treated via the Perdew, Burke, and Ernzerhof (PBE)60 implementation of the generalised gradient approximation (GGA).61 GGA builds on what is known as the local density approximation (LDA), by considering both the local electron density and its gradient, as the electron density can vary rapidly over a small region of space.
Long-range considerations: what is dispersion-corrected DFT?
Considering dispersion corrections in DFT calculations is important as the exchange functionals have difficulty in reproducing long-range behaviour, even those explicitly parameterised for long range behaviour.62 This is because approximations such as GGA within these functionals63 result in potential energy surfaces that lack sufficient crystal packing effects (CPEs) without the addition of a dispersion correction.64 These are influenced by van der Waals forces that are better estimated through dispersion corrections as their inclusion follows a simple formula where the displacement energy is added to the exchange correlation function so as not to be included in the initial DFT calculations.A vital aspect to the dispersion correction is dampening, with methods that lack an adequate dampening failing to give consistent results for crystal structure and energies.65 The dampening function within the dispersion correction determines the range at which the dispersion correction acts66 as well as the steepness of the cut off of the dispersion correction.67 The dampening function means that the dispersion effects approach 1 at long distances, this meaning that it is purely a dispersion interaction, but at as the distance between the dipoles shortens the dispersion correction gets dampened eventually going to zero.68 This means that there is no dispersion effect at shorter distances where the XC functionals perform better. The dampening effects are also intended to reduce double counting effects.69 Further studies are needed on which dampening function performs best with each dispersion correction and exchange functional.68 However with increasing numbers of atoms in the unit cell the difficulty arises in deciding where dampening should take place, as this needs to be symmetric.70
Dispersion corrections can be calculated in several ways. This can be with a pairwise approach, a three-body approach or a many body approach. The pairwise approach which is chosen in dispersion corrections schemes such as Grimme-D2 (ref. 71 and 72) and Tkatchenko–Scheffler (TS)73 summates over the C6R−6 potential where R is the atomic distance and the C6 is the dispersion coefficient. For the Grimme-D2 method these are multiplied by a global scaling factor.71 where the TS scheme calculates the pairwise dispersion energy using the formula:
where θ represents the internal angles formed by RAB, RBC and RCA.76 This uses a C9 triple dipole constant that can be approximated in two possible ways, either through integrating the average dipole polarizability at an imaginary frequency for all three atoms, or through calculating the square root of the three-atoms dispersion coefficient.76 This three-body treatment has been found to contribute minimally to the overall dispersion energy with one paper saying that the three body treatment contributes <5–10% of the dispersion energy,77 and another paper stating that the three body effect contributes 7.2% of the lattice energy.78
The many body dispersion method, as used in the many body dispersion scheme (MBD), builds on the pairwise TS approach and addresses the fact that the nature of long-range energy is many-body in nature.74 The main drawback of the MBD scheme is the high computational cost70 which is due to the fact that within this method it involves having to calculate both pairwise and three-body dispersion energy utilising the formula:
Elastic properties of electroactive materials
Our work to date studying biomolecular crystals using DFT relies on the Vienna ab initio simulation package (VASP)80 which uses plane wave basis sets,81 and the projector augmented-wave (PAW) method.82 However, many DFT packages, such as CASTEP,83 ABINIT,84 and CP2K85 also have efficient schemes for calculating elastic properties. For VASP standard PAW pseudopotentials are used in all calculations, as supplied with the software. As our focus has been on the piezoelectric properties86 of crystals, elastic constant calculation is part of a calculation workflow, as the elastic stiffness constants ckj, are required to calculate the piezoelectric strain constants dik. The elastic compliance (skj) can easily be derived from the stiffness and measured alongside electromechanical properties using impedance spectroscopy,87,88 as can the various elastic moduli. Using the piezoelectric charge coefficients, eij, which are also calculated directly by VASP,89 and the elastic stiffness constants, ckj, we can calculate the more useful piezoelectric strain coefficient, dik, using the relationship| dik = eij/ckj |
Using this methodology, we have calculated to a high accuracy versus experiment the elastic constants of amino acid90,98–100 and peptide crystals,101,102 co-crystals,103,104 and biominerals105 (Fig. 2). We have also recently calculated the elastic properties of large protein crystals using classical force fields. Elastic constants of the transmembrane protein ba3 cytochrome c oxidase, as well as lysozyme, and aldehyde dehydrogenase were predicted using the classical CHARMM forcefield model for the protein, ions and water with structures calculated using the CP2K modelling software augmented with homemade subroutines to impose crystal symmetry. In any calculation of elastic properties if crystal symmetry is not preserved then stiffness and compliance tensors will be incorrect. To evaluate the mechanical stability of the crystal we can apply the Born–Huang elastic stability criteria for the appropriate crystal system. As an example for the cubic crystal system, it is required that c11 − c12 > 0, c11 + 2c12 > 0, c44 > 0. If one or more of these criteria is violated, one or more of the elastic tensor eigenvalues is negative and the crystal is mechanically unstable.
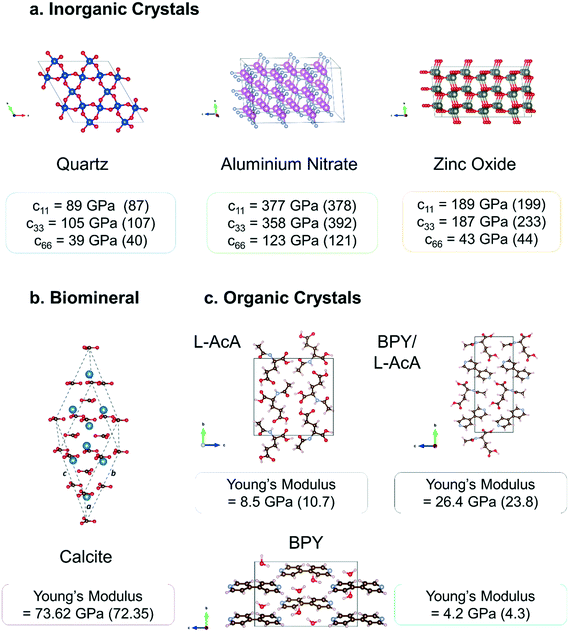 | ||
| Fig. 2 Crystal structures and mechanical properties of different classes of crystal calculated using a PBE-only DFT methodology as published in previous literature90,103,105 and summarised in the previous section a. inorganic piezoelectric crystals quartz (SiO2), aluminium nitrate (AlN), and zinc oxide (ZnO) b. the biomineral calcite (CaCO3) c. molecular crystals 4,4′-bipyridine (BPY), N-acetyl-L-alanine (AcA), and their combined BPY/AcA cocrystal. Experimental values are shown in brackets. | ||
Fig. 2 shows the high quantitative accuracy that can be obtained using the above PBE-only methodology for individual stiffness tensor components and derived Young's modulus values for a small sample of the different classes of crystal that we have studied. As the piezoelectric response is inversely proportional to the elastic stiffness if the material is predicted to be more flexible than it is this will lead to an overestimation of the electromechanical coupling. Full mechanical testing of piezoelectric materials is always recommended as properties such as fracture limit and hardness ultimately determine the specific applications and environments the material can be used in.
Pei & Zeng106 computed structural and elastic properties of nine phases of piezoelectric polyvinylidene fluoride (PVDF) crystals using DFT with and without a variety of dispersion corrections. In addition to the four known crystalline forms the mechanical properties of five theoretically predicted crystalline forms of PVDF were also investigated. The DFT/PBE calculations show that the cell parameters of four known crystalline forms are in good agreement with experiment. However, they identified that including empirical van der Waals corrections, specifically the Grimme-D2 method, led to a large error in the calculated unit cell lattice parameters. By comparing conventional PBE (without dispersion corrections) and DFT-D2 calculations the authors could highlight that the PBE method provides a better description of the structural and mechanic properties of PVDF crystals.
Complex hybrid systems: limitations of DFT
Kosa et al. recently demonstrated a combined computational and experimental approach in studying the elastic anisotropy of a zinc phosphate phosphonoacetate (ZnPA)107 metal–organic framework (MOF). This 3D framework is composed of Zn–O–Zn layers that are connected by phosphate groups bridging the ZnO4 tetrahedra. This in turn sections off small channels that run parallel to the crystallographic a-axis. DFT calculations rationalise that the pore morphology contributes towards the elastic anisotropy. An efficient computational scheme Again a simple and efficient GGA calculation scheme was used, in this case to predict the Young's modulus and the Poisson's ratio (n) along the primary crystallographic axes. Notably, they avoided a finite difference methodology in order to circumvent computing the full elastic stiffness tensor (cij), which can be a computationally heavy approach for low-symmetrical crystal systems.38,108 The relative stiffness of the different crystal facets was found to be in reasonably good agreement with experiments. In terms of their absolute values, however, the calculated moduli are consistently higher, by as much as 25% to 40%, than those determined experimentally. Given that the hybrid compound considered here was not moisture sensitive the Young's moduli measured by nanoindentation are expected to be reliable,109 as in the authors' previous work. This study pointed out that the higher stiffness calculated by DFT could be due both from the derivation scheme and deficiencies associated with the electronic structure methods used. They discuss how theoretical calculations at 0 K are expected to overestimate the elastic stiffness when compared to experiments performed at ambient 300 K. In relation to the electronic structure method, the authors note that an incorrect description of the position of transition metal d-states can cause over-hybridization of the Zn–O bonds within GGA because of a self-interaction error (SIE). This can lead to artificial stiffening in the zinc–oxygen cores of the ZnPA framework and thus an overestimation of mechanical strength. They emphasise that due to the current limitations of DFT, elastic property predictions for complex hybrid systems are potentially sensitive to the choice of, among others, the exchange–correlation functional and the pseudopotential.Choosing your functional for high accuracy elastic constants
Dengetal et al. highlight the benefits of testing multiple functionals to obtain accurate bulk moduli predictions. The elastic moduli from all functionals (PBE, PBEsol, optB88-vdW) are significantly higher than the values reported experimentally, with PBEsol deviating the least from experimental measurements. The authors attribute this difference to many factors. For example, the samples for characterization in the reported experiments were polycrystalline with both finite grain size and porosity. They are modelled however, as infinite single crystals in plane-wave DFT. The elastic moduli of samples with different grain sizes or porosities can vary, which can also lead to discrepancies in experimental values. The authors also derive Pugh's ratio, G/B, which is commonly used to evaluate the brittleness of materials, with a larger G/B indicating that the material is more brittle.Another excellent screening of DFT functionals for elastic constant prediction was carried out by Rego & de Koning in their recent study on hexagonal proton-disordered ice using the Quantum ESPRESSO software package.110 They evaluated nine different exchange–correlation functionals, four of which include long-range dispersion interactions through the non-local van der Waals (vdW) approach. While we have observed that dispersion corrections can over-bind crystals and induce polymorphic transitions in small crystals,90,106 they are known to play an important role in the condensed phases of water. The authors utilise the well-established energy-strain approach to calculate the elastic constants, in which one exploits the relation between the energy of a crystal and its state of deformation, using the equation
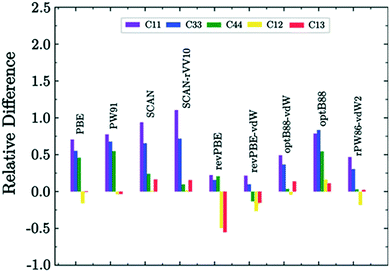 | ||
| Fig. 3 Relative difference of DFT values with respect to experimental data for the structural parameters of ice.110,111 Reproduced with permission from AIP Publishing. | ||
DFT screening of mechanical properties and database generation
Efforts aimed at developing databases of elastic moduli from first-principles computational methods have been undertaken in numerous studies.112,113 These computational approaches are advantageous as all of the data can be derived in a consistent manner, allowing for unambiguous comparisons across many classes of material. De Jong and colleagues have expanded on this approach, producing the largest database of calculated elastic properties of crystalline inorganic compounds to date, ranging from metals and metallic compounds to semiconductors and insulators. The calculations formed part of the larger high-throughput effort,114 undertaken by the Materials Project.115 Using DFT the calculated elastic constants were consistently shown to be within 15% of experimental values, which represents a smaller scatter than that observed in experimental measurements in some cases (Fig. 4). Pearson (r) and Spearman (ρ) coefficients indicate that the calculations performed in this work yield elastic properties that show an excellent correlation with experimental values, making the database useful for screening materials with properties based on elastic tensors.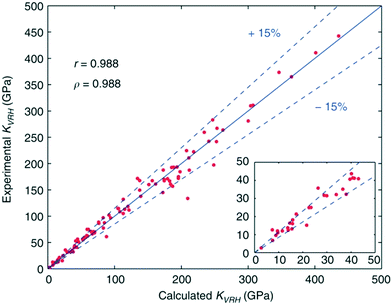 | ||
| Fig. 4 Comparison of experimental and calculated bulk moduli for a selected set of systems, with calculated Pearson correlation coefficient r and Spearman correlation coefficient ρ reported.19 | ||
For this study the elastic constants were calculated using a stress–strain methodology. Starting from a relaxed structure for each compound, a set of distorted structures is generated. For each of the applied strains ∈ij, the full stress tensor is obtained from a DFT calculation in which ionic positions are relaxed. One row (or equivalently, column) of the elastic matrix is obtained from a linear fit of the calculated stresses over the range of imposed strains. Repeating this procedure for each of the 6 independent strain components, all elements of the elastic modulus tensor can be calculated. The result is a calculated set of cij values that can be used to calculate properties such as the bulk modulus K and the shear modulus G as in previously mentioned studies.
Mechanical properties of crystal polymorphs
DFT is widely used to study crystal polymorphism, most commonly through the calculation of the ground state energy difference between polymorphic crystal structures,116 or a simpler analysis of intermolecular interactions (Fig. 5).117 From this, the relative stability of polymorphs can be determined, though high accuracy functionals and dispersion corrections are required for this.118 For molecular crystals the highest level of theory needed for calculating accurate relative stabilities is still being debated.118–121 As with any crystal, DFT-calculated physical properties, be they mechanical,122 dielectric,116 or physiochemical123 can also be used to distinguish and rationalize polymorphic behaviour. Since both polymorphism and distinct mechanical properties arise from differences in crystal packing of molecules (in the case of packing polymorphism), polymorphs can be identified by their unique mechanical properties. In addition to colour or morphology, mechanical properties can also be used for the rapid screening and sorting of concomitant polymorphic forms.47 This is especially useful for structurally similar polymorphic forms, such as the aspirin polytypes. The structural differences in aspirin I and aspirin II are not obvious. They both constitute hydrogen-bonded dimers ordered in layers, with the layers arranged differently relative to each other.124 Reilly and Tkatchenko have shown that their Young's moduli exhibit distinct anisotropies.125 In their work they use dispersion-inclusive DFT, by incorporating many-body van der Waals (vdW) interactions to calculate the elastic tensor of the two polymorphic forms. Their elastic property analysis shows that both forms are expected to be mechanically stable under compression and shearing at room temperature – shedding light on the widely-discussed mechanical stability of form II.38,126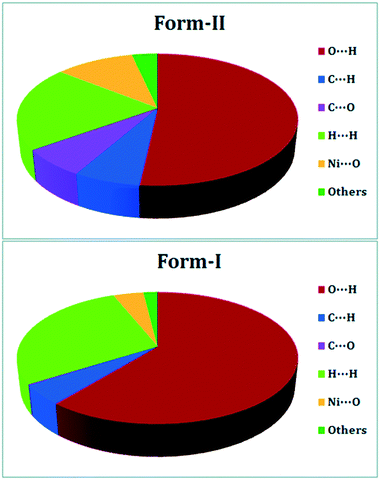 | ||
| Fig. 5 DFT-calculated intermolecular interactions that contribute to the Hirshfeld surfaces of polymorphic form-II (top) and form-I (bottom) of a 1D Ni(II) polymer with iminodiacetic acid (IDA), namely diaquaiminodiacetatonickel(II). Reproduced from ref. 117 with permission from the Royal Society of Chemistry. | ||
The work of Reilly and Tkatchenko shows that extensive characterization of polymorphic forms can be achieved from the determination of elastic tensor using DFT and other in silico methods. A strong interconnect between molecular modelling and experiment is preferable, as even with structure–property correlations, a polycrystalline lens is needed to fully understand properties like plasticity and tabletability. The tabletability of a polycrystalline material is influenced by factors such as the relative movements of grains and grain size, which are difficult to extrapolate from single crystal DFT. Karki et al. have successfully used the eigenvalues of the compliance tensor to rationalize the differences in mechanical behavior of paracetamol polymorphic forms – which show significant differences in structural features – as well as paracetamol form II cocrystals.48 They used the value of the highest compliance eigenvalue to draw conclusions about the compliance of a crystal and the relative strengths of shear planes. From that, they establish that form II shows a higher compliance eigenvalue compared to form I, because it is compliant to shearing, which leads to plastic deformation during tableting. This result is consistent with the layered structure of form II which grants it preferable compaction properties.127 Despite these milestones of linking mechanical behavior to structure using DFT, crystal engineering of pharmaceuticals with desired mechanical behavior is still to be achieved. With the maturity of DFT, crystal structure prediction, and ever-increasing computational power, there is continued opportunity for new insights.
The right direction: the importance of elastic anisotropy
The mechanical properties of crystals are naturally anisotropic, with different stress–strain responses depending on the crystallographic axis of interest. Azuri et al., in their investigation of the high mechanical strength of amino acid crystals, demonstrated that experimental measurements perpendicular to different crystal planes yield unique Young's modulus values.128 The mechanical properties of cellulose nanocrystals (CNCs) have been difficult to experimentally characterize owing largely to extreme anisotropy and uncertainties about the structure of these materials. For example, reported experimental values for the Young modulus of cellulose Iβ show a wide variation that is hard to explain considering the defect-free crystalline structure typically observed in CNCs.129–131 Three dimensional surfaces, which are colour contours showing the crystallographic dependence of the Young's modulus and Poisson's ratio, were computed by Dri et al. to examine the extreme anisotropy of these important elastic properties using DFT.132 A clear correlation between the stiffness of the crystal and the different deformation mechanisms was noted. The largest Young's modulus (206 GPa) was found to be aligned with the crystallographic c-axis where covalent bonds drive the mechanical response of the crystal. Perpendicular to the cellulose chain axis, the b-direction shows the next greatest value for the Young modulus (98 GPa), explained by the presence of the hydrogen bond network linking the cellulose chains. Finally, a Young modulus value of only 19 GPa was computed along the direction perpendicular to the previous two, where weak vdW interactions play a dominant role in the mechanical response of the material. The 0 K calculations, carried out with dispersion-corrected DFT in VASP predicted a transverse Young modulus for crystalline cellulose in the range between 13 and 98 GPa, in good agreement with the reported range of experimental results.The elastic stiffness tensor predicted by some DFT methods is calculated as a 6 × 6 matrix that naturally describes the elastic anisotropy of a crystalline system. However, it is only recently that elastic anisotropy has begun to be considered in experimental measurement of mechanical properties. Mishra and co-workers systematically examined the mechanical properties of dimorphic forms, forms I and II, of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 caffeine–glutaric acid cocrystal on multiple faces. Here nanoindentation was used to fully understand the co-crystal mechanical anisotropy and mechanical stability under an applied load.133 The higher hardness and elastic modulus of stable form II was rationalized on the basis of its corrugated layers, higher interlayer energy, lower interlayer separation, and the presence of more intermolecular interactions in the crystal structure compared to metastable form I. The results show that mechanical anisotropy in both polymorphs arises due to the difference in orientation of the identical 2D structural features, namely, the number of possible slip systems and the strength of the intermolecular interactions with respect to the indentation direction. It is hoped that studies like these will influence future experimental investigations, where directional elastic stiffness can be correlated with DFT-predicted tensors to rationalise mechanical properties from the nanoscale up.
1 caffeine–glutaric acid cocrystal on multiple faces. Here nanoindentation was used to fully understand the co-crystal mechanical anisotropy and mechanical stability under an applied load.133 The higher hardness and elastic modulus of stable form II was rationalized on the basis of its corrugated layers, higher interlayer energy, lower interlayer separation, and the presence of more intermolecular interactions in the crystal structure compared to metastable form I. The results show that mechanical anisotropy in both polymorphs arises due to the difference in orientation of the identical 2D structural features, namely, the number of possible slip systems and the strength of the intermolecular interactions with respect to the indentation direction. It is hoped that studies like these will influence future experimental investigations, where directional elastic stiffness can be correlated with DFT-predicted tensors to rationalise mechanical properties from the nanoscale up.
Looking forward: room temperature property predictions
Current standard ab initio methods describe ground-state properties at zero temperature and pressure. One implication of this that the theoretical structures do not expand with increasing temperature and the elastic constants do not account for zero-point or temperature effects. A quick fix for this is to compare the ground-state properties determined from theoretical structures to those of experimental XRD structures grown and characterized at the lowest-possible temperature, where temperature effects are dampened. However, even with this work-around, elastic constants can still be overestimated by up to 40%.134Thermal contributions to the elastic constants can be incorporated by treating the lattice dynamics of a crystal structure within the quasi-harmonic approximation (QHA), as opposed to the more commonly adopted harmonic approximation (HA) approach.135 In the QHA, the lattice dynamics of the structure are modelled within the HA at several unit-cell volumes, therefore incorporating the volume dependence missing in the pure HA. It follows then that with the volume dependence, elastic constants now depend on temperature. The incorporation of temperature effects into elastic constant predictions from QHA calculations accounts for approximately 30% of the disagreement observed134,136 compared to elastic constants at 0 K (Fig. 6).
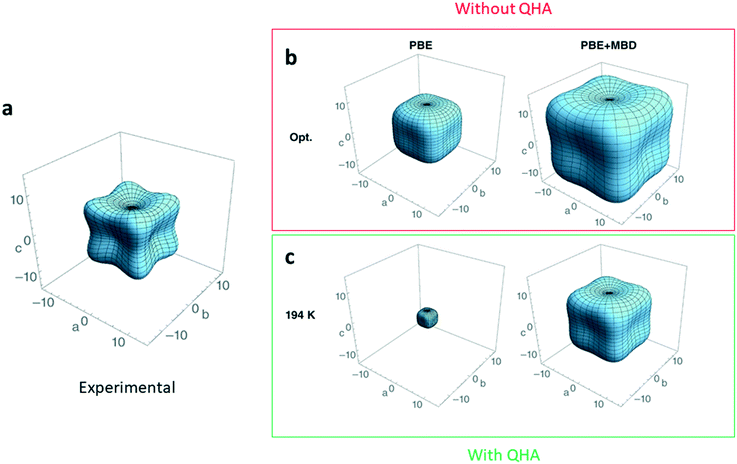 | ||
| Fig. 6 Three-dimensional plot in GPa showing the magnitude and anisotropy of the material's Young modulus a. experimental measurement137 for deuterated ammonia (ND3) b. DFT-calculated Young's modulus with no dispersion corrections (PBE), and many-body dispersion corrections (PBE + MBD). c. DFT-calculated Young's modulus using the same two methods but with the inclusion of the quasi-harmonic approximation (QHA) to simulate the Young's modulus at a temperature of 194 K. Adapted from ref. 134 with permission from Wiley. | ||
Treating lattice dynamics in this way is known to increase computational expense and effort when considering complex systems, and even more so with the inclusion of dispersion corrections and many-body effects. Lower-level density-functional based methods can be considered in efforts to reduce computational expense.138 Density-functional tight binding (DFT-B) is one such method,139 being an approximate treatment of the Kohn–Sham DFT formalism with less empirical parameters compared to classical force fields. It therefore lies between ab initio methods and classical force fields in terms of time scales and attainable system sizes. Despite its computational efficiency, DFT-B is still to be fully explored as a tool for predicting the elastic constants of materials.
Conclusions
In this Highlight we have introduced the theory of DFT, and multiple methodologies and software packages that can be used to calculate the elastic properties of periodic systems. From these calculations further mechanical properties can be derived, and if desired fed into FEA models for structural and behavioural analysis. While all DFT methodologies overestimate elastic constants to some extent, many combinations of exchange–correlation functional and dispersion corrections match well with experimental values. Extensive benchmarking is recommended for any DFT investigation into the mechanical response of materials, not only to ensure accuracy but to confirm mechanical stability and correct imposition of symmetry. It is envisioned that the accuracy of DFT predictions of elastic constants will continue to improve with advances in high-performance computing power, as well as the incorporation of more efficient many-body interaction schemes with quasi-harmonic approximations in order to overcome the negative effects of calculations carried out at absolute zero.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was supported by Science Foundation Ireland (SFI) under award number 12/RC/2275_P2.References
- J. N. Coleman, U. Khan, W. J. Blau and Y. K. Gun'ko, Small but strong: a review of the mechanical properties of carbon nanotube–polymer composites, Carbon, 2006, 44(9), 1624–1652 CrossRef CAS.
- W. A. Curtin, Theory of mechanical properties of ceramic-matrix composites, J. Am. Ceram. Soc., 1991, 74(11), 2837–2845 CrossRef CAS.
- K. Ravikumar, K. Kiran and V. Sreebalaji, Characterization of mechanical properties of aluminium/tungsten carbide composites, Measurement, 2017, 102, 142–149 CrossRef.
- A. Ainurofiq, R. Mauludin, D. Mudhakir, D. Umeda, S. N. Soewandhi, O. D. Putra and E. Yonemochi, Improving mechanical properties of desloratadine via multicomponent crystal formation, Eur. J. Pharm. Sci., 2018, 111, 65–72 CrossRef CAS PubMed.
- M. Meier, E. John, D. Wieckhusen, W. Wirth and W. Peukert, Influence of mechanical properties on impact fracture: Prediction of the milling behaviour of pharmaceutical powders by nanoindentation, Powder Technol., 2009, 188(3), 301–313 CrossRef CAS.
- K. Wang, M. K. Mishra and C. C. Sun, Exceptionally elastic single-component pharmaceutical crystals, Chem. Mater., 2019, 31(5), 1794–1799 CrossRef CAS.
- S. Lv, D. M. Dudek, Y. Cao, M. Balamurali, J. Gosline and H. Li, Designed biomaterials to mimic the mechanical properties of muscles, Nature, 2010, 465(7294), 69–73 CrossRef CAS PubMed.
- S. Mitragotri and J. Lahann, Physical approaches to biomaterial design, Nat. Mater., 2009, 8(1), 15–23 CrossRef CAS PubMed.
- L. Wang, C. Wang, S. Wu, Y. Fan and X. Li, Influence of the mechanical properties of biomaterials on degradability, cell behaviors and signaling pathways: current progress and challenges, Biomater. Sci., 2020, 8(10), 2714–2733 RSC.
- J. Pelleg, Mechanical properties of materials, Springer Science & Business Media, 2012, vol. 190 Search PubMed.
- H. Gu, et al., Phase engineering and supercompatibility of shape memory alloys, Mater. Today, 2018, 21(3), 265–277 CrossRef CAS.
- A. Nathan, A. Ahnood, M. T. Cole, S. Lee, Y. Suzuki, P. Hiralal, F. Bonaccorso, T. Hasan, L. Garcia-Gancedo and A. Dyadyusha, Flexible electronics: the next ubiquitous platform, Proc. IEEE, 2012, 100(Special Centennial Issue), 1486–1517 Search PubMed.
- L. Wang, D. Chen, K. Jiang and G. Shen, New insights and perspectives into biological materials for flexible electronics, Chem. Soc. Rev., 2017, 46(22), 6764–6815 RSC.
- S. Baek, H. Jang, C. Folkman, Y. Li, B. Winchester, J. Zhang, Q. He, Y. Chu, C. Nelson and M. Rzchowski, Ferroelastic switching for nanoscale non-volatile magnetoelectric devices, Nat. Mater., 2010, 9(4), 309–314 CrossRef CAS PubMed.
- Y. Hu, L. You, B. Xu, T. Li, S. A. Morris, Y. Li, Y. Zhang, X. Wang, P. S. Lee and H. J. Fan, Ferroelastic-switching-driven large shear strain and piezoelectricity in a hybrid ferroelectric, Nat. Mater., 2021, 1–6 Search PubMed.
- T. Seki, C. Feng, K. Kashiyama, S. Sakamoto, Y. Takasaki, T. Sasaki, S. Takamizawa and H. Ito, Photoluminescent ferroelastic molecular crystals, Angew. Chem., 2020, 132(23), 8924–8928 CrossRef.
- K. Balasubramanian, N. Rajeswari and K. Vaidheeswaran, Analysis of mechanical properties of natural fibre composites by experimental with FEA, Mater. Today: Proc., 2020, 28, 1149–1153 CAS.
- S. Eshraghi and S. Das, Micromechanical finite-element modeling and experimental characterization of the compressive mechanical properties of polycaprolactone–hydroxyapatite composite scaffolds prepared by selective laser sintering for bone tissue engineering, Acta Biomater., 2012, 8(8), 3138–3143 CrossRef CAS PubMed.
- M. De Jong, W. Chen, T. Angsten, A. Jain, R. Notestine, A. Gamst, M. Sluiter, C. K. Ande, S. Van Der Zwaag and J. J. Plata, Charting the complete elastic properties of inorganic crystalline compounds, Sci. Data, 2015, 2(1), 1–13 Search PubMed.
- H. Niu, X.-Q. Chen, P. Liu, W. Xing, X. Cheng, D. Li and Y. Li, Extra-electron induced covalent strengthening and generalization of intrinsic ductile-to-brittle criterion, Sci. Rep., 2012, 2(1), 1–6 Search PubMed.
- D. G. Cahill, S. K. Watson and R. O. Pohl, Lower limit to the thermal conductivity of disordered crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(10), 6131 CrossRef CAS PubMed.
- D. R. Clarke, Materials selection guidelines for low thermal conductivity thermal barrier coatings, Surf. Coat. Technol., 2003, 163, 67–74 CrossRef.
- G. J. Snyder and E. S. Toberer, Complex thermoelectric materials, Materials for sustainable energy: a collection of peer-reviewed research and review articles from Nature Publishing Group, 2011, pp. 101–110 Search PubMed.
- Z. Hashin and S. Shtrikman, A variational approach to the theory of the elastic behaviour of multiphase materials, J. Mech. Phys. Solids, 1963, 11(2), 127–140 CrossRef.
- T. Zohdi and P. Wriggers, Aspects of the computational testing of the mechanical properties of microheterogeneous material samples, Int. J. Numer. Methods Eng., 2001, 50(11), 2573–2599 CrossRef.
- O. L. Anderson, E. Schreiber, R. C. Liebermann and N. Soga, Some elastic constant data on minerals relevant to geophysics, Rev. Geophys., 1968, 6(4), 491–524 CrossRef CAS.
- B. B. Karki, L. Stixrude and R. M. Wentzcovitch, High-pressure elastic properties of major materials of Earth's mantle from first principles, Rev. Geophys., 2001, 39(4), 507–534 CrossRef CAS.
- K. Burke, Perspective on density functional theory, J. Chem. Phys., 2012, 136(15), 150901 CrossRef PubMed.
- C. Fiolhais, F. Nogueira and M. A. Marques, A primer in density functional theory, Springer Science & Business Media, 2003, vol. 620 Search PubMed.
- R. G. Parr, Density functional theory of atoms and molecules, in Horizons of quantum chemistry, Springer, 1980, pp. 5–15 Search PubMed.
- R. Astala, S. M. Auerbach and P. Monson, Density functional theory study of silica zeolite structures: Stabilities and mechanical properties of SOD, LTA, CHA, MOR, and MFI, J. Phys. Chem. B, 2004, 108(26), 9208–9215 CrossRef CAS.
- F. Colmenero, J. Cobos and V. Timón, Periodic density functional theory study of the structure, Raman spectrum, and mechanical properties of Schoepite mineral, Inorg. Chem., 2018, 57(8), 4470–4481 CrossRef CAS PubMed.
- A. Fereidoon, M. G. Ahangari, M. D. Ganji and M. Jahanshahi, Density functional theory investigation of the mechanical properties of single-walled carbon nanotubes, Comput. Mater. Sci., 2012, 53(1), 377–381 CrossRef CAS.
- M. A. Neumann and M.-A. Perrin, Energy ranking of molecular crystals using density functional theory calculations and an empirical van der Waals correction, J. Phys. Chem. B, 2005, 109(32), 15531–15541 CrossRef CAS PubMed.
- P. Ravindran, L. Fast, P. A. Korzhavyi, B. Johansson, J. Wills and O. Eriksson, Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi 2, J. Appl. Phys., 1998, 84(9), 4891–4904 CrossRef CAS.
- S. Refaely-Abramson, S. Sharifzadeh, M. Jain, R. Baer, J. B. Neaton and L. Kronik, Gap renormalization of molecular crystals from density-functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88(8), 081204 CrossRef.
- R. Golesorkhtabar, P. Pavone, J. Spitaler, P. Puschnig and C. Draxl, ElaStic: A tool for calculating second-order elastic constants from first principles, Comput. Phys. Commun., 2013, 184(8), 1861–1873 CrossRef CAS.
- J. D. Bauer, E. Haussühl, B. R. Winkler, D. Arbeck, V. Milman and S. Robertson, Elastic properties, thermal expansion, and polymorphism of acetylsalicylic acid, Cryst. Growth Des., 2010, 10(7), 3132–3140 CrossRef CAS.
- J. C. Tan and A. K. Cheetham, Mechanical properties of hybrid inorganic–organic framework materials: establishing fundamental structure–property relationships, Chem. Soc. Rev., 2011, 40(2), 1059–1080 RSC.
- T. D. Bennett, J. C. Tan, S. A. Moggach, R. Galvelis, C. Mellot-Draznieks, B. A. Reisner, A. Thirumurugan, D. R. Allan and A. K. Cheetham, Mechanical Properties of Dense Zeolitic Imidazolate Frameworks(ZIFs): A High-Pressure X-ray Diffraction, Nanoindentation and Computational Study of the Zinc Framework Zn(Im) 2, and its Lithium Boron Analogue, LiB(Im) 4, Chem. – Eur. J., 2010, 16(35), 10684–10690 CrossRef CAS PubMed.
- C. Boissiere, D. Grosso, S. Lepoutre, L. Nicole, A. B. Bruneau and C. Sanchez, Porosity and mechanical properties of mesoporous thin films assessed by environmental ellipsometric porosimetry, Langmuir, 2005, 21(26), 12362–12371 CrossRef CAS PubMed.
- A. C. Fischer-Cripps and D. Nicholson, Nanoindentation. Mechanical engineering series, Appl. Mech. Rev., 2004, 57(2), B12 CrossRef.
- D. M. Ebenstein and L. A. Pruitt, Nanoindentation of biological materials, Nano Today, 2006, 1(3), 26–33 CrossRef.
- H. Attar, S. Ehtemam-Haghighi, D. Kent, I. Okulov, H. Wendrock, M. Bönisch, A. Volegov, M. Calin, J. Eckert and M. Dargusch, Nanoindentation and wear properties of Ti and Ti-TiB composite materials produced by selective laser melting, Mater. Sci. Eng., A, 2017, 688, 20–26 CrossRef CAS.
- G. Konstantopoulos, E. P. Koumoulos and C. A. Charitidis, Classification of mechanism of reinforcement in the fiber-matrix interface: Application of Machine Learning on nanoindentation data, Mater. Des., 2020, 192, 108705 CrossRef CAS.
- R. He, S. Gahlawat, C. Guo, S. Chen, T. Dahal, H. Zhang, W. Liu, Q. Zhang, E. Chere and K. White, Studies on mechanical properties of thermoelectric materials by nanoindentation, Phys. Status Solidi A, 2015, 212(10), 2191–2195 CrossRef CAS.
- C. M. Reddy, S. Basavoju and G. R. Desiraju, Sorting of polymorphs based on mechanical properties. Trimorphs of 6-chloro-2, 4-dinitroaniline, Chem. Commun., 2005,(19), 2439–2441 RSC.
- S. Karki, T. Friščić, L. Fabian, P. R. Laity, G. M. Day and W. Jones, Improving mechanical properties of crystalline solids by cocrystal formation: new compressible forms of paracetamol, Adv. Mater., 2009, 21(38–39), 3905–3909 CrossRef CAS.
- K. R. Morris, U. J. Griesser, C. J. Eckhardt and J. G. Stowell, Theoretical approaches to physical transformations of active pharmaceutical ingredients during manufacturing processes, Adv. Drug Delivery Rev., 2001, 48(1), 91–114 CrossRef CAS PubMed.
- G. G. Zhang, D. Law, E. A. Schmitt and Y. Qiu, Phase transformation considerations during process development and manufacture of solid oral dosage forms, Adv. Drug Delivery Rev., 2004, 56(3), 371–390 CrossRef CAS PubMed.
- I. Tumanov, A. Achkasov, S. Myz, E. Boldyreva and V. Boldyrev, in Different effect of impact and shear mechanical treatment on mechanochemical cocrystallization of piroxicam and succinic acid, Doklady Chemistry, Pleiades Publishing, 2014, pp. 154–159 Search PubMed.
- J. Bauer, S. Spanton, R. Henry, J. Quick, W. Dziki, W. Porter and J. Morris, Ritonavir: an extraordinary example of conformational polymorphism, Pharm. Res., 2001, 18(6), 859–866 CrossRef CAS PubMed.
- I. B. Rietveld and R. Céolin, Rotigotine: unexpected polymorphism with predictable overall monotropic behavior, J. Pharm. Sci., 2015, 104(12), 4117–4122 CrossRef CAS PubMed.
- M. F. Manning, Exact solutions of the Schrödinger equation, Phys. Rev., 1935, 48(2), 161 CrossRef.
- P. A. M. Dirac, The principles of quantum mechanics, Oxford university press, 1981 Search PubMed.
- W. Kohn, A. D. Becke and R. G. Parr, Density functional theory of electronic structure, J. Phys. Chem., 1996, 100(31), 12974–12980 CrossRef CAS.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136(3), B864 CrossRef.
- W. Koch and M. C. Holthausen, A chemist's guide to density functional theory, John Wiley & Sons, 2015 Search PubMed.
- J. P. Perdew and M. Levy, Physical content of the exact Kohn-Sham orbital energies: band gaps and derivative discontinuities, Phys. Rev. Lett., 1983, 51(20), 1884 CrossRef CAS.
- J. P. Perdew and W. Yue, Accurate and simple density functional for the electronic exchange energy: Generalized gradient approximation, Phys. Rev. B, 1986, 33(12), 8800 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- S. Kristyán and P. Pulay, Can(semi) local density functional theory account for the London dispersion forces?, Chem. Phys. Lett., 1994, 229(3), 175–180 CrossRef.
- J. G. Brandenburg and S. Grimme, Dispersion corrected Hartree–Fock and density functional theory for organic crystal structure prediction, Prediction and Calculation of Crystal Structures, 2013, pp. 1–23 Search PubMed.
- J. Moellmann and S. Grimme, Importance of London dispersion effects for the packing of molecular crystals: a case study for intramolecular stacking in a bis-thiophene derivative, Phys. Chem. Chem. Phys., 2010, 12(30), 8500–8504 RSC.
- P. Xu, M. Alkan and M. S. Gordon, Many-Body Dispersion, Chem. Rev., 2020, 120(22), 12343–12356 CrossRef CAS PubMed.
- S. Grimme, Density functional theory with London dispersion corrections, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1(2), 211–228 CAS.
- M. D. King and T. M. Korter, Modified corrections for London forces in solid-state density functional theory calculations of structure and lattice dynamics of molecular crystals, J. Phys. Chem. A, 2012, 116(25), 6927–6934 CrossRef CAS PubMed.
- Y. Liu and W. A. I. Goddard, A universal damping function for empirical dispersion correction on density functional theory, Mater. Trans., 2009, 50(7), 1664–1670 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32(7), 1456–1465 CrossRef CAS PubMed.
- A. Otero-de-la-Roza, L. M. LeBlanc and E. R. Johnson, What is “many-body” dispersion and should I worry about it?, Phys. Chem. Chem. Phys., 2020, 22(16), 8266–8276 RSC.
- S. Grimme, Accurate description of van der Waals complexes by density functional theory including empirical corrections, J. Comput. Chem., 2004, 25(12), 1463–1473 CrossRef CAS PubMed.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27(15), 1787–1799 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data, Phys. Rev. Lett., 2009, 102(7), 073005 CrossRef PubMed.
- L. Kronik and A. Tkatchenko, Understanding molecular crystals with dispersion-inclusive density functional theory: pairwise corrections and beyond, Acc. Chem. Res., 2014, 47(11), 3208–3216 CrossRef CAS PubMed.
- G.-X. Zhang, A. Tkatchenko, J. Paier, H. Appel and M. Scheffler, Van der Waals interactions in ionic and semiconductor solids, Phys. Rev. Lett., 2011, 107(24), 245501 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, A generally applicable atomic-charge dependent London dispersion correction, J. Chem. Phys., 2019, 150(15), 154122 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction(DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- W. Jankiewicz, R. Podeszwa and H. A. Witek, Dispersion-corrected DFT struggles with predicting three-body interaction energies, J. Chem. Theory Comput., 2018, 14(10), 5079–5089 CrossRef CAS PubMed.
- A. Tkatchenko, R. A. DiStasio Jr, R. Car and M. Scheffler, Accurate and efficient method for many-body van der Waals interactions, Phys. Rev. Lett., 2012, 108(23), 236402 CrossRef PubMed.
- J. Hafner, Ab-initio simulations of materials using VASP: Density-functional theory and beyond, J. Comput. Chem., 2008, 29(13), 2044–2078 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B, 1996, 54(16), 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B, 1999, 59(3), 1758 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr. - Cryst. Mater., 2005, 220(5–6), 567–570 CrossRef CAS.
- X. Gonze, F. Jollet, F. A. Araujo, D. Adams, B. Amadon, T. Applencourt, C. Audouze, J.-M. Beuken, J. Bieder and A. Bokhanchuk, Recent developments in the ABINIT software package, Comput. Phys. Commun., 2016, 205, 106–131 CrossRef CAS.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt and F. Schiffmann, CP2K: An electronic structure and molecular dynamics software package-Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152(19), 194103 CrossRef PubMed.
- S. Guerin, S. A. Tofail and D. Thompson, Organic piezoelectric materials: milestones and potential, NPG Asia Mater., 2019, 11(1), 1–5 CrossRef.
- S. Dutta, R. Choudhary, P. Sinha and A. K. Thakur, Microstructural studies of(PbLa)(ZrTi) O 3 ceramics using complex impedance spectroscopy, J. Appl. Phys., 2004, 96(3), 1607–1613 CrossRef CAS.
- V. V. Ganesan, M. Dhanasekaran, N. Thangavel and A. Dhathathreyan, Elastic compliance of fibrillar assemblies in type I collagen, Biophys. Chem., 2018, 240, 15–24 CrossRef CAS PubMed.
- X. Wu, D. Vanderbilt and D. Hamann, Systematic treatment of displacements, strains, and electric fields in density-functional perturbation theory, Phys. Rev. B, 2005, 72(3), 035105 CrossRef.
- S. Guerin, A. Stapleton, D. Chovan, R. Mouras, M. Gleeson, C. McKeown, M. R. Noor, C. Silien, F. M. Rhen and A. L. Kholkin, Control of piezoelectricity in amino acids by supramolecular packing, Nat. Mater., 2018, 17(2), 180–186 CrossRef CAS PubMed.
- P. Tulip and S. Clark, Structural and electronic properties of L-amino acids, Phys. Rev. B, 2005, 71(19), 195117 CrossRef.
- P. Tulip and S. Clark, Dielectric and vibrational properties of amino acids, J. Chem. Phys., 2004, 121(11), 5201–5210 CrossRef CAS PubMed.
- J. F. Nye, Physical properties of crystals: their representation by tensors and matrices, Oxford university press, 1985 Search PubMed.
- D. Chung and W. Buessem, The Voigt-Reuss-Hill(VRH) approximation and the elastic moduli of polycrystalline ZnO, TiO2(Rutile), and α-Al2O3, J. Appl. Phys., 1968, 39(6), 2777–2782 CrossRef CAS.
- R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65(5), 349 CrossRef.
- R. Gaillac, P. Pullumbi and F.-X. Coudert, ELATE: an open-source online application for analysis and visualization of elastic tensors, J. Phys.: Condens. Matter, 2016, 28(27), 275201 CrossRef PubMed.
- A. Marmier, Z. A. Lethbridge, R. I. Walton, C. W. Smith, S. C. Parker and K. E. Evans, ElAM: A computer program for the analysis and representation of anisotropic elastic properties, Comput. Phys. Commun., 2010, 181(12), 2102–2115 CrossRef CAS.
- S. Guerin, J. O'Donnell, E. U. Haq, C. McKeown, C. Silien, F. M. Rhen, T. Soulimane, S. A. Tofail and D. Thompson, Racemic amino acid piezoelectric transducer, Phys. Rev. Lett., 2019, 122(4), 047701 CrossRef CAS PubMed.
- J. O'Donnell, S. Guerin, P. Makam, P.-A. Cazade, E. U. Haq, K. Tao, E. Gazit, C. Silien, T. Soulimane and D. Thompson, Atomistic-Benchmarking towards a protocol development for rapid quantitative metrology of piezoelectric biomolecular materials, Appl. Mater. Today, 2020, 21, 100818 CrossRef.
- J. O'Donnell, S. M. Sarkar, S. Guerin, G. G. Borda, C. Silien, T. Soulimane, D. Thompson, E. O'Reilly and S. A. Tofail, Piezoelectricity in the proteinogenic amino acid L-leucine: A novel piezoactive bioelectret, IEEE Trans. Dielectr. Electr. Insul., 2020, 27(5), 1465–1468 Search PubMed.
- V. Basavalingappa, et al., Diphenylalanine-derivative peptide assemblies with increased aromaticity exhibit metal-like rigidity and high piezoelectricity, ACS Nano, 2020, 14(6), 7025–7037 CrossRef CAS PubMed.
- S. Guerin, T. A. Syed and D. Thompson, Deconstructing collagen piezoelectricity using alanine-hydroxyproline-glycine building blocks, Nanoscale, 2018, 10(20), 9653–9663 RSC.
- W. Ji, et al., Tunable Mechanical and Optoelectronic Properties of Organic Cocrystals by Unexpected Stacking Transformation from H-to J-and X-Aggregation, ACS Nano, 2020, 14(8), 10704–10715 CrossRef CAS PubMed.
- W. Ji, et al., Modulation of physical properties of organic cocrystals by amino acid chirality, Mater. Today, 2021, 42, 29–40 CrossRef CAS.
- S. Guerin, S. A. Tofail and D. Thompson, Longitudinal piezoelectricity in natural calcite materials: Preliminary studies, IEEE Trans. Dielectr. Electr. Insul., 2018, 25(3), 803–807 CAS.
- Y. Pei and X. C. Zeng, Elastic properties of poly(vinyldene fluoride)(PVDF) crystals: A density functional theory study, J. Appl. Phys., 2011, 109(9), 093514 CrossRef.
- M. Kosa, J. C. Tan, C. A. Merrill, M. Krack, A. K. Cheetham and M. Parrinello, Probing the Mechanical Properties of Hybrid Inorganic–Organic Frameworks: A Computational and Experimental Study, ChemPhysChem, 2010, 11(11), 2332–2336 CrossRef CAS PubMed.
- F. M. Capaldi, M. C. Boyce and G. C. Rutledge, The mechanical properties of crystalline cyclopentyl polyhedral oligomeric silsesquioxane, J. Chem. Phys., 2006, 124(21), 214709 CrossRef PubMed.
- J. Tan, C. Merrill, J. Orton and A. Cheetham, Anisotropic mechanical properties of polymorphic hybrid inorganic–organic framework materials with different dimensionalities, Acta Mater., 2009, 57(12), 3481–3496 CrossRef CAS.
- J. Santos Rego and M. de Koning, Density-functional theory prediction of the elastic constants of ice I h, J. Chem. Phys., 2020, 152(8), 084502 CrossRef CAS PubMed.
- K. Röttger, A. Endriss, J. Ihringer, S. Doyle and W. Kuhs, Lattice constants and thermal expansion of H2O and D2O ice Ih between 10 and 265 K, Acta Crystallogr., Sect. B: Struct. Sci., 1994, 50(6), 644–648 CrossRef.
- C. R. Da Silva, P. R. da Silveira, B. Karki, R. M. Wentzcovitch, P. A. Jensen, E. F. Bollig, M. Pierce, G. Erlebacher and D. A. Yuen, Virtual laboratory for planetary materials: System service architecture overview, Phys. Earth Planet. Inter., 2007, 163(1–4), 321–332 CrossRef.
- P. R. Da Silveira, C. R. da Silva and R. M. Wentzcovitch, Metadata management for distributed first principles calculations in VLab—A collaborative cyberinfrastructure for materials computation, Comput. Phys. Commun., 2008, 178(3), 186–198 CrossRef CAS.
- S. Curtarolo, G. L. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, The high-throughput highway to computational materials design, Nat. Mater., 2013, 12(3), 191–201 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002 CrossRef.
- S. Roy, A. Hazra, A. Bandyopadhyay, D. Raut, P. L. Madhuri, D. S. Rao, U. Ramamurty, S. K. Pati, S. Krishna Prasad and T. K. Maji, Reversible Polymorphism, Liquid Crystallinity, and Stimuli-Responsive Luminescence in a Bola-amphiphilic π-System: Structure–Property Correlations Through Nanoindentation and DFT Calculations, J. Phys. Chem. Lett., 2016, 7(20), 4086–4092 CrossRef CAS PubMed.
- S. K. Seth, A. Bauzá and A. Frontera, Screening polymorphism in a Ni(II) metal–organic framework: experimental observations, Hirshfeld surface analyses and DFT studies, CrystEngComm, 2018, 20(6), 746–754 RSC.
- S. Wen and G. J. Beran, Crystal polymorphism in oxalyl dihydrazide: Is empirical DFT-D accurate enough?, J. Chem. Theory Comput., 2012, 8(8), 2698–2705 CrossRef CAS PubMed.
- A. Pedone, D. Presti and M. C. Menziani, On the ability of periodic dispersion-corrected DFT calculations to predict molecular crystal polymorphism in para-diiodobenzene, Chem. Phys. Lett., 2012, 541, 12–15 CrossRef CAS.
- K. Hongo, M. A. Watson, R. S. Sánchez-Carrera, T. Iitaka and A. Aspuru-Guzik, Failure of conventional density functionals for the prediction of molecular crystal polymorphism: a Quantum Monte Carlo Study, J. Phys. Chem. Lett., 2010, 1(12), 1789–1794 CrossRef CAS.
- J. Van De Streek and M. A. Neumann, Validation of experimental molecular crystal structures with dispersion-corrected density functional theory calculations, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66(5), 544–558 CrossRef CAS PubMed.
- O. U. O. Mota, R. A. Araujo, H. Wang and T. Çağın, Mechanical properties of metal nitrides for radiation resistant coating applications: a DFT study, Phys. Procedia, 2015, 66, 576–585 CrossRef CAS.
- L. F. L. Silva, W. Paschoal, G. S. Pinheiro, J. G. da Silva Filho, P. T. Freire, F. F. de Sousa and S. G. Moreira, Understanding the effect of solvent polarity on the polymorphism of octadecanoic acid through spectroscopic techniques and DFT calculations, CrystEngComm, 2019, 21(2), 297–309 RSC.
- A. D. Bond, R. Boese and G. R. Desiraju, On the polymorphism of aspirin: crystalline aspirin as intergrowths of two “polymorphic” domains, Angew. Chem., Int. Ed., 2007, 46(4), 618–622 CrossRef CAS PubMed.
- A. M. Reilly and A. Tkatchenko, Understanding the role of vibrations, exact exchange, and many-body van der Waals interactions in the cohesive properties of molecular crystals, J. Chem. Phys., 2013, 139(2), 024705 CrossRef PubMed.
- S. Varughese, M. Kiran, K. A. Solanko, A. D. Bond, U. Ramamurty and G. R. Desiraju, Interaction anisotropy and shear instability of aspirin polymorphs established by nanoindentation, Chem. Sci., 2011, 2(11), 2236–2242 RSC.
- T. Beyer, G. M. Day and S. L. Price, The prediction, morphology, and mechanical properties of the polymorphs of paracetamol, J. Am. Chem. Soc., 2001, 123(21), 5086–5094 CrossRef CAS PubMed.
- I. Azuri, E. Meirzadeh, D. Ehre, S. R. Cohen, A. M. Rappe, M. Lahav, I. Lubomirsky and L. Kronik, Unusually large Young's moduli of amino acid molecular crystals, Angew. Chem., Int. Ed., 2015, 54(46), 13566–13570 CrossRef CAS PubMed.
- I. Diddens, B. Murphy, M. Krisch and M. Müller, Anisotropic elastic properties of cellulose measured using inelastic X-ray scattering, Macromolecules, 2008, 41(24), 9755–9759 CrossRef CAS.
- A. Ishikawa, T. Okano and J. Sugiyama, Fine structure and tensile properties of ramie fibres in the crystalline form of cellulose I, II, IIII and IVI, Polymer, 1997, 38(2), 463–468 CrossRef CAS.
- R. Wagner, R. Moon, J. Pratt, G. Shaw and A. Raman, Uncertainty quantification in nanomechanical measurements using the atomic force microscope, Nanotechnology, 2011, 22(45), 455703 CrossRef PubMed.
- F. L. Dri, L. G. Hector, R. J. Moon and P. D. Zavattieri, Anisotropy of the elastic properties of crystalline cellulose I β from first principles density functional theory with Van der Waals interactions, Cellulose, 2013, 20(6), 2703–2718 CrossRef CAS.
- M. K. Mishra, et al., Structural Basis for Mechanical Anisotropy in Polymorphs of a Caffeine–Glutaric Acid Cocrystal, Cryst. Growth Des., 2020, 20(10), 6306–6315 CrossRef CAS.
- J. Hoja, A. M. Reilly and A. Tkatchenko, First-principles modeling of molecular crystals: structures and stabilities, temperature and pressure, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7(1), e1294 Search PubMed.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- A. Erba, J. Maul and B. Civalleri, Thermal properties of molecular crystals through dispersion-corrected quasi-harmonic ab initio calculations: the case of urea, Chem. Commun., 2016, 52(9), 1820–1823 RSC.
- H. Kiefte, S. Breckon, R. Penney and M. Clouter, Elastic constants of ammonia by Brillouin spectroscopy, J. Chem. Phys., 1985, 83(9), 4738–4743 CrossRef CAS.
- T. Kamencek, S. Wieser, H. Kojima, N. Bedoya-Martínez, J. P. Dürholt, R. Schmid and E. Zojer, Evaluating Computational Shortcuts in Supercell-Based Phonon Calculations of Molecular Crystals: The Instructive Case of Naphthalene, J. Chem. Theory Comput., 2020, 16(4), 2716–2735 CrossRef CAS PubMed.
- J. G. Brandenburg and S. Grimme, Accurate modeling of organic molecular crystals by dispersion-corrected density functional tight binding(DFTB), J. Phys. Chem. Lett., 2014, 5(11), 1785–1789 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |