Open Access Article
Open Access ArticleMeasuring the end-face of silicon boules using mid-infrared laser scanning
Mathias Novik
Jensen
 and
Olav Gaute
Hellesø
and
Olav Gaute
Hellesø
 *
*
Department of Physics and Technology, UiT The Arctic University of Norway, 9037 Tromsø, Norway. E-mail: olav.gaute.helleso@uit.no
First published on 9th June 2021
Abstract
Laser scanning is investigated to measure the deflection of the crystal–melt interface during Czochralski-growth of silicon. A mid-infrared laser is used to take advantage of the IR-transparency of silicon. The method is tested at room temperature on the end-face of three crystal-samples prematurely separated from the melt (‘body-pops’). For these samples, the end-face closely resembles the crystal–melt interface during crystal growth. The laser beam is sent through the crystal boule and detected on the far side, depending on whether it is reflected by the end-face or not. Two scanning methods are tested, one assuming no reflection, i.e. direct transmission, and the second assuming reflection by the end-face, with triangulation used to find the end-face deflection. The transmission scan distinguished the end-face from other changes in transmission in >87% of measurement points along the samples, with the resolution determined by the step-size used (1 mm). The end-face reflection method only worked for two of the three samples, with a mean error of ≤0.3 mm and a standard deviation of ≤0.8 mm. This is sufficient to distinguish normal from abnormal end-face deflections. Challenges for in situ implementation of the methods are discussed.
1 Introduction
In the production of monocrystalline silicon via the Czochralski-process, a seed crystal is lowered into a crucible containing the molten silicon. The liquid material of the melt then adheres to the seed crystal due to capillary forces and, due to the relatively low temperature of the seed, crystallizes as part of the same crystalline structure as the seed. The seed is then slowly retracted from the melt, causing the crystallization front (the crystal–melt interface) to remain stationary while a growing crystal is “pulled” from the melt, as shown in Fig. 1, eventually producing a silicon boule. The shape and deflection of the crystal–melt interface has been shown in the works of Noghabi et al.,1 Shiraishi et al.2 and Popescu et al.3 to be dependent on multiple factors, including boule and crucible rotation, and with a strong dependence on the temperature gradient near the interface. As investigated by Jiptner et al.,4 the magnitude and nature of the temperature gradient has a causal link to the development of thermal stress-induced crystal dislocations resulting in lower crystal quality. This implies a correlation between the deflection h of the interface (Fig. 1) and the likelihood of the grown crystal having reduced quality due to high dislocation density. A method for process-monitoring of the deflection would thus be a valuable tool for improving the quality and reduce the cost of high quality Czochralski-grown silicon, which is the main method for making crystalline silicon for the large, silicon-based, electronics and nanotechnology industries.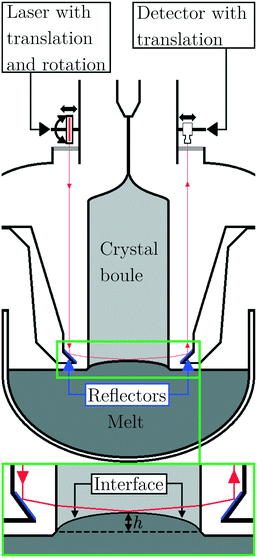 | ||
| Fig. 1 Sketch of proposed in situ measurement system. The experimental setup used is shown in Fig. 2. | ||
A few systems for measuring the interface geometry during Czochralski-growth have been proposed previously. Kakimoto et al.5 used X-ray radiography to form lateral images of the boule near the interface. A system developed by Zhu et al.,6,7 focused on the electro-chemical mechanisms of crystallization in Czochralski-growth of lithium niobate to indirectly measure the interface deflection. The methods of Kakimoto et al. and Zhu et al. have been experimentally tested in small-scale Czochralski-growth and showed encouraging results, but have not yet been implemented in large-scale production. A reason for this is that both methods require significant alteration of the hardware of the common Czochralski-furnace. Another method, suggested by Ding et al.,8 employs a thermal model of the crystal to find the relationship between the temperature distribution and the interface deflection. Thus, by taking point measurements of the surface temperature of the boule, the deflection can be found. This method is relatively easy to implement, but the model relies on certain assumptions being valid. This makes the method vulnerable to changes in factors that are not well accounted for, such as variations in melt flow conditions and thermal properties due to contamination.
We propose a system, as shown in Fig. 1, using laser scanning9,10 and triangulation10 to detect the pseudo-parabolic interface1 and measure its deflection. Laser triangulation has been employed for various applications11 and is a mature technique for precision measurement of surface features in industrial applications.12 In this system, a mid-infrared laser is used to exploit the relatively low optical absorption of silicon13 for photon energies below its band gap energy. Due to the high temperatures near the melt, and the necessity of the funnel assembly, a pair of reflectors must be used to relay the beam, as shown in Fig. 1. In this article, a simplified version of the system is tested at room temperature, omitting these reflectors (see Fig. 2). Three crystal-samples prematurely separated from the melt (‘body-pops’) are used. For these boules, the end-face closely resembles the crystal–melt interface during crystal growth and the deflection of the end-face is the same as when they separated from the melt.
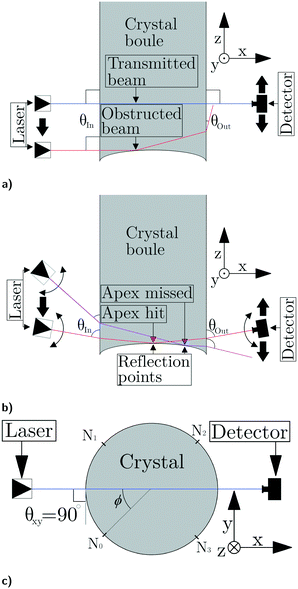 | ||
| Fig. 2 Outline of experimental setup, omitting the reflectors shown in Fig. 1. The crystal boule and beam paths are shown for a) transmission scan, vertical cross-section, b) end-face reflection, vertical cross-section, and c) horizontal cross-section for both methods, with crystal nodes N0 to N3. | ||
Two methods are investigated to measure the deflection of the end-face, both based on sending a laser beam through the centre of the boule and detecting it on the far side. The first method scans through the boule and finds the apex of the end-face, and thereby the deflection, as the position where the transmission decreases due to obstruction of the beam by the end-face. Whereas the first method assumes no reflection from the end-face, the second method relies on pointing the beam onto the end-face where it is reflected, and using laser triangulation to find the deflection based on the positions and angles of the laser and the detector. We will refer to the two methods as transmission scan and end-face reflection, respectively. Based on experimental results obtained with silicon boules at room temperature, it is discussed how the system and the two methods can be adapted to provide real-time process monitoring of the crystal–melt interface during the production of silicon boules.
2 Measurement principles and methods
2.1 Choice of wavelength
Laser scanning using a wavelength in the mid-infrared is proposed to take advantage of the relatively low optical absorption of light for photon energies below the intrinsic band gap energy of silicon. The indirect band gap energy of silicon can be approximated using a semi-empirical expression:14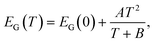 | (1) |
2.2 Transmission scan
For the transmission scan method, the angle of incidence between the laser beam and boule sidewall is fixed and aligned to be orthogonal to the surface of the boule, as shown in Fig. 2. Note that the reflecting mirrors affixed to the funnel above the melt, shown in Fig. 1, are not included in the experimental setup. A beam transmitted through the cylindrical section of the boule (the “body”), above the end-face, will pass unobstructed through the bulk material, while a beam intersecting the end-face will be reflected by the end-face, giving a sharp drop in transmission as the beam falls outside the detector's cone of acceptance. The deflection h of the end-face can be determined by varying the z-position of the laser, looking for the drop in transmission.The direct transmission, i.e. for smooth entrance and exit surfaces, no obstruction by the end-face and no internal scattering, can be calculated from the absorption and the refractive index of crystalline silicon. Given the findings of Schroder et al.16 and a manufacturer specified dopant (boron) concentration, increasing from 1.45 × 1016 atoms per cm3 at the top to 2.8 × 1016 atoms per cm3 at full length (>1500 mm), the estimated absorption coefficient is 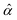 = 0.21 ± 0.07 cm−1 for the entire length and λ = 2.55 μm. Factoring in the reflection upon entering and exiting the boule, assuming normal angle of incidence on a planar surface and a refractive index of 3.44 at 300 K,17 the estimated transmission through a 210 mm diameter boule is −22 ± 6 dB. The large uncertainty is due to the variation in doping. A boule has four nodes given by the crystal structure, visible as ridges along the growth direction. It is expected that these nodes and growth striation in the boule will give a variation in the transmission as a function of the rotation angle (see Fig. 2c). This is not reflected by the calculated transmission and was investigated experimentally.
= 0.21 ± 0.07 cm−1 for the entire length and λ = 2.55 μm. Factoring in the reflection upon entering and exiting the boule, assuming normal angle of incidence on a planar surface and a refractive index of 3.44 at 300 K,17 the estimated transmission through a 210 mm diameter boule is −22 ± 6 dB. The large uncertainty is due to the variation in doping. A boule has four nodes given by the crystal structure, visible as ridges along the growth direction. It is expected that these nodes and growth striation in the boule will give a variation in the transmission as a function of the rotation angle (see Fig. 2c). This is not reflected by the calculated transmission and was investigated experimentally.
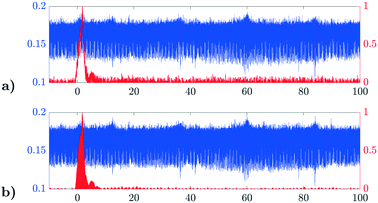
The aim of the transmission scan is to find the position where the transmission decreases due to intersection of the beam and the end-face. To validate the method, the entire length of the boule is scanned, giving a graph of the transmission through the centre of the boule. This may show changes in transmission due to defects, either on the surface or internally, which may disturb the detection of the end-face. The scan is performed by moving the laser to a position, scanning the detector around that position to find the transmitted beam, before moving the laser to the next position. For each laser position, the detector is first swept at high speed (8 mm s−1) over its entire travel range, while continuously sampling at the maximum rate (24 kHz) of the data-acquisition card. The peak response and its corresponding detector position is found from the smoothed data (see Fig. 3), and subsequently verified and refined by a narrow sweep around the detected peak at a reduced speed. The transmission is determined from the peak response, the responsivity (9.2 V mW−1) of the detector/DAQ-system and the open-air transmission of −2.9 dB measured during calibration. Due to significant high-frequency noise in the detector and its amplifier, the raw signal is filtered by a 120-point moving mean filter. A different filtering method is used to remove the noise for the end-face reflection method, see next paragraph.
2.3 End-face reflection
The end-face reflection method (Fig. 2b) uses a beam, with an oblique angle of incidence in the xz-plane, that is refracted as it enters the boule, reflected internally from the end-face and again refracted as it exits the boule. By knowing the angles and positions of the entering and exiting beams, as well as the refractive index of the crystal, the position of the reflection point on the end-face (in the xz-plane) can be determined by triangulation. This is illustrated in Fig. 2b for a beam hitting the apex at the centre of the end-face and an (exaggerated) beam hitting off the centre.The transmission can be calculated as for the transmission scan by taking into account the oblique angle of incidence and the reflection coefficient at the end-face. Due to the high refractive index and relatively low angles of incidence (≈15°), the beam makes a small angle (≈4.3°) with the x-axis inside the boule. This results in a very small increase (≈0.6 mm) in path length inside the boule compared to the normal incidence for the transmission scan. The small angle of the refracted beam results in a large angle of incidence (≈85.7°) with the end-face near its apex, well above the critical angle (16.9° for silicon/air). The beam is thus totally internally reflected by the end-face. Using the Fresnel-equations (assuming TE-polarization) and the small increase in path-length and thus absorption, the expected transmission is just 3.5% lower than for the transmission scan, also giving an estimated total transmission of −22 ± 6 dB.
The optical properties of melted silicon resemble those of a metal.18 Thus, with air replaced by melted silicon as the adjoining material, the reflection coefficient is expected to be high, comparable to that for total internal reflection. Our setup thus resembles the in situ situation regarding reflection from the end-face.
The end-face reflection method relies on hitting the apex of the end-face with the laser and detect the reflected beam. A complete scan-procedure would thus have four variables, with positions and angles for both the laser and the detector. To simplify the problem, we chose to set the detector (manually) to a specified angle, while an algorithm attempts to find a combination of laser angle, laser position, and detector position to hit the apex and detect the reflected beam.
The loss for the beam reflected from the end-face was found to be significantly higher than for the transmission scan, giving a poor signal-to-noise ratio. This can be due to surface irregularities giving increased loss for the oblique angle of incidence, small and concave area for reflection and poor beam-capture by the detector. To enhance the signal-to-noise ratio, the moving-mean filter was replaced by a 50 Hz square wave modulation of the laser and a complementary matched filtering of the detector signal. The matched filter is defined by:
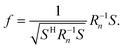 | (2) |
The search-algorithm assumes a parabolic end-face with an initial guess for the deflection at the apex. Given the detector half-cone angle of 1.4° and a refractive index 3.44 (ref. 17) for silicon, a “hit” must be on a portion of the end-face with a surface normal less than 0.4° from the z-axis to be captured. As this angle is small, the triangulation algorithm considers the end-face apex to be flat and orthogonal to the sidewalls when calculating the reflection points.
The algorithm acquires a set of measurements through a series of trials designed to make the beam intersect the end-face apex where each trial consists of a unique combination of angles and positions for both laser and detector. The set of trials is arranged into a set of four nested subsets:
1. Detector angle
• A set of manually set detector angles.
2. Laser angle
• For each detector angle, a discrete set of laser angles in a narrow range surrounding the detector angle.
3. Laser position
• A set of laser positions surrounding the estimated laser position required to hit the end-face apex given by entering each detector/laser angle combination and current best estimate of the deflection into the triangulation formula.
4. Detector position
• A narrow, continuous sweep around the expected beam exit position given by the triangulation formula and each of the preceding variables.
Each trial then returns either a negative (“miss”) or a positive (“hit”) giving the combination resulting in an actual beam intersecting the end-face apex.
The result of a series of trials using only the laser and detector angles of 9° and 10°, respectively, on sample 2 can be seen in Fig. 4.
 | ||
| Fig. 4 Raw dataset from end-face reflection trials near estimated laser/detector positions for triangulation of sample 2 end-face apex. | ||
For laser positions in the range 26–32 mm, the maximum detector response is above the noise level (≈ −30 ± 2 dB), and thus constitute valid beam captures corresponding to “hits” on the end-face. For the same range, the detector positions giving maximum response for each laser position (solid blue), converge to a narrow range of approximately 22–23 mm. The twin peaks for the detector response in Fig. 4 and the corresponding two detector positions at 22 and 23 mm, indicate that “hits” can be slightly away from the apex, on both sides of it. The cause of the two peaks is likely due to a slight discrepancy between the approximated parabolic end-face shape and the true end-face shape which, for 200 mm boules, can form an “M”-shaped cross-section due to melt flow conditions induced by crystal/crucible rotation.1
The corresponding reflection point (xz-plane) and deflection for each “hit” is determined through triangulation (accounting for refraction). The value found for the deflection is used to update the trial values for the angles and positions for subsequent scans. The aim of this iterative approach is that successful trials will improve the “hit”-rate of subsequent trials, thereby producing converging results.
2.4 Samples and experimental setup
The three samples used experimentally are shown in Fig. 5a. The samples are boules that prematurely separated from the melt and closely resembles a boule during crystal-growth. Due to the sudden separation from the melt and subsequent termination of the growth process, the interface solidifies and retains its shape as it was at the time of separation. The end-faces of the samples are thus solid “snapshots” of the crystal–melt interface during crystal growth. The pseudo-parabolic shape of the end-face (interface) can be clearly seen in Fig. 5b as distortions in the image reflected by the bottom (i.e. end-face) of sample 1. | ||
| Fig. 5 Images of samples. a) Side-by-side comparison of samples 1–3 (from left), b) image of mm-scale alignment card reflected by the end-face of sample 1, c) image of sample 1 placed in setup. | ||
The end-face deflection of the three samples was measured using a mechanical probe mounted on a translation stage (Standa 7 T175-100). The specified read-accuracy of this stage is 10 μm, but due to uncertainties regarding the probe itself, the accuracy is taken as 0.1 mm. The measured dimensions and mass of the samples are given in Table 1.
| Length (mm) | Diameter (mm) | Mass (kg) | h (mm) | |
|---|---|---|---|---|
| Sample 1 | 276 ± 1 | 213 ± 1 | 23.7 | 19.7 ± 0.1 |
| Sample 2 | 162 ± 1 | 211 ± 1 | 10.1 | 11.0 ± 0.1 |
| Sample 3 | 389 ± 1 | 212 ± 1 | 34.4 | 13.8 ± 0.1 |
To test the transmission scan and the end-face reflection methods in the laboratory, the samples were positioned horizontally, as shown in Fig. 5c. The xz-plane in Fig. 2a and b was thus horizontal. This made handling easier and simplified the setup. As the reflectors shown in Fig. 1 are intended to be stationary, the behavior of the beam being relayed can be considered equivalent to the laser and detector mounted in place of the reflectors, thus the reflectors are omitted from the experimental setup.
The setup uses a DFB laser diode (NanoPlus, 2550 nm) mounted on motorized rotation and translation stages (Standa, 8MR151 and 8MT175–50) and an amplified, extended-range InGaAs photodiode (ThorLabs, PDA10D2) mounted on a manual rotation stage (ThorLabs, XRR1) and a motorized translation stage (Standa, 8MT50-150BS1). Additionally, a plano-convex lens is mounted on the detector (CaF, 1/2′′, f = 20 mm) to focus incoming light onto the detector active area, giving an effective sensing area of 127 mm2 with NA 0.025. The sample itself is held by a purpose-built holder mounted on a manual translation stage (Standa, 7 T175-100). All motorized stages are controlled by a common controller (Standa, 8SMC5-USB) and data is acquired from the detector using a data-acquisition card (NI, USB-6009). Both stage-control and data-acquisition are performed by algorithms run in Python (3.8.6 ×64) using the manufacturer libraries (pyximc and NI-DAQmx).
For measuring the transmission as function of rotation, the samples were positioned vertically on a rotation stage and rotated with a DC-motor running at a fixed speed. This was thus different from the setup used for the scanning methods.
2.5 Calibration
Before scanning starts, some initiation and calibration steps are carried out. The rotation-angle of the laser is calibrated such that at 0°, the laser beam is perpendicular to the translation axis of the sample holder. The position along the z-axis for the laser (Fig. 2a and b) is set to 0 mm with the translation-stage at the end-position. The detector reference position is subsequently aligned with the laser, such that a detector position of 0 mm optimally captures a beam from the laser at position 0 mm. The laser and detector zero-positions are automatically calibrated at the beginning of each scan. The maximum open-air transmission (i.e. beam not intersecting the sample) was measured by optimally aligning the detector and laser and found to be 51% (−2.9 dB), this loss is likely due to misalignment resulting in overfilling of the detector. This measurement was carried out for a laser-power not saturating the detector, while maximum laser power was used for transmission through the samples.Upon placing the sample in the setup, the height (y-axis of Fig. 2a and b) of the laser is manually adjusted such that the beam intersects the boule at its widest point, giving normal angle of incidence as shown in Fig. 2c. The height of the detector is then adjusted to match that of the laser by maximizing the measured open-air transmission. Lastly, the sample z-position is calibrated such that the lowermost edge (end-face side) obscures 50% of the beam for a laser position of 0 mm and angle 0°.
3 Experimental results and discussion
3.1 Transmission scan
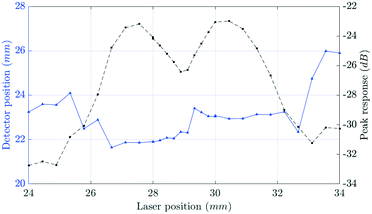
Before measuring transmission along the samples, the transmission was measured as function of rotation of the samples, at one position above the end-face and one below. The results are shown in Fig. 6. The difference in transmission for the two positions is up to 15 dB between the DC-corrected signals. Note that the transmission varies significantly with rotation. At the four nodes of the crystal, the beam is refracted such that no signal is obtained. For sample 2 and 3, the transmissions is relatively constant through the “clear” quadrants of the crystal cross section. On the other hand, sample 1 produced eight distinct peaks corresponding to approximately 15° leading and lagging the four nodes. This can be caused by loss of structure prior to separation and related to the large-scale slip dislocations, as shown by the slip lines in Fig. 8a. The large differences in transmission with rotation can be related to the quality of the grown crystal, but it is necessary to measure more samples and compare with other methods to draw a conclusion. For sample 2 and particularly sample 3, the transmission in the “clear” quadrants is approximately −20 dB which is in agreement with the estimate of −22 ± 6 dB from sec. 2.2. For all three samples, there is a significant difference between the transmission above and below the end-face apex, which is the basis for the transmission scan method. However, the variation in transmission with rotation may impose averaging over a full rotation to obtain a valid result.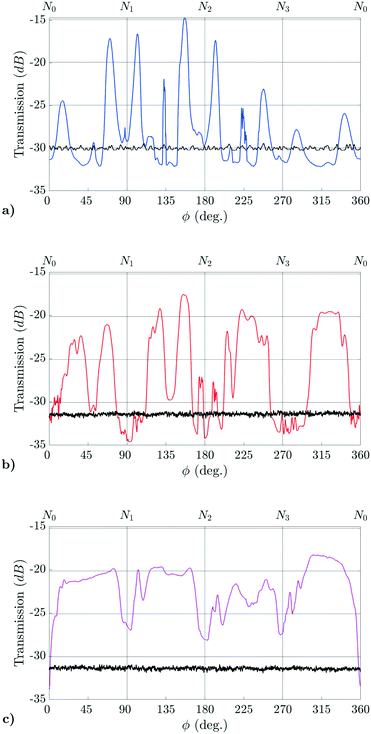 | ||
| Fig. 6 Transmission above (color) and below (black) the apex of the end-face for a) sample 1, b) sample 2, and c) sample 3. The first node encountered has been defined as N0 at 0°. | ||
The transmission scan method was tested by running full scans along the samples, as described in sec. 2.2, with steps of 1 mm for the laser position. A rotation angle was chosen that gave high transmission. The transmission through sample 1, shown in Fig. 7a, shows a sharp increase as the laser position exceeds 19 mm. Omitting the lowest three measurements (0–2 mm) due to parts of the beam being transmitted below the sample, the transmission below 19 mm is −32 ± 2 dB, increasing by 11 dB to −21 ± 2 dB in the range of 20 – 62 mm. The latter value is in agreement with the estimated transmission through the boule of −22 ± 6 dB from sec. 2.2. The transmission shows a dip for 65–110 mm, which is unique for sample 1. The four nodes along the side of the sample, caused by the cubic nature of silicon crystals, terminate 42 mm above the lowermost edge of sample 1, indicating a loss of monocrystalline structure. This is supported by the presence of slip lines at 60 mm to 140 mm, as shown in Fig. 8a, indicating macroscopic crystal dislocations. The abnormally high end-face deflection of 19.7 ± 0.1 mm, in combination with the loss of structure, indicate insufficient cooling relative to crystal growth rate and serves to underscore the motivation for in-situ monitoring of the deflection.
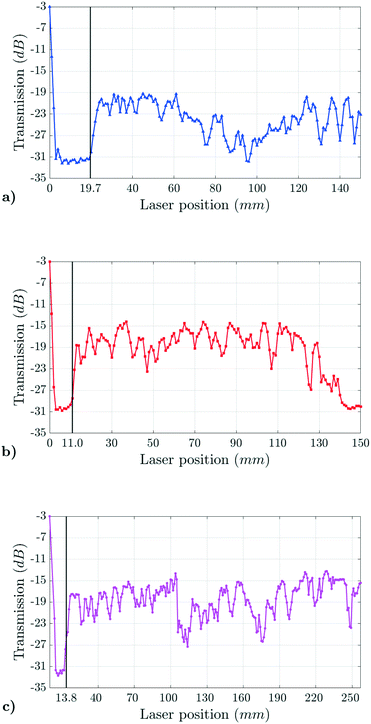 | ||
| Fig. 7 Transmission scan results. a) Sample 1 from 0–150 mm, b) sample 2 from 0–150 mm, c) sample 3 from 0–257 mm. | ||
Measurements of sample 2 show a similar jump in transmission as the height exceeds 11 mm, increasing by 10 dB from 11 mm to 13 mm. Again omitting the lowermost three results, the transmission is −30 ± 2 dB below 11 mm and −18 ± 6 dB from 12 mm to the beginning of the drop-off at 125 mm. The transmission through the bulk material overlaps with the estimated value and the transmission of sample 1, although the mean value is higher. This can be due to lower doping concentration, cleaner material or lower dislocation density than in sample 1. Sample 2 has a full-diameter length of 162 mm, and from 125–150 mm, the beam intersects the lower part of the shoulder, which has an indent as shown in Fig. 8b. The indent gives a non-zero angle of incidence for the beam, thus giving a non-zero angle for the internal beam. This may cause the beam to be refracted out of the acceptance-cone of the detector and thus cause the drop in transmission observed at 140 mm.
The transmission of sample 3, see Fig. 7c, shows less variation than samples 1 and 2. The increase in transmission due to the deflection peak is 7 dB from 12 mm to 17 mm, which is a smaller increase and a flatter slope than for samples 1 and 2. The transmission is −32 ± 4 dB below 13 mm and −19 ± 9 dB from 14 mm and up, with the latter overlapping with the estimate of −22 ± 6 dB from sec. 2.2. The mean values for the transmission through the bulk are higher for samples 2 and 3 than for sample 1, which might be linked to the loss of monocrystalline structure for sample 1. Sample 3 is longer than the two other samples. This made additional alignment and adjustment necessary, which, together with the heavier load on the translation stage, might have given small errors in the recorded positions, although this is not evident from the results.
The nature of each response is determined by thresholding on the transmission and classifying the responses as above end-face apex if transmission is above the threshold, or as intersecting the end-face if under the transmission threshold. The apex of the end-face, and thereby its deflection, is then found as between the lowermost response classified as above the apex and the uppermost response intersecting the end-face. Using the results presented in Fig. 7, the optimum threshold is found to be −27.7 dB and the results are shown in Table 2. The measured deflection deviates from the true deflection by less than the uncertainty of the measurement, and the accuracy is high. Based on this, it is concluded that a transmission scan can determine the end-face deflection with an accuracy of ±0.5 mm using a transmission threshold of −27.7 dB. Note that the transmission scans presented here are designed primarily to serve as a demonstration of the transmission change as the beam passes the apex of the end-face, therefore the method was implemented as a mapping algorithm with a chosen resolution of 1 mm. This means that the accuracy of ±0.5 mm is the limit set by the resolution and not an inherent limitation in the method itself. This method could potentially become both faster and more accurate by using a search algorithm with decreasing scan intervals to find the fast change in transmission identifying the end-face.
| Transmission scan | End-face reflection | Mechanical probe | ||
|---|---|---|---|---|
| CA | Result (mm) | Result (mm) | Result (mm) | |
| Sample 1 | 87.2% | 19.5 ± 0.5 | 19.4 ± 0.8 | 19.7 ± 0.1 |
| Sample 2 | 99.3% | 11.5 ± 0.5 | 11.0 ± 0.4 | 11.0 ± 0.1 |
| Sample 3 | 100% | 13.5 ± 0.5 | — | 13.8 ± 0.1 |
Regarding the classification accuracy (CA), see Table 2, for samples 1 and 2 there are significant deviations caused by anomalous properties of the crystals, as shown in Fig. 8. However, the slip line defects on sample 1 and the diameter anomalies on sample 2 are both far removed from the end-face. In a practical implementation, only the area surrounding the end-face and its apex would be of interest, such that these defects would only be included when the boules were in the beginning of the growth process. If only the lowermost 50 mm are considered here, then the threshold becomes −27.4 dB, resulting in only the measurement at 20 mm on sample 1 giving a false negative, giving a total accuracy of 99.3%.
3.2 End-face reflection
For each scan series, the detector was rotated to an angle in the range 5–30° (1° intervals), followed by using the search-algorithm to find the reflection from the end-face. The search was repeated several times for each angle, including calibration, to obtain valid measurements. For sample 1, approximately 77% of trials gave valid results (see sec. 2.3), for sample 2 this was reduced to 34% and for sample 3 no valid measurements were obtained. As is seen in Fig. 8c, the surface of sample 2 (and 3) exhibits defects that reduces the external reflectivity of the end-face whereas sample 1 (see Fig. 5b) does not. Given that the growth of samples 2 and 3 was terminated due to loss of power, it is conceivable that the shutdown of the heating elements caused the melt beneath the interface to become severely undercooled. As shown in the work of Fujiwara et al.,19 strong undercooling of the melt can induce the growth of facets on the interface, which would manifest as opaque features on the surface. It is possible that these defects can also affect the internal surface, resulting in attenuation and/or scattering of beams reflected from it. Valid reflections might thus only be possible in regions without defects, giving a lower ratio of valid measurements. Another likely reason for the lack of valid measurements from sample 3 is that the foam padding between the sample and holder became significantly compressed due to the higher weight of sample 3 (see Table 1), causing misalignment of the sample. This indicates that the end-face reflection method is less reliable than the transmission scan and more sensitive to alignment and defects.The result of the end-face reflection measurements of sample 1 (see Fig. 9a) reveals two main clusters of reflection points, centered around 37 mm and 72 mm from the center of the sample. For illustration, the parabolic approximation of the end-face cross section is shown, with peak deflection h0, crystal radius r0 and radial position r. Due to the cluster at 72 mm representing a minority of the measurements and being far from the center, only the main cluster centered around 37 mm is considered. This gives a measured end-face deflection of 19.4 ± 0.8 mm compared to the previously measured ‘true’ deflection of 19.7 ± 0.1 mm (see Table 2). This implies a mean error of 0.3 mm (1.5%) and a maximum error of 1.2 mm (6.1%). The result for sample 2 (see Fig. 9b) shows a single cluster centered around 19 mm from the center of the sample. This cluster gives a resulting measured deflection of 11.0 ± 0.4 mm compared to the ‘true’ deflection of 11.0 ± 0.1 mm (see Table 2), and thus zero mean error but a maximum error of 0.5 mm (4.5%).
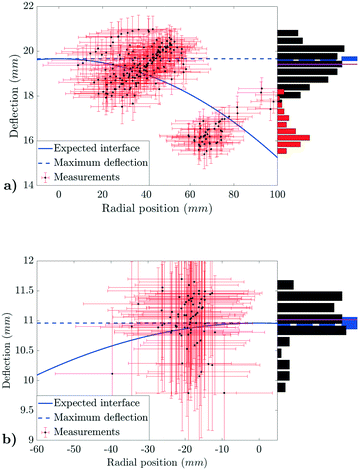 | ||
| Fig. 9 Result of triangulation of reflection points and estimated end-face deflection compared to the idealized parabolic interface shape (h (1 − r2/r02)). a) Sample 1, b) sample 2. | ||
The purpose of the measurement system will most likely be to detect abnormally large interface deflections rather than give a precise reading of the deflection. Considering sample 3 to be representative of a normal case and sample 1 to be an abnormal case, the difference in deflection between normal and abnormal is approximately 6 mm. With a mean error below 0.5 mm for the transmission scan (given by the step-size), and 0.3 mm for the end-face reflection, this is well within the capability of the two methods.
While the measured deflections are shown to be sufficiently accurate, the results reveal that there are significant deviations in the measured radial positions of the reflection points. The high refractive index of silicon causes a large change in the angle of the refracted beam, even for relatively small angles of incidence. Considering that the incidence angle for the measurements was 15°, the beam internal to the boules is expected to have an angle of 4.3° relative to the x-axis. This makes the estimate for the radial position highly sensitive to errors in the angle and z-position of both the detector and the laser. The triangulation formula considers the side-walls of the boules to be flat, while they actually have a wave-like texture (see the reflection in Fig. 8a). It is likely that such features also induce errors, especially in the x-axis.
4 Practical implementation in situ
The experiments at room-temperature demonstrate the principles, but the methods and setups have to be modified for implementation in a furnace, as outlined in Fig. 1. Reflectors must be added to keep the laser and detector away from the high temperatures, thus adding two sources of misalignment and making the beam-path longer, resulting in higher sensitivity to misalignment. Regarding the transmission scan, the beam must be orthogonal to the boule, and thus parallel to the surface of the melt. The minimum detectable interface deflection is thus given by the lower edge of the reflectors. Due to the high temperatures, the reflectors must probably be too high above the melt for the method to be useful. Also, calibration cannot be performed by scanning below the boule as was done at room-temperature, and the zero-height must thus be found separately. The end-face reflection method uses an oblique angle of incidence, which makes it possible for the beam to interact with features below the lower edge of the reflectors. This potentially makes it possible to measure interface deflections down to 0 mm, while fixing the reflectors higher on the funnel, where the temperature is lower. Calibration of the zero-height can be done by reflecting the beam from the surface of the melt and use triangulation, as for reflection from the (inner) surface of the boule. The method did not give results for one of the samples, and the cause of this has to be investigated further. Both methods are likely insensitive to the gas flow within the furnace as this is a non-absorbing gas at low pressure (commonly argon at <6.7 kPa20). However, the methods may respond differently to variations in melt flow conditions. As illustrated by Noghabi et al.,1 high flow caused by rotation of crystal and crucible may induce an “M” shaped cross section. The transmission scan would be insensitive to this as it detects the maximum deflection independently of the cross section. On the other hand, the end-face reflection would return the height at the center, which for an M-shaped interface would not be the maximum deflection. The rotation itself, as shown by the results in Fig. 6, gives intermittent transmission related to the nodes of the crystals. Laser scanning is generally fast and can handle this, but it may be necessary to measure over a full rotation to get reliable results. Finally, regarding integration into existing furnaces, the required physical modifications of a furnace are relatively minor compared to alternative methods as described in sec. 1, but clearly poses a significant challenge in implementation due to the requirements on alignment for both methods.5 Conclusions
Two methods have been proposed, based on laser scanning, to measure the crystal–melt interface deflection of a silicon boule. Both methods give sufficiently precise results at room-temperature to be relevant for in situ use. The transmission scan method is shown to achieve a minimum accuracy of 87% in differentiating the bulk material from the end-face in all three samples when implemented as a mapping method with a fixed step-size of 1 mm, which dictates the measurement error of 0.5 mm. The end-face reflection method measured the deflection of two out of three samples with a mean measurement error of less than 0.3 mm (1.5%) with maximum errors of less than 1.2 mm (6%) when using incidence angles between 5° and 30°.The transmission scan method is superior in reliability as it successfully measured the deflection of all three samples, while the end-face reflection method failed to acquire measurements for sample 3. The transmission scan method is also shown to remain viable with constant crystal rotation. An interesting topic for further study is to search for a link between the variation in transmission during rotation and the quality of the grown crystal.
The end-face reflection method is superior in flexibility as its use of oblique angles of incidence allows for fixing the reflectors higher on the funnel, while the transmission scan method requires the reflectors to be placed in close proximity of the melt.
A mid-infrared laser is used, to avoid absorption due to band-to-band transitions in silicon at high temperatures. This requires the use of detectors prone to high noise, resulting in low signal-to-noise ratio. This ratio can be improved by changing from the uncooled detector used here, to a cooled one. By also changing the optical components to avoid the open-air loss of 2.9 dB, the signal-to-noise ratio can probably be increased from 11.5 dB at present, to upwards of 20 dB. The influence of absorption for photon energies lower than the band-gap must be investigated for high temperatures, as an increase in absorption will reduce the signal-to-noise ratio correspondingly, possibly compromising the success of the proposed methods.
Author contributions
The first author suggested the problem and the authors conceived the measurement methods together. The first author conducted the experimental work and the data analysis. The authors contributed equally on the written work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Norwegian Crystals AS for supplying the samples and relevant reference information. Also thanks to Dr. Eivind Johannes Øverlid (SINTEF Industry) and Dr. Per Anders Eidem (SINTEF Helgeland) for advice.Notes and references
- O. Asadi Noghabi, M. M'Hamdi and M. Jomâa, J. Cryst. Growth, 2011, 318, 173–177 Search PubMed.
- Y. Shiraishi, S. Maeda and K. Nakamura, J. Cryst. Growth, 2004, 266, 28–33 Search PubMed.
- A. Popescu and D. Vizman, Cryst. Growth Des., 2012, 12, 320–325 Search PubMed.
- K. Jiptner, B. Gao, H. Harada, Y. Miyamura, M. Fukuzawa, K. Kakimoto and T. Sekiguchi, J. Cryst. Growth, 2014, 408, 19–24 Search PubMed.
- K. Kakimoto, M. Eguchi, H. Watanabe and T. Hibiya, J. Cryst. Growth, 1988, 91, 509–514 Search PubMed.
- Y. Zhu, D. Ma, S. Long, F. Tang, S. Lin and B. Wang, J. Cryst. Growth, 2017, 475, 70–76 Search PubMed.
- Y. Zhu, S. Lin, Z. Liu, W. Wang, D. Ma and B. Wang, CrystEngComm, 2019, 21, 1107–1113 Search PubMed.
- J. Ding and L. Liu, CrystEngComm, 2018, 20, 6925–6931 Search PubMed.
- Handbook of Optical and Laser Scanning, ed. G. F. Marshall and G. E. Stutz, CRC Press, 2nd edn, 2011 Search PubMed.
- In Laser in der Technik/Laser in Engineering, ed. W. Waidelich, Springer, 1994 Search PubMed.
- In Laser scanning: Theory and Application, ed. C.-C. Wang, IntechOpen, 2011 Search PubMed.
- K. Haug and G. Pritschow, IECON '98. Proceedings of the 24th Annual Conference of the IEEE Industrial Electronics Society (Cat. No.98CH36200), 1998, vol. 2, pp. 1236–1241 Search PubMed.
- C. Schinke, P. Christian Peest, J. Schmidt, R. Brendel, K. Bothe, M. R. Vogt, I. Kröger, S. Winter, A. Schirmacher, S. Lim, H. T. Nguyen and D. MacDonald, AIP Adv., 2015, 5, 067168 Search PubMed.
- Y. Varshni, Physica, 1967, 34, 149–154 Search PubMed.
- V. Alex, S. Finkbeiner and J. Weber, J. Appl. Phys., 1996, 79, 6943–6946 Search PubMed.
- D. K. Schroder, R. N. Thomas and J. C. Swartz, IEEE J. Solid-State Circuits, 1978, 13, 180–187 Search PubMed.
- D. Chandler-Horowitz and P. M. Amirtharaj, J. Appl. Phys., 2005, 97, 123526 Search PubMed.
- K. Li and P. Fauchet, Solid State Commun., 1987, 61, 207–209 Search PubMed.
- K. Fujiwara, R. Gotoh, X. Yang, H. Koizumi, J. Nozawa and S. Uda, Acta Mater., 2011, 59, 4700–4708 Search PubMed.
- N. Machida, Y. Suzuki, K. Abe, N. Ono, M. Kida and Y. Shimizu, J. Cryst. Growth, 1998, 186, 362–368 Search PubMed.
| This journal is © The Royal Society of Chemistry 2021 |