New insights into the role of solution additive anions in Mg²⁺ dehydration: implications for mineral carbonation

Abstract

Simulations of hydrated Mg²⁺, in the absence and presence of several solution additive anions, show that in pure liquid water Mg(H₂O)₆²⁺ is the only stable coordination state; yet anions may stabilise undercoordinated five-hydration configurations. Solution composition can lower the barrier to Mg²⁺ dehydration and subsequent incorporation into the lattice of Mg-carbonates, promoting low-temperature crystallisation.

---

Formed via aqueous mineral carbonation of Mg²⁺ ions, the crystallisation of magnesite (MgCO₃) represents an industrially effective route to CO₂ storage and utilisation, generating stable, inert, non-hazardous, and ready-to-use carbonate-based materials,¹ revenues of which are expected to reach $1 trillion per year by 2030.² Mg²⁺ sources are widespread and plenty and include Mg-silicate deposits (>100 000 Gt)³ and alkaline industrial residues.⁴ However, CO₂ mineralisation is limited by the slow rates of MgCO₃ precipitation.⁵

Magnesite production is an energy-intensive process due to the high temperatures (120 ≤ T ≤ 600 °C) required to prevent the formation of metastable hydrated phases nesquehonite (MgCO₃·3H₂O) and hydromagnesite, (Mg₅(CO₃)₄(OH)₂·4H₂O).⁶ The high T conditions necessary to promote the direct precipitation of anhydrous MgCO₃, increased solid mass and volume of the hydrated Mg-carbonate phases per mole of CO₂ sequestered and their inferior mechanical properties, all have negative impacts on the industrial viability and profitability of CO₂ mineralisation.⁷

Due to the highly hydrated character of Mg²⁺ in aqueous solutions (Δ_hydG° = −455 kcal mol⁻¹),⁸ the difficulty in precipitating magnesite has long been ascribed to the slow kinetics of Mg²⁺ dehydration.⁹ However, geological records show that magnesite, MgCO₃, and dolomite, CaMg(CO₃)₂, form during weathering of ultramafic rocks (Mg-rich and low silica) and sedimentary processes (precipitation and/or replacement) taking place at low-T,¹⁰ which are different from the conditions necessary to stimulate the synthesis of the anhydrous forms of Mg-carbonates. This conundrum, known as the “dolomite problem”, represents one of the most long-standing questions in low-temperature geochemistry.¹¹

Natural solutions are far from pure water, being rich in ions, making solution environments highly influential on the rate determining Mg²⁺ dehydration step. Resolving the catalytic role of composition is imperative in determining what catalyses MgCO₃ formation in sedimentary environments. The goal of this communication is to provide a computational characterisation of the mechanism of Mg²⁺⋯H₂O dissociation reaction in the presence of several solution additive anions. We reason that the root of these effects may reside in the ability of organic ligands and inorganic anions that are typically present in aqueous environments to activate Mg²⁺ dehydration, and subsequent nucleation and growth steps, by influencing the hydration structure of Mg²⁺.

Here, we report a computational characterisation of the rate determining Mg²⁺ (de)hydration process. We conducted simulations of Mg²⁺ in pure liquid water and in solutions containing ions (X) commonly found in groundwater (F⁻, Cl⁻, NO₃⁻, HCO₃⁻, CO₃²⁻, SO₄²⁻) including bisulfide (HS⁻)¹² and carboxylate (CH₃COO⁻) ions thought to catalyse carbonation.¹³ The computational details of the molecular dynamics (MD) and enhanced sampling metadynamics (MetaD) simulations and of the electronic structure analyses adopted are reported in ESI,† together with the details of the electrolyte solutions considered (number of ions and H₂O molecules, equilibrated cell length).

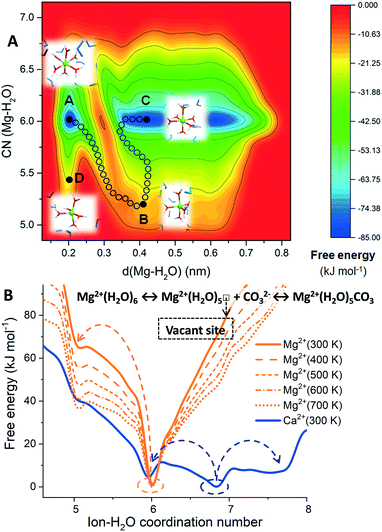
Fig. 1A shows the free energy landscape, computed using MetaD, of a hydrated Mg²⁺ (isolated metal ion, without any counterions) as a function of the ion–water distance, d(Mg–H₂O), and ion–water coordination number, CN(Mg–H₂O). Letters A, B, C and D correspond to representative configurations on the free energy landscape. The octahedral six-fold coordination with water (configurations A and C) represents the only thermodynamically stable state for hydrated Mg²⁺ in pure liquid water. Configuration B corresponds to the metastable five-fold trigonal bipyramidal coordination state, which lies on the lowest energy pathway between the six-fold configurations A and C. Configuration D is another five-coordinated intermediate Mg(H₂O)₅²⁺ on the free energy surface of hydrated Mg²⁺. Our metadynamics results are consistent with gas-phase density functional theory (DFT) calculations of Mg²⁺ hydrates containing up to 18 water molecules, which showed that the process of going from the six- to the five-coordinated states (the two lowest energy hydrated structures) is highly unfavorable.¹⁴ The arrangement of H₂O molecules around the five-coordinated intermediate B also shows that the Mg²⁺ dehydration proceeds with the assistance of out-of-shell solvent water molecules, in agreement with static electronic structure calculations of small hydrated Mg²⁺ cluster models.¹⁵

Fig. 1 (A) Free energy contour plot of hydrated Mg²⁺ as a function of the Mg–H₂O coordination number, CN(Mg–H₂O), and of the Mg–H₂O distance, d(Mg–H₂O), of one of the six water molecules (H₂O*) that at the start of the MetaD simulation is part of the first hydration shell of Mg²⁺. A and C correspond to the six-coordinated state. B and D are the five-coordinated intermediate Mg(H₂O)₅²⁺ when H₂O* is inside or outside of the first hydration shell of Mg²⁺, respectively. (B) Free energy profiles of hydrated Ca²⁺ and Mg²⁺ ions as a function of the ion–water coordination number. For the hydrated Mg²⁺, MetaD simulations were conducted at temperatures ranging from 300 K to 700 K.

In Fig. 1B, the free energy profiles of hydrated Mg²⁺ as a function of the ion–water coordination number are compared to that of Ca²⁺. From these profiles, we can extract thermodynamic information on the accessible coordination states for these cations. For the calcium ion, the seven-coordinate Ca(H₂O)₇²⁺ is the most likely hydration state and not the six-coordinate as for Mg²⁺, but the six- and eight-fold coordination states are also accessible at room temperature (Fig. 1B, in blue). The calcium incorporation in calcite or dolomite may occur through dissociative (7 → 6) or associative (7 → 8) pathways. The hydrated Mg²⁺ has a very stable minimum corresponding to six-fold coordination with water, Mg(H₂O)₆²⁺. On the other hand, the five-coordinated intermediate, Mg(H₂O)₅²⁺, is inaccessible at 300 K due to the 65 kJ mol⁻¹ activation barrier between six- and five-coordinated configurations of Mg²⁺, which is significantly larger than the thermal energy at 300 K (kT = 2.5 kJ mol⁻¹). Consequently, water exchange is drastically retarded in the first hydration shell of Mg²⁺. MD simulations showed no water exchange around Mg²⁺ (no dehydration) after 100 ns compared to aqueous Ca²⁺ which underwent ∼50 water exchanges in only 180 ps (facile dehydration) (Fig. S2†). Even a single H₂O dissociated from Mg²⁺ would still translate to a ∼36 000-fold retardation compared to Ca²⁺. The subsequent steps of nucleation and growth are likewise susceptible to Mg-(re)hydration. Consequently, the precipitate rates of MgCO₃ and CaMg(CO₃)₂, are six and four orders of magnitude slower, respectively than CaCO₃ at 300 K.¹⁶

The generation of a vacant site at the central magnesium ion, to which carbonate can bind to initiate the MgCO₃ nucleation process, requires the displacement of a water molecule from the first coordination shell of Mg²⁺. However, the Mg²⁺ dehydration is a highly activated process, restricted by a free energy barrier of 65 kJ mol⁻¹ for the transformation from the six to the five-coordinated states (Fig. 1B). By increasing the temperature from 300 K to 700 K, a gradual stabilisation of Mg(H₂O)₅²⁺ occurs and the activation barrier between six- and five-coordinated Mg²⁺ decreases (Fig. 1B, in orange), which is consistent with the experimental evidence that higher temperatures promote the direct precipitation of magnesite.^6,7

Towards resolving the bases of the faster kinetics of MgCO₃ precipitation observed within the nanoconfined space of adsorbed H₂O films, compared to the bulk solution, Miller et al. proposed a reduction in coordinating water molecules (fewer than six) for Mg²⁺.¹⁷ Similarly, Mergelsberg conjectured that the greater salinity in natural systems may stabilise the five-coordinated intermediate.¹⁸ A substantial proportion of Mg(H₂O)₅²⁺ in solution will lower the barrier to cationic dissolution, and its incorporation in the crystal lattice of Mg-carbonates.

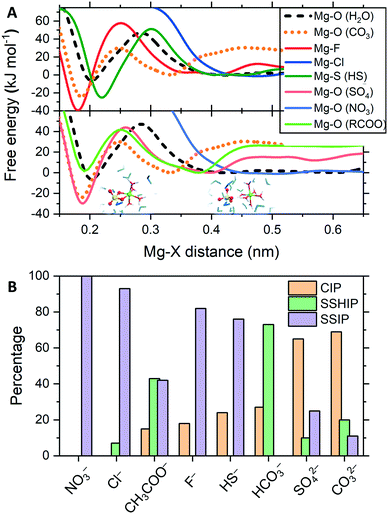
In electrolyte solutions, ions are not purely hydrated and can form contact ion pairs (CIPs), when the cation and anion are in direct contact, or solvent-shared ion pairs (SSHIPs), when separated by one water molecule. Ion pairs interspersed by two or more water molecules are labelled solvent-separated ion pairs (SSIP). The tendency of Mg²⁺ and a counterion (X) of forming CIP, SSHIP or SSIP depends on the competition between Mg²⁺⋯H₂O and Mg²⁺⋯X interactions. The strength of ion-pairing was assessed by computing, using MetaD, the free energy profiles as a function of the Mg²⁺⋯X distance and compare them to the free energy profile of removing a water molecule from hydrated Mg²⁺ (Fig. 2A). Key features of the free energy profiles for the formation of Mg²⁺⋯X CIPs, the standard Gibbs energy of activation (Δ^‡G) and Gibbs free energy of reaction (ΔG), are summarised in Table S2 (ESI†). Fig. 2B reports the distribution of ion pairs in the solutions, where we have sorted additive anions based on their ability to form a CIP with Mg²⁺.

Fig. 2 (A) The free energy profiles as a function of the distance between Mg²⁺ and the centre of mass of the additive X (CO₃²⁻, F⁻, Cl⁻, HS⁻, SO₄²⁻, NO₃⁻, CH₃COO⁻) are compared with the free energy profile for the removal of H₂O from Mg(H₂O)₆²⁺. Structures of Mg(η₂-SO₄)(H₂O)₄, with SO₄²⁻ coordinated in a bidentate mode and the hydration number four, and of Mg²⁺ and SO₄²⁻ interspersed by one water molecule. (B) Distribution of Mg²⁺ and X contact ion pairs (CIP), and solvent shared (SSHIP) and solvent separated (SSIP) ion pairs obtained from the analysis of the MetaD simulations.

The free energies for the Mg²⁺⋯CO₃²⁻ (ΔG = −26 kJ mol⁻¹) and Mg²⁺⋯SO₄²⁻ (−30 kJ mol⁻¹) pairing are significantly lower than Mg(H₂O)₆²⁺ (−7 kJ mol⁻¹), whilst the Gibbs energy of activation of these CIPs are lower than Mg²⁺⋯H₂O dissociation (Δ^‡G = +48 kJ mol⁻¹). Consequently, both Mg²⁺⋯CO₃²⁻ and Mg²⁺⋯SO₄²⁻ CIPs are thermodynamically and kinetically favourable compared to Mg(H₂O)₆²⁺. That is why in Fig. 2B, carbonate and sulfate display a high propensity towards CIP. Such a result corroborates the significant body of knowledge in low-temperature geochemistry showing the prerequisite for dolomite precipitation in sedimentary environments is the low concentrations of sulfate ions, and that such a low concentration is due to the activity of sulfate reducing bacteria (forming bisulfide ions).¹⁹ Using AFM, King et al. showed that even small amounts of sulfate in solution is detrimental to the growth of both anhydrous and hydrated Mg-carbonate phases.²⁰ The authors interpreted the detrimental effect of sulphate ions in solution to Mg-carbonation to the formation of Mg²⁺⋯SO₄²⁻ ion pairs, which lower the activity of the free Mg²⁺ ion, reducing the solution supersaturation with respect to magnesite. Our results also agree with Raman spectra of aqueous solutions of MgSO₄ reported by Rudolph et al., where the changes to the ν₁-SO₄²⁻ mode at ∼980 cm⁻¹ was associated with the formation of an Mg²⁺⋯SO₄²⁻ contact ion pairs.²¹ Based on our simulations, sulfate ions may inhibit the nucleation and growth of magnesite because ion pairing of Mg²⁺⋯SO₄²⁻ is competitive to Mg²⁺⋯CO₃²⁻.

The formation of the Mg²⁺⋯F⁻ CIP is thermodynamically very favourable (ΔG = −41 kJ mol⁻¹ at r(Mg–F) = 0.18 nm in Fig. 2A). However, the lower propensity towards ion-pairing observed in our simulations is likely to be caused by the very high Gibbs energy of activation for the formation of the Mg²⁺⋯F⁻ CIP (Δ^‡G = 60 kJ mol⁻¹ at r(Mg–F) = 0.25 nm in Fig. 2A). Such a value is significantly higher than removing an H₂O molecule from the Mg(H₂O)₆²⁺ complex (Δ^‡G = 47 kJ mol⁻¹ at r(Mg–O) = 0.29 nm in Fig. 2A). Similar behaviour is observed for bisulfide. The Mg²⁺⋯HS⁻ is thermodynamically favourable (ΔG = −26 kJ mol⁻¹) but the high activation barrier (Δ^‡G = 51 kJ mol⁻¹) limits the formation of CIPs.

Due to the absence of a minimum on the free energy profile, Cl⁻ and NO₃⁻ form almost exclusively SSIPs. For these ions, no disturbance in the inner hydration shell of Mg²⁺ occurs priory to the energetically costly replacement of a water molecule with one Cl or O (nitrate) atom. For MgCl₂(aq), such a result confirms recent broadband dielectric relaxation spectroscopic measurements on the aqueous solution of MgCl₂ where no evidence for the significant formation of contact ion pairs was observed.²² Also, a combined Raman spectroscopic study and MD simulation using an ad hoc force field for aqueous MgCl₂ solutions also supported the absence of Mg²⁺⋯Cl pairing.²³Fig. 2B shows that CH₃COO⁻ and HCO₃⁻ have a propensity for SSHIP because the free energy difference between contact, Mg²⁺⋯X, and solvent shared, Mg²⁺⋯H₂O⋯X, pairs are close to zero (Table S2†). The values of ΔG = 1 kJ mol⁻¹ and Δ^‡G = 41 kJ mol⁻¹ for the carboxylate group, deemed responsible for Mg²⁺ dehydration, imply that CH₃COO⁻ does not inhibit MgCO₃ pairing. The low propensity of the acetate anion towards pairing with Mg²⁺ observed in our simulations qualitatively agrees with the positive value of the free energy for water ↔ formate (HCOO⁻) substitution exchange reaction [Mg(H₂O)₆]²⁺ + HCOO⁻ → [Mg(H₂O)₅(HCOO)]⁺ + H₂O computed using DFT and continuum dielectric methods.²⁴

To determine the influence of additive anions on the kinetics of Mg²⁺ dehydration, we computed the free energy as a function of the Mg²⁺–water coordination number, CN(Mg–H₂O), for solutions containing counterions. Exploring the dynamical aspects of the CN(Mg–H₂O) reaction coordinate allows us to examine the ability of solution additive anions to influence the transition between coordination states of Mg²⁺ during the dynamics of cation solvation. Fig. 3A compares the free energy profiles of Mg²⁺ in pure liquid water with that of Mg²⁺ in solutions containing anions with a propensity for SSHIP or SSIP as they are not competitive to CIP MgCO₃ formation.

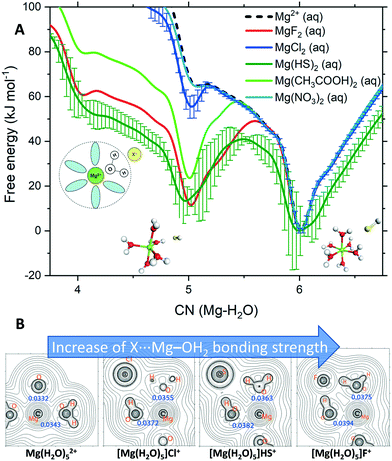Fig. 3 (A) Free energy as a function of the Mg²⁺–H₂O coordination number, CN(Mg–H₂O), for hydrated Mg²⁺ (single Mg²⁺, no counterions) and solvated Mg²⁺ with a counterion in the second hydration shell. The structures are the five- and six-coordinated states in Mg(HS)₂(aq). Standard deviation computed from the average of the profiles of four independent MetaD simulations (300 K). Error bars are presented for the cases with the largest uncertainty, others have been removed for clarity (see Fig. S3†). (B) 2-D Laplacians of electronic density (∇²ρ) in the plane of the Mg, O, H and X atoms in Mg(H₂O)₅²⁺ and [Mg(H₂O)₅]·X⁺ (X = F⁻, Cl⁻, HS⁻). Values of ρ_b (in e bohr⁻³) at selected bond critical points are provided in blue.

In these MetaD simulations, we have kept the separation between Mg²⁺ and the counterion at ∼4.5 Å, which corresponds to a solvent shared Mg²⁺⋯H₂O⋯X ion pair. According to Fig. 3A, the nitrate ion does not affect the kinetics of Mg²⁺–H₂O dissociation because the free energy profile of Mg(NO₃)₂(aq) overlaps that of hydrated Mg²⁺ (isolated metal ion, without any counterions). In both solutions, the Mg²⁺ six-coordinated state is the only one accessible at room T. Chloride shows a small stabilisation of the five-coordinated Mg²⁺. In comparison, the bisulfide ion has a dramatic effect on the thermodynamics and kinetics of Mg²⁺ dehydration. In Mg(HS)₂(aq), the five-coordinated Mg(H₂O)₅²⁺ state is as stable as its six-coordinate compliment Mg(H₂O)₆²⁺ and the Gibbs free energy barrier to jump between these two states is 49 kJ mol⁻¹ compared to 66 kJ mol⁻¹ in pure liquid water. Our simulations thus show, for the first time, that additive anions such as HS⁻ forming SSHIP with Mg²⁺ can promote the dehydration of the Mg²⁺ cation. Such a process may generate a large proportion in the aqueous solution of undercoordinated hydrated Mg²⁺ states with a vacant coordination site to which CO₃²⁻ can bind, initiating the process of MgCO₃ nucleation or promoting the Mg²⁺ incorporation into the crystal lattice. Our result supports McKenzie's hypothesis that bisulfides, delivered by sulfate-reducing bacteria, promote natural dolomite formation by catalysing Mg²⁺–H₂O dissociation.¹² Similarly, the dehydration of Mg²⁺via surface-bound carboxyl groups has been proposed by Kenward et al. to explain the low-T precipitation of dolomite on carboxylated polystyrene spheres.²⁵ The result for the carboxylate ion in Fig. 3A confirms Kenward's hypothesis since CH₃COO⁻ in the second hydration shell of Mg²⁺ stabilises the five-hydration state in a more energetically favourable process than in pure liquid water, thus promoting Mg-carbonate nucleation. The fluoride ion shows similar stabilisation behaviour (Fig. 3A). Further, the role of fluoride in facilitating Mg²⁺ dehydration may help to explain natural deposits of thin alternating layers of fluorite and dolomite, known as zebra rocks.²⁶ For the solutions containing Mg²⁺⋯X CIPs, the free energy profiles show stabilisation of configurations with three and four water molecules in the first shell (Fig. S4†). Therefore, Mg²⁺ is dehydrated even when directly coordinated to the solution additive anion.

The electronic structure of Mg(H₂O)_n²⁺ and [Mg(H₂O)_n]·X⁺ (n = 5, 6) were determined using Bader's atoms-in-molecules analyses of the wavefunctions generated from their DFT geometry-optimised structures (Fig. S5†). The rho-b (ρ_b/e bohr⁻³) values (Fig. 3B, in blue) indicate a progressive increase in the electron density at the bond critical point of the Mg–O bond with the axial-H₂O group interacting with the incoming X ion. Such a bond strengthening is concomitant with the weakening of other Mg–O bonds, the opposing axial in particular (Fig. S4†); an anti-type effect in classical inorganic coordination. In Fig. 3B, the 2-D Laplacians of the electronic density in the plane of the Mg, O, H and X atoms show iso-density contour lines progressively widening ‘saddle points’ between Mg²⁺ and O. These trends point to a continuing stabilisation of the five-coordinate species, with the allosteric weakening of the other Mg–O bonds, effectively readying the complex for subsequent dehydration. The widening of the free-energy potentials for the five-coordinate minimums (Fig. 3A) support such a conclusion, implying more structurally flexible geometries.

Conclusions

We have computationally characterised the mechanism of Mg²⁺–H₂O dissociation in the absence and presence of several solution additive anions. The slow kinetics of Mg²⁺ dehydration in pure liquid water is due a high-energy metastable five-coordinated intermediate. Anions such as bisulfide, carboxylate and fluoride ions can stabilise undercoordinated Mg²⁺ hydration configurations, even when they are in the second hydration shell of Mg²⁺. Wavefunction analyses revealed the changes in bonding responsible for the equilibration of five and six hydrated states, with insight into the mechanisms by which these can inter-change and open-up coordination sites on the central Mg²⁺ ion. The characterisation of the rate-determining Mg²⁺ dehydration process in a series of solutions, as covered in our work, contributes to resolving the catalytic role of solution composition in promoting Mg²⁺ dehydration, and subsequent MgCO₃ formation in natural and industrial environments.

This project is funded through the ACT programme (Accelerating CCS Technologies, Horizon2020 Project No 294766). Financial contributions made from Department for Business, Energy & Industrial Strategy together with extra funding from NERC and EPSRC research councils (UK), ADEME (FR), MINECO-AEI (ES). We thank the UK MMM Hub (EP/P020194/1), HEC MCC (EP/L000202, EP/R029431), and Queen Mary's Research-IT for computing resources. GAC thanks McMaster University and Hong Kong Univ. for his adjunct and honorary positions.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. A. Sanna, M. Uibu, G. Caramanna, R. Kuusik and M. M. Maroto-Valer, Chem. Soc. Rev., 2014, 43, 8049–8080.
2. Mission Innovation, Accelerating Breakthrough Innovation in Carbon Capture, Utilization, and Storage, Houston, Texas, 2017.
3. K. S. Lackner, Annu. Rev. Energy Environ., 2002, 27, 193–232.
4. E. R. Bobicki, Q. Liu, Z. Xu and H. Zeng, Prog. Energy Combust. Sci., 2012, 38, 302–320.
5. D. E. Giammar, R. G. Bruant Jr. and C. A. Peters, Chem. Geol., 2005, 217, 257–276.
6. E. J. Swanson, K. J. Fricker, M. Sun and A.-H. A. Park, Phys. Chem. Chem. Phys., 2014, 16, 23440–23450.
7. V. Prigiobbe, M. Hänchen, M. Werner, R. Baciocchi and M. Mazzotti, Energy Procedia, 2009, 1, 4885–4890.
8. J. Burgess, Metal ions in solution, Ellis Horwood Ltd., Chichester, 1978.
9. F. L. Sayles and W. S. Fyfe, Geochim. Cosmochim. Acta, 1973, 37, 87–99.
10. M. Kralik, P. Aharon, E. Schroll and D. Zachmann, in Monograph Series on Mineral Deposits, 1989, vol. 28, pp. 197–223.
11. H. Zimmermann, Int. Geol. Rev., 2000, 42, 481–490.
12. J. McKenzie and C. Vasconcelos, Sedimentology, 2009, 56, 205–219.
13. I. M. Power, P. A. Kenward, G. M. Dipple and M. Raudsepp, Cryst. Growth Des., 2017, 17, 5652–5659.
14. C. W. Bock, G. D. Markham, A. K. Katz and J. P. Glusker, Inorg. Chem., 2003, 42, 1538–1548.
15. Z. Qian, H. Feng, C. Wang and J. Chen, Inorg. Chim. Acta, 2010, 363, 3627–3631.
16. G. D. Saldi, G. Jordan, J. Schott and E. H. Oelkers, Geochim. Cosmochim. Acta, 2009, 73, 5646–5657.
17. Q. R. S. Miller, J. P. Kaszuba, H. T. Schaef, M. E. Bowden, B. P. McGrail and K. M. Rosso, Chem. Commun., 2019, 55, 6835–6837.
18. S. T. Mergelsberg, S. N. Kerisit, E. S. Ilton, O. Qafoku, C. J. Thompson and J. S. Loring, Chem. Commun., 2020, 56, 12154–12157.
19. P. A. Baker and M. Kastner, Science, 1981, 213, 214–216.
20. H. E. King and C. V. Putnis, Geochim. Cosmochim. Acta, 2013, 109, 113–126.
21. W. W. Rudolph, G. Irmer and G. T. Hefter, Phys. Chem. Chem. Phys., 2003, 5, 5253–5261.
22. S. Friesen, G. Hefter and R. Buchner, J. Phys. Chem. B, 2019, 123, 891–900.
23. K. M. Callahan, N. N. Casillas-Ituarte, M. Roeselová, H. C. Allen and D. J. Tobias, J. Phys. Chem. A, 2010, 114, 5141–5148.
24. T. Dudev, J. A. Cowan and C. Lim, J. Am. Chem. Soc., 1999, 121, 7665–7673.
25. J. A. Roberts, P. A. Kenward, D. A. Fowle, R. H. Goldstein, L. A. González and D. S. Moore, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 14540–14545.
26. U. Kelka, M. Veveakis, D. Koehn and N. Beaudoin, Sci. Rep., 2017, 7, 14260.

---

Footnote

† Electronic supplementary information (ESI) available: Computational details and data. See DOI: 10.1039/d1ce00052g

---