High-pressure and low-temperature structural study of claudetite I, a monoclinic layered As₂O₃ polymorph

High-pressure structural studies of arsenic(III) oxide polymorphs are completed by presenting crystal structures of claudetite I determined using synchrotron powder X-ray diffraction up to ∼30 GPa. The crystal structure of claudetite I is also redetermined based on synchrotron single-crystal X-ray diffraction measurements at room and low temperatures. Claudetite I undergoes no phase transitions under high pressure nor at low temperature. It is the densest and least compressible ambient-pressure As₂O₃ polymorph with the following third-order Vinet equation of state parameters: V₀ = 312.1(13) ų, B₀ = 21.0(11) GPa, and = 6.72(17). Fitting of a simple Berman thermal equation of state to the low-temperature single-crystal data yields V₀₀ = 307.4(4) ų and α₀ = 9.1(7) × 10⁻⁵ K⁻¹ with a reference temperature of 298 K. The coordination sphere of arsenic atoms is thoroughly characterized by the valence entropy coordination number and the description of their lone electron pair stereoactivity using bond-valence vectors. Surprisingly, it is found that although claudetite I is the densest ambient-pressure arsenic(III) oxide polymorph, it does not exhibit the highest arsenic coordination numbers. The pressure dependence of secondary As⋯O bond lengths follows the same trends for all crystalline As₂O₃ polymorphs confirming the same nature of the interactions in all forms. It is also found that pressure does not affect the stereoactivity of arsenic lone electron pairs.

Introduction

Arsenic(III) oxide has been known to humanity since antiquity. Initially used as a poison, it has found numerous applications in medicine, where it is used in the treatment of acute promyelocytic leukemia, and in industry, where it is used as an additive to various glasses and for the production of elemental arsenic, wood preservatives and pesticides. The basic building block of all arsenic(III) compounds is the AsO₃ ψ-tetrahedron containing three O²⁻ ligands and a stereoactive lone electron pair (LEP) acting as a pseudoligand. The ψ-tetrahedra have to share all oxide ligands to yield As₂O₃ stoichiometry which gives rise to rich polymorphism of arsenic(III) oxide. It occurs in nature in the form of two minerals – cubic arsenolite built of As₄O₆ molecules and layered monoclinic claudetite I. In the 1940s, the third polymorph was discovered and called α-claudetite II due to its resemblance to claudetite I (see Fig. S1 and Table S1† for comparison of the crystal structures of ambient-pressure As₂O₃ polymorphs).¹ A few years ago, three more layered polymorphs of arsenic(III) oxide were discovered when claudetite II was subjected to high pressure (HP). It transformed at 2 GPa and 6GPa into α′- and α′′-claudetite II, respectively, gradually losing the symmetry of inversion centers until it formed polar β-claudetite II at 11 GPa.² It was also found that arsenolite does not undergo phase transitions under (quasi)hydrostatic conditions up to 40 GPa,^3,4 but undergoes amorphization at around 15 GPa when the non-hydrostaticity of pressure transmitting media is significant.^5,6 Claudetite I is formed from highly corrugated As₂O₃ layers and crystallizes in the P2₁/n space group with the following unit cell parameters at ambient pressure and temperature: a = 5.25(1) Å; b = 12.99(3) Å; c = 4.53(1) Å; β = 93.9(3) Å; V = 308.2(12) ų (see Fig. 1).⁷ There are two independent arsenic atoms in the structure whose coordination modes may be described as 3 + 1 and 3 + 2. Soignard et al. carried out HP Raman measurements of claudetite I crystals up to 40 GPa and observed no signs of amorphization up to this pressure.⁸ The appearance of new peaks and changes in relative intensities for peaks below 400 cm⁻¹ were noted between 7 and 13 GPa and, according to a recent review, these could indicate a phase transition.^8,9 Herein, we finalize the HP structural characterization of arsenic(III) oxide crystalline polymorphs by presenting a HP powder synchrotron X-ray diffraction study of claudetite I supplemented by room temperature (RT) and low temperature (LT) single-crystal diffraction measurements. The obtained structural models are compared to other As₂O₃ polymorphs as well as studied using the recently proposed valence entropy coordination number (VECN)¹⁰ and the experimental data are supplemented by DFT computations.

Fig. 1 Claudetite I crystal structure with the unit cell and crystallographic directions denoted. As and O atoms are depicted as green and red spheres, respectively.⁷

Experimental and methodology

HP synchrotron powder X-ray diffraction

HP powder diffraction experiments were carried out at the ID09A beamline of the European Synchrotron Radiation Facility.¹¹ Claudetite I powder was obtained by slow decomposition of ammonium arsenite (NH₄AsO₂) crystals dissolved in water carried out at around 10 °C.¹² Claudetite I pellets were loaded together with ruby chips and helium as the pressure transmitting medium into a membrane diamond anvil cell. Diamonds with culets of 500 μm and a stainless-steel gasket with a hole of 250 μm in diameter were used. Diffraction data were collected with X-ray radiation of 0.41421 Å wavelength and were recorded on a Mar555 flat panel detector. The pressure was determined from the shift in the ruby fluorescence line.^13,14 One static image was recorded for every pressure point. Instrument model parameters were refined against diffraction data of polycrystalline Si. The 2D images were integrated using Fit2D and were subsequently analysed using GSAS-II.^15,16 The background was fitted with Chebyshev polynomials typically with 15 coefficients. First Pawley refinements were carried out to obtain the unit cell parameters and instrument parameters. Then profile refinements (usually referred to as Rietveld refinements) were performed to obtain the positions of arsenic and oxygen atoms in the asymmetric unit.¹⁷ Only one isotropic displacement parameter was refined for all atoms. Due to the weak scattering power of oxygen, the As–O bond lengths were restrained to 1.77 Å with an estimated standard deviation of 0.01 Å. The pressure and thermal equation of states were fitted using the EosFit7 program.^18,19 CCDC 2031863–2031890 records contain the supplementary crystallographic data for the HP crystal structures. These data can be obtained free of charge from the joint CCDC's and FIZ Karlsruhe's service to view and retrieve structures viahttps://www.ccdc.cam.ac.uk/structures/.

LT synchrotron single-crystal X-ray diffraction

Single-crystal X-ray diffraction experiments were carried out at the ID-15B ChemMatCARS beamline of the Advanced Photon Source synchrotron in Argonne National Laboratory. Diffraction data were collected using an Apex detector and X-ray radiation with a wavelength of 0.41328 Å. Details of scans are provided in the ESI.† Two crystals were used for measurements – one for the experiments from RT down to 100 K and another one for the experiments in the 10–50 K temperature range. The diffraction data were imported to and processed in the CrysAlis^PRO software suite.²⁰ SHELXL-2018 was used for structural refinements and was invoked from within the Olex2 program.^21,22 All structural data were analyzed using PLATON.²³ CCDC 2031535–2031545 records contain the supplementary crystallographic data for the LT crystal structures.

Bond valence vectors (BVVs) and VECN calculations

The bond valences of As–O bonds were calculated according to the exponential correlation s_i = exp((R₀ − r_i)), where R₀ is the bond length of a bond with unit valence, r_i is the bond length and B is the bond softness, using parameters derived by Gagné and Hawthorne.²⁴ The dependence of R₀ on pressure was taken into account using the approach proposed by Brown and co-workers.²⁵ The BVV is defined according to Zachara as an integral of the electric field across a surface corresponding to a particular bond irrespective of the direction of that surface.²⁶ Such a definition results in (1) BVVs aligned along the bonds they correspond to; (2) sum of BVVs around an unstrained coordination center being a zero vector and (3) magnitude of a BVV v_i being related to the bond valence (BV) s_i according to the following relationship: ∥v_i∥ = s_i(1 − s_i/Q_cc), where Q_cc is the electric charge of the coordination center's atomic core. If a coordination center is electronically strained e.g. due to the presence of a stereoactive LEP, the sum of BVVs around a coordination center can be brought back to zero by treating the LEP as a pseudoligand bonded to the coordination centre with s_LEP ≤ 2 and the equality holds when the LEP is fully stereoactive. When calculating BVVs, arsenic was treated as being in the +5 oxidation state since the LEP was treated as a pseudoligand.

The valence entropy coordination number of order n (ⁿVECN), defined by Guńka and Zachara, was calculated according to the following formula:¹⁰

where , n is the VECN order and N is the number of ligands taken into calculations. LibreOffice functions provided by Guńka and Zachara were used for the computations of the ¹VECN.¹⁰

DFT computations

Density functional theory (DFT) computations were carried out with VASP ver. 5.4.4.³⁸ Projector augmented plane waves were used with an energy cut-off of 1200 eV.^27,28 The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional based on general gradient approximation was applied together with Grimme's D3 correction for dispersion interactions and the Becke–Johnson damping function which, according to our experience, works best for arsenic(III) oxide.^29–31 SCF computations and geometry optimizations were considered converged when the energy difference between consecutive steps was smaller than 0.1 μeV and when forces acting on atoms were smaller than 1 meV Å⁻¹. The calculations were performed in three steps with external pressure applied by using the PSTRESS keyword. The first and second steps involved optimizations of both unit cell parameters and atomic positions with Fermi smearing of partial orbital occupancies, whereas the third step involved only optimization of atomic positions, and the tetrahedron method with Blöchl corrections was applied for smearing of partial occupancies.³² The length parameter controlling the automatic generation of the Γ-centered Monkhorst–Pack k-point grid was set to 40 in the KPOINTS file.³³ No convergence study was carried out and we used the strictest parameters from previous convergence tests that we found to work well for arsenolite and its inclusion compound with helium.⁴

Results

Pawley and profile fittings of claudetite I HP powder X-ray diffraction patterns reveal that it undergoes monotonic compression up to 30 GPa (see Fig. 2 for the V(p) curve and Fig. S2† for exemplary diffraction patterns and profile fits) with no signs of phase transitions. The volume decrease of 32.9% at 29.91(5) GPa with respect to V₀ determined by the equation of state fit (EoS, see below) results mainly from a 13.7% compression along the crystallographic a direction and to a smaller extent from compressions of 11.0% and 11.1% along the b and c crystallographic directions, respectively (see Fig. 3 and S3† for variation of the β angle with pressure). These relative shrinkages correspond well to the values of linear moduli of claudetite I along the crystallographic a, b and c directions obtained with linearized third-order Vinet EoS. These linear moduli amount to 35(3), 69(2) and 108(4) GPa, respectively. LT single-crystal X-ray diffraction measurements indicate that claudetite I does not undergo any phase transitions down to 10 K either (see Fig. 2). Fitting of a simple Berman thermal EoS of the form V_0T = V₀₀(1 + α₀(T − T_ref)) to the LT single crystal data yields V₀₀ = 307.4(4) ų and α₀ = 9.1(7) × 10⁻⁵ K⁻¹ with a reference temperature of 298 K.³⁴

Fig. 2 Experimental and DFT (small black filled circles) unit cell volumes of claudetite I plotted as a function of pressure (axis at the bottom) and temperature (axis at the top). Big red open and filled circles for experimental data correspond to the pressure increase and decrease, respectively. Blue filled squares correspond to a variable temperature run. The solid red line and dashed blue line correspond to the third-order Vinet EoS and to Berman thermal EoS, respectively, fitted to experimental data points.^34–36 Standard uncertainties on volume, temperature and pressure of data points are all smaller than the symbol size.

Fig. 3 Experimental (large symbols) and DFT (small symbols) unit cell parameters of claudetite I plotted as a function of pressure. Open and filled symbols for experimental data correspond to the pressure increase and decrease, respectively.

The herein described room-temperature (294 K) structural model of claudetite I determined from single-crystal diffraction is significantly better than the model refined by Pertlik in 1978 although the general picture of the structure does not change.⁷ In particular, the precision and accuracy of As−O bond lengths are much better and they lie in the range of 1.754(3)–1.790(3) Å compared to 1.72(1)–1.81(1) Å reported by Pertlik. The same is true for bond angles spanning a range from 91.20(14)° to 102.26(14)° in our model compared to 89.7(6)°–103.3(6)° in Pertlik's model. Tables S1–S3† contain numerical values of unit cell parameters from the HP and LT experiments as well as from DFT computations.

The third-order Vinet EoS fitted to the herein presented HP data yields parameters which are listed in Table 1 together with analogous parameters of other As₂O₃ polymorphs.^35,36 The comparison of all arsenic(III) oxide polymorphs' densities reveals that claudetite I is the densest of all of them with the exception of β-claudetite II which is a high-pressure polymorph formed above 11 GPa (see Fig. S4†). As expected based on our results of DFT computations for arsenolite, the PBE-D3(BJ) model reproduces the experimental V(p) curve of claudetite I even better than the previously applied PBE-D2 model (see Fig. S5†).^4,12 Interestingly, the value of unit cell parameter a predicted by DFT is overestimated while b and c parameters are underestimated by computations. This indicates that in the DFT modelled crystal structure, As₂O₃ layers are less corrugated than in reality (see Fig. 1). It is noteworthy that herein DFT calculations were carried out with initially set external pressure (using the PSTRESS tag in the INCAR file) before constant volume optimizations had been run. Nonetheless, tests carried out for arsenolite and for claudetite I (using the DFT-D2 model) both revealed that the results are independent of the way external pressure is administered in the input files.

Table 1 Third-order Vinet EoS parameters for As₂O₃ polymorphs

Parameter	V 0/Z^d/Å^3	B 0/GPa
a One set of parameters fitted to α, α′ and α′′ polymorphs. b V(p) data for fitting taken from ref. 2. c EoS parameters taken from ref. 4. d V 0 per As2O3 formula unit.
Claudetite I	78.0(3)	21.0(11)	6.72(17)
α-Claudetite II^a^,^b	82.21(2)	15.4(3)	6.7(2)
β-Claudetite II^b	76(3)	30(10)	5(1)
Arsenolite^c	84.90(4)	10.78(14)	8.14(6)

---

Fig. 4 presents the comparison of experimentally determined primary As–O bond and secondary As⋯O bond lengths plotted as a function of pressure. Secondary bonds were chosen such that the As⋯O distance is not greater than 3.0 Å at ambient pressure and they are situated approximately trans with respect to primary As–O bonds. It was also assumed that no new As⋯O interactions are formed at HP and all new close contacts between As and O atoms result only from compression of the structure. The distances are very similar for claudetite I and arsenolite and they follow the same trend as a function of pressure.

Fig. 4 Experimental primary As–O and secondary As⋯O bond lengths plotted as a function of pressure for various As₂O₃ polymorphs. Data for α-, α′-, α′′- and β-claudetite II as well as arsenolite come from ref. 2 and 3, respectively.

The primary As–O and secondary As⋯O bond lengths as well as valence angles were utilized to calculate the bond valences (BVs) of all these bonds and then the bond valence sums (BVS), resultant bond valence vectors (BVVs)²⁶ and first-order valence entropic coordination numbers (¹VECNs)¹⁰ for both symmetry independent As atoms from the claudetite I asymmetric unit (see the Experimental and methodology section for the definitions of the quantities and details of these calculations). The results are plotted together with the same quantities for other As₂O₃ polymorphs in Fig. 5. The BVSs for claudetite I are practically constant in the whole studied pressure range although they are scattered. The magnitude of As resultant BVVs which represents the stereoactivity of the As LEP is fairly constant around 1.03 v. u. and is slightly smaller than the values observed for arsenolite. The BVV lengths are noisier for claudetite I than those for arsenolite, which is probably the case because the structural data for claudetite I were refined against powder diffraction patterns. The noise which was also present in the BVS values vanishes for ¹VECN dependence on pressure which is attributed to the fact that the ¹VECN is based on ratios between individual bond valences and bond valence sums. It is noteworthy that despite the fact that claudetite I is the densest of all ambient-pressure arsenic(III) oxide polymorphs, it exhibits the lowest coordination numbers of arsenic atoms among them.

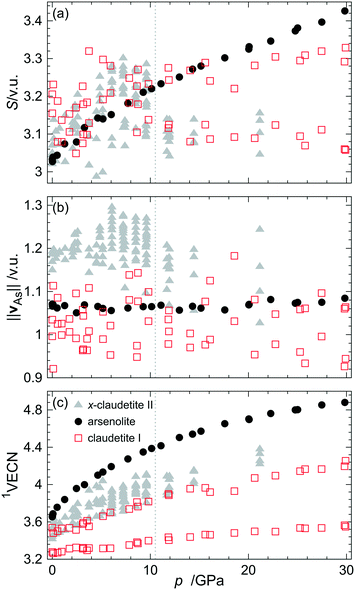Fig. 5 (a) Bond valence sum, (b) magnitude of the resultant bond valence vector of As atoms and (c) first-order valence entropic coordination number of As atoms for various As₂O₃ polymorphs plotted as a function of pressure. Data for α-, α′-, α′′- and β-claudetite II as well as arsenolite come from ref. 10. The grey dotted line indicates the pressure of the first-order phase transition from α′′- to β-claudetite II.²

Discussion

Smooth compression of claudetite I unit cell parameters and volume agrees with the results of Soignard et al. and confirms their conclusion that the observed changes in Raman spectra between 7 and 13 GPa are changes in Raman activity of vibrations rather than indications of possible phase transitions as Manjón and co-workers suggested.^8,9 The third-order Vinet EoS parameters of As₂O₃ polymorphs show that claudetite I is the densest and least compressible ambient-pressure arsenic(III) oxide polymorph. The analysis of EoS parameters reveals that the compressibility of claudetite I is comparable to that of the high-pressure β-claudetite II form and that the less dense a polymorph is, the more compressible it is. The same trend can be observed for silica polymorphs.³⁷ It is noteworthy that, unlike for α-, α′-, α′′- and β-claudetite II, all unit cell parameters of claudetite I decrease with increasing pressure. This indicates that not only interlayer distances shrink with increasing pressure but also As₂O₃ layers become more corrugated and denser as the pressure increases. The secondary As⋯O interactions fall on the same line for all As₂O₃ polymorphs (see Fig. 4) which demonstrates that the nature of As⋯O interactions is the same in all compounds. The stereoactivity of the LEP for arsenolite and claudetite I, which are stable As₂O₃ polymorphs, does not change with pressure. Similarly, it is constant for α-, α′- and α′′-claudetite II and decreases abruptly upon the first-order phase transition to β-claudetite II. This shows that pressure exerts additional strain on the arsenic coordination sphere, which is independent of the electronic strain coming from LEP stereoactivity. The fairly constant value of the LEP BVV of 1.03 v. u. for claudetite I and 1.05 v. u. for arsenolite corresponds to the LEP valence of 1.45 and 1.50 v. u., respectively, indicating that the LEPs are not fully stereoactive. If the LEPs were fully stereoactive, their valence would be 2 and the corresponding BVV magnitude would be 1.2 v. u. The stereoactivity of arsenic LEPs is lower than that of nitrogen and phosphorus LEPs observed in nitrogen(III) and phosphorus(III) organic compounds, respectively, where a resultant BVV average length of 1.15 v. u. corresponding to an average LEP valence of 1.78 was found.²⁶ This is in agreement with the prevalent trend observed in the periodic table of elements that LEPs of elements lying in higher periods are less stereoactive than those of lighter congeners.

Surprisingly, the ¹VECNs of As atoms in claudetite I are the lowest among all arsenic(III) oxide polymorphs even though it is the densest ambient-pressure polymorph. This is the case because of the different numbers of primary and secondary As–O bonds that one may observe in the polymorphs. In arsenolite, there is one symmetry independent As atom which forms 3 primary and 3 secondary bonds and its coordination number may be described as 3 + 3. For claudetite I and α-, α′- and α′′-claudetite II, there are more symmetry independent As atoms whose coordination numbers may be denoted as 3 + 1 and 3 + 2 while for β-claudetite II there is even one As atom that does not form any secondary bonds (see Table 2 for details). These results indicate that higher density of a polymorph does not necessarily imply higher coordination numbers of the constituting atoms and, vice versa, higher coordination numbers of atoms do not have to imply higher density of a material.

Table 2 Coordination numbers of As atoms in various As₂O₃ polymorphs

Polymorph	Number of independent As atoms	Coordination number ratios of As
		3 + 0	3 + 1	3 + 2	3 + 3
Arsenolite	1	0	0	0	1
Claudetite I	2	0	1	1	0
α-Claudetite II	2	0	1	1	0
α′-Claudetite II	4	0	1	3	0
α′′-Claudetite II	12	0	1	1	0
β-Claudetite II	4	1	2	1	0

---

Conclusions

The herein presented HP powder X-ray diffraction study performed on claudetite I confirms earlier supposition from HP Raman measurements that claudetite I does not undergo any phase transitions up to at least 30 GPa.⁸ The comparison of the structural data of claudetite I with those of other As₂O₃ polymorphs revealed that no direct and simple relationship between the coordination number of arsenic atoms, herein expressed as ¹VECN, in a polymorph and the density of that crystalline form exists. In particular, the coordination numbers of arsenic atoms in claudetite I are not the highest among all As₂O₃ polymorphs at a particular pressure even though it is the densest polymorph at that pressure. The pressure dependence of the arsenic resultant bond-valence vector indicates that the stereoactivity of arsenic lone electron pairs is not affected by pressure.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The DFT computations were performed using resources provided by the Wrocław Centre for Networking and Supercomputing (http://wcss.pl), grant no. 260. We acknowledge the European Synchrotron Radiation Facility (ESRF) for provision of beamtime for the high-pressure diffraction experiments at the ID09A beamline under proposal CH4272. The low-temperature single-crystal measurements were carried out at NSF's ChemMatCARS Sector 15 which is supported by the Divisions of Chemistry (CHE) and Materials Research (DMR), National Science Foundation, under grant number NSF/CHE-1834750. The use of the Advanced Photon Source, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science by Argonne National Laboratory, was supported by the U.S. DOE under contract no. DE-AC02-06CH11357. This work was also supported in part by the Warsaw University of Technology.

Notes and references

1. E. Kürbs, K. Plieth and I. N. Stranski, Z. Anorg. Chem., 1949, 258, 238–246.
2. P. A. Guńka, M. Dranka, M. Hanfland, K. F. Dziubek, A. Katrusiak and J. Zachara, Cryst. Growth Des., 2015, 15, 3950–3954.
3. P. A. Guńka, K. F. Dziubek, A. Gładysiak, M. Dranka, J. Piechota, M. Hanfland, A. Katrusiak and J. Zachara, Cryst. Growth Des., 2015, 15, 3740–3745.
4. P. A. Guńka, M. Hapka, M. Hanfland, M. Dranka, G. Chałasiński and J. Zachara, ChemPhysChem, 2018, 19, 857–864.
5. J. A. Sans, F. J. Manjón, C. Popescu, V. P. Cuenca-Gotor, O. Gomis, A. Muñoz, P. Rodríguez-Hernández, J. Contreras-García, J. Pellicer-Porres, A. L. J. Pereira, D. Santamaría-Pérez and A. Segura, Phys. Rev. B, 2016, 93, 054102.
6. V. P. Cuenca-Gotor, O. Gomis, J. A. Sans, F. J. Manjón, P. Rodríguez-Hernández and A. Muñoz, J. Appl. Phys., 2016, 120, 155901.
7. F. Pertlik, Monatsh. Chem., 1978, 109, 277–282.
8. E. Soignard, S. A. Amin, Q. Mei, C. J. Benmore and J. L. Yarger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 144113.
9. F. J. Manjón, J. A. Sans, J. Ibáñez and A. L. D. J. Pereira, Crystals, 2019, 9, 630.
10. P. A. Guńka and J. Zachara, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 86–96.
11. M. Merlini and M. Hanfland, High Pressure Res., 2013, 33, 511–522.
12. P. A. Guńka, M. Dranka, J. Piechota, G. Z. Żukowska, A. Zalewska and J. Zachara, Cryst. Growth Des., 2012, 12, 5663–5670.
13. H. K. Mao, J. Xu and P. M. Bell, J. Geophys. Res., [Solid Earth Planets], 1986, 91, 4673–4676.
14. K. Syassen, High Pressure Res., 2008, 28, 75–126.
15. A. P. Hammersley, J. Appl. Crystallogr., 2016, 49, 646–652.
16. B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549.
17. B. van Laar and H. Schenk, Acta Crystallogr., Sect. C: Struct. Chem., 2018, 74, 88–92.
18. J. Gonzalez-Platas, M. Alvaro, F. Nestola and R. Angel, J. Appl. Crystallogr., 2016, 49, 1377–1382.
19. R. J. Angel, M. Alvaro and J. Gonzalez-Platas, Z. Kristallogr., 2014, 229, 405–419.
20. CrysAlisPro Software system ver. 171.40.71a, Rigaku OD, Oxford, UK, 2019.
21. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
22. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
23. A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155.
24. O. C. Gagné and F. C. Hawthorne, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 562–578.
25. I. D. Brown, P. Klages and A. Skowron, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 439–448.
26. J. Zachara, Inorg. Chem., 2007, 46, 9760–9767.
27. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
28. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
30. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
31. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
32. P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233.
33. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
34. R. G. Berman, J. Petrol., 1988, 29, 445–522.
35. P. Vinet, J. Ferrante, J. R. Smith and J. H. Rose, J. Phys. C: Solid State Phys., 1986, 19, L467–L473.
36. P. Vinet, J. Ferrante, J. H. Rose and J. R. Smith, J. Geophys. Res.: Solid Earth, 1987, 92, 9319–9325.
37. W. Pabst and E. Gregorová, Ceram.-Silik., 2013, 57, 167–184.
38. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54(16), 11169–11186.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2031535–2031545 and 2031863–2031890. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ce01401j

---