Unprecedented superstructure in the type I family of clathrates

Abstract

The first arsenic-based clathrate exhibiting superstructural ordering due to optimization of Au–As, As–As, and Ba–Au bonding is reported. Ba₈Au₁₆As₃₀ crystallizes in a unique P2₁/c monoclinic clathrate structure. The synthesis, crystal and electronic structure, and transport properties are discussed.

---

Clathrates have “guest atoms” that reside in cages and “framework” atoms that compose the cages. Type I clathrates are an expansive group of compounds typically crystallizing in the Pm3̄n space group with a framework composed of tetrel elements, Si, Ge, or Sn.^1,2 As the type I clathrate has expanded into the regime of late transition metals and pnictogens forming the framework, there has been evidence of different superstructural orderings in selected compounds.³ Most notably, Ba₈Cu₁₆P₃₀ crystallizes in Pbcn with a primitive cell containing 4 formula units.^4,5 Ba₈Au₁₆P₃₀ was shown to be twinned down to the nano domain using transmission electron microscopy and was determined to crystallize with the same superstructure as the Cu analogue.⁶ Several ternary clathrates with late transition metals and arsenic are reported: Ba₈Cu₁₆As₃₀, Cs₈Zn₁₈As₂₈, Rb₈Zn₁₈As₂₈, and Cs₈Cd₁₈As₂₈.^7,8 All the arsenide-based clathrates have been reported to crystallize in the archetype clathrate I structure (cubic Pm3̄n space group) with mixed M/As sites in the framework. Moving down the pnictogen group, a new story has emerged for antimony-based clathrates. Originally investigated in 2009, single crystal X-ray diffraction (SXRD) suggested that Cs₈Zn₁₈Sb₂₈ and Cs₈Cd₁₈Sb₂₈ crystallize in Pm3̄n.⁹ Recent reinvestigation has shown that the antimony-based clathrates Cs₈Zn₁₈Sb₂₈ and Cs₈Cd₁₈Sb₂₈ exhibit ordered superstructures with segregation of M and Sb over different framework sites as evidenced using transmission electron microscopy and high-resolution synchrotron X-ray powder diffraction (HR-PXRD).¹⁰ A similar ordering was found for In-Sb and Ga-Sb clathrates.¹¹

Contrary to the observation of superstructural ordering among the phosphorous- and antimony-based clathrates, no superstructural ordering has been reported for arsenide clathrates. The superstructural ordering can be due to the energy gain attained by avoiding metal–metal bonds. In Pm3̄n, the framework filling of the 6c, 16i, and 24k sites cannot simultaneously fulfill the stoichiometry while avoiding metal–metal bonds and the structure is forced to reduce the overall symmetry and enlarge the unit cell volume. For phosphides, the known type I clathrates have crystallized in either Pbcn or P4₂/ncm, while the antimonides exhibited complex ordering in the Ia3̄, Ia3̄d, and P2 space groups (the latter was proposed using microscopy studies). Herein, we report the first arsenide clathrate Ba₈Au₁₆As₃₀ with unique superstructural ordering in the monoclinic space group P2₁/c.

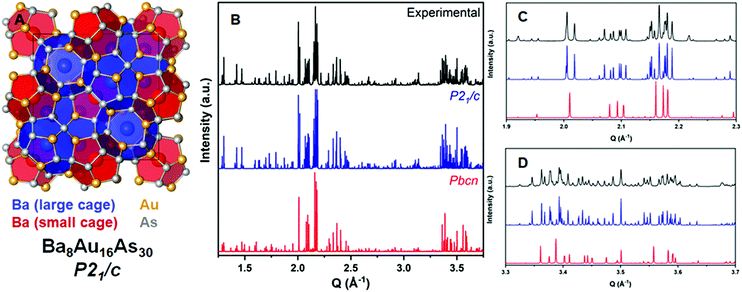
The direct synthesis from elements at 600 °C resulted in a polycrystalline sample of Ba₈Au₁₆As₃₀. Elemental energy dispersive analysis confirms presence of only Ba, Au, and As in the sample. A separate reaction utilizing a CsBr/CsI flux and an excess of As resulted in crystals suitable for single crystal X-ray diffraction (SCXRD). Ba₈Au₁₆As₃₀ crystallizes in the P2₁/c space group as determined using SCXRD with a = 15.147(1) Å, b = 15.218(1) Å, c = 10.954(1) Å, and β = 90.502(2)° (Table S1, ESI†). Refinement of the crystal structure shows that all atomic sites are fully occupied (Fig. 1A). Like many other pnictide clathrates with superstructures, no metal–metal (Au–Au) bonds are formed in this framework. There are five Ba positions inside the Au–As cages: Ba1@Au₆As₁₄, Ba2@Au₈As₁₂, Ba3@Au₉As₁₅, Ba4@Au₈As₁₆, and Ba5@Au₈As₁₆. Ba1 and Ba2 occupy the 5¹² pentagonal dodecahedra (Fig. 1A, red cage), while Ba3, Ba4, and Ba5 occupy the 5¹²6² tetrakaidecahedra (Fig. 1A, blue cage). Although the data suggested a monoclinic space group, the lattice parameters and beta angle were suspiciously close to tetragonal symmetry. The supergroups Pm3̄n, P4₂/mmc, and P4₂/ncm were considered as possible solutions but failed to give a good refinement. To confirm the small but robust beta angle deviation from 90° and the correct symmetry, a sample synthesized from elements was prepared and studied with HR-PRXD.

Fig. 1 (A) Crystal structure of Ba₈Au₁₆As₃₀, Ba: blue/red; Au: gold; As: grey. (B) Experimental (black) HR-PXRD pattern and theoretical patterns for P2₁/c (blue) and hypothetical Pbcn derived from Ba₈Au₁₆P₃₀ (red); (C and D) zoomed-in regions of (B).

Aside from a few minor peaks attributed to admixtures, the calculated diffraction pattern from the single crystal model fit extremely well once the room temperature unit cell parameters (a = 15.197 Å, b = 15.261 Å, c = 10.979 Å, and β = 90.444°) were refined (Fig. 1). HR-PXRD ruled out the aristotype cubic and orthorhombic (Pbcn) structural models. In Fig. 1C a zoomed-in region from 1.9 to 2.3 Q explicitly demonstrates that the Pbcn model fails to generate enough peaks to even begin fitting the experimental diffraction pattern. In Fig. 1D a similar conclusion can be made while noticing an agreeable peak splitting from the P2₁/c model and the experimentally collected data. The formation energy and stability of Ba₈Au₁₆As₃₀ was calculated and compared with other ternary Ba–Au–As phases using density functional theory (Fig. S1, ESI†). The atomization energy is negative (−0.429 eV per atom) and Ba₈Au₁₆As₃₀ is a thermodynamically stable phase when considering all experimentally reported binary and ternary compounds in the Ba–Au–As system. However, inclusion of the hypothetical BaAu₂As₄ (isostructural to BaAu₂P₄)^12,13 shows that Ba₈Au₁₆As₃₀ could decompose to BaAu₂As₄, BaAuAs, and Au (Fig. S1, ESI†). Our experimental efforts to synthesize BaAu₂As₄ have instead resulted in the formation of Ba₈Au₁₆As₃₀.

The reduction of symmetry from Pm3̄n to P2₁/c stems from the ordering of the framework elements (Au and As). The Bärnighausen tree (Fig. S2, ESI†) shows the relationship between the two space groups as well as the Wyckoff site splitting. In the first reduction of symmetry to the space group P4₂/mmc almost all the framework sites remain mixed occupied except for the 2e site. The second transformation to P4₂/ncm is accompanied by a doubling of the unit cell volume ( × × 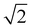1). In this space group a hypothetical distribution of Au and As among the Wyckoff sites could result in a completely ordered structure that fulfills the stoichiometry of the framework (16Au:30As) in analogy with the reported ordered structure for La_1.6Ba_6.4Cu₁₆P₃₀.¹⁴ Further reduction of symmetry may be caused by optimization of the As–As and Ba–Au interactions (Table S2, ESI†). The next transformation lowers the symmetry to the orthorhombic space group Pccn. In the final transformation to P2₁/c all the framework sites are identified as general position 4e sites and are fully occupied by either Au or As. All the Au atoms are surrounded by four As atoms and no Au–Au distance shorter than 3.91 Å is present.

The Bärnighausen tree demonstrates that single atom type site occupation is possible in P2₁/c but the same ordering can be accomplished in Pbcn, as was found for Ba₈Au₁₆P₃₀ and Ba₈Cu₁₆P₃₀. What is the driving force for this reduction of symmetry as opposed to Pbcn found in Ba₈Au₁₆P₃₀? In the structure of Ba₈Au₁₆Pn₃₀ (Pn = P, As) pnictogen atoms account for almost 2/3 of the framework atoms. The replacement of all smaller P atoms with As leads to an overall 13.7% increase of the unit cell volume per formula unit. Assuming an isotropic structure expansion in the Pbcn space group, this would lead to the increase of the Ba-framework distances and the volume of the polyhedral cages, which may become oversized for the Ba guest cations. Reducing the crystal symmetry of Ba₈Au₁₆As₃₀ down to P2₁/c allows optimization of the Ba-framework interactions. The volumes of the Ba polyhedra in Ba₈Au₁₆As₃₀ are 14% larger than those of the respective polyhedra in Ba₈Au₁₆P₃₀ (Table S2, ESI†). However, the average and shortest Ba-framework distances in both polyhedra increase only by 4% as compared to the distances in the phosphide analogue. The simplest model of Pbcn Ba₈Au₁₆As₃₀ was produced using the atomic coordinates of Ba₈Au₁₆P₃₀ and isotropically expanding the volume per formula unit to match that of Ba₈Au₁₆As₃₀. The analysis of the consequent atomic distances shows that for cages of the same volume, P2₁/c allows for optimized Ba–Au distances (Table S2.2, ESI†). Relaxing of the produced hypothetical Pbcn Ba₈Au₁₆As₃₀ using DFT still results in the structure with ∼0.1 Å longer Ba–Au distances, e.g. the shortest Ba–Au distance in relaxed Pbcn is 3.49 Å while in P2₁/c the shortest Ba–Au distance is 3.39 Å. Another important difference between Ba₈Au₁₆As₃₀ and Ba₈Au₁₆P₃₀ is the pnictogen–pnictogen bonding. While there are no Au–Au bonds in either structure, there are homoatomic pnictogen–pnictogen bonds. The sum of covalent radii for P is 2.20 Å while the sum of covalent radii for As is 2.40 Å. In the case of Ba₈Au₁₆P₃₀, very long P–P bonds are observed with distances up to 2.72 Å.⁶ This is not the case for Ba₈Au₁₆As₃₀ where the longest As–As distance is 2.53 Å. The Zintl phases Ba₃As₁₄¹⁵ and Ba₂As₇I¹⁶ feature As₇ clusters where the longest As–As bond is 2.52–2.53 Å, while BaAs₂¹⁷ features one-dimensional As chains with a longest distance of 2.50 Å, which suggests that the As–As distances in Ba₈Au₁₆As₃₀ are not unusual. The substantial differences between Ba₈Au₁₆As₃₀ and Ba₈Au₁₆P₃₀ are in the polypnictide anions. While there are two fragments in Ba₈Au₁₆P₃₀, P₁₂ and P₁₈, only one type of As fragment, As₁₅, exists in Ba₈Au₁₆As₃₀ (Fig. S3, ESI†). We hypothesize that the differences in the superstructural ordering for Ba₈Au₁₆As₃₀ and Ba₈Au₁₆P₃₀ are due to optimization of pnictogen–pnictogen bonding and Ba–Au interactions.

To confirm the superstructural ordering determined using HR-PXRD and SCXRD, transmission electron microscopy was employed. The selected area electron diffraction (ED) patterns collected from the main crystallographic zone axes show agreement with the P2₁/c space group determined using the other methods (Fig. 2). In the [001] zone axis, the absence of 4-fold symmetry excludes tetragonal or cubic symmetry and the absence of the (010) diffraction peak is in line with the systematic absence condition for 0k0, k = 2n, which is a general condition for P2₁/c as well as Pccn. The presence of the (100) reflection shows that Pccn cannot be used to index the ED patterns, because of the violation of the h00, h = 2n condition. The [011] zone axis, which corresponds to [111] in the cubic aristotype structure, confirms an absence of the 3-fold rotation axis and shows only the presence of two-fold symmetry. This zone confirms the presence of the (100) reflection seen in the [001].

Fig. 2 Top: ED of the [001], [011], and [112] zones of Ba₈Au₁₆As₃₀ indexed in the P2₁/c model; middle: low magnification HAADF-STEM image of the single crystallite and the corresponding EDX elemental mapping of Au M (red), Ba L (green), As K (blue), and the overplayed image; bottom: high resolution [011] and [112] HAADF-STEM images. The simulated images are given as insets.

Elemental mapping and high resolution HAADF-STEM imaging show the homogeneous distribution of all chemical elements within a composition close to nominal (As – 54.6 at%, Ba – 15.0 at%, and Au – 31.8 at%) and good crystallinity (free of twinning and defects). The simulated high resolution [001] and [011] HAADF-STEM images are in agreement with the experimental ones (inset in Fig. 2, bottom panel).

Low thermal conductivity is ubiquitous among clathrates.² The large number of atoms in the unit cell and the rattling guest atoms give rise to localized modes, which reduces the lattice contribution to thermal conductivity (κ_lattice). Additionally, the presence of heavy atoms in the framework reduces κ_lattice by lowering the optical phonon frequency range. Au is the third heaviest atom that has been incorporated into the framework of any clathrate, behind Bi and Hg.^2,18–20 The incorporation of Au and other heavy framework atoms has been shown to lower the thermal conductivity significantly. For the Ba₈Ga_16−3xAu_xGe_30+2x system, substitution of Au (x = 4) lowered the lattice thermal conductivity from 1.6 W K⁻¹ m⁻¹ in Ba₈Ga₁₆Ge₃₀ to 1.0 W K⁻¹ m⁻¹.²¹ Ba₈Au₁₆P₃₀ has an exceptionally low lattice thermal conductivity even for clathrates.⁶ Considering the substitution of As for P it is reasonable to expect an even further reduction of the κ_lattice for Ba₈Au₁₆As₃₀. However, that is not the case. As seen in Fig. 3, the lattice thermal conductivity for Ba₈Au₁₆As₃₀ is ∼0.85 W K⁻¹ m⁻¹ at room temperature. The thermal conductivity is comparable to that for Ba₈Au₆Ge₄₀ considering that Ge and As are comparable in atomic mass and Ba₈Au₁₆As₃₀ has substantially more Au allowing the lattice thermal conductivity to be lowered from ∼1.0 W K⁻¹ m⁻¹ for Ba₈Au₆Ge₄₀²¹ to ∼0.85 W K⁻¹ m⁻¹ for Ba₈Au₁₆As₃₀. The thermal conductivity of Ba₈Au₁₆As₃₀ is lower than most type I clathrates including Ba₈Cu₁₆P₃₀ however it is still ∼50% higher than Ba₈Au₁₆P₃₀. It may be that Ba₈Au₁₆P₃₀ is an outlier due to an extrinsic lowering of the thermal conductivity caused by the grain boundaries and nanoscale twinning detected using HAADF-STEM.⁶ The extent of the twinning in Ba₈Au₁₆As₃₀ is currently unknown but the presence of twinning to nano-domains seems unlikely as a structural solution from a single crystal was easily obtained and no twinning was detected during HAADF-STEM studies.

Fig. 3 Left: projected density of states in the GGA+U approximation. Right: temperature dependence of resistivity (blue), Seebeck coefficient (black), and thermal conductivity (red). The total thermal conductivity trend is shown with a black line to guide the eye.

Ba₈Au₁₆As₃₀ exhibits a metal-like temperature behavior of electrical resistivity with values similar to that for Ba₈Au₁₆P₃₀. This is expected for compositions that are not electron balanced. Ba₈Au₁₆As₃₀ has 182 electrons per 46 framework atoms, 8 × 2(Ba) + 16 × 1(Au) + 30 × 5(As) = 182, while an electron balanced composition requires 46 × 4 = 184 electrons. Electronic structure calculations confirm the expected metallic nature of Ba₈Au₁₆As₃₀. The Fermi level is about 0.25 eV below the maximum of the valence band, which makes this material p-type. The Seebeck coefficient of Ba₈Au₁₆As₃₀ is positive and increases with temperature. The room temperature absolute value (13 μV K⁻¹) is close to those for other metallic pnictide clathrates, such as Ba₈Au₁₆P₃₀ (15 μV K⁻¹)⁶ and Cs₈Cd₁₈As₂₈ (11 μV K⁻¹).⁸ The major charge carriers are holes, which is expected for an electron deficient clathrate. The absolute values for the Seebeck coefficient below 75 K were lower than 1 μV K⁻¹ and were omitted due to a high level of noise. While the Seebeck coefficient is low; zT ∼ 2.2 × 10⁻³, the low thermal conductivity and electron deficiency means that Ba₈Au₁₆As₃₀ is well positioned for substitution and alloying to optimize the electronic transport properties, as was shown for clathrates developed from Ba₈Cu₁₆P₃₀.^14,22–24 To probe potential of Ba₈Au₁₆As₃₀ for thermoelectric applications, the transport properties were calculated as a function of the energy of the Fermi level (Fig. S4, ESI†). Shifting the Fermi level via substitutional doping to the top of the valence band increases the Seebeck coefficient by an order of magnitude. However, the resistivity also increased by a similar amount. Due to the counteracting effects of resistivity and Seebeck coefficient, the overall zT of the material did not surpass 0.07. Even if the material was doped to n-type, zT will not exceed 0.1 (Fig. S4, ESI†). These results indicate that only modifying the carrier concentration will not provide a feasible route to a “state-of-the-art” thermoelectric material. Adjusting the hole-mobility may be an alternative route to further increase the thermoelectric performance of Ba₈Au₁₆As₃₀, as was demonstrated for La_xBa_8–xCu₁₆P₃₀.¹⁴

In conclusion, Ba₈Au₁₆As₃₀ is a new type I clathrate crystallizing in the unprecedented superstructural space group P2₁/c that features a singular repeating As fragment and the absence of Au–Au bonds. We hypothesize that factors such as cage volume, and optimization of the Au–As, As–As, and Ba-framework interactions are the reasons for Ba₈Au₁₆As₃₀ crystallizing in a different superstructure compared to Ba₈Au₁₆P₃₀. The transport properties of Ba₈Au₁₆As₃₀ are expected for a metallic clathrate but point to Ba₈Au₁₆P₃₀ as an outlier in terms of its thermal conductivity. The theoretical transport properties indicate that modification of carrier mobility is required to substantially increase the zT of Ba₈Au₁₆As₃₀-based thermoelectric materials.

The authors would like to thank Dr Saul Lapidus (APS) for help collecting synchrotron the HR-PXRD data and Prof. J. Zaikina (ISU) for access to the SPS. This research was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Science and Engineering, grant DE-SC0022288. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility, operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357.

Conflicts of interest

There are no conflicts to declare.

References

1. G. Nolas, The Physics and Chemistry of Inorganic Clathrates, Springer, Netherlands, 1 edn, 2014.
2. J.-A. Dolyniuk, B. Owens-Baird, J. Wang, J. V. Zaikina and K. Kovnir, Mater. Sci. Eng., 2016, 108, 1–46.
3. J. Wang, J.-A. Dolyniuk and K. Kovnir, Acc. Chem. Res., 2018, 51, 31–39.
4. J. Dünner and A. Mewis, Z. Anorg. Allg. Chem., 1995, 621, 191–196.
5. D. Huo, T. Sasakawa, Y. Muro and T. Takabatake, Appl. Phys. Lett., 2003, 82, 2640–2642.
6. J. Fulmer, O. I. Lebedev, V. V. Roddatis, D. C. Kaseman, S. Sen, J.-A. Dolyniuk, K. Lee, A. V. Olenev and K. Kovnir, J. Am. Chem. Soc., 2013, 135, 12313–12323.
7. K. Wei, A. R. Khabibullin, D. Hobbis, W. Wong-Ng, T. Chang, S. G. Wang, I. Levin, Y.-S. Chen, L. M. Woods and G. S. Nolas, Inorg. Chem., 2018, 57, 9327–9334.
8. H. He, A. Zevalkink, Z. M. Gibbs, G. J. Snyder and S. Bobev, Chem. Mater., 2012, 24, 3596–3603.
9. Y. Liu, L.-M. Wu, L.-H. Li, S.-W. Du, J. D. Corbett and L. Chen, Angew. Chem., 2009, 121, 5409–5412.
10. B. Owens-Baird, P. Yox, S. Lee, X. B. Carroll, S. Grass Wang, Y.-S. Chen, O. I. Lebedev and K. Kovnir, Chem. Sci., 2020, 11, 10255–10264.
11. B. Owens-Baird, J. Wang, S. G. Wang, Y.-S. Chen, S. Lee, D. Donadio and K. Kovnir, J. Am. Chem. Soc., 2020, 142, 2031–2041.
12. J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509.
13. J. Fulmer, D. Kaseman, J. Dolyniuk, K. Lee, K. S. Sen and K. Kovnir, Inorg. Chem., 2013, 52, 7061–7067.
14. J. Wang, Y. He, N. E. Mordvinova, O. I. Lebedev and K. Kovnir, Chem, 2018, 4, 1465–1475.
15. W. Schmettow and H. G. Von Schnering, Angew. Chem., Int. Ed. Engl., 1977, 16, 857.
16. J.-A. Dolyniuk, S. Lee, N. Tran, J. Wang, L.-L. Wang and K. Kovnir, J. Solid State Chem., 2018, 263, 195–202.
17. F. Emmerling, D. Petri and C. Röhr, Z. Anorg. Allg. Chem., 2004, 630, 2490–2501.
18. T. F. Fassler and C. Kronseder, Z. Anorg. Allg. Chem., 1998, 624, 561–568.
19. A. Kaltzoglou, S. Ponou and T. F. Fässler, Eur. J. Inorg. Chem., 2008, 4507–4510.
20. A. Kaltzoglou, S. Ponou and T. F. Fässler, Z. Anorg. Allg. Chem., 2008, 538–542.
21. Z. Ye, J. Y. Cho, M. M. Tessema, J. R. Salvador, R. A. Waldo, J. Yang, H. Wang, W. Cai, M. J. Kirkham, J. Yang and W. Zhang, J. Alloys Compd., 2014, 587, 747–754.
22. J. Wang, O. I. Lebedev, K. Lee, J.-A. Dolyniuk, P. Klavins, S. Bux and K. Kovnir, Chem. Sci., 2017, 8, 8030–8038.
23. J. Dolyniuk, P. S. Whitfield, K. Lee, O. I. Lebedev and K. Kovnir, Chem. Sci., 2017, 8, 3650–3659.
24. J. Dolyniuk, J. Wang, M. Marple, S. Sen, Y. Cheng, A. J. Ramirez-Cuesta and K. Kovnir, Chem. Mater., 2018, 30, 3419–3428.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2109533. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1cc05167a

---