Simultaneous analyte indicator binding assay (SBA) for the monitoring of reversible host–guest complexation kinetics

Abstract

Very little information is available on the kinetics of the self-assembly and dissociation of optically silent building blocks despite the importance of such data in the rational design of tailor-made host–guest systems. We introduce here a novel time-resolved method that enables the simultaneous determination of complex formation and complex dissociation rate constants for inclusion-type host–guest complexes. The simultaneous analyte indicator binding assay (SBA) gives also direct access to binding affinities, thus largely simplifying the experimental procedure for a full kinetic and thermodynamic characterisation of host–guest systems.

---

The knowledge of the inclusion and release kinetics of various host–guest complexes is essential for their utilization, e.g. in molecular devices, drug delivery vehicles, stimuli-responsive materials, functional nanostructures, and supramolecular polymeric hydrogels.^1–8 The understanding of the major factors influencing the rate constants of association and dissociation is crucial also for the application of cavitands in the biomedical field,⁹ catalysis,^10,11 and self-sorting multicomponent systems.^12,13 Time-resolved measurements provide insights into the subtle mechanistic details of the inclusion of simple^14,15 and ditopic guests^16–18 as well as those of the cation-induced release of encapsulated molecules.¹⁹ Moreover, the importance of ligand–receptor binding kinetics is increasingly recognized as the selection criterion in the search for potent pharmaceutical ingredients.²⁰ The dissociation rate constants of drug–receptor complexes are often more preferable parameters to predict in vivo drug efficacy and optimal duration of action than the traditionally used equilibrium-based binding constants.²¹ Besides, association rates play also a significant role in drug research due to their capability of modulating the onset of biological response.²²

In contrast to the large amount of biomedical related kinetic measurements, much less attention has been paid to the dynamics of host–guest complex formation of simple macrocyclic compounds^23–26 despite the increasing need for estimating the equilibration time or response time after an external stimulus, as are crucial for fine-tuning in sensing, materials and drug delivery applications.²⁷ So far, the rate constants of reversible encapsulation processes have been mainly studied via direct-binding assays (kinDBA) for environment-sensitive fluorescent guests by monitoring the alteration of their emission intensity upon host–receptor binding.²⁴ However, the methodological restriction to emissive guests has been limiting as many host–guest complexes of interest, including those of metabolites, drugs and other bioactive compounds, are not fluorescent or only show modest emission signal alterations.

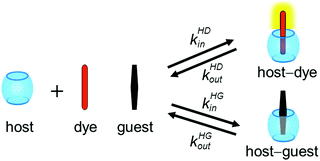
We recently introduced the kinetic indicator displacement assay (kinIDA) and kinetic guest displacement assay (kinGDA) that allow probing of the temporal characteristics of host–guest inclusion complexes of nonchromophoric or nonluminescent guests.²⁸ One drawback of these competitive-binding methods is the need to independently determine the binding affinity a priori, e.g. by titration experiments, in order to allow a reliable fitting of the kinetic ingression and egression rates. Moreover, the use of high concentrations of the displacement agent, e.g. guest (kinGDA) or dye (kinIDA), can potentially lead to complications in the kinetic mechanism, e.g., if ternary host–dye–guest complexes are formed as transient species.²⁸ The aim of the present study was to develop an alternative accurate procedure whose signal shape provides an immediate qualitative insight into the relationship among the rate constants of the reversible binding of the guest and indicator molecules. Fig. 1 presents the principle of the herein introduced kinetic simultaneous analyte indicator binding assay (kinSBA).

Fig. 1 Kinetic simultaneous binding assay (kinSBA).

In kinSBA, a solution of a host (H) is rapidly mixed with a solution of an indicator dye (D), whose kinetic parameters are already known, and a solution of a spectroscopically silent guest (G), whose kinetic rate constants are to be determined. Upon mixing, the temporal changes in the spectroscopic signal, indicative of the time-dependent ratio of free (D) and bound (HD) indicator dyes, are monitored. Generally, the recording of the alteration of the fluorescence intensity is preferable because of the high sensitivity of this technique but kinSBA can also be applied to other spectroscopic signals.

A fine-tuning of kinSBA measurements can be achieved by selecting a suitable dye–guest combination with comparable rate parameters. Thus, three natural isoquinoline alkaloids berberine, palmatine and dehydrocorydaline (DHC) (Fig. 2) were selected as fluorescent indicators for the macrocyclic host cucurbit[7]uril (CB7) in this study as the half-life of their CB7 complexes varies more than 200 fold in the conveniently measurable time range.^14,29 These indicators strongly emit when bound in the host cavity but show negligible fluorescence in water, thus providing large signal changes. In addition, the environment-sensitive stilbazolium-type dye DSMI was selected to examine the confinement effects on the rate constants of cucurbit[6]uril (CB6)–guest complexes.

Fig. 2 Chemical structure of the compounds used in the present study. The cations contained the Cl⁻ counterion, except DSMI, which was I⁻ salt.

Fig. 3 displays mathematically computed kinSBA traces where we first compared a D and a G with exactly identical binding affinity, while the ingression and egression rates were varied in inverse proportion (K = k_in/k_out). The temporal changes of the calculated concentrations are shown in Fig. S1 in the ESI.† The simulation uncovers the unique signal shapes of the kinSBA method. In the scenario displayed in Fig. 3A, the ingression and egression rates, k^HG_in and k^HG_out, of G were set to be each 10 fold faster than the corresponding k^HD_in and k^HD_out rates of D. In this case, a steep initial signal rise is followed by a slower signal growth. In contrast, a signal plateau is quickly reached after the initial increase when k^HG_in = k^HD_in and k^HG_out = k^HD_out (Fig. 3B). Finally, when both the ingression and egression rates were set to be 10 fold slower for G than for D, then the initial rapid signal increase is followed by a slow intensity decay (Fig. 3C).

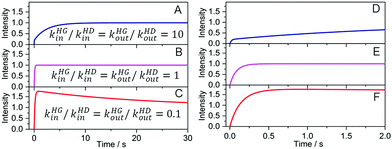Fig. 3 Simulated fluorescence intensity vs. time traces after mixing H solution with the solutions of G and D. Concentrations at t = 0 s are [H] = 0.25 μM and [D] = [G] = 1.2 μM. Negligible fluorescence was assumed for the unbound indicator. The rate constants k^HD_in = 5.4 × 10⁶ M⁻¹ s⁻¹ and k^HD_out = 0.20 s⁻¹ were fixed and corresponded to those of palmatine binding with CB7; see also Table 1. (A–C) k^HG_in and k^HG_out were varied with keeping K^HG = 2.7 × 10⁷ M⁻¹ constant. (D–F) represent the zoomed views.

The simulated kinSBA plots reveal that the initial slope and the intensity profile can provide useful information on k^HG_in (compared to the ingression rate of the dye), while the shape of the kinetic traces is mostly controlled by the k^HG_out kinetic parameter. A deeper analysis of additional scenarios, wherein also different binding affinities (K^HG ≠ K^HD) were considered, are presented in the ESI.† The main conclusions are as follows: firstly, a change of the k^HG_in[G]/(k^HG_in[D]) ratio affects the initial slope and the intensity of the kinSBA signal after the steep incipient growth (Fig. 3 and Fig. S1A–C in the ESI†). Secondly, if the binding equilibrium is much more rapidly reached for G than for D (k^HG_in[G] ≫ k^HD_in[D] and k^HG_out ≫ k^HD_out), then the intensity–time profiles rise more slowly in the presence than in the absence of the spectroscopically silent guest since the fast establishment of the HG formation equilibrium diminishes the concentration of the unbound host (Fig. S1D and E, ESI†). In this case, a larger association constant of HG formation (K^HG = k^HG_in/k^HG_out) decreases the initial slope and the intensity at the plateau and the kinetics is sensitive to K^HG but insensitive to the individual k^HG_in and k^HG_out values. The simulations also revealed that the shape profile of kinSBA sensitively reflects the relative comparisons of k^HG_invs. k^HD_in and k^HG_outvs. k^HD_out. In other words, a fine-tuning of kinSBA is readily feasible by selecting one or several appropriate indicator dyes with known, suitable kinetic rate constants.

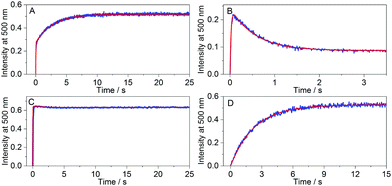
The anticipated trends from simulations were indeed observed in different kinSBA experiments: Fig. 4 shows representative examples for the four types of experimentally recorded fluorescence intensity profiles obtained using kinSBA, whereas the concentrations of the various species vs. time are plotted in Fig. S3 in the ESI.† The data traces were fitted with the numerical solution of the system of differential equations characterizing the inclusion kinetics (S4–S8 in the ESI†) taking the rate constants of complexation (k^HD_in) and dissociation (k^HD_out) of D as fixed input parameters as they can be determined from independent experiments by mixing the H and D solutions.²⁹ The rate constants of ingression (k^HG_in) and egression (k^HG_out) of the guest G can then be determined by a least-squares fitting routine. The thus-obtained kinetic parameters are summarized in Table 1. As shown in Fig. 4, the kinSBA measurements of cyclohexanone inclusion in CB7 provided three fundamentally different types of signals depending on the indicator chosen. When palmatine served as D, whose ingression into CB7 is slower than that of cyclohexanone (Table 1), the fluorescence intensity first quickly “spiked”, after which it further grew much more slowly and levelled off at ≥10 s (Fig. 4A). In the first “spike-phase”, both D and G bind to free CB7. However, initially a higher amount of the CB7–cyclohexanone than that of the CB7–palmatine complex is produced because k^HG_in > k^HD_in, despite their similar K_a values. Thus, in the second phase a subsequent slower partial dissociation of the CB7–cyclohexanone complex occurs coupled with the rise of the CB7–palmatine concentration and the corresponding signal increase until the equilibrium is reached. To achieve the best accuracy for the fitted rate constants in such a scenario, i.e. for k^HG_in > k^HD_in, the initial [D] and [G] concentrations should be adjusted to ensure that the intensity at the breakpoint of the signal is about half of the intensity at the equilibrium.

Fig. 4 Fluorescence intensity changes at 500 nm after rapid mixing of 0.25 μM CB7 solution with (A) 2.5 μM cyclohexanone and 2.5 μM palmatine solution, (B) 2.5 μM cyclohexanone and 2.5 μM DHC solution, (C) 2.5 μM cyclohexanone and 2.5 μM berberine solution, and (D) 13.6 μM 6-methoxy-1-methylquinolinium and 2.5 μM palmatine solution (total concentrations are given at t = 0 s). Excitation occurred at 345 nm (A–C) or 422 nm (D). The red line represents the fitted function.

Table 1 Rate constants and binding constants for CBn inclusion complexes in water determined by the kinetic simultaneous analyte indicator binding assay^a

Guest	Indicator	k in/10^5 M^−1 s^−1	k out/10^−3 s^−1	K /10^7 M^−1	K /10^7 M^−1
a The errors are less than ± 10% for the rate constants, and measurements were performed at 298 K using low micro- to nanomolar concentrations of the host, guest and dye. For exact values, see the figure captions in the ESI. b K = k^HGin/k^HGout. c From isothermal titration calorimetry unless otherwise noted. d Ref. 14. e Ref. 29. f From steady-state fluorescence titrations. g Ref. 28.
Host: CB7 0.25 μM
	Berberine^d	190	810		2.4
	Palmatine^e	54	200		2.7
	DHC^e	43	2200	0.19
Cyclohexanone	Berberine	140	760	1.8
Cyclohexanone	Palmatine	130	680	1.9	1.9
Cyclohexanone	DHC	130	660	2.0
Norcamphor	Berberine	150	96	15
Norcamphor	Palmatine	140	94	15	13^f
Norcamphor	DHC	150	98	15
2,2,6-Trimethylcyclohexanone	Berberine	2.8	33	0.85	0.93
(+)-Fenchone	Berberine	0.84	3.0	2.8	2.7
2-Adamantanone	Berberine	29	0.074	3900
5-Chloro-2-adamantanone	Berberine	68	0.64	110
5-Bromo-2-adamantanone	Berberine	5.5	1.8	32
Host: CB6 2 μM
	DSMI^g	1950	790	0.79
4-MBA	DSMI	0.31	0.60	5.0
4-MBA in 1 : 1 HCOOH–H2O^30	—	7.55 × 10^−6	1.55	4.87 × 10^−5
CAD	DSMI	2200	7.1	3100

---

An entirely differently shaped kinetic trace was obtained (Fig. 4B) when DHC served as the fluorescent indicator, whose k^HD_in is only ∼25% smaller than that of palmatine but whose k^HD_out rate constant is 11 times larger (Table 1). In accordance with the simulations in Fig. 3C, the kinetically controlled initial complexation results in a DHC–CB7 complex built up in the beginning phase, followed by signal decay towards the equilibrium plateau. Consequently, a signal maximum that was higher in magnitude than the equilibrium signal was observed.

When berberine is employed as the indicator for the study of the CB7–cyclohexanone system (Fig. 4C), the fluorescence intensity only slightly changed after the steep growth has nearly instantaneously reached the equilibrium signal level. After free CB7 has been used up in the first fast phase, almost no further macroscopic changes occurred due to the similarity of k^HG_in to k^HD_in and of k^HG_out to k^HD_out (Table 1). In the third scenario, we recorded kinSBA traces for the guest 6-methoxy-1-methylquinolinium, which nearly instantaneously binds to CB7³¹ such that one can assume a pre-equilibrium between the host and guest is established, while the reaction with palmatine as the indicator occurs on a much slower time scale (Fig. 4D). In this case, it was infeasible to accurately determine k^HG_in or k^HG_out due to the fast equilibration of the guest with the host.³¹ A faster ingressing indicator dye should be used under such circumstances.

Despite the low (30 μM) water solubility of CB6,⁹ the kinSBA method allowed the determination of kinetic parameters for its inclusion complexes in neat water (see Fig. S17 in the ESI†), which previously was feasible only in the presence of salt or acid solubility enhancers. The K value reported for 4-MBA in the HCOOH–H₂O 1 : 1 mixture³⁰ at 298.3 K is about five orders of magnitude smaller than the one we found in water (Table 1). The kinSBA experiments revealed that the enormous difference in affinity in HCOOH–H₂O (1 : 1) vs. pure water primarily arises from the much slower ingression of 4-MBA into CB6 in the HCOOH–H₂O 1 : 1 mixture, whereas the release from CB6 is only slightly affected by the solvent change. The protonation of CB6 and/or association with HCOOH/H₃O⁺ not only reduce the amount of free CB6 decelerating and therefore the second order complexation process, but also electrostatically or sterically hinders the ingression of 4-MBA. In contrast, the first order dissociation rate of the 4-MBA–CB6 complex is not sensitive to such effects. Cadaverine (CAD) easily threads into CB6 on account of the small size of ammonium and methylene groups. Consequently, a much larger but still not diffusion-controlled k^HG_in was found (Table 1). The length of CAD permits an optimal interaction between the ammonium moieties of the guest and the two electron-rich carbonyl-laced portals of CB6, resulting in strong binding and a slow guest egression kinetics.

To accurately determine k^HG_in and k^HG_out by kinSBA, the signals should resemble those displayed in Fig. 4A or B, which can be accomplished by the proper choice of the dye and concentrations. The comparison of the rate constants obtained for cyclohexanone or norcamphor complexation with CB7 using different dyes (Table 1) demonstrates that the results are of high precision and independent of the chosen indicator dye. The data derived for norcamphor and (+)-fenchone show excellent agreement with our previously published values measured by kinGDA and kinIDA.²⁸ The studies on alicyclic ketone–CB7 and organic ammonium–CB6 complexations confirm the applicability of the kinSBA method for the measurement of k^HG_in and k^HG_out covering a range of several orders of magnitude (Table 1). The kinSBA method can be applied for direct determination of the equilibrium constants of host–guest binding defined as K_HG = k^HG_in/k^HG_out. This is a more accurate procedure than the usually applied multistep sequential competition titrations,^28,32 in which experimental errors accumulate. It is also advisable to check the agreement between the directly measured K_HG and the value calculated as the k^HG_in/k^HG_out ratio. The last column of Table 1 displays good accordance between the K_HG values derived from the rate constants and the ones measured directly by calorimetry or fluorescence titrations.

In conclusion, the kinSBA method can become a convenient-to-use and powerful tool for the determination of the kinetic and thermodynamic parameters of host–guest complexation, including protein–ligand systems. It provides signals that are very responsive to the alteration of the rate constants and curve shape analysis gives an immediate qualitative insight into the relationship between the ingression and egression rates. Moreover, kinSBA can serve as a sensitive rapid test to screen the time required to reach the host–guest binding equilibrium, which will be of immediate use to estimate the assay time needed when aiming to determine the binding constants of high-affinity or slowly-equilibrating systems.

This work was supported by NKFIH (Grant K123995) and the Emmy-Noether Programme of the DFG (BI1850/2).

Conflicts of interest

There are no conflicts of interest to declare.

Notes and references

1. L. Zhu, M. Zhu and Y. Zhao, ChemPlusChem, 2017, 82, 30–41.
2. E. Pazos, P. Novo, C. Peinador, A. E. Kaifer and M. D. García, Angew. Chem., Int. Ed., 2019, 58, 403–416.
3. E. A. Appel, J. del Barrio, X. J. Loh and O. A. Scherman, Chem. Soc. Rev., 2012, 41, 6195–6214.
4. K. M. Park, M. Y. Hur, S. K. Ghosh, D. R. Boraste, S. Kim and K. Kim, Chem. Commun., 2019, 55, 10654–10664.
5. H. Yin and R. Wang, Isr. J. Chem., 2018, 58, 188–198.
6. M. A. Romero, R. J. Fernandes, A. J. Moro, N. Basílio and U. Pischel, Chem. Commun., 2018, 54, 13335–13338.
7. H. Chen, Z. Huang, H. Wu, J.-F. Xu and X. Zhang, Angew. Chem., Int. Ed., 2017, 56, 16575–16578.
8. Y. Yan, J. Huang and B. Z. Tang, Chem. Commun., 2016, 52, 11870–11884.
9. D. Das, K. I. Assaf and W. M. Nau, Front. Chem., 2019, 7, 619.
10. S. Funk and J. Schatz, J. Inclusion Phenom. Macrocyclic Chem., 2020, 96, 1–27.
11. Q.-Q. Wang, in Handbook of Macrocyclic Supramolecular Assembly, ed. Y. Liu, Y. Chen and H.-Y. Zhang, Springer Singapore, Singapore, 2019, pp. 1–47.
12. Y.-C. Liu, W. M. Nau and A. Hennig, Chem. Commun., 2019, 55, 14123–14126.
13. K. Kotturi and E. Masson, Chem. – Eur. J., 2018, 24, 8670–8678.
14. Z. Miskolczy, L. Biczók and G. Lendvay, Phys. Chem. Chem. Phys., 2018, 20, 15986–15994.
15. B. Held, H. Tang, P. Natarajan, C. P. da Silva, V. de Oliveira Silva, C. Bohne and F. H. Quina, Photochem. Photobiol. Sci., 2016, 15, 752–757.
16. M. H. Tootoonchi, S. Yi and A. E. Kaifer, J. Am. Chem. Soc., 2013, 135, 10804–10809.
17. S. S. Thomas, H. Tang and C. Bohne, J. Am. Chem. Soc., 2019, 141, 9645–9654.
18. X. Ling, E. L. Samuel, D. L. Patchell and E. Masson, Org. Lett., 2010, 12, 2730–2733.
19. H. Tang, D. Fuentealba, Y. H. Ko, N. Selvapalam, K. Kim and C. Bohne, J. Am. Chem. Soc., 2011, 133, 20623–20633.
20. R. A. Copeland, Nat. Rev. Drug Discovery, 2016, 15, 87–95.
21. H. Lu and P. J. Tonge, Curr. Opin. Chem. Biol., 2010, 14, 467–474.
22. A. P. Ijzerman and D. Guo, Trends Biochem. Sci., 2019, 44, 861–871.
23. C. Bohne, Chem. Soc. Rev., 2014, 43, 4037–4050.
24. E. Masson, M. Raeisi and K. Kotturi, Isr. J. Chem., 2018, 58, 413–434.
25. C. Schönbeck, J. Phys. Chem. B, 2019, 123, 9831–9838.
26. R. Shusterman-Krush, L. Grimm, L. Avram, F. Biedermann and A. Bar-Shir, Chem. Sci., 2021, 12, 865–871.
27. C. L. Maikawa, A. I. d’Aquino, E. T. Vuong, B. Su, L. Zou, P. C. Chen, L. T. Nguyen, A. A. A. Autzen, J. L. Mann, M. J. Webber and E. A. Appel, Biomacromolecules, 2021, 22, 3565–3573.
28. A. Prabodh, S. Sinn, L. Grimm, Z. Miskolczy, M. Megyesi, L. Biczók, S. Bräse and F. Biedermann, Chem. Commun., 2020, 56, 12327–12330.
29. Z. Miskolczy, M. Megyesi, O. Toke and L. Biczók, Phys. Chem. Chem. Phys., 2019, 21, 4912–4919.
30. W. L. Mock and N. Y. Shih, J. Org. Chem., 1986, 51, 4440–4446.
31. Z. Miskolczy, J. G. Harangozó, L. Biczók, V. Wintgens, C. Lorthioir and C. Amiel, Photochem. Photobiol. Sci., 2014, 13, 499–508.
32. M. V. Rekharsky, T. Mori, C. Yang, Y. H. Ko, N. Selvapalam, H. Kim, D. Sobransingh, A. E. Kaifer, S. M. Liu, L. Isaacs, W. Chen, S. Moghaddam, M. K. Gilson, K. M. Kim and Y. Inoue, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20737–20742.

---

Footnote

† Electronic supplementary information (ESI) available: Materials and methods, evaluation of rate constants, simulated and measured signals. See DOI: 10.1039/d1cc04888k

---