A simple liquid state ¹H NMR measurement to directly determine the surface hydroxyl density of porous silica

Abstract

Silica is widely used in industrial applications and its performance is partially decided by its surface hydroxyl density α_OH. Here we report a quick, simple liquid ¹H NMR method to determine α_OH using a benchtop ¹H NMR spectrometer. The results show excellent agreement with the literature with an α_OH range from 4.16 to 6.56 OH per nm².

---

Silicas (SiO₂) are a class of porous materials which exhibit high surface areas, and whose available surfaces are populated, to varying degrees, with hydroxyl (silanol) groups. Hydroxyl moieties make silica useful in a number of applications including chromatography,¹ drug delivery^2–4 and catalysis.^5–8 In drug delivery, hydroxyls can be functionalised providing controllable drug release,⁹ and in catalysis hydroxyls are sites where metal ions can coordinate onto the silica surface.¹⁰ Therefore, it becomes important to characterise, quantify and understand the behaviour of surface hydroxyls.

A key measurement regarding surface (available) hydroxyls is their total density on the silica surface. The total surface hydroxyl density, α_OH, can impact the performance of silica for a given application. A higher surface density has a greater quantity of hydroxyls that can be functionalised,¹¹ and a low surface density leads to a more hydrophobic surface more suited to catalytic systems where water can hinder catalytic reaction such as olefin hydrogenation.¹² Subsequently, quantifying the total surface hydroxyl density, α_OH, has been the subject of much research using analytical techniques including infrared spectroscopy,^1,13–15 mass spectrometry^16–19 and solid state NMR.^20–28 Infrared spectroscopy (IR) is able to discriminate between absorbed water and surface hydroxyls. Gallas et al.¹³ showed that the H₂O IR stretch peak at 5260 cm⁻¹ representing absorbed water disappeared around 200 °C leaving behind OH stretch peaks between 4200–4800 cm⁻¹ representing hydroxyls. The presence of internal water complicating α_OH measurements was discussed by Davydov et al.²⁹ who showed that an infrared peak at 3650 cm⁻¹ persisted following deuterium (D₂O vapour) exchange, and its intensity increased with silica particle size. In most cases, infrared spectroscopy has been used in conjunction with other techniques to make their estimates of α_OH more insightful and less prone to error. Christy and Egeberg¹⁴ use IR spectroscopy data and partial least squares analysis to quantify α_OH with an error of around 10% on a series of silica gels. However, their method was limited to silicas with high surface areas (≥400 m² g⁻¹).

Mass spectrometry (MS) paired with temperature programmed desorption (TPD)^16–19 has been used to quantify the absorbed water (dehydration) and hydroxyl groups (dehydroxylation) removed by applying heat to silica samples. Zhuravlev reported that the combined use of MS and TPD can measure minimal amounts of water from silica ranging 0.04 μL to 4 μL with 1–5% relative error.¹⁶ Zhuravlev et al.¹⁷ have also presented results for the total surface hydroxyl density of 100 different silicas. The results from the different silicas ranged between α_OH = 4.2–5.7 OH per nm² and had an arithmetic mean, α_OH,average = 4.9 OH per nm². These results highlighted that the surface hydroxyl density is similar regardless of the geometry, surface area and pore size distribution of the silica. The total surface hydroxyl density average, α_OH,average = 4.9 OH per nm², is supported by a theoretical method developed by Kiselev et al.³⁰ based on crystallographic data. This theoretical model also predicted single hydroxyl (silanol) O₃–Si–OH was the most probable species on a ‘fully’ hydroxylated silica surface.

Solid state ¹H Magic Angle Spinning (MAS) NMR, ²⁹Si Direct Polarisation (DP) and ²⁹Si–{¹H} Cross Polarisation (CP) have all been used to quantify hydroxyl densities in silicas.^{20–27,31,32} For example, Sindorf and Maciel,²⁶ grafted trimethylsilane onto silica through a reaction that only affects hydroxyls on the surface, and by measuring the corresponding weight gained, they calculated for a ‘fully’ hydroxylated silica an α_OH ≈ 5.0 OH per nm². One of the major drawbacks with solid state ¹H MAS NMR for direct α_OH calculation is that a reference silica with a known total hydroxyl density^24,33 is required. Moreover, solid state ¹H MAS-NMR does not distinguish between internal and external hydroxyl groups. To quantify external hydroxyls Schrader et al.³⁴ recently reported a liquid state ¹H NMR based method to calculate silanol densities from a commercial silica. However, their method involved several steps including the use of an internal standard, sonication and centrifugation of the sample.

In this paper, we present a simple liquid phase ¹H NMR technique based upon D₂O/surface-OH exchange to determine α_OH. The following materials were used: D₂O (deuterium oxide 99.96% in Septum Vial, Eurisotop); H₂O (deionised water, 15 MΩ), 5 mm diameter 8 inch length NMR Tubes (Wilmad Inc, USA); Silica beads (Fuji Silysia Chemical Ltd, Japan 1.70–4.00 mm particle size) were from the CARiACT Q Series and labelled as: Q6, Q10, Q15, Q30 and Q50 where the number in the label indicates the average pore size diameter (e.g. Q6 has a pore diameter of 6 nm).

To remove residual OH groups present on the walls of the 5 mm NMR tube 0.5 mL of D₂O was added to the tube and then sealed with a lid. The NMR tube is then rigorously shaken for duration of 5 minutes. Then the lid was then removed and the D₂O was emptied out. The calibration of the NMR system is as follows:

I. Approximately 1.0 mL of D₂O (99.96%) is placed into a 5 mm NMR tube. The sample is then weighed using a Precisa 205 A balance capable of weighing to a precision of ±0.0001 g. A ‘background’ ¹H signal is then acquired and subsequently Fourier transformed to give a ¹H NMR spectrum.

II. Approximately 2 μL of deionised H₂O is then added to the sample tube in (i). The sample is then capped with a lid, vigorously shaken for 5 minutes and then a ¹H NMR signal is acquired from this system.

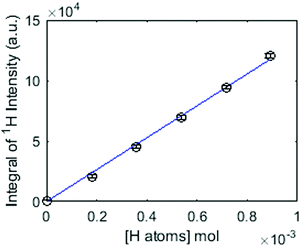
III. Step (ii) is repeated for the same sample tube until the cumulative volume of H₂O in the sample is 10 μL. The mass of added hydrogen atoms is calculated for each step and the integral of ¹H signal intensity is then plotted against the known mass of added hydrogen atoms as shown in the calibration plot in Fig. 1.

Fig. 1 Calibration plot showing the integral of ¹H signal intensity against the mass concentration of H atoms. A linear regression (blue line) is displayed and has a gradient of 1.3335e + 08 (intensity units g⁻¹).

The data points shown in Fig. 1 are fitted to a simple linear equation to give the mass of hydrogen atoms from a sample containing an unknown amount of exchangeable hydrogen.

In order to measure hydroxyl densities of the CARiACT Q-series silicas the following procedure was adopted and repeated 3 times for each different Q-series silica (n = 3).

(1) Ten Q-series beads are heated in an oven at 120 °C for 12 h.

(2) Following (1), the silica beads are transferred to a 5 mL plastic vessel and weighed using a precision scale.

(3) 1 mL of D₂O (99.96) is syringed into the plastic vessel containing the silica beads.

(4) The silica beads are left to equilibrate for 3 h. The equilibration time was confirmed to be sufficient for our system as described in in ESI† S5.

(5) D₂O (500–600 μL) is then pipetted from the plastic vessel into a 5 mm NMR tube.

(6) The NMR tube is then capped and shaken for a duration of 5 minutes.

(7) The ¹H signal is then acquired, Fourier transformed, and the resulting spectrum is integrated to obtain the ¹H intensity. This integral is background corrected by subtracting the integral obtained by performing only steps (3) to (7), i.e. the same procedure but without the silica beads.

Using pelletized/granulated materials ensures an easy separation of liquid and solid materials; in principle the method is suitable for powdered samples provided a suitable separation of powder and liquid is possible, e.g., by mild centrifugation during step (4). Overall, we assume that any liquid density changes are negligible. The vertical liquid height must exceed the entire active region of the (RF) coil to ensure all ¹H NMR measurements are from the same control volume. In these experiments, a sample length of ∼42 mm was used which was significantly longer than the length of the coil over which any signal was received (see ESI† S6). ¹H NMR spectra were collected using a Magritek Spinsolve 43 MHz NMR benchtop spectrometer and details of pulse sequence parameters may be found in ESI† S1.

There are several sources of experimental error that need to be accounted for when producing the calibration plot in Fig. 1, the details of which are given in ESI† S2. The calculation of hydroxyl density is taken directly from Zhuralev¹⁶ using eqn (1):

α_OH = δ_OH × N_A × 10⁻²¹ × (S.A.)⁻¹ g⁻¹ catalyst (1)

where, α_OH is the hydroxyl density in OH per nm², δ_OH is the concentration of H atoms, obtained from the calibration plot expressed in mmol per gram of catalyst, N_A is Avagadro's number and S.A. is the surface area of the catalyst, which was obtained with BET N₂ (details found in ESI† S3). Table 1 describes the results from the as-received CARiACT Q series silica beads. The OH density values of silicas with pore sizes larger than 10 nm (Q15, Q30 and Q50) show excellent agreement with the results reported by Zhuravlev which ranged between 4.1 and 6.1 OH per nm².¹⁸ Theoretically, it is expected that the OH densities of Q6 and Q10 silicas should also have been in this range. However, the OH densities calculated for Q6 and Q10 silicas show statistically significant deviations from Zhuravlev's arithmetic mean, with OH densities of 1–2 OH per nm².

Table 1 As-received CARiACT Q-series silica beads and their respective total surface hydroxyl densities as measured by NMR. Further sample details are given in ESI S4

Sample	Average mass (n = 3) of silica beads (g^−1)	Average mass concentration δOH (mmol g^−1)	Average αOH (nm^−2)
BET N2 surface areas for the samples were the following: 407 m^2 g^−1 (Q6), 312 m^2 g^−1 (Q10), 207 m^2 g^−1 (Q15), 107 m^2 g^−1 (Q30) and 70 m^2 g^−1 (Q50).
Q6	0.1772 g	1.02	1.51 ± 0.13
Q10	0.1454 g	0.67	1.29 ± 0.17
Q15	0.1188 g	1.55	4.52 ± 0.36
Q30	0.1687 g	0.95	5.35 ± 0.81
Q50	0.1705 g	0.60	5.16 ± 0.70

---

It has been previously reported using ¹H magic angle spinning NMR³⁵ data that, as received CARiACT Q6 and Q10 also exhibit these lower OH densities. It is unclear what causes the lower OH densities in as received Q6 and Q10 silicas, but the evidence from ¹H magic angle spinning NMR³⁵ and additional experiments shown in ESI† S5 rule out slower kinetics or diffusion in smaller pores as a cause of these low OH densities. We also note that the OH densities reported by Zhuravlev et al.¹⁷ are based on ‘fully hydroxylated’ samples, and ‘as received’ does not always equate to ‘fully hydroxylated’. Therefore, rehydroxylation is required for samples such as Q6 and Q10 in order to make a fairer comparison with previous research. Q-series silicas were rehydroxylated by being placed in boiling water for 100 h in a reflux condenser setup with heating mantle and cooling water. Fig. 2 highlights that rehydroxylation increases the total surface hydroxyl density of Q6 and Q10 silicas. The α_OH values for Q6 and Q10 following rehydroxylation (but using the as received surface area) are 2.82 and 3.54 OH per nm² respectively and remain below the expected Zhuravlev constant of around 5.0 OH per nm². However, by taking a further BET surface area measurement of Q6 and Q10 after rehydroxylation for 100 h in boiling water, both silicas show a significant reduction in surface area: Q6 reduces from 407 to 191 m² g⁻¹ and Q10 from 312 to 233 m² g⁻¹. The rightmost columns in Fig. 2 show that when reduction in surface area is considered, the α_OH values are more in line with those seen in literature. This group of ‘fully hydroxylated’ silicas has an α_OH range of 4.16 to 6.56 OH per nm², and is consistent with the average Zhuravlev constant. This consistency could not have been achieved without considering the surface area decrease as a result of rehydroxylation (Fig. 2). The literature^18,32,36 often does not specify and/or neglects ‘when’ BET measurements for specific surface area are made, though it is clear that this could be a significant source of error if the surface area is being affected by any treatment. A surface area reduction has also been observed by Zhuravlev,¹⁶ who reported a surface area reduction in an aerosilogel after 60 h in boiling water from 168 to 108 m² g⁻¹. It is noted that changing the surface hydroxyl content by heating alone does not change the BET surface area calculation significantly. Previous research^19,32,37 limits the discussion of rehydroxylation to a surface reaction that converts siloxanes (Si–O–Si) into hydroxyls (Si–OH), and therefore does not consider any structural implications rehydroxylation may have on the silica. To investigate the effect of dehydroxylation CARiACT Q15 silica beads were dehydroxylated by heating under vacuum for a duration of 8 h under the following temperatures: 325, 425 and 800 °C. The Q15 samples were then subject to exactly the same the D₂O exchange procedure outlined in (1–7) on the previous page.

Fig. 2 The total surface hydroxyl density of Q6, Q10 and Q50 silica as received (0 h) and after rehydroxylation. The rehydroxylation was done by placing silica in boiling water for 100 h. The specific surface area S.A. was measured when as received (S.A. as received) and after rehydroxylation (S.A. rehydroxylated).

Table 2 highlights the clear trend that the total surface hydroxyl density decreases with increasing pre-treatment temperature under vacuum. The surface area variation with the heat treatments described in Table 2 do not vary significantly from the as received silica: 207 m² g⁻¹vs. 203, 199, 202 m² g⁻¹ for 325, 425, 800 °C respectively. This constant surface area trend with respect to pre-treatments of 800 °C and below was also found by Shioji et al.³⁷ The dehydroxylated total surface hydroxyl densities obtained through this ¹H liquid phase technique do not diverge further than 0.4 OH per nm² from the results of Zhuravlev^17,19 (noting slightly different temperatures were used). The dehydroxylation trend and the absolute values of dehydroxylated total surface hydroxyl densities are both consistent with the literature, and therefore support the validity of this technique. In addition, our technique is further able to measure a significantly dehydroxylated silica sample heated at 800 °C demonstrating this technique has a suitable degree of sensitivity.

Table 2 Total surface hydroxyl density of CARiACT Q15 when heated under vacuum at pre-treatment temperatures of 325, 425 and 800 °C

Pre-treatment temperature/°C	325	425	800
Average αOH/nm^−2	3.31 ± 0.44	2.70 ± 0.24	0.90 ± 0.15

---

Some of the absolute OH densities, such as rehydroxylated Q6 (with surface area change) and the dehydroxylated measurements may be considered slightly higher than the literature (by less than 0.3 OH per nm²). Small differences between our results and those presented in the literature are possible since the Q-series silicas used here were briefly exposed to moisture from the atmosphere once removed from the oven till full immersion in the D₂O; therefore, through rehydration, some adsorbed surface water could contribute to the OH density which would increase the α_OH value slightly. To reduce this effect, we minimised the exposure time; alternatively, an inert atmosphere could be used at the expense of experimental complexity.

A question that this technique does not answer is that of the ratio of the total hydroxyl density of the silica to that of exchangeable OH groups on the silica. The amount of intraskeletal or intraglobule (internal)²⁹ OH sites that are inaccessible to D₂O molecules cannot be determined by this method. It is unlikely that such sites are involved in catalysis, as they would be inaccessible to reactant molecules, and hence it is felt that the question of quantifying the amount of intraskeletal/intraglobule OH sites is rather superfluous. One final remark regarding this technique is that it should, in theory, be possible to measure the concentration of any exchangeable hydrogen moiety providing (i) the D₂O is in vast excess and (ii) a suitable calibration of the NMR spectrometer is performed.

To summarise we have demonstrated a simple benchtop ¹H NMR based liquid deuterium exchange technique that is able to measure the total surface hydroxyl density α_OH of silica. Fully hydroxylated silicas give α_OH values between 4.16 and 6.56 OH per nm² which is in excellent agreement with the literature. This technique is sensitive enough to measure samples with low α_OH values such as CARiACT Q15 dehydroxylated at 800 °C with an α_OH = 0.90 ± 0.15 OH per nm². It is also evident that a correction step for specific surface area may be required for accurate determination of OH densities by this method, particularly if a sample has undergone any thermal and/or chemical treatment. Overall, the methods described demonstrates a similar performance and results to other techniques used in the literature but has the significant advantages in terms of speed and expense and has the potential to be used by non-experts.

P. S. and C. P. would like to thank the EPSRC and Johnson Matthey Plc. for funding this work under grant numbers GR/R47523/01 and EP/R511870/1 respectively.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. V. Y. Davydov, A. V. Kiselev, S. A. Kiselev and V. O.-V. Polotnyuk, J. Colloid Interface Sci., 1980, 74, 378–383.
2. S. Y. Tan, C. Y. Ang and Y. Zhao, J. Controlled Release, 2015, 213, e100.
3. K. Naghdipari, L. Shojaei, A. Heidari, M. Heidarifard, M. Sharbati, A. Mahari and R. Hosseinzadeh-Khanmiri, Polyhedron, 2019, 170, 659–665.
4. N. Hao, K. W. Jayawardana, X. Chen and M. Yan, ACS Appl. Mater. Interfaces, 2015, 7, 1040–1045.
5. J. Xu, Z. Qu, G. Ke, Y. Wang and B. Huang, Appl. Surf. Sci., 2020, 513, 145910.
6. R. Antony, S. T. D. Manickam and S. Balakumar, J. Inorg. Organomet. Polym., 2017, 27, 418–426.
7. K. Usui, K. Miyashita, K. Maeda, Y. Manaka, W.-J. Chun, K. Inazu and K. Motokura, Org. Lett., 2019, 21, 9372–9376.
8. R. H. Vekariya and H. D. Patel, Synth. Commun., 2015, 45, 1031–1054.
9. V.-C. Niculescu, G. Paun and V. Parvulescu, Appl. Organomet. Chem., 2018, 32, e4590.
10. E. Groppo, C. Lamberti, S. Bordiga, G. Spoto and A. Zecchina, Chem. Rev., 2005, 105, 115–184.
11. S.-C. Shen, W. K. Ng, L. S. O. Chia, Y.-C. Dong and R. B. H. Tan, Applications of Mesoporous Materials as Excipients for Innovative Drug Delivery and Formulation, http://www.eurekaselect.com/115562/article, accessed May 1, 2020.
12. P. P. M. M. Wittgen, C. Groeneveld, P. J. C. J. M. Zwaans, H. J. B. Morgenstern, A. H. van Heughten, C. J. M. van Heumen and G. C. A. Schuit, J. Catal., 1982, 77, 360–381.
13. J.-P. Gallas, J.-M. Goupil, A. Vimont, J.-C. Lavalley, B. Gil, J.-P. Gilson and O. Miserque, Langmuir, 2009, 25, 5825–5834.
14. A. A. Christy and P. K. Egeberg, Analyst, 2005, 130, 738–744.
15. W. K. Hall, H. P. Leftin, F. J. Cheselske and D. E. O’Reilly, J. Catal., 1963, 2, 506–517.
16. L. T. Zhuravlev, Colloids Surf., A, 2000, 173, 1–38.
17. L. T. Zhuravlev, Langmuir, 1987, 3, 316–318.
18. L. T. Zhuravlev, Colloids Surf., A, 1993, 74, 71–90.
19. L. T. Zhuravlev, React. Kinet. Catal. Lett., 1993, 50, 15–25.
20. F. M. Wisser, M. Abele, M. Gasthauer, K. Müller, N. Moszner and G. Kickelbick, J. Colloid Interface Sci., 2012, 374, 77–82.
21. Y. Cabrera, A. Cabrera, F. H. Larsen and C. Felby, Holzforschung, 2016, 70, 709–718.
22. C. C. Liu and G. E. Maciel, J. Am. Chem. Soc., 1996, 118, 5103–5119.
23. S. Haukka and A. Root, J. Phys. Chem., 1994, 98, 1695–1703.
24. S. Ek, A. Root, M. Peussa and L. Niinistö, Thermochim. Acta, 2001, 379, 201–212.
25. G. E. Maciel and D. W. Sindorf, J. Am. Chem. Soc., 1980, 102, 7606–7607.
26. D. W. Sindorf and G. E. Maciel, J. Phys. Chem., 1983, 87, 5516–5521.
27. M. Ide, M. El-Roz, E. D. Canck, A. Vicente, T. Planckaert, T. Bogaerts, I. V. Driessche, F. Lynen, V. V. Speybroeck, F. Thybault-Starzyk and P. V. D. Voort, Phys. Chem. Chem. Phys., 2012, 15, 642–650.
28. N. Millot, C. C. Santini, F. Lefebvre and J.-M. Basset, C. R. Chim, 2004, 7, 725–736.
29. V. Y. Davydov, A. V. Kiselev and L. T. Zhuravlev, Trans. Faraday Soc., 1964, 60, 2254–2264.
30. L. D. Belyakova and A. V. Kiselev, Preparation, Structure and Characteristics of Sorbents, Goskhimizdat, Leningrad, 1959.
31. E. Lippmaa, M. Maegi, A. Samoson, G. Engelhardt and A. R. Grimmer, J. Am. Chem. Soc., 1980, 102, 4889–4893.
32. D. W. Sindorf and G. E. Maciel, J. Am. Chem. Soc., 1983, 105, 1487–1493.
33. G. Hartmeyer, C. Marichal, B. Lebeau, S. Rigolet, P. Caullet and J. Hernandez, J. Phys. Chem. C, 2007, 111, 9066–9071.
34. A. M. Schrader, J. I. Monroe, R. Sheil, H. A. Dobbs, T. J. Keller, Y. Li, S. Jain, M. S. Shell, J. N. Israelachvili and S. Han, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2890–2895.
35. C. I. Robertson, PhD thesis, University of Cambridge, 2018.
36. V. I. Lygin, Russ. J. Gen. Chem., 2001, 71, 1368–1372.
37. S. Shioji, M. Kawaguchi, Y. Hayashi, K. Tokami and H. Yamamoto, Adv. Powder Technol., 2001, 12, 331–342.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cc03959h

---