Magnetic shielding paints an accurate and easy-to-visualize portrait of aromaticity

Abstract

Chemists are trained to recognize aromaticity semi-intuitively, using pictures of resonance structures and Frost-Musulin diagrams, or simple electron-counting rules such as Hückel's 4n + 2/4n rule. To quantify aromaticity one can use various aromaticity indices, each of which is a number reflecting some experimentally measured or calculated molecular property, or some feature of the molecular wavefunction, which often has no visual interpretation or may not have direct chemical relevance. We show that computed isotropic magnetic shielding isosurfaces and contour plots provide a feature-rich picture of aromaticity and chemical bonding which is both quantitative and easy-to-visualize and interpret. These isosurfaces and contour plots make good chemical sense as at atomic positions they are pinned to the nuclear shieldings which are experimentally measurable through chemical shifts. As examples we discuss the archetypal aromatic and antiaromatic molecules of benzene and square cyclobutadiene, followed by modern visual interpretations of Clar's aromatic sextet theory, the aromaticity of corannulene and heteroaromaticity.

---

Peter B. Karadakov

Peter B. Karadakov is a Reader in the Department of Chemistry at the University of York. He received his MSc from Sofia University, Bulgaria, and his PhD from the Bulgarian Higher Degrees Commission. He has worked as Lecturer at Sofia University, Research Associate at the Bulgarian Academy of Sciences and the University of Bristol, and Lecturer at the University of Surrey. His research is equally divided between the development and applications of modern valence bond theory, and the use of off-nucleus NMR shieldings to describe bonding, aromaticity and antiaromaticity in the ground and excited states of molecular systems.

Brett VanVeller

Brett VanVeller is an Associate Professor in the Department of Chemistry at Iowa State University. He received his PhD from the Massachusetts Institute of Technology under the supervision of Prof. Timothy M. Swager. He later completed postdoctoral studies as a Canadian Institutes of Health Research Fellow under Prof. Ronald T. Raines, then at the University of Wisconsin–Madison. His research interests focus on physical organic chemistry, photochemistry, synthetic and bioorganic chemistry, and peptide science.

---

1. Introduction

One intriguing question that does not require a long stretch of chemical imagination is what would we see if we were able to measure magnetic shieldings not just at nuclei, as in NMR spectroscopy, but also at any point in space close to a molecule? According to NMR theory, if a molecule is placed in an external magnetic field B₀, the magnetic field B_J felt at nucleus J is different from B₀; for an isolated molecule, this change in the magnetic field is due to the shielding of that nucleus by the electrons. Chemically different nuclei are surrounded by different electronic environments and exhibit different extents of shielding. B_J and B₀ are related through the equation

B_J = (1 − σ_J)B₀ (1)

where σ_J is the shielding tensor of nucleus J defined as a 3 × 3 matrix with rows and columns labelled by the coordinate axes symbols x, y and z, and 1 is a 3 × 3 unit matrix. Isotropic shieldings, the differences between which are associated with chemical shifts, are obtained by averaging the diagonal elements of the shielding tensor

While experimental NMR can currently provide data about shieldings at nuclei only, quantum chemical methods allow calculation of shielding tensors not only at nuclei, but also at arbitrary positions r in space close to a molecule. It turns out that these “off-nucleus” shielding tensors, σ(r), studied as a function of position, provide valuable information about chemical bonding and the aromaticity of cyclic conjugated systems.

The interest towards “off-nucleus” shieldings can be traced back to 1958 when Johnson and Bovey introduced a convenient approach for approximating ring current effects based on Pauling's free electron model.¹ Using proton shieldings calculated at different points in the neighbourhood of a benzene ring, these authors were able to construct a contour plot of “isoshielding” lines. The most well-known and widely used off-nucleus shielding is the nucleus-independent chemical shift (NICS) suggested by Schleyer and co-workers.² The original NICS [currently referred to as NICS(0)], defined as the isotropic shielding evaluated at the centre of an aromatic or antiaromatic ring and taken with a reversed sign, −σ_iso(at ring centre), has become a popular aromaticity probe. Other aromaticity probes derived from shielding tensors calculated at selected points in space include NICS(1), −σ_iso(at 1 Å above ring centre),³ NICS(0)_zz, the out-of-plane component of the shielding tensor at the ring centre with reversed sign, −σ_zz(at ring centre),^4,5 NICS(1)_zz, defined as −σ_zz(at 1 Å above ring centre),⁶ as well as various “dissected”' NICS indices.⁶ In 1997 Wolinski proposed “to analyze the magnetic shielding tensor as a continuous function of space point coordinates in atoms and molecules”,⁷ and examined the changes in the shielding tensor σ(r) along the molecular axes of a series of linear molecules including LiH, LiF, Li₂, HF, HCN, NHC and ethyne. Wolinski observed that, in general, the variations in the isotropic shielding σ_iso(r) and in the shielding components parallel and perpendicular to the molecular axes were similar to the behaviour of the total electronic density but showed certain differences which could be attributed to the fact that the total electron density is responsible for the electron charge distribution, whereas magnetic properties, including shielding, are determined by the induced current density. Schleyer and co-workers³ analysed the changes in isotropic NICS and “dissected” NICS above the molecular planes of benzene and cyclobutadiene by calculating and interpolating the values of these quantities at two-dimensional grids of points perpendicular to the molecular planes. The first systematic calculations of the isotropic shielding isosurfaces surrounding a range of molecules including ethene, formaldehyde, butadiene, ethyne, benzene and naphthalene were carried out by Klod and Kleinpeter.⁸ In subsequent studies Kleinpeter and co-workers showed that analyses of the isotropic shielding isosurfaces surrounding a large selection of molecular species provide interesting information about aromaticity, antiaromaticity, the diatropic and paratropic regions within molecules, and the anisotropic effects due to specific substituents (see ref. 9–11 and references therein). To construct isotropic shielding isosurfaces for various molecules, Kleinpeter and co-workers were using regular three-dimensional grids of points with a spacing of 0.5 Å. While grids of this type can reproduce the general features of σ_iso(r) within the volume surrounding a molecule, obtaining a detailed picture of the changes in σ_iso(r), especially in the regions of space close to atoms and chemical bonds, requires a finer grid so as to allow probing σ_iso(r) at a reasonable number of points within the covalent radius of even the smallest atom, H (ca. 0.32 Å). The shielding increment plots employed by Martin and co-workers^12–14 are closely related to the isotropic shielding isosurfaces. To generate these plots, a molecular probe (most often, an H₂ molecule), is placed at each point from a grid above and parallel to the plane of a conjugated system and the shielding increments are calculated by subtracting the isotropic shielding for a nucleus in the isolated probe from the corresponding value obtained at a grid point.

More accurate and higher-resolution isotropic shielding isosurfaces and contour plots, constructed from dense grids of points (as established in a series of applications, see ref. 15 and 16 and references therein, a reasonable compromise between level of detail and computational effort is achieved by using a spacing of 0.05 Å) and calculated, if required, using correlated wavefunctions, allow very clear distinction between aromaticity and antiaromaticity in the low-lying electronic states of cyclic conjugated systems and reveal how pronounced differences in aromatic character are reflected in chemical bonding. Similarly to the Laplacian of the electron density, ∇²ρ(r), used in the theory of atoms in molecules (AIM)¹⁷ and the electron localization function (ELF),^18,19 the isotropic shielding amplifies the changes in electron activity within the space encompassing a molecule and, especially, along chemical bonds, making the differences between bonds much easier to visualize.²⁰ One advantage of the isotropic shielding is that at atomic positions it is pinned to the experimentally verifiable nuclear shieldings.

The spatial variation in the values of σ_iso(r) highlights regions of positive σ_iso(r) that can be associated with more intensive electron presence and movement, leading to stronger bonding and, in conjugated rings, greater aromatic character. Alternatively, regions of negative σ_iso(r) spreading out from the centres of conjugated rings are indicative of antiaromaticity and weakened bonding. The profoundly different shielding distributions observed in aromatic and antiaromatic systems can be viewed as aromatic and antiaromatic “fingerprints” that allow for unambiguous and quantitative classification of the local degree of aromaticity.¹⁵ This attribute leads to an inherently pictorial yet quantitative analysis of aromaticity which has been used to produce a visual interpretation of Clar's aromatic sextet theory based on isotropic shielding contour plots.²¹ There is an important difference between σ_iso(r) isosurfaces and contour plots and NICS that needs to be emphasized: We treat increased shielding as a bond-enhancing factor and decreased shielding as a bond-disrupting factor; this is not the case with NICS, for which the sign inversion (vide supra) facilitates comparison to proton chemical shifts.

The aim of this feature article is to explain, through easy-to-visualize examples, the essential features of the isotropic shielding analysis of aromaticity, antiaromaticity and chemical bonding. The main focus will be on aromaticity, a fuzzy concept that does not lend itself to widely applicable and clear-cut definitions. The International Union of Pure and Applied Chemistry (IUPAC) defines “aromatic” as “in the traditional sense, having a chemistry typified by benzene”,²² a definition that is not particularly helpful when it comes to identifying and quantifying aromaticity. Chemists often use simple qualitative aids such as resonance structures, or Hückel's 4n + 2/4n electron-counting rules and the familiar Frost-Musulin diagrams,²³ both of which have their roots in simple Hückel molecular orbital (HMO) theory. As we show here, the isotropic shielding isosurfaces and contour plots calculated using ab initio and density functional theory (DFT) methods provide a much more capable, reliable and theoretically sound approach for describing aromaticity in a wide range of molecules.

2. Benzene and cyclobutadiene

It is instructive to start by examining the shielding around the archetypal examples of aromatic and antiaromatic rings, benzene and square cyclobutadiene (C₆H₆ and C₄H₄), in their electronic ground states at geometries of D_6h and D_4h symmetry, respectively (Fig. 1). The data for the shielding isosurfaces and contour plots shown in Fig. 1 come from calculations utilizing CASSCF(6,6)-GIAO and CASSCF(4,4)-GIAO wavefunctions (π-space complete active space self-consistent field wavefunctions constructed from gauge-including atomic orbitals with 6 electrons in 6 active orbitals for benzene and 4 electrons in 4 active orbitals for cyclobutadiene) in the 6-311++G(2d,2p) basis (for further details, see ref. 15). The most important feature of the shielding isosurface plot for benzene (Fig. 1a) is the thick shielded “doughnut” enclosing the carbon ring which demonstrates strong bonding interactions and aromatic stability. The antiaromatic destabilization in square C₄H₄ follows from the central deshielded region (Fig. 1b) which eliminates most of the shielding over carbon–carbon bonds, weakens these bonds and pushes the remaining shielding towards the exterior of the ring. Note that while the extensive deshielding in square cyclobutadiene suggests substantial decrease in strength for all carbon–carbon bonds, this is very much an exaggeration as, in fact, high-level computational estimates indicate a carbon–carbon bond length of about 1.45 Ų⁴ which is shorter than a typical C–C single bond.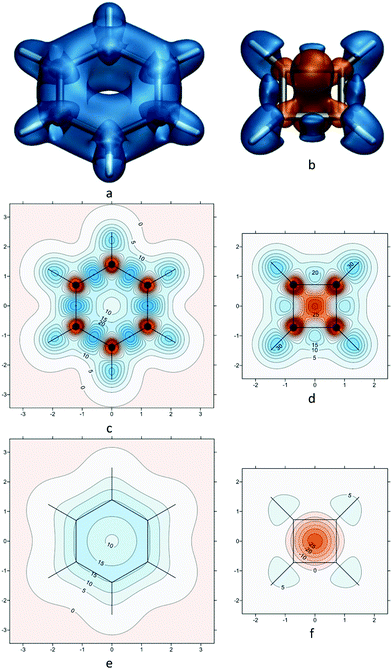

Fig. 1 Isotropic shielding in the ground electronic states of benzene and square cyclobutadiene. (a) and (b): isosurfaces at σ_iso(r) = ±16 ppm (blue/orange); (c) and (d): σ_iso(r) contour plots in the molecular planes; (e) and (f): σ_iso(r) contour plots in planes 1 Å above the molecular planes. σ_iso(r) in ppm, axes in Å. All recreated using shielding data computed for ref. 15.

The contour plots in Fig. 1c–e provide more detailed information about the shielding variations in the molecular planes (Fig. 1c and d) and in planes 1 Å above the molecular planes (Fig. 1e and f). The shielding over each C–C bond in benzene increases towards the midpoint of the bond where it reaches 45 ppm (Fig. 1c); the maximum shielding for a C–C bond in square cyclobutadiene is much lower, 25 ppm at an off-bond location (Fig. 1d). On the other hand, the C–H bonds in square cyclobutadiene are more shielded and stronger than those in benzene (larger shielded regions, maximum shielding values of 35 ppm in C₄H₄ against 31 ppm in C₆H₆). These observations are in line with the expected differences between aromatic and antiaromatic rings. The carbon nuclei in the ground electronic states of C₆H₆ and C₄H₄ are surrounded by small ovoid deshielded regions inside which the σ_iso(r) values are negative (Fig. 1c and d). In the antiaromatic C₄H₄ these ovoid deshielded regions around carbons merge with the larger deshielded region in the centre of the molecule. Similar deshielded “halos”' around sp² and sp hybridized carbons and other sp² hybridized first main row atoms have been observed in not only in conjugated rings,^15,25–28 but also in in open-chain conjugated molecules such as ethene, ethyne and s-trans-1,3-butadiene.²⁰ The occurrence of such “halos” has been attributed to a specific type of π electron behaviour characteristic of some sp² and sp hybridized first main row atoms that is different from traditional ring currents.¹⁵ While intriguing, these deshielded “halos” complicate the σ_iso(r) contour plots in the molecular planes (Fig. 1c and d) and do not offer much insight into chemical bonding and aromaticity. A recently developed approach for studying the spatial contributions to nuclear magnetic shieldings²⁹ has the potential to provide a better understanding of the deshielded “halos” but it still has not been applied to off-nucleus shieldings.

The contour plots in planes 1 Å above the molecular planes (Fig. 1e and f) are much simpler in appearance. While the choice of height is somewhat arbitrary, it is just the same as for the NICS(1) aromaticity index³ and it is sufficient to retain most of the π electron contributions to shielding, while eliminating most of the σ electron contributions and helping stay above the deshielded “halos” surrounding the carbons. The deshielded “halos” have been found to disappear in σ_iso(r) contour plots at the lower height of 0.5 Å above the molecular planes of various conjugated heterocycles,^26,27 but the shielding at this lower height still shows some σ electron contributions. The differences between the “aromatic” and “antiaromatic” σ_iso(r) contour plots in Fig. 1e and f are still very pronounced: In benzene we observe significant shielding delocalization in the form of a circular band of σ_iso(r) ≥ 15 ppm values, whereas the region over the carbon ring in cyclobutadiene is strongly deshielded; interestingly, even at 1 Å above the C₄H₄ molecular plane there is increased shielding over the C–H bonds which indicates that the shielded regions surrounding these bonds extend significantly higher in the vertical direction in comparison to those around C–H bonds in C₆H₆. The shielding delocalization in the contour plot for benzene (Fig. 1e) can be thought of as the consequence of the resonance between the two familiar Kekulé resonance structures;^30,31 we can expect to see high levels of shielding delocalization in σ_iso(r) contour plots in planes 1 Å above the molecular planes in all other aromatic compounds.

3. Making aromaticity “klar”

If we now turn our attention to polycyclic aromatic hydrocarbons (PAHs) such as phenanthrene (Fig. 2), which have multiple fused rings, the situation becomes more complicated, as we need to account not only for the overall aromaticity of the molecule (global aromaticity), but also for the varying degrees of aromatic character of the individual rings (local aromaticity). To address this problem, in the 1960s Erich Clar developed his sextet rule, which states that the dominant resonance structure in a molecule is the one with the largest number of disjoint aromatic π electron sextets.^32–34 Isotropic shielding contour plots for PAHs provide an intuitive and yet quantitative picture of aromaticity, both global and local, not only replicating but also going beyond Clar's rule.²¹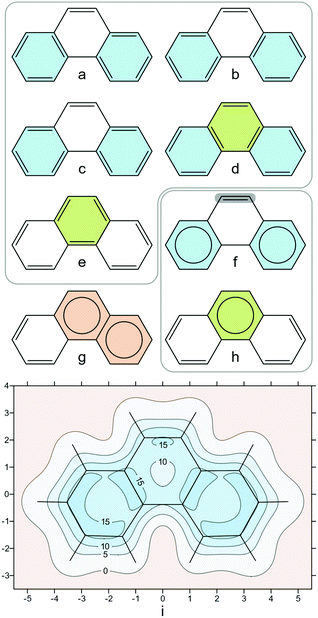

Fig. 2 (a)–(e): Kekulé resonance structures of phenanthrene showing the rings with 6 π electrons; (f) and (h): Clar aromatic π sextets (rings with circles inside) resulting from resonance structures (a)–(e), the most reactive site in phenanthrene is shaded grey in (f); (g): incorrect assignment of Clar sextets, adjacent rings cannot have 6 π electrons each; (i): isotropic shielding contour plot in a plane 1 Å above the molecular plane, recreated from shielding data computed using DFT for ref. 21, at the B3LYP-GIAO/6-311++G(d,p)//B3LYP-D3BJ/def2-TZVP level, σ_iso(r) in ppm, axes in Å.

As a first example, let us examine phenanthrene. Phenanthrene has five Kekulé resonance structures (Fig. 2a–e), four of which back the form in Fig. 2f with two disjoint Clar sextets (rings shaded in blue), and just two back the form in Fig. 2h with one Clar sextet (rings shaded in green), hence the dominant form is the one in Fig. 2f. The isotropic shielding contour plot in a plane 1 Å above the molecular plane (Fig. 2i) shows clearly that the two terminal phenanthrene rings feature shielding delocalization very similar to that in benzene (cf.Fig. 1e), provides justification for Clar's dominant form with two disjoint sextets in Fig. 2f without any use of resonance structures and highlights, at the same time, through increased shielding, the most reactive site in the molecule.

Our second example is coronene. Coronene has 20 Kekulé resonance structures which support two symmetry-equivalent forms with three disjoint Clar sextets each (Fig. 3a and b). Of course, either form is equally valid and, in order to deal with this situation, the Clar sextets can be thought to be “migrating” around the central ring following the dashed arrows in Fig. 3c—as a result, the electronic structure becomes the average of the two forms in very much the same way as benzene can be considered as the average of its two Kekulé resonance structures. The shielding contour plot in Fig. 3d captures this averaged description perfectly, showing immediately, at a glance, that all peripheral rings in coronene exhibit the same degree of aromatic character and that the central ring is less aromatic than the peripheral rings. The higher aromaticity of the peripheral rings in comparison to the central ring does not come as a surprise, as most aromaticity indices make the same prediction (see ref. 34 and references therein); however, the contour plot in Fig. 3d is much easier to visualize and, arguably, more convincing than a pair of NICS values or one-dimensional NICS-X-scan and NICS-XY-scan plots.^35,36

Fig. 3 (a) and (b): the two symmetry-equivalent forms with three disjoint Clar sextets each for coronene; (c): “migrating” Clar sextets demonstrating the equivalence of forms (a) and (b); (d): isotropic shielding contour plot in a plane 1 Å above the molecular plane, details as for Fig. 2i.

To enable comparison of the results obtained with the current approach to those coming from methods utilizing the out-of-plane zz-component of the off-nucleus shielding tensor, σ_zz(r) (the z axis is assumed to be perpendicular to the molecular plane), such as NICS_zz(0), NICS_zz(1), NICS-X-scans and NICS-XY-scans, as well as to ring current plots, in Fig. 4 we show σ_zz(r) contour plots for phenanthrene and coronene in the respective molecular planes and in planes 1 Å above the molecular planes. The σ_zz(r) values for these plots were extracted from the computational data obtained while preparing ref. 21.

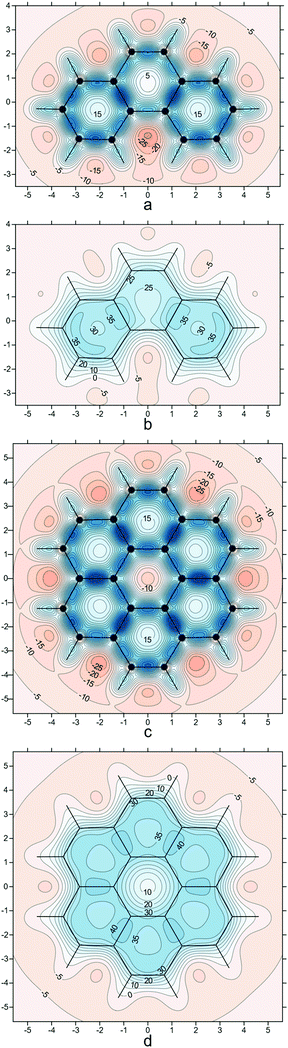Fig. 4 σ _zz (r) contour plots for phenanthrene (a and b) and coronene (c and d) in the respective molecular planes (a and c) and in planes 1 Å above the molecular planes (b and d), details as for Fig. 2i (results obtained during the work on but not included in ref. 21).

Whereas at first glance the σ_zz(r) contour plots look like accentuated versions of the σ_iso(r) contour plots in Fig. 1c–f, 2i and 3d, careful examination reveals some interesting and important differences. The deshielded “halos” around carbons observed in Fig. 1c and d have all but disappeared in Fig. 4a and c, which is an indication that the main contributions to these “halos” come from the in-plane components of the shielding tensor σ(r). The central ring in coronene includes a region of negative σ_zz(r) values (Fig. 4c); this is in line with ring current studies indicating the presence of a diamagnetic ring current along the ring formed by the 18 peripheral carbons and a weak paramagnetic ring current in the central ring.^5,37–39 On the other hand, at 1 Å above the molecular plane this region of negative σ_zz(r) values disappears completely (Fig. 4d) which suggests that it is due mainly to σ electron effects. The contour plot in Fig. 4c shows that NICS(0)_zz for the central ring in coronene is positive and over 15 ppm, which could be interpreted as an indication of local antiaromaticity; however, NICS(1)_zz for this ring is clearly negative (Fig. 4d) and, according to the computational data from ref. 21, so are NICS(0) and NICS(1) (see also Fig. 3d and ref. 40). However, NICS(0) is very small in magnitude, just −0.15 ppm and can change sign at another level of theory: A small positive NICS(0) value of 0.5 ppm has been reported at the B3LYP/cc-pVTZ//B3LYP/cc-pVTZ level.⁴¹ The more reliable NICS(1) and NICS(1)_zz indices and, especially, the contour plots in Fig. 3d and 4d indicate that the central ring in coronene is weakly aromatic.

Ring current plots^5,37–39 do not appear to include regions corresponding to the sizeable regions of negative σ_zz(r) values observed just outside the peripheral carbon rings in both phenanthrene and coronene (Fig. 4). There are no such regions in the σ_iso(r) contour plots if Fig. 2i and 3d, just very slightly deshielded areas surrounding both molecules. Another discrepancy, between the σ_zz(r) contour plots for coronene (Fig. 4c, d) and ring current studies, is associated with the regions of increased σ_zz(r) values (above 40 ppm in Fig. 4d) over radial (spoke) carbon–carbon bonds—as a result, one would expect to see strong currents over these bonds, but ring current plots indicate that there are next to no radial currents (see ref. 34 and references therein). The comparison between the σ_iso(r) and σ_zz(r) contour plots for phenanthrene at a height of 1 Å (Fig. 2i and 4b) shows that the former has certain interpretational advantages: The more aromatic peripheral rings are outlined better and there is a shielded region highlighting the most reactive site in phenanthrene which has no equivalent in the σ_zz(r) plot. Our conclusion derived from comparing the σ_iso(r) and σ_zz(r) contour plots for phenanthrene, coronene and other PAHs studied in ref. 21 is that it is simpler and more informative to work with the σ_iso(r) plots which retain relation to bonding, rather than with the σ_zz(r) plots which reflect some of the features of ring currents but prove more complicated to analyse. Still, as demonstrated by the plots in Fig. 4 and the work of other authors,^42–44σ_zz(r) and related plots remain a viable alternative when studying planar conjugated molecules. While we can choose between σ_iso(r) and σ_zz(r) contour plots when describing planar molecules, for nonplanar molecules we need to use σ_iso(r) isosurfaces. As an example, in Fig. 5 we show the σ_iso(r) = ±16 ppm isosurfaces for corannulene, a bowl-shaped PAH of C_5v symmetry.⁴⁵ Similarly to coronene, the shielding around the peripheral six-membered carbon rings follows closely the pattern observed in benzene (cf.Fig. 1a), which suggests strong bonding interactions and aromatic stability; once again, the spoke bonds are very well-shielded, in contrast to the findings of ring current studies which show next to no current density along these bonds.⁵ For a further example, see ref. 46 where σ_iso(r) isosurfaces are used in order to study bonding and aromaticity in another nonplanar molecule, norcorrole.

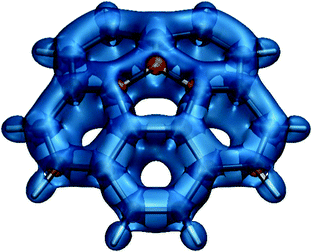Fig. 5 Isotropic shielding isosurfaces at σ_iso(r) = ±16 ppm (blue/orange) for corannulene recreated from shielding data computed using DFT for ref. 45, at the B3LYP-GIAO/6-311++G(d,p)//B3LYP-D3BJ/def2-TZVP level.

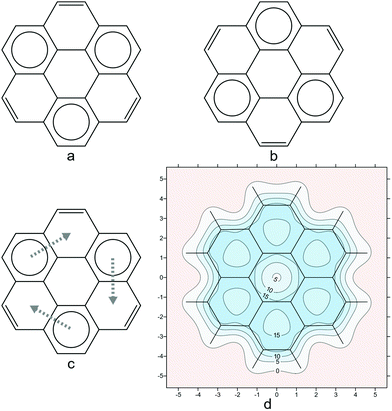
As a final example, we examine circumcoronene (Fig. 6). Circumcoronene has just one Clar form with seven disjoint sextets (Fig. 6a). The isotropic shielding plot in Fig. 6b reproduces the Clar picture in surprising detail, down to the positions of the peripheral carbon–carbon double bonds. However, the σ_iso(r) variations provide additional information which is not present in the Clar form: The local aromaticity of each of the peripheral sextets is higher than that of the central sextet—this is demonstrated by the regions with shielding over 20 ppm in each of the corresponding six-membered rings. This observation is supported by the various NICS values extracted from our shielding data, as well as by NICS results reported by other authors.⁴¹

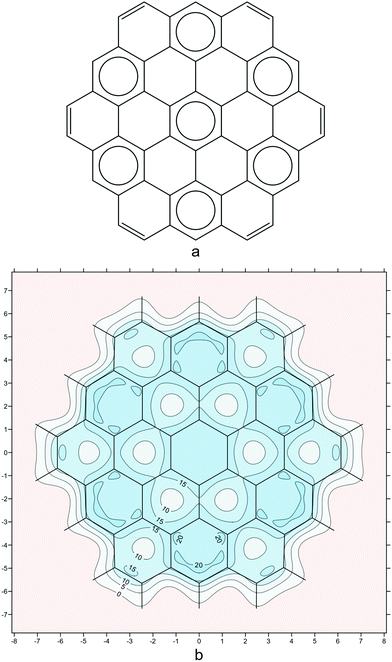Fig. 6 (a): the Clar form with seven disjoint sextets for circumcoronene; (b): isotropic shielding contour plot in a plane 1 Å above the molecular plane, details as for Fig. 2i (results obtained during the work on but not included in ref. 21).

4. Heteroaromaticity

It is hard to underestimate the importance of heteroaromatic compounds which are all around us—according to Balaban et al. “Among approximately 20 million chemical compounds identified by the end of the second millennium, more than two-thirds are fully or partially aromatic, and approximately half are heteroaromatic.”⁴⁷

Heteroaromaticity is more difficult to quantify than the aromaticity of conjugated carbocycles because, as a rule, there is “less” of it: For example, one qualitative measure of the degree of aromaticity of heterocycles is associated with their diene character manifested by their reactivity in Diels–Alder reactions and polymerizations. According to this measure, furan is less aromatic than pyrrole which, in turn, is less aromatic than benzene. As many biologically important compounds contain at least one of the five-membered heterocycles furan, pyrrole, thiophene, oxazole, imidazole and thiazole, the degrees of aromaticity of these heterocycles have been the subject of a number of investigations making use of different aromaticity criteria.^48–52 Isotropic shielding contour plots have been found to provide quantitative and yet easy-to-visualize pictures of heteroaromaticity in furan, pyrrole, thiophene, oxazole, imidazole and thiazole.^26,27

The contour plots included in Fig. 7 show clearly that the extent of isotropic shielding delocalization in these six five-membered heterocycles, in planes 1 Å above the respective molecular planes, increases in the order oxazole < furan < imidazole < pyrrole < thiazole < thiophene; arguably, aromaticity increases in the same order. Oxazole and furan are more difficulty to compare, as in oxazole the combined area enclosed by σ_iso(r) = 15 ppm contours is larger than that in furan; however, this is largely due to the presence of a nitrogen atom contributing one π electron (a similar effect is observed in imidazole and thiazole) and, on the other hand, the “hole” of σ_iso(r) < 10 ppm values near the centre of the ring is larger in oxazole. Finally, the contour plots reveal more localized diene character for furan than pyrrole and accordingly, furan is a more willing reaction partner in Diels–Alder chemistry than pyrrole.

Fig. 7 Relative aromaticities of furan, pyrrole, thiophene, oxazole, imidazole and thiazole suggested by the extent of shielding delocalization in the isotropic shielding contour plots in planes 1 Å above the respective molecular planes. All recreated from MP2-GIAO (second-order Møller–Plesset perturbation theory with GIAOs) shielding data at experimental or MP2(FC)/aug-cc-pVTZ geometries (“FC” stands for frozen-core) computed for ref. 26 and 27. σ_iso(r) in ppm.

The aromaticity ordering following from Fig. 7 makes good chemical sense as it is logical to expect that the introduction of a second heteroatom in furan, pyrrole and thiophene, yielding oxazole, imidazole and thiazole, respectively, would have, in each case, detrimental effect on aromaticity, as it restricts π electrons to smaller regions of increased activity. It is interesting to note that, according to the NICS(1) results for furan, pyrrole, thiophene, oxazole, imidazole and thiazole, extracted from the data used to construct Fig. 7,^26,27 the inclusion of a second heteroatom leads to a slight increase in the aromaticity of a five-membered heterocycle. This is not that surprising, taking into account the certain arbitrariness in the choice of the positions where NICS(1) are calculated, and the more general argument that the use of any NICS index is equivalent to reducing aromaticity, a global property, to a single numerical value. The two-dimensional nature of our approach, which is based on comparisons between the extents of isotropic shielding delocalization in planes 1 Å above the molecular planes, can be expected to provide more reliable and consistent results, especially when trying to differentiate between systems with similar levels of aromaticity such as the pairs furan and oxazole, pyrrole and imidazole and thiophene and thiazole.

5. Conclusions

When attempting to explain fuzzy concepts such as aromaticity and antiaromaticity one should always keep in mind the fact that chemists are visual creatures who are adept at discerning reactivity and chemical behaviour from pictures of molecular properties coming from experiment and theory, aided by various drawings, including resonance structures and curly arrow mechanisms. This was aptly described by Roald Hoffman as “People like pictures. Chemists live off of them.”⁵³ The isotropic magnetic shielding plots present visually appealing maps of areas featuring increases and decreases in electron activity that provide quantitative descriptions not just of local aromaticity but also of chemical bonding in general. For planar conjugated mono and polycyclic hydrocarbons and heterocyclic compounds the extent of isotropic shielding delocalization in the contour plots in a plane 1 Å above the molecular plane can be viewed as a highly sensitive visual two-dimensional aromaticity criterion which, while costlier to obtain computationally, has clear advantages over single-point NICS and one-dimensional aromatic ring chemical shielding (ARCS),⁵⁴ NICS-X-scan and NICS-XY-scan plots.^35,36

Coronene (Fig. 3) provides a suitable example for comparing isotropic shielding plots to other tools used to visualize the aromaticity of the whole molecule, such as the anisotropy of the induced current density (ACID)³⁹ and the gauge including magnetically induced current method (GIMIC).³⁸ It is difficult to think of a way in which the ACID and GIMIC pictures of magnetic ring currents in coronene could be associated directly with the migrating Clar sextets (Fig. 3a and b). ACID shows no π electron activity along radial carbon–carbon bonds³⁹ which makes much less chemical sense than the σ_iso(r) and σ_zz(r) results shown in Fig. 3d and 4d, respectively. The more complicated combination of diatropic and paratropic currents depicted in the GIMIC plot³⁸ is not straightforward to analyse; however, the integration of these currents should result in the shielding distribution surrounding coronene, a slice of which is shown in Fig. 3d. Ring currents are often referred to as subobservables⁵⁵ and, as a consequence, cannot be measured experimentally. On the other hand, the isotropic shielding σ_iso(r) is pinned, at atomic positions, to the nuclear shieldings which are experimentally measurable through chemical shifts.

In contrast to ring currents, obtaining the data used to construct isotropic shielding surfaces and contour plots does not require specialized computer codes and can be done with any computational package capable of calculating magnetic shielding tensors. For example, GAUSSIAN⁵⁶ can calculate shielding tensors at the HF-GIAO (Hartree–Fock wavefunction with GIAOs), DFT-GIAO and MP2-GIAO levels of theory, Dalton⁵⁷ can perform this task for CASSCF-GIAO wavefunctions, CFOUR⁵⁸ can calculate HF-GIAO, MP2-GIAO, MP3-GIAO and MP4-GIAO shielding tensors, as well as shielding tensors at several coupled-cluster levels of theory, CC2-GIAO, CCD-GIAO, QCISD-GIAO, CCSD-GIAO, QCISD(T)-GIAO, CCSD(T-GIAO), CCSDT-n-GIAO (n = 1–4), CC3-GIAO, CCSDT-GIAO. As a result, it is possible to calculate isotropic shielding surfaces and contour plots including non-dynamic and dynamic electron correlation effects. Of course, the computational expense associated with shielding calculations utilizing CASSCF-GIAO wavefunctions with large active spaces, Møller–Plesset perturbation theory of order higher than two and coupled-cluster approaches beyond CC2 or CCD would be prohibitive for all but very small molecules. However, computational experience suggests that the inclusion of dynamic electron correlation effects and the use of larger basis sets affect mainly shielding tensors at nuclear or close to nuclear positions; away from nuclei it proves sufficient to use lower levels of theory and smaller basis sets.

The availability of a CASSCF-GIAO code in Dalton allows the calculation of NICS, isotropic shielding surfaces and contour plots for the low-lying excited states of cyclic conjugated systems; this has made it possible to extend Baird's rule,⁵⁹ which states that Hückel's 4n + 2/4n criteria for electronic ground state aromaticity in cyclic conjugated hydrocarbons are switched in the lowest triplet state, with rings with 4n π electrons becoming aromatic and those with 4n + 2 π electrons ending up as antiaromatic, to the lowest singlet excited state.^15,60,61 Excited state aromaticity switching has been shown to have important implications for excited-state intramolecular proton transfers.⁶²

Whereas triplet antiaromatic electronic states can be described reasonably well using spin-unrestricted approaches such as UHF and UDFT, singlet antiaromatic electronic states require at least a two-configuration wavefunction. It has been shown that a simple “two electrons in two orbitals” CASSCF(2,2)-GIAO wavefunction can be sufficient for obtaining qualitative correct results for the first singlet excited state of larger molecules.⁶³

The versatile nature of isotropic shielding surfaces and contour plots which combine quantitative assessments of differences in aromaticity and bonding for both ground and excited state molecules make these plots a valuable tool for rationalizing aromatic behaviour and molecular structure in general.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

B. V. wishes to acknowledge the National Science Foundation, Division of Chemistry (grant 1848261) for support.

Notes and references

1. C. E. Johnson and F. A. Bovey, J. Chem. Phys., 1958, 29, 1012–1014.
2. P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
3. P. v. R. Schleyer, M. Manoharan, Z. X. Wang, B. Kiran, H. Jiao, R. Puchta and N. J. R. van Eikema Hommes, Org. Lett., 2001, 3, 2465–2468.
4. I. Cernusak, P. W. Fowler and E. Steiner, Mol. Phys., 2000, 98, 945–953.
5. E. Steiner, P. W. Fowler and L. W. Jenneskens, Angew. Chem., Int. Ed., 2001, 40, 362–366.
6. H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Org. Lett., 2006, 8, 863–866.
7. K. J. Wolinski, Chem. Phys., 1997, 106, 6061–6067.
8. S. Klod and E. J. Kleinpeter, J. Chem. Soc., Perkin Trans. 2, 1989, 1893–1898.
9. E. Kleinpeter, S. Klod and A. Koch, THEOCHEM, 2007, 811, 45–60.
10. E. Kleinpeter and A. Koch, Phys. Chem. Chem. Phys., 2012, 14, 8742–8746.
11. E. Kleinpeter and A. Koch, J. Phys. Chem. A, 2012, 116, 5674–5680.
12. N. H. Martin, D. M. Loveless and D. C. Wade, J. Mol. Graphics Modell., 2004, 23, 285–290.
13. N. H. Martin, M. R. Teague and K. H. Mills, Symmetry, 2010, 2, 418–436.
14. N. H. Martin and J. D. Robinson, J. Mol. Graphics Modell., 2012, 38, 26–30.
15. P. B. Karadakov, P. Hearnshaw and K. E. Horner, J. Org. Chem., 2015, 81, 11346–11352.
16. P. B. Karadakov, M. A. H. Al-Yassiri and D. L. Cooper, Chem. – Eur. J., 2018, 24, 16791–16803.
17. R. F. W. Bader, Atoms in Molecules - A Quantum Theory, Oxford University Press, Oxford, 1990.
18. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
19. A. Savin, R. Nesper, S. Wengert and T. E. Fässler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832.
20. P. B. Karadakov and K. E. Horner, J. Chem. Theory Comput., 2016, 12, 558–563.
21. B. J. Lampkin, P. B. Karadakov and B. VanVeller, Angew. Chem., Int. Ed., 2020, 59, 19275–19281.
22. P. Muller, Pure Appl. Chem., 1994, 66, 1077–1184 ; see also https://goldbook.iupac.org/terms/view/A00441.
23. A. A. Frost and B. Musulin, J. Chem. Phys., 1953, 21, 572–573.
24. M. Eckert-Maksić, M. Vazdar, M. Barbatti, H. Lischka and Z. B. Maksić, J. Chem. Phys., 2006, 125, 064310.
25. P. B. Karadakov and K. E. Horner, J. Phys. Chem. A, 2013, 117, 518–523.
26. K. E. Horner and P. B. Karadakov, J. Org. Chem., 2013, 78, 8037–8043.
27. K. E. Horner and P. B. Karadakov, J. Org. Chem., 2015, 80, 7150–7157.
28. P. B. Karadakov, M. Di and D. L. Cooper, J. Phys. Chem. A, 2020, 124, 9611–9616.
29. R. K. Jinger, H. Fliegl, R. Bast, M. Dimitrova, S. Lehtola and D. Sundholm, J. Phys. Chem. A, 2021, 125, 1778–1786.
30. D. L. Cooper, J. Gerratt and M. Raimondi, Nature, 1986, 323, 699–701.
31. J. Gerratt, Chem. Br, 1987, 23, 327–329.
32. E. Clar, Polycyclic Hydrocarbons, Springer, Berlin, Heidelberg, 1964, vol. 1.
33. E. Clar, Polycyclic Hydrocarbons, Springer, Berlin, Heidelberg, 1964, vol. 2.
34. E. Clar, The Aromatic Sextet, Wiley, London, New York, Sydney, Toronto, 1972.
35. A. Kumar, M. Duran and M. Solà, J. Comput. Chem., 2017, 38, 1606–1611.
36. R. Gershoni-Poranne and A. Stanger, Chem. – Eur. J., 2014, 20, 5673–5688.
37. S. Fias, P. W. Fowler, J. L. Delgado, U. Hahn and P. Bultinck, Chem. – Eur. J., 2008, 14, 3093–3099.
38. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518.
39. D. Geuenich, K. Hess, F. Köhler and R. Herges, Chem. Rev., 2005, 105, 3758–3772.
40. A. Ciesielski, M. K. Cyrański, T. M. Krygowski, P. W. Fowler and M. Lillington, J. Org. Chem., 2006, 71, 6840–6845.
41. I. A. Popov and A. I. Boldyrev, Eur. J. Org. Chem., 2012, 3485–3491.
42. G. Merino, T. Heine and G. Seifert, Chem. – Eur. J., 2004, 10, 4367–4371.
43. T. Heine, C. Corminboeuf and G. Seifert, Chem. Rev., 2005, 105(10), 3889–3910.
44. T. Heine, R. Islas and G. Merino, J. Comput. Chem., 2007, 28, 302–309.
45. P. B. Karadakov, Chemistry, 2021, 3, 861–872.
46. P. B. Karadakov, Org. Lett., 2020, 22, 8676–8680.
47. A. T. Balaban, D. C. Oniciu and A. R. Katritzky, Chem. Rev., 2004, 104, 2777–2812.
48. C. W. Bird, Tetrahedron, 1985, 41, 1409–1414.
49. K. Jug and A. M. Koster, J. Phys. Org. Chem., 1991, 4, 163–169.
50. A. R. Katritzky, M. Karelson, S. Sild, T. M. Krygowski and K. Jug, J. Org. Chem., 1998, 63, 5228–5231.
51. M. K. Cyrański, T. M. Krygowski, A. R. KatritSchleyerzky and P. v. R. Schleyer, J. Org. Chem., 2002, 67, 1333–1338.
52. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888.
53. R. Hoffmann, in Roald Hoffmann on the Philosophy, Art, and Science of Chemistry, ed. J. Kovac and M. Weisberg, Oxford University Press, New York, 2012.
54. J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 1999, 1, 3429–3435.
55. J. O. Hirschfelder, J. Chem. Phys, 1978, 68, 5151–5162.
56. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016; see also http://gaussian.com.
57. K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansik, H. J. Aa. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. Rybkin, P. Salek, C. C. M. Samson, A. Sánchez de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 ; see also http://daltonprogram.org.
58. D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108 (1–35); R57, Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package by J. F. Stanton, J. Gauss, L. Cheng, M. E. Harding, D. A. Matthews, P. G. Szalay with contributions from A. A. Auer, A. Asthana, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, S. Blaschke, Y. J. Bomble, S. Burger, O. Christiansen, D. Datta, F. Engel, R. Faber, J. Greiner, M. Heckert, O. Heun, M. Hilgenberg, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, T. Kirsch, K. Klein, G. M. Kopper, W. J. Lauderdale, F. Lipparini, J. Liu, T. Metzroth, L. A. Mück, T. Nottoli, D. P. O'Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J.D. Watts and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen; see also http://www.cfour.de.
59. N. C. Baird, J. Am. Chem. Soc., 1972, 94, 4941–4948.
60. P. B. Karadakov, J. Phys. Chem. A, 2008, 112, 7303–7309.
61. P. B. Karadakov, J. Phys. Chem. A, 2008, 112, 12707–12713.
62. B. J. Lampkin, Y. H. Nguyen, P. B. Karadakov and B. VanVeller, Phys. Chem. Chem. Phys., 2019, 21, 11608–11614.
63. P. B. Karadakov and S. Saito, Angew. Chem., Int. Ed., 2020, 59, 9228–9230.

---