DOI:
10.1039/D1CC02579A
(Communication)
Chem. Commun., 2021,
57, 8264-8267
Direct enantiomeric discrimination through antisymmetric hyperfine coupling†‡
Received
17th May 2021
, Accepted 23rd June 2021
First published on 29th July 2021
Abstract
Chiral open-shell molecules possessing permanent electric dipole moments have an EPR signal at the difference frequency of the electron and nuclear resonances, allowing direct enantiomeric discrimination by signal phase. The effect depends on the vector antisymmetry of the hyperfine coupling. Quantum chemistry suggests chiral bisfluorene methyl radical derivatives as promising for experiments.
The hyperfine coupling (HFC) between the spins of an unpaired electron and a nucleus provides important information about the molecular structure and interactions.1,2 However, the techniques used in electron paramagnetic resonance (EPR) spectroscopy can so far only indirectly be applied to distinguish the enantiomers of chiral molecules, e.g., by transforming the molecule to a diastereoisomeric entity by chiral environment such as a gel or a chiral solvent, or by conducting a reaction with a chiral derivatizing agent.3,4 In this letter we propose a new effect that allows direct chiral discrimination from the vector of antisymmetric HFC, A*. Typically the sensitivity of measurements of the electron spin transitions surpasses that of nuclear transitions by several orders of magnitude.5 Thus, the effect caused by A* puts us in a good position to achieve direct sensitivity to chirality in EPR. Ref. 6–11 discuss other chirality-sensitive nuclear spin effects. An alternative possibility provided by the chiral-induced spin selectivity effect (CISS) is presented in ref. 12 and 13.
The spin Hamiltonian 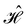 for an unpaired electron S interacting with a
for an unpaired electron S interacting with a  nucleus I,14
nucleus I,14
| |  | (1) |
includes the HFC of the corresponding spin operators
Ŝ and
Î,
| |  | (2) |
and the Zeeman interactions with the magnetic field
B0:
| |  | (3) |
| |  | (4) |
Here,
A (in MHz) is the HFC tensor, and
gS and
gI are the
g-tensors of
S and
I. Overlooking the very small parity non-conservation effects,
15eqn (1) holds for both enantiomers.
For a liquid sample of molecules with permanent electric dipole μe, its isotropic average due to  at temperature T is
at temperature T is
| |  | (5) |
with
Ω denoting the molecular orientation and assuming that the eigenvalues of
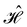
are small compared to
kBT, and hence,
| | | 〈μce〉 = 〈μc,Ae〉 + 〈μc,Be〉, | (6) |
| | | 〈μc,Be〉 = (μBgcSŜ + μNgcIÎ) × B0. | (8) |
with the pseudoscalars
| |  | (9) |
| |  | (10) |
| |  | (11) |
The two-index tensors
A,
gS, and
gI can be decomposed as the sums of three irreducible tensors: the rank-0 isotropic (
e.g.,
Aiso), the rank-1 antisymmetric (
Aanti) and the rank-2 (traceless) symmetric (
Asym) parts.
16 We have in
eqn (9)–(11) expressed
Aanti as the vector
A* whose components are

.
While μe is a polar vector, A* is axial, since the part of the Hamiltonian  relevant to A* transforms under inversion as A*·(Ŝ × Î) →(−A*)·{−[(−Ŝ) × (−Î)]}.17 Therefore, the product μe·A* changes its sign under mirror reflection of the molecule and, consequently, the pseudoscalar Ac has opposite signs for enantiomers. It follows that, in an achiral dipolar molecule, μe·A* = 0, hence μe and A* are perpendicular to each other and Ac = 0. The same applies to the pseudoscalars gcS and gcI drawn from the g-tensors gS and gI (Fig. 1A).
relevant to A* transforms under inversion as A*·(Ŝ × Î) →(−A*)·{−[(−Ŝ) × (−Î)]}.17 Therefore, the product μe·A* changes its sign under mirror reflection of the molecule and, consequently, the pseudoscalar Ac has opposite signs for enantiomers. It follows that, in an achiral dipolar molecule, μe·A* = 0, hence μe and A* are perpendicular to each other and Ac = 0. The same applies to the pseudoscalars gcS and gcI drawn from the g-tensors gS and gI (Fig. 1A).
 |
| | Fig. 1 (A) Permanent electric dipole moment (μe) and the vector antisymmetries of the hyperfine coupling tensor (A*) and g-tensors of the electron and the  nucleus ( nucleus ( and and  ) for a chiral molecule and its mirror image. (B) Expected signals of the enantiomers due to the precession of the magnetization (M, red color) and the oscillation of the chirality-sensitive electric polarization (PcA, blue, and PcB, green) for two different initial states of the spin system. The total signal shown in black. ) for a chiral molecule and its mirror image. (B) Expected signals of the enantiomers due to the precession of the magnetization (M, red color) and the oscillation of the chirality-sensitive electric polarization (PcA, blue, and PcB, green) for two different initial states of the spin system. The total signal shown in black. | |
When a sample is excited by electromagnetic field, the observed signal  arises from the electron and nuclear magnetization
arises from the electron and nuclear magnetization
| |  | (12) |
and the chirality-sensitive electric polarization
| |  | (13) |
Here,
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif)
is the number density of the molecules and
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif)
(
t) is the density matrix of the spin system. The expected signal is proportional to the time derivative of the magnetization
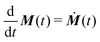
and the polarization

as
| |  | (14) |
B1 and
E1 are the amplitude vectors of the magnetic and electric field, respectively, which can be generated by the detector at frequency
ν.
18 The integration is over the volume of the sample.
Assume B0 along the laboratory z axis. Due to the vector products in eqn (7) and (8), the observation of Pc is only possible for states whose spin vectors have a non-vanishing component perpendicular to B0 (e.g., Ŝy) or possess mutually perpendicular components (e.g., ŜyÎx).
The time-dependence of the density operator ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) (t) is found by solving the Liouville–von Neumann equation
(t) is found by solving the Liouville–von Neumann equation
| |  | (15) |
with the appropriate initial condition
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif)
(0). At high field, the Hamiltonian [
eqn (1)] can be approximated as
| | 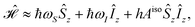 | (16) |
where
ħωS = −
μBgisoSB0 and
ħωI = −
μNgisoIB0.
19 Let us next consider two experiments beginning from the thermal equilibrium
| | ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) eq = 1/4 + 〈Ŝz〉eqŜz + 〈Îz〉eqÎz + 〈ŜzÎz〉eqŜzÎz, eq = 1/4 + 〈Ŝz〉eqŜz + 〈Îz〉eqÎz + 〈ŜzÎz〉eqŜzÎz, | (17) |
where 〈
Ŝz〉
eq = −
ħωS/(4
kBT), 〈
Îz〉
eq = −
ħωI/(4
kBT), and 〈
ŜzÎz〉
eq = −
hAiso/(4
kBT).
Case I. A  pulse of the B1 field on
pulse of the B1 field on ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) eq generates the state
eq generates the state
| | ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) 1(0) = −〈Ŝz〉eqŜy + 〈Îz〉eqÎz − 〈ŜzÎz〉eqŜyÎz. 1(0) = −〈Ŝz〉eqŜy + 〈Îz〉eqÎz − 〈ŜzÎz〉eqŜyÎz. | (18) |
Solving
eqn (15) one finds
| | ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) 1(t) = [cos(πAisot) 1(t) = [cos(πAisot)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωSt)Ŝx + sin(πAisot) sin(ωSt)Ŝx + sin(πAisot)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωSt)ŜxÎz] 〈Ŝz〉eq +… cos(ωSt)ŜxÎz] 〈Ŝz〉eq +… | (19) |
with the detection defined by
B1 =
B1ex and
E1 =
E1ey,
Mx and
Pcy in
eqn (12) and (13) may contribute to the signal. In
eqn (19), both terms that (i) do not contribute to
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif)
(
ν) and/or (ii) are much smaller than 〈
Ŝz〉
eq,
i.e., proportional to 〈
ŜzÎz〉
eq, are omitted. Then, the expected signal is
| |  | (20) |
The signals of
Pc appear at the same frequencies as
M, forcing discrimination between the two require the measurement of the amplitude difference of the components of the EPR doublet (
Fig. 1B, the first spectrum).
Case II. For a different initial spin state
| | ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) 2(0) = −〈Ŝz〉eqŜyÎx + 〈Îz〉eqÎx − 〈ŜzÎz〉eqŜy, 2(0) = −〈Ŝz〉eqŜyÎx + 〈Îz〉eqÎx − 〈ŜzÎz〉eqŜy, | (21) |
which can be obtained by applying the pulse sequence

on
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) eq
eq, one finds the density matrix
| |  | (22) |
If the electric field detection is changed into
E1 =
E1ez, the signal becomes
| | 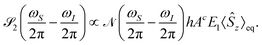 | (23) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) 2
2(
t) only generates signal of the chirality-sensitive
PcA at the difference frequency
ωS −
ωI. This allows to distinguish the postulated chirality-sensitive effect from other, nonchiral effects.
PcA has the same direction as
B0 (
Fig. 1B, the second spectrum).
The phases and amplitudes of B1 and E1 depend on the particular experimental implementation (see ref. 20 for examples). If the electronic relaxation time is long in comparison with the  pulse, one can presume that the case II, i.e.,
pulse, one can presume that the case II, i.e., ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) 2(0) ∝ ŜyÎx, represents a promising initial state. Spin relaxation toward the thermodynamic equilibrium causes Ŝz and Îz to appear. However, being parallel to B0, they do not generate any observable signals. One can hypothesize the inverse effect to that described above, i.e., that excitation by oscillating electric field would cause changes of the spin state that are dependent on the molecular chirality. Observing the inverse effect would be, however, complicated by dielectric heating since, due to the smallness of chirality-sensitive effects, an electric field of high amplitude is required.
2(0) ∝ ŜyÎx, represents a promising initial state. Spin relaxation toward the thermodynamic equilibrium causes Ŝz and Îz to appear. However, being parallel to B0, they do not generate any observable signals. One can hypothesize the inverse effect to that described above, i.e., that excitation by oscillating electric field would cause changes of the spin state that are dependent on the molecular chirality. Observing the inverse effect would be, however, complicated by dielectric heating since, due to the smallness of chirality-sensitive effects, an electric field of high amplitude is required.
We study neutral organic radicals depicted in Fig. 2: nitroxyls, i.e., 2,2,6,6-tetramethyl-1-piperidinyloxy (1a; TEMPO), the TEMPO derivative of (R)-alanine [(R)-1b], 1,3,5-trimethyl-6-oxoverdazyl (2a), and the verdazyl derivative of (R)-phenylalanine [(R)-2b], as well as carbon-centered radicals: triphenylmethyl (3a), bis(fluoren-9-yl)methyl (3b), and bisfluorene methyl derivative of (R)-alanine [(R)-3c]. 3a and 3b, whose rigid structures are non-superposable on their mirror images, do not exhibit chiral properties due to fast interconversion of their enantiomers. Chiral samples are 1b, 2b, and 3c.
 |
| | Fig. 2 Antisymmetric parts of the hyperfine coupling tensors A* and permanent electric dipole moments μe of the studied radicals. | |
The molecular structures were computationally optimized as described in ESI.‡ The A tensors were calculated using unrestricted density-functional theory (DFT) at the fully relativistic matrix-Dirac–Kohn–Sham (mDKS) level21,22 on the ReSpect code,23,24 using mainly the PBE0 hybrid functional25 and the pcH-2 large-component basis sets of ref. 26. See ESI‡ for further details. The results of computed eigenvalues of A are in a reasonable agreement which literature (Table S9 in the ESI‡). The experiments have been at various temperatures and physical states, whereas the computations were performed for single molecules at the equilibrium geometry in vacuo. However, such differences can easily be masked by the dependence of A on the chosen functional.27,28
In contrast to the antisymmetry gS* of the electronic g-tensor, which is a few times larger than the nuclear gI* (Tables S10 and S11 in ESI‡ and ref. 29, 30), the antisymmetry A* of the HFC tensor is larger by about three orders of magnitude than the antisymmetric part of the indirect spin–spin coupling tensor in diamagnetic molecules.31 The direction of A* and its magnitude are mainly determined by the local electronic structure of the molecule and vary weakly when a chiral substituent is placed in a distal position with respect to the maximum of the unpaired electron density (Table 1; all components of HFC tensors and dipole moments are given in Tables S12–S20 of the ESI‡). E.g., AN* of the nitroxyl nitrogen and AC* of the adjacent carbons differ by less than 1% in 1a and (R)-1b. Similarly, the antisymmetries AN* of radicals 2a and (R)-2b are almost unaffected by the chiral amino acid substituent.
Table 1 Permanent electric dipole moment μe (D), the isotropic part Aiso (MHz) and the length of antisymmetry vector, A* (kHz), of the hyperfine coupling tensor, and the pseudoscalar Ac (µHz m V−1). Ac is only listed for chiral species whose enantiomers do not interconvert in solution
| Radical |
μ
e
|
Nucleus/position |
A
iso
|
A
*
|
A
c
|
|
1a
|
3.03 |
15N |
−51.3 |
161.8 |
|
13![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) NO˙ NO˙ |
−9.4 |
203.8 |
|
| (R)-syn-1b |
4.85 |
15N |
−51.4 |
166.9 |
−30.5 |
13![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) NO˙ NO˙ |
−9.6 |
199.9 |
27.3 |
| (R)-anti-1b |
4.80 |
15N |
−51.6 |
166.9 |
49.4 |
13![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) NO˙ NO˙ |
−9.5 |
200.2 |
−31.5 |
|
2a
|
1.12 |
15N |
−22.6 |
46.4 |
|
| (R)-2b |
2.23 |
15N |
−22.6 |
49.5 |
2.3 |
|
13C |
−32.5 |
21.9 |
−8.3 |
|
3a
|
0.000193 |
13C |
−11.2 |
9.8 |
|
|
3b
|
0.0375 |
13![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) C˙H C˙H |
40.7 |
12.2 |
|
| CC˙1H |
42.8 |
23.3 |
|
| (R)-3c |
2.69 |
13![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) C˙C C˙C |
43.3 |
13.5 |
−6.4 |
C13![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ˙C ˙C |
−40.7 |
11.3 |
4.4 |
CC13˙![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) |
43.7 |
15.9 |
6.9 |
Chiral substituent may noticeably change the permanent electric dipole μe. For an achiral molecule, μe is perpendicular to A* [eqn (9)]. The sum of the scalar products μe·A* of two equivalent nuclei may vanish also in a chiral system. E.g., in 1a (Fig. 2), μe is in the σv plane of the molecule, whereas  of the nitroxyl nitrogen is perpendicular to that plane. While the
of the nitroxyl nitrogen is perpendicular to that plane. While the  and
and  of the adjacent carbons are not perpendicular to the σv plane, their projections onto this plane cancel, and the overall chirality-sensitive effect vanishes. However, if the molecule were isotopically 13C-labeled at the C position with 12C at the C′ position, 1a would be chiral and the predicted effect might be observed.
of the adjacent carbons are not perpendicular to the σv plane, their projections onto this plane cancel, and the overall chirality-sensitive effect vanishes. However, if the molecule were isotopically 13C-labeled at the C position with 12C at the C′ position, 1a would be chiral and the predicted effect might be observed.
To maximize Ac, one has to orient the chiral substituent such that μe is maximally parallel to A*. For (R)-1b, the (R)-alanine substituent is placed at the opposite site to the nitroxyl group and its presence causes a tilt of μe. However, (R)-1b has two dominating conformers: syn with the carbonyl oxygen atom nearby the CH3 group and anti, where the CO and CH3 groups are distant (Fig. S1 in ESI‡). The dipole moments μe of the two conformers are oppositely tilted, thus AcN,syn ≈ −AcN,anti and the chirality-sensitive effect is greatly suppressed. While AcC and  cancel out entirely for the isotopically unsubstituted molecule (vide supra), the effect of the substitution on AisoC is of the order of a fraction of MHz and, therefore, the chiral signal would presumably average to almost zero. A similar result is obtained for the nitrogen atoms of (R)-2b.
cancel out entirely for the isotopically unsubstituted molecule (vide supra), the effect of the substitution on AisoC is of the order of a fraction of MHz and, therefore, the chiral signal would presumably average to almost zero. A similar result is obtained for the nitrogen atoms of (R)-2b.
Comparison of 3a and 3b with (R)-3c shows that the carbon-centered radicals require a chiral substituent that ensures a sufficiently large μe.  of 3b is only weakly affected by the (R)-alanine group but, due to more favorable orientation of μe with respect to
of 3b is only weakly affected by the (R)-alanine group but, due to more favorable orientation of μe with respect to  , AcC reaches a much higher amplitude of 10–15 kHz. In this case, the amplitude of the expected chiral effect is at last 5 nHz m V−1, meaning that its detection by the equipment currently used in electron-nucleus double resonance experiments is feasible. When X-band
, AcC reaches a much higher amplitude of 10–15 kHz. In this case, the amplitude of the expected chiral effect is at last 5 nHz m V−1, meaning that its detection by the equipment currently used in electron-nucleus double resonance experiments is feasible. When X-band  or W-band (
or W-band ( ) EPR is applied, the signal of PcA will not overlap with any residual standard EPR signal, which could be present due to the finite purity of the desired initial state, i.e., −SyIx.
) EPR is applied, the signal of PcA will not overlap with any residual standard EPR signal, which could be present due to the finite purity of the desired initial state, i.e., −SyIx.
A further advantage of the 3c over 1b or 2b is the more efficient generation of the initial spin state, since the expected relaxation time of 3c is approx. 10 µs based on T2 for an unsubstituted 3c.32 This is comparable with the length of the π/2 pulse, whereas the typical TEMPO relaxation time does not exceed several dozen ns. Assuming that the ratio between the electric and magnetic fields of the detector is cB1/E1= 103 and selectively 13C-enriched 3c, one finds that the amplitude of the expected chirality-sensitive signal of PcA is of the order of 10−4 of the standard EPR signal.
To conclude, it is predicted that with a suitably chosen initial spin state, the electron-nucleus system generates an electric polarization Pc whose phase directly identifies the handedness of the molecule. Pc oscillates at the difference frequency of the electron and nuclear resonances in the direction of the main, static magnetic field. Largest magnitude of the effect is obtained if the permanent electric dipole and the antisymmetric HFC tensor, represented as a vector, are parallel to each other. This condition is fulfilled by a chiral derivative of bisfluorene 3c, which is a good candidate for forthcoming experiments. We believe that the predicted effect has potential for EPR investigations of chiral systems.
PG acknowledges the National Science Centre, Poland, for the financial support through OPUS 16 Grant No. 2018/31/B/ST4/02570 and Bartosz Kreft (U. Warsaw) for his help in computations. JV has received funding from the Academy of Finland (grant 331008) and U. Oulu (Kvantum Institute). Computations were carried at CSC-the Finnish IT Centre for Science and the Finnish Grid and Cloud Infrastructure project (persistent identifier urn:nbn:fi:research-infras-2016072533).
Note added after first publication
This article replaces the version published on 29th July 2021, which contained errors in eqn (2), (3), (4), (7), (8) and (9).
Conflicts of interest
There are no conflicts to declare.
Notes and references
- K. Möbius, W. Lubitz, N. Cox and A. Savitsky, Magnetochemistry, 2018, 4, 50 CrossRef.
- M. M. Roessler and E. Salvadori, Chem. Soc. Rev., 2018, 47, 2534–2553 RSC.
- H. B. Stegmann, H. Wendel, H. Dao-Ba, P. Schuler and K. Scheffer, Angew. Chem., Int. Ed. Engl., 1986, 25, 1007–1008 CrossRef.
- C. D. Stevenson, A. L. Wilham and E. C. Brown, J. Phys. Chem. A, 1998, 102, 2999–3001 CrossRef CAS.
-
G. A. Rinard, R. W. Quine, S. S. Eaton and G. R. Eaton, in Frequency Dependence of EPR Sensitivity, ed. L. J. Berliner and C. J. Bender, Springer US, Boston, MA, 2004, p. 118 Search PubMed.
- P. Garbacz and A. D. Buckingham, J. Chem. Phys., 2016, 145, 204201 CrossRef CAS PubMed.
- A. D. Buckingham, J. Chem. Phys., 2014, 140, 011103 CrossRef PubMed.
- P. Garbacz, J. Chem. Phys., 2016, 145, 224202 CrossRef PubMed.
- J. P. King, T. F. Sjolander and J. W. Blanchard, J. Phys. Chem. Lett., 2017, 8, 710–714 CrossRef CAS PubMed.
- A. Soncini and S. Calvello, Phys. Rev. Lett., 2016, 116, 163001 CrossRef PubMed.
- S. Calvello and A. Soncini, Phys. Chem. Chem. Phys., 2020, 22, 8427–8441 RSC.
- R. Naaman, Y. Paltiel and D. Waldeck, Nat. Rev. Chem., 2019, 3, 250–260 CrossRef CAS.
- R. Naaman and D. Waldeck, Annu. Rev. Phys. Chem., 2015, 66, 263–281 CrossRef CAS PubMed.
-
A. Schweiger and G. Jeschke, Principles of pulse electron paramagnetic resonance, Oxford University Press, Oxford, 2001, p. 29 Search PubMed.
- A. L. Barra and J. B. Robert, Mol. Phys., 1996, 88, 875–886 CrossRef CAS.
-
D. A. Varshalovich, A. N. Moskalev and V. K. Khersonskii, Quantum Theory of Angular Momentum, World Scientific, 1989, p. 63 Search PubMed.
- We found by quantum-chemical computations that the relation A*′ = det(R)RA* of the pseudovector transformation holds (R is a rotation matrix of radical coordinates). Thus, the coupling of the electron spin with molecular rotation may be neglected.
- The signal depends on the sensitivity of the detector to the excitation by Ṁ and Ṗc. According to the reciprocity theorem, the sensitivity is proportional to the magnitude of the field that the detector would generate if voltage of the same amplitude as observed would be used for exciting the detector.
- For an electron, gS < 0, thus the angular frequency ωS > 0 and the spin S precesses anticlockwise according to the right-hand rule. The reverse is true for a nucleus with gI > 0 (such as 1H and 13C); in this case the angular frequency ωI < 0, i.e., the spin I precesses clockwise.
-
E. Reijerse and A. Savitsky, EPR Spectroscopy: Fundamentals and Methods, Wiley, 2018, pp. 242–251 Search PubMed.
- E. Malkin, M. Repiský, S. Komorovský, P. Mach, O. Malkina and V. G. Malkin, J. Chem. Phys., 2011, 134, 044111 CrossRef PubMed.
- S. Gohr, P. Hrobárik, M. Repiský, S. Komorovský, K. Ruud and M. Kaupp, J. Phys. Chem. A, 2015, 119, 12892–12905 CrossRef CAS PubMed.
- M. Repiský, S. Komorovský, M. Kadek, U. Konecny, L. Ekström, E. Malkin, M. Kaupp, K. Ruud, O. L. Malkina and V. G. Malkin, J. Chem. Phys., 2020, 152, 184101 CrossRef PubMed.
-
M. Repisky, S. Komorovsky, V. G. Malkin, O. L. Malkina, M. Kaupp and K. Ruud, ReSpect, version 5.1.0 ( 2019); Relativistic Spectroscopy DFT program, with contributions from R. Bast, U. Ekström, M. Kadek, S. Knecht, L. Konecny, E. Malkin and I. Malkin-Ondik. See http://www.respectprogram.org.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- P. Jakobsen and F. Jensen, J. Chem. Phys., 2019, 151, 174107 CrossRef PubMed.
- M. Bühl, Chem. Phys. Lett., 1997, 267, 251–257 CrossRef.
- J. Vaara, Phys. Chem. Chem. Phys., 2007, 9, 5399–5418 RSC.
- P. Garbacz, J. Cukras and M. Jaszuński, Phys. Chem. Chem. Phys., 2015, 17, 22642–22651 RSC.
- A. D. Buckingham, P. Lazzeretti and S. Pelloni, Mol. Phys., 2015, 113, 1780–1785 CrossRef CAS.
- P. Garbacz, Mol. Phys., 2018, 116, 1397–1408 CrossRef CAS.
- V. Meyer, S. S. Eaton and G. R. Eaton, Appl. Magn. Reson., 2014, 45, 993–1007 CrossRef CAS.
Footnotes |
| † This article is dedicated to the memory of Prof. A. D. Buckingham (1930–2021), whose theoretical research laid the foundation for the magnetic resonance spectroscopy of chiral molecules. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cc02579a |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
Juha
Vaara
*a and
Juha
Vaara
 b
b
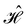 for an unpaired electron S interacting with a
for an unpaired electron S interacting with a  nucleus I,14
nucleus I,14



 at temperature T is
at temperature T is
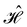 are small compared to kBT, and hence,
are small compared to kBT, and hence, 


 .
.
 relevant to A* transforms under inversion as A*·(Ŝ × Î) →(−A*)·{−[(−Ŝ) × (−Î)]}.17 Therefore, the product μe·A* changes its sign under mirror reflection of the molecule and, consequently, the pseudoscalar Ac has opposite signs for enantiomers. It follows that, in an achiral dipolar molecule, μe·A* = 0, hence μe and A* are perpendicular to each other and Ac = 0. The same applies to the pseudoscalars gcS and gcI drawn from the g-tensors gS and gI (Fig. 1A).
relevant to A* transforms under inversion as A*·(Ŝ × Î) →(−A*)·{−[(−Ŝ) × (−Î)]}.17 Therefore, the product μe·A* changes its sign under mirror reflection of the molecule and, consequently, the pseudoscalar Ac has opposite signs for enantiomers. It follows that, in an achiral dipolar molecule, μe·A* = 0, hence μe and A* are perpendicular to each other and Ac = 0. The same applies to the pseudoscalars gcS and gcI drawn from the g-tensors gS and gI (Fig. 1A). arises from the electron and nuclear magnetization
arises from the electron and nuclear magnetization

![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) is the number density of the molecules and
is the number density of the molecules and ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) (t) is the density matrix of the spin system. The expected signal is proportional to the time derivative of the magnetization
(t) is the density matrix of the spin system. The expected signal is proportional to the time derivative of the magnetization 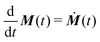 and the polarization
and the polarization  as
as
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) (t) is found by solving the Liouville–von Neumann equation
(t) is found by solving the Liouville–von Neumann equation
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) (0). At high field, the Hamiltonian [eqn (1)] can be approximated as
(0). At high field, the Hamiltonian [eqn (1)] can be approximated as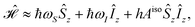
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) eq = 1/4 + 〈Ŝz〉eqŜz + 〈Îz〉eqÎz + 〈ŜzÎz〉eqŜzÎz,
eq = 1/4 + 〈Ŝz〉eqŜz + 〈Îz〉eqÎz + 〈ŜzÎz〉eqŜzÎz, pulse of the B1 field on
pulse of the B1 field on ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) eq generates the state
eq generates the state![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) 1(0) = −〈Ŝz〉eqŜy + 〈Îz〉eqÎz − 〈ŜzÎz〉eqŜyÎz.
1(0) = −〈Ŝz〉eqŜy + 〈Îz〉eqÎz − 〈ŜzÎz〉eqŜyÎz.![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) 1(t) = [cos(πAisot)
1(t) = [cos(πAisot)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωSt)Ŝx + sin(πAisot)
sin(ωSt)Ŝx + sin(πAisot)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωSt)ŜxÎz] 〈Ŝz〉eq +…
cos(ωSt)ŜxÎz] 〈Ŝz〉eq +…![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (ν) and/or (ii) are much smaller than 〈Ŝz〉eq, i.e., proportional to 〈ŜzÎz〉eq, are omitted. Then, the expected signal is
(ν) and/or (ii) are much smaller than 〈Ŝz〉eq, i.e., proportional to 〈ŜzÎz〉eq, are omitted. Then, the expected signal is
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) 2(0) = −〈Ŝz〉eqŜyÎx + 〈Îz〉eqÎx − 〈ŜzÎz〉eqŜy,
2(0) = −〈Ŝz〉eqŜyÎx + 〈Îz〉eqÎx − 〈ŜzÎz〉eqŜy, on
on ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) eq, one finds the density matrix
eq, one finds the density matrix
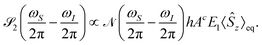
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) 2(t) only generates signal of the chirality-sensitive PcA at the difference frequency ωS − ωI. This allows to distinguish the postulated chirality-sensitive effect from other, nonchiral effects. PcA has the same direction as B0 (Fig. 1B, the second spectrum).
2(t) only generates signal of the chirality-sensitive PcA at the difference frequency ωS − ωI. This allows to distinguish the postulated chirality-sensitive effect from other, nonchiral effects. PcA has the same direction as B0 (Fig. 1B, the second spectrum).
 pulse, one can presume that the case II, i.e.,
pulse, one can presume that the case II, i.e., ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b7.gif) 2(0) ∝ ŜyÎx, represents a promising initial state. Spin relaxation toward the thermodynamic equilibrium causes Ŝz and Îz to appear. However, being parallel to B0, they do not generate any observable signals. One can hypothesize the inverse effect to that described above, i.e., that excitation by oscillating electric field would cause changes of the spin state that are dependent on the molecular chirality. Observing the inverse effect would be, however, complicated by dielectric heating since, due to the smallness of chirality-sensitive effects, an electric field of high amplitude is required.
2(0) ∝ ŜyÎx, represents a promising initial state. Spin relaxation toward the thermodynamic equilibrium causes Ŝz and Îz to appear. However, being parallel to B0, they do not generate any observable signals. One can hypothesize the inverse effect to that described above, i.e., that excitation by oscillating electric field would cause changes of the spin state that are dependent on the molecular chirality. Observing the inverse effect would be, however, complicated by dielectric heating since, due to the smallness of chirality-sensitive effects, an electric field of high amplitude is required.
![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) NO˙
NO˙![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) NO˙
NO˙![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) NO˙
NO˙![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) C˙H
C˙H![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) C˙C
C˙C![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ˙C
˙C![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
 of the nitroxyl nitrogen is perpendicular to that plane. While the
of the nitroxyl nitrogen is perpendicular to that plane. While the  and
and  of the adjacent carbons are not perpendicular to the σv plane, their projections onto this plane cancel, and the overall chirality-sensitive effect vanishes. However, if the molecule were isotopically 13C-labeled at the C position with 12C at the C′ position, 1a would be chiral and the predicted effect might be observed.
of the adjacent carbons are not perpendicular to the σv plane, their projections onto this plane cancel, and the overall chirality-sensitive effect vanishes. However, if the molecule were isotopically 13C-labeled at the C position with 12C at the C′ position, 1a would be chiral and the predicted effect might be observed. cancel out entirely for the isotopically unsubstituted molecule (vide supra), the effect of the substitution on AisoC is of the order of a fraction of MHz and, therefore, the chiral signal would presumably average to almost zero. A similar result is obtained for the nitrogen atoms of (R)-2b.
cancel out entirely for the isotopically unsubstituted molecule (vide supra), the effect of the substitution on AisoC is of the order of a fraction of MHz and, therefore, the chiral signal would presumably average to almost zero. A similar result is obtained for the nitrogen atoms of (R)-2b. of 3b is only weakly affected by the (R)-alanine group but, due to more favorable orientation of μe with respect to
of 3b is only weakly affected by the (R)-alanine group but, due to more favorable orientation of μe with respect to  , AcC reaches a much higher amplitude of 10–15 kHz. In this case, the amplitude of the expected chiral effect is at last 5 nHz m V−1, meaning that its detection by the equipment currently used in electron-nucleus double resonance experiments is feasible. When X-band
, AcC reaches a much higher amplitude of 10–15 kHz. In this case, the amplitude of the expected chiral effect is at last 5 nHz m V−1, meaning that its detection by the equipment currently used in electron-nucleus double resonance experiments is feasible. When X-band  or W-band (
or W-band ( ) EPR is applied, the signal of PcA will not overlap with any residual standard EPR signal, which could be present due to the finite purity of the desired initial state, i.e., −SyIx.
) EPR is applied, the signal of PcA will not overlap with any residual standard EPR signal, which could be present due to the finite purity of the desired initial state, i.e., −SyIx.



