DOI:
10.1039/D1CC01551F
(Feature Article)
Chem. Commun., 2021,
57, 5737-5749
Enhanced activity of catalysts on substrates with surface protonic current in an electrical field – a review
Received
22nd March 2021
, Accepted 14th May 2021
First published on 19th May 2021
Abstract
It has over the last few years been reported that the application of a DC electric field and resulting current over a bed of certain catalyst-support systems enhances catalytic activity for several reactions involving hydrogen-containing reactants, and the effect has been attributed to surface protonic conductivity on the porous ceramic support (typically ZrO2, CeO2, SrZrO3). Models for the nature of the interaction between the protonic current, the catalyst particle (typically Ru, Ni, Co, Fe), and adsorbed reactants such as NH3 and CH4 have developed as experimental evidence has emerged. Here, we summarize the electrical enhancement and how it enhances yield and lowers reaction temperatures of industrially important chemical processes. We also review the nature of the relevant catalysts, support materials, as well as essentials and recent progress in surface protonics. It is easily suspected that the effect is merely an increase in local vs. nominal set temperature due to the ohmic heating of the electrical field and current. We address this and add data from recent studies of ours that indicate that the heating effect is minor, and that the novel catalytic effect of a surface protonic current must have additional causes.

Truls Norby
| Truls Norby (b. 1955), PhD from University of Oslo (UiO) 1986, became professor at the Department of Chemistry UiO 1994 and since 1997 has headed the Group for Electrochemistry. He works with defects and transport in materials for solid-state fuel cells, electrolysers, batteries, membranes, and sensors, specialising in protons and protonic transport in oxides and on their surfaces. Norby has published 275 journal papers, graduated >100 Master- and PhD-students, and is a member of the Norwegian Academy of Science and Letters and other national academies. He has founded 4 companies, won the UiO Innovation Prize 2012 and the Norwegian Guldberg-Waage medal for chemistry 2018. |

Yasushi Sekine
| Yasushi Sekine (b. 1968), PhD from The University of Tokyo 1998, became professor at the Department of Applied Chemistry, Waseda University in 2012. He works with low temperature catalysis, specialising in protons and protonic transport in oxides and on their surfaces. Sekine has published 202 journal papers, supervised 96 Master- and 11 PhD-students, and is a fellow of the RSC (FRSC) and a member of other national academies. |
Many important and large-scale chemical reactions are carried out efficiently by means of catalysts to limit temperature, footprint and cost, and increase yield and reactor lifetime. The need to incorporate renewable energy into chemical reactions is gaining importance, such as operation of on-demand chemical reactions at relatively low temperatures. Non-equilibrium plasmas, photochemical, photoelectrochemical, and electrochemical reactions (electrosynthesis) as well as catalytic reactions with the application of electric fields and currents have been proposed as means of realizing such on-demand chemical reactions.
Through the development and study of systematic methodologies for a number of heterogeneous catalytic reactions, it has been found that the application of electric fields and small currents to various metal catalysts on ceramic semiconducting supports can significantly enhance the reaction rates.1–20 Also, non-equilibrium electrocatalytic processes include non-faradaic electrochemical modification of catalytic activity (NEMCA)21–25 and reactions in plasmas and electrical discharges26–33 have been proposed. NEMCA works at rather higher temperatures thanks to the oxygen anion migration in the oxide by the application of an electric field. Plasma-aided catalytic reactions have been attracting much attention recently, but it requires a high electrical energy consumption and it is difficult to maintain a stable catalyst structure. Compared to these processes, the catalytic effect of the electric field appears to be operative and maintaining high yields and selectivity and hence cost efficiency of various chemical reactions at low temperatures. Activation of catalysts by the application of an electric field evidently results from the migration of protons on the surface of the catalyst support and their interaction with reactant molecules such as N2, CO2, and CH4 at the catalyst support–metal interface.1,2,34–44 We have studied several reactions and catalysts and used a wide range of techniques to demonstrate the general principle of catalytic activation and to clarify the mechanism. Regarding the effect of electric fields (denoted as “EF”) on reactions, it was found that the apparent activation energy of the reaction is greatly reduced.
Here, we summarize the fundamentals, applications, theories, and developments of catalytic reactions in the electric field to help further research and development. In addition, as a means of applying the reaction to a wide variety of applications, examples of its application to ammonia synthesis, hydrogen and syngas production (steam reforming, dry reforming), hydrocarbon dehydrogenation, carbon dioxide activation, etc. will be introduced in detail, and the reaction mechanism will be summarized to provide a roadmap for further energy efficiency improvement. In laboratory demonstrations so far, the electrical energy required is relatively high for exothermic reactions including ammonia synthesis. For instance typically 1 kW h per kg NH3 synthesized from N2 + 3H2 is required for ammonia synthesis, and this needs to be reduced by at least an order of magnitude at scale-up if the EF enhanced catalysis is to be viable, as such requiring that the enhancement is not by ohmic Joule heating. On the other hand, the energy efficiency is rather high, about ∼70% on the endothermic reactions including reverse water gas shift, hydrogen evolution from methylcyclohexane, steam/dry reforming of hydrocarbons or alcohols.
General description and considerations
Here we first provide an introductory overview of the general principles and approaches.
The catalysts
For heterogeneous catalysts, which are reported to enable enhanced catalytic activity upon application of an electric field, ceramic supports with a relatively high bandgap (i.e., semiconducting) and negligible bulk electrical conductivity are important. By taking the form of powdered catalysts or porous ceramics and providing the surface with adsorbed species, the surface exhibits proton conduction by the Grotthuss mechanism. For this purpose, fluorite binary oxides such as CeO234 and perovskites such as SrZrO341,42 are good candidates. The choice of catalyst support should be considered based on its physical properties:45 conductors such as Fe2O3 can sustain an electric current but do not promote catalytic activity, whereas insulators such as Al2O3 cannot sustain sufficient surface protonic current, and the electric field results only in discharge. Only semiconducting type supports such as CeO2 and SrZrO3 appear to satisfy the required physical properties: surface protonic conductivity is a key factor, but also the presence of redox-active cations and possibly electronic transport seem important. For preparing active catalysts, various active metals, such as Ru, Pt, Pd or Ni, which show high catalytic activity, are loaded on the support by an impregnation method. The supported metal catalyst is calcined at 673–973 K for 2–12 hours. After calcination, the solid is pressed and sieved into agglomerates of diameter 355–500 μm. The catalyst structure and composition are evaluated by X-ray diffraction (XRD) and surface area analysis using the Brunauer–Emmett–Teller (BET) method before and after activity tests under the electric field.
Reactor and temperature measurement
The structure of a typical reactor is shown in Fig. 1. It consists of a conventional fixed-bed flow reactor in a furnace and two electrodes for applying an electric field on the catalyst.1,2 Usually, several hundred mg of catalyst is packed between the electrodes in the form of mesh or plates of Au or other materials, and the two electrodes are mounted vertically or coaxially on a fixed catalyst bed. A small current (a few mA) is applied to this catalyst bed at a DC voltage of 70–800 V. The stability of the voltage required for a given current is checked using a digital oscilloscope. The field strength in this process (on the order of 105 V m−1) is intermediate between other methods such as NEMCA (103 V m−1)46 and plasma (>107 V m−1).47 The catalyst layer acts as a kind of solid electrolyte. A thermocouple is attached to the reactor to measure the temperature of the catalyst layer. The products released from the gas outlet are qualitatively and quantitatively analyzed using gas chromatography with flame ionization detector (GC-FID), gas chromatography with thermal conductivity detector (GC-TCD), quadrupole mass spectrometer (Q-Mass), or ion chromatography.34,42
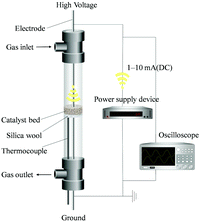 |
| | Fig. 1 Schematic image of the standard fixed-bed reactor. | |
When a weak electric current is applied to the catalyst bed by the electric field, Joule heat is generated, which may increase the temperature of the bed and the reaction rate. However, the power consumption by the field and current is low (typically 2 W, maximum 8 W) and the effect of the temperature rise of the catalyst bed on the reaction is small, confirmed by the thermocouple. Therefore, the induced Joule heat is estimated to be negligible in this process.48,49
Attempts to measure the catalyst temperature during the application of the electrical current in ammonia synthesis experiments have also been made in a setup at University of Oslo employing a ProboStat™ sample holder system (NORECS AS, Norway) with a wider quartz tube bed reactor equipped with Au mesh electrodes and taking up to 1 g catalyst. Thermocouples to the side of the quartz tube, in the exiting gas just under the frit, and in a protrusion of the quartz glass wall into the catalyst were used to more closely – yet still crudely – evaluate temperature effects. It was confirmed that application of 5 mA of current and typically 2 W of power caused temperature increases of only a few degrees at a nominal furnace and reactor temperature of 400 °C, increasing to typically 10 K at 200 °C and 20 K below 100 °C.
Rough calculations show that the gas flow can only absorb minute amounts of the ohmic heat, that radiation accounts for only a small fraction, and that heat conduction through the quartz walls to the surrounding reactor and furnace accounts for most of the heat transport, and indeed rationalizes the observed modest increase of only a few degrees.
For measuring and assuring the “real” catalytic temperature, we have evaluated it by operando-EXAFS comprising Debye–Waller factor analysis.50 We measured Pd K-edge for PdO in samples of Pd catalyst on CeO2 support with and without electrical field and current by EXAFS (BL14B2, SPring-8 at Hyogo, Japan) and compared with measurements of PdO samples at various temperatures, see Fig. 2. The σ2 value at 473 K with the electric field is a little larger than at 473 K without the electric field, but it does not exceed the value of PdO at 473 K (Fig. 2). If the difference is interpreted along the same slope as for the PdO sample, the electrical power leads to an increase of <50 K in the Pd catalyst. This means that the local heating effect by the electric field is rather small in the electric field over the catalyst of Pd/CeO2.
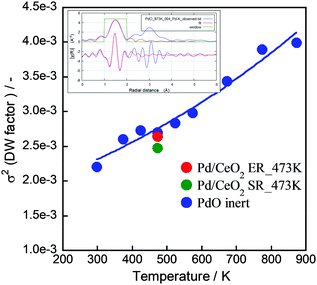 |
| | Fig. 2 Local heat evaluation using EXAFS. “ER” is a sample under the electric field and current, “SR” is without. | |
Reaction mechanism
We have reported that by applying a DC electric field over the catalyst and conducting a small current, the catalytic activity is enhanced, the reaction proceeds at a much lower temperature than ever, and the apparent activation energy is significantly decreased.34,42,43 Here, while the apparent activation energy decreases, the pre-exponential of the rate decreases with the electric field, suggesting an experimental correlation between the two or a change in the mechanism or geometry of the reaction site.
In addition, the correlation between the turnover frequency (TOF) and the metal particle size in the presence and absence of the electric field has also been investigated. They classify the TOF into those dependent on the surface area of the metal particles (TOF-s) and those dependent on the periphery of the metal particles (TOF-p), as described in eqn (1) and (2). In general catalytic reactions with heating, the TOF divided by the surface area (TOF-s) takes a constant value, while the TOF divided by the perimeter area (TOF-p) takes a constant value in reactions with the addition of an electric field.34,40,43 The TOF (TOF-p) takes a constant value for reactions with an applied electric field.34,40,43 This is evidence that the reaction with an applied electric field is active only around the supporting metal. Furthermore, only when an electric field was applied, a unique peak related to the Grotthuss mechanism was detected in situ infrared measurements, suggesting the appearance of proton hopping on the catalyst surface.34,40,42,51 These findings suggest that the reaction under the applied electric field has a completely different reaction pathway from the conventional process, as generalized in Fig. 3, but on the other hand the ohmic Joule heating does indeed come from the transport of protons on the surface of the support, since this is the dominating conduction mechanism in the catalyst material. In the case of catalysis by heat without an applied electric field, the reaction takes place on the metal catalyst surface based on the Langmuir–Hinshelwood mechanism, whereas the catalysis with an applied electric field appears to proceed with the activated protons reacting with the reactants around the metal. The proton transfer can be assigned to proton conduction from dissociated water and hydrogen adsorbed on the catalyst support surface, resulting in a net flux of protons as a result of the current due to the DC electric field.
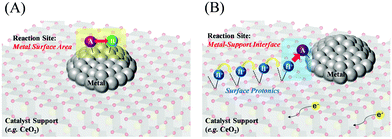 |
| | Fig. 3 Schematic reaction mechanisms; (A) without an applied electric field, (B) with an applied electric field. | |
Equally interestingly, in the presence of an electric field, some reactions appear to proceed beyond thermodynamic equilibrium. This has been suggested to be due to the activation of irreversible reaction pathways.18,19,34,35,37,38,49,52
In the following, we discuss the contribution of surface protonics to various catalytic reactions: (1) ammonia synthesis,39,41–44 (2) methane steam/dry reforming,34 (3) water gas shift,51 and (4) methylcyclohexane dehydrogenation.37,38 Irreversible properties derived from the electric field will also be discussed.
| |  | (1) |
| |  | (2) |
Detailed assessment of selected reactions
Here, we describe each reaction studied, discussing thermodynamics and catalysis, and the enhanced catalysis achieved by the electrical field.
Ammonia synthesis
More than 180 million tons of ammonia is produced annually on a very large industrial scale and is widely used as a raw material for chemical fertilizers, textiles, and refrigeration. The most established industrial route for ammonia synthesis is the Haber–Bosch process,53–55 which uses iron-based catalysts for the exothermic reaction:| | | N2(g) + 3H2(g) ↔ 2NH3(g) ΔH0298 = −45.94 kJ mol−1 | (3) |
This process is an artificial nitrogen fixation process. The reaction mechanism over a heterogeneous catalyst is called the “dissociation mechanism”.56,57 Nitrogen dissociation is the rate-determining step in the Haber–Bosch process, which requires harsh reaction conditions of 20–40 MPa and 673–873 K due to its thermodynamic and kinetic limitations.58
Many possibilities to increase the efficiency of ammonia production have been extensively studied. The most popular catalyst for ammonia synthesis is based on iron-promoted complexes.59 However, in 1972, Aika et al. reported that supported Ru is a more active catalyst that allows lower temperatures and hence also lower operating pressures.60,61 The study of supported Ru catalysts allowed us to reduce the reaction temperature and pressure required for the Haber–Bosch process.62–68
Alternative ammonia synthesis routes including plasma,69 photocatalysis,70 and electrolysis71 have been studied, showing the potential for low-temperature ammonia synthesis with better yields and efficiency.
Recently, Manabe et al. demonstrated a new catalytic ammonia synthesis process using an electric field and were the first to show surprisingly high ammonia synthesis rates at low temperatures.42 Such a process has a higher energy efficiency than the plasma-based process. With electric field and current enhancement, a supported Ru/SrZrO3 catalyst achieved an astonishing ammonia synthesis rate of more than 30 mmol gcat−1 h−1 and 0.9 MPa at a low temperature. Fig. 4(B) shows Arrhenius plots for ammonia synthesis at 0.1–0.9 MPa in the region 463–634 K with and without the electric field.
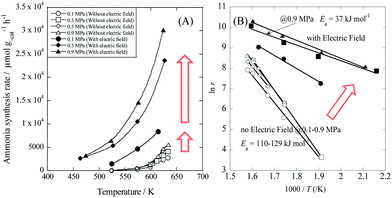 |
| | Fig. 4 Temperature and pressure dependence of ammonia synthesis rate with/without an electric field. (A) Temperature dependence of the ammonia synthesis rate at 0.1–0.9 MPa. (B) Arrhenius plots for each reaction: catalyst bed temperature, 463–634 K; catalyst, Cs/Ru/SrZrO3, 200 mg; flow, N2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 = 1 H2 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, total 240 sccm; current, 0 or 6 mA. Reproduced with permission from literature.42 3, total 240 sccm; current, 0 or 6 mA. Reproduced with permission from literature.42 | |
Application of an electric field at 0.9 MPa decreased the apparent activation energy from 121 kJ mol−1 to 37 kJ mol−1. Furthermore, the partial pressure dependence of H2 increased from −0.2 to 0, and that of N2 decreased from 0.7 to 0.2. The difference in these trends is so large that the reaction mechanism is considered to be changed by the application of an electric field.42
Isotope exchange studies with isotopic nitrogen (30N2) confirmed that N2 dissociation was significantly enhanced by the application of an electric field.42 In addition, H/D isotope effect tests demonstrated that proton hopping on the catalyst surface plays an important role in catalyzing ammonia synthesis;41 N2 dissociation is thought to proceed through a milder pathway by using adsorbed protons in the electric field to hydrogenate N2. Such a mechanism is called the “association mechanism”.39
Density functional theory (DFT) calculations were used to investigate the effect of active metals on the rate of ammonia synthesis, both with and without an electric field.44 Comparing several supported metals (Ru, Fe, Co, Ni, Pd, and Pt), the order was Ru > Fe > Co > Ni > Pd = Pt in the absence of the electric field, while a different trend was observed in the presence of electric field (Fe > Ni > Ru > Co > Pd > Pt). In addition, TOF-p and EN2H formation showed a linear correlation with the electric field (see Fig. 5). This is important evidence for a unique reaction pathway leading to the formation of N2H intermediates.
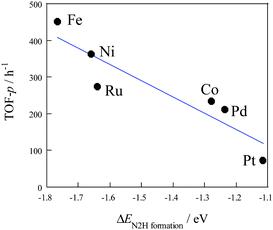 |
| | Fig. 5 TOF-p as a function of ΔEN2H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) formation with an electric field, 0.1 MPa, 373 K, 6 mA. Reproduced with permission from literature.44 formation with an electric field, 0.1 MPa, 373 K, 6 mA. Reproduced with permission from literature.44 | |
A deviation from Arrhenius behavior in an intermediate-temperature region (373 K < T < 473 K) was observed over 1 wt% Ru/CeO2 catalyst on the ammonia synthesis in the electric field (Fig. 6).72 Two investigations of (i) PH2 dependence on catalytic activity and (ii) the observation of surface OH group using in situ IR measurements revealed that the proton coverage over the catalyst surface is a critical factor for this non-Arrhenius behavior. In this temperature region, the proton coverage increases with lowering the temperature, and activated surface protonics leads to the higher ammonia synthesis rate. The appearance of surface protonics under NH3 synthesis (i.e. dry atmosphere) has also been concluded from AC impedance measurements73 on porous (R.D. = 60%) as compared to dense (R.D. = 90%) SrZrO3 pellets: only the porous sample showed enhancement of conductivity at lower temperatures (<723 K) when the gas atmosphere was switched from N2 to N2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 = 1
H2 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. Furthermore, the porous sample exhibited a H/D isotope effect, contrary to the dense sample. These observations emphasize that the proton conduction takes place mainly on the grain surface, not in bulk, and that surface protons are dominant charge carriers under ammonia synthesis atmospheres. So far, the energy efficiency of this reaction in the electric field is >1 kW h kg−1-NH3, and it is still rather high. We have to decrease it by the better catalyst design.
3. Furthermore, the porous sample exhibited a H/D isotope effect, contrary to the dense sample. These observations emphasize that the proton conduction takes place mainly on the grain surface, not in bulk, and that surface protons are dominant charge carriers under ammonia synthesis atmospheres. So far, the energy efficiency of this reaction in the electric field is >1 kW h kg−1-NH3, and it is still rather high. We have to decrease it by the better catalyst design.
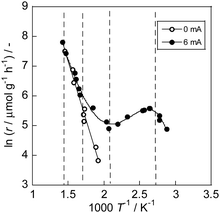 |
| | Fig. 6 Arrhenius plots for NH3 synthesis rate (r) over 1 wt% Ru/CeO2 with/without an electric field (0 or 6 mA) under PH2 = 0.75 atm. Reproduced with permission from literature.72 | |
In the NH3 synthesis using the electric field, the hydrogenation of N2 proceeds by the “associative mechanism” that can proceed under milder conditions than the “dissociative mechanism”; this allows the reaction to proceed at temperatures as low as 473 K. In particular, the increase in surface proton coverage at lower temperatures contributes significantly to the improvement of catalytic activity.
Steam reforming and dry reforming of methane
The demand for hydrogen is increasing every year thanks to its wide range of use and high potential as a clean secondary energy source that can be easily converted into electricity by fuel cells with water as the only by-product. Most of the industrially produced hydrogen is formed by steam reforming (SR) with methane by the eqn (4).| | | CH4 + H2O → CO + 3H2, ΔH0298 = 206 kJ mol−1 | (4) |
This reaction is usually carried out at high temperatures of at least 973 K using Ni catalysts because it is a very endothermic reaction, and methane has high structural stability.74,75 Such harsh conditions are associated with several problems, such as catalyst deactivation and the need for complex processes with heat exchangers and highly thermostable structural materials. Therefore, a novel process which can work at lower temperatures is promising. It has been shown that the use of Pd-supported catalysts with a DC electric field promotes methane steam reforming, in what was referred to as an irreversible path and named electroreforming, ER.34,35 By applying the electric field (EF) on the catalyst (Fig. 7(A)), high catalytic activity was observed even at low temperatures such as 473 K, where otherwise no reaction occurs. From the partial pressure dependence, the reaction rate equations with/without the electric field can be described as follows (eqn (5) and (6)).| | 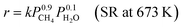 | (5) |
| | 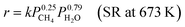 | (6) |
Thus, for the same methane conversion rate, SR and ER showed completely different partial pressure dependencies. When an electric field was applied, the methane partial pressure dependence decreased and the water pressure dependence increased, with the water partial pressure dependence exceeding the methane partial pressure dependence. As shown in Fig. 8(B), the Arrhenius plots of SR and ER show that the apparent activation energy of ER decreases significantly from 54.4 kJ mol−1 to 14.3 kJ mol−1 when the electric field is applied. These results indicate that ER proceeds through a different reaction pathway from that of SR, which has lower activation energy at temperatures below 623 K.
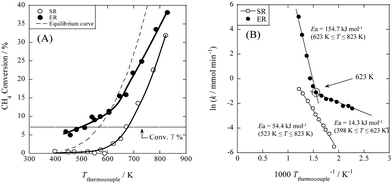 |
| | Fig. 7 Temperature dependencies of catalytic activity with or without electric field (EF). (A) Activities for catalytic steam reforming by heat (SR) and applying EF (ER); (B) Arrhenius plots for both reactions, preset temperature, 398–823 K; catalyst, 1.0 wt% Pd/CeO2, 80 mg; flow, CH4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar Ar![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) He = 12 He = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72, total flow rate 120 sccm; current, 0 or 5 mA. Reproduced with permission from literature.34 72, total flow rate 120 sccm; current, 0 or 5 mA. Reproduced with permission from literature.34 | |
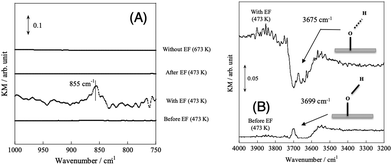 |
| | Fig. 8
Operando-DRIFTS spectra with/without EF. (A) O–H rotating region, (B) O–H stretching region, catalyst, CeO2 or 1.0 wt% Pd/CeO2; flow, CH4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 1 Ar = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62, total flow rate 65 sccm; current, 0 or 5 mA. Reproduced with permission from literature.34 62, total flow rate 65 sccm; current, 0 or 5 mA. Reproduced with permission from literature.34 | |
In order to elucidate the reaction mechanism with EF in more detail, we performed operando diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) measurements for both SR and ER. Fig. 8(A) shows the results of comparison under several conditions: the peak observed at 855 cm−1 is attributed to the rotation of adsorbed water,76,77 indicating that proton hopping occurs via O–H groups and water molecules based on the Grotthuss mechanism. As shown in Fig. 8(B), when an electric field was applied, the peak of O–H bond shifted to a lower wavenumber due to the stretching of O–H bond length, indicating the weakening of the O–H bond. Furthermore, AC impedance measurements of porous CeO2 pellets were performed to evaluate their electrical properties in terms of surface proton conduction.78 As shown in Fig. 9, the temperature dependence was different between the dry (Ar) and wet (Ar + H2O) conditions, and the conductivity enhancement in the low-temperature region was observed only in the wet condition. This phenomenon can be attributed to the increase of adsorbed water on the grain surface with decreasing temperature, which enhanced the surface proton conduction.79–90 This result is in good agreement with the results of the operando-DRIFTS measurements. To further investigate the contribution of proton hopping, we evaluated the quantitative changes in gas-phase methane at 3016.6 cm−1.91 The infrared band intensity of gas-phase methane at 473 K was not identical in the presence or absence of H2O, and the infrared band intensity decreased sharply while H2O was supplied. These results suggest that H2O is strongly involved in the activation of methane in the ER. In order to confirm whether methane is activated by proton collisions originating from the Grotthuss mechanism, kinetic isotope effects were evaluated using D2O. As a result, the decrease in infrared intensity was larger when D2O was used than when H2O was used, suggesting that the reverse kinetic isotope effect (KIE) appears.92–95 In addition, from the potential energy point of view, the energy levels with steep potential curves are formed in the triatomic transition state, and the discrepancy of the zero-point energy (ZPE) is enlarged.35 Thus, the activation energy is lower when the isotope (D2O) is used. These results indicate that the dissociative adsorption of methane at low temperatures is facilitated by the protonic nature of the surface, which promotes proton collisions with methane. The operando-DRIFTS study and AC impedance measurements revealed that the proton hopping on the catalyst surface is an essential factor for high methane conversion at low temperatures during ER.
 |
| | Fig. 9 Electrical conductivity of porous CeO2 as a function of inverse temperature under dry and wet conditions (PH2O = 0.026 atm). Reproduced with permission from literature.78 | |
Dry reforming of methane (DRM) is recognized as another important hydrogen and/or syngas production processes, as shown in eqn (7).96–100
| | | CH4 + CO2 → 2H2 + 2CO, ΔH0298 = 247.2 kJ mol−1 | (7) |
Recently, DRM is attracting attention from the viewpoint of efficient utilization of natural gas and suppressing global warming.
101–104 Nevertheless, this reaction requires a high temperature, above 1073 K, because of its thermodynamic limitations, so some issues including expensive material for the reactor and coke deposition on the catalyst are known.
105,106 For resolving these problems and proceeding reaction efficiency even at low temperatures, a new DRM process that proceeds with less coke deposition has been strongly desired. Recently, Yabe
et al. have achieved the promotion of DRM at low temperatures such as 473 K by imposing EF.
40,107 In their research, 1 wt% Ni/10 mol% La–ZrO
2 catalyst was used.
Fig. 10 shows the temperature dependence of catalytic activity with/without the EF. Both CH
4 and CO
2 conversions are enhanced drastically at low temperatures by applying the EF, although the conventional catalytic reaction hardly proceeds. The apparent activation energy based on CH
4 and CO
2 consumption rates was evaluated at temperatures of 505–880 K with EF and 764–897 K without EF at similar conversion conditions. As shown in
Table 1, the apparent activation energy was much lower by applying EF for each reactant, indicating that DRM with the EF proceeded
via a totally different reaction path from the heated catalytic reaction. We have proposed that surface protonics on the catalyst surface induced by imposing EF promotes the catalytic reaction at low temperatures.
36 Assuming that the proton conduction on the catalyst surface contributes to high CH
4 and CO
2 conversion for DRM with EF, the apparent electrical conductivity behavior was assessed as shown in
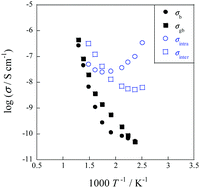
Fig. 11. The conductivity was calculated using eqn (8), where
L denotes the catalyst bed height,
S represents the area of electrodes,
I shows the applied current and
V stands for the response voltage.
| | 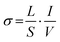 | (8) |
As shown in
Fig. 11, conductivity increased with decreasing temperature below 573 K in the CH
4 + CO
2 reaction, while conductivity decreased in the same temperature range in the CO
2 + Ar reaction. This behavior is close to that of the water-supplying state (under the wet condition), and the enhanced conductivity at low temperatures is interpreted as an increase in the amount of surface adsorbed species such as H
2O and hydroxyl groups with decreasing temperatures.
108–110 In this case, it is inferred that the surface proton species were formed by CH
4 and surface hydroxyl groups on La–ZrO
2via the reverse water–gas shift reaction (RWGS: H
2 + CO
2 → CO + H
2O).
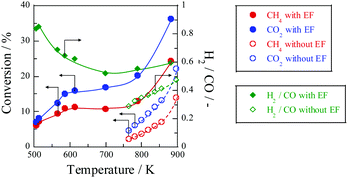 |
| | Fig. 10 Temperature dependence for catalytic activities with EF over 0.88 wt% Ni/10 mol% La–ZrO2 catalyst, CH4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 1 Ar = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, total flow rate: 20–200 sccm; input current: 3 mA; catalyst weight: 100 mg; furnace temperature: 505–880 K (with EF) and 764–897 K (without EF). Reproduced with permission from literature.40 2, total flow rate: 20–200 sccm; input current: 3 mA; catalyst weight: 100 mg; furnace temperature: 505–880 K (with EF) and 764–897 K (without EF). Reproduced with permission from literature.40 | |
Table 1 Apparent activation energy Ea, calculated from CH4 and CO2 consumption rate, for dry reforming of CH4 with/without the EF over 0.88 wt% Ni/10 mol% La–ZrO2 catalyst.a (Reproduced with permission from literature40)
|
|
E
a/kJ mol−1 |
R
2 value/— |
Reaction conditions: CH4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 1 Ar = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2; 100 sccm total flow rate; 3.0 mA input current; 100 mg catalyst weight; 505–880 K (with EF) and 764–897 K (without EF) catalyst bed temperature. 2; 100 sccm total flow rate; 3.0 mA input current; 100 mg catalyst weight; 505–880 K (with EF) and 764–897 K (without EF) catalyst bed temperature.
|
| Without EF |
CH4 |
66.1 |
0.96 |
| CO2 |
62.3 |
0.97 |
|
|
| With EF |
CH4 |
8.2 |
0.99 |
| CO2 |
12.1 |
0.99 |
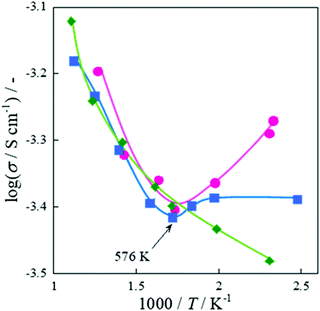 |
| | Fig. 11 Logarithmic apparent electrical conductivity as a function of inverse temperature with EF over 0.88 wt% Ni/10 mol% La–ZrO2 catalyst, CH4 (or CD4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 1 Ar = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 or CO2 2 or CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 1 Ar = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3; total flow rate, 100 sccm; 3.0 mA input current; 100 mg catalyst weight; 404–856 K catalyst bed temperature. Reproduced with permission from literature.40 3; total flow rate, 100 sccm; 3.0 mA input current; 100 mg catalyst weight; 404–856 K catalyst bed temperature. Reproduced with permission from literature.40 | |
In the case of the CD4 + CO2 reaction, the conductivity in the low-temperature region was lower than that of the CH4 + CO2 reaction because the D species, such as D2O and OD groups derived from CD4, are heavier than the H species. Furthermore, we investigated the KIE of DRM with EF using CH4/CD4 and CO2 (Fig. 12). In this experiment, pre-reduction with H2 or D2 was performed to produce H or D species, rH and rD were calculated as the CO production rate, and the value of rD/rH was evaluated. As a result, CO from CH4 was calculated to be 1.23 ± 0.08 and CO from CO2 was calculated to be 1.39 ± 0.03. These results indicate an “inverse” KIE for the dissociation of both CH4 and CO2.92,111–116 Furthermore, operando-DRIFTS measurements were performed to observe the surface adsorbed species of DRM in the presence of an electric field. According to the overall (Fig. 13(A)) and magnified (Fig. 13(B)) spectra, a specific peak corresponding to the rotation of adsorbed water at 850 cm−1 at 573 K was observed in the difference spectrum between the EF-applied and post-applied spectra, i.e., only in the EF-applied spectrum. This water rotation is based on the Grotthuss mechanism, and this result is evidence of the appearance of surface proton conduction.
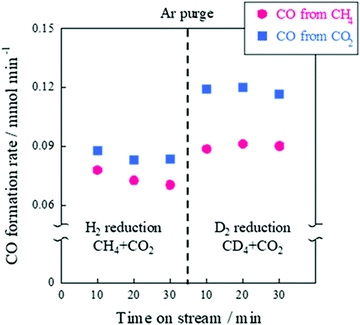 |
| | Fig. 12 CO formation rate with the EF over 0.88 wt% Ni/10 mol% La–ZrO2 catalyst, CH4 (or CD4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 1 Ar = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2; total flow rate, 100 sccm; 3.0 mA input current; 100 mg catalyst weight; 423 K furnace temperature. Reproduced with permission from literature.40 2; total flow rate, 100 sccm; 3.0 mA input current; 100 mg catalyst weight; 423 K furnace temperature. Reproduced with permission from literature.40 | |
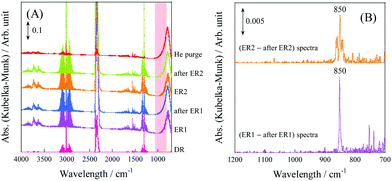 |
| | Fig. 13
Operando-DRIFTS spectra with/without EF. (A) Comparison of before/with/after applying EF (without EF, DR; with EF, ER). (B) Differential spectra with/after applying EF in H2O rotation: 0.88 wt% Ni/10 mol% La–ZrO2 catalyst; CH4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) He = 3 He = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34; 40 Sccm total flow rate; 9 mA current; 573 K preset temperature. Reproduced with permission from literature.40 34; 40 Sccm total flow rate; 9 mA current; 573 K preset temperature. Reproduced with permission from literature.40 | |
On the steam and dry reforming of methane, the energy efficiency is rather high compared to the exothermic reaction (i.e. ammonia synthesis, etc.). So far, about ∼70% of the electric power consumption has been used for the endothermic reaction, and it depends on the catalyst structure. Further improvement on the reaction energy efficiency is anticipated.
By thorough investigations on steam reforming and dry reforming of methane, it was revealed that surface protonics efficiently promotes these reactions at low temperatures by the application of EF, which was evidenced by studies of operando-DRIFTS measurement, “inverse” KIE, and the electrical property of catalyst support.
Water gas shift reaction
The water gas shift (WGS) reaction is important for industrial hydrogen production. This reaction enables purifying produced hydrogen by steam reforming and adjusting the synthesis gas composition. Carbon monoxide (CO), which is produced as a byproduct in steam reforming, poisons electrodes in polymer electrolyte membrane fuel cells (PEMFCs).117–119 The WGS reaction is exothermic as presented in eqn (9).| | | CO + H2O → CO2 + H2 ΔH0298 = −41.2 kJ mol−1 | (9) |
Thus, it is thermodynamically favorable at low temperatures, but kinetically limited. Accordingly, the WGS reaction is well suited for catalytic promotion at lower temperatures.
An effective solution to these problems is to apply an electric field to the heterogeneous catalyst.51 When a DC electric field was applied (3 mA, 2.9 W) to a Pt/La–ZrO2 catalyst, the CO conversion increased from 0% to 47.1% even at 423 K.1 To investigate the difference in the reaction rate with and without the electric field, we compared the apparent activation energy. As a result, the apparent activation energy was reduced to almost half when the electric field was applied (98.3 kJ mol−1 without EF, 50.9 kJ mol−1 with EF). In order to compare the behavior with and without the applied electric field, the partial pressure dependence of each reactant (CO, H2O) on the rate was investigated. The results showed that when the electric field was applied at 553 K, the reaction partial pressure of CO changed from −0.28 to 0.33 and that of H2O from 0.49 to 0.57. In the case of WGS with the electric field, the CO partial pressure dependence changed from negative to positive and CO adsorption was suppressed; the change in the H2O partial pressure dependence was assumed to originate from the surface ionic conductivity based on the Grotthuss mechanism. By this mechanism, protons move through the rotating surface adsorbed water with a weak electric current, thus accelerating the surface catalytic reaction. The changes in the partial pressure dependence of each reactant indicate that the electric field accelerates the reaction at low temperatures. These changes suggest that the WGS reaction using an electric field proceeds through a different pathway than the conventional reaction. In order to clarify this reaction pathway, we evaluated the H/D isotope effect. As shown in Table 2, the primary isotope effect was confirmed, with rD/rH having the same value of 0.317 in the presence and absence of EF. This result indicates that H2O is activated on the catalyst support, but not on the overloaded Pt, and that O–H dissociation is not part of the rate-determining step for both reactions. Next, we performed a transient experiment in which the reactants (CO and H2O) were periodically introduced. The transient production of CO and H2 was monitored using a quadrupole mass spectrometer (Q-Mass). It is clear from the results summarized in Table 3 that in the reaction without EF, the amount of CO2 and H2 produced was almost the same at the fourth introduction of CO, which was stoichiometric. On the other hand, in the reaction with EF, the amount of CO2 produced exceeded that of H2 in all cycles. This suggests that a redox mechanism using surface-lattice oxygen and H2O occurred during the EF reaction. Based on this, we investigated the transient production of CO2 using the 18O isotope. As shown in Fig. 14, C18O2 was not observed at all in the reaction without EF, while C18O2 and C18O16O were detected in abundance in the reaction with EF. These results indicate that the lattice oxygen plays an important role and that the reaction mechanism in the EF reaction is the Mars–van Krevelen mechanism. These investigations indicate that it is possible to promote the WGS reaction at low temperatures by surface reactions based on the Mars–van Krevelen mechanism by applying an electric field.
Table 2 H/D isotope effect for WGS (reproduced with permission from literature51)
|
|
r
D/mmol min−1 |
r
H/mmol min−1 |
r
D/rH/— |
| Without EF |
0.004 |
0.013 |
0.317 |
| With EF |
0.025 |
0.078 |
0.317 |
Table 3 Transient responses during cyclic introductions of CO and H2O over Pt/La–ZrO2 with/without EF, at 553 K for with EF and at 723 K for without EF (reproduced with permission from literature51)
|
|
With EF at 553 K |
Without EF at 723 K |
| CO2 formation/mmol |
H2 formation/mmol |
CO2 formation/mmol |
H2 formation/mmol |
| 1st |
CO introduction |
24.65 |
7.42 |
12.17 |
1.77 |
| H2O introduction |
0.00 |
8.24 |
0.00 |
2.16 |
| 2nd |
CO introduction |
12.13 |
6.52 |
2.64 |
1.91 |
| H2O introduction |
0.00 |
6.59 |
0.00 |
3.41 |
| 3rd |
CO introduction |
14.99 |
9.96 |
3.04 |
2.87 |
| H2O introduction |
0.00 |
0.00 |
0.00 |
0.00 |
| 4th |
CO introduction |
7.13 |
3.29 |
2.40 |
2.22 |
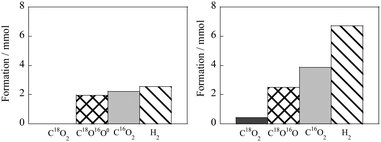 |
| | Fig. 14 Transient formation amounts of isotopic CO2 during transient tests using 18O, left: without EF, right: with EF. Reproduced with permission from literature.51 | |
Methylcyclohexane dehydrogenation
The methylcyclohexane (MCH)–toluene–hydrogen cycle is promising and interesting as a liquid organic hydrogen carrier system. Dehydrogenation of MCH, eqn (10), is an endothermic reaction. It typically requires temperatures above 623 K due to its kinetic limitations, even over Pt catalysts.120| | | C7H14 → C7H8 + 3H2, ΔH0298 = 204.8 kJ mol−1 | (10) |
If this dehydrogenation temperature could be lowered efficiently, a clean energy society e.g. reducing energy consumption or using low-grade heat can be realized.120–123 Nevertheless, this reaction is strictly limited by the thermodynamic equilibrium, particularly at low temperatures. To exceed this equilibrium limitation and promote the dehydrogenation at low temperatures irreversibly, we have investigated irreversible MCH dehydrogenation with a DC electric field over supported Pt catalysts.37,38,49 Results presented in Table 4 show that the catalytic activity was enhanced markedly by the DC electric field at low temperatures.
Table 4 Temperature dependences of catalytic activity in a kinetic condition on 3 wt% Pt/CeO2 with and without the electric field; gas supply: MCH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 6.4
Ar = 6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 (total flow rate 36.4 mL min−1), EF: constant current of 3 mA.a (Reproduced with permission from literature37)
30 (total flow rate 36.4 mL min−1), EF: constant current of 3 mA.a (Reproduced with permission from literature37)
| Reaction temperature/K |
Equilibrium limitation/% |
With EF |
Without EF |
|
T
tc/K |
H2 yield/% |
CH4 production/10−2 μmol min−1 |
T
tc/K |
H2 yield/% |
CH4 production/10−2 μmol min−1 |
|
T
tc: catalyst bed temperature measured using a thermocouple.
|
| 423 |
5.5 |
442 |
21.6 |
1.1 |
422 |
0.8 |
n.d. |
| 473 |
25.2 |
479 |
30.2 |
2.4 |
468 |
5.6 |
n.d. |
| 523 |
72.0 |
522 |
51.8 |
4.1 |
523 |
21.5 |
1.6 |
| 573 |
98.7 |
572 |
88.3 |
14.0 |
566 |
52.5 |
5.2 |
Notably, at 423 K, the catalytic activity showed 21.6% hydrogen yield, which exceeds the thermodynamic equilibrium hydrogen yield of 5.5% at this temperature. From the Arrhenius plots (Fig. 15), the apparent activation energies with and without electric field were 28.6 and 55.6 kJ mol−1, respectively. These results indicate that the applied electric field promotes the MCH dehydrogenation, and that the reaction mechanism involved must be different from the one in operation without the electric field.
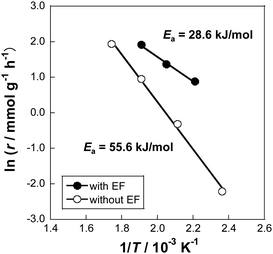 |
| | Fig. 15 Arrhenius plots for 3 wt% Pt/CeO2 catalyst with and without the electric field (EF): gas supply, MCH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 6.4 Ar = 6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 (total flow rate 36.4 mL min−1); EF: constant current of 3 mA. Reproduced with permission from literature.37 30 (total flow rate 36.4 mL min−1); EF: constant current of 3 mA. Reproduced with permission from literature.37 | |
To investigate the reaction mechanism, partial pressure dependencies of MCH, toluene and hydrogen were assessed and are shown in Table 5, allowing the MCH dehydrogenation reaction rate to be expressed by eqn (11)
| | | rdehydrogenation = k[MCH]a[Toluene]b[H2]c | (11) |
Generally, gaseous hydrogen promotes the hydrogenation of toluene, which is the reverse reaction in this case. In the absence of the electric field, there was a negative dependence on the hydrogen partial pressure (
c < 0) in
eqn (11). On the other hand, when an electric field was applied, the reaction rate showed an unusual positive dependence on the hydrogen partial pressure. It has been reported that the positive dependence of the hydrogen partial pressure indicates the acceleration of the reaction by proton hopping at the catalyst surface.
34,36 Therefore, proton species may be an important factor in accelerating the MCH dehydrogenation reaction in an electric field.
Table 5 Dependence of partial pressure and reaction rate for (a) methylcyclohexane, (b) toluene, and (c) hydrogen over 3 wt% Pt/CeO2 in methylcyclohexane dehydrogenation with the electric field at 423 K and without electric field at 523 K; EF: constant current 3 mA; gas supply: C7H14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = (3.2, 6.4, 9.6, 11.3)
Ar = (3.2, 6.4, 9.6, 11.3)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (53.2, 50.0, 46.8, 45.1), C7H14
(53.2, 50.0, 46.8, 45.1), C7H14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C7H8
C7H8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 6.4
Ar = 6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.0, 2.0, 3.0, 4.0)
(1.0, 2.0, 3.0, 4.0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (49.0, 48.0, 47.0, 46.0) and C7H14
(49.0, 48.0, 47.0, 46.0) and C7H14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2
H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 6.4
Ar = 6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (4.0, 7.0, 9.0, 12.0)
(4.0, 7.0, 9.0, 12.0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (46.0, 43.0, 41.0, 38.0). (Reproduced with permission from literature37)
(46.0, 43.0, 41.0, 38.0). (Reproduced with permission from literature37)
| Condition |
a (MCH) |
b (toluene) |
c (H2) |
| With EF (423 K) |
0.35 |
−0.07 |
0.15 |
| Without EF (523 K) |
0.49 |
−0.18 |
−0.13 |
Furthermore, the isotope effect was investigated by supplying MCHD (i.e., C7D14) and D2 during the reaction with and without an electric field, as shown in Table 6. The isotope effects were evaluated using the isotope ratio of the rate constants, kD/kH. This value is typically less than 1 due to the higher stability of the chemical bonds of the heavier isotopes (low zero-point energy (ZPE)).35 The results for no electric field are consistent with those for MCHD, which are 0.67 for MCHD/H2 and 0.69 for MCHD/D2. The results confirmed the kinetic isotope effect (KIE) in the case without the electric field. However, it was found that the kD/kH value increased with increasing deuterium supply when an electric field was applied. This inverse KIE was observed due to the extended ZPE discrepancy between the isotopes in the physisorbed to three-atom transition state when the C–H–H configuration was formed by proton collisions.35,92,94,95,124 Thus, the inverse KIE indicates that proton collisions promote MCH dehydrogenation in the electric field. It has also been suggested that when MCH dehydrogenation passes through the three-atom transition due to proton hopping, it has an inhibitory effect on the reverse reaction, toluene hydrogenation, because hydrogenation in an electric field requires large apparent activation energy.37 As discussed in this section, surface protonation by the application of an electric field can achieve irreversible MCH dehydrogenation and highly efficient hydrogen production even at temperatures as low as 423 K. The electrical energy demand for this reaction in the electric field is rather small, and about 70% of energy efficiency based on the electric power consumption and the reaction enthalpy has been achieved.
Table 6 MCH dehydrogenation using isotope; 3 wt% Pt/CeO2 catalyst; gas supply: MCH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 (or D2)
H2 (or D2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 6.4
Ar = 6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46 (total flow 56.4 mL min−1); EF: constant current of 3 mA. (Reproduced with permission from literature37)
46 (total flow 56.4 mL min−1); EF: constant current of 3 mA. (Reproduced with permission from literature37)
| Condition |
T
tc
/K |
H2 production rate/μmol min−1 |
H2 yield/% |
k
D/kH/— |
|
T
tc: catalyst bed temperature measured using a thermocouple.
|
| With EF (423 K) |
MCHH/H2 |
445 |
148 |
18.8 |
— |
| MCHH/D2 |
441 |
178 |
22.6 |
1.20 |
| MCHD/H2 |
445 |
180 |
22.9 |
1.22 |
| MCHD/D2 |
442 |
209 |
26.6 |
1.42 |
|
|
| Without EF (523 K) |
MCHH/H2 |
519 |
247 |
31.5 |
— |
| MCHH/D2 |
519 |
255 |
32.5 |
1.03 |
| MCHD/H2 |
518 |
165 |
21.0 |
0.67 |
| MCHD/D2 |
520 |
170 |
21.7 |
0.69 |
Discussion
As described in “Detailed Evaluation of Selected Reactions,” we have thoroughly elucidated the significance of the effects of electric field on the catalytic activity. As a result, we discovered a novel catalytic reaction mechanism that proceeds in a low-temperature electric field, different from conventional (heated) catalytic reactions.1,2 The enhancement seems not to stem from ohmic Joule heating, based on temperature measurements with thermocouples near and in the catalyst and by the Debye–Waller factor in EXAFS. The frequency factor was small because the apparent activation energy was greatly reduced by the application of the electric field, and the reaction mechanism changed from a reaction on the metal surface to a reaction at the interface of the metal and the substrate. There are three important phenomena: (i) in situ DRIFTS measurements to evaluate the behavior of surface adsorbents showed proton hopping on the catalyst support surface based on the Grotthuss mechanism.34,35 (ii) Considering the “inverse” KIE theory, protons with kinetic energy collide with stable reactants and accelerate the rate-determining step of the reaction.34,37,38 (iii) EIS measurements revealed that surface ionic conduction occurs on the catalyst support at lower temperatures.34,36 These three are strong evidence to support a significant increase in the reaction rate of the catalytic process by the application of this electric field. In order to further explain the apparent irreversibility, further studies from the perspective of “dynamics” such as ab initio molecular dynamics (AIMD) simulations are desirable. One example is the quantitative evaluation of the collision frequency of protons. This allows us to know how much kinetic energy is consumed to form an intermediate in the transition state. It is also important to find new catalytic materials that can improve the efficiency and performance of this process. We propose “topological ionic conductors” as a unique candidate for this purpose. As their physicochemical properties, we expect partial activation of ion conduction (surface proton conduction) and reduction of Joule heat loss. In order to create such a material, we need to evaluate in parallel (a) the bulk conductivity by DC conduction measurements and (b) the surface ionic conductivity by AC impedance measurements. If this can be achieved, the process will allow for much higher catalytic activity and also control the selectivity to the desired product. If this happens, highly efficient processes for small-scale, on-site, and on-demand production could be established in the future.
Conclusion
A method of applying an electric field to semiconductor catalysts was proposed as a way to make catalytic reactions low temperature and on-demand. The working theory of the method is summarized and its application is described. For further development, it is suggested to develop new materials and structures that can promote surface protonics, and simpler evaluation methods for them. Further research in this area is highly anticipated.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Authors at University of Oslo acknowledge financial support from the ENERGIX program of The Research Council of Norway, project #280495.
Notes and references
- S. Ogo and Y. Sekine, Chem. Rec., 2017, 17(8), 726–738 CrossRef CAS PubMed.
- M. Torimoto, K. Murakami and Y. Sekine, Bull. Chem. Soc. Jpn., 2019, 92(10), 1785–1792 CrossRef CAS.
- F. Shen, K. Li, D. Xu, R. Yan, T. Chen, R. Zhan and H. Lin, Mol. Catal., 2019, 476, 110536 CrossRef CAS.
- K. Li, K. Liu, H. Ni, B. Guan, R. Zhan, Z. Huang and H. Lin, Mol. Catal., 2018, 459, 78–88 CrossRef CAS.
- K. Liu, K. Li, D. Xu, H. Lin, B. Guan, T. Chen and Z. Huang, J. Shanghai Jiaotong Univ., 2018, 23(1), 8–17 CrossRef.
- K. Li, K. Liu, D. Xu, H. Ni, F. Shen, T. Chen, B. Guan, R. Zhan, Z. Huang and H. Lin, Chem. Eng. J., 2019, 369, 660–671 CrossRef CAS.
- K. Li, D. Xu, K. Liu, H. Ni, F. Shen, T. Chen, B. Guan, R. Zhan, Z. Huang and H. Lin, J. Phys. Chem. C, 2019, 123(16), 10377–10388 CrossRef CAS.
- F. Che, J. T. Gray, S. Ha, N. Kruse, S. L. Scott and J.-S. McEwen, ACS Catal., 2018, 8(6), 5153–5174 CrossRef CAS.
- F. Che, J. T. Gray, S. Ha and J.-S. McEwen, ACS Catal., 2017, 7(10), 6957–6968 CrossRef CAS.
- F. Che, J. T. Gray, S. Ha and J.-S. McEwen, ACS Catal., 2017, 7(1), 551–562 CrossRef CAS.
- F. Che, S. Ha and J. McEwen, Angew. Chem., Int. Ed., 2017, 56, 3557–3561 CrossRef CAS PubMed.
- F. Che, S. Ha and J.-S. McEwen, Appl. Catal., B, 2016, 195, 77–89 CrossRef CAS.
- F. Che, J. T. Gray, S. Ha and J.-S. McEwen, J. Catal., 2015, 332, 187–200 CrossRef CAS.
- V.-J. Lee, Science, 1966, 152(3721), 514 CrossRef CAS PubMed.
- J.-S. McEwen, A. G. C. Ros, P. Gaspard, T. V. de Bocarmé and N. Kruse, Catal. Today, 2010, 154(1–2), 75–84 CrossRef CAS.
- C. Périllat-Merceroz, G. Gauthier, P. Roussel, M. Huvé, P. Gélin and R.-N. Vannier, Chem. Mater., 2011, 23(6), 1539–1550 CrossRef.
- D. Bhattacharyya and R. Rengaswamy, Ind. Eng. Chem. Res., 2009, 48(13), 6068–6086 CrossRef CAS.
- Y. Sekine, M. Haraguchi, M. Matsukata and E. Kikuchi, Catal. Today, 2011, 171(1), 116–125 CrossRef CAS.
- K. Oshima, T. Shinagawa, M. Haraguchi and Y. Sekine, Int. J. Hydrogen Energy, 2013, 38(7), 3003–3011 CrossRef CAS.
- Y. Sekine, M. Haraguchi, M. Tomioka, M. Matsukata and E. Kikuchi, J. Phys. Chem. A, 2010, 114(11), 3824–3833 CrossRef CAS PubMed.
- C. G. Vayenas, S. Bebelis and S. Neophytides, J. Phys. Chem., 1988, 92(18), 5083–5085 CrossRef CAS.
- A. de Lucas-Consuegra, A. Princivalle, A. Caravaca, F. Dorado, C. Guizard, J. L. Valverde and P. Vernoux, Appl. Catal., B, 2010, 94(3–4), 281–287 CrossRef CAS.
- A. Caravaca, A. de Lucas-Consuegra, C. Molina-Mora, J. L. Valverde and F. Dorado, Appl. Catal., B, 2011, 106(1–2), 54–62 CAS.
- I. V. Yentekakis, Y. Jiang, S. Neophytides, S. Bebelis and C. G. Vayenas, Ionics, 1995, 1(5–6), 491–498 CrossRef CAS.
- M. Stoukides and C. G. Vayenas, J. Catal., 1981, 70(1), 137–146 CrossRef CAS.
- S. Kado, K. Urasaki, Y. Sekine and K. Fujimoto, Chem. Commun., 2001,(5), 415–416 RSC.
- M. Kraus, B. Eliasson, U. Kogelschatz and A. Wokaun, Phys. Chem. Chem. Phys., 2001, 3(3), 294–300 RSC.
- T. Jiang, Y. Li, C. J. Liu, G. H. Xu, B. Eliasson and B. Z. Xue, Catal. Today, 2002, 72(3–4), 229–235 CrossRef CAS.
- S. Kado, Y. Sekine, T. Nozaki and K. Okazaki, Catal. Today, 2004, 89(1–2), 47–55 CrossRef CAS.
- Y. Sekine, K. Urasaki, S. Asai, M. Matsukata, E. Kikuchi and S. Kado, Chem. Commun., 2005,(1), 78–79 RSC.
- C. J. Liu, A. Marafee, B. Hill, G. H. Xu, R. Mallinson and L. Lobban, Ind. Eng. Chem. Res., 1996, 35(10), 3295–3301 CrossRef CAS.
- C. J. Liu, A. Marafee, R. Mallinson and L. Lobban, Appl. Catal., A, 1997, 164(1–2), 21–33 CrossRef CAS.
- A. Marafee, C. J. Liu, G. H. Xu, R. Mallinson and L. Lobban, Ind. Eng. Chem. Res., 1997, 36(3), 632–637 CrossRef CAS.
- R. Manabe, S. Okada, R. Inagaki, K. Oshima, S. Ogo and Y. Sekine, Sci. Rep., 2016, 6, 38007 CrossRef CAS PubMed.
- S. Okada, R. Manabe, R. Inagaki, S. Ogo and Y. Sekine, Catal. Today, 2018, 307, 272–276 CrossRef CAS.
- R. Inagaki, R. Manabe, Y. Hisai, Y. Kamite, T. Yabe, S. Ogo and Y. Sekine, Int. J. Hydrogen Energy, 2018, 43(31), 14310–14318 CrossRef CAS.
- K. Takise, A. Sato, K. Murakami, S. Ogo, J. G. Seo, K. Imagawa, S. Kado and Y. Sekine, RSC Adv., 2019, 9(11), 5918–5924 RSC.
- K. Takise, A. Sato, S. Ogo, J. G. Seo, K.-I. Imagawa, S. Kado and Y. Sekine, RSC Adv., 2019, 9(48), 27743–27748 RSC.
- K. Murakami, Y. Tanaka, S. Hayashi, R. Sakai, Y. Hisai, Y. Mizutani, A. Ishikawa, T. Higo, S. Ogo, J. G. Seo, H. Tsuneki, H. Nakai and Y. Sekine, J. Chem. Phys., 2019, 151(6), 064708 CrossRef.
- T. Yabe, K. Yamada, K. Murakami, K. Toko, K. Ito, T. Higo, S. Ogo and Y. Sekine, ACS Sustainable Chem. Eng., 2019, 7(6), 5690–5697 CrossRef CAS.
- K. Murakami, R. Manabe, H. Nakatsubo, T. Yabe, S. Ogo and Y. Sekine, Catal. Today, 2018, 303, 271–275 CrossRef CAS.
- R. Manabe, H. Nakatsubo, A. Gondo, K. Murakami, S. Ogo, H. Tsuneki, M. Ikeda, A. Ishikawa, H. Nakai and Y. Sekine, Chem. Sci., 2017, 8(8), 5434–5439 RSC.
- A. Gondo, R. Manabe, R. Sakai, K. Murakami, T. Yabe, S. Ogo, M. Ikeda, H. Tsuneki and Y. Sekine, Catal. Lett., 2018, 148(7), 1929–1938 CrossRef CAS.
- K. Murakami, Y. Tanaka, R. Sakai, K. Toko, K. Ito, A. Ishikawa, T. Higo, T. Yabe, S. Ogo, M. Ikeda, H. Tsuneki, H. Nakai and Y. Sekine, Catal. Today, 2020, 351, 119–124 CrossRef CAS.
- R. Sakai, K. Murakami, Y. Mizutani, Y. Tanaka, S. Hayashi, A. Ishikawa, T. Higo, S. Ogo, H. Tsuneki, H. Nakai and Y. Sekine, ACS Omega, 2020, 5(12), 6846–6851 CrossRef CAS PubMed.
- A. D. Frantzis, S. Bebelis and C. G. Vayenas, Solid State Ionics, 2000, 136, 863–872 CrossRef.
- Y. Sekine, K. Urasaki, S. Kado, M. Matsukata and E. Kikuchi, Energy Fuels, 2004, 18(2), 455–459 CrossRef CAS.
- K. Takise, A. Sato, K. Muraguchi, S. Ogo and Y. Sekine, Appl. Catal., A, 2019, 573, 56–63 CrossRef CAS.
- M. Kosaka, T. Higo, S. Ogo, J. G. Seo, S. Kado, K. Imagawa and Y. Sekine, Int. J. Hydrogen Energy, 2020, 45(1), 738–743 CrossRef CAS.
- T. Ano, S. Tsubaki, A. Liu, M. Matsuhisa, S. Fujii, K. Motokura, W.-J. Chun and Y. Wada, Commun. Chem., 2020, 3, 86 CrossRef CAS.
- Y. Sekine, K. Yamagishi, Y. Nogami, R. Manabe, K. Oshima and S. Ogo, Catal. Lett., 2016, 146(8), 1423–1428 CrossRef CAS.
- T. Yabe, K. Mitarai, K. Oshima, S. Ogo and Y. Sekine, Fuel Process. Technol., 2017, 158, 96–103 CrossRef CAS.
- J. S. Anderson, J. Rittle and J. C. Peters, Nature, 2013, 501(7465), 84–87 CrossRef CAS PubMed.
- A. Mittasch, Adv. Catal., 1950, 2, 81–104 Search PubMed.
- G. Ertl, D. Prigge, R. Schloegl and M. Weiss, J. Catal., 1983, 79, 359–377 CrossRef CAS.
- K. Honkala, A. Hellman, I. N. Remediakis, A. Logadottir, A. Carlsson, S. Dahl, C. H. Christensen and J. K. Nørskov, Science, 2005, 307, 555–558 CrossRef CAS PubMed.
-
J. R. Jennings, Catalytic ammonia synthesis, fundamentals and practice, Springer, US, 1991, pp. 109–131 Search PubMed.
- P. Stoltze and J. K. Norskov, Phys. Rev. Lett., 1985, 55(22), 2502–2505 CrossRef CAS PubMed.
- B. Wilk, R. Pelka and W. Arabczyk, J. Phys. Chem. C, 2017, 121(15), 8548–8556 CrossRef CAS.
- K. Aika, A. Ozaki and H. Hori, J. Catal., 1972, 27(3), 424–431 CrossRef CAS.
- K. Aika, A. Ohya, A. Ozaki, Y. Inoue and I. Yasumori, J. Catal., 1985, 92(2), 305–311 CrossRef CAS.
- Y. Ogura, K. Sato, S. Miyahara, Y. Kawano, T. Toriyama, T. Yamamoto, S. Matsumura, S. Hosokawa and K. Nagaoka, Chem. Sci., 2018, 9(8), 2230–2237 RSC.
- M. Kitano, Y. Inoue, H. Ishikawa, K. Yamagata, T. Nakao, T. Tada, S. Matsuishi, T. Yokoyama, M. Hara and H. Hosono, Chem. Sci., 2016, 7(7), 4036–4043 RSC.
- M. Kitano, Y. Inoue, Y. Yamazaki, F. Hayashi, S. Kanbara, S. Matsuishi, T. Yokoyama, S.-W. Kim, M. Hara and H. Hosono, Nat. Chem., 2012, 4(11), 934 CrossRef CAS PubMed.
- Y. Lu, J. Li, T. Tada, Y. Toda, S. Ueda, T. Yokoyama, M. Kitano and H. Hosono, J. Am. Chem. Soc., 2016, 138(12), 3970–3973 CrossRef CAS PubMed.
- J. Wu, Y. Gong, T. Inoshita, D. C. Fredrickson, J. Wang, Y. Lu, M. Kitano and H. Hosono, Adv. Mater., 2017, 29(36), 1700924 CrossRef PubMed.
- M. Kitano, Y. Inoue, M. Sasase, K. Kishida, Y. Kobayashi, K. Nishiyama, T. Tada, S. Kawamura, T. Yokoyama and M. Hara, Angew. Chem., Int. Ed., 2018, 57(10), 2648–2652 CrossRef CAS PubMed.
- Y. Inoue, M. Kitano, K. Kishida, H. Abe, Y. Niwa, M. Sasase, Y. Fujita, H. Ishikawa, T. Yokoyama and M. Hara, ACS Catal., 2016, 6(11), 7577–7584 CrossRef CAS.
- R. Hawtof, S. Ghosh, E. Guarr, C. Y. Xu, R. M. Sankaran and J. N. Renner, Sci. Adv., 2019, 5(1), eaat5778 CrossRef PubMed.
- J. John, D. K. Lee and U. Sim, Nano Convergence, 2019, 6, 15 CrossRef PubMed.
- T. Murakami, T. Nohira, T. Goto, Y. H. Ogata and Y. Ito, Electrochim. Acta, 2005, 50(27), 5423–5426 CrossRef CAS.
- K. Murakami, Y. Tanaka, R. Sakai, Y. Hisai, S. Hayashi, Y. Mizutani, T. Higo, S. Ogo, J. G. Seo, H. Tsuneki and Y. Sekine, Chem. Commun., 2020, 56, 3365–3368 RSC.
- Y. Hisai, K. Murakami, Y. Kamite, Q. Ma, E. Vøllestad, R. Manabe, T. Matsuda, S. Ogo, T. Norby and Y. Sekine, Chem. Commun., 2020, 56, 2699–2702 RSC.
- J. R. Rostrup-Nielsen, J. Catal., 1973, 31(2), 173–199 CrossRef CAS.
- C. Bernardo, I. Alstrup and J. Rostrup-Nielsen, J. Catal., 1985, 96(2), 517–534 CrossRef CAS.
- S. Ashihara, Ensemble, 2009, 11(2), 20–24 Search PubMed.
- G. Jacobs, L. Williams, U. Graham, G. A. Thomas, D. E. Sparks and B. H. Davis, Appl. Catal., A, 2003, 252(1), 107–118 CrossRef CAS.
- R. Manabe, S. Ø. Stub, T. Norby and Y. Sekine, Solid State Commun., 2018, 270, 45–49 CrossRef CAS.
- S. Ø. Stub, E. Vøllestad and T. Norby, J. Mater. Chem. A, 2018, 6, 8265–8270 RSC.
- I. G. Tredici, F. Maglia, C. Ferrara, P. Mustarelli and U. Anselmi-Tamburini, Adv. Funct. Mater., 2014, 24, 5137–5146 CrossRef CAS.
- B. Scherrer, M. V. F. Schlupp, D. Stender, J. Martynczuk, J. G. Grolig, H. Ma, P. Kocher, T. Lippert, M. Prestat and L. J. Gauckler, Adv. Funct. Mater., 2013, 23, 1957–1964 CrossRef CAS.
- S. Miyoshi, Y. Akao, N. Kuwata, J. Kawamura, Y. Oyama, T. Yagi and S. Yamaguchi, Chem. Mater., 2014, 26, 5194–5200 CrossRef CAS.
- S. Ø. Stub, E. Vøllestad and T. Norby, J. Phys. Chem. C, 2017, 121, 12817–12825 CrossRef CAS.
- C. Tandé, D. Pérez-Coll and G. C. Mather, J. Mater. Chem., 2012, 22, 11208–11213 RSC.
- S. Ø. Stub, K. Thorshaug, P. M. Rørvik, T. Norby and E. Vøllestad, Phys. Chem. Chem. Phys., 2018, 20, 15653–15660 RSC.
- M. Takayanagi, T. Tsuchiya, K. Kawamura, M. Minohara, K. Horiba, H. Kumigashira and T. Higuchi, Solid State Ionics, 2017, 311, 46–51 CrossRef CAS.
- S. Raz, K. Sasaki, J. Maier and I. Riess, Solid State Ionics, 2001, 143, 181–204 CrossRef CAS.
- S. Miyoshi, Y. Akao, N. Kuwata, J. Kawamura, Y. Oyama, T. Yagi and S. Yamaguchi, Solid State Ionics, 2012, 207, 21–28 CrossRef CAS.
- G. Gregori, M. Shirpour and J. Maier, Adv. Funct. Mater., 2013, 23, 5861–5867 CrossRef CAS.
- A. Takahashi, R. Inagaki, M. Torimoto, Y. Hisai, T. Matsuda, Q. Ma, J. G. Seo, T. Higo, H. Tsuneki, S. Ogo, T. Norby and Y. Sekine, RSC Adv., 2020, 10, 14487–14492 RSC.
- C. Li and Q. Xin, J. Phys. Chem., 1992, 96(19), 7714–7718 CrossRef CAS.
- K. B. Wiberg, Chem. Rev., 1955, 55(4), 713–743 CrossRef CAS.
- B. N. Kerkeni and D. C. Clary, Phys. Chem. Chem. Phys., 2006, 8(8), 917–925 RSC.
- M. J. Kurylo, G. A. Hollinden and R. B. Timmons, J. Chem. Phys., 1970, 52(4), 1773–1781 CrossRef CAS.
- G. C. Schatz, A. F. Wagner and T. H. Dunning, J. Phys. Chem., 1984, 88(2), 221–232 CrossRef CAS.
- M. C. J. Bradford and M. A. Vannice, Catal. Rev., 1999, 41(1), 1–42 CrossRef CAS.
- M. S. Fan, A. Z. Abdullah and S. Bhatia, ChemCatChem, 2009, 1(2), 192–208 CrossRef CAS.
- Y. C. Gao, J. G. Jiang, Y. Meng, F. Yan and A. Aihemaiti, Energy Convers. Manage., 2018, 171, 133–155 CrossRef CAS.
- Y. Wang, L. Yao, S. H. Wang, D. H. Mao and C. W. Hu, Fuel Process. Technol., 2018, 169, 199–206 CrossRef CAS.
- G. Zhang, J. Liu, Y. Xu and Y. Sun, Int. J. Hydrogen Energy, 2018, 43(32), 15030–15054 CrossRef CAS.
- J. Baltrusaitis and W. L. Luyben, ACS Sustainable Chem. Eng., 2015, 3(9), 2100–2111 CrossRef CAS.
- M. M. B. Noureldin, N. O. Elbashir, K. J. Gabriel and M. M. El-Halwagi, ACS Sustainable Chem. Eng., 2015, 3(4), 625–636 CrossRef CAS.
- P. Zhang, J. Tong and K. Huang, ACS Sustainable Chem. Eng., 2016, 4(12), 7056–7065 CrossRef CAS.
- S. Afzal, D. Sengupta, A. Sarkar, M. El-Halwagi and N. Elbashir, ACS Sustainable Chem. Eng., 2018, 6(6), 7532–7544 CrossRef CAS.
- S. Shoji, X. B. Peng, T. Imai, P. S. M. Kumar, K. Higuchi, Y. Yamamoto, T. Tokunaga, S. Arai, S. Ueda, A. Hashimoto, N. Tsubaki, M. Miyauchi, T. Fujita and H. Abe, Chem. Sci., 2019, 10(13), 3701–3705 RSC.
- M. Li and A. C. van Veen, Appl. Catal., B, 2018, 237, 641–648 CrossRef CAS.
- T. Oguri, K. Sugiura, T. Yabe, S. Ogo and Y. Sekine, J. Jpn. Pet. Inst., 2017, 60(5), 232–240 CrossRef CAS.
- P. C. Rieke and N. E. Vanderborgh, J. Membr. Sci., 1987, 32(2–3), 313–328 CrossRef CAS.
- G. Alberti, M. Casciola, L. Massinelli and B. Bauer, J. Membr. Sci., 2001, 185(1), 73–81 CrossRef CAS.
- B. Scherrer, M. V. F. Schlupp, D. Stender, J. Martynczuk, J. G. Grolig, H. Ma, P. Kocher, T. Lippert, M. Prestat and L. J. Gauckler, Adv. Funct. Mater., 2013, 23(15), 1957–1964 CrossRef CAS.
- P. M. Guyon, W. A. Chupka and J. Berkowitz, J. Chem. Phys., 1976, 64(4), 1419–1436 CrossRef CAS.
- M. D. Fenn and E. Spinner, J. Phys. Chem., 1984, 88(18), 3993–3997 CrossRef CAS.
- T. Y. Cheng and R. M. Bullock, J. Am. Chem. Soc., 1999, 121(13), 3150–3155 CrossRef CAS.
- D. G. Churchill, K. E. Janak, J. S. Wittenberg and G. Parkin, J. Am. Chem. Soc., 2003, 125(5), 1403–1420 CrossRef CAS PubMed.
- G. Jacobs, S. Khalid, P. M. Patterson, D. E. Sparks and B. H. Davis, Appl. Catal., A, 2004, 268(1–2), 255–266 CrossRef CAS.
- G. Parkin, Acc. Chem. Res., 2009, 42(2), 315–325 CrossRef CAS PubMed.
- T. Utaka, K. Sekizawa and K. Eguchi, Appl. Catal., A, 2000, 194, 21–26 CrossRef.
- H. A. Gasteiger, N. Markovic, P. N. Ross and E. J. Cairns, J. Phys. Chem., 1994, 98(2), 617–625 CrossRef CAS.
- V. M. Schmidt, P. Brockerhoff, B. Hohlein, R. Menzer and U. Stimming, J. Power Sources, 1994, 49(1–3), 299–313 CrossRef CAS.
- F. Alhumaidan, D. Cresswell and A. Garforth, Energy Fuels, 2011, 25(10), 4217–4234 CrossRef CAS.
- D. Teichmann, K. Stark, K. Muller, G. Zottl, P. Wasserscheid and W. Arlt, Energy Environ. Sci., 2012, 5(10), 9044–9054 RSC.
- G. W. H. Scherer and E. Newson, Int. J. Hydrogen Energy, 1998, 23(1), 19–25 CrossRef CAS.
- G. W. H. Scherer, E. Newson and A. Wokaun, Int. J. Hydrogen Energy, 1999, 24(12), 1157–1169 CrossRef CAS.
- B. Kerkeni and D. C. Clary, J. Phys. Chem. A, 2004, 108(41), 8966–8972 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Truls
Norby
*b and
Yasushi
Sekine
a,
Truls
Norby
*b and
Yasushi
Sekine
 *a
*a





![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 = 1
H2 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, total 240 sccm; current, 0 or 6 mA. Reproduced with permission from literature.42
3, total 240 sccm; current, 0 or 6 mA. Reproduced with permission from literature.42
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) formation with an electric field, 0.1 MPa, 373 K, 6 mA. Reproduced with permission from literature.44
formation with an electric field, 0.1 MPa, 373 K, 6 mA. Reproduced with permission from literature.44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 = 1
H2 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. Furthermore, the porous sample exhibited a H/D isotope effect, contrary to the dense sample. These observations emphasize that the proton conduction takes place mainly on the grain surface, not in bulk, and that surface protons are dominant charge carriers under ammonia synthesis atmospheres. So far, the energy efficiency of this reaction in the electric field is >1 kW h kg−1-NH3, and it is still rather high. We have to decrease it by the better catalyst design.
3. Furthermore, the porous sample exhibited a H/D isotope effect, contrary to the dense sample. These observations emphasize that the proton conduction takes place mainly on the grain surface, not in bulk, and that surface protons are dominant charge carriers under ammonia synthesis atmospheres. So far, the energy efficiency of this reaction in the electric field is >1 kW h kg−1-NH3, and it is still rather high. We have to decrease it by the better catalyst design.
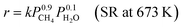
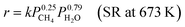

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O
H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar
Ar![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) He = 12
He = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72, total flow rate 120 sccm; current, 0 or 5 mA. Reproduced with permission from literature.34
72, total flow rate 120 sccm; current, 0 or 5 mA. Reproduced with permission from literature.34
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O
H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 1
Ar = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62, total flow rate 65 sccm; current, 0 or 5 mA. Reproduced with permission from literature.34
62, total flow rate 65 sccm; current, 0 or 5 mA. Reproduced with permission from literature.34
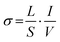

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2
CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 1
Ar = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, total flow rate: 20–200 sccm; input current: 3 mA; catalyst weight: 100 mg; furnace temperature: 505–880 K (with EF) and 764–897 K (without EF). Reproduced with permission from literature.40
2, total flow rate: 20–200 sccm; input current: 3 mA; catalyst weight: 100 mg; furnace temperature: 505–880 K (with EF) and 764–897 K (without EF). Reproduced with permission from literature.40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2
CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 1
Ar = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2; 100 sccm total flow rate; 3.0 mA input current; 100 mg catalyst weight; 505–880 K (with EF) and 764–897 K (without EF) catalyst bed temperature.
2; 100 sccm total flow rate; 3.0 mA input current; 100 mg catalyst weight; 505–880 K (with EF) and 764–897 K (without EF) catalyst bed temperature.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2
CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 1
Ar = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 or CO2
2 or CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 1
Ar = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3; total flow rate, 100 sccm; 3.0 mA input current; 100 mg catalyst weight; 404–856 K catalyst bed temperature. Reproduced with permission from literature.40
3; total flow rate, 100 sccm; 3.0 mA input current; 100 mg catalyst weight; 404–856 K catalyst bed temperature. Reproduced with permission from literature.40
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2
CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 1
Ar = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2; total flow rate, 100 sccm; 3.0 mA input current; 100 mg catalyst weight; 423 K furnace temperature. Reproduced with permission from literature.40
2; total flow rate, 100 sccm; 3.0 mA input current; 100 mg catalyst weight; 423 K furnace temperature. Reproduced with permission from literature.40
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2
CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) He = 3
He = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34; 40 Sccm total flow rate; 9 mA current; 573 K preset temperature. Reproduced with permission from literature.40
34; 40 Sccm total flow rate; 9 mA current; 573 K preset temperature. Reproduced with permission from literature.40
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 6.4
Ar = 6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 (total flow rate 36.4 mL min−1), EF: constant current of 3 mA.a (Reproduced with permission from literature37)
30 (total flow rate 36.4 mL min−1), EF: constant current of 3 mA.a (Reproduced with permission from literature37)

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 6.4
Ar = 6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 (total flow rate 36.4 mL min−1); EF: constant current of 3 mA. Reproduced with permission from literature.37
30 (total flow rate 36.4 mL min−1); EF: constant current of 3 mA. Reproduced with permission from literature.37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = (3.2, 6.4, 9.6, 11.3)
Ar = (3.2, 6.4, 9.6, 11.3)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (53.2, 50.0, 46.8, 45.1), C7H14
(53.2, 50.0, 46.8, 45.1), C7H14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C7H8
C7H8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 6.4
Ar = 6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.0, 2.0, 3.0, 4.0)
(1.0, 2.0, 3.0, 4.0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (49.0, 48.0, 47.0, 46.0) and C7H14
(49.0, 48.0, 47.0, 46.0) and C7H14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2
H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 6.4
Ar = 6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (4.0, 7.0, 9.0, 12.0)
(4.0, 7.0, 9.0, 12.0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (46.0, 43.0, 41.0, 38.0). (Reproduced with permission from literature37)
(46.0, 43.0, 41.0, 38.0). (Reproduced with permission from literature37)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 (or D2)
H2 (or D2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar = 6.4
Ar = 6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46 (total flow 56.4 mL min−1); EF: constant current of 3 mA. (Reproduced with permission from literature37)
46 (total flow 56.4 mL min−1); EF: constant current of 3 mA. (Reproduced with permission from literature37)



